Похожие презентации:
Магнитное поле
1. Л8-9 Магнитное поле
2.
Магнитное поле токаПЛАН
1. Магнитное поле и его характеристики
2. Закон Био — Савара — Лапласа
3. Закон Ампера. Взаимодействие
параллельных токов
4. Единицы измерения магнитных величин.
5. Сила Лоренца.
6. Циркуляция и поток вектора В для магнитного
поля в вакууме. Теорема Гаусса для поля
7. Магнитное поле соленоида и тороида.
8. Работа по перемещению проводника с током в
магнитном поле
9. Эффект Холла.
3. 1.1. Магнитные взаимодействия
В пространстве, окружающем намагниченные
тела, возникает магнитное поле.
Помещенная в это поле маленькая магнитная
стрелка устанавливается в каждой его точке вполне
определенным образом, указывая тем самым
направление поля.
Тот конец стрелки, который в магнитном поле
Земли указывает на север, называется северным, а
противоположный – южным.
4.
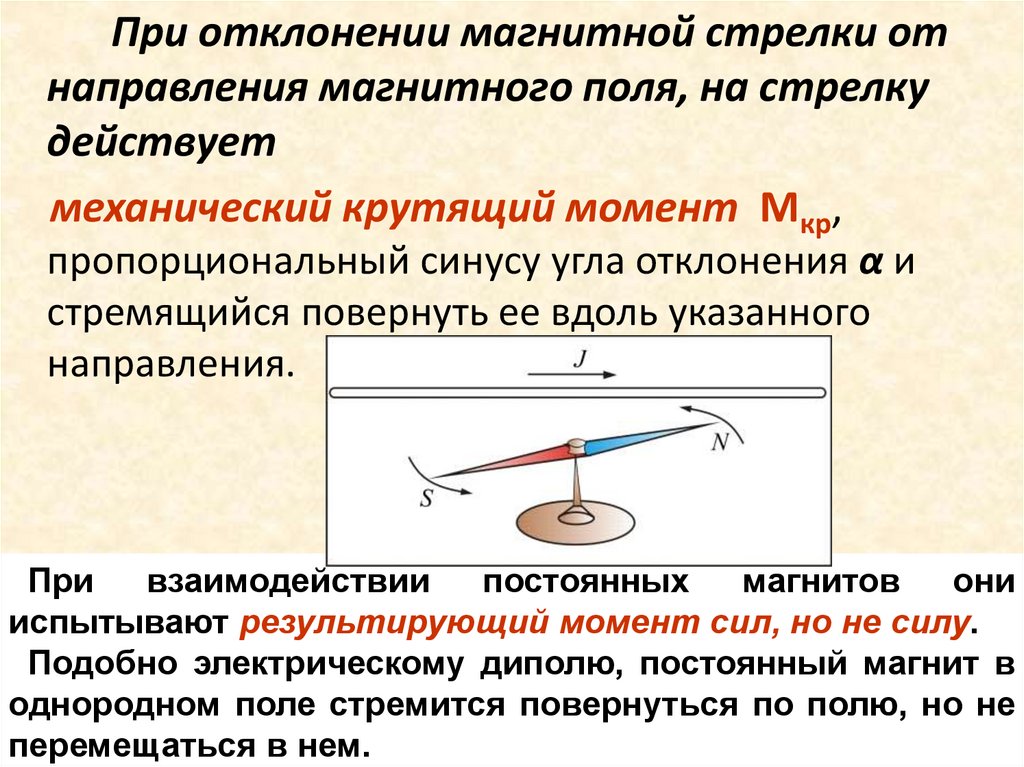
При отклонении магнитной стрелки отнаправления магнитного поля, на стрелку
действует
механический крутящий момент Мкр,
пропорциональный синусу угла отклонения α и
стремящийся повернуть ее вдоль указанного
направления.
При
взаимодействии
постоянных
магнитов
они
испытывают результирующий момент сил, но не силу.
Подобно электрическому диполю, постоянный магнит в
однородном поле стремится повернуться по полю, но не
перемещаться в нем.
5.
Отличие постоянных магнитов от
Электрических диполей заключается в
следующем:
Электрический диполь всегда состоит из зарядов,
равных по величине и противоположных по знаку.
Постоянный же магнит, будучи разрезан пополам,
превращается в два меньших магнита, каждый из
которых имеет и северный и южный полюса.
6.
Подводя итогисведениям о магнетизме,
накопленным к 1600 г.,
английский ученыйфизик Уильям Гильберт
написал труд
«О магните,
магнитных телах и
большом магните –
Земле»
7.
8.
В своих трудах У. Гильберт высказал
мнение, что, несмотря на некоторое
внешнее сходство, природа
электрических и магнитных явлений
различна.
Все же, к середине XVIII века, окрепло
убеждение о наличии тесной связи между
электрическими и магнитными
явлениями.
9.
• В 1820 г. Х. Эрстед открыл магнитное полеэлектрического тока.
• А. Ампер установил законы магнитного
взаимодействия токов.
• Ампер объяснил магнетизм веществ
существованием молекулярных токов.
10.
11.
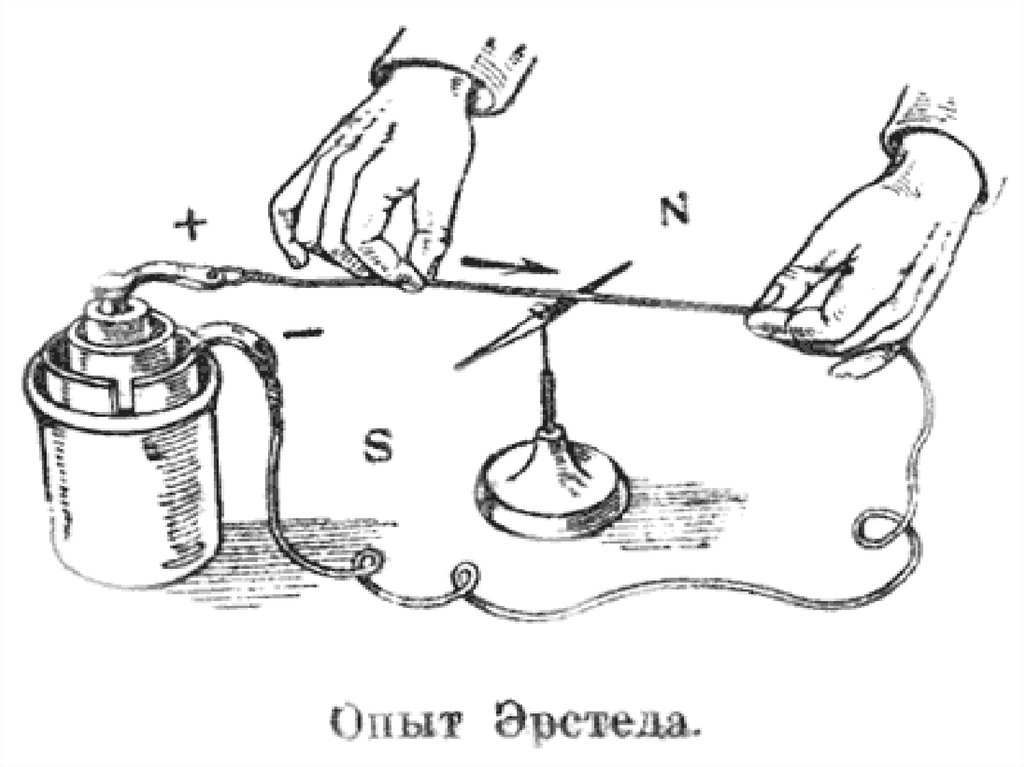
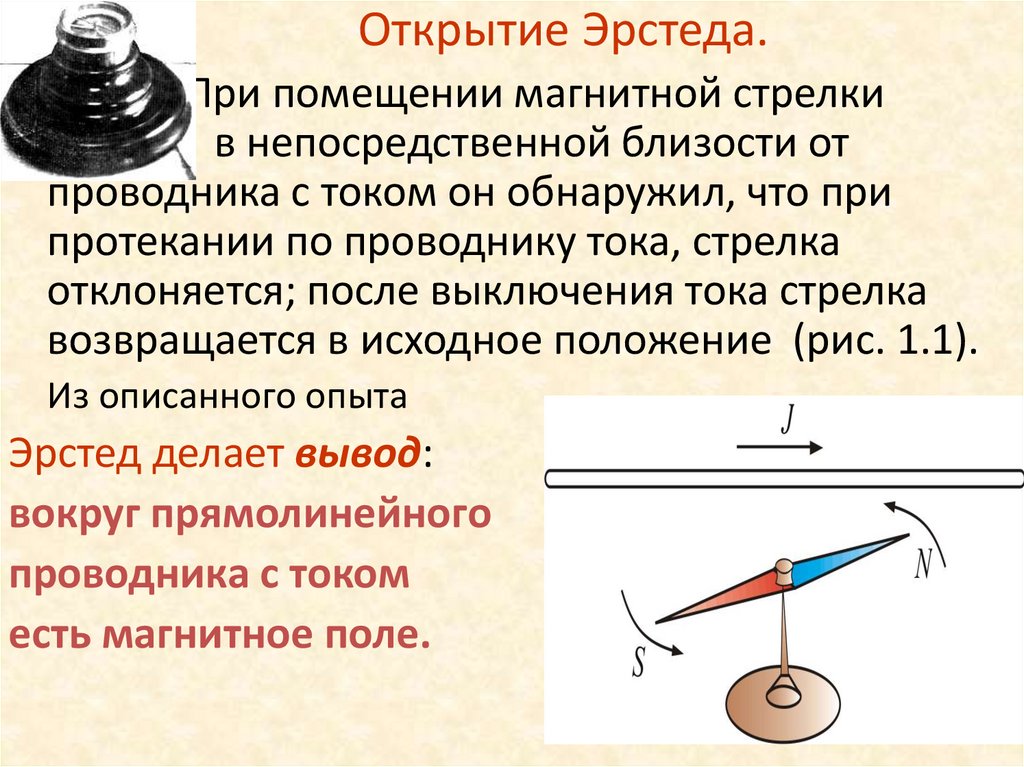
Открытие Эрстеда.При помещении магнитной стрелки
в непосредственной близости от
проводника с током он обнаружил, что при
протекании по проводнику тока, стрелка
отклоняется; после выключения тока стрелка
возвращается в исходное положение (рис. 1.1).
Из описанного опыта
Эрстед делает вывод:
вокруг прямолинейного
проводника с током
есть магнитное поле.
12.
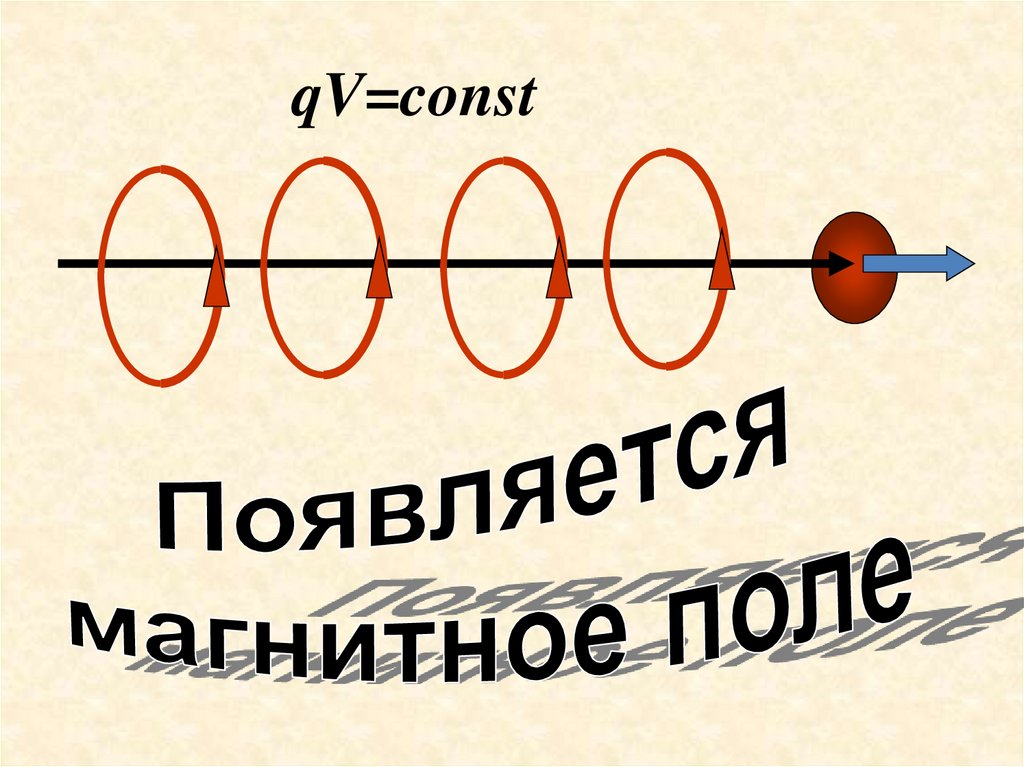
• Общий вывод: вокруг всякого проводника стоком есть магнитное поле.
• Но ведь ток – это направленное движение
зарядов.
• Опыты подтверждают: магнитное поле
появляется вокруг электронных пучков и вокруг
перемещающихся в пространстве заряженных
тел.
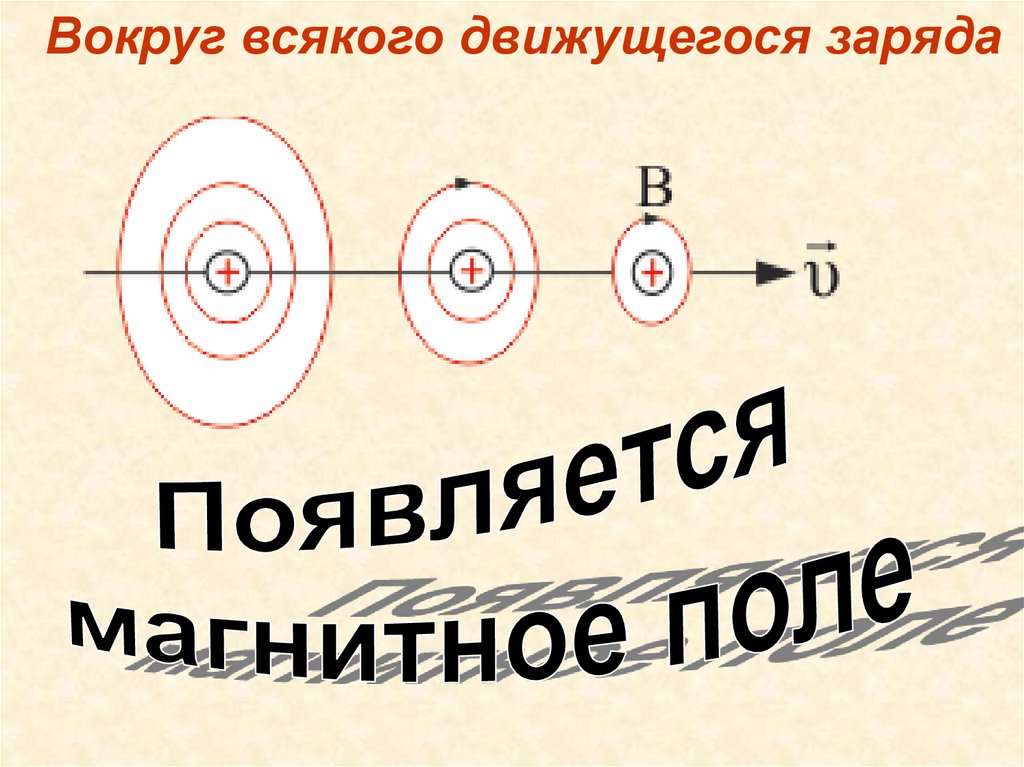
• Вокруг всякого движущегося заряда помимо
электрического поля существует еще и
магнитное.
13.
qV=const14.
Вокруг всякого движущегося заряда15.
16.
17.
18.
Магнитное поле материально. Подобноэлектрическому полю, оно обладает
энергией и, следовательно, массой.
Определение магнитного поля:
Магнитное поле – это материя,
связанная с движущимися зарядами и
обнаруживающая себя по действию на
магнитные стрелки и движущиеся
заряды, помещенные в это поле.
19.
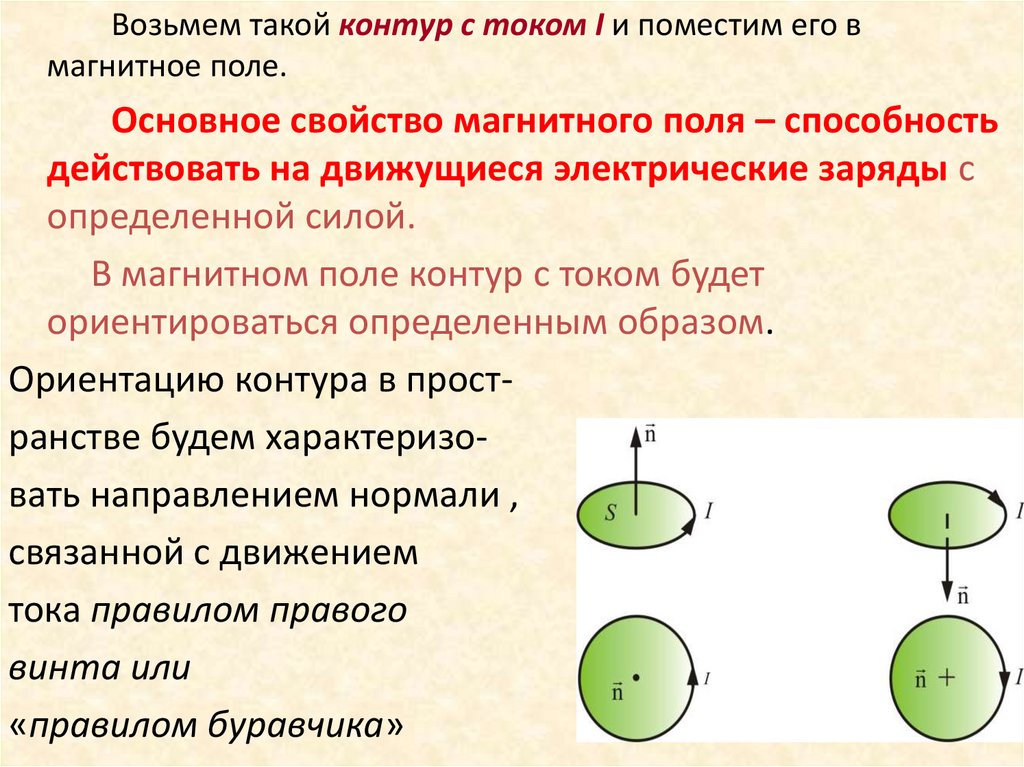
Возьмем такой контур с током I и поместим его вмагнитное поле.
Основное свойство магнитного поля – способность
действовать на движущиеся электрические заряды с
определенной силой.
В магнитном поле контур с током будет
ориентироваться определенным образом.
Ориентацию контура в пространстве будем характеризовать направлением нормали ,
связанной с движением
тока правилом правого
винта или
«правилом буравчика»
20.
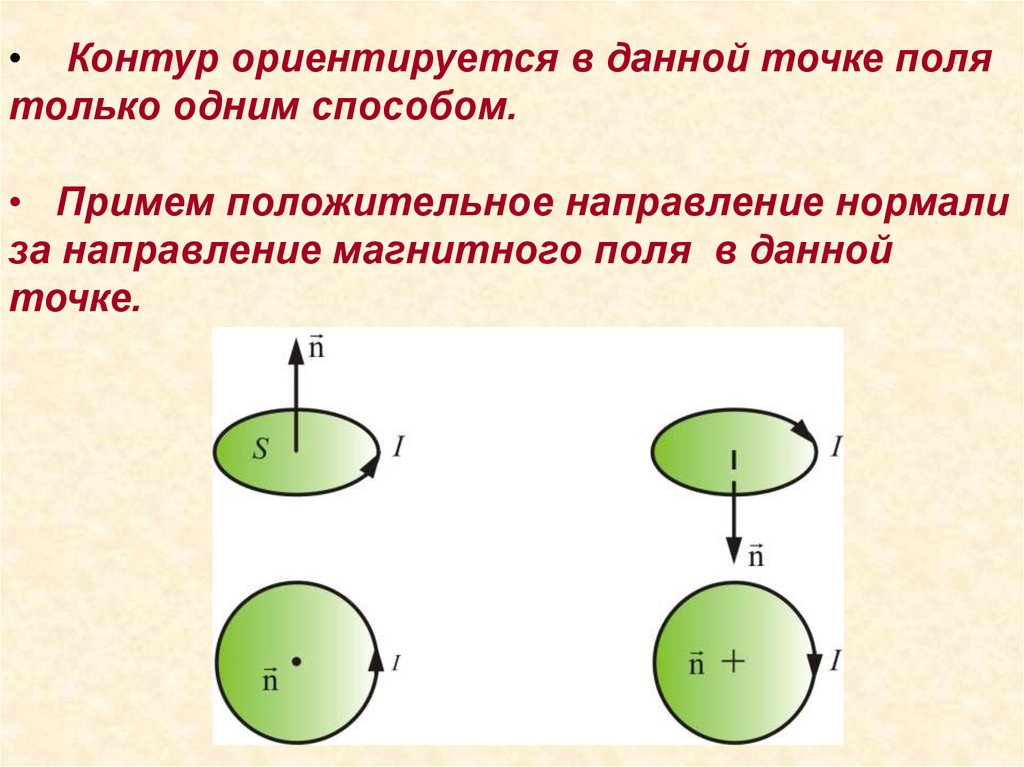
• Контур ориентируется в данной точке полятолько одним способом.
• Примем положительное направление нормали
за направление магнитного поля в данной
точке.
21.
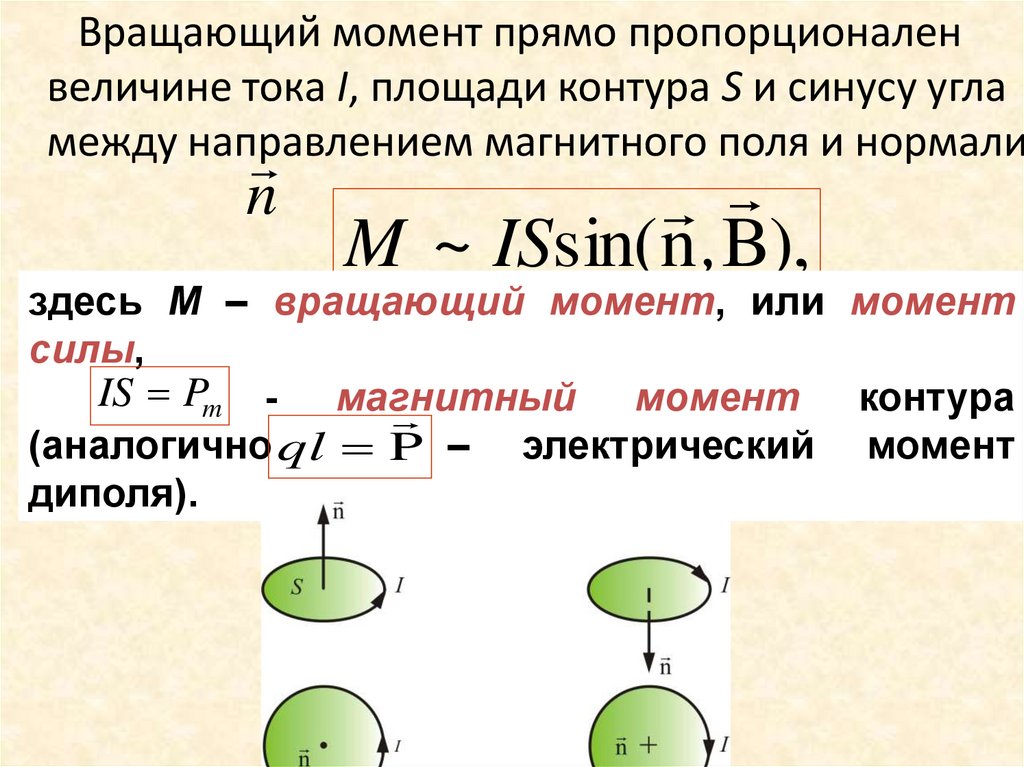
Вращающий момент прямо пропорционаленвеличине тока I, площади контура S и синусу угла
между направлением
магнитного поля и нормали
n
M ~ ISsin( n ,B),
здесь М – вращающий момент, или момент
силы,
IS Pm - магнитный
момент контура
(аналогично ql P – электрический момент
диполя).
22.
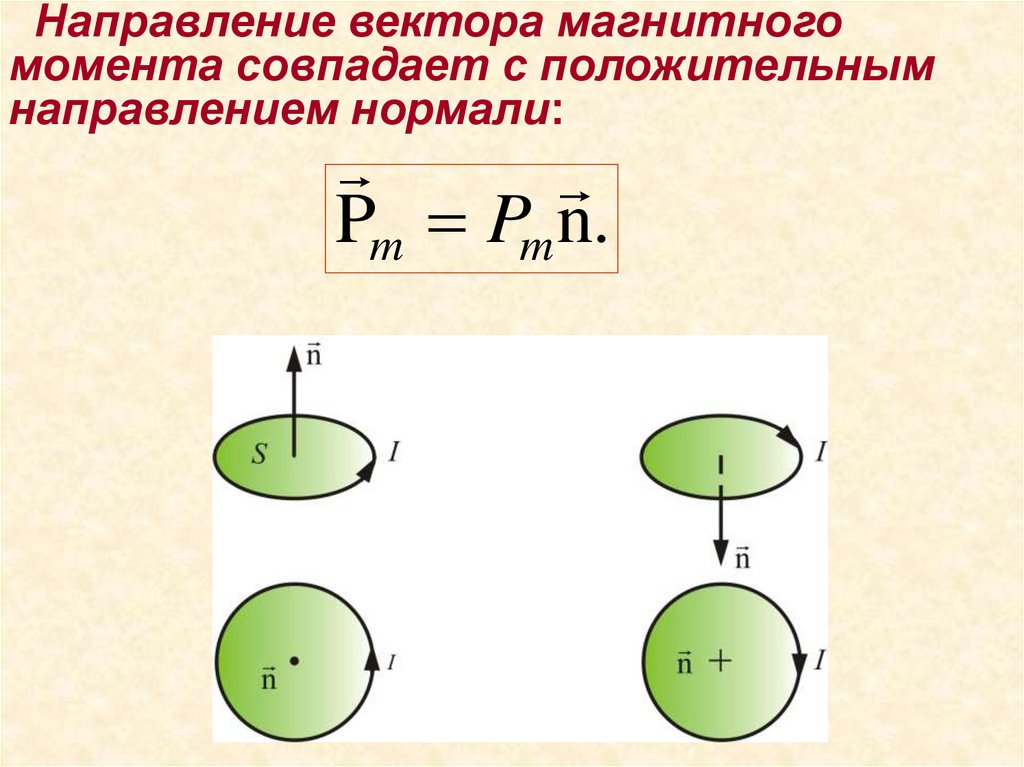
Направление вектора магнитногомомента совпадает с положительным
направлением нормали:
Pm Pm n.
23.
Отношение момента силы к магнитному моментуM
Pm
для данной точки магнитного поля
будет одним и тем же и может служить
характеристикой
магнитного
поля,
названной магнитной индукцией:
M
B
Pmsin (n, B)
M max
B ,
Pm
B – вектор магнитной индукции, совпадающий с нормалью n
F
По аналогии с электрическим полем
E .
q
24.
BМагнитная индукция
характеризует силовое
действие магнитного поля на ток (аналогично,
характеризует силовое действие электрического поля на
заряд).
B– силовая характеристика магнитного поля, ее можно
изобразить с помощью магнитных силовых линий.
Поскольку М – момент силы и
– магнитный моме
являются характеристиками вращательного
Pm движения, то
можно предположить, что магнитное поле – вихревое.
25.
Условились, за направление B принимать
направление северного конца магнитной стрелки.
• Силовые линии выходят из северного полюса, а
входят, соответственно, в южный полюс магнита.
• Для графического изображения полей удобно пользоваться
силовыми линиями (линиями магнитной индукции).
Линиями магнитной индукции называются кривые,
касательные к которым в каждой точке совпадают с
направлением вектора
в этой точке.
B
26.
Конфигурациюсиловых линий легко
установить с помощью
мелких железных опилок
которые
намагничиваются
в
исследуемом магнитном
поле и ведут себя
подобно
маленьким
магнитным
стрелкам
(поворачиваются вдоль
силовых линий).
(рис. 1.3)
27.
Три способа задать вектор магнитнойиндукции В
28.
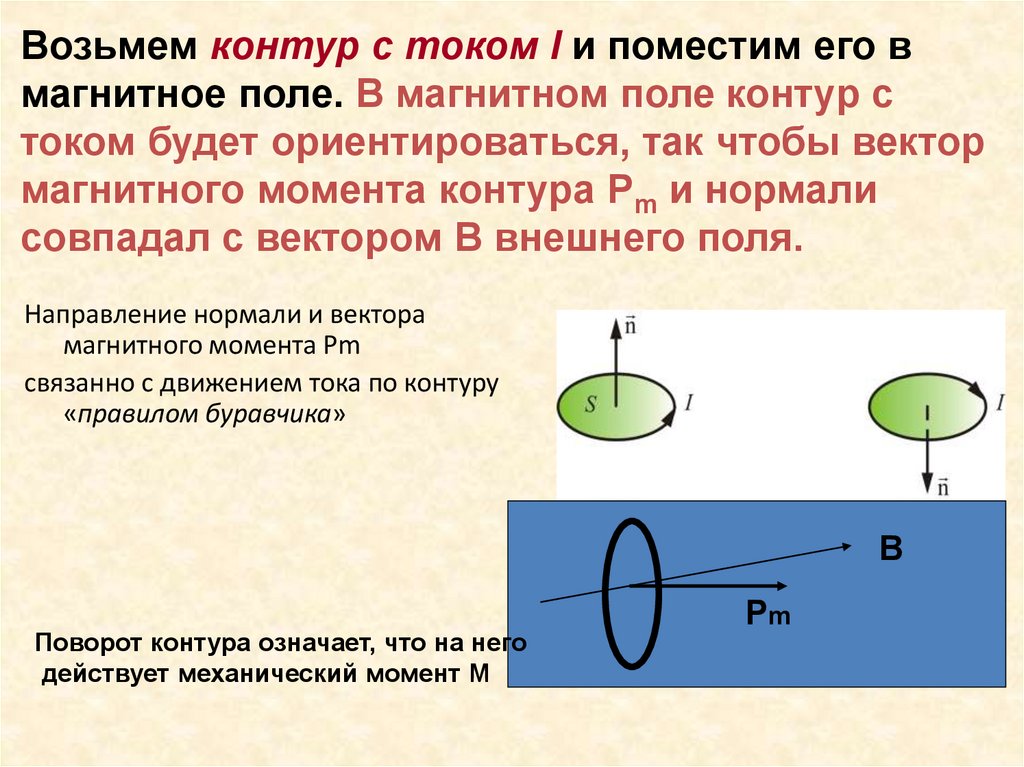
Возьмем контур с током I и поместим его вмагнитное поле. В магнитном поле контур с
током будет ориентироваться, так чтобы вектор
магнитного момента контура Рm и нормали
совпадал с вектором В внешнего поля.
Направление нормали и вектора
магнитного момента Рm
связанно с движением тока по контуру
«правилом буравчика»
В
Поворот контура означает, что на него
действует механический момент М
Рm
29.
Вращающий момент М прямо пропорционален величинетока I, площади контура S, вектору В и синусу угла между
направлением магнитного поля и нормали n.
M ISBsin( n , B) [Pm, B]
B
FA
I
Pm
IS Pm
- магнитный момент контура
30.
Отношение момента силы к магнитному моментуM
Pm
для данной точки магнитного поля
будет одним и тем же и может служить
характеристикой
магнитного
поля,
названной магнитной индукцией В:
M
B
Pmsin (n, B)
M max
B ,
Pm
B – вектор магнитной индукции,
совпадающий с нормалью n
По аналогии с электрическим полем
F
E .
q
31.
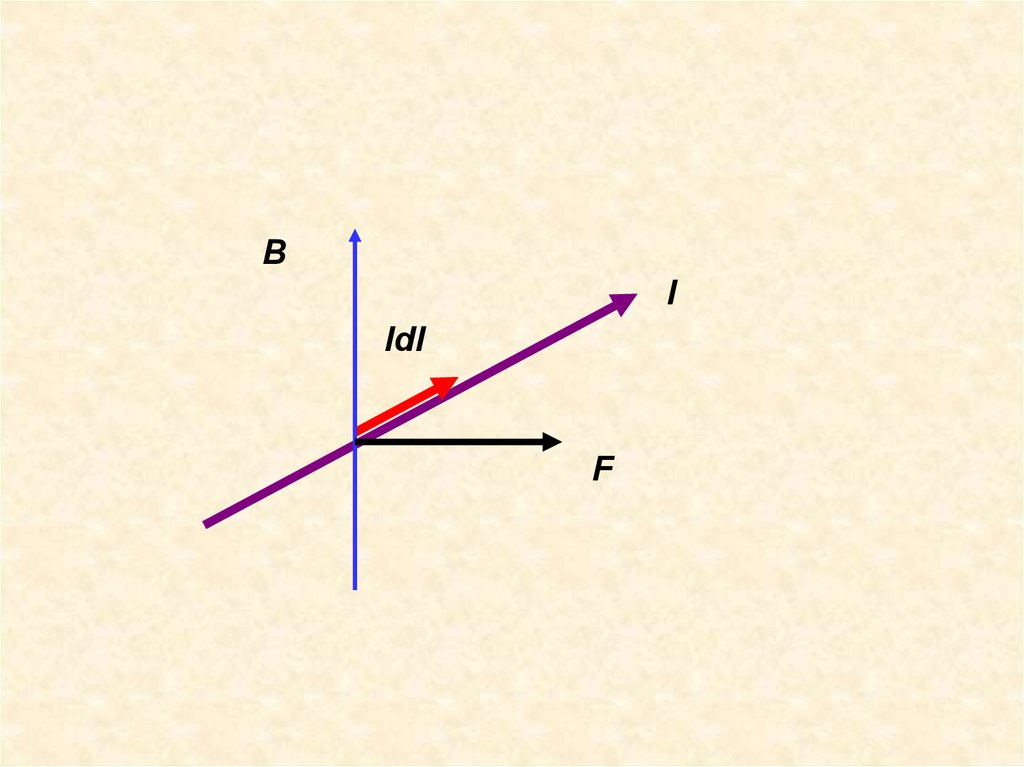
Второй способ по силе Ампера.Сила Ампера действует на проводник dl с током I,
В, направлена перпендикулярно
векторам dl и В и
определяется по правилу
произведения векторов: наблюдаемое со стороны
конца вектора dF вращение векторов dl и В на
помещенный в магнитное поле
наименьший угол, происходит против часовой стрелки.
dF=[Idl,B] или F=[Jl,B]
B=Fmax / Jl
32.
BI
Idl
F
33.
Третий способ: по силе ЛоренцаСила, действующая на электрический заряд
q во внешнем магнитном поле, зависит от
скорости его движения V и величины
индукции магнитного поля В(x,y,z).
F = q[V,B].
34.
Выражение для силы былополучено Лоренцем путем
обобщения опытных данных
F = q[V,B].
Вектор B является силовым
вектором и не зависит от величины
и движения заряда q, он
характеризует только магнитное
поле, в котором движется заряд q.
B Fmax /( qV )
35.
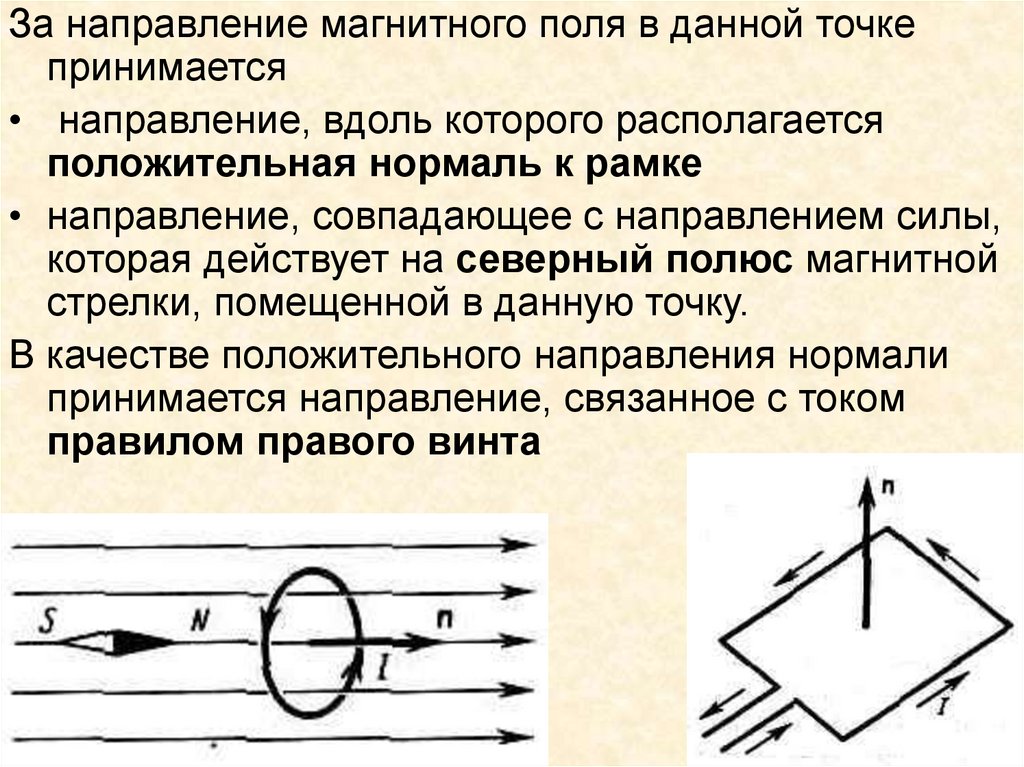
За направление магнитного поля в данной точкепринимается
• направление, вдоль которого располагается
положительная нормаль к рамке
• направление, совпадающее с направлением силы,
которая действует на северный полюс магнитной
стрелки, помещенной в данную точку.
В качестве положительного направления нормали
принимается направление, связанное с током
правилом правого винта
36.
• Рамка с током поворачивается в магнитном поле.• Вращающий момент сил зависит как от свойств
поля в данной точке, так и от свойств рамки:
M Pm B ,
M Pm B sin
• В - вектор магнитной индукции,
• Pm - вектор магнитного момента рамки с током.
• Для плоского контура с током I
Pm ISn ,
Pm IS
• S - площадь поверхности контура (рамки),
• n - единичный вектор нормали к поверхности
рамки.
Направление Pm совпадает с направлением
положительной нормали.
37.
Магнитная индукция в данной точке однородногомагнитного поля определяется максимальным
вращающим моментом, действующим на рамку с
магнитным моментом, равным единице, когда
нормаль к рамке перпендикулярна направлению
поля
M max
B
Pm
Вектор магнитной индукции В может быть выведен
также из закона Ампера и из выражения для силы
Лоренца.
38.
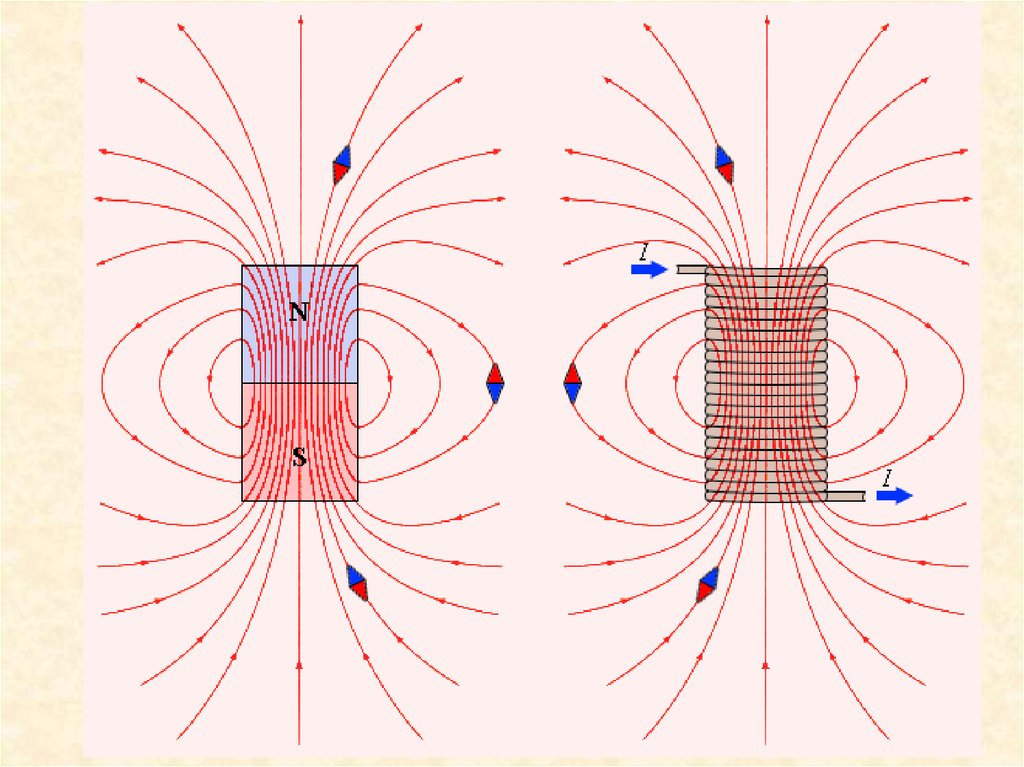
Магнитное поле изображают с помощью линиймагнитной индукции — линий, касательные к
которым в каждой точке совпадают с
направлением вектора В.
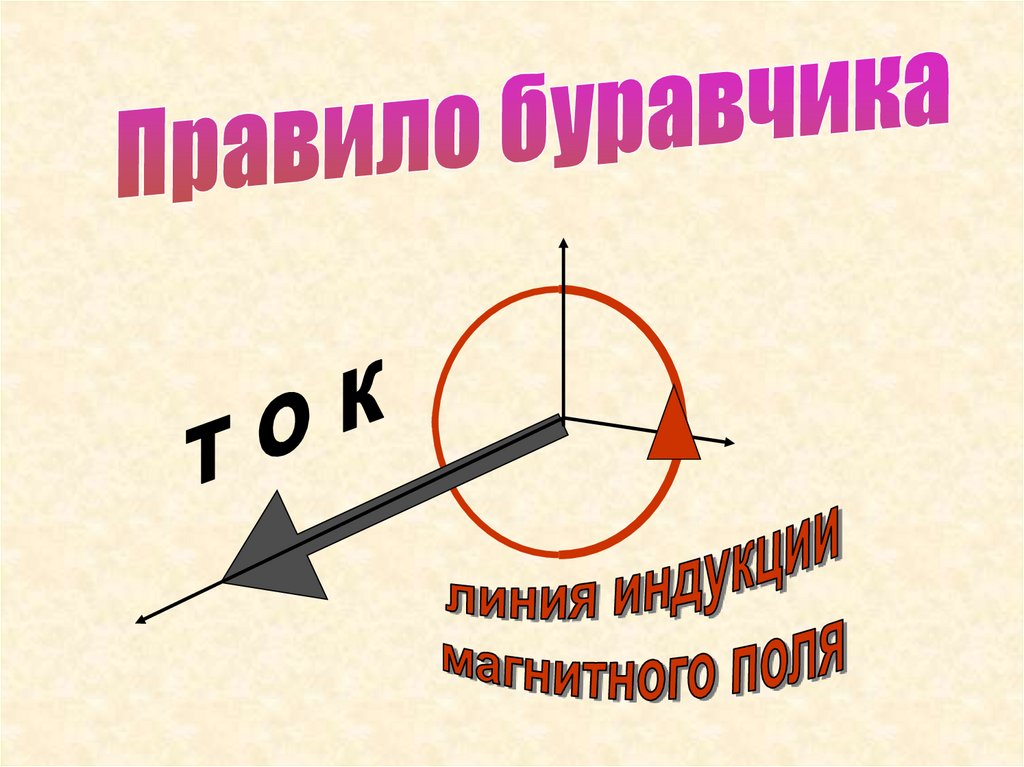
Их направление задается правилом правого
винта(Правило Буравчика).
Линии магнитной индукции всегда замкнуты и
охватывают проводники с током.
Магнитное поле не имеет источников – магнитных
зарядов. Силовые поля, обладающие этим
свойством, называются вихревыми.
39.
40.
• Гипотеза А. Ампера: в любом теле существуютмикроскопические токи, обусловленные движением
электронов в атомах и молекулах.
• Молекулярные токи создают свое магнитное поле и
могут поворачиваться в магнитных полях
макротоков.
• Вектор магнитной индукции В характеризует
результирующее магнитное поле, создаваемое
всеми макро- и микротоками
• Магнитное поле макротоков описывается
вектором напряженности Н.
• Для однородной изотропной среды:
В= 0 Н,
0 — магнитная постоянная
— магнитная проницаемость среды,
показывающая, во сколько раз магнитное поле
макротоков Н усиливается за счет поля микротоков
среды.
41.
2. Закон Био — Савара — ЛапласаМагнитное поле постоянных токов различной формы
изучалось французскими учеными Ж. Био и Ф.
Саваром.
Результаты этих опытов были обобщены
французским математиком и физиком П.
Лапласом.
Принцип суперпозиции:
Если магнитное поле создается несколькими
проводниками с током, то индукция
результирующего поля есть векторная сумма
индукций полей, создаваемых каждым
проводником в отдельности.
B Bi
n
i 1
42.
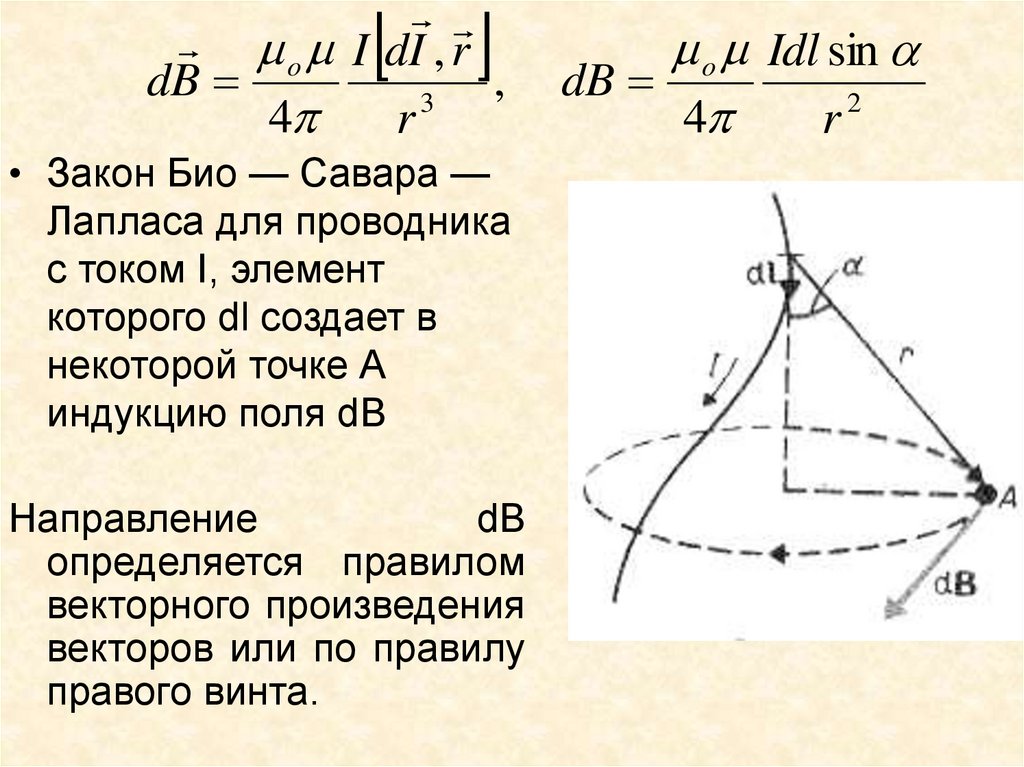
o I dI , rdB
,
3
4
r
• Закон Био — Савара —
Лапласа для проводника
с током I, элемент
которого dl создает в
некоторой точке А
индукцию поля dB
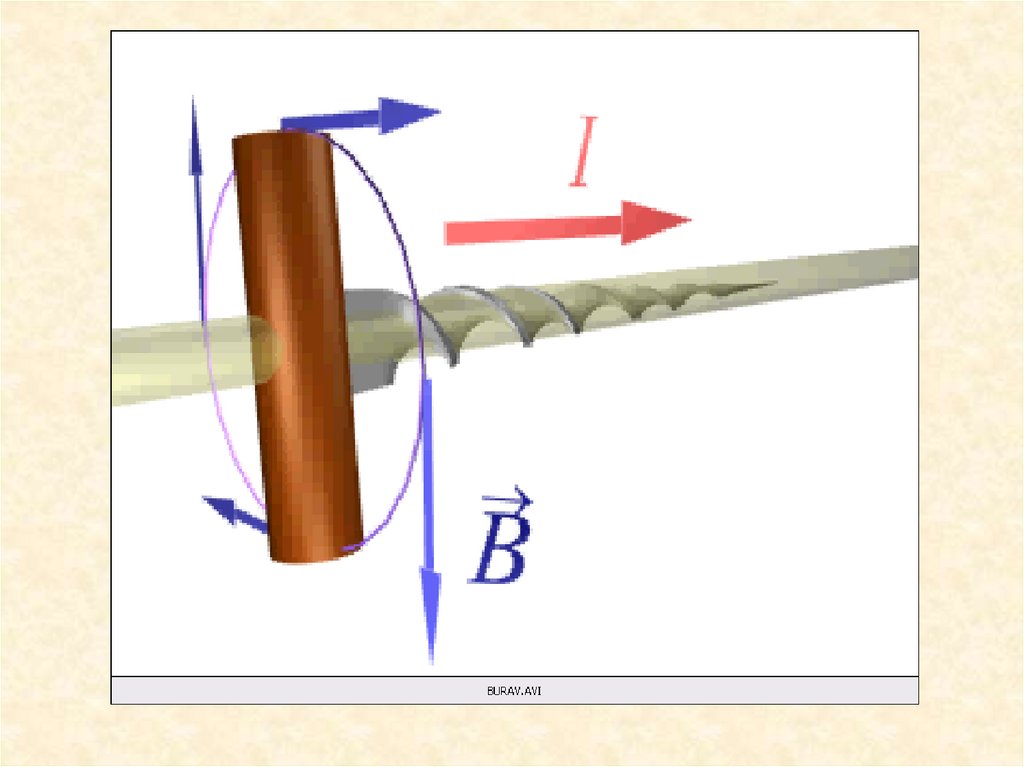
Направление
dB
определяется правилом
векторного произведения
векторов или по правилу
правого винта.
o Idl sin
dB
2
4
r
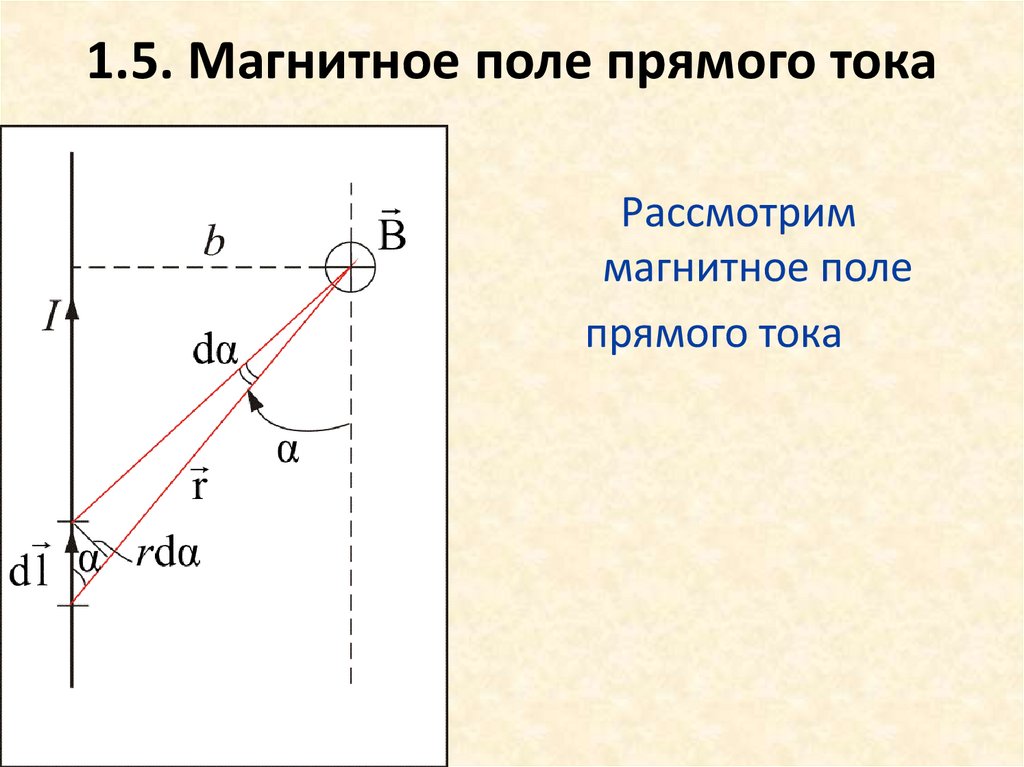
43. 1.5. Магнитное поле прямого тока
Рассмотриммагнитное поле
прямого тока
44.
Пусть точка, в которой определяетсямагнитное поле, находится на расстоянии b
от провода. Из рис. 1.6 видно, что:
b
r
;
sinα
rdα
bdα
dl
.
2
sinα sin α
Подставив найденные значения r и dl в закон
Био–Савара–Лапласа, получим:
μ 0 Ib dα sinα sin α μ 0 I
dB
sinα dα.
2
2
4π
4π b
sin α b
2
45.
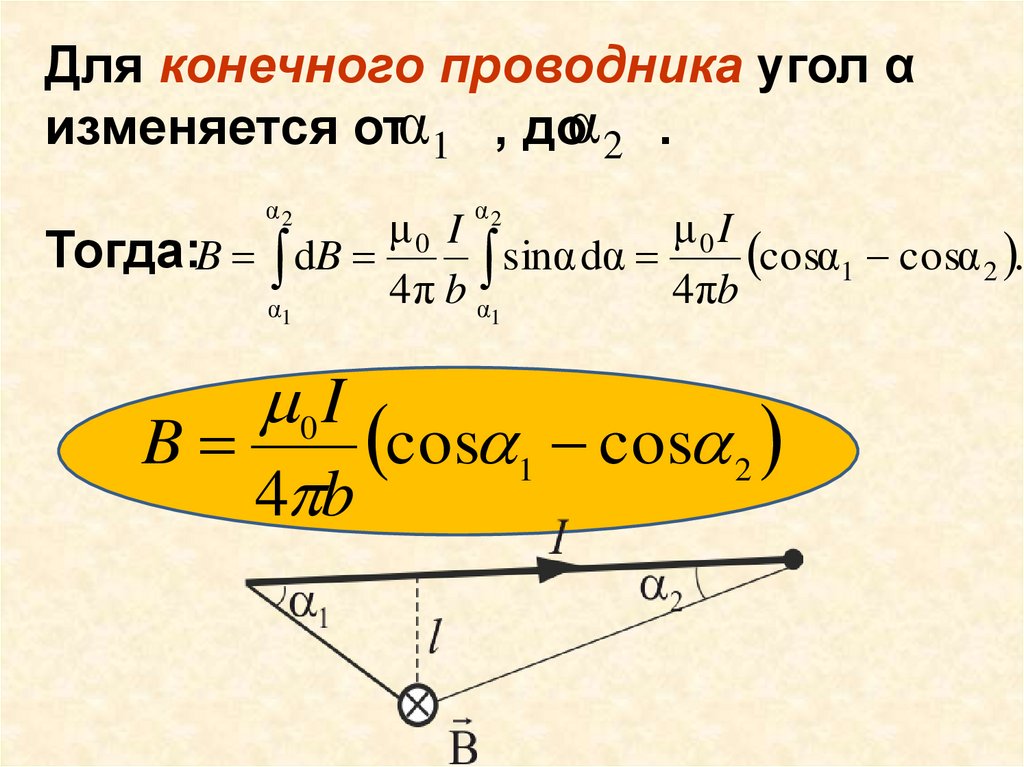
Для конечного проводника угол αизменяется отα1 , доα 2 .
α2
α2
μ0 I
μ0I
Тогда:B dB
cosα1 cosα 2 .
sinα dα
4 π b α1
4 πb
α1
0 I
cos 1 cos 2
B
4 b
46.
Для бесконечно длинного проводникааα1 0,
, тогда:
α2 π
0 I
B
2 b
или
0 2I
B
.
4 b
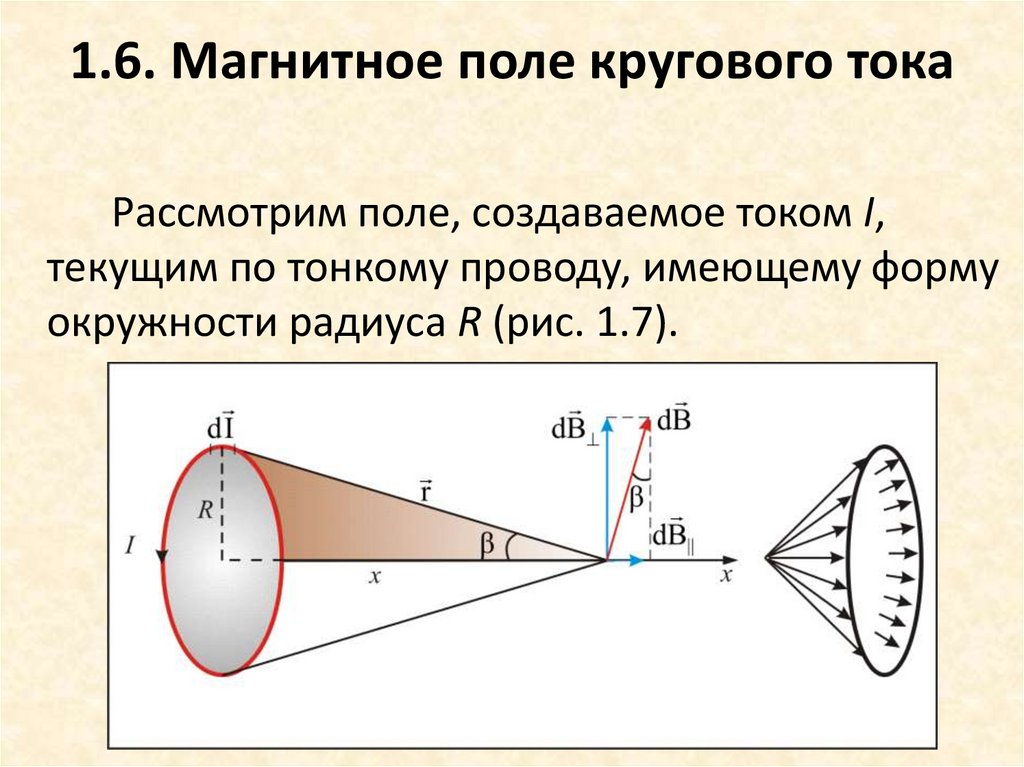
47. 1.6. Магнитное поле кругового тока
Рассмотрим поле, создаваемое током I,текущим по тонкому проводу, имеющему форму
окружности радиуса R (рис. 1.7).
48.
Rsinβ
r
т.к. угол между
тогда
sinполучим:
α 1,
dB| | dBsinβ
d lи
αr – прямой, то
R μ 0 Idl R
dB| | dB
.
2
r 4π r r
49.
2 и, 2Подставив в (1.6.1)
r R x
проинтегрировав по всему контуру
l 2 πR
получим выражение для нахождения
магнитной индукции кругового тока:
(1.6.2)
2 R
2 R
0 IR
0 2 R I
B dB||
d
l
.
3
3
2
2
4 r 0
4 R x 2
0
При ,
получим магнитную индукцию в
2
центре
x 0кругового тока:
B
0 I
2R
(1.6.3)
50. 3. Закон Ампера
АМПЕР Андре Мари (1775 –1836)
–
французский
физик
математик и химик.
Основные физические работы
посвящены
электродинамике.
Сформулировал
правило
для
определения действия магнитного
поля тока на магнитную стрелку.
Обнаружил влияние магнитного поля
Земли на движущиеся проводники с
током.
51.
В 1820 г. А. М. Ампер экспериментально установил,что два проводника с током взаимодействуют друг с
другом с силой:
I1 I 2
F k
b
где b – расстояние между проводниками, а k –
коэффициент пропорциональности зависящий от
системы единиц.
52.
В современной записи в системе СИ, закон Амперавыражается формулой:
dF I [d l , B]
Это сила с которой магнитное поле действует на
бесконечно малый проводник с током I.
Модуль силы действующей на проводник
dF IBdlsin d l , B .
53.
Если магнитное поле однородно и проводникперпендикулярен силовым линиям магнитного поля,
то
F IlB,
Работа силы Ампера
dA FA dх I B dх
dA I ( B dх cos )
dA I d
54.
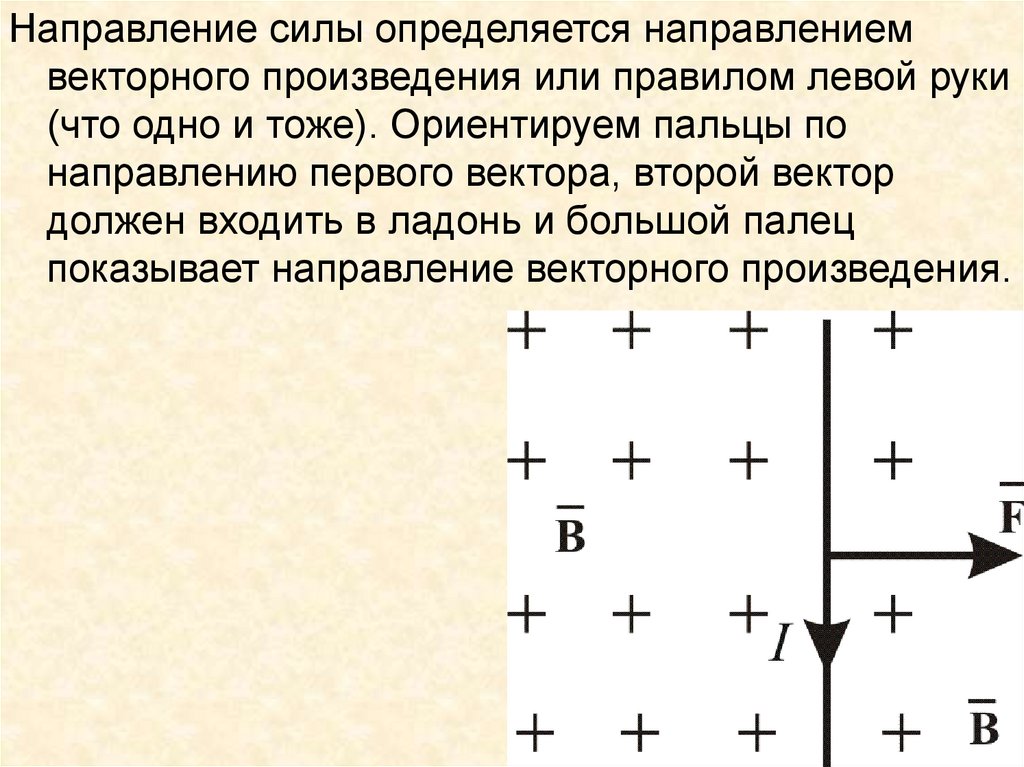
Направление силы определяется направлениемвекторного произведения или правилом левой руки
(что одно и тоже). Ориентируем пальцы по
направлению первого вектора, второй вектор
должен входить в ладонь и большой палец
показывает направление векторного произведения.
55.
Физический смысл магнитной индукции:В – величина, численно равная силе, с которой
магнитное поле действует на проводник единичной
длины, по которому течет единичный ток.
B
F
Il
Размерность индукции
Н
B
.
А м
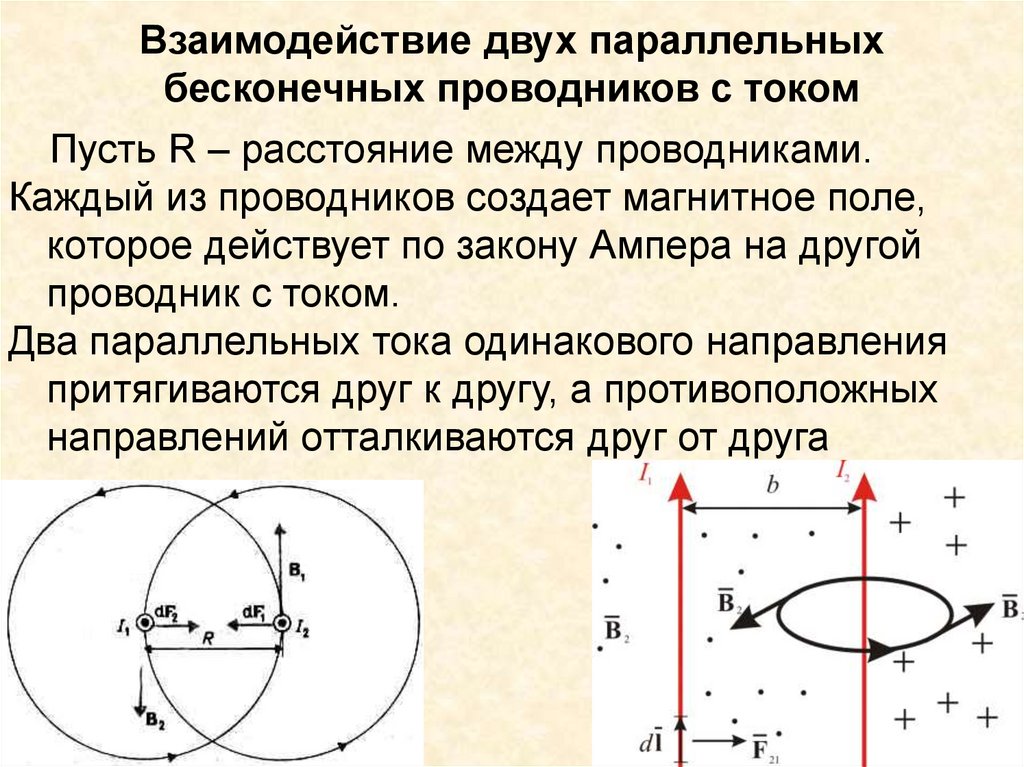
56. Взаимодействие двух параллельных бесконечных проводников с током
Пусть R – расстояние между проводниками.Каждый из проводников создает магнитное поле,
которое действует по закону Ампера на другой
проводник с током.
Два параллельных тока одинакового направления
притягиваются друг к другу, а противоположных
направлений отталкиваются друг от друга
57.
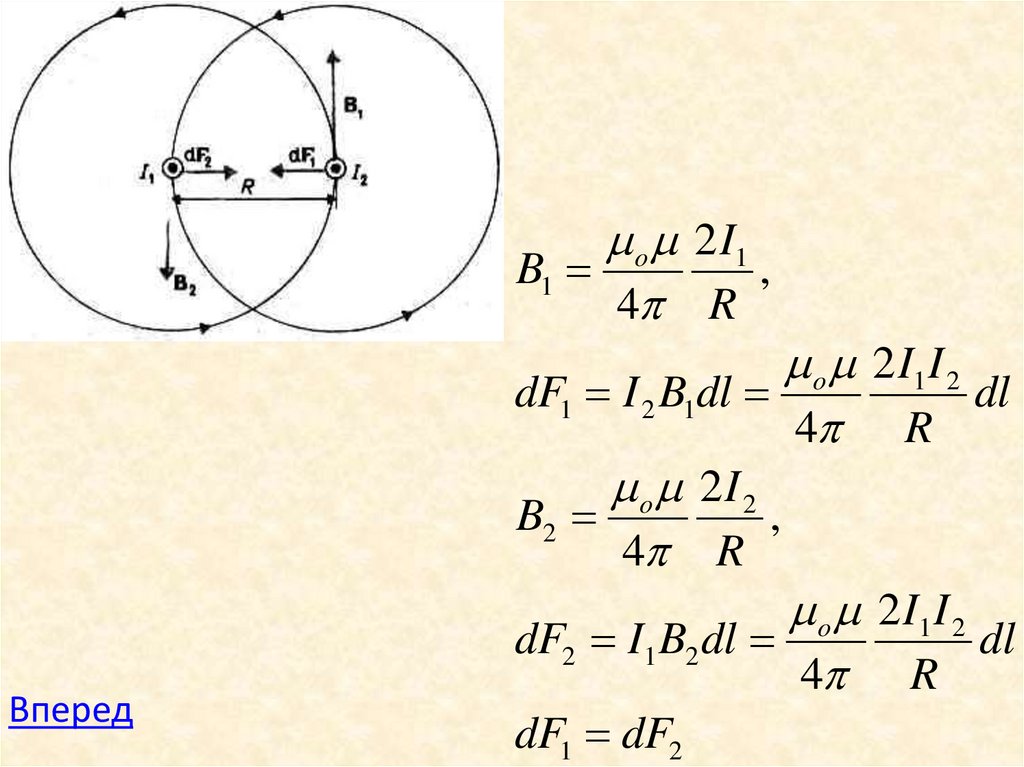
o 2 I1B1
,
4 R
Вперед
o 2 I1 I 2
dF1 I 2 B1dl
dl
4 R
o 2 I 2
B2
,
4 R
o 2 I1 I 2
dF2 I1 B2 dl
dl
4 R
dF1 dF2
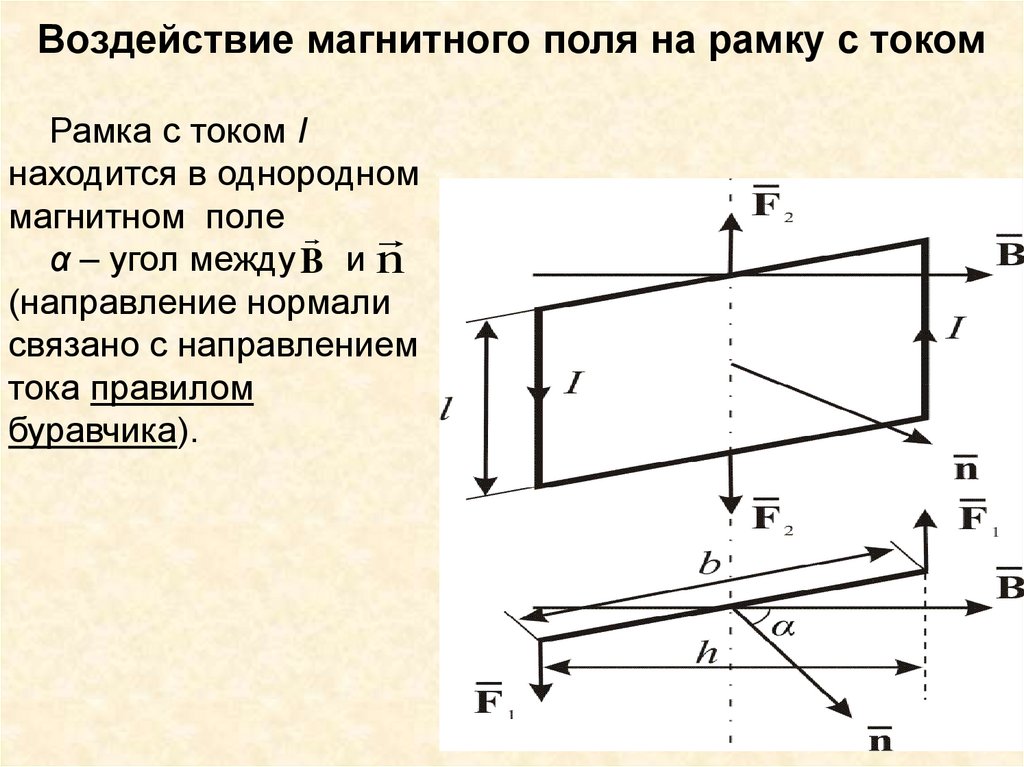
58. Воздействие магнитного поля на рамку с током
Рамка с током Iнаходится в однородном
магнитном поле
α – угол между B и n
(направление нормали
связано с направлением
тока правилом
буравчика).
B
n
59.
• Сила Ампера, действующая на сторону рамкидлиной l, равна:
F1 IlB
• Вращающий момент равен:
M F1h IlBb sin ,
M IBS sin BPm sin
M
B
Pm sin
M макс
B
Pm
M – вращающий момент силы,
P – магнитный момент.
h b sin .
60. 4. Единицы измерения магнитных величин
Закон Ампера используется для установленияединицы силы тока – ампер.
dF
2I I
0
dl 4 R
1
dl 1 м R 1 м I1 I 2 1 А
dF
7 Н
2 10
.
dl
м
2
61.
Ампер – сила тока неизменного по величине,который, проходя по двум параллельным
прямолинейным проводникам бесконечной длины и
ничтожно малого сечения, расположенным на
расстоянии один метр, один от другого в вакууме
7
вызывает между этими проводниками силу 2 10 Í
• Тогда
0
2
2 10 Н
2А
4
0 4 10
7
7
0 4 10
Н
2
А
7
Гн
м
0 I
B
4 b
Н А
Н
[ B] 2
1Тл
А м А м
62.
1 Тл (один тесла равен магнитной индукцииоднородного магнитного поля, в котором) на плоский
контур с током, имеющим магнитный момент 1 А·м2
действует вращающий момент 1 Н·м.
1 Тл равен магнитной индукции при которой
магнитный поток сквозь площадку 1 м2,
перпендикулярную направлению поля равен 1 Вб
dÔ B BdS cos(dn, B)
Ф Bn dS .
S
63.
ТЕСЛА Никола (1856 - 1943)сербскийученый
в
области
электротехники, радиотехники
Разработал
ряд
конструкций
многофазных генераторов, электродвигателей
и
трансформаторов. Сконструировал ряд радиоуправляемых
самоходных
механизмов.
Изучал физиологическое действие
токов высокой частоты. Построил в
1899 радиостанцию на 200 кВт в
Колорадо и радиоантенну высотой
57,6 м в Лонг-Айленде. Изобрел
электрический счетчик, частотомер
и др.
64.
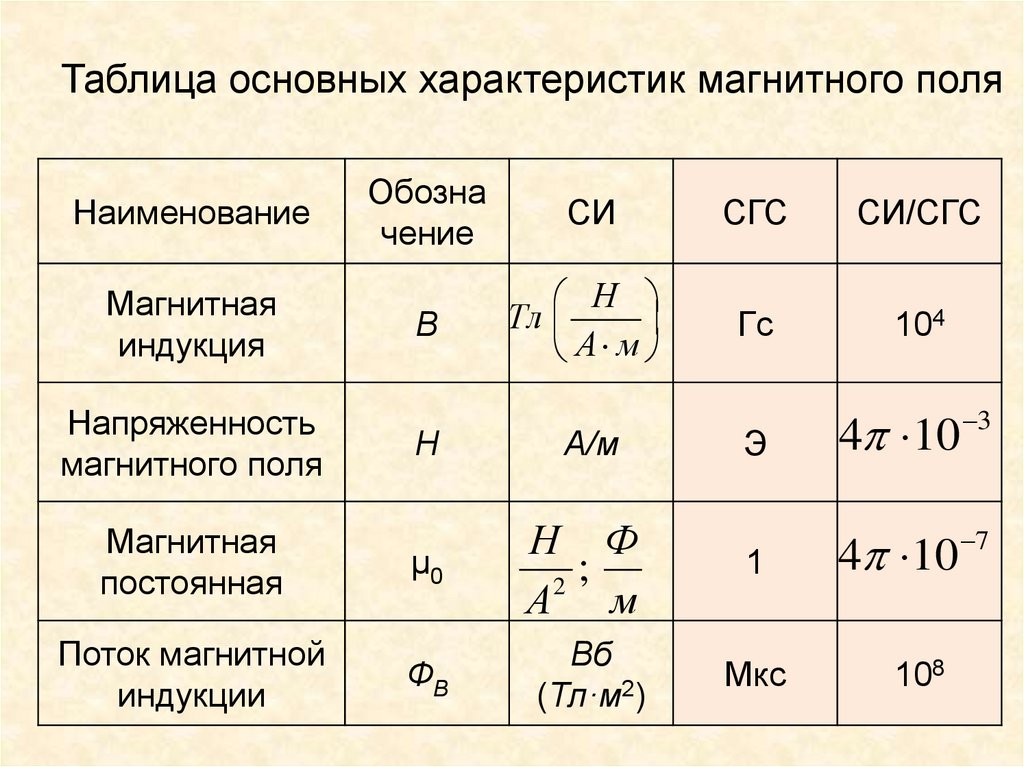
Таблица основных характеристик магнитного поляНаименование
Магнитная
индукция
Напряженность
магнитного поля
Магнитная
постоянная
Поток магнитной
индукции
Обозна
чение
СИ
СГС
СИ/СГС
В
Н
Тл
А м
Гс
104
Э
4 10
μ0
Н Ф
;
2
А м
1
4 10
ФB
Вб
(Тл·м2)
Мкс
Н
А/м
108
3
7




























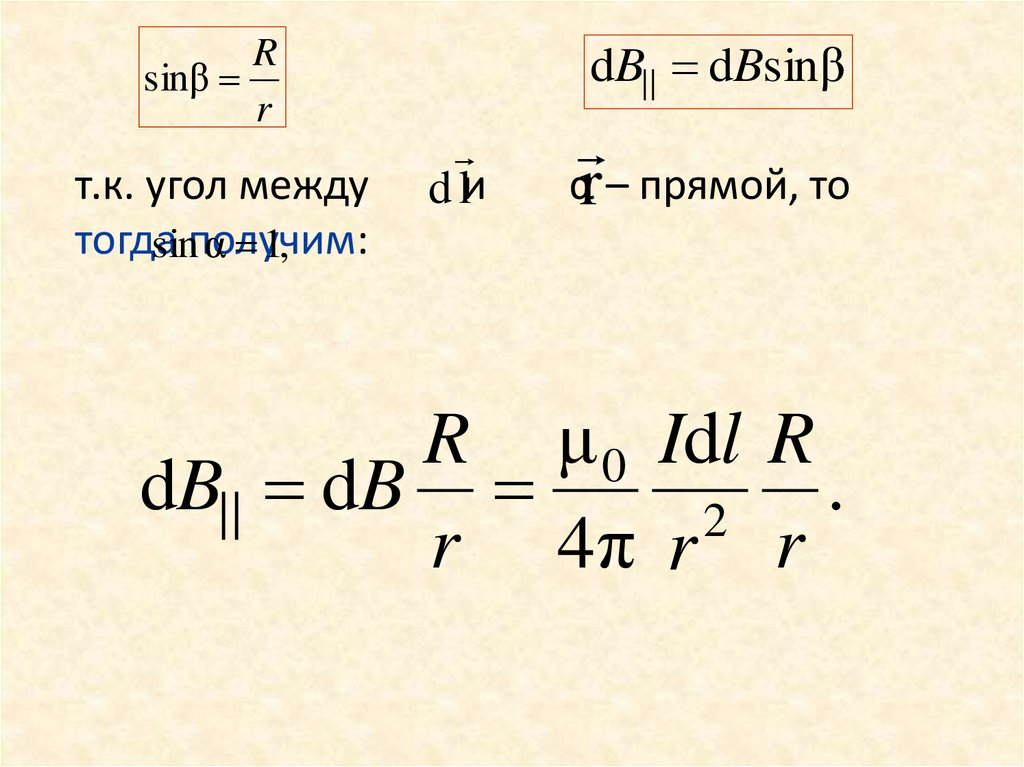











 Физика
Физика








