Случайные блуждания и их компьютерное моделирование 2020

1. Случайные блуждания и их компьютерное моделирование

2020

2. Случайные блуждания

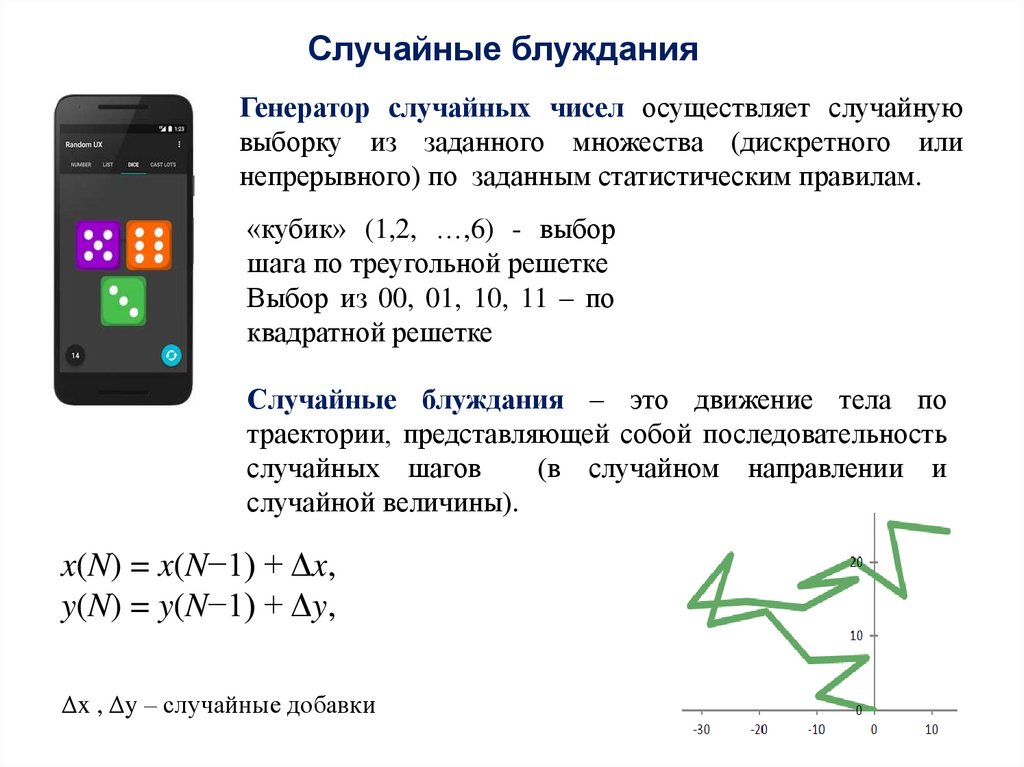
Генератор случайных чисел осуществляет случайную
выборку из заданного множества (дискретного или
непрерывного) по заданным статистическим правилам.
«кубик» (1,2, …,6) - выбор
шага по треугольной решетке
Выбор из 00, 01, 10, 11 – по
квадратной решетке
Случайные блуждания – это движение тела по
траектории, представляющей собой последовательность
случайных шагов
(в случайном направлении и
случайной величины).
x(N) = x(N−1) + Δx,
y(N) = y(N−1) + Δy,
Δx , Δy – случайные добавки

3.

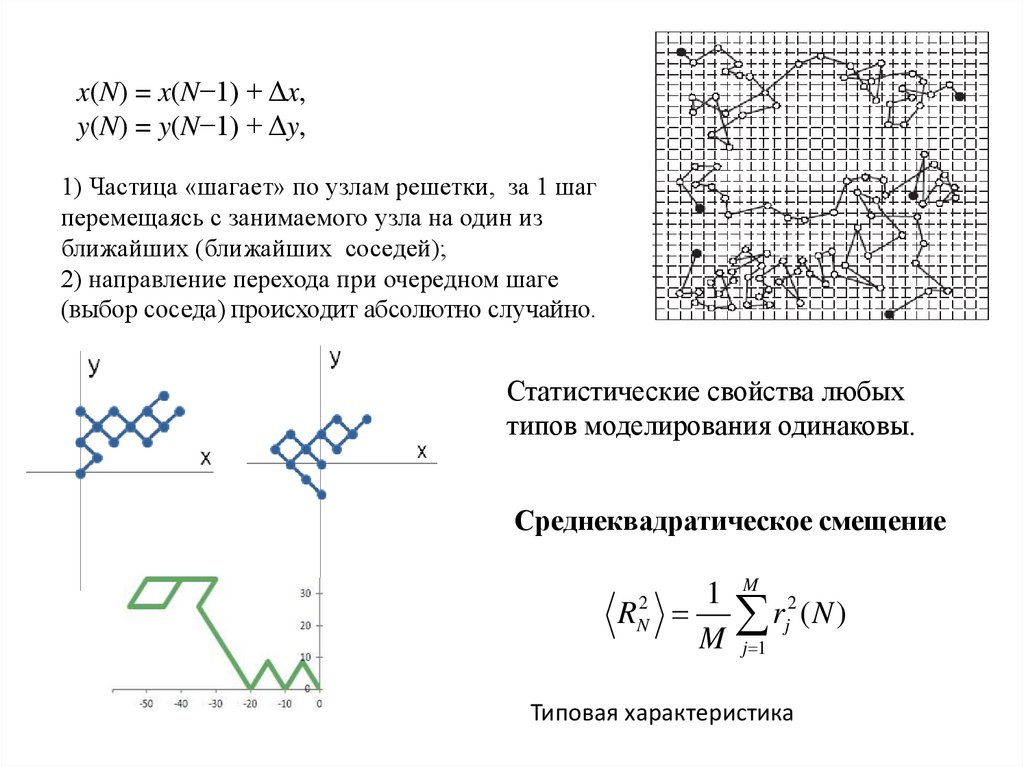
x(N) = x(N−1) + Δx,
y(N) = y(N−1) + Δy,
1) Частица «шагает» по узлам решетки, за 1 шаг
перемещаясь с занимаемого узла на один из
ближайших (ближайших соседей);
2) направление перехода при очередном шаге
(выбор соседа) происходит абсолютно случайно.
Статистические свойства любых
типов моделирования одинаковы.
Среднеквадратическое смещение
2
N
R
1
M
M
2
r
j (N )
j 1
Типовая характеристика

4. Связь модели случайных блужданий с явлением диффузии

В 1906 году коллега Эйнштейна польский физик
Мариан Смолуховский получил набор формул,
связывающих параметры, явления диффузии и
случайных блужданий. Основная идея - диффузия
частиц есть независимые случайные блужданий этих
частиц, происходящих одновременно.
для среднего диффузионного расстояния
(среднего размера «облака» частиц как
функции времени) получено:
(XДифф) 2 = 2Dt
Коэффициент диффузии
D=h2/(2t)
Результат моделирования за N =12 и N =24 шага.
Радиус окружн. R соответствует формуле R2 = dh2N

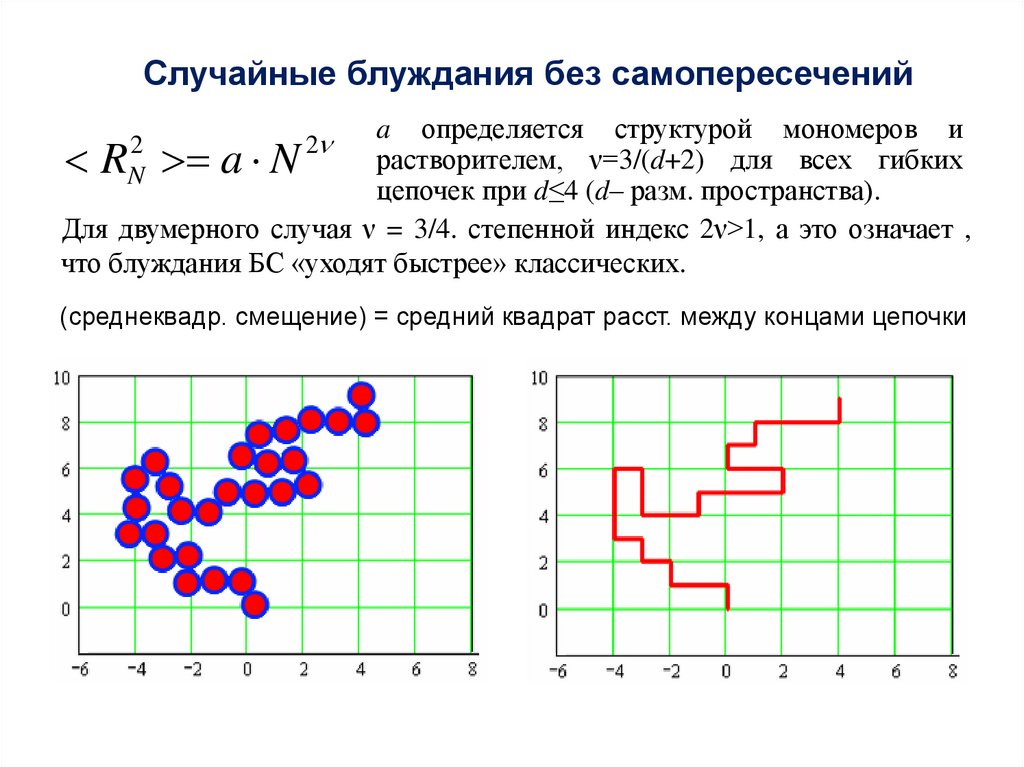
5. Случайные блуждания без самопересечений

a определяется структурой мономеров и
растворителем, ν=3/(d+2) для всех гибких
R a N
цепочек при d≤4 (d– разм. пространства).
Для двумерного случая ν = 3/4. степенной индекс 2ν>1, а это означает ,
что блуждания БС «уходят быстрее» классических.
2
N
2
(среднеквадр. смещение) = средний квадрат расст. между концами цепочки

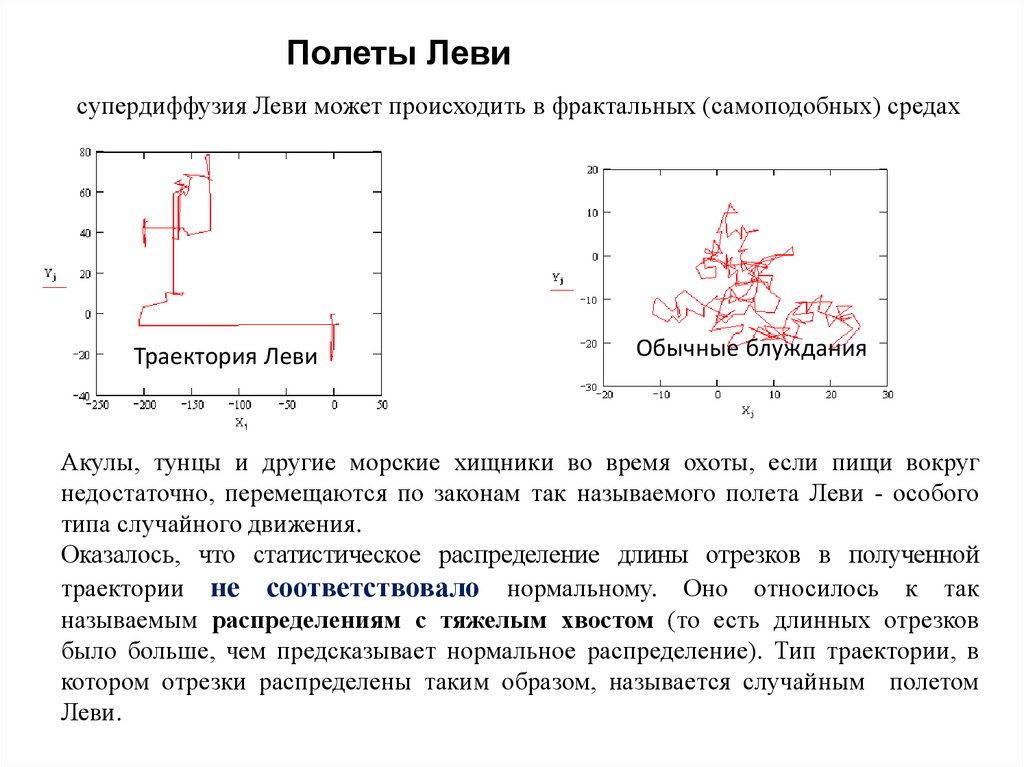
6. Полеты Леви

супердиффузия Леви может происходить в фрактальных (самоподобных) средах
Траектория Леви
Обычные блуждания
Акулы, тунцы и другие морские хищники во время охоты, если пищи вокруг
недостаточно, перемещаются по законам так называемого полета Леви - особого
типа случайного движения.
Оказалось, что статистическое распределение длины отрезков в полученной
траектории не соответствовало нормальному. Оно относилось к так
называемым распределениям с тяжелым хвостом (то есть длинных отрезков
было больше, чем предсказывает нормальное распределение). Тип траектории, в
котором отрезки распределены таким образом, называется случайным полетом
Леви.

7.

Типы
моделей
Формальные
характеристики
Классические
блуждания
R t , N
Блуждания без
самопересечений
R a N
Аномальная
диффузия
R (t ) A t
Полеты
Леви
«Береговая
линия»
Комментарии
Броуновское движение,
классическая диффузия
2
N
2
N
2
R
2
N
2
2
( 2 )
Диффузия по фракталам
θ - индекс аномальной
диффузии
Супердиффузия во
фрактальном композите
блуждающий хищник
RN2 a N
Полимерная цепочка в
разбавленном растворе
2
F
Одномерн. случ. фрактал,
модель береговой линии
F>1 – фрактальная размерн.

8.

Фракта́л (лат. Fractus - дроблёный, сломанный, разбитый) — множество,
обладающее свойством самоподобия (объект, в точности или приближённо
совпадающий с частью себя самого, то есть целое имеет ту же форму, что и
одна или более частей).
Квадрат Серпинского

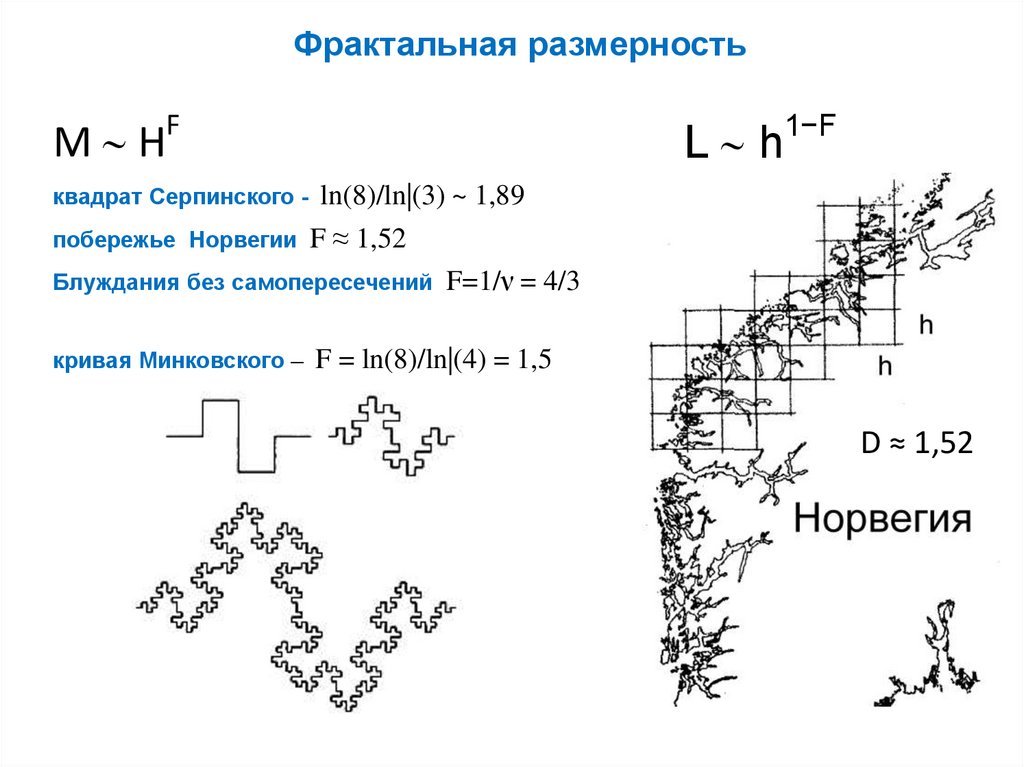
9. Фрактальная размерность

1−F
M H
F
L h
квадрат Серпинского -
ln(8)/ln|(3) ~ 1,89
побережье Норвегии F ≈ 1,52
Блуждания без самопересечений F=1/ν = 4/3
кривая Минковского –
F = ln(8)/ln|(4) = 1,5
D ≈ 1,52