Тригонометрические функции y = sin x и y = cos x . Их свойства и графики

1.

2.

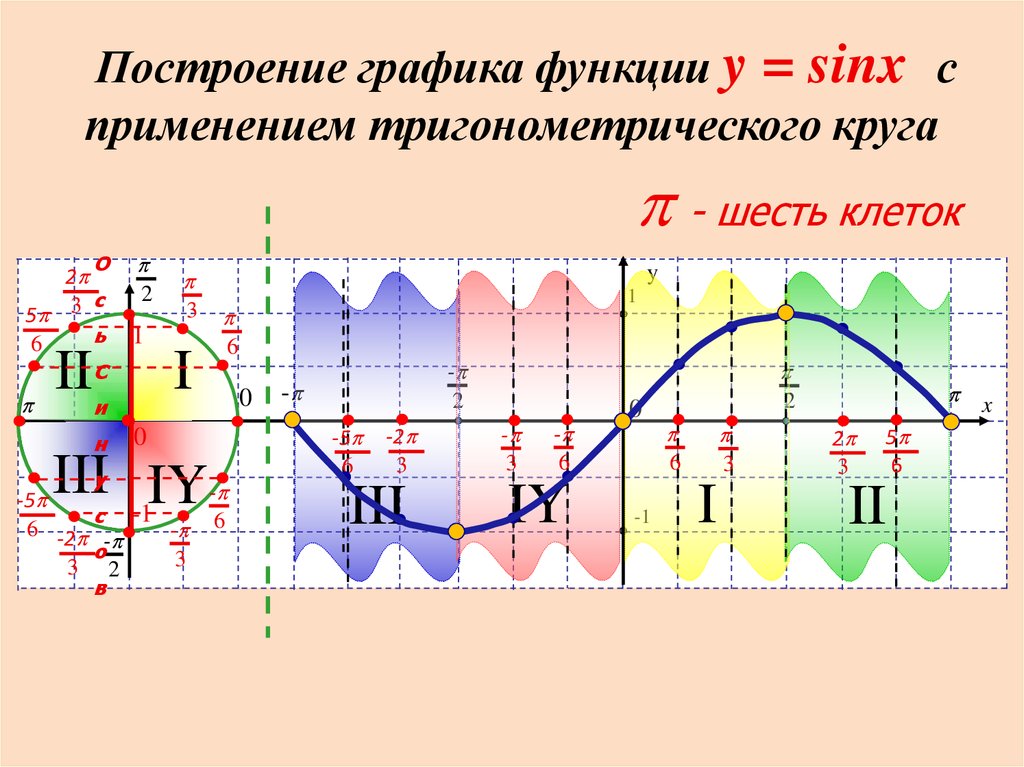
Построение графика функции y = sinx с
применением тригонометрического круга
p - шесть клеток
О
2p
с
5p 3
ь
6
p
II
p
2
I
и
н
III
у
3
1
С
y
p
p
6
0
IY
-p
-5p
с -1
6
6 -2p
p
-p
о
3
3 2
в
1
0
-p
2
-p
-5p
6
-2p
3
III
p
-p
3
-p
6
IY
0
-1
p x
2
p
p
6
3
I
2p
3
5p
6
II

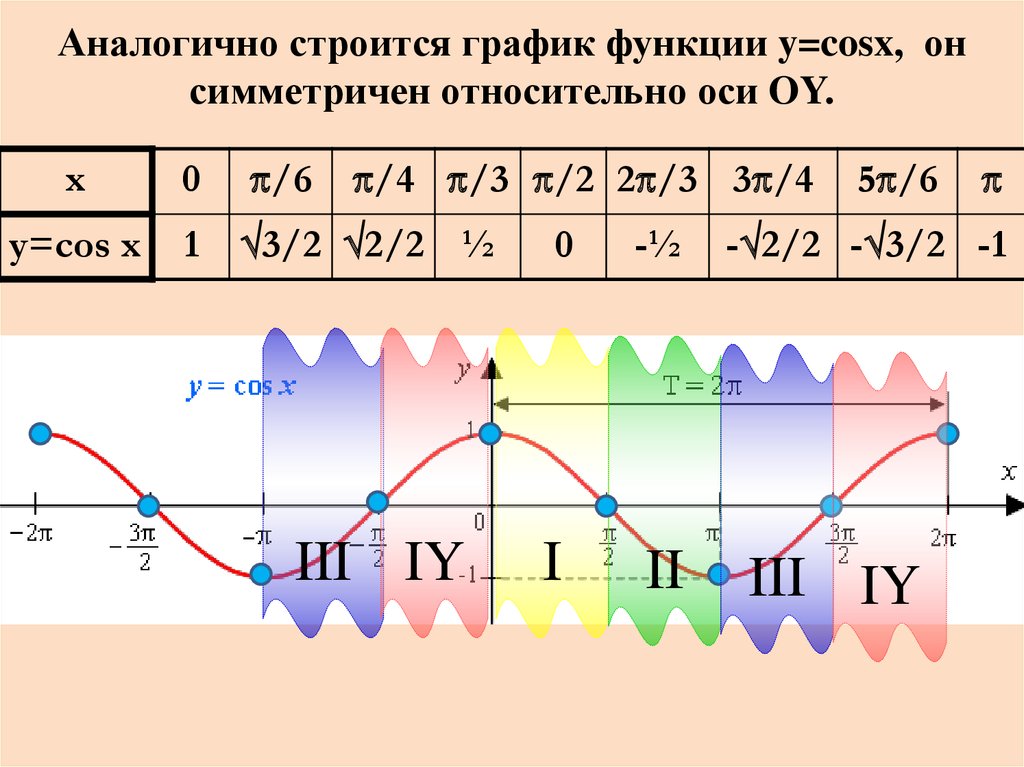
3. Аналогично строится график функции y=cosx, он симметричен относительно оси OY.

x
0
p/6
p/4 p/3 p/2 2p/3 3p/4
y=cos x
1
3/2 2/2 ½
III IY
0
-½
I
II
5p/6
p
- 2/2 - 3/2 -1
III IY

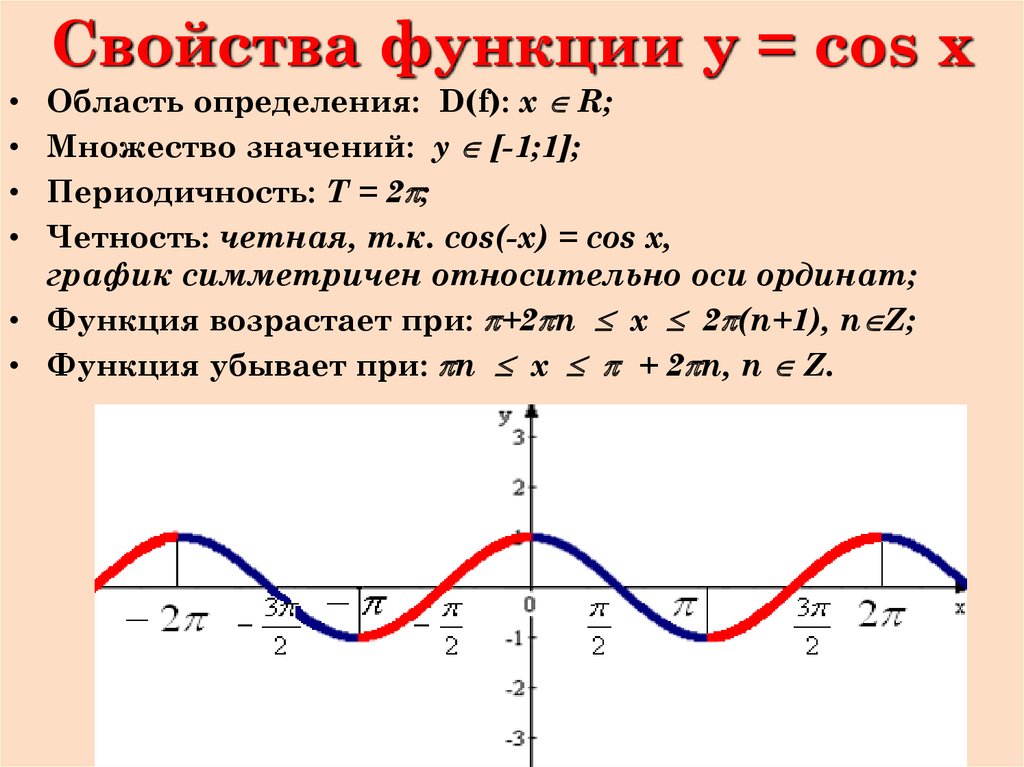
4. Свойства функции y = cos x

Область определения: D(f): х R;
Множество значений: у [-1;1];
Периодичность: Т = 2p;
Четность: четная, т.к. cos(-x) = cos x,
график симметричен относительно оси ординат;
• Функция возрастает при: p+2pn x 2p(n+1), n Z;
• Функция убывает при: pn x p + 2pn, n Z.

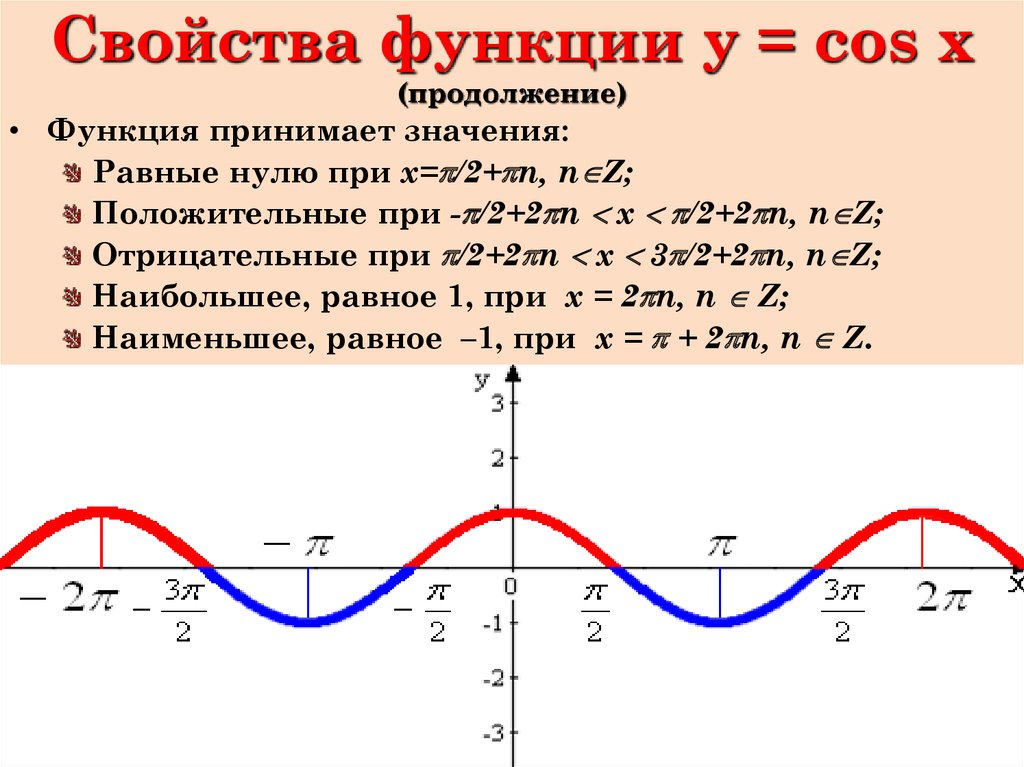
5. Свойства функции y = cos x (продолжение)

• Функция принимает значения:
Равные нулю при х=p/2+pn, n Z;
Положительные при -p/2+2pn x p/2+2pn, n Z;
Отрицательные при p/2+2pn x 3p/2+2pn, n Z;
Наибольшее, равное 1, при x = 2pn, n Z;
Наименьшее, равное –1, при x = p + 2pn, n Z.

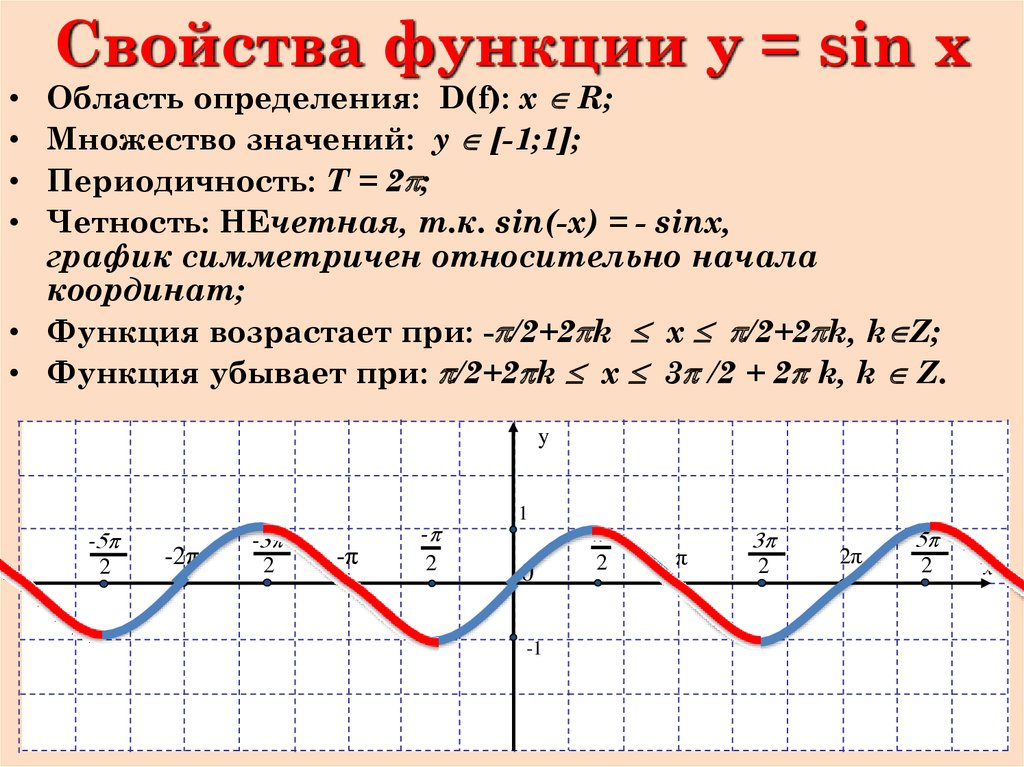
6. Свойства функции y = sin x

Область определения: D(f): х R;
Множество значений: у [-1;1];
Периодичность: Т = 2p;
Четность: НЕчетная, т.к. sin(-x) = - sinx,
график симметричен относительно начала
координат;
• Функция возрастает при: -p/2+2pk x p/2+2pk, k Z;
• Функция убывает при: p/2+2pk x 3p /2 + 2p k, k Z.
y
-5p
2
-2π
-3p
2
-π
-p
2
1
0
-1
p
2
π
3p
2
2π
5p
2
x

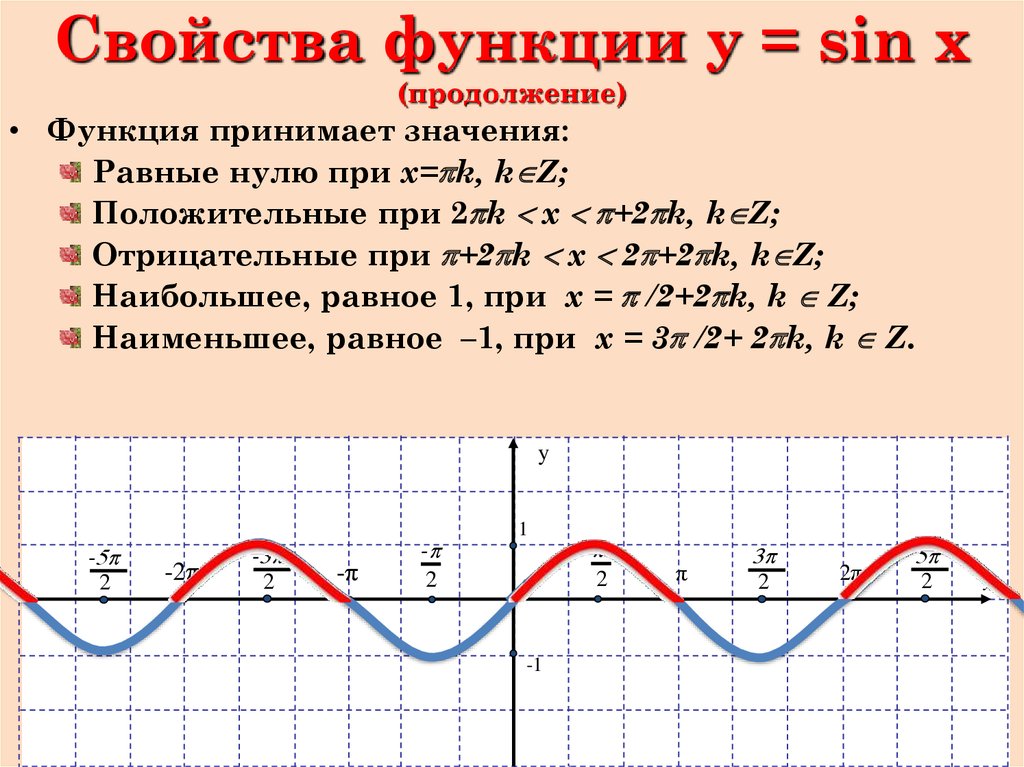
7. Свойства функции y = sin x (продолжение)

• Функция принимает значения:
Равные нулю при х=pk, k Z;
Положительные при 2pk x p+2pk, k Z;
Отрицательные при p+2pk x 2p+2pk, k Z;
Наибольшее, равное 1, при x = p /2+2pk, k Z;
Наименьшее, равное –1, при x = 3p /2+ 2pk, k Z.
y
-5p
2
-2π
-3p
2
-π
-p
2
1
0
-1
p
2
π
3p
2
2π
5p
2
x

8.

9.

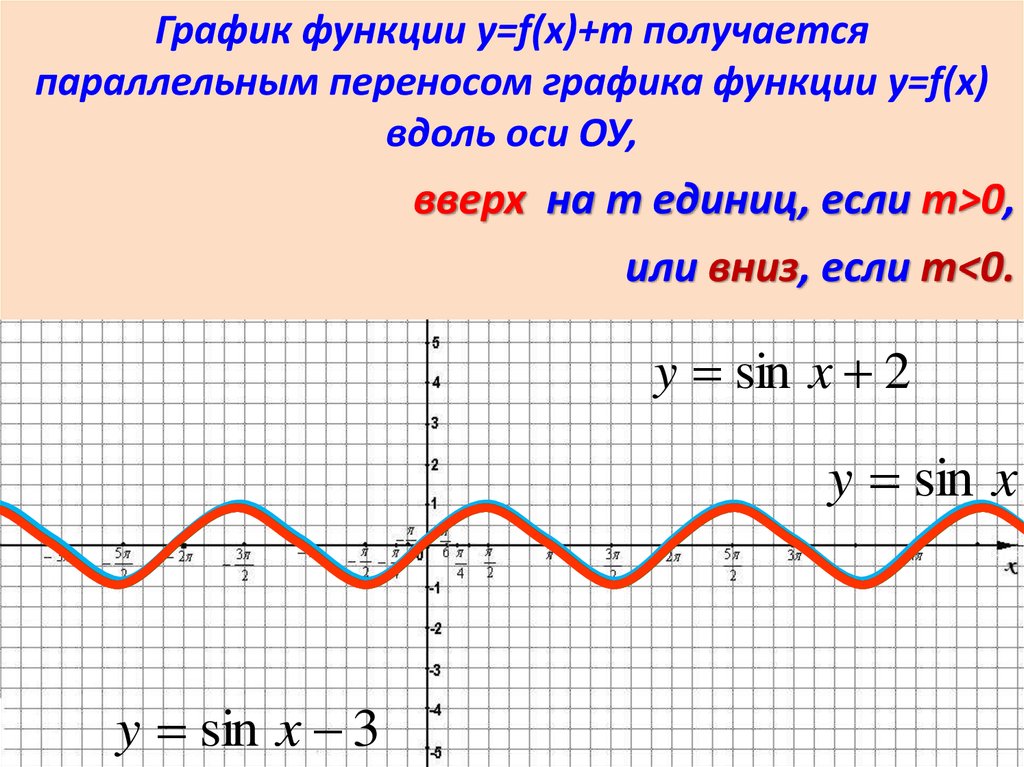
График функции y=f(x)+m получается
параллельным переносом графика функции y=f(x)
вдоль оси ОУ,
вверх на m единиц, если m>0,
или вниз, если m<0.
y sin x 2
y sin x
y sin x 3

10.

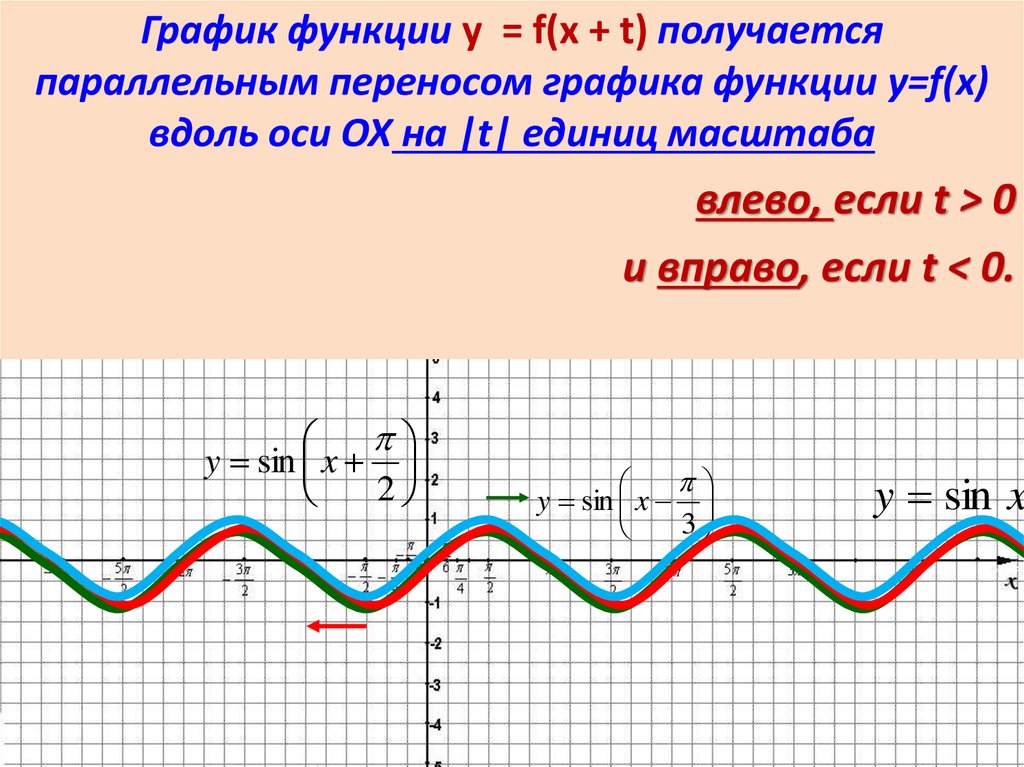
График функции y = f(x + t) получается
параллельным переносом графика функции y=f(x)
вдоль оси ОХ на |t| единиц масштаба
влево, если t > 0
и вправо, если t < 0.
p
y sin x
2
p
y sin x
3
y sin x

11.

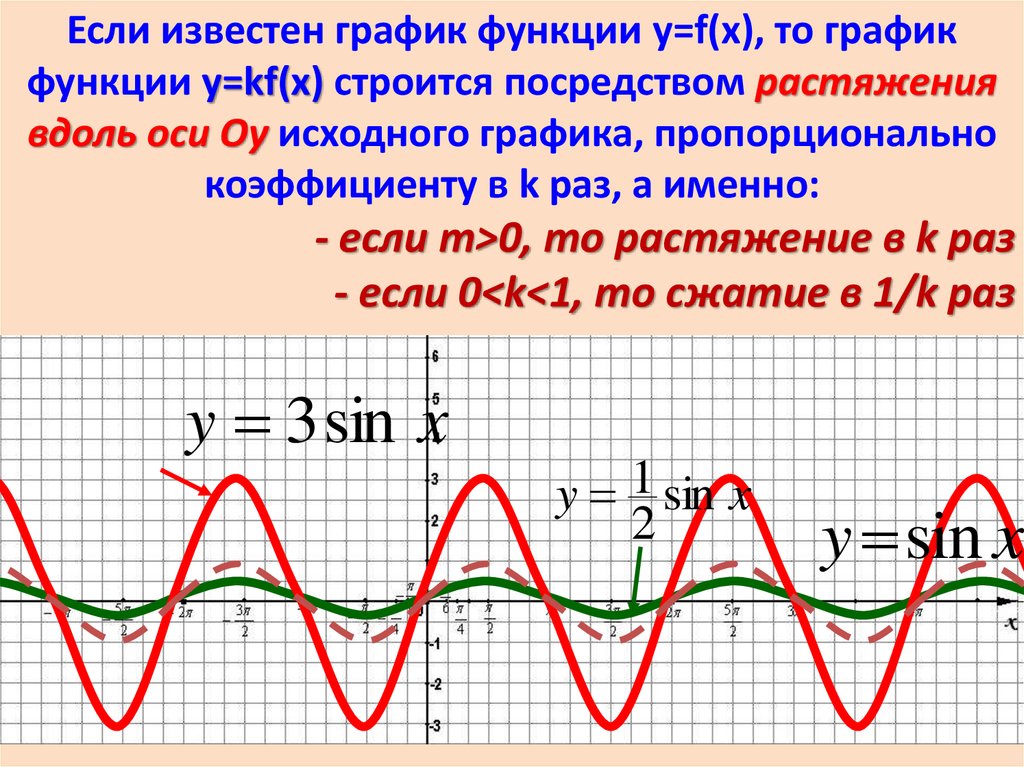
Если известен график функции y=f(x), то график
функции y=kf(x) строится посредством растяжения
вдоль оси Оy исходного графика, пропорционально
коэффициенту в k раз, а именно:
- если m>0, то растяжение в k раз
- если 0<k<1, то сжатие в 1/k раз
y 3 sin x
y 1 sin x
2
y sin x

12.

Если известен график функции y=f(x), то график
функции y=f(kx) строится посредством
сжатия по оси Оx исходного графика
пропорционально коэффициенту k при аргументе, а
именно:
- если k>1, то сжатие в k раз
- если 0<k<1, то растяжение в 1/k раз
y sin 2 x
x
y sin
3
y sin x

13.

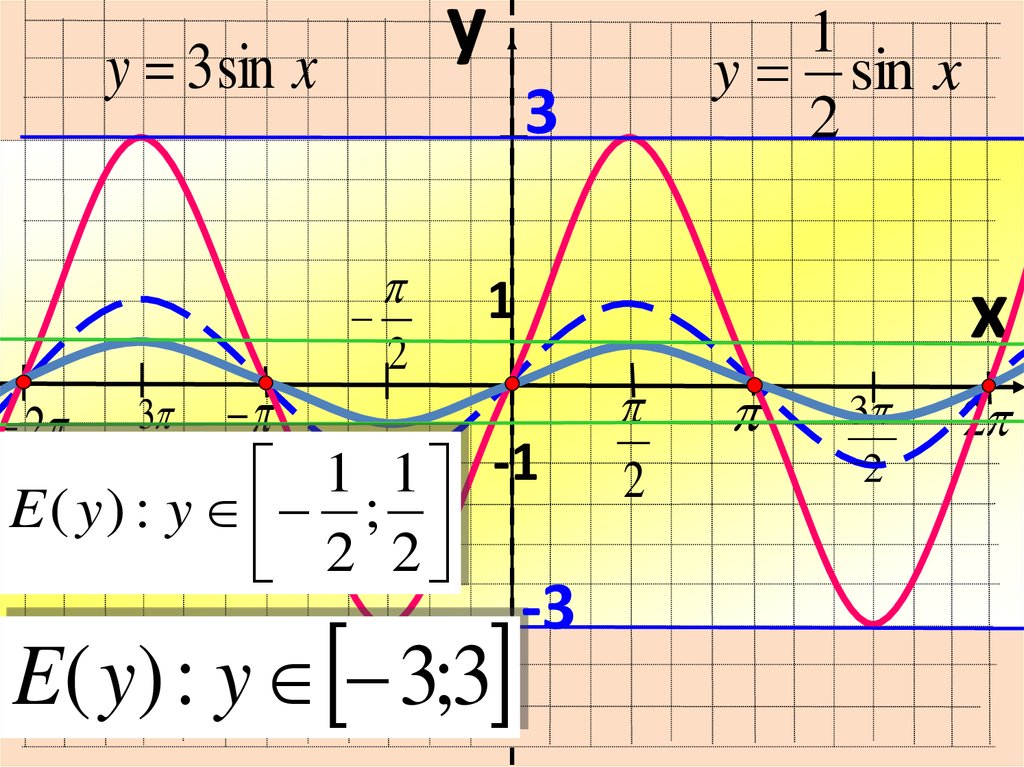
y
y 3 sin x
3
p
2
x
1
p
1 1 -1
E ( y ) : y ;
2 2
2p
1
y sin x
2
3p
2
E( y) : y 3;3
-3
p
2
p
3p
2
2p

14.

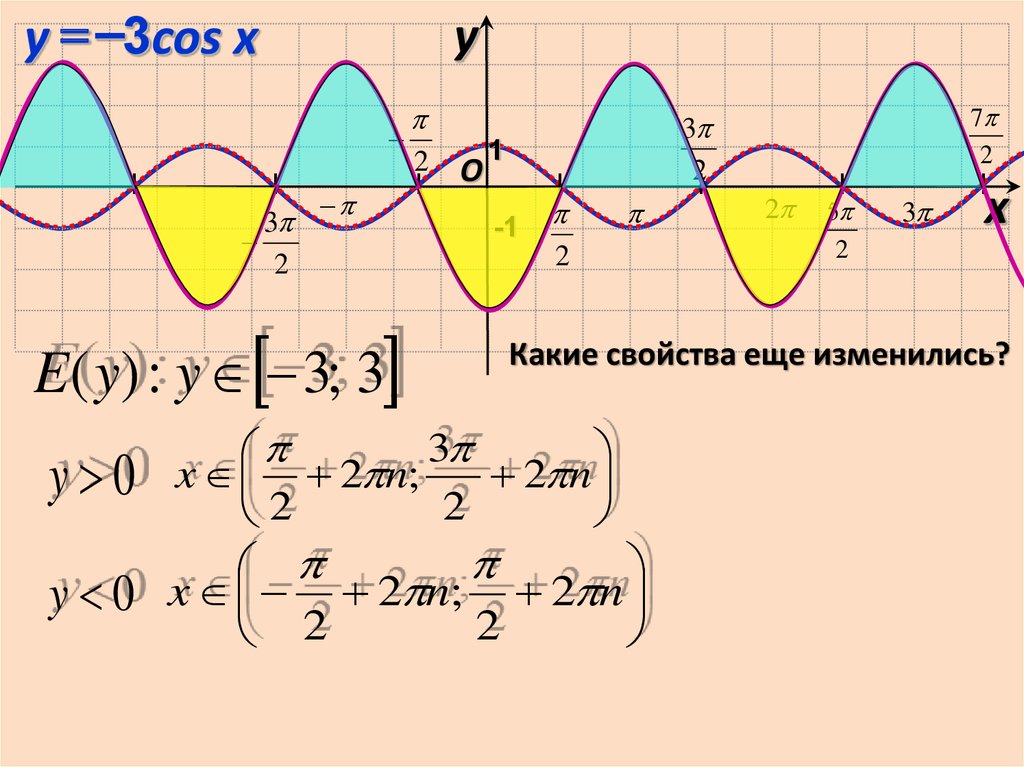
y –3cos x
y
I
I
p
3p
2
E( y) : y 3; 3
y 0
p
2
I
O
1
I
-1
p
2
p
3p
2I
7p
2
2p
I
5p
3p
I
x
2
Какие свойства еще изменились?
3p
p
x 2pn;
2pn
2
2
p
p
y 0 x 2pn; 2pn
2
2

15.

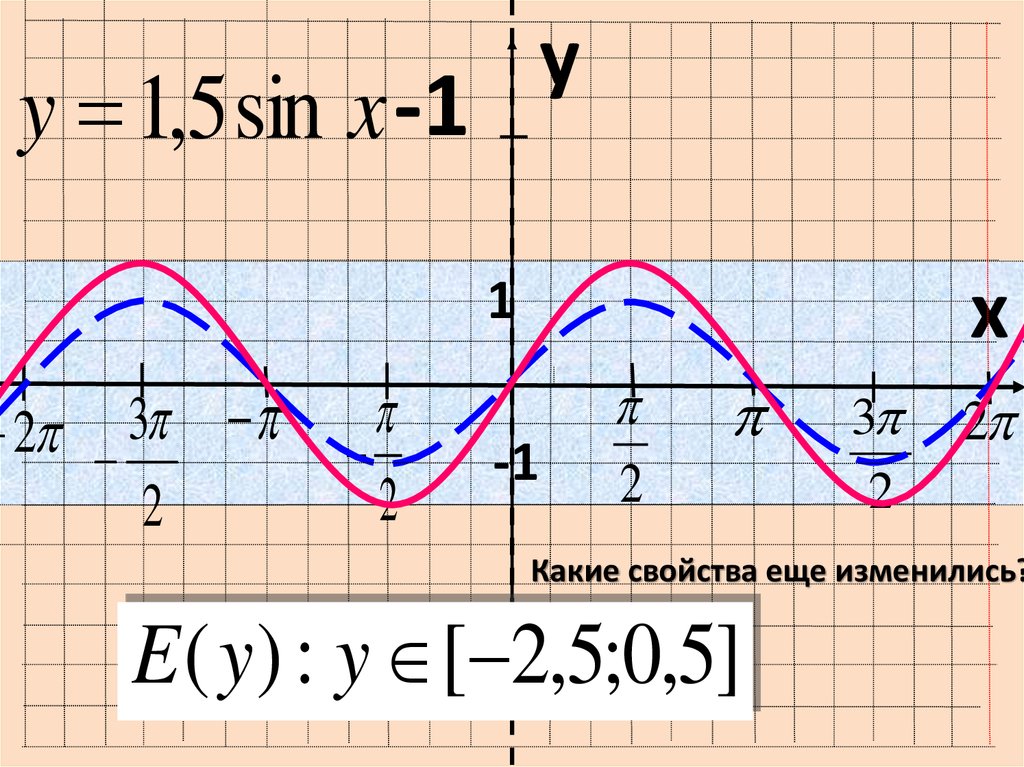
y
y 1,5 sin x -1
x
1
2p 3p p
2
p
2
-1
p
2
p
3p
2
2p
Какие свойства еще изменились?
E ( y) : y [ 2,5;0,5]

16.

y
I
I
p
3p
2
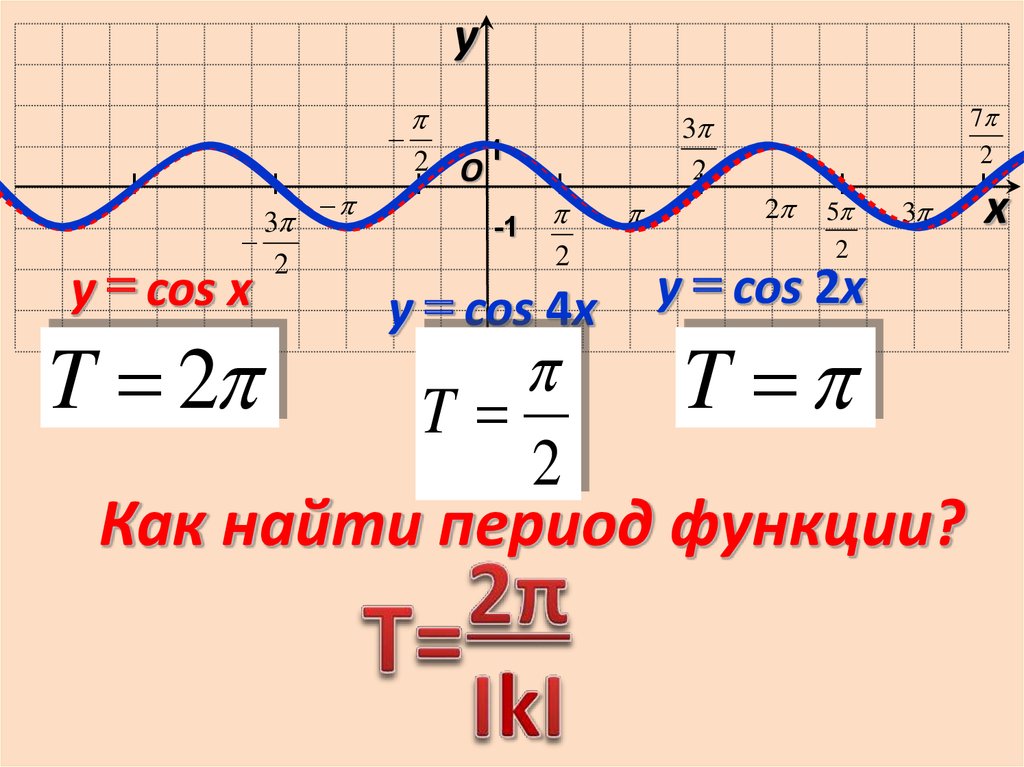
y cos x
T 2p
p
2
I
O
1
I
-1
p
2
y cos 4x
p
3p
2I
7p
2
2p
I
5p
3p
2
y cos 2x
p
T
p
T
2
Как найти период функции?
I
x

17.

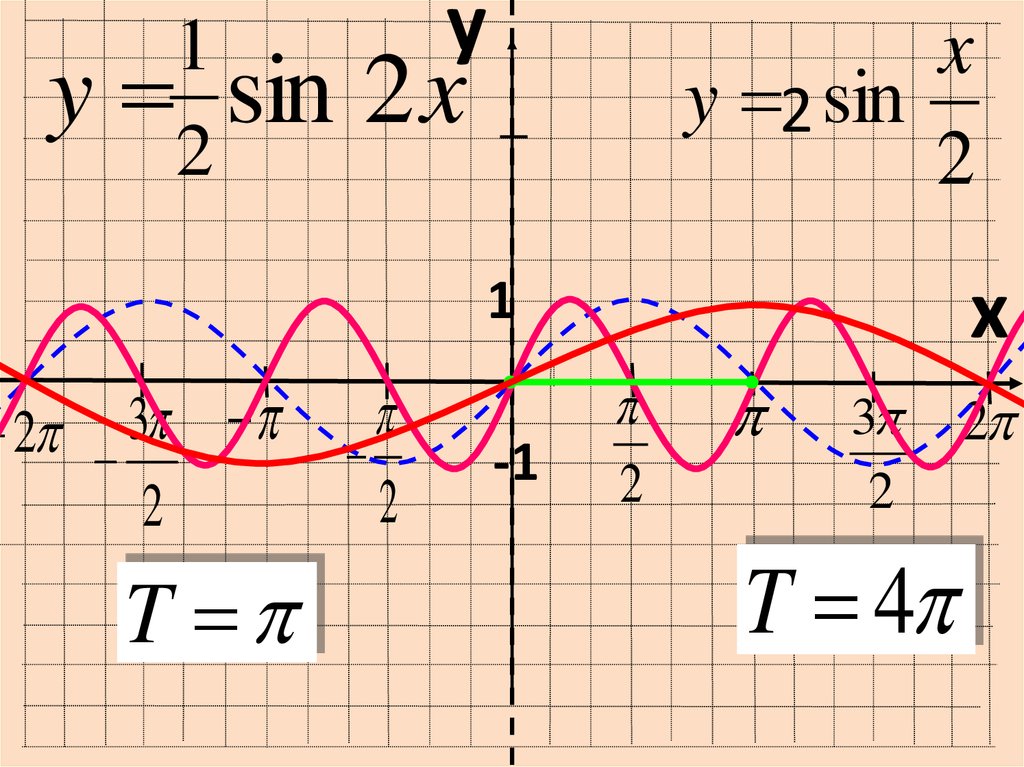
y
1
sin
2
y
x
y 2 sin
2
2x
x
1
2p 3p p
2
T p
p
2
-1
p
2
p
3p
2
T 4p
2p