Похожие презентации:
Графики тригонометрических функций у = sin x и y = cos x и их свойства
1. Графики тригонометрических функций у =sin x и y =cos x и их свойства Задание: 1. Посмотрите презентацию 2. Начертите графики
функций3. Заполните таблицу
1
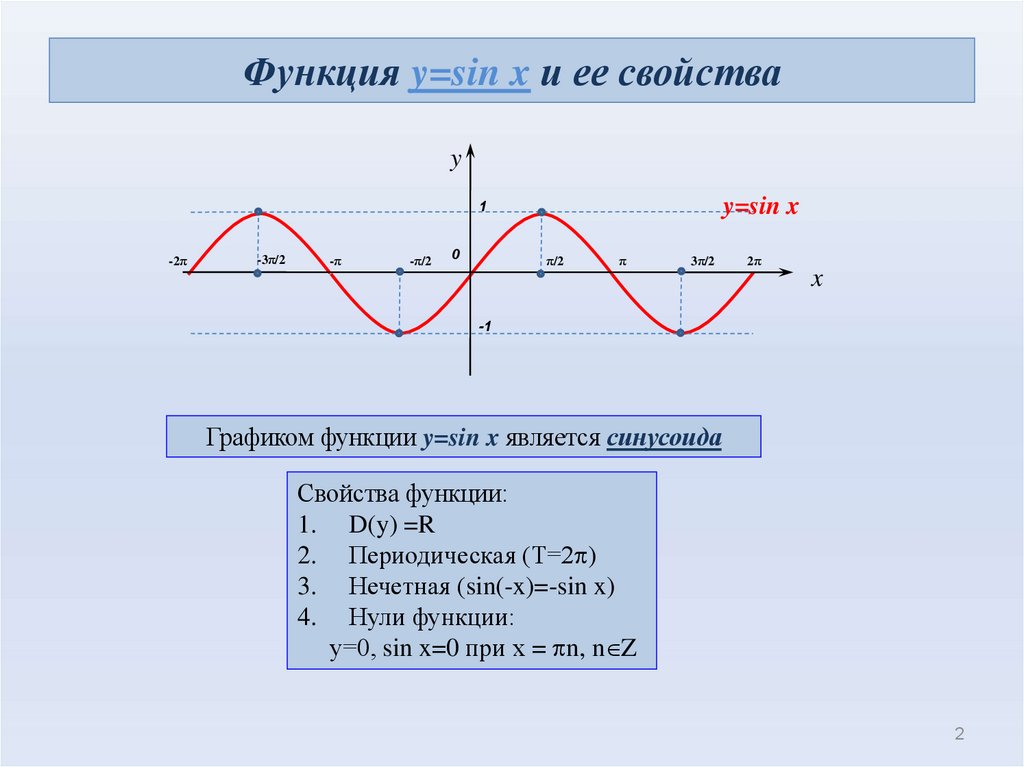
2. Функция y=sin x и ее свойства
yy=sin x
1
-2π
-3π/2
-π
-π/2
0
π/2
π
3π/2
2π
x
-1
Графиком функции y=sin x является синусоида
Свойства функции:
1. D(y) =R
2. Периодическая (Т=2p)
3. Нечетная (sin(-x)=-sin x)
4. Нули функции:
у=0, sin x=0 при х = pn, n Z
2
3.
y1
-2π
-3π/2
-π
-π/2
0
y=sin x
π/2
π
3π/2
2π
x
-1
5. Промежутки знакопостоянства:
У>0 при х (0+2pn; p+2pn), n Z
У<0 при x (-p+2pn; 0+2pn), n Z
y
y=sin x
1
-2π
-3π/2
-π
-π/2
0
π/2
π
3π/2
2π
x
-1
6. Промежутки монотонности:
функция возрастает на промежутках
вида: [-p/2+2pn; p/2+2pn], n Z
функция убывает на промежутках
вида: [p/2+2pn; 3p/2+2pn], n Z
3
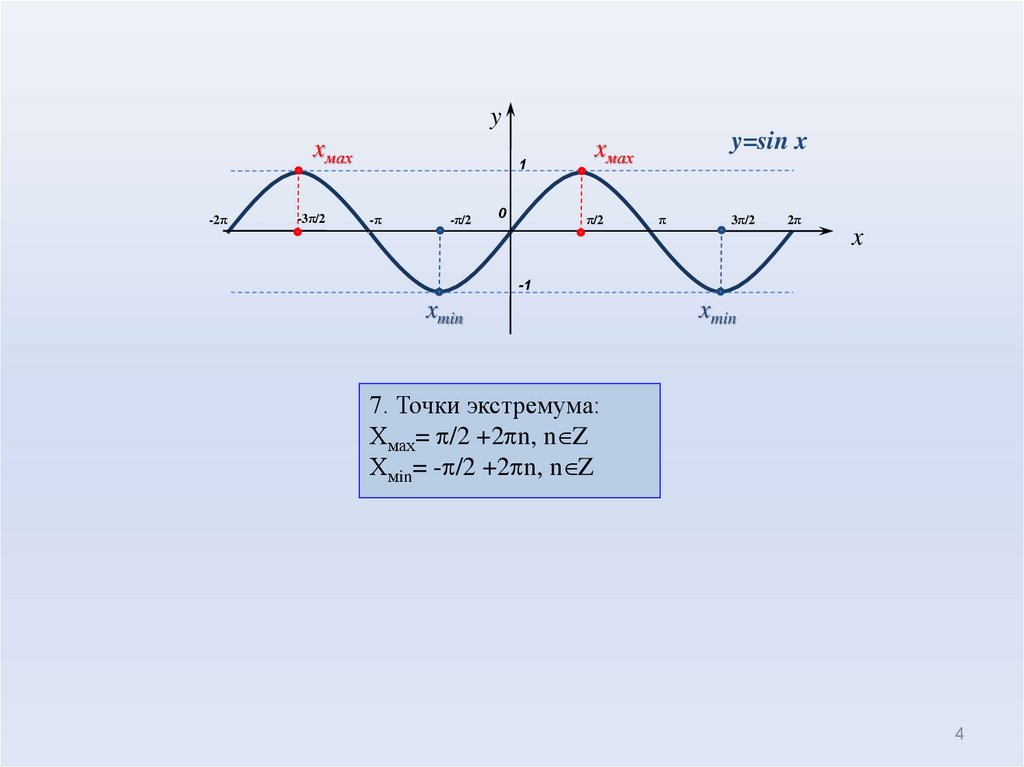
4.
yxмах
-2π
-3π/2
1
-π
-π/2
0
y=sin x
xмах
π/2
π
3π/2
2π
x
-1
xmin
xmin
7. Точки экстремума:
Хмах= p/2 +2pn, n Z
Хмin= -p/2 +2pn, n Z
4
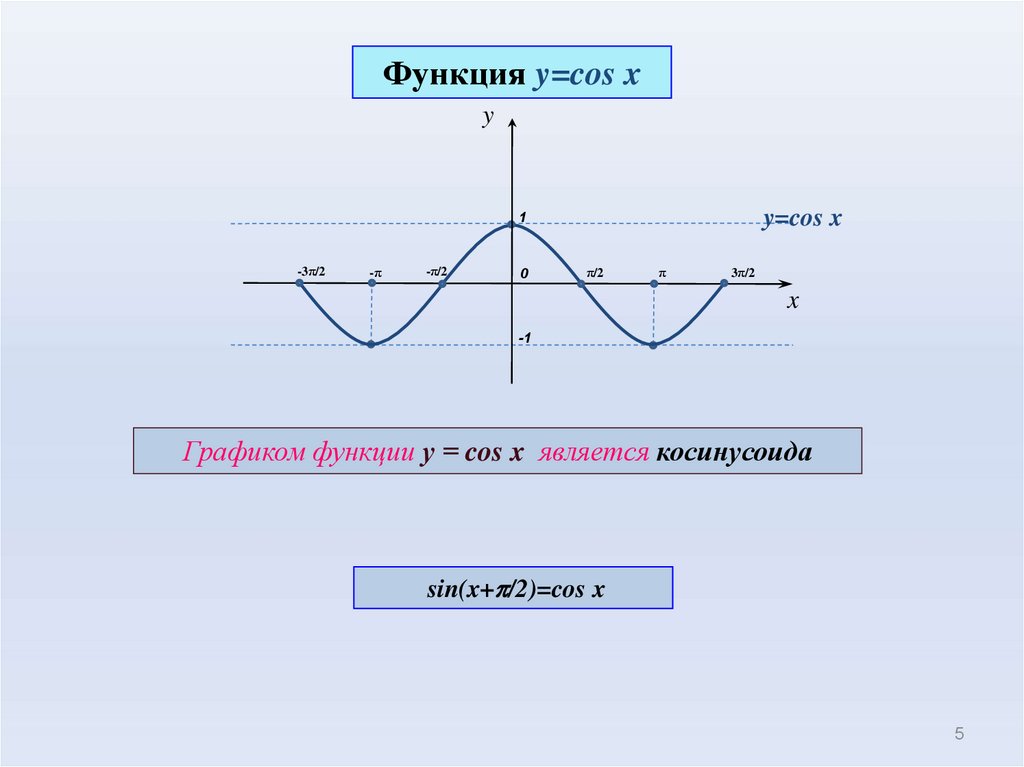
5.
Функция y=cos xy
y=cos x
1
-3π/2
-π
-π/2
0
π/2
π
3π/2
x
-1
Графиком функции у = cos x является косинусоида
sin(x+p/2)=cos x
5
6.
Свойства функции y=cos x1.
2.
3.
4.
D(y) =R
Периодическая Т=2p
Четная
cos(-x)=cos x
Нули функции:
у=0, cos x=0 при х = 1/2pn, n Z
5. Промежутки знакопостоянства:
У>0 при х (-p/2+2pn; p/2+2pn), n Z
У<0 при x (p/2+2pn; 3p/2+2pn), n Z
6. Промежутки монотонности:
функция возрастает на промежутках вида:
[p+2pn; 2p+2pn], n Z
функция убывает на промежутках вида:
[0+2pn; p+2pn], n Z
7. Точки экстремума:
Хмах= 0 +2pn, n Z
Хмin = p +2pn, n Z
6
7. Сравнение свойств функций y = sinx и y = cosx
Функцияy = sinx
y = cosx
Область определения
D(sinx) = ......
D(cosx) = ......
Множество значений
E(sinx) = [........]
E(cosx) = [.......]
Четность и нечетность
………………
…………………
Нули функции
x = ......, k ∈ ℤ
x =............., k ∈ ℤ
y(x)>0
x ∈ (......; .....)
x ∈ ( …..; ……) k ∈ ℤ
y(x)<0
x ∈ (....; ......), k ∈ ℤ
x ∈ ( .….; ……) k ∈ ℤ
f(x)
x ∈ ( ……; …...) k ∈ ℤ
x ∈ ( …..; …..) k ∈ ℤ
f(x)
x ∈ ( …..; …..) k ∈ ℤ
x ∈ ( ….; …..) k ∈ ℤ
………………….
.......................
Промежутки
знакопостоянства
Промежутки
монотонности
Точки экстремума




 Математика
Математика








