Похожие презентации:
Применение производной для исследования функции на монотонность и экстремумы
1.
Вопросы к зачету по теме : Применение производной дляисследования функции на монотонность и экстремумы
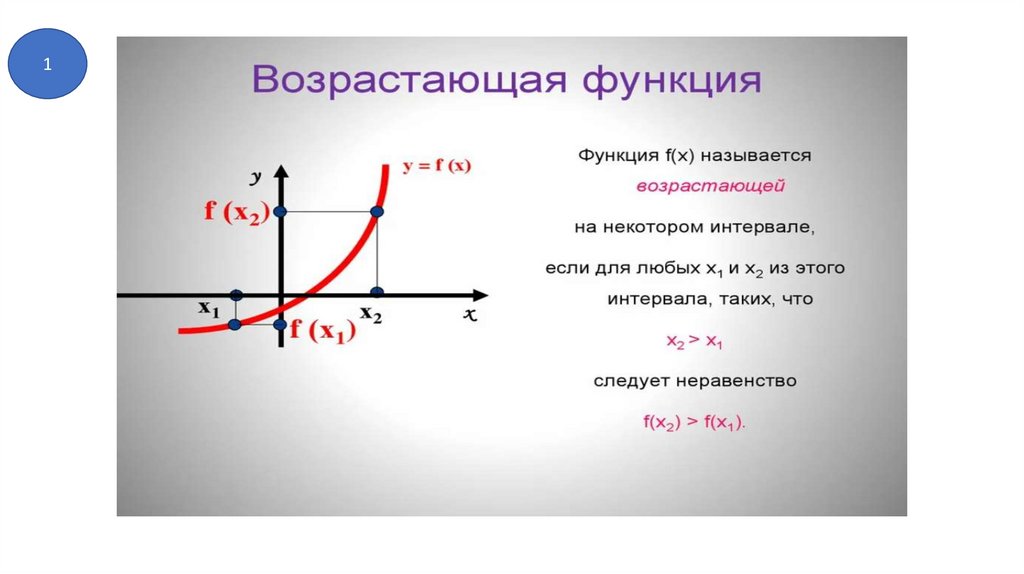
1) Какая функция называется возрастающей (определение +
свойство производной, график ) . Примеры.
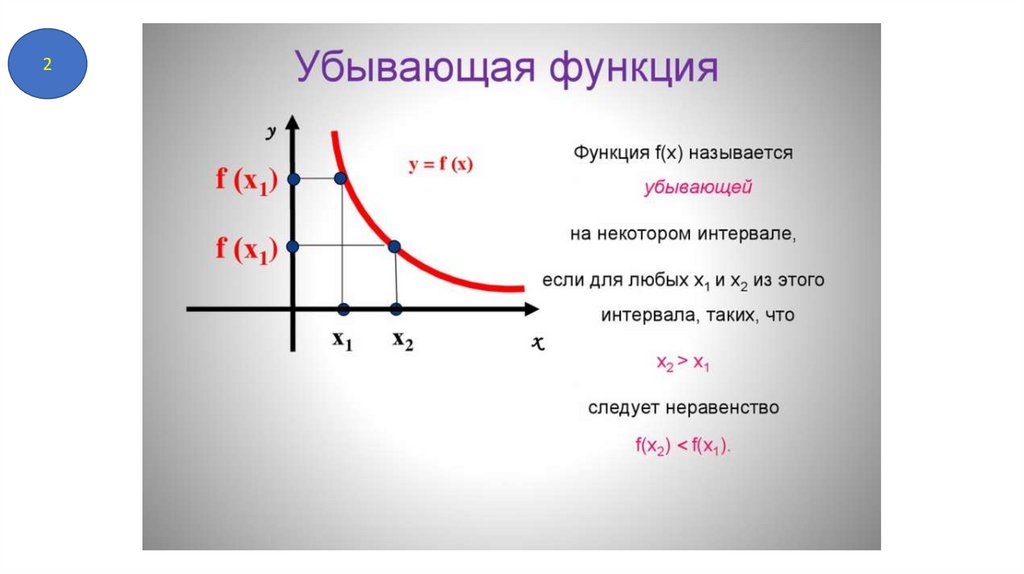
2) Какая функция называется убывающей.
(определение + свойство производной, график). Примеры.
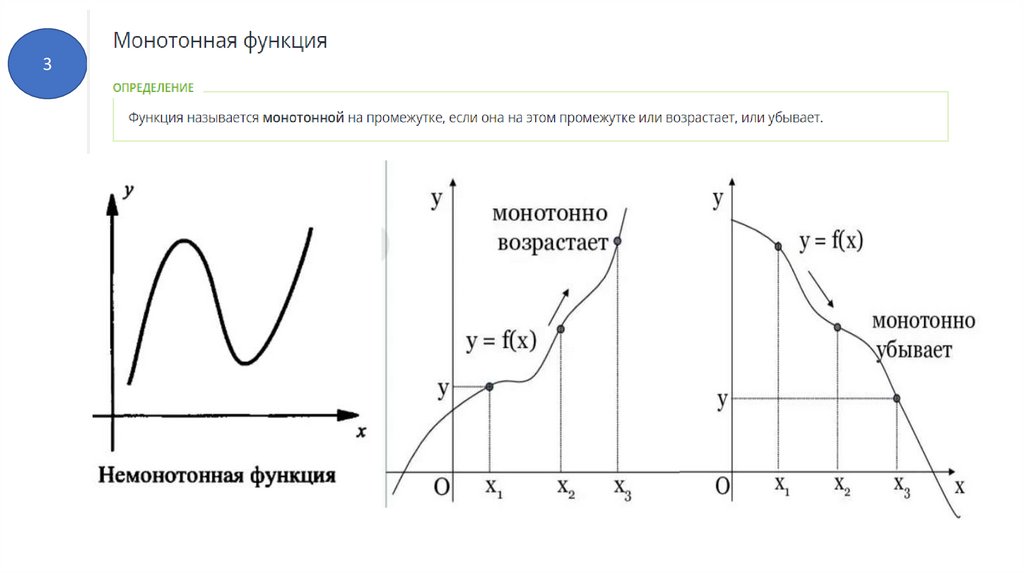
3) Какие функции называются монотонными. Монотонно
возрастающие, монотонно убывающие функции. Примеры.
4) Способы исследования функции на монотонность. Алгоритм
нахождения промежутков монотонности функции с помощью
производной. Решение примера.
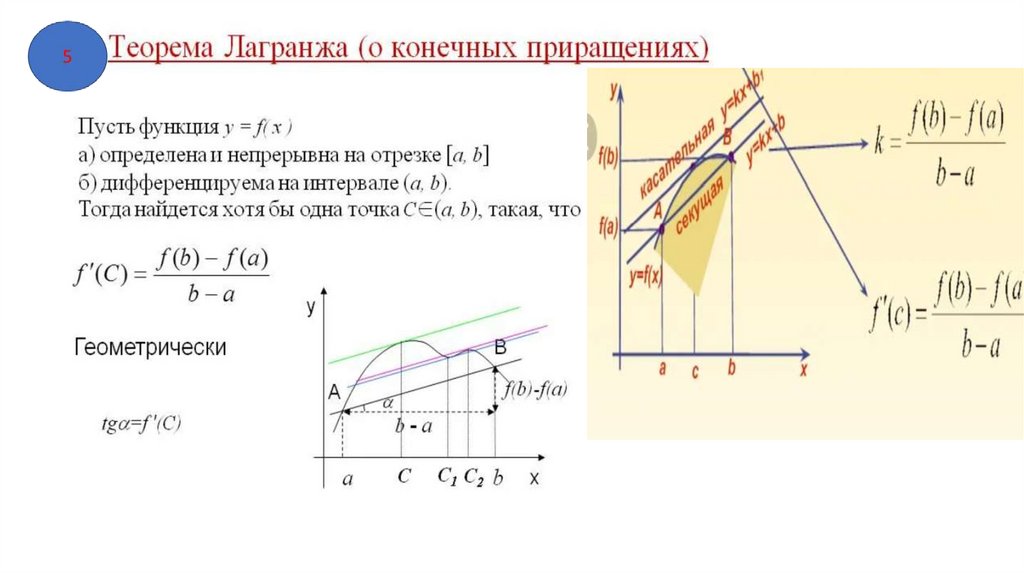
5) Теорема Лагранжа. Геометрический смысл теоремы Лагранжа.
6) Теорема о достаточном условии возрастания и убывания функции.
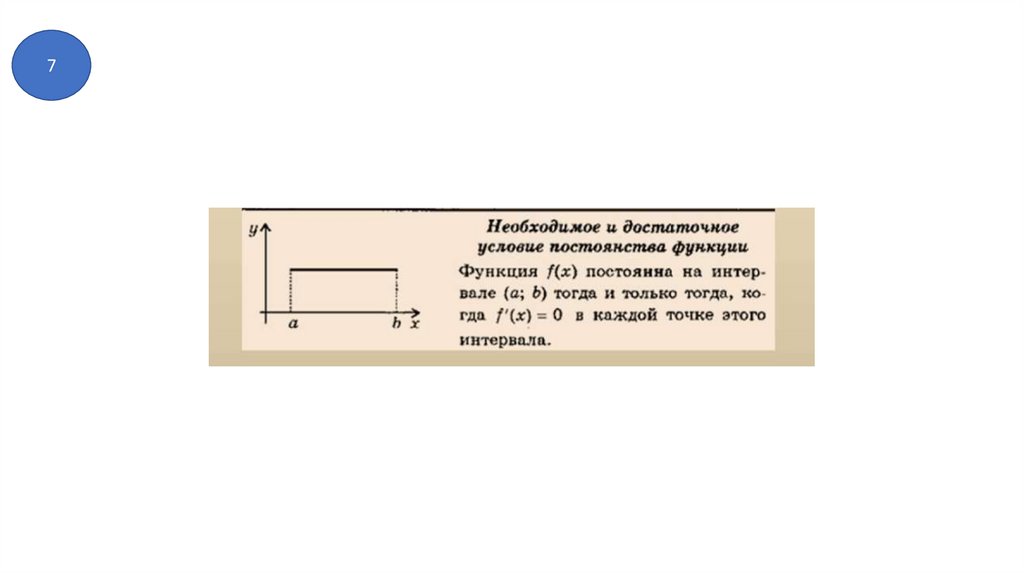
7) Необходимые и достаточные условия постоянства функции.
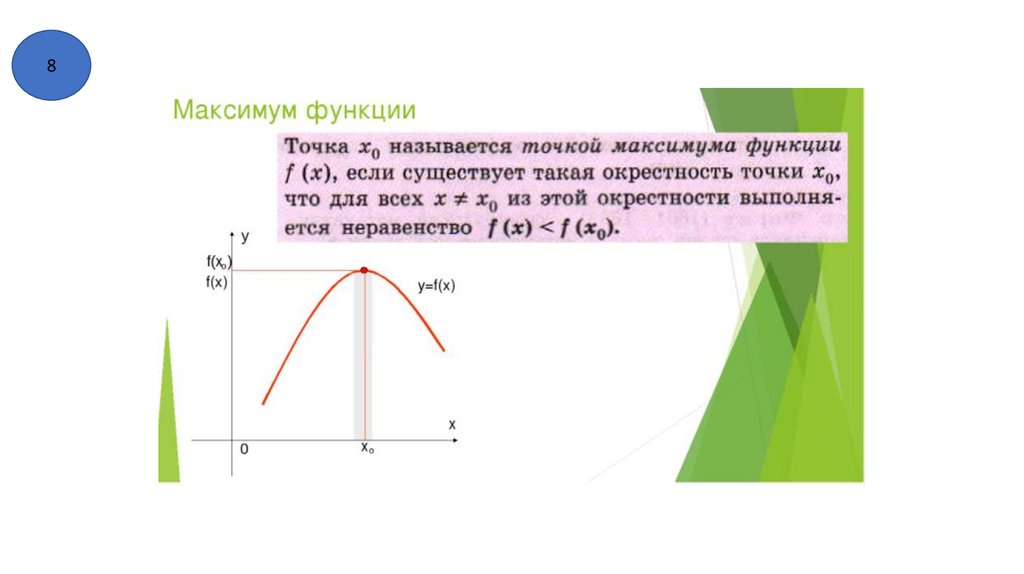
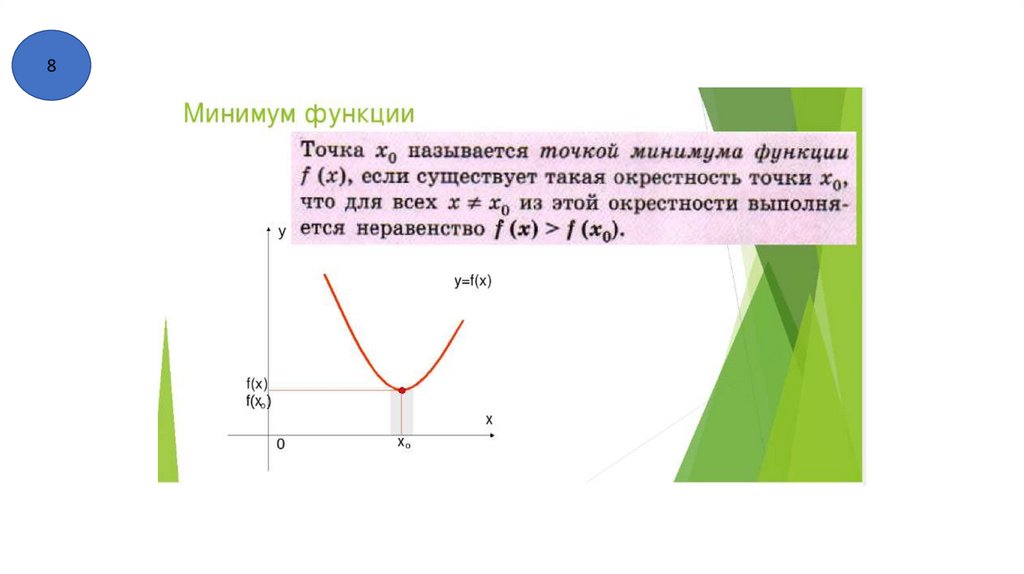
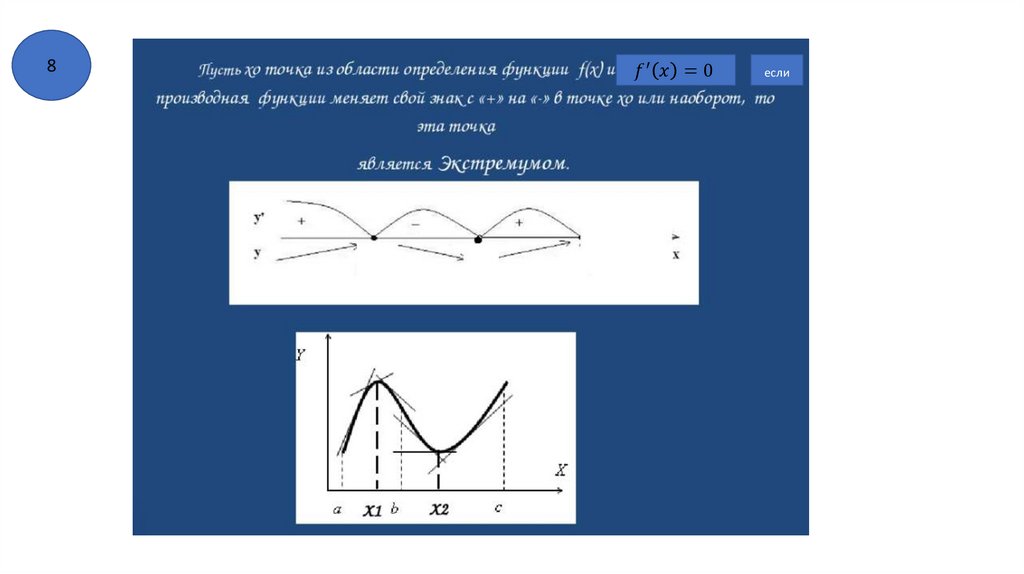
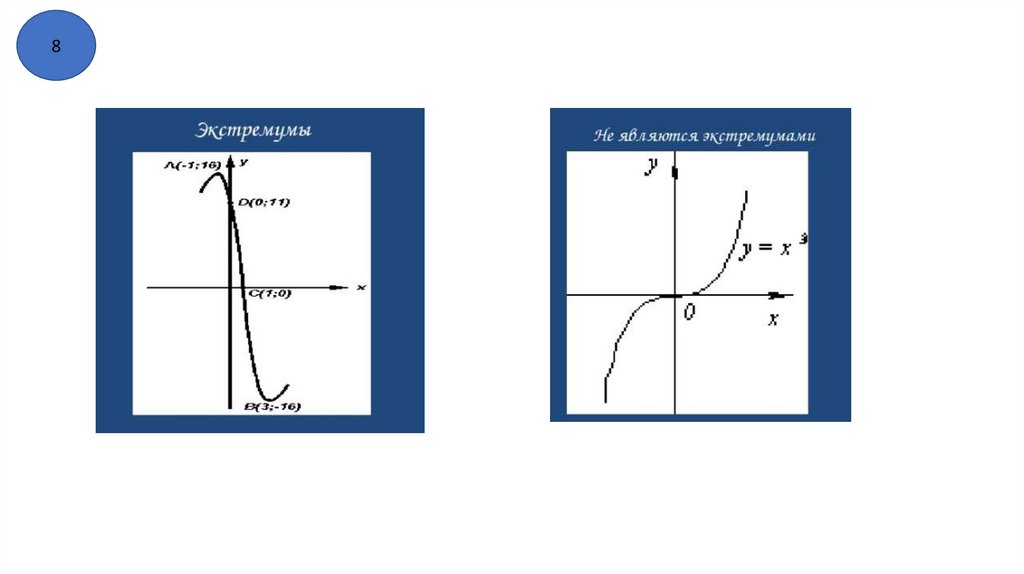
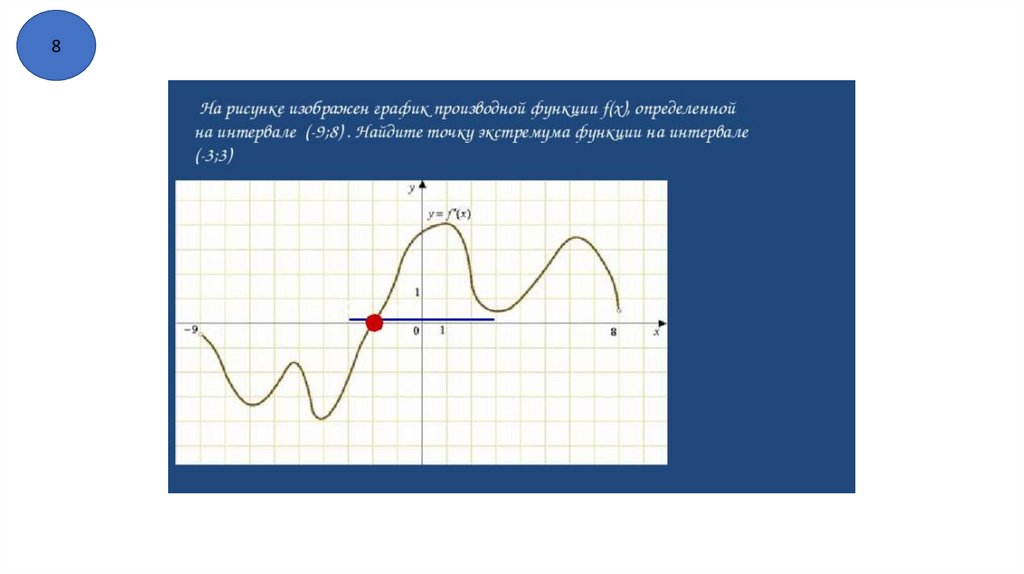
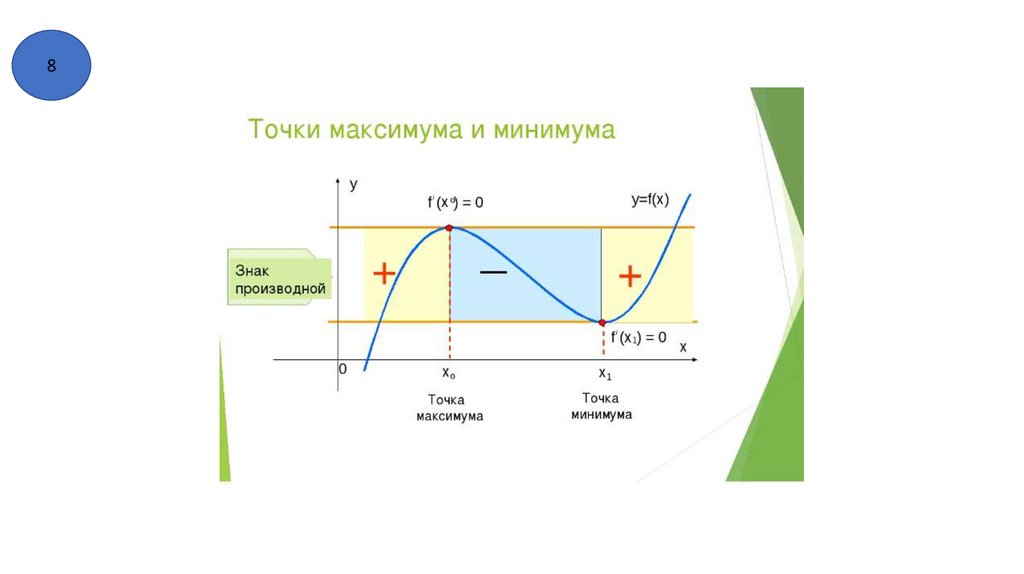
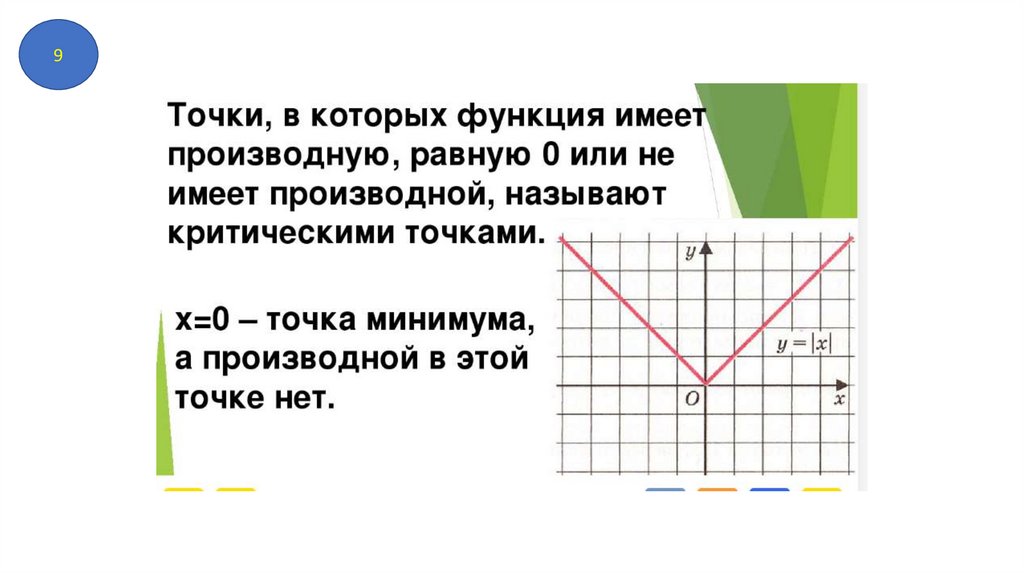
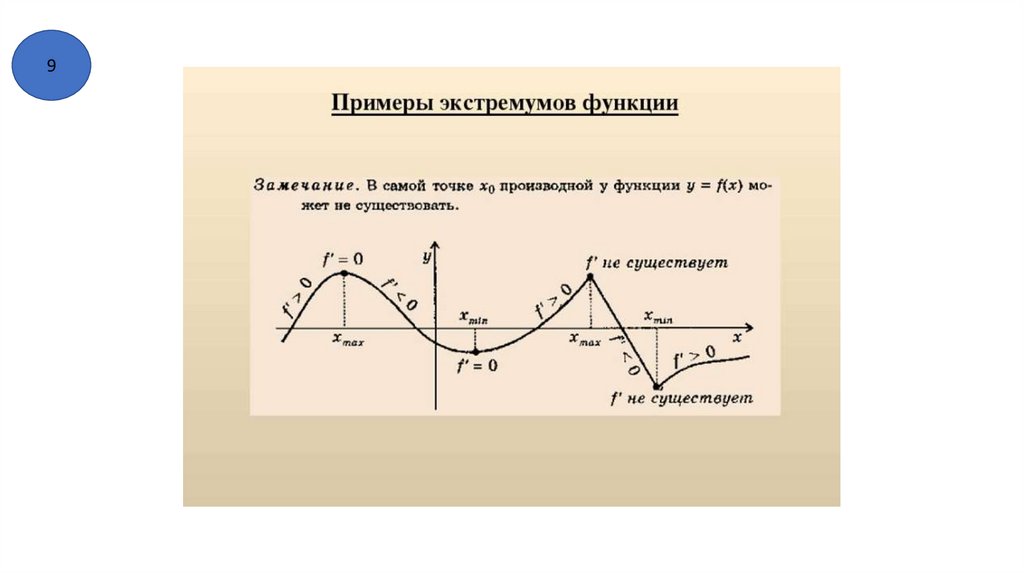
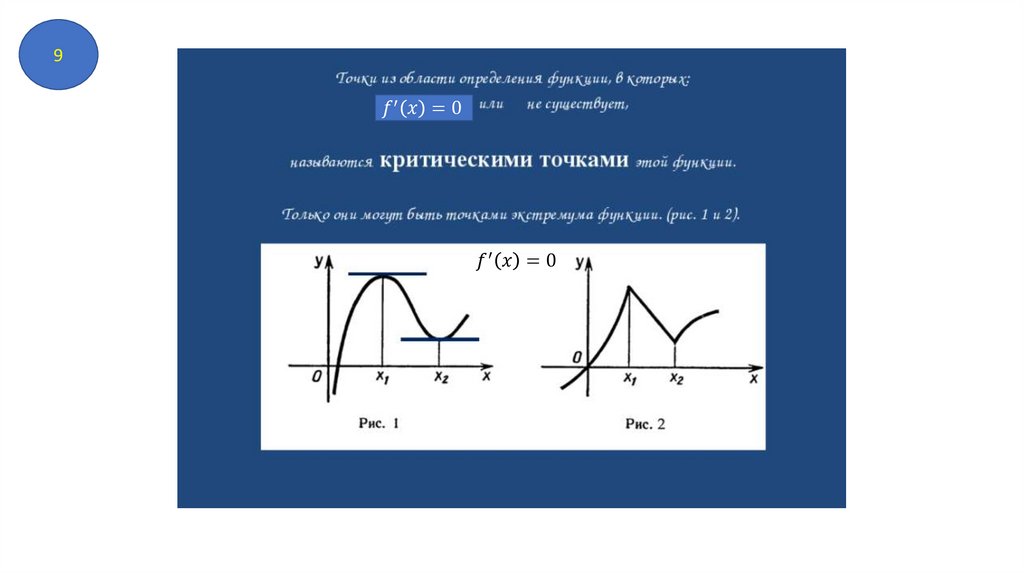
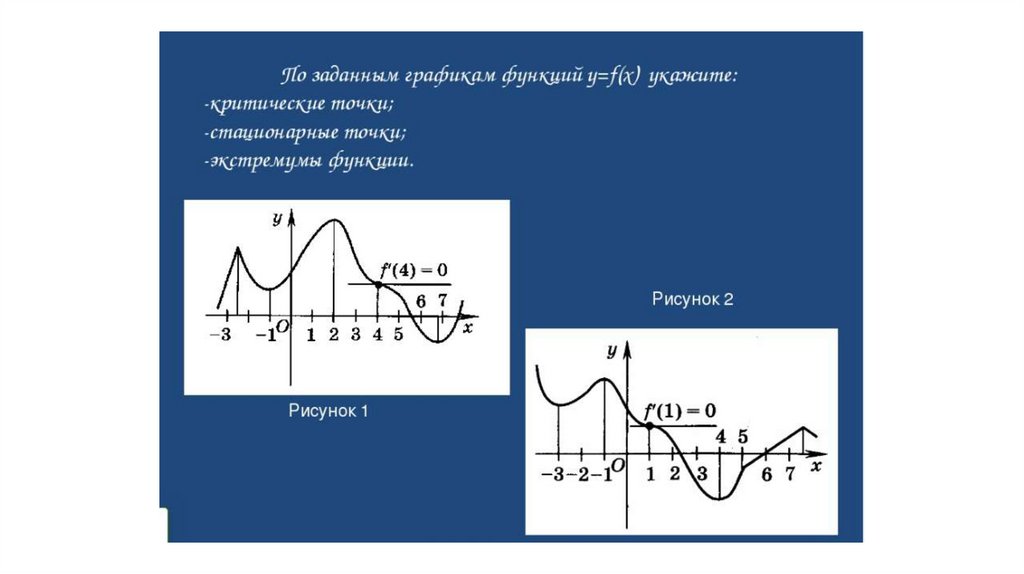
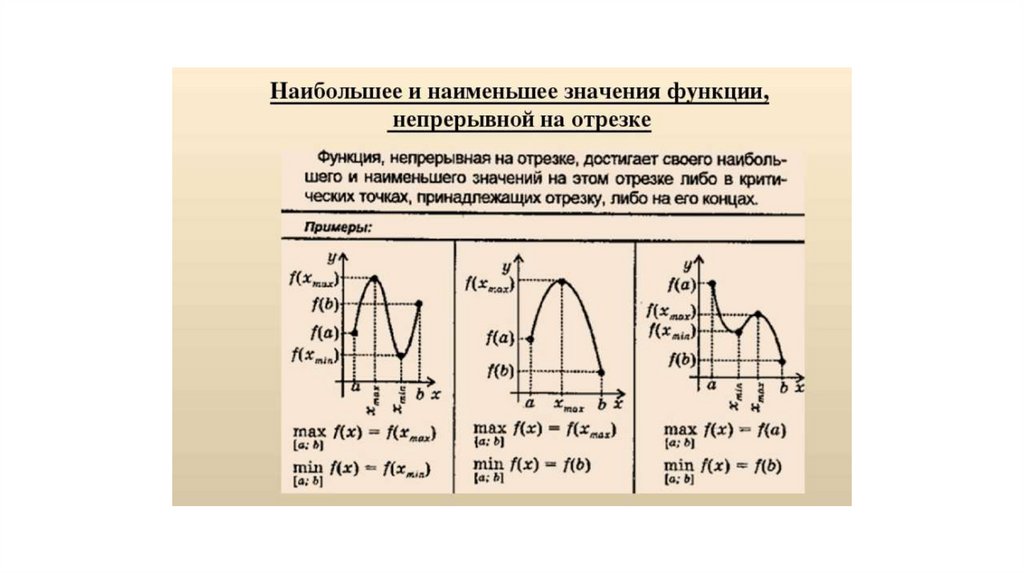
8) Точки экстремума . Точки минимума и точки максимума.
9) Стационарные точки и критические точки.
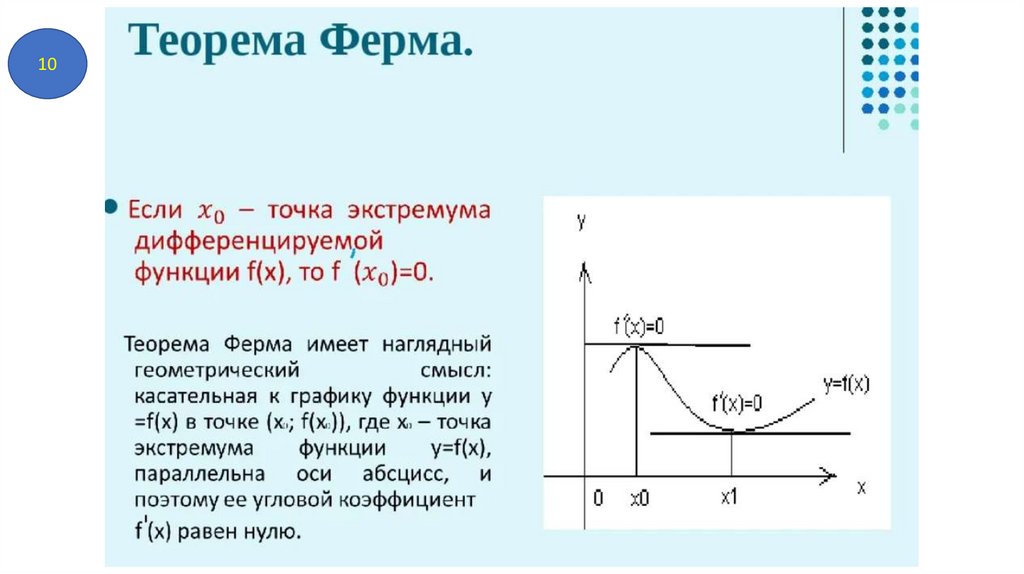
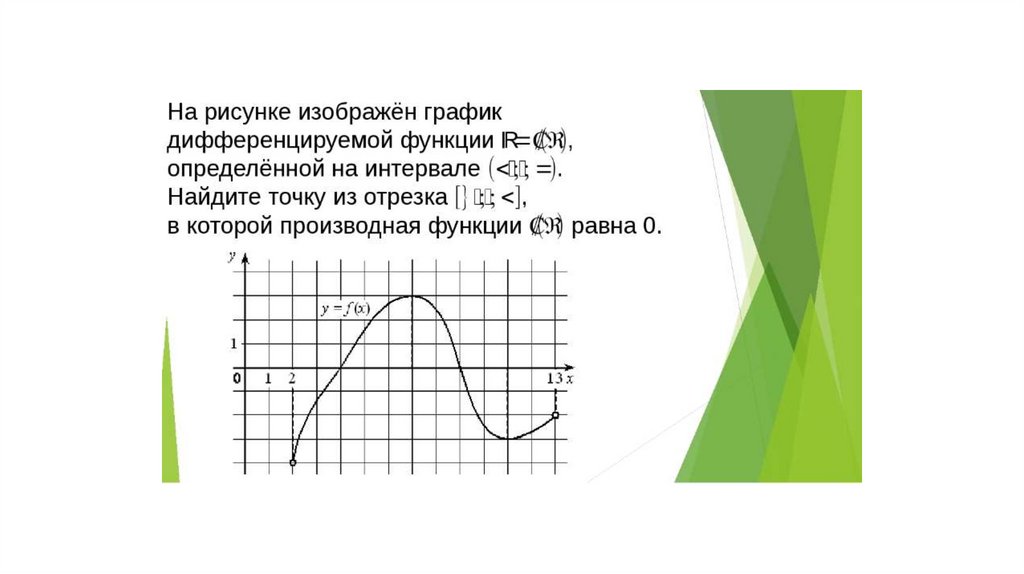
10) Теорема Ферма. Геометрический смысл теоремы Ферма.
11) Необходимое и достаточное условие Теоремы Ферма
Эта фотография, автор: Неизвестный автор,
лицензия: CC BY
2.
13.
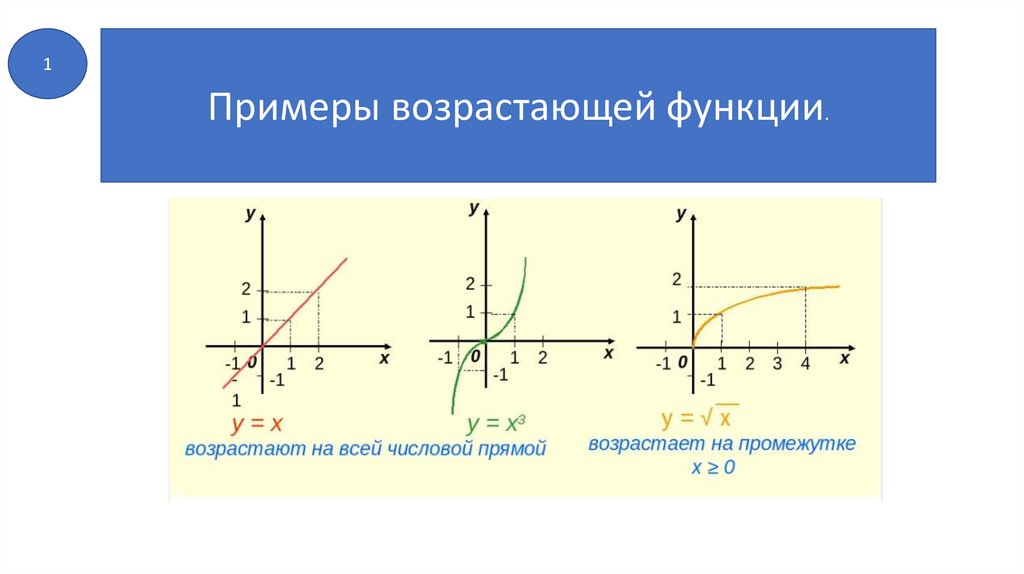
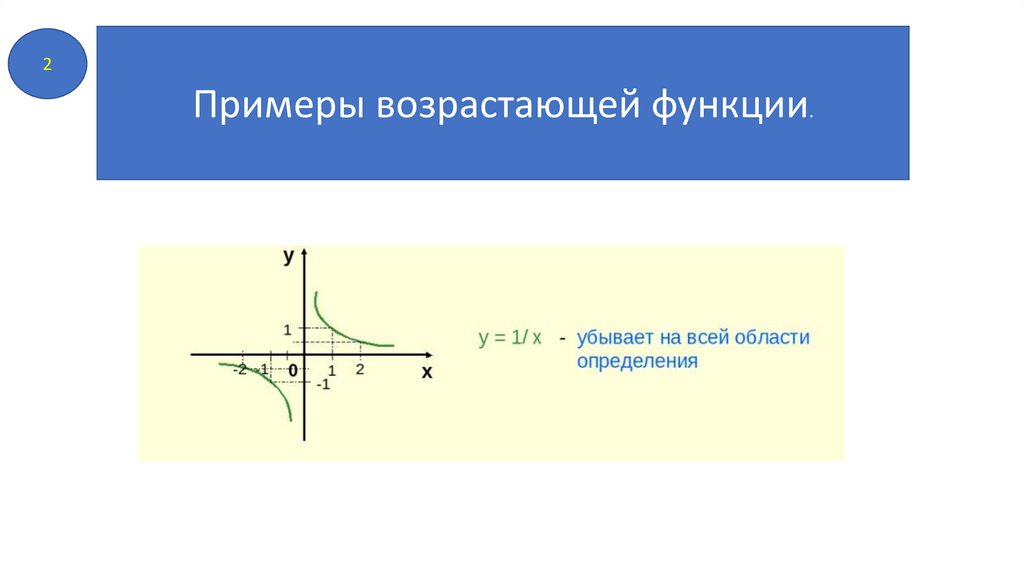
1Примеры возрастающей функции.
4.
15.
26.
2Примеры возрастающей функции.
7.
28.
39.
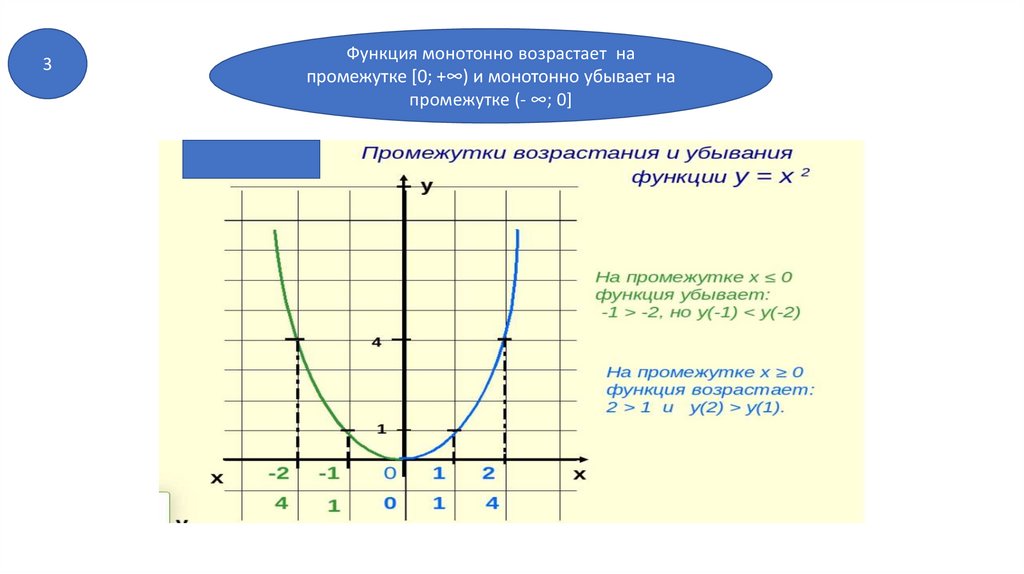
3Функция монотонно возрастает на
промежутке [0; +∞) и монотонно убывает на
промежутке (- ∞; 0]
10.
3Монотонно возрастающие
степенные функции
Монотонно убывающая
степенная функция
11.
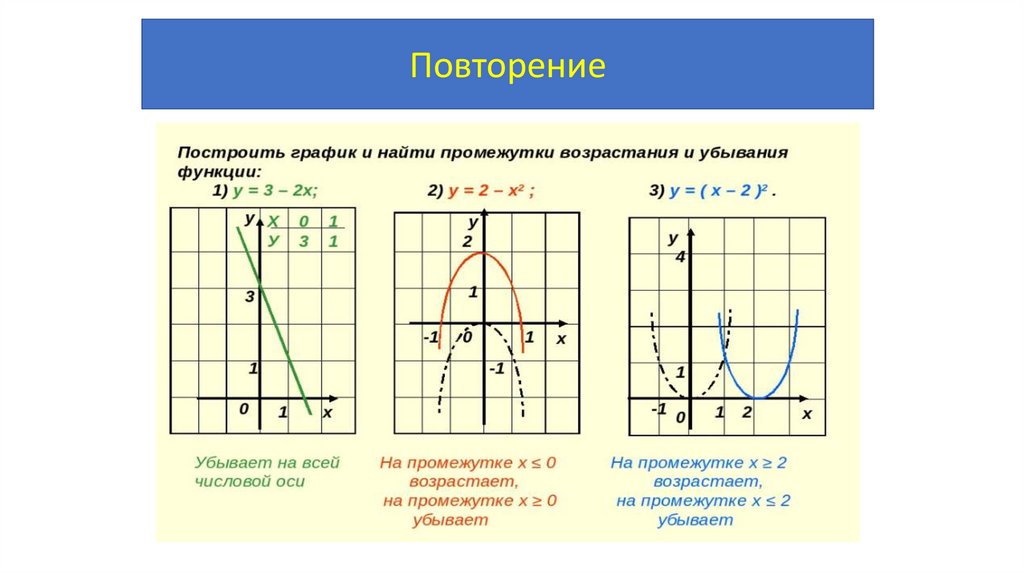
Повторение12.
Повторение13.
414.
415.
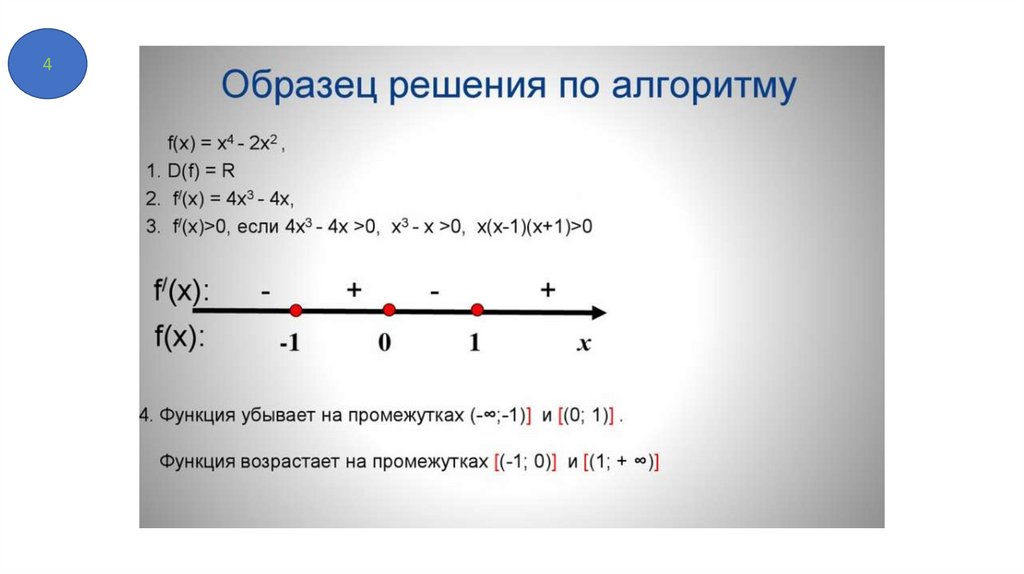
4Алгоритм нахождения промежутков монотонности
функции.
16.
417.
Повторение18.
Повторение19.
20.
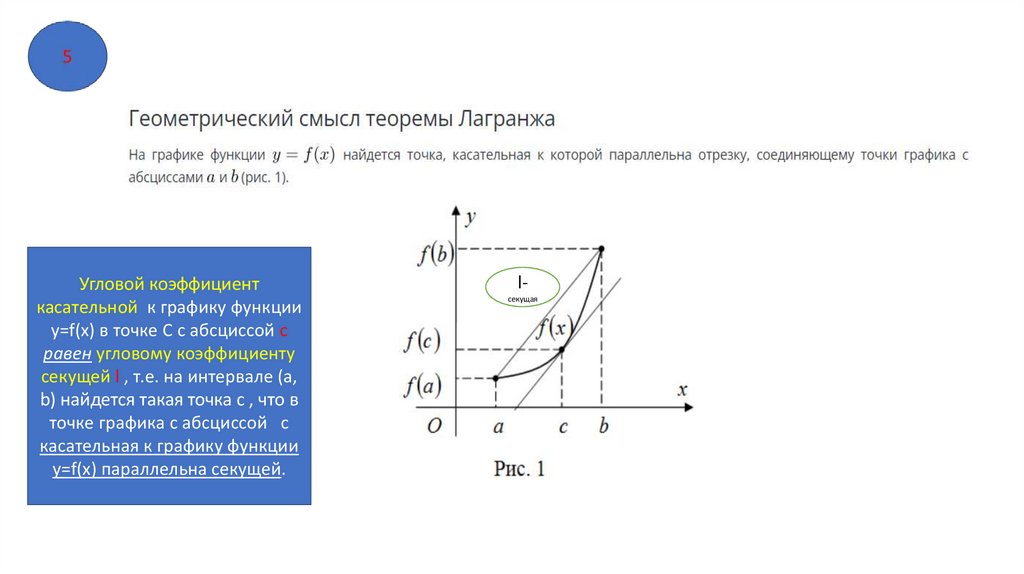
Угловой коэффициенткасательной к графику функции
у=f(x) в точке С с абсциссой с
равен угловому коэффициенту
секущей l , т.е. на интервале (а,
b) найдется такая точка с , что в
точке графика с абсциссой с
касательная к графику функции
у=f(x) параллельна секущей.
lсекущая
21.
22.
23.
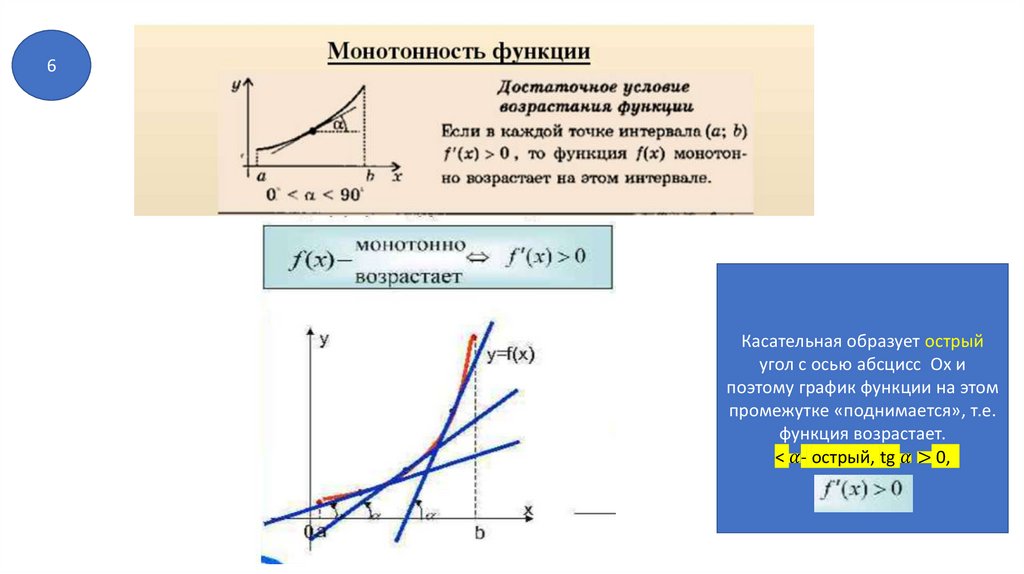
624.
6Касательная образует острый
угол с осью абсцисс Ох и
поэтому график функции на этом
промежутке «поднимается», т.е.
функция возрастает.
<



















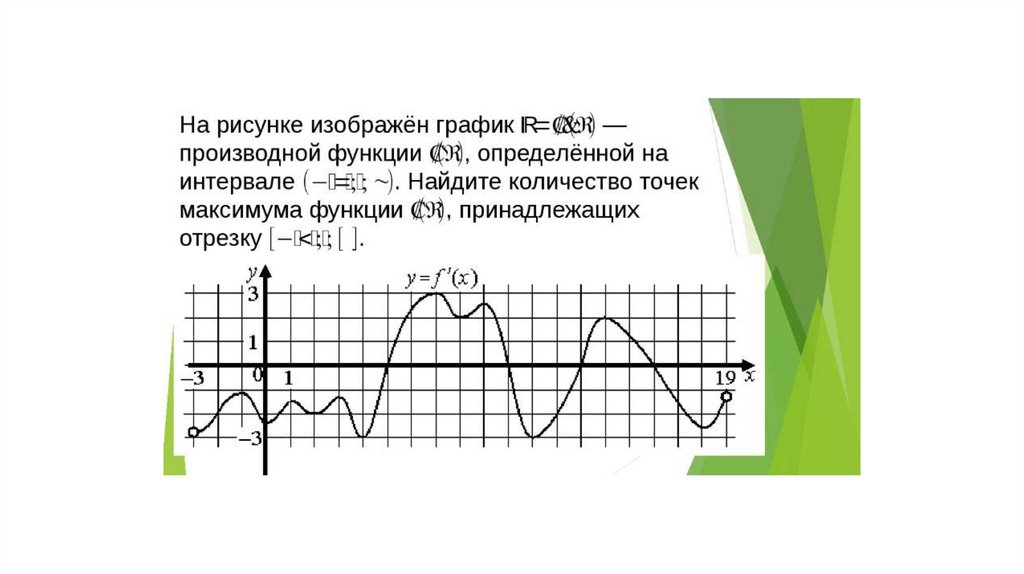
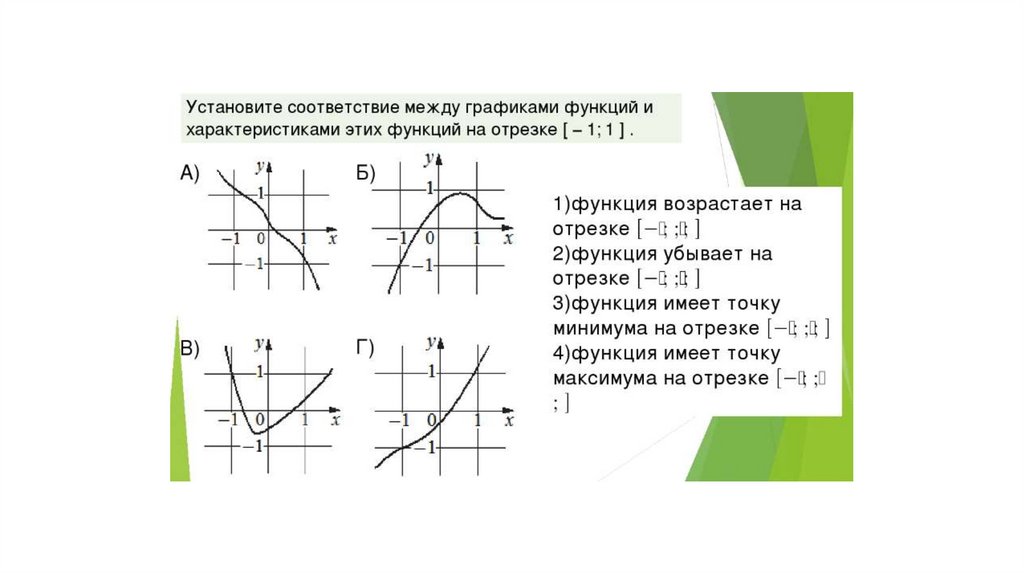

 Математика
Математика








