Похожие презентации:
Основы обеспечения отказоустойчивости ПК. Тема 2
1. Основы обеспечения отказоустойчивости ПК
Показатели безотказности2. Основные показатели безотказности
•вероятность безотказной работы;•плотность распределения отказов;
•интенсивность отказов;
•средняя наработка до отказа.
3. Схема испытаний
• Пусть на испытания поставлено Nодинаковых серийных объектов.
• T = {0, t1, … tN } = {t} – случайная величина
наработки объекта до отказа;
• N(t) – число объектов, работоспособных к
моменту наработки t;
• n(t) – число объектов, отказавших к моменту
наработки t;
• Δn(t, t +Δt) – число объектов, отказавших в
интервале наработки [t, t +Δt ];
• Δt – длительность интервала наработки.
4. 1. Вероятность безотказной работы
Статистическая оценкаN (t )
ˆ
P (t )
N
Поскольку N(t) = N - n(t), то
n(t )
ˆ
P(t ) 1
1 Qˆ (t )
N
5.
Вероятностное определениеP(t ) P{T t}
Q(t ) P{T t}
P(t ) P(t t )
Q(t , t t ) 1 P(t , t t )
P(t )
6. 2. Плотность распределения отказов
Статистическая оценкаˆf (t ) n(t , t t) [ед.наработки 1 ]
N t
Поскольку Δ n ( t, t + Δt ) = n ( t + Δt ) - n(t)
ˆ (t , t t )
n
(
t
t
)
n
(
t
)
1
Q
fˆ (t )
(Qˆ (t t ) Qˆ (t ))
N t
t
t
7.
Вероятностное определениеQˆ (t , t t ) dQ(t ) d[1 P(t )]
dP(t )
f (t ) lim
t
dt
dt
dt
t 0
Поскольку Q(t) = P{T < t}, то
t
Q(t ) P{0 T t} P{T (0, t )} f (t )dt
0
P(t ) P{t T } f (t )dt
t
t
0
0
t
f (t )dt f (t )dt f (t )dt Q(t ) Р(t ) 1
8. 3. Интенсивность отказов
Статистическая оценкаn(t , t t )
ˆ
(t )
[ед.наработки 1]
N (t ) t
Вероятностная оценка
n(t , t t ) N n(t , t t ) N
ˆ
(t )
N (t ) t
N
N t
N (t )
ˆ (t , t t ) 1
Q
ˆ (t )
t
Pˆ (t )
Qˆ (t , t t ) 1
dQ(t ) 1
f (t )
(t ) lim
t
dt P (t ) P (t )
t 0
Pˆ (t )
9. Уравнение связи показателей надежности
f (t )(t )
P (t )
dP (t ) dt (t ) P (t )
умножив обе части на dt / P(t), получим
dP(t) / P(t) = -λ(t) dt.
Интегрируя от 0 до t и принимая во внимание, что при t= 0 ВБР
объекта P(0) = 1, получаем
t
t
dP(t )
0 P(t ) ln P(t ) 0| ln P(t ) 0 (t )dt
t
10. Откуда уравнение связи основных показателей надежности имеет вид:
tP(t ) exp{ (t )dt}
0
Величина λ (t) dt – есть вероятность того, что элемент,
безотказно проработавший в интервале наработки [0, t],
откажет в интервале [t, t + dt].
Уравнение связи показывает, что все показатели надежности
P(t), Q(t), f(t) и λ (t) равноправны в том смысле, что зная один
из них, можно определить другие.
11. 4. Средняя наработка до отказа
Статистическая оценка1
ˆ
T0
N
N
t
i
1
где ti – наработка до отказа i-го объекта.
При вероятностном определении средняя наработка до
отказа представляет собой математическое
ожидание (МО) случайной величины T и
определяется:
T0 M {T } t f (t )dt
0
12. Используя выражение для плотности распределения отказов
dP(t )f (t )
dt
и интегрирование по частям
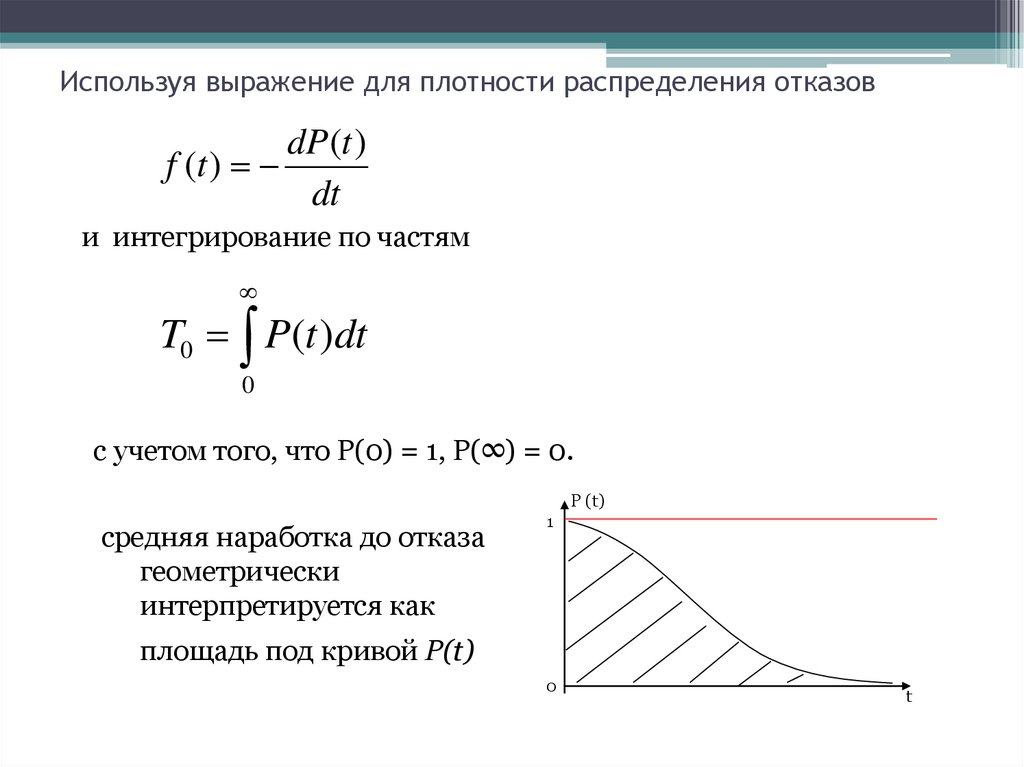
T0 P(t )dt
0
с учетом того, что P(0) = 1, P(∞) = 0.
P (t)
средняя наработка до отказа
геометрически
интерпретируется как
1
площадь под кривой P(t)
0
t
13.
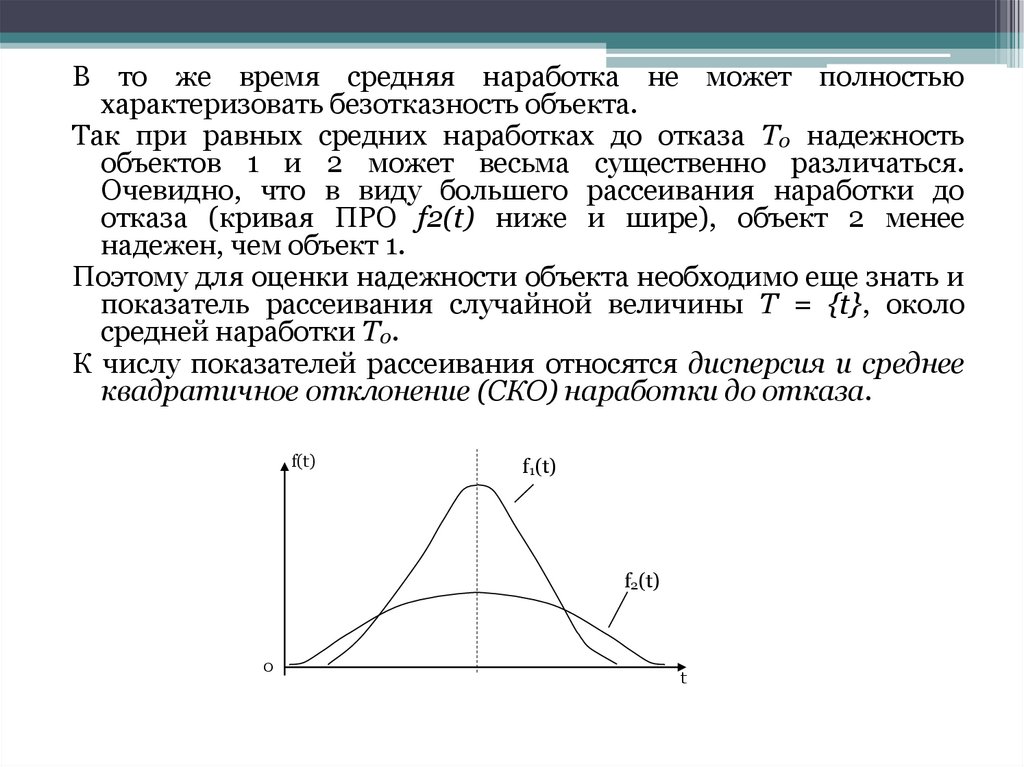
В то же время средняя наработка не может полностьюхарактеризовать безотказность объекта.
Так при равных средних наработках до отказа T0 надежность
объектов 1 и 2 может весьма существенно различаться.
Очевидно, что в виду большего рассеивания наработки до
отказа (кривая ПРО f2(t) ниже и шире), объект 2 менее
надежен, чем объект 1.
Поэтому для оценки надежности объекта необходимо еще знать и
показатель рассеивания случайной величины T = {t}, около
средней наработки T0.
К числу показателей рассеивания относятся дисперсия и среднее
квадратичное отклонение (СКО) наработки до отказа.
f(t)
f1(t)
f2(t)
0
t
14.
Дисперсия случайной величины наработки:статистическая оценка
N
1
2
ˆ
Dˆ
(
t
T
)
i
0
N 1 1
вероятностное определение
D D{T } M {(T T0 ) 2 } (t T0 ) 2 f (t )dt
0
СКО случайной величины наработки:
ˆ
Sˆ 2 D
S 2 D{T }
Средняя наработка до отказа T0 и СКО наработки S имеют
размерность [ед. наработки], а дисперсия D - [ед. наработки2].












 Информатика
Информатика