Похожие презентации:
Моделирование и основы системного анализа. Модели и элементы теории систем. (Часть 1)
1.
Ульяновский государственный университетКумунжиев К.В.
МОДЕЛИРОВАНИЕ И ОСНОВЫ
СИСТЕМНОГО АНАЛИЗА
Краткий конспект лекций
Часть 1: Модели и элементы теории систем
1
2.
Ульяновск - 20092
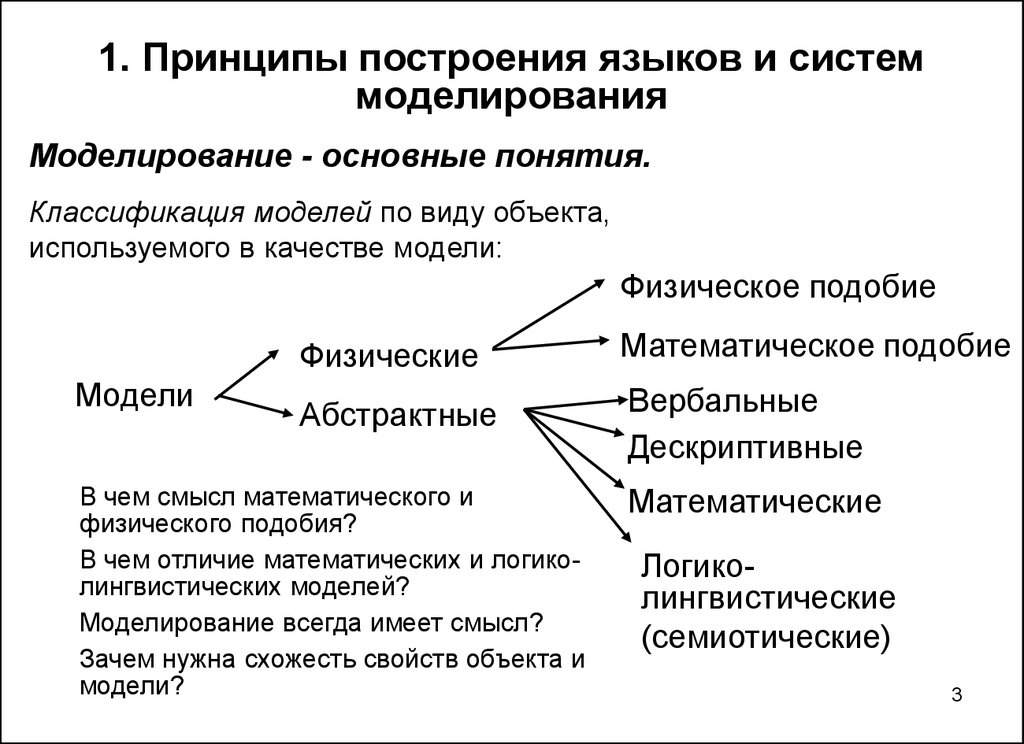
3. Классификация моделей по виду объекта, используемого в качестве модели:
1. Принципы построения языков и системмоделирования
Моделирование - основные понятия.
Классификация моделей по виду объекта,
используемого в качестве модели:
Физическое подобие
Модели
Физические
Математическое подобие
Абстрактные
Вербальные
Дескриптивные
В чем смысл математического и
физического подобия?
В чем отличие математических и логиколингвистических моделей?
Моделирование всегда имеет смысл?
Зачем нужна схожесть свойств объекта и
модели?
Математические
Логиколингвистические
(семиотические)
3
4.
Классификация моделей по характеру связи междувходами и выходами:
-Кибернетические (элементные) модели:
- Имитационные (системные) модели:
- Имитационное моделирование?
Модель – стратифицированное описание объекта??
Общение - двусторонний процесс передачи с определенными
целями связных сведений о некотором мире, реальном или
гипотетическом, Сведения передаются в виде текстов на языке
общения от одного участника (автора) к другому (адресату) при
условии понятности этих сведений для автора и адресата.
- Какие факторы влияют на «понятность» сведений?
Проранжируйте их по степени влияния?
- Как выглядит схема общения человек-компьютер? Есть ли что-то общее со схемой человек-человек? Если
4
есть, в чем особенности?
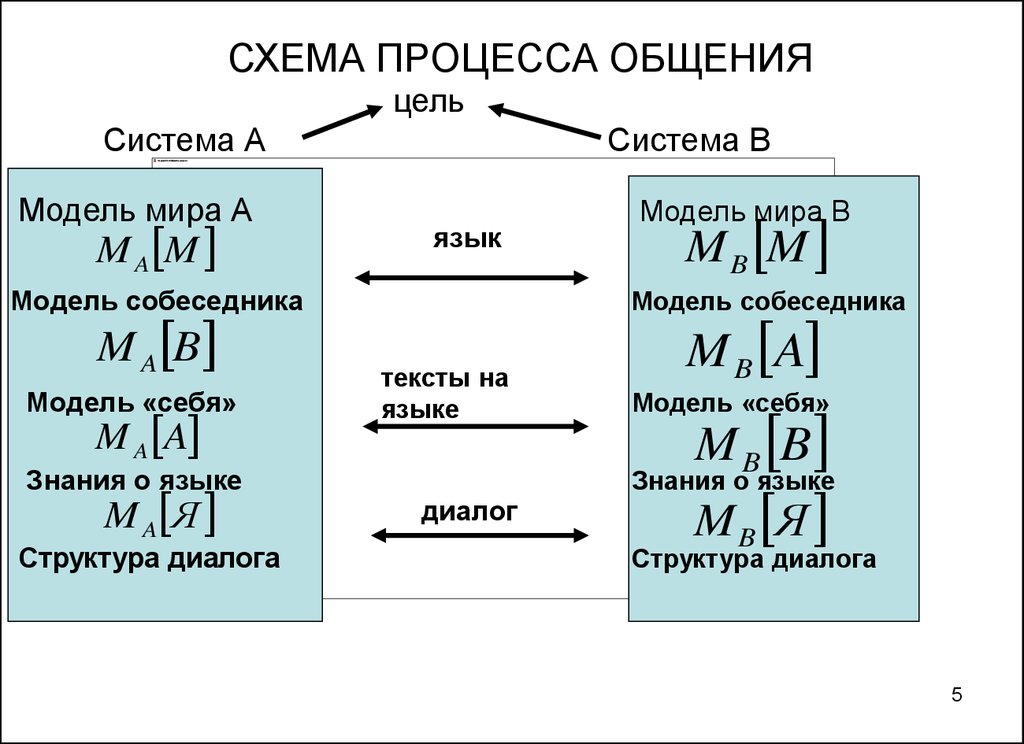
5. СХЕМА ПРОЦЕССА ОБЩЕНИЯ
цельСистема А
Модель мира А
M A M
Система B
язык
Модель собеседника
M A B
Модель «себя»
M A A
Структура диалога
M B M
Модель собеседника
тексты на
языке
Знания о языке
M A Я
Модель мира В
M B A
Модель «себя»
M B B
Знания о языке
диалог
M B Я
Структура диалога
5
6. Формализация знаний
Элемент - часть системы, не подлежащая дроблениюв условиях данной задачи.
- Два типа элементов: неопределяемый, определяемый?
-Правила композиции: синтаксические, семантические?
- Формальная система: что это? в чем ее ценность?
- Общая схема построения языка описания моделей?
- Какими средствами должен располагать язык описания
моделей?
- Что означает «вторичность» языка описания?
- Что подтверждает построение естественного языка по той
же схеме??
- Возможности модели в зависимости от степени
проработки класса?
6
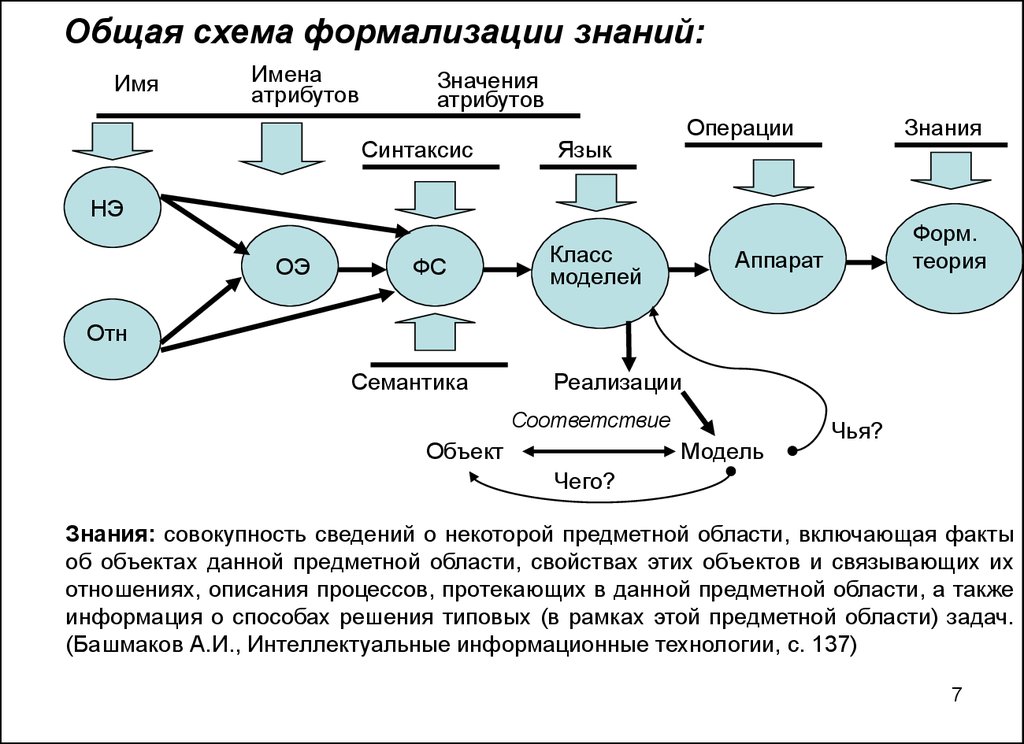
7. Общая схема формализации знаний:
ИмяИмена
атрибутов
Значения
атрибутов
Синтаксис
Операции
Язык
Знания
НЭ
ОЭ
ФС
Класс
моделей
Форм.
теория
Аппарат
Отн
Семантика
Реализации
Соответствие
Объект
Модель
Чья?
Чего?
Знания: совокупность сведений о некоторой предметной области, включающая факты
об объектах данной предметной области, свойствах этих объектов и связывающих их
отношениях, описания процессов, протекающих в данной предметной области, а также
информация о способах решения типовых (в рамках этой предметной области) задач.
(Башмаков А.И., Интеллектуальные информационные технологии, с. 137)
7
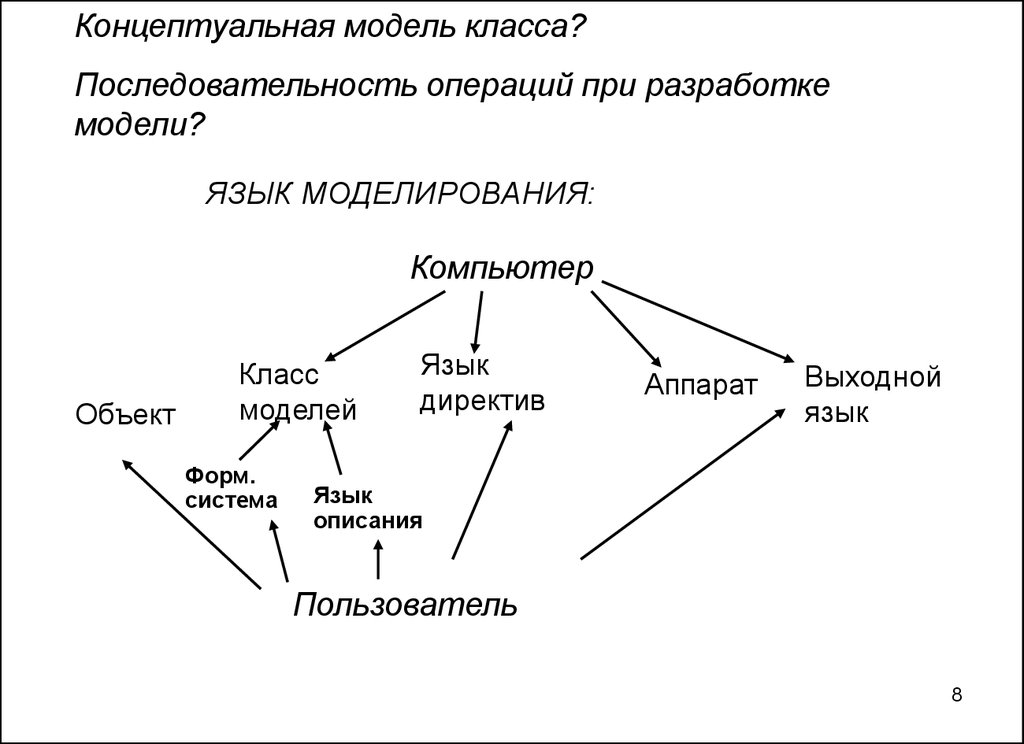
8. ЯЗЫК МОДЕЛИРОВАНИЯ:
Концептуальная модель класса?Последовательность операций при разработке
модели?
ЯЗЫК МОДЕЛИРОВАНИЯ:
Компьютер
Объект
Класс
моделей
Форм.
система
Язык
директив
Аппарат
Выходной
язык
Язык
описания
Пользователь
8
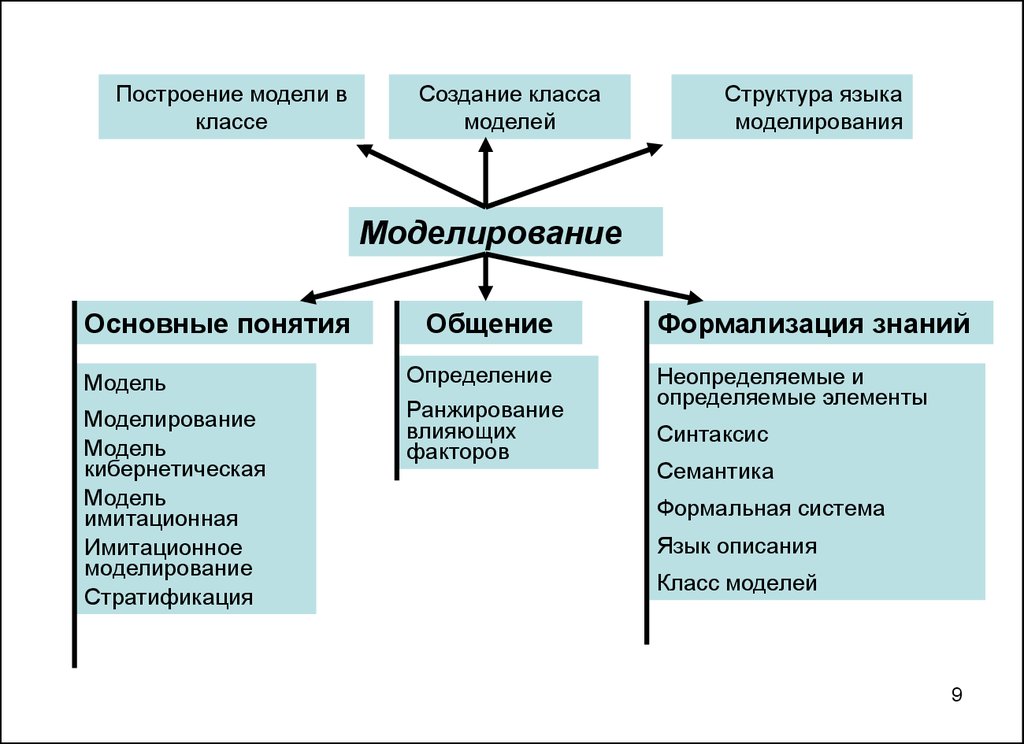
9.
Построение модели вклассе
Создание класса
моделей
Структура языка
моделирования
Моделирование
Основные понятия
Общение
Модель
Определение
Моделирование
Модель
кибернетическая
Модель
имитационная
Имитационное
моделирование
Стратификация
Ранжирование
влияющих
факторов
Формализация знаний
Неопределяемые и
определяемые элементы
Синтаксис
Семантика
Формальная система
Язык описания
Класс моделей
9
10.
Контрольные вопросы1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
Определите понятия модель, моделирование?
Что такое кибернетическая модель?
Что такое имитационная модель?
Как формально описывается элемент?
Что такое неопределяемый элемент?
Что такое определяемый элемент?
Раскройте понятие: синтаксические правила композиции?
Раскройте понятие семантические правила композиции?
Определите понятие формальная система?
Какое свойство формальной системы обеспечивает ее широкое применение?
Что такое реализация в формальной системе?
При каких условиях реализация может использоваться как модель некоторого
объекта?
Какую информацию необходимо передать средствами языка описания модели?
Как выглядит общая схема процесса структуризации и формализации знаний?
Как строится модель в классе?
Как выглядит процесс построения класса моделей применительно к некоторой
предметной области?
Чем подтверждаются вторичность по отношению к реальности и договорной характер
естественного языка?
Определите понятие язык моделирования?.
10
11.
2. Алгебро-дифференциальные уравнения каккласс моделей
Системы
Непрерывные
Системы с расп.
параметрами
Уравнения
матфизики
Дискретные
Системы с соср.
параметрами
Обыкнов.
АДУ
Синхронные
системы
Конечные
автоматы
Асинхронные
системы
Сети Петри,
Стейтчарты,
СМО
11
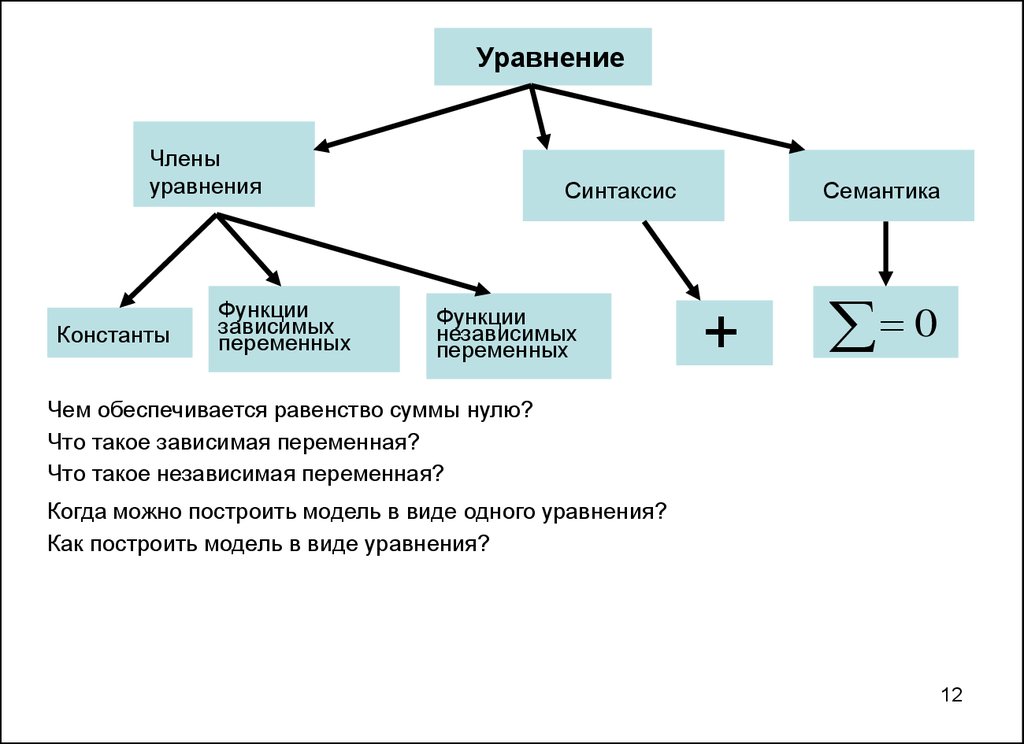
12.
УравнениеЧлены
уравнения
Константы
Функции
зависимых
переменных
Синтаксис
Функции
независимых
переменных
Семантика
+
0
Чем обеспечивается равенство суммы нулю?
Что такое зависимая переменная?
Что такое независимая переменная?
Когда можно построить модель в виде одного уравнения?
Как построить модель в виде уравнения?
12
13. Формы записи линейных уравнений:
Аналитическое решение дифференциальныхуравнений.
Как классифицируют уравнения по виду коэффициентов при
зависимых переменных:
- Принцип суперпозиции – что это? Для каких систем он
справедлив? В чем его ценность?
dy1
a11 y1 ..... a1n yn f1 ( x )
Формы записи линейных
dt
уравнений:
dY
dy
AY F
dt
n an1 y1 ..... ann yn f n ( x )
dt
an y n an 1 y n 1 ... a0 y bm x m ... b0 x
Как перейти от одной формы записи к другой??
Переменные
x
и y в уравнениях – чем они отличаются??
13
14. СИСТЕМЫ ПЕРВОГО ПОРЯДКА
a1dy
a0 y x
dt
a1 p a0 0;
p 1 0; a1 / a0 ;
p
1
,
A
y
a0
t
1 e
1
p ,
Где на этих рисунках установившееся (вынужденное) и собственное
движение??
14
15. СИСТЕМЫ ВТОРОГО ПОРЯДКА
2a2
d y
dy
a
a 0 y x (t )
1
2
dt
dt
a 2 p 2 a1 p a 0 0;
2
p1, 2
a
a
a1
2
1 0 2 0 ,
2a 2
a2
2a 2
2
2
0
y y уст 1 e t
sin 02 2 t arctg 0 2
02 2
- При каких условиях переходный процесс будет
колебательным? апериодическим?
-Поясните физический и математический смысл перехода
от колебательного движения к апериодическому и
обратно??
- Собственная частота, показатель затухания, степень
успокоения – что это?
15
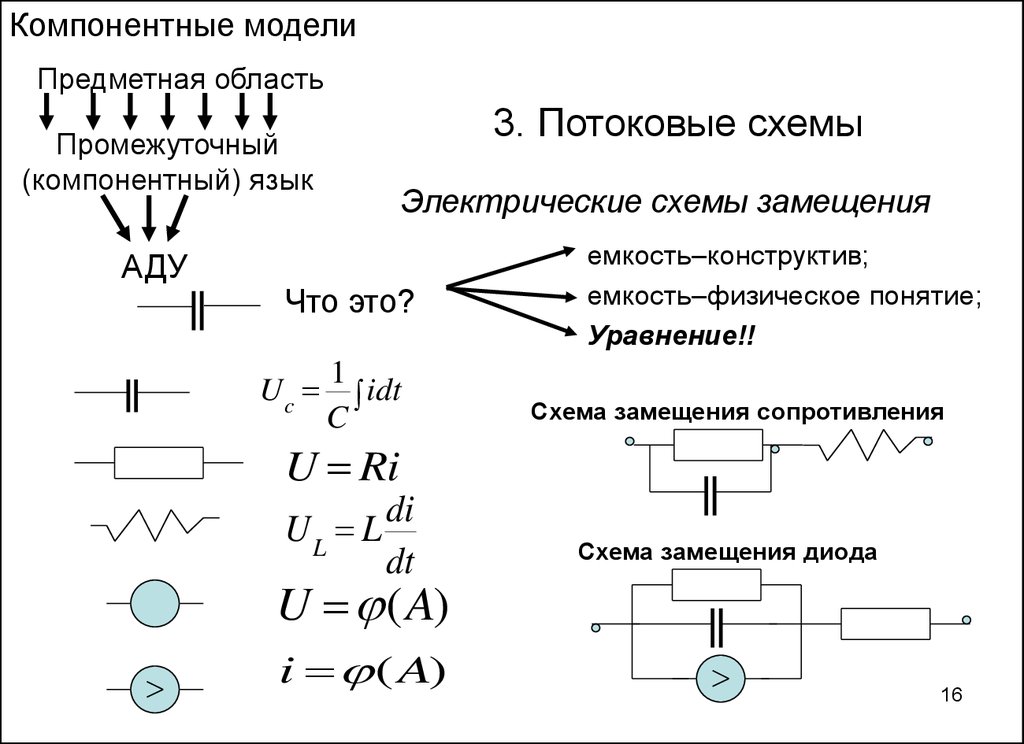
16. Электрические схемы замещения
Компонентные моделиПредметная область
3. Потоковые схемы
Промежуточный
(компонентный) язык
АДУ
Электрические схемы замещения
Что это?
Uc
1
idt
C
емкость–конструктив;
емкость–физическое понятие;
Уравнение!!
Схема замещения сопротивления
U Ri
UL L
di
dt
Схема замещения диода
U (A)
i ( A)
16
17. Гидравлические схемы
P f (t)Источник давления:
q f (t)
Источник расхода:
Гидравлическое сопротивление
q 1 Rг *( P1 P2 )
q 1 Rг *( P1 P2 )1 2
- ламинарный режим;
- турбулентный режим.
( P1 P2 ) 1 Cг * qdt Гидравлическая емкость
( P1 P2 ) m
P1
P2
d
dt
Гидравлическая
индуктивность
17
18.
Неопределяемые элементы: МатематическиеРазностная переменная
Потоковая переменная
Параметры K , R, P, A
№
Тип
операции
df
Графический
знак
di
f
, , /,*,
dj
Уравнение
1
Y
f ij 0
Y
2
D
di d j A
E
3
P
d i d j P fdt
4
R
d i d j Rf
R
5
K
d i d j Kdf / dt
L
6
F
f ij A
I
7
Z
di d j 0
Z
1/C
18
19.
Правила композиции:1. Все элементы соединяются в узлах, значение разностной
переменной для всех соединяемых в узле переменных
одинаково.
2. Каждый элемент присоединяется к двум узлам;
соответственно, схема содержит только замкнутые контура.
3. Для каждого узла выполняется
условие
4. Для каждого контура выполняется
условие
f
i
0
(d
i
dj) 0
5. Запрещено последовательное соединение элементов
типа D и параллельное соединение элементов типа F .
Что явилось основанием для введения правил 3 и 4??
Откуда следуют правило 5??
19
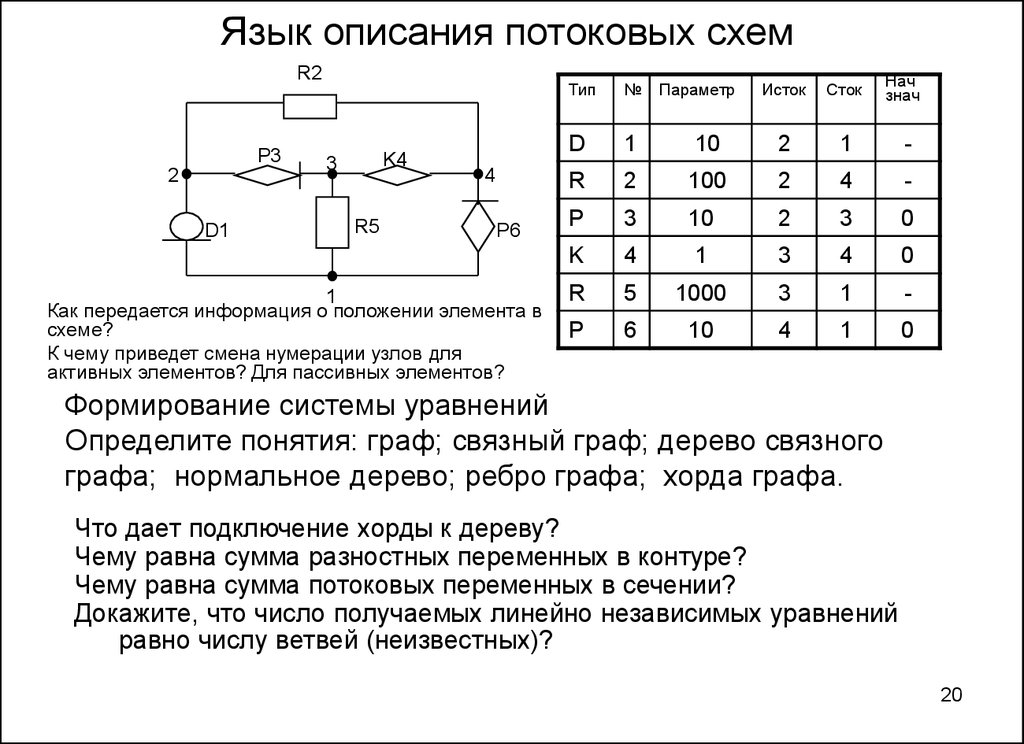
20. Язык описания потоковых схем
R2P3
2
D1
K4
3
R5
4
P6
1
Как передается информация о положении элемента в
схеме?
К чему приведет смена нумерации узлов для
активных элементов? Для пассивных элементов?
Тип
№
D
1
R
Параметр
Нач
знач
Исток
Сток
10
2
1
-
2
100
2
4
-
P
3
10
2
3
0
K
4
1
3
4
0
R
5
1000
3
1
-
P
6
10
4
1
0
Формирование системы уравнений
Определите понятия: граф; связный граф; дерево связного
графа; нормальное дерево; ребро графа; хорда графа.
Что дает подключение хорды к дереву?
Чему равна сумма разностных переменных в контуре?
Чему равна сумма потоковых переменных в сечении?
Докажите, что число получаемых линейно независимых уравнений
равно числу ветвей (неизвестных)?
20
21.
Контрольные вопросы:1. Что такое потоковая схема?
2. Перечислите базовый набор элементов потоковой схемы и приведите их математическое
описание?
3. Назовите правила композиции для потоковых схем?
4. Почему нельзя включать параллельно элементы типа D, последовательно элементы типа
F?
5. Как в языке описания потоковых схем передаётся информация о наборе элементов и их
соединении в схеме?
6. Что означает в языке описания потоковых схем смена исток-сток?
7. Как преобразовать потоковую схему в систему уравнений?
8. Что такое граф, связный граф, дерево графа, сечение графа?
9. Какие элементы потоковой схемы должны входить в дерево? Не могут входить в дерево?
10. Чему в потоковой схеме равно число рёбер в дереве графа? Число хорд?
11. Схемы LR, RC: покажите, что это уравнения 1 порядка; их постоянные времени?
12. Как выглядит реакция LR и RC цепей на стандартные испытательные сигналы?
13. RLC цепь: покажите, что она описывается уравнением 2 порядка?
14. RLC цепь: чему равны показатель затухания, степень успокоения и собственная частота
цепи?
15. Как выглядит реакция RLC цепи на стандартные испытательные сигналы?
21
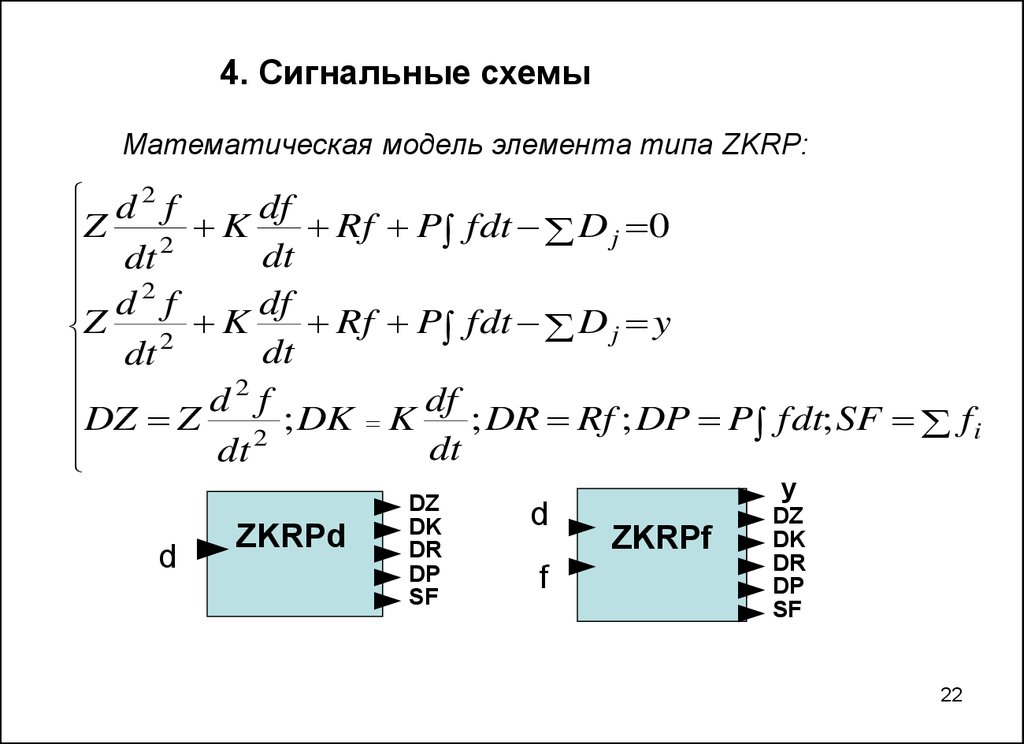
22.
4. Сигнальные схемыМатематическая модель элемента типа ZKRP:
2
d
f
df
Z
K
Rf P fdt D j 0
2
dt
dt
2
df
d f
Z
K
Rf P fdt D j y
2
dt
dt
2
d
f
df
DZ Z
;
DK
K
; DR Rf ; DP
2
dt
dt
d
ZKRPd
DZ
DK
DR
DP
SF
d
f
P fdt; SF f i
y
KRPd
ZKRPf
DZ
DK
DR
DP
SF
22
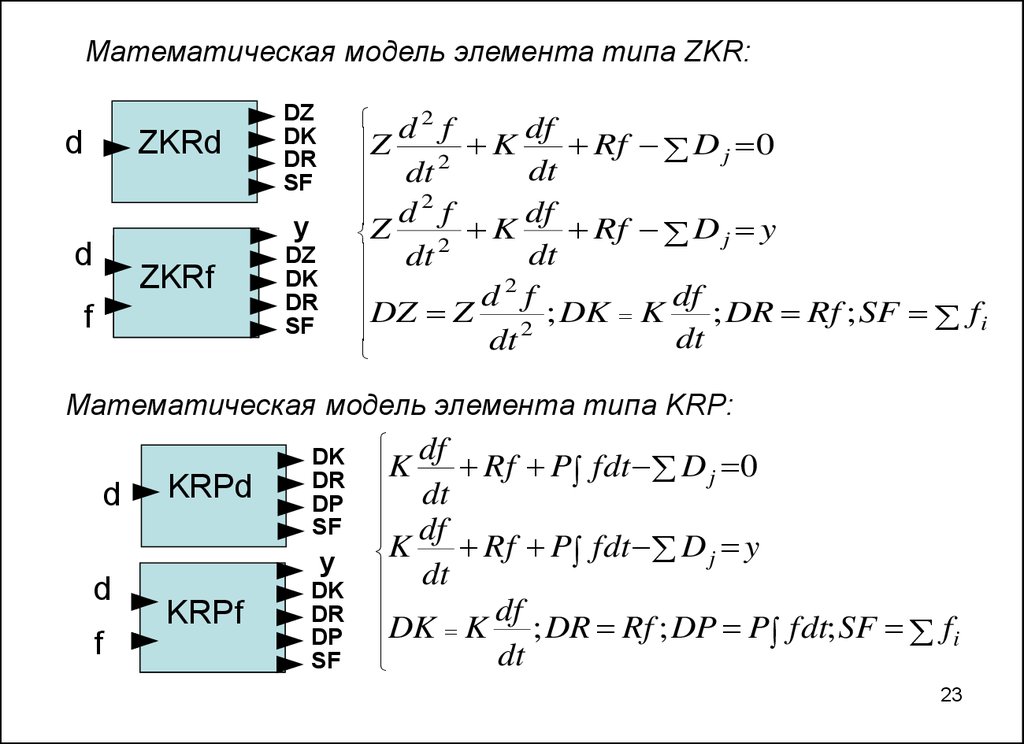
23.
Математическая модель элемента типа ZKR:d
ZKRd
DZ
DK
DR
SF
2
d
f
df
Z
K
Rf D j 0
2
dt
dt
2
df
d f
K
Rf D j y
Z
2
dt
dt
2
d
f
df
DZ Z
;
DK
K
; DR
2
dt
dt
y
d
ZKRf
KRPd
f
DZ
DK
DR
SF
Rf ; SF f i
Математическая модель элемента типа KRP:
d
d
f
KRPd
DK
DR
DP
SF
y
KRPf
KRPd
DK
DR
DP
SF
df
K
Rf P fdt D j 0
dt
df
Rf P fdt D j y
K
dt
df
DK
K
; DR Rf ; DP P
dt
fdt; SF fi
23
24.
dKRd
d
KRPd
KRf
f
Математическая модель элемента типа KR:
DK
df
DR
K
Rf D j 0
SF
dt
df
Rf D j y
K
y
dt
DK
DR
df
DK
K
; DR Rf ; SF f i
SF
dt
Математическая модель элемента типа RP:
d
RPd
y
d
RPf
KRPd
f
DR
DP
SF
DR
DP
SF
Rf P fdt D 0
j
Rf P fdt D j y
DR Rf ; DP P fdt; SF
fi
KRP , KR, KP, RP , K , R, P
24
25.
dy3d 2 y3
k1 y3 k 2 dt k 3 dt 2 1,5
dy4
k
4
y4 0,1
dt
Z=? K=? R=? d -?
y3 y5 y4
1.5
ZKRd
y3
SF
0.1
KRd
RPd
KRd
y5
y4
SF
Kg
m2
W
(f)
(f)
S
F
Kd
2
Q
SF
RPf
Y
+1
Kd
1
(d)
-1
K2: K=J2; D1=Mт; D2=RP2, y, +1
RP3: R=Kд; P=w; F1=K1,SF,+1;
F2=K2,SF,-1
Как найти:
+1
-1
(d)
K1: K=J1; D1=Mвр; D2=RP3, y, -1
m1
Q
(d)
Скорости масс? Силу пружины? Силу
демпфирования? Расстояние между грузами?
Как будут меняться скорости масс, если:
Сила Q – ступенчатый сигнал?
Сила Q – прямоугольник заданной
длительности и амплитуды?
25
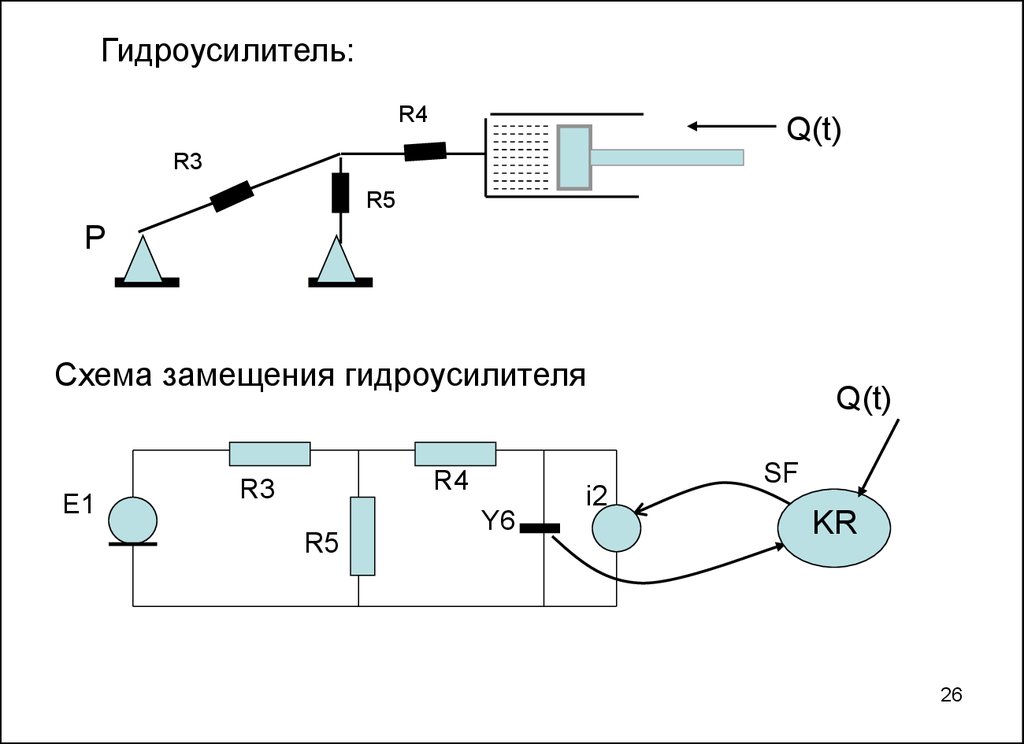
26.
Гидроусилитель:R4
Q(t)
R3
R5
P
Схема замещения гидроусилителя
E1
R4
R3
R5
Y6
i2
Q(t)
SF
KR
26
27.
Контрольные вопросы1. Какие отношения связывают понятия класс моделей, АДУ, потоковая
схема, сигнальная схема?
2. Как выглядит базовое уравнение класса моделей сигнальные схемы?
3. Какие входы и выходы может иметь элемент KRP класса сигнальные
схемы?
4. Дайте физическую интерпретацию выходов DK,DP,DR.SF,y подсистемы
KRP применительно к моделированию механических систем?
5. Дайте физическую интерпретацию входов D, F подсистемы сигнальной
схемы применительно к моделированию механических систем?
6. Как вводятся остальные (кроме подсистемы KRP) элементы класса
сигнальные схемы?
7. Опишите процесс построения модели в классе сигнальные схемы?
8. Что понимается под однокоординатной подсистемой?
9. Как определить в сигнальных схемах тип входа?
10. В каких случаях подсистемы в сигнальных схемах имеют выход типа
Y?
11. Как определить тип подсистемы в сигнальных схемах?
12. Какая информация должна содержаться в описании сигнальной
схемы?
27
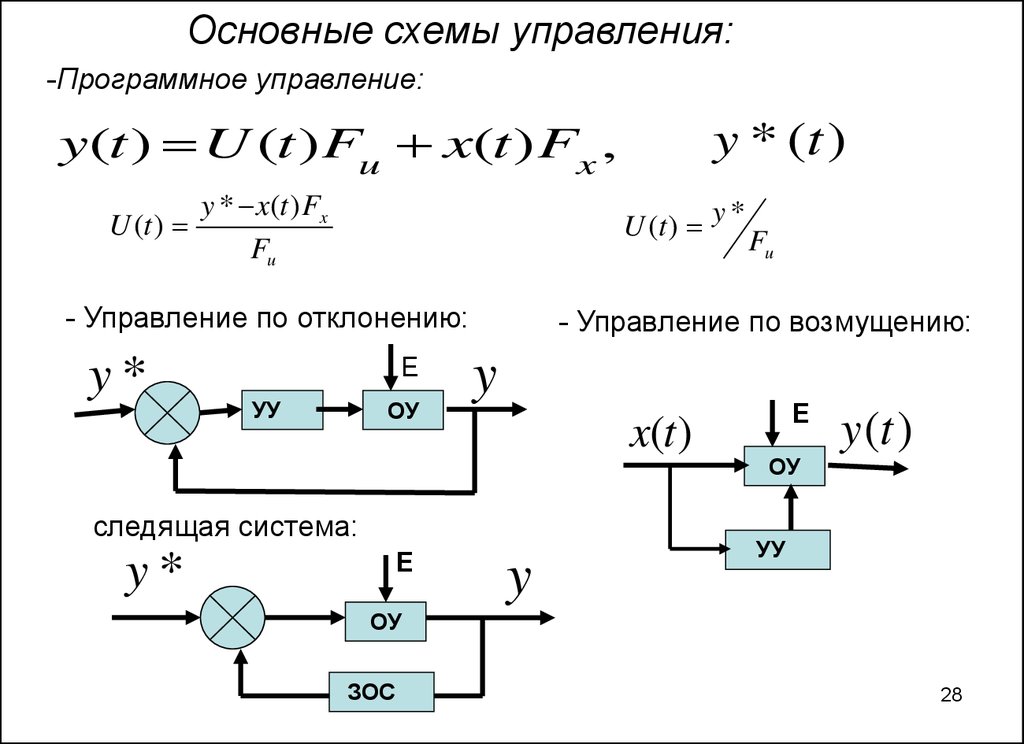
28. - Управление по отклонению:
Основные схемы управления:-Программное управление:
y(t ) U (t ) Fu x(t ) Fx ,
U (t )
y * x(t ) Fx
Fu
U (t ) y *
- Управление по отклонению:
y*
E
УУ
ОУ
E
Fu
- Управление по возмущению:
y
x(t )
следящая система:
y*
y * (t )
y
E
ОУ
y (t )
УУ
ОУ
ЗОС
28
29. 5.2 Операторный метод и передаточная функция
Преобразование Лапласа:f (t ) : t 0, f (t ) 0; p s j
f ( p) e pt f t dt,
1
f (t )
2 j
s j
pt
e
f ( p)dp
0
s j
- для большинства встречающихся на практике функций преобразование
Лапласа существует;
- для широкого класса функций интеграл Лапласа является регулярной
функцией от
;
p
- для заданного изображения соответствующий оригинал существует и
является единственным во всей области, за исключением точек разрыва.
Алгебраизация
ДУ
Решение
АУ
Обратное
преобразование
f ( p)
f (t )
Кроме того, существуют методы исследования систем,
основанные на представлении модели в операторной форме.
29
30.
Для алгебраизации линейного дифференциальногоуравнения с нулевыми начальными условиями необходимо:
dk
x(t ) x( p); y (t ) y ( p ); k p k
dt
Для широкого класса линейных систем:
dn
dm
(an n ... a0 ) y (t ) (bm m ... b0 ) x(t )
dt
dt
(an p n ... a0 ) y ( p ) (bm p m ... b0 ) x ( p )
Передаточная функция:
y ( p) Q( p)
W ( p)
,
x ( p ) P( p )
где
P( p) an p n ... a0 ;
Q( p) bm p m ... b0 ;
30
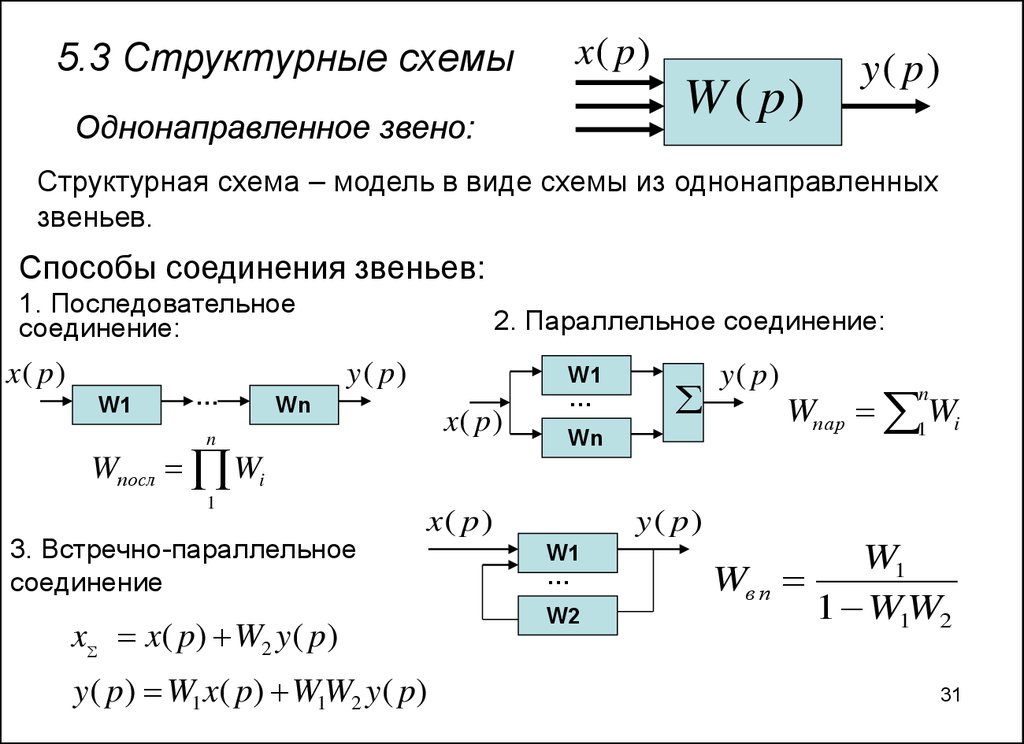
31.
5.3 Структурные схемыx( p)
W ( p)
Однонаправленное звено:
y( p)
Структурная схема – модель в виде схемы из однонаправленных
звеньев.
Способы соединения звеньев:
1. Последовательное
соединение:
x( p)
W1
…
2. Параллельное соединение:
y( p)
Wn
x( p)
n
Wпосл Wi
1
3. Встречно-параллельное
соединение
W1
…
Wn
x( p)
x x( p) W2 y( p)
y ( p) W1 x( p) W1W2 y( p)
y( p)
Wпар 1Wi
n
y( p)
W1
…
W2
W1
Wв п
1 W1W2
31
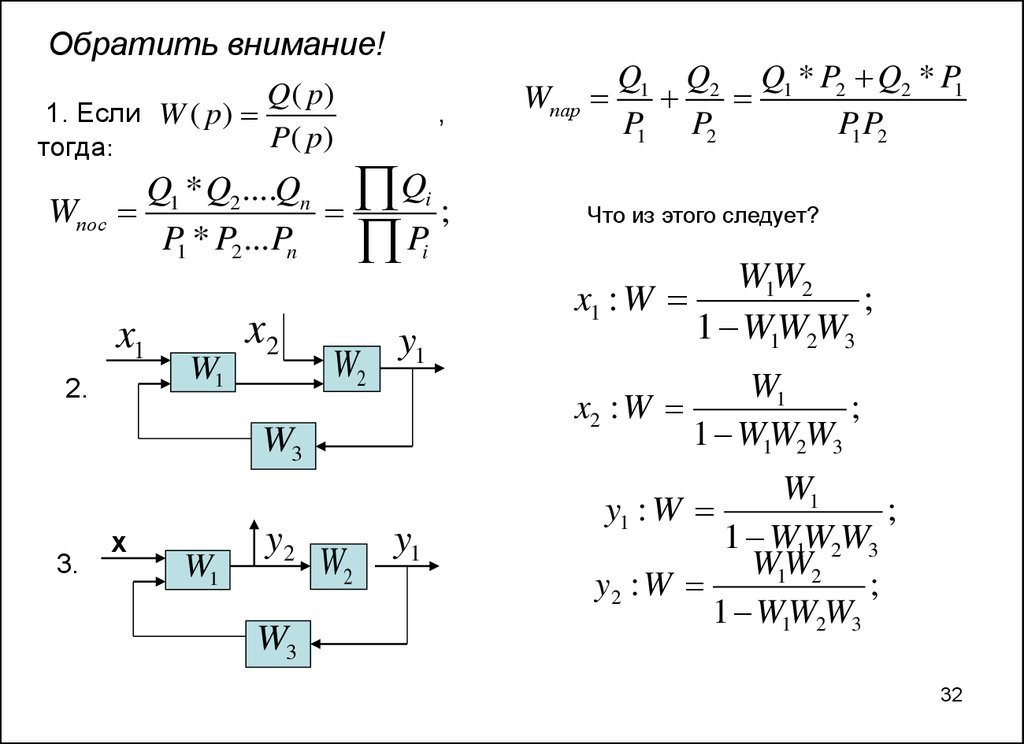
32.
Обратить внимание!Q( p)
1. Если W ( p )
P( p )
тогда:
,
Q1 * Q2 ....Qn Qi
Wпос
;
P1 * P2 ...Pn
Pi
x1
2.
W1
x2
W2
y1
3.
W1
y2
W3
W2
Q1 Q2 Q1 * P2 Q2 * P1
P1 P2
P1P2
Что из этого следует?
W1W2
x1 : W
;
1 W1W2W3
x2 : W
W3
x
Wпар
y1
W1
;
1 W1W2W3
W1
;
1 W1W2W3
W1W2
y2 : W
;
1 W1W2W3
y1 : W
32
33.
Основные динамические звенья:1. Динамическое звено общего вида:
(an p n ... a0 ) y ( p) (bm p m ... b0 ) x( p);
2.Апериодическое звено
( a1 p a0 ) y ( p ) b0 x ( p ); W
3. Дифференцирующее звено:
( a1 p a0 ) y ( p ) b1 x ( p ); W
4. Интегратор:
5.Усилитель
6. Сумматор:
bm p m ... b0
W ( p)
;
n
an p ... a0
k
a
; k b0 / a0 ; 0 .
p 1
b0
kp
b
a
; k 1 ; 1 .
p 1
a0
a0
( a1 p ) y ( p ) b0 x ( p ); W
k
b
;k 0 .
p
a1
b
a0 y ( p ) b0 x ( p );W k ; k 0 .
a0
y xi ;
7. Звено запаздывания:
y (t ) x(t ), W e
p
Набор соединительных звеньев: элементарные функции;
рациональные функции; кусочно-линейные функции; табличные
функции и т.д.
.
33
34.
Контрольные вопросы1. Что лежит в основе операторного метода?
2. Зачем нужен операторный метод?
3. Как производится алгебраизация системы линейных АДУ с нулевыми начальными
условиями?
4. Что понимается под передаточной функцией?
5. Как записывается передаточная функция линейной системы с одним входом и одним
выходом?
6. Что отображают числитель и знаменатель передаточной функции линейной системы с
одним входом и выходом?
7. Однонаправленное звено – что это такое?
8. Что понимается под структурной схемой?
9. Назовите основные виды соединения звеньев структурных схем?
10. Каковы передаточные функции для различных способов соединения звеньев последовательного, параллельного и встречно параллельного.
11. Что изменяется в передаточной функции при переносе точки приложения воздействия и
наблюдаемой величины?
12. Перечислите динамические звенья структурной схемы, реализуемые обычно в системах
моделирования систем управления?
13. Какое уравнение соответствует динамическому звену общего вида?
14. Какая передаточная функция соответствует динамическому звену общего вида?
15. Что такое звенья связи? Какие звенья возможны в системах моделирования?
16. Как строится модель в классе «Структурные схемы»?
34
35.
6. Сигналы в частотной областиt2
f (t ) * f
1
2
(t ) 0
t1
-Тригонометрические:
cos n 0t , sin n 0t , n 0,1,2......
- Экспоненциальные:
e jn 0t , n 0, 1, 2.....
- Полиномы Лежандра, Чебышева, функции Бесселя.
Разложение периодических сигналов
Периодический сигнал:
f (t ) f (t T ), t
gi (t ), интервал(t1 t2 ),
Если
f (t ) c1g1 (t ) c2 g2 (t ) ... cn gn (t ) 1 ci gi (t )
n
t2
ci
f ( t ) g i ( t ) dt
t1
t2
g
t1
2
i
( t ) dt
35
36.
Тригонометрический ряд Фурье: cos n 0t , sin n 0t (n=0,1,2…)f t a0 a1 cos 0t a2 cos 2 0t a3 cos 3 0t
b1 sin 0t b2 sin 2 0t b3 sin 3 0t
аn
2
T
t 0 T
f (t ) cos n 0tdt
t0
f (t ) a0
0
2
bn
T
t 0 T
f (t ) sin n 0tdt
t0
cn cos(n 0t n )
n 1
0
2 0
3 0
1
a0
T
сn
t0 T
f (t )dt
t0
a b
2
n
2
n
bn
n arctg
an
36
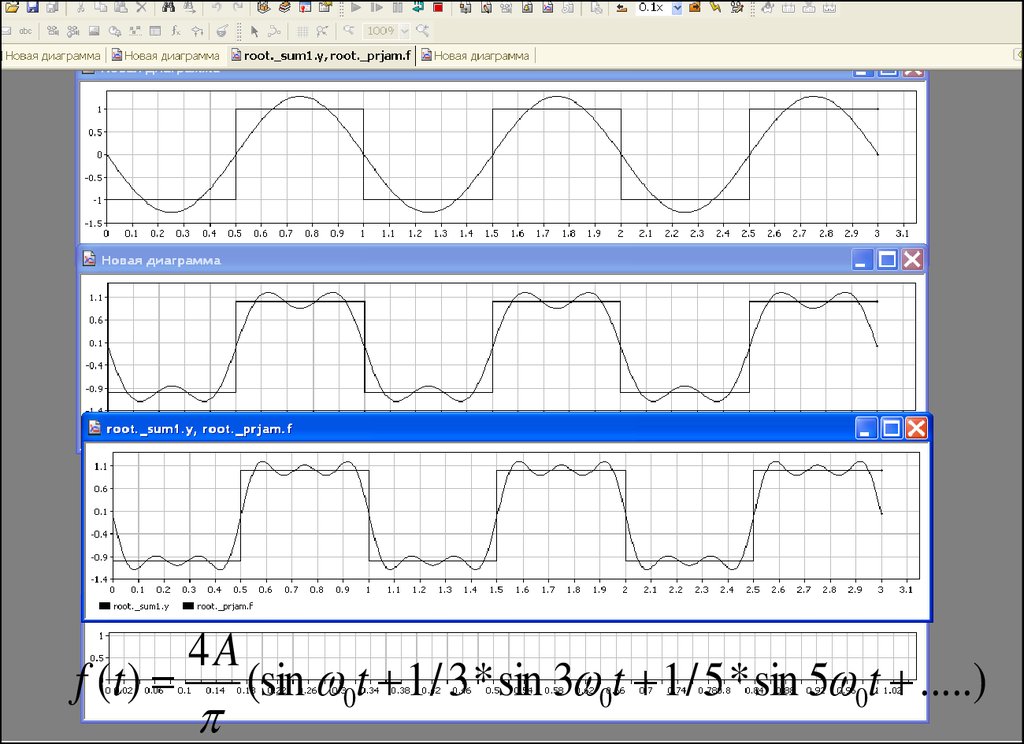
37.
4Af (t ) (sin 0t 1 / 3 * sin 3 0t 1 / 5 * sin 5 0t .....)
37
38.
Любой сигнал f (t ), удовлетворяющий условиям Дирихле иабсолютно интегрируемый, может быть представлен в виде
спектра:
f (t ) F ( )
F ( ) f (t )e
j t
1
f (t )
2
dt
0
j t
F
(
)
e
d
Условия Дирихле:
-интервал может быть разбит на конечное число подин-тервалов,
в каждом из которых функция непрерывна и моно- тонна, а в
точках разрыва существует
f (t 0; ), f (t 0)
- функция абсолютно интегрируема.
Абсолютная интегрируемость:
M – конечная величина
,
/ f (t ) / dt M
38
39. Свойства преобразования Фурье
1.Свойство изменения масштаба:f (t ) F ( )
1
f ( at )
F( )
/a/
a
2. Свойство линейности:
f1 (t ) F1 ( )
f 2 (t ) F2 ( )
af1 (t ) af 2 (t ) aF1 ( ) aF2 ( )
3. Свойство частотного и временного сдвига
f (t ) F ( )
f (t ) F ( )
f (t t0 ) F ( )e j t0
f (t )e j 0t F ( 0 )
t
e j 0t
0
39
40. 7. Системы в частотной области
t p s jx (t )
y (t )
x( p)
W ( p)
y( p)
y( p)
x( p)
Частный случай интеграла Лапласа – интеграл Фурье:
p j
f ( p ) f (t )e dt
0
f (t )
1
2 j
pt
F ( j ) f (t )e j t dt
0
c j
f ( p )e pt dt
c j
Комплексный коэффициент
передачи:
1
f (t )
2
j t
F
(
)
e
dt
0
K ( j ) W ( p ) p j
Амплитудно-фазовая характеристика
K ( j ) K ( )e
j ( )
40
41.
Амплитудно-частотная характеристикаK ( ) / K ( j ) /
Фазо-частотная характеристика
( ) arg K ( j )
Система 1 порядка:
W
k
p 1
K ( )
K ( j )
k
1
2 2
k
;
1 j
;
( ) arctg ;
T 3 T 2 T1
41
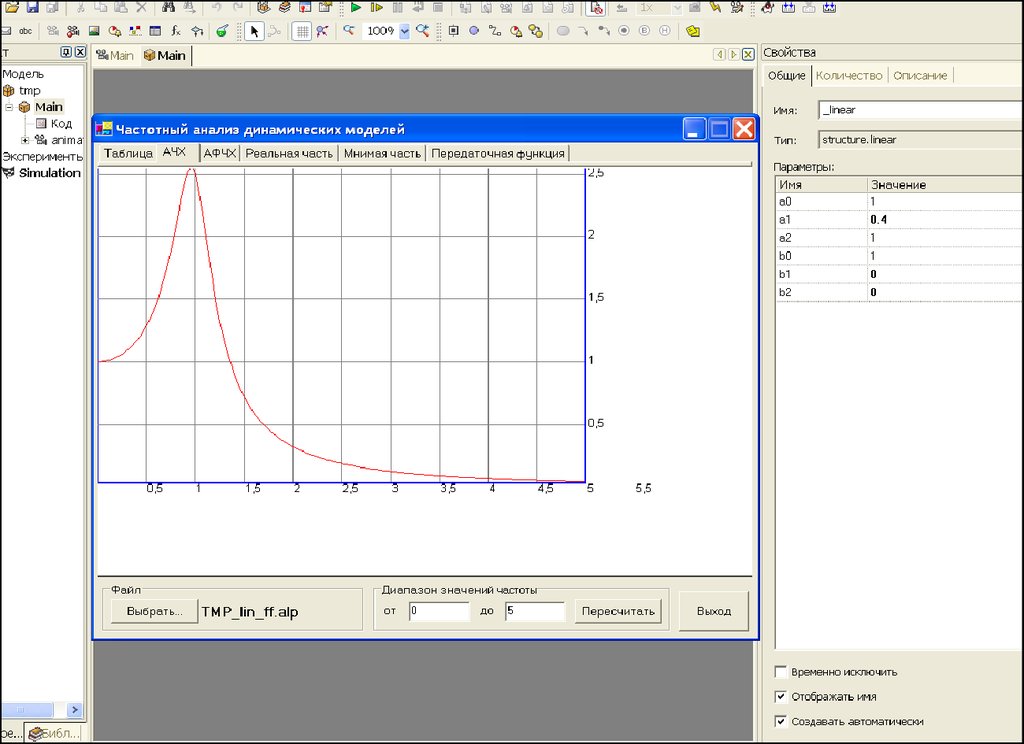
42.
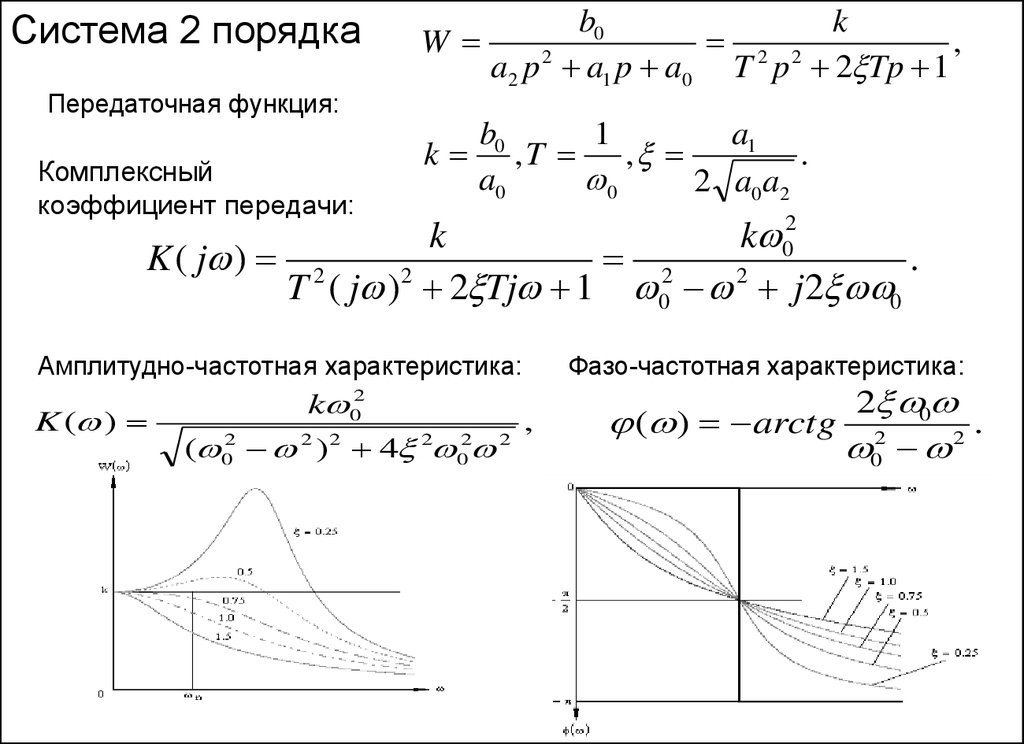
4243.
Система 2 порядкаПередаточная функция:
Комплексный
коэффициент передачи:
W
b0
k
,
2
2 2
a2 p a1 p a0 T p 2 Tp 1
b0
1
a1
k ,T
,
.
a0
0
2 a0 a 2
k
k 02
K ( j ) 2
2
.
2
2
T ( j ) 2 Tj 1 0 j 2 0
Амплитудно-частотная характеристика:
K ( )
k 02
( 02 2 ) 2 4 2 02 2
Фазо-частотная характеристика:
,
( ) arctg
2 0
.
2
2
0
43
44.
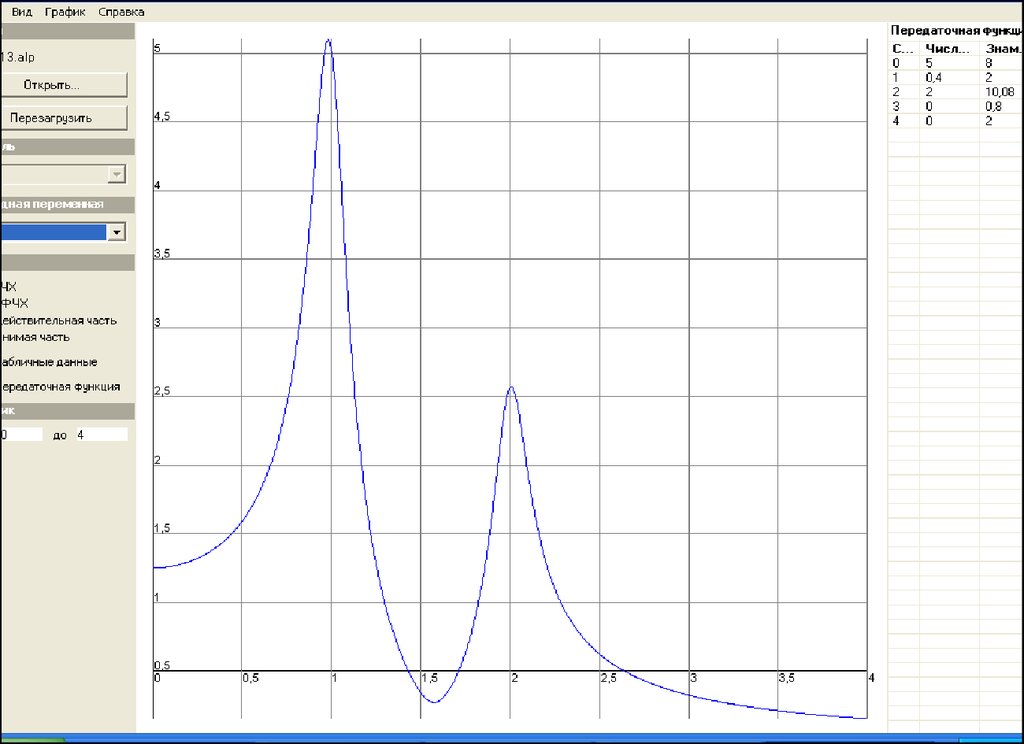
4445.
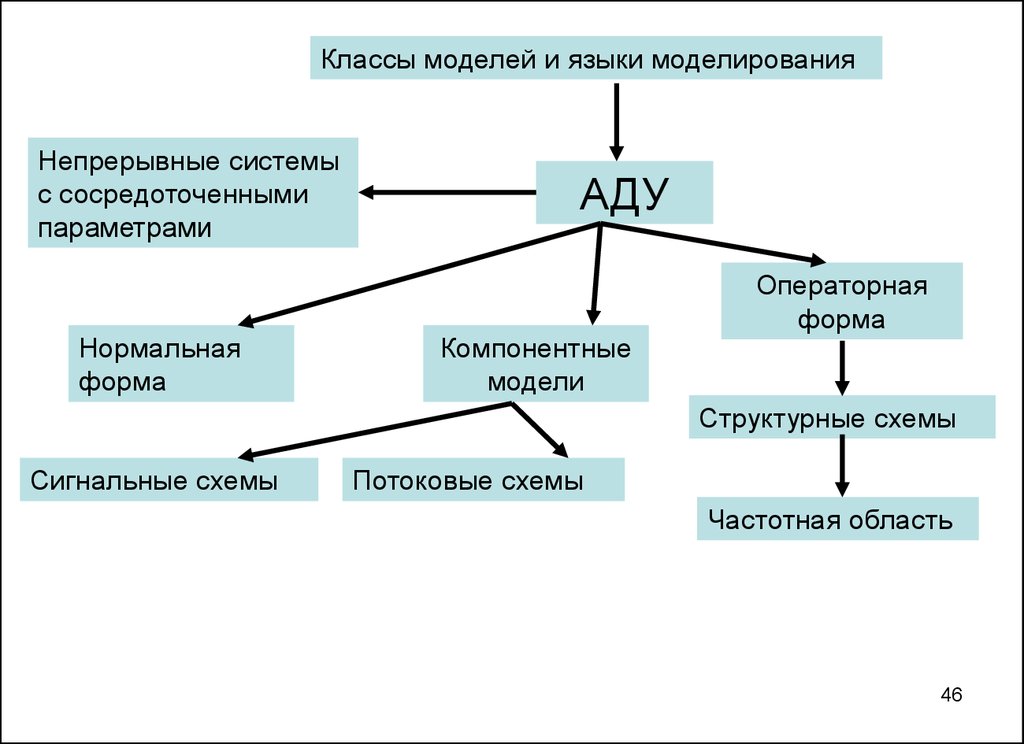
4546.
Классы моделей и языки моделированияНепрерывные системы
с сосредоточенными
параметрами
Нормальная
форма
АДУ
Компонентные
модели
Операторная
форма
Структурные схемы
Сигнальные схемы
Потоковые схемы
Частотная область
46
47.
Контрольные вопросы1.Что понимается под системой ортогональных функций, где и как она
используется?
2. Приведите примеры ортогональных функций?
3. Тригонометрический ряд Фурье – как он выглядит?
4. Как выглядит разложение в тригонометрический ряд Фурье, выраженное
через амплитуду и фазу гармоник?
5. Как выглядит спектр периодического сигнала и чем отличаются спектры
периодического и непериодического сигналов?
6. Смысловое содержание и формализм свойства изменения масштаба
преобразования Фурье?
7. Смысловое содержание и формализм свойства линейности
преобразования Фурье?
8. Смысловое содержание и формализм свойства частотного и временного
сдвига преобразования Фурье?
9. Как перейти от комплексной амплитудно-частотной характеристики к
амплитудно-частотной и фазовой характеристикам?
10. Комплексный коэффициент передачи: что это и как его найти?
11. Как выглядят АЧХ и ФЧХ системы 1 порядка?
12. Как выглядят АЧХ и ФЧХ системы 2 порядка?
47
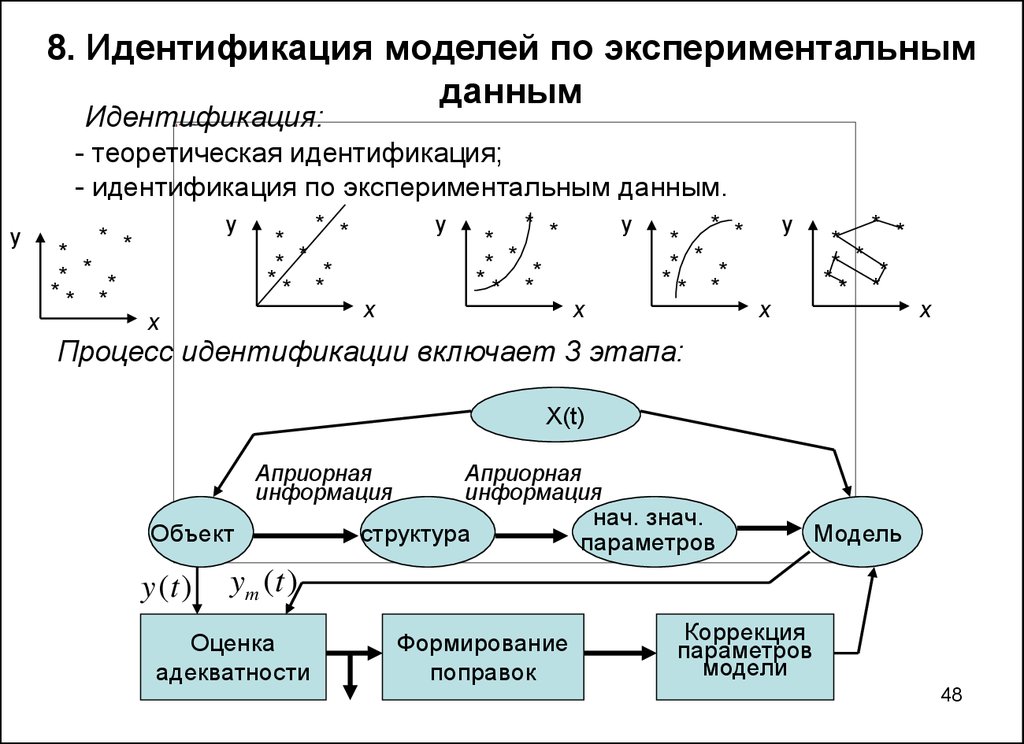
48.
8. Идентификация моделей по экспериментальнымданным
Идентификация:
- теоретическая идентификация;
- идентификация по экспериментальным данным.
y
y
* *
*
* * *
** *
* *
*
* *
* * **
y
* *
*
* *
* * **
x
x
y
* *
*
* *
* * **
x
y
* *
*
* *
* * **
x
x
Процесс идентификации включает 3 этапа:
X(t)
Априорная
информация
Объект
y (t )
Априорная
информация
структура
нач. знач.
параметров
Модель
ym (t )
Оценка
адекватности
Формирование
поправок
Коррекция
параметров
модели
48
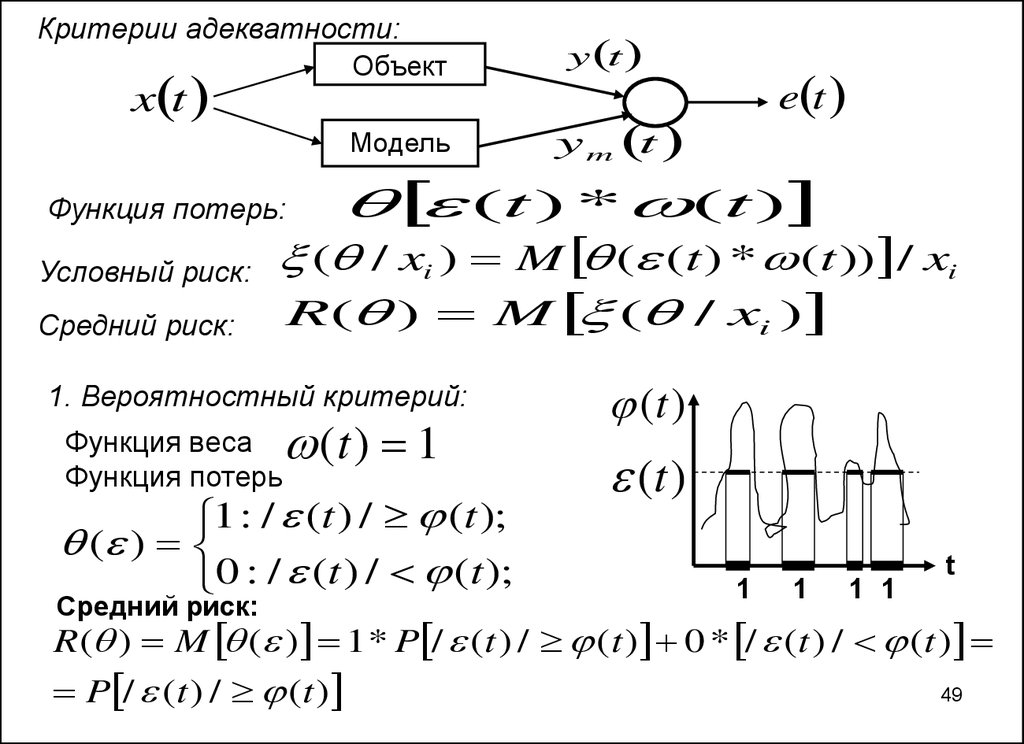
49. Критерии адекватности:
Объектx t
Модель
y t
e t
y m t
(t ) * (t )
( / xi ) M ( (t ) * (t )) / xi
R( ) M ( / xi )
Функция потерь:
Условный риск:
Средний риск:
1. Вероятностный критерий:
Функция веса
Функция потерь
(t ) 1
1 : / (t ) / (t );
( )
0 : / (t ) / (t );
Средний риск:
(t )
(t )
1
1
1 1
t
R ( ) M ( ) 1 * P / (t ) / (t ) 0 * / (t ) / (t )
49
P / (t ) / (t )
50. Метод наименьших квадратов
2. Среднеквадратичный критерий:(t ) 1; (t ) 2 (t );
3. Равномерный критерий:
T
R( ) 1 / T 2 (t )dt.
0
(t ) 1; ( ) / (t ) /:
T
R( ) 1 / T / (t ) / dt.
0
4. Равномерный критерий с учетом времени:
T
(t ) t; ( ) / (t ) / : R( ) 1 / T / (t ) / tdt.
Метод наименьших квадратов
Многомерный статический объект:
X x1 ,... xn ;
Информация:
0
Y F ( X , A)
A a1 ,...ak ;
Y y1..... ym ;
I xi , yi , i 1,... N ; ?? a1 ,...ak ;
Сведение к одному выходу:
y1 f ( X 1 , A);
.......................
y N f ( X N , A);
y f ( X , A)
N ???
50
51. Если:
1 2(t ) 1, ( ) (t ) : R( ) (t )dt;
T
2
1
R ( )
N
min R
1
N
2
(
y
y
)
im i ;
f ( X , A) y )
n
i 1
Частный случай:
min
2
i
2
i
y f ( x, A) f ( x, a1,...ak )
yi f ( x, A)
Дифференцируя и приравнивая
производную нулю:
2
*
A
*
A
n
f
y
f
(
x
,
A
)
0;
i
i
a1
i 1
......................................
n
yi f ( xi , A) f 0;
ak
i 1
51
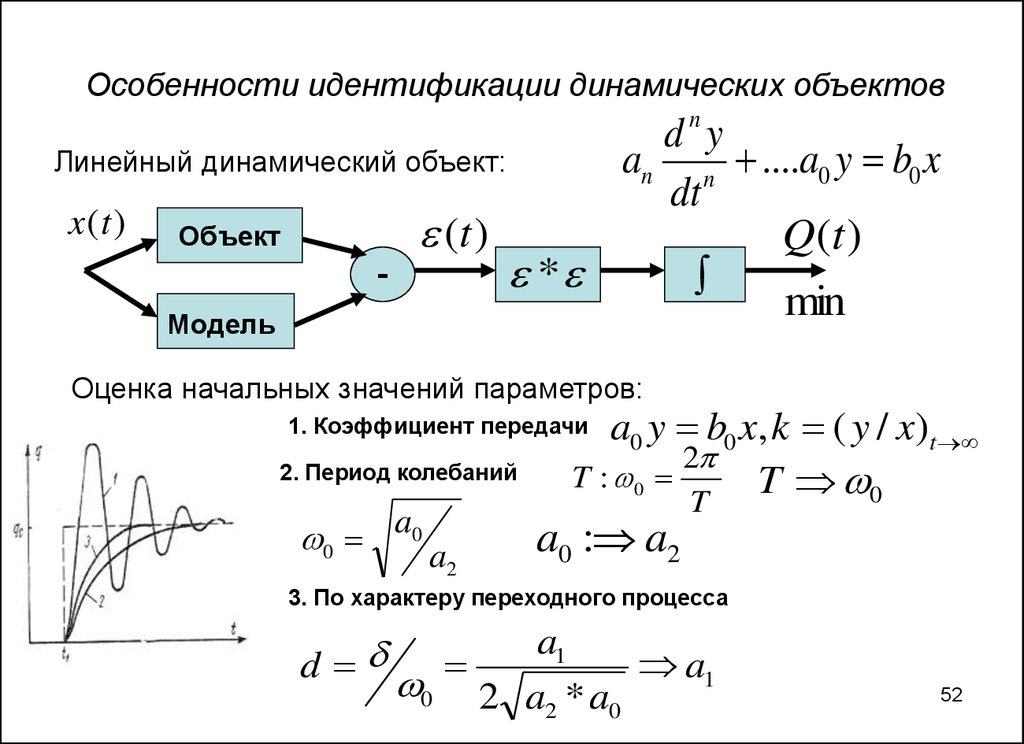
52. Особенности идентификации динамических объектов
dnyЛинейный динамический объект:
an n ....a0 y b0 x
dt
x (t ) Объект
(t )
Q(t )
*
min
Модель
Оценка начальных значений параметров:
a0 y b0 x, k ( y / x)t
2
T : 0
T 0
T
1. Коэффициент передачи
2. Период колебаний
0 a0 a
2
a0 : a2
3. По характеру переходного процесса
a1
d
0 2 a * a a1
2
0
52
53. Идентификация в частотной области
- Синусоидальный сигнал:- Прямоугольный сигнал:
x x0 sin t
y K ( ) sin( t ( ))
4A
x(t ) (sin 0t 1 sin 3 0t 1 sin 5 0t ...)
3
5
1
K ( 0 ) sin( 0t 0 ) K (3 0 ) sin( 3 0t 3 ) .......
y (t )
3
4A
- Случайный сигнал:
X (t )
K x ( )
S x ( )
Y (t )
K y (t )
S y ( )
S y ( )
S x ( )
K 2 ( ) K ( )
53
54.
5455. Регрессионный анализ
r rкр :rкр
t 2n
( t n 2)
2
n
t n - критерий Стъюдента,
Критерий Стъюдента для
1
2
-доверительная вероятность
0.9
5
10
30
120
t n
2.1
1.8
1.7
1.7
1.6
rкр
0.8
0.5
0.3
0.15
0
n
55
56.
Контрольные вопросы1. Определите понятие "Идентификация"?
2. Определите понятие "Теоретическая идентификация"?
3. В каких ситуациях приходится идентифицировать модель по экспериментальным
данным?
4. Перечислите основные этапы (процедуры) процесса идентификации модели по
экспериментальным данным?
5. Что такое «критерий адекватности»?
6. Перечислите основные типы задач идентификации и их особенности?
11. Как строятся оценки степени адекватности?
12. Какие критерии адекватности наиболее часто используются на практике?
13. Как выглядит и где используется критерий адекватности «средний риск»?
14. Как выглядит и где используется среднеквадратичный критерий?
15. Что такое «метод наименьших квадратов» в задачах идентификации моделей?
16. Как выглядит математическая формулировка метода наименьших квадратов?
17. В чем особенность идентификации динамических моделей?
18. Как строится процедура идентификации в частотной области?
19. Как можно имитировать гармонический сигнал?
20. Регрессионный анализ - что это?
21. Как в общем виде выглядит решение задачи регрессионного анализа?
22. От чего зависит и как определяется критический коэффициент корреляции в
регрессионном анализе?
56
57.
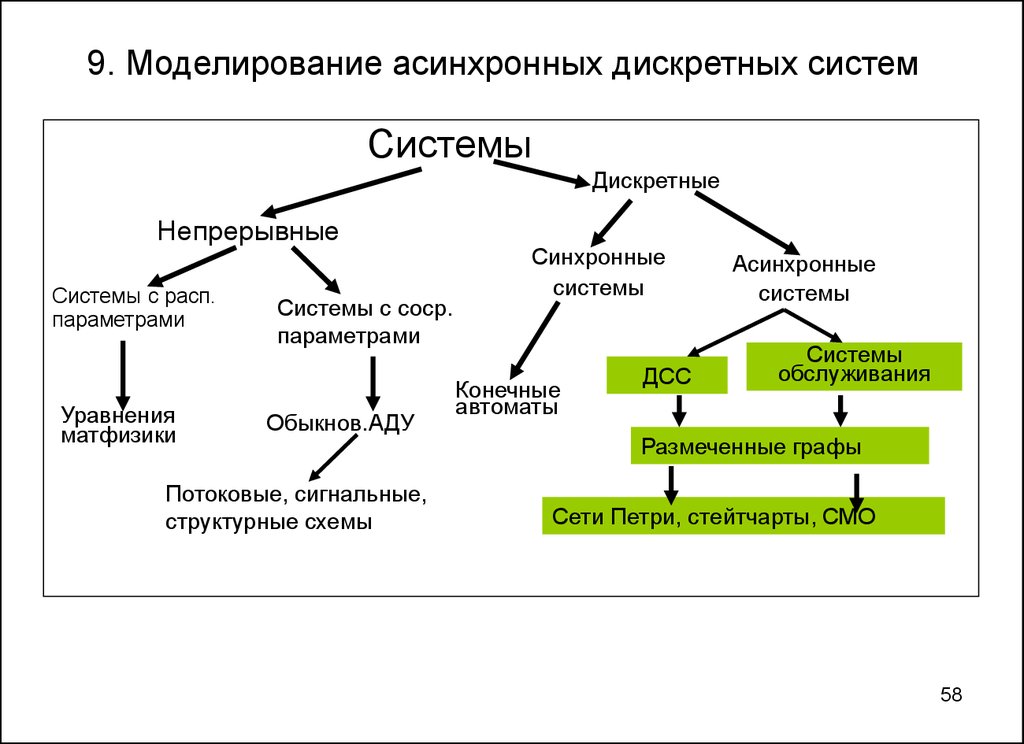
5758. 9. Моделирование асинхронных дискретных систем
СистемыДискретные
Непрерывные
Системы с расп.
параметрами
Уравнения
матфизики
Системы с соср.
параметрами
Обыкнов.АДУ
Потоковые, сигнальные,
структурные схемы
Синхронные
системы
Конечные
автоматы
ДСС
Асинхронные
системы
Системы
обслуживания
Размеченные графы
Сети Петри, стейтчарты, СМО
58
59.
Дискретно-событийные системы:Событие
Условия
Состояние 2
Состояние 1
Событие
Условия
Системы массового обслуживания:
Уход
Приход
Очередь
Прибор
59
60.
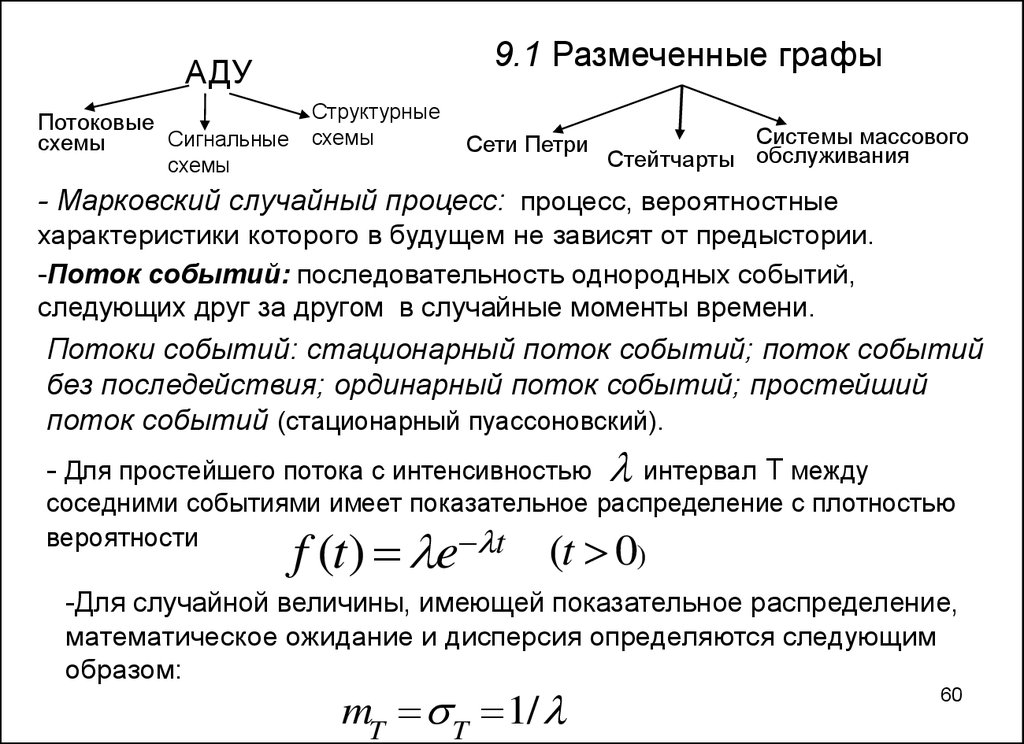
9.1 Размеченные графыАДУ
Структурные
Потоковые
Сигнальные схемы
схемы
схемы
Сети Петри
Системы массового
Стейтчарты обслуживания
- Марковский случайный процесс: процесс, вероятностные
характеристики которого в будущем не зависят от предыстории.
-Поток событий: последовательность однородных событий,
следующих друг за другом в случайные моменты времени.
Потоки событий: стационарный поток событий; поток событий
без последействия; ординарный поток событий; простейший
поток событий (стационарный пуассоновский).
- Для простейшего потока с интенсивностью
интервал T между
соседними событиями имеет показательное распределение с плотностью
вероятности
t
f (t) e
(t 0)
-Для случайной величины, имеющей показательное распределение,
математическое ожидание и дисперсия определяются следующим
образом:
mT T 1/
60
61.
Уравнения Колмогорова:Система включает два канала связи с отказами. Может находиться в
трех состояниях:
S0
S1
S2
-оба канала свободны;
Размеченный граф системы:
-один из каналов занят;
01
-оба канала заняты.
S0
S1
10
Для любого момента времени:
2
12
21
S2
p (t ) p (t ) p (t ) p (t ) 1.
i 0
i
0
1
2
Элемент вероятности – вероятность попадания на малый интервал хотя бы одного
события потока
t
p
t
61
62.
Вероятность того, что в момент временинаходиться в состоянии
s1
t t
система будет
p1 (t t ) p1 (t ) 1 ( 10 12 ) t
t
t
p0 (t ) 01 t p2 (t ) 21 t.
S1
Если
t 0
01
S0
10
S1
dp1
dt
12
21
p0 01 p2 21 p1 ( 10 12 ).
S2
dp0
dt p1 10 p0 01
dp1
p0 01 p2 21 p1 ( 10 12 )
dt
dp2
dt p1 12 21 p2
Общее правило составления
уравнений Колмогорова:
Левая часть – производные вероятности
каждого из возможных
состояний.
Правая часть – сумма произведений
вероятностей всех состояний, из которых
идут стрелки в данное состояние, на
интенсивности соответствующих потоков
событий, минус суммарная интенсивность
всех потоков, выводящих систему из
данного состояния, умноженная на
вероятность данного состояния.
62
63.
Для решения системы уравнений необходимо задать начальныеусловия: p0 (0) 1; p1 (0) p2 (0) 0
Финальные вероятности состояний – значения вероятностей
к которым они стремятся при t
.
pi (t )
Интерпретация: финальная вероятность состояния – среднее
относительное время пребывания системы в этом состоянии.
Для установившегося состояния
соответственно получим:
производные
Для решения системы одно
нормировочным условием:
уравнений
равны
нулю;
01 p0 10 p1
( 10 12 ) p1 01 p0 21 p2
p p
21 2 12 1
из
необходимо
заменить
p1 p2 p3 1
63
64.
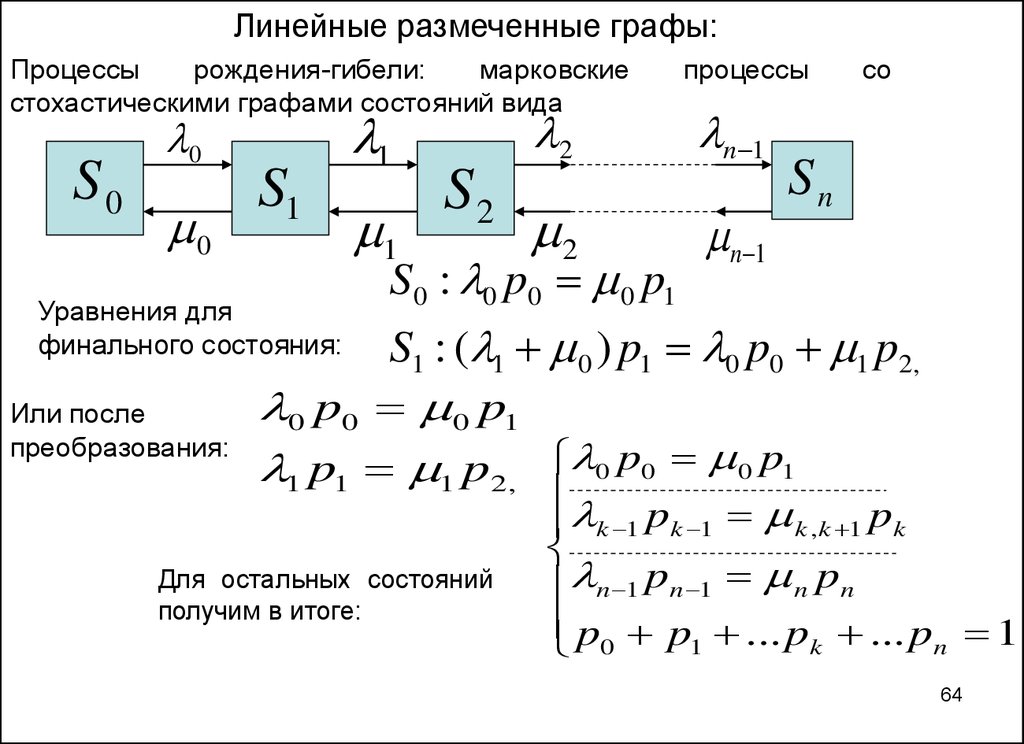
Линейные размеченные графы:Процессы
рождения-гибели:
марковские
стохастическими графами состояний вида
S0
0
0
S1
Уравнения для
финального состояния:
Или после
преобразования:
1
1
S2
процессы
2
n 1
2
n 1
S0 : 0 p0 0 p1
со
Sn
S1 : ( 1 0 ) p1 0 p0 1 p2,
0 p0 0 p1
1 p1 1 p2, 0 p0 0 p1
Для остальных состояний
получим в итоге:
p
k 1 k 1 k , k 1 pk
n 1 pn 1 n pn
p0 p1 ... pk ... pn 1
64
65.
Решение системы в компактной форме примет вид:n i
p0 ik 0
k 1
m
m 1
k 1
1
k 1
, pk
i
i 0
k
, k 1, n.
m
m 1
К описанной выше модели сводятся многие простые задачи
асинхронных дискретных систем.
Приведенная интенсивность потока заявок – среднее
число
заявок,
приходящее
за
среднее
время
обслуживания одной заявки:
Формулы Эрланга:
1
k
p0 ; pk
p0 ; .
k!
k 0 k!
n
k
65
66.
Формулы ЛиттлаДля любой СМО, при любом характере потока заявок, при
любом распределении времени обслуживания, при любой
дисциплине обслуживания:
- Среднее время пребывания заявки в системе равно среднему
числу заявок в системе, деленному на интенсивность потока
заявок:
1
Wсист
Lсист
- Среднее время пребывания заявки в очереди равно среднему
числу заявок в очереди, деленному на интенсивность потока
заявок:
Wоч
1
Lоч
Поскольку речь идет об установившемся режиме, входной поток заявок
равен выходному. Тогда среднее время пребывания заявки в очереди
при ее единичной длине 1/ . Так как реально в очереди стоит L, то
время надо умножить на эту величину.
1
66
67.
Одноканальная СМО с отказами в обслуживании:Модель в виде размеченного графа:
S0
S1
Система дифференциальных
уравнений Колмогорова:
Откуда:
dp0
( ) p0 (t ) .
dt
Решение при нулевых
начальных условиях:
В установившемся режиме,
при
p0 (0) 1; p1 (0) 0;
p0 (t )
dp0 (t )
dt p0 (t ) p1 (t );
dp1 (t )
p1 (t ) p0 (t );
dt
p0 (t ) p1 (t ) 1.
e
( ) t
p1 (t )
(1 e ( )t );
;
p0
t
; p1
67
.
68.
В установившемся режиме,при
t
p0
; p1
.
Относительная пропускная способность
Q p0 (t ).
Абсолютная
пропускная
способность
обслуживаемых в единицу времени):
(число
заявок,
A
Q.
Доля заявок, которым отказано в обслуживании:
Pотк p1
.
Число не обслуженных заявок в единицу времени:
Pотк
2
68
69.
Многоканальная СМО с отказами (задача Эрланга)S0
S1
Sk
k
2
( k 1)
n
Sn
Приведенная интенсивность потока заявок – среднее число
заявок, приходящее за среднее время обслуживания одной заявки:
;
Формулы Эрланга:
1
k
p0
; .
; p k p0
k!
k 0 k!
n
k
69
70.
Вероятность отказа:pотк pn p0
Относительная пропускная
способность:
Абсолютная пропускная
способность:
Среднее число занятых каналов:
n
n!
; k n;
Q pобсл 1 pотк 1 pn ;
A pобсл ;
n зан pобсл A / ;
Задачи, имеющие аналитическое решение:
-Одноканальная СМО с ограниченной длиной очереди.
- Одноканальная СМО с неограниченной очередью.
- Многоканальная СМО с ограниченной длиной очереди.
- Многоканальная СМО с неограниченной очередью.
70
71.
10. Асинхронные дискретно-событийные процессыЕсть билет
Успел
Нужно!
Быть в
Москве
Я в Москве
Купил!
Есть
деньги
Покупка
Есть в продаже
Прибыл по
расписанию
- Однонаправленные связи
- Маркеры
Сети Петри
Позиция
Переход
Основное
синтаксическое
правило:
Активный переход??
Срабатывание перехода:
71
72.
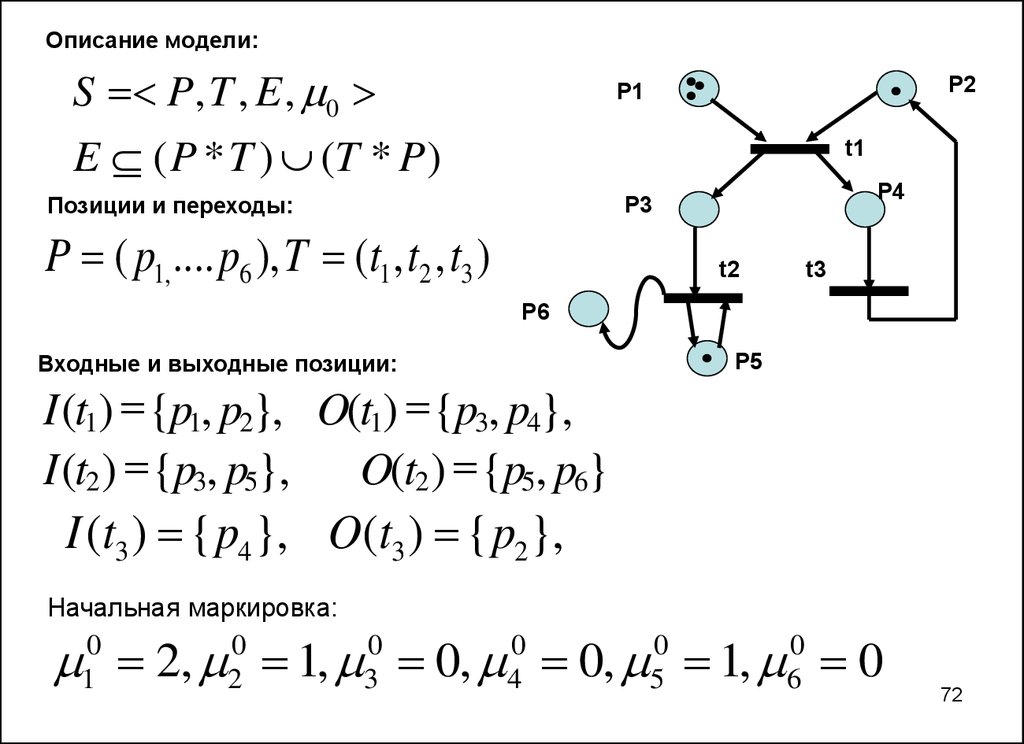
Описание модели:S P, T , E , 0
P2
P1
E ( P * T ) (T * P )
t1
Позиции и переходы:
P4
P3
P ( p1, .... p6 ), T (t1 , t2 , t3 )
t2
t3
P6
Входные и выходные позиции:
P5
I (t1) {p1, p2}, O(t1) {p3, p4},
I (t2 ) {p3, p5},
O(t2 ) {p5, p6}
I (t3 ) { p4 }, O(t3 ) { p2},
Начальная маркировка:
2, 1, 0, 0, 1, 0
0
1
0
2
0
3
0
4
0
5
0
6
72
73.
а73
74.
d1d2
ВН
СЖ
ВП
ВВ
ОТП
ВЛ
74
75.
P1P0
t0
t5
t1
P2
t2
P4
P3
t3
P5
t6
t4
P9
P8
P7
P6
Распараллеливание обработки сложных данных
75
76.
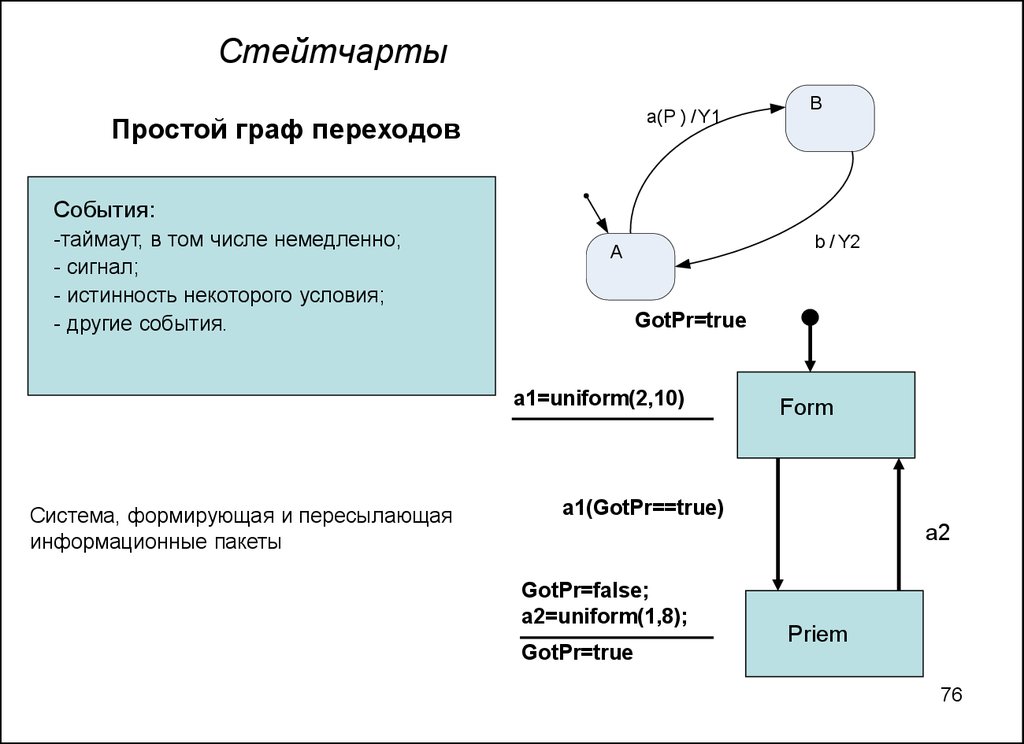
Стейтчартыa(P ) / Y1
Простой граф переходов
B
События:
-таймаут, в том числе немедленно;
- сигнал;
- истинность некоторого условия;
- другие события.
b / Y2
A
GotPr=true
a1=uniform(2,10)
Система, формирующая и пересылающая
информационные пакеты
Form
a1(GotPr==true)
a2
GotPr=false;
a2=uniform(1,8);
GotPr=true
Priem
76
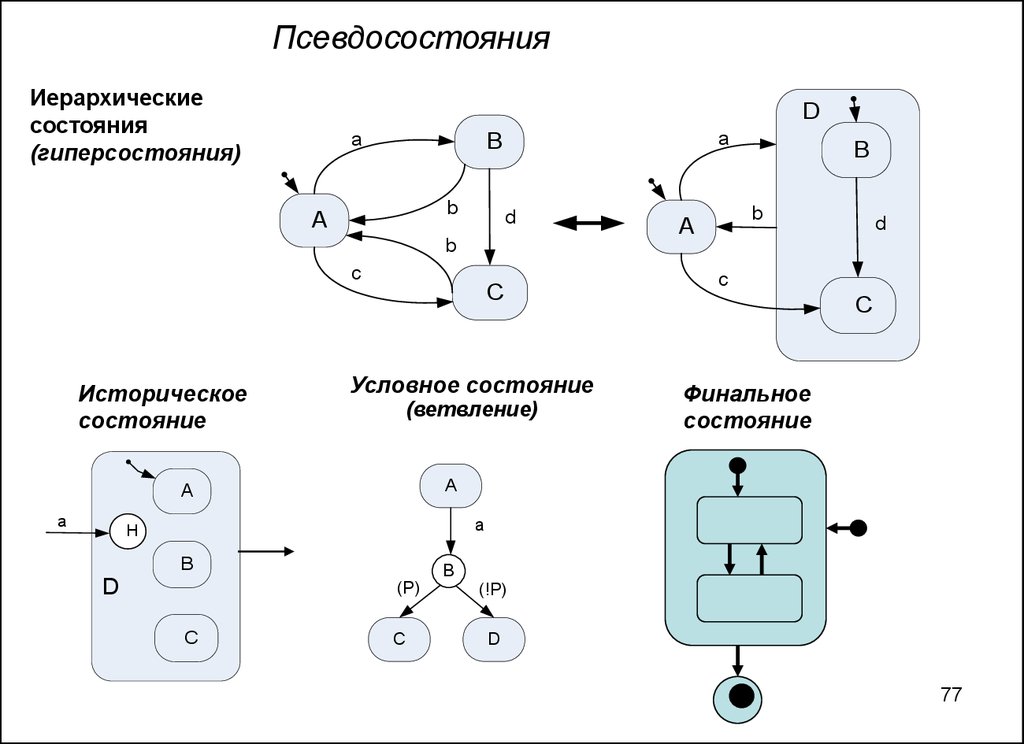
77.
ПсевдосостоянияИерархические
состояния
(гиперсостояния)
D
a
a
B
b
A
d
b
c
Историческое
состояние
C
Условное состояние
(ветвление)
b
A
d
c
C
Финальное
состояние
A
A
a
B
a
H
B
D
B
(P)
C
C
(!P)
D
77
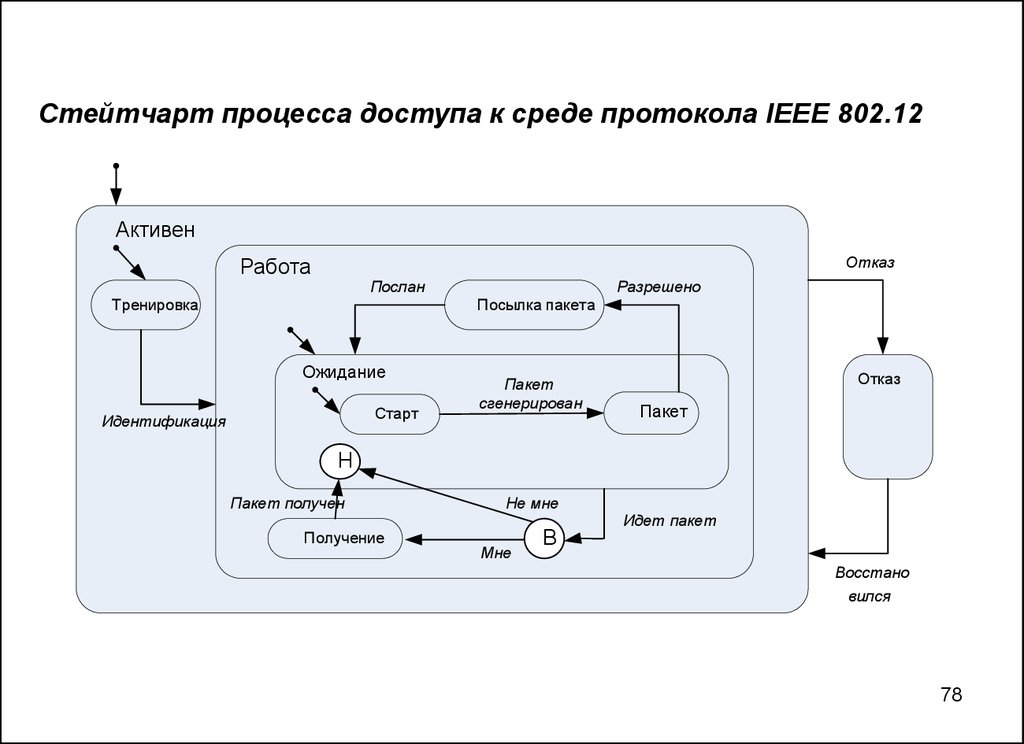
78.
Стейтчарт процесса доступа к среде протокола IEEE 802.12Активен
Отказ
Работа
Послан
Тренировка
Ожидание
Старт
Идентификация
Посылка пакета
Пакет
сгенерирован
Разрешено
Отказ
Пакет
Н
Пакет получен
Получение
Не мне
Мне
В
Идет пакет
Восстано
вился
78
79.
i1t3
L
t2
B
i2
t1
M
t4
i3
N
Находимся в состоянии N,
срабатывает переход t1
1) Д. выхода из N.
2) Д. выхода из М.
3) Д. перехода t1.
4) Д. состояния ветвления.
Выбран переход t2:
5) Д. перехода t2.
6) Д. указателя i2.
7) Д. входа в M.
8) Д. указателя i3.
9) Д. входа в N.
Выбран переход t3:
10) Д. выхода из L.
11) Д. перехода t3.
Находимся в начальном состоянии:
1) Д. указателя i1.
2) Д. входа в L.
3) Д. указателя i2.
4) Д. входа в M.
5) Д. указателя i3.
6) Д. входа в N.
Срабатывает переход t4:
1) Д. перехода t4.
2)
79
80.
Пример 1Движение
dy
dt v;
dv g ;
dt
y 0 A;
v 0 0.
GotPr=true
a1=uniform(2,10)
y 0 & &v 0;
v k *v;
Form
a1(GotPr==true)
a2
GotPr=false;
a2=uniform(1,8);
Priem
GotPr=true
80
81.
Пример 2t0
Зеленый
t1,25
t2,1
A
Зеленый - 25 с
Миг. зеленый – 7 с
Красный – 20 с
Красный + желтый – 4 с
B
Green=true
Green=false
Green=true
Green=false
t3,1
t4,7
Красный
t5,20
t6,4
Красный +
желтый
Red=true
Red=false
Red=true
Yellow=true
Red=false
Red=false
81
82.
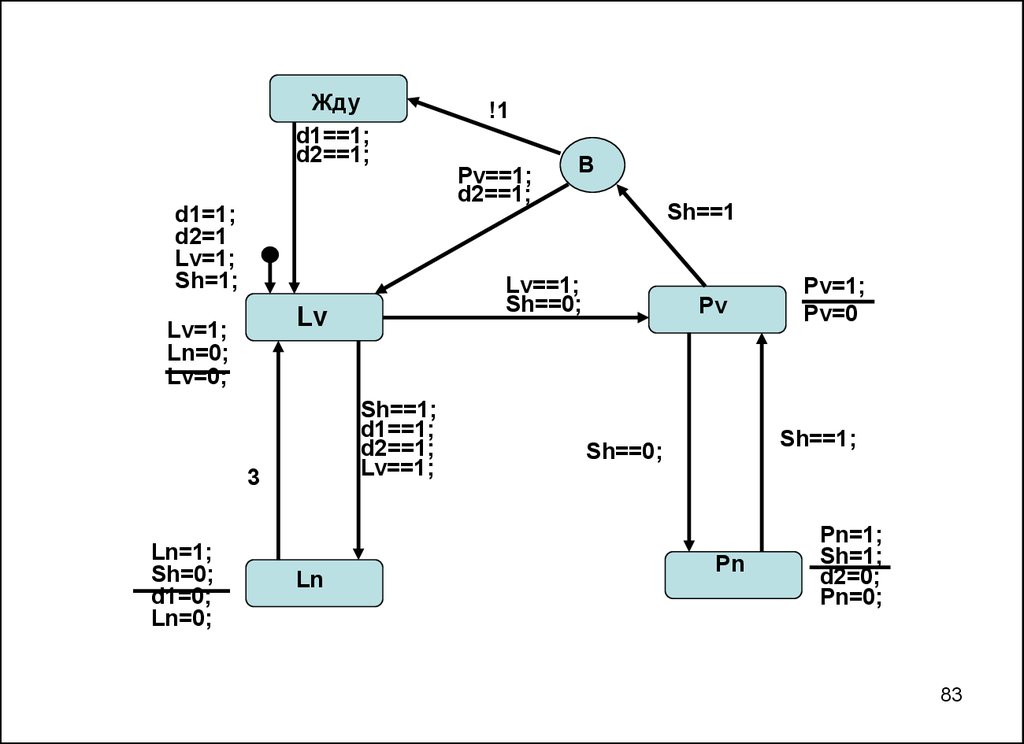
8283.
Ждуd1==1;
d2==1;
d1=1;
d2=1
Lv=1;
Sh=1;
Sh==1;
d1==1;
d2==1;
Lv==1;
3
Ln=1;
Sh=0;
d1=0;
Ln=0;
Ln
Pv==1;
d2==1;
В
Sh==1
Lv==1;
Sh==0;
Lv
Lv=1;
Ln=0;
Lv=0;
!1
Pv
Pv=1;
Pv=0
Sh==1;
Sh==0;
Pn
Pn=1;
Sh=1;
d2=0;
Pn=0;
83
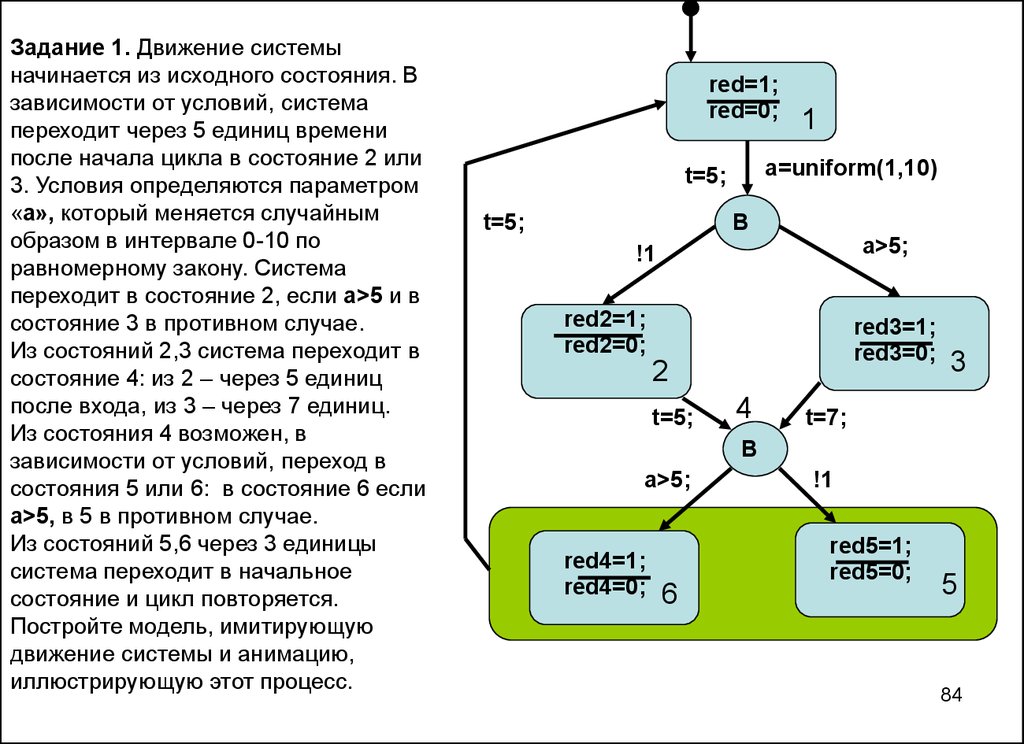
84.
Задание 1. Движение системыначинается из исходного состояния. В
зависимости от условий, система
переходит через 5 единиц времени
после начала цикла в состояние 2 или
3. Условия определяются параметром
«а», который меняется случайным
образом в интервале 0-10 по
равномерному закону. Система
переходит в состояние 2, если а>5 и в
состояние 3 в противном случае.
Из состояний 2,3 система переходит в
состояние 4: из 2 – через 5 единиц
после входа, из 3 – через 7 единиц.
Из состояния 4 возможен, в
зависимости от условий, переход в
состояния 5 или 6: в состояние 6 если
а>5, в 5 в противном случае.
Из состояний 5,6 через 3 единицы
система переходит в начальное
состояние и цикл повторяется.
Постройте модель, имитирующую
движение системы и анимацию,
иллюстрирующую этот процесс.
red=1;
red=0;
1
a=uniform(1,10)
t=5;
В
t=5;
a>5;
!1
red2=1;
red2=0;
red=1;
red3=1;
red=0;
red3=0;
2
t=5;
4
3
t=7;
В
a>5;
red4=1;
red4=0;
6
!1
red5=1;
red5=0;
5
84
85.
Контрольные вопросы:1. На какую предметную область ориентирован класс моделей Сети Петри (СП)?
2. Перечислите элементы и правила композиции класса СП?
3. Какой переход в СП считается активным, что происходит при срабатывании активного
перехода?
4. Как выглядит язык описания для СП?
5. На какую предметную область ориентирован класс моделей Стейтчарты?
6. Перечислите элементы и правила композиции класса Стейтчарты?
7. Когда в классе Стейтчарты возможен переход из одного состояния в другое?
8. С чем возможно связывание действий в классе Стейтчарты?
9. Иерархическое состояние в классе Стейтчарты?
10. Историческое состояние в классе Стейтчарты?
11. Условное состояние (ветвление) в классе Стейтчарты?
12. Финальное состояние в классе Стейтчарты?
13. Порядок срабатывания элементов Стейтчарта при входе в иерархическое состояние?
14. Порядок срабатывания элементов Стейтчарта при выходе из иерархического
состояния?
15. Как срабатывают элементы Стейтчарта при входе в состояние ветвления?
85
86.
11. Системы массового обслуживанияУход
Приход
Очередь
Прибор
-Опишите простейшую систему массового обслуживания? Что
входит в ее состав?
-Перечислите основные подсистемы системы массового
обслуживания? Дайте их характеристику?
- Назовите наиболее часто встречающиеся дисциплины
обслуживания?
-Назовите наиболее часто встречающиеся цели моделирования?
86
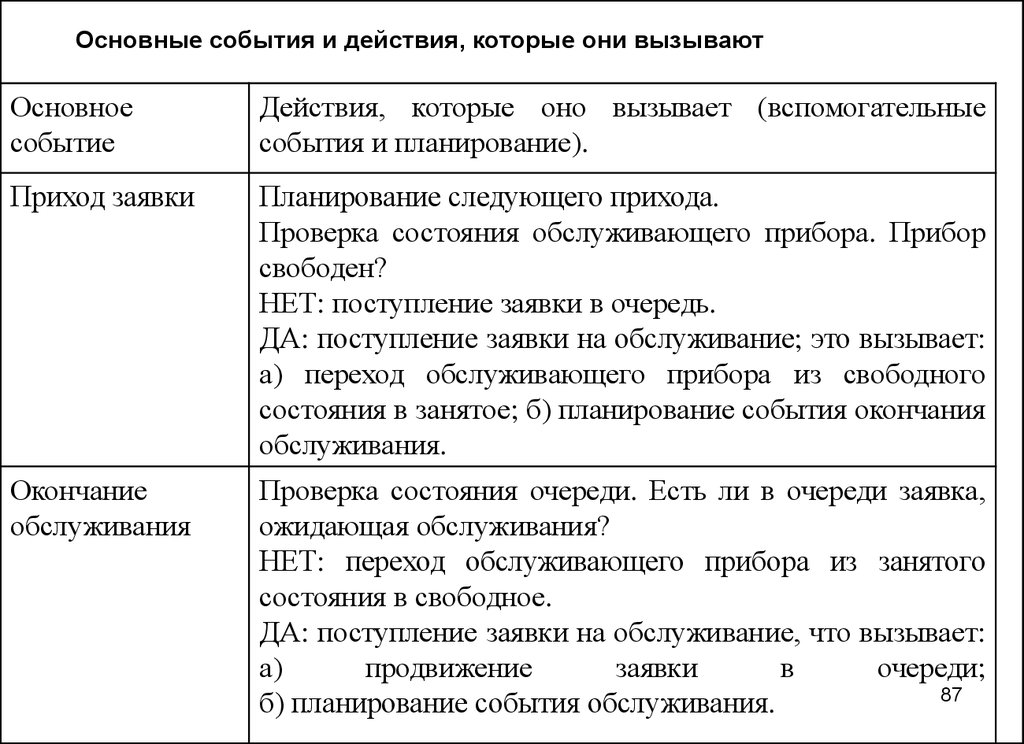
87.
Основные события и действия, которые они вызываютОсновное
событие
Действия, которые оно вызывает (вспомогательные
события и планирование).
Приход заявки
Планирование следующего прихода.
Проверка состояния обслуживающего прибора. Прибор
свободен?
НЕТ: поступление заявки в очередь.
ДА: поступление заявки на обслуживание; это вызывает:
а) переход обслуживающего прибора из свободного
состояния в занятое; б) планирование события окончания
обслуживания.
Окончание
обслуживания
Проверка состояния очереди. Есть ли в очереди заявка,
ожидающая обслуживания?
НЕТ: переход обслуживающего прибора из занятого
состояния в свободное.
ДА: поступление заявки на обслуживание, что вызывает:
а)
продвижение
заявки
в
очереди;
87
б) планирование события обслуживания.
88.
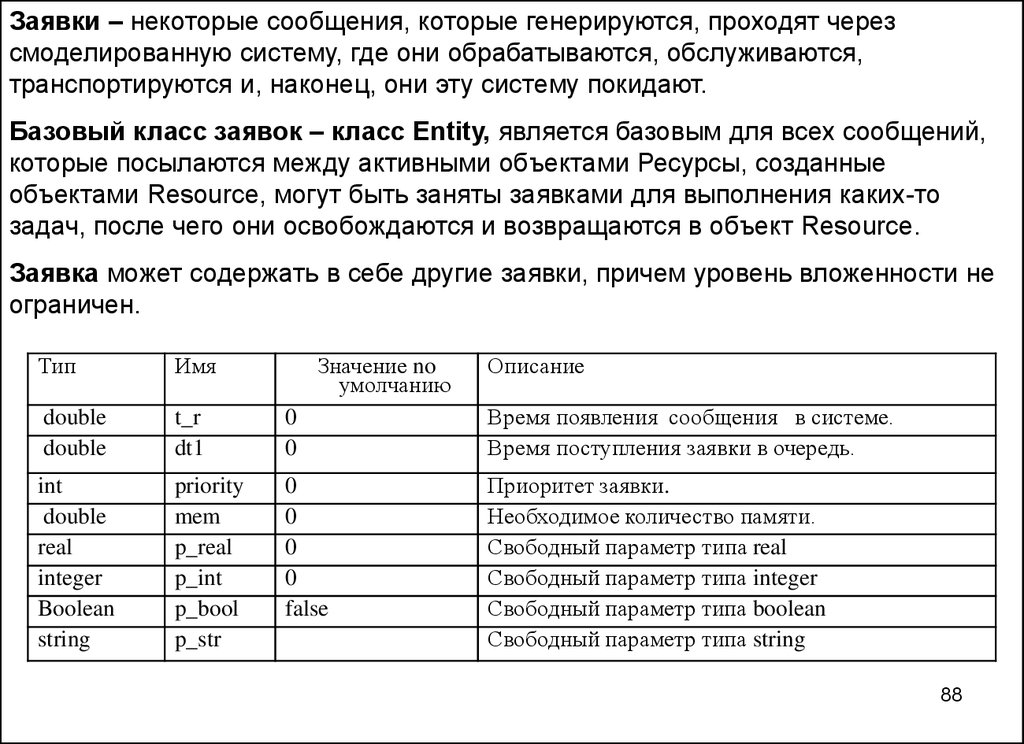
Заявки – некоторые сообщения, которые генерируются, проходят черезсмоделированную систему, где они обрабатываются, обслуживаются,
транспортируются и, наконец, они эту систему покидают.
Базовый класс заявок – класс Entity, является базовым для всех сообщений,
которые посылаются между активными объектами Ресурсы, созданные
объектами Resource, могут быть заняты заявками для выполнения каких-то
задач, после чего они освобождаются и возвращаются в объект Resource.
Заявка может содержать в себе другие заявки, причем уровень вложенности не
ограничен.
Тип
Имя
Значение no
умолчанию
Описание
double
double
t_r
dt1
0
0
Время появления сообщения в системе.
Время поступления заявки в очередь.
int
double
real
integer
Boolean
string
priority
mem
p_real
p_int
p_bool
p_str
0
0
0
0
false
Приоритет заявки.
Необходимое количество памяти.
Свободный параметр типа real
Свободный параметр типа integer
Свободный параметр типа boolean
Свободный параметр типа string
88
89.
ТипИмя
Значение no
умолчанию
Описание
double
t_r
0
Время появления сообщения в системе.
double
dt1
0
Время поступления заявки в очередь.
Вычисляется в блоке queue.
int
priority
0
double
mem
0
Приоритет заявки. Чем больше значение, тем
выше приоритет.
Количество памяти, необходимое для решения
задачи.
real
p_real
0
Свободный параметр типа real
integer
p_int
0
Свободный параметр типа integer
Boolean
p_bool
false
Свободный параметр типа boolean
string
p_str
Свободный параметр типа string
89
90.
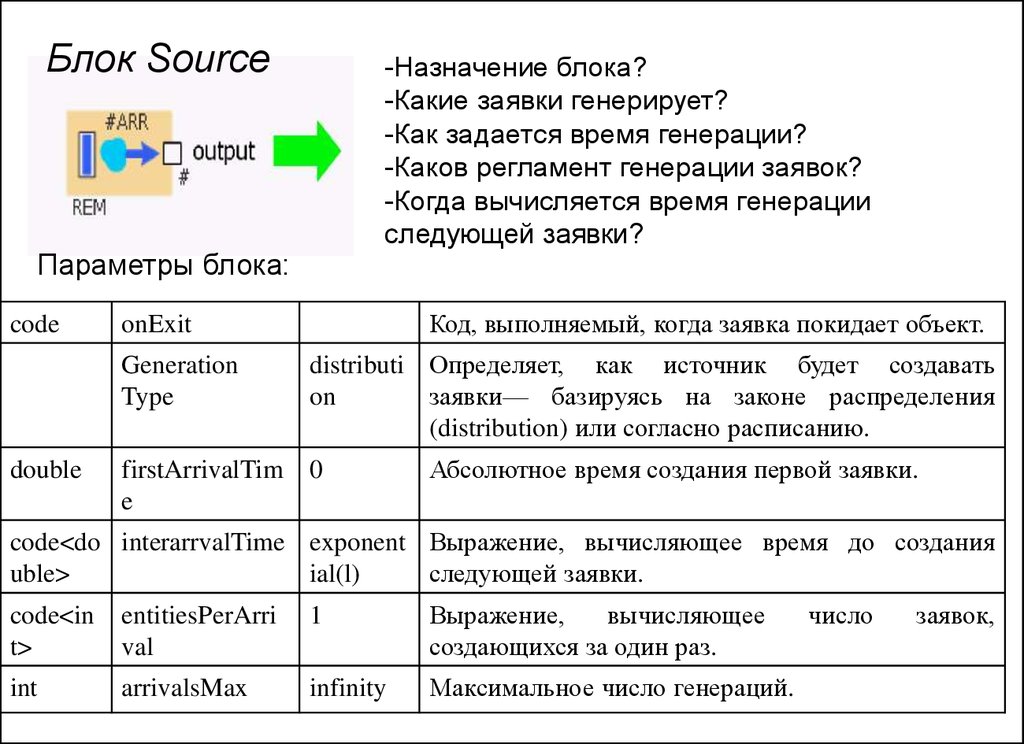
Блок Source-Назначение блока?
-Какие заявки генерирует?
-Как задается время генерации?
-Каков регламент генерации заявок?
-Когда вычисляется время генерации
следующей заявки?
Параметры блока:
code
Generation
Type
double
Код, выполняемый, когда заявка покидает объект.
onExit
distributi Определяет, как источник будет создавать
on
заявки— базируясь на законе распределения
(distribution) или согласно расписанию.
firstArrivalTim 0
e
Абсолютное время создания первой заявки.
code<do interarrvalTime exponent Выражение, вычисляющее время до создания
uble>
ial(l)
следующей заявки.
code<in
t>
entitiesPerArri
val
1
Выражение,
вычисляющее
создающихся за один раз.
int
arrivalsMax
infinity
Максимальное число генераций.
число
заявок,
90
91.
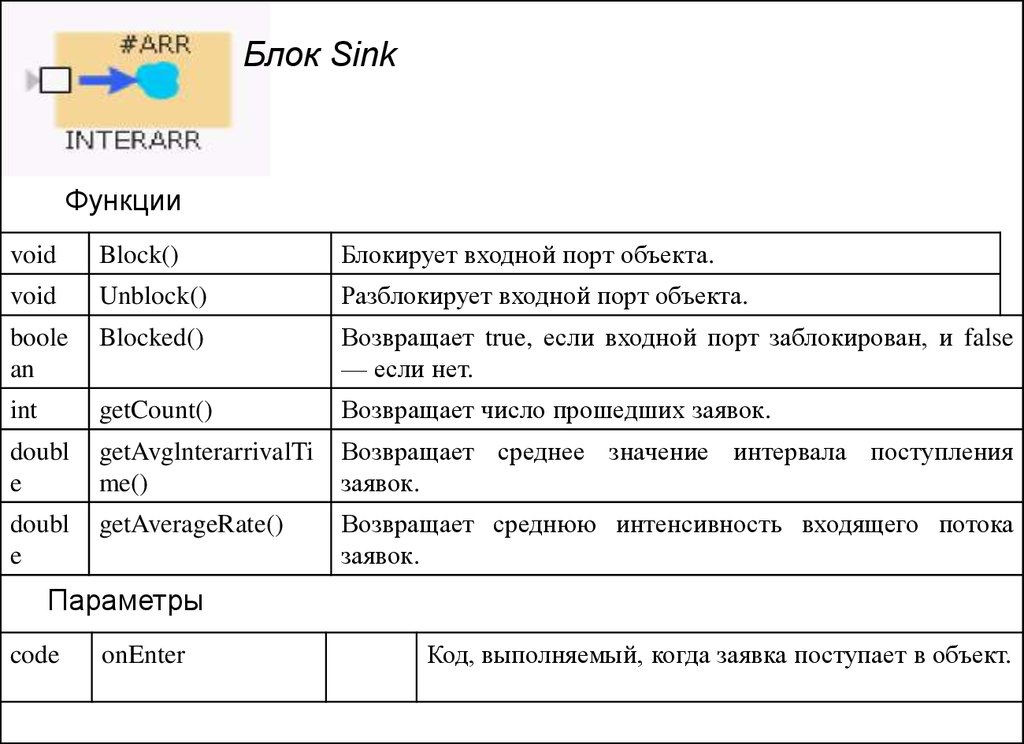
Блок SinkФункции
void
Block()
Блокирует входной порт объекта.
void
Unblock()
Разблокирует входной порт объекта.
boole
an
Blocked()
Возвращает true, если входной порт заблокирован, и false
— если нет.
int
getCount()
Возвращает число прошедших заявок.
doubl
e
getAvglnterarrivalTi
me()
Возвращает среднее значение интервала поступления
заявок.
doubl
e
getAverageRate()
Возвращает среднюю интенсивность входящего потока
заявок.
Параметры
code
onEnter
Код, выполняемый, когда заявка поступает в объект.
91
92.
Блок DelayПеременные
1. Назначение блока?
2. Как задается время задержки?
3. Сколько заявок одновременно
могут быть задержаны?
4. Время задержки для всех заявок
одинаково?
5. Что происходит, если блок
заполнен полностью?
Тип
Имя
Описание
Entity
entity
Текущая заявка.
double
delayTime Value
Значение задержки для текущей заявки.
92
93.
ФункцииТип
Имя
Описание
void
block()
Блокирует входной порт.
void
unblock()
Разблокировывает входной порт.
boolean
blocked()
Возвращает true, если входной порт заблокирован, и false —
если нет.
int
size()
Число задержанных (находящихся в объекте) в данный
момент заявок.
Entity
get(inti)
Возвращает i-ю заявку.
boolean
canEnter()
Возвращает true, если новая заявка может быть принята
TimedDataSet
getStatsUtilization()
Возвращает статистику использования объекта.
93
94.
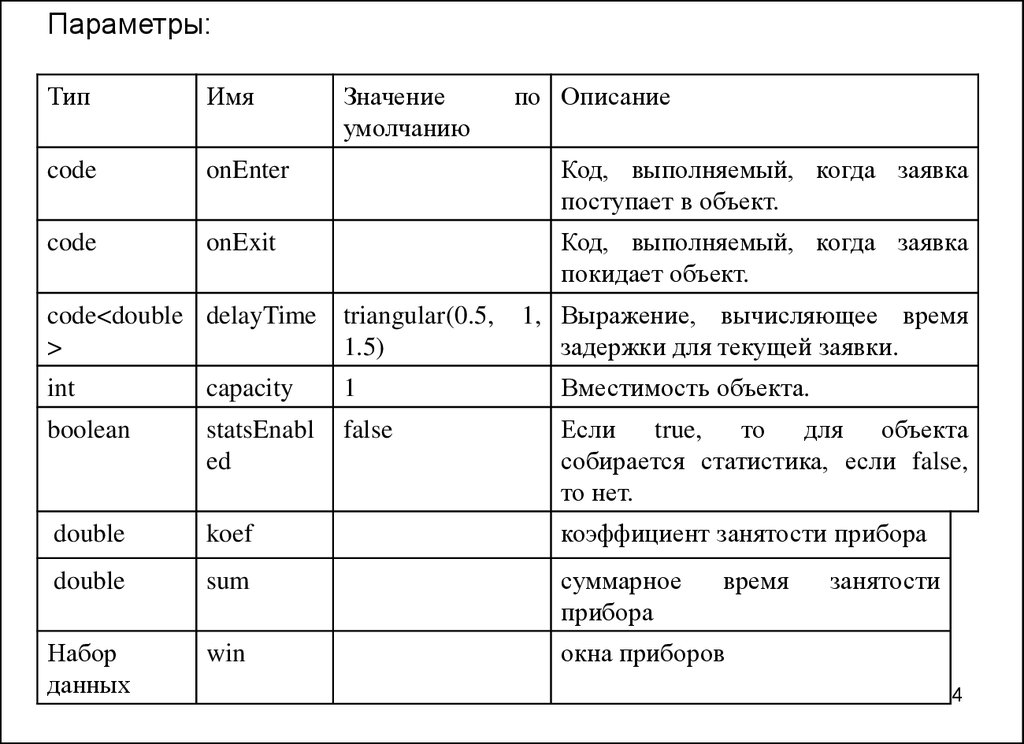
Параметры:Тип
Имя
Значение
умолчанию
по Описание
code
onEnter
Код, выполняемый, когда заявка
поступает в объект.
code
onExit
Код, выполняемый, когда заявка
покидает объект.
1, Выражение, вычисляющее время
задержки для текущей заявки.
code<double delayTime
>
triangular(0.5,
1.5)
int
capacity
1
Вместимость объекта.
boolean
statsEnabl
ed
false
Если true, то для объекта
собирается статистика, если false,
то нет.
double
koef
коэффициент занятости прибора
double
sum
суммарное
прибора
Набор
данных
win
окна приборов
время
занятости
94
95.
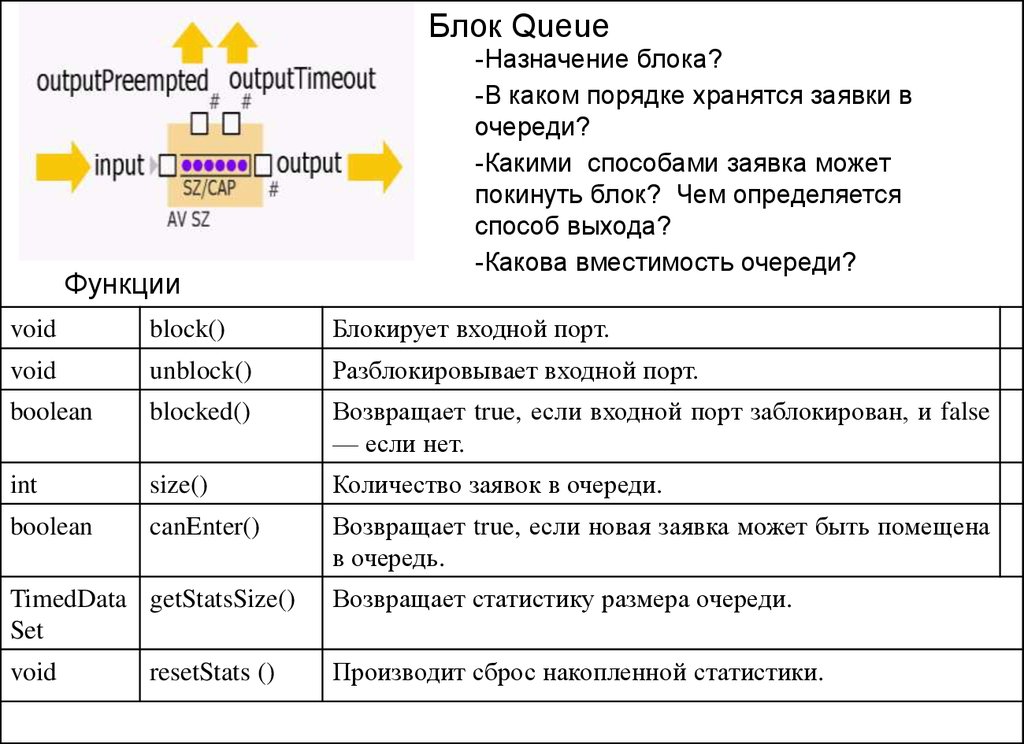
Блок QueueФункции
-Назначение блока?
-В каком порядке хранятся заявки в
очереди?
-Какими способами заявка может
покинуть блок? Чем определяется
способ выхода?
-Какова вместимость очереди?
void
block()
Блокирует входной порт.
void
unblock()
Разблокировывает входной порт.
boolean
blocked()
Возвращает true, если входной порт заблокирован, и false
— если нет.
int
size()
Количество заявок в очереди.
boolean
canEnter()
Возвращает true, если новая заявка может быть помещена
в очередь.
TimedData getStatsSize()
Set
Возвращает статистику размера очереди.
void
Производит сброс накопленной статистики.
resetStats ()
95
96.
Параметры:Тип
Имя
Пo
умолчани
ю
Описание
code
onEnter
Код, выполняемый, когда заявка поступает в
объект.
code
onExit
Код, выполняемый, когда заяка покидает объект
или через порт output
code
onExitPreempt
ed
Код, выполняемый, когда заявка покидает объект
через порт outputPreempted
code
onExitTimeout
Код, выполняемый, когда заявка покидает объект
через порт outputTimeout
int
queueType
FIFO
Тип очереди: FIFO, LIFO,
RANDOM, PRIORITY
integer
capacity
100
Вместимость очереди.
boolean
preemption
false
Если true, то включен режим вытеснения.
boolean
timeout
false
Если true, то включен режим таймаута.
96
97.
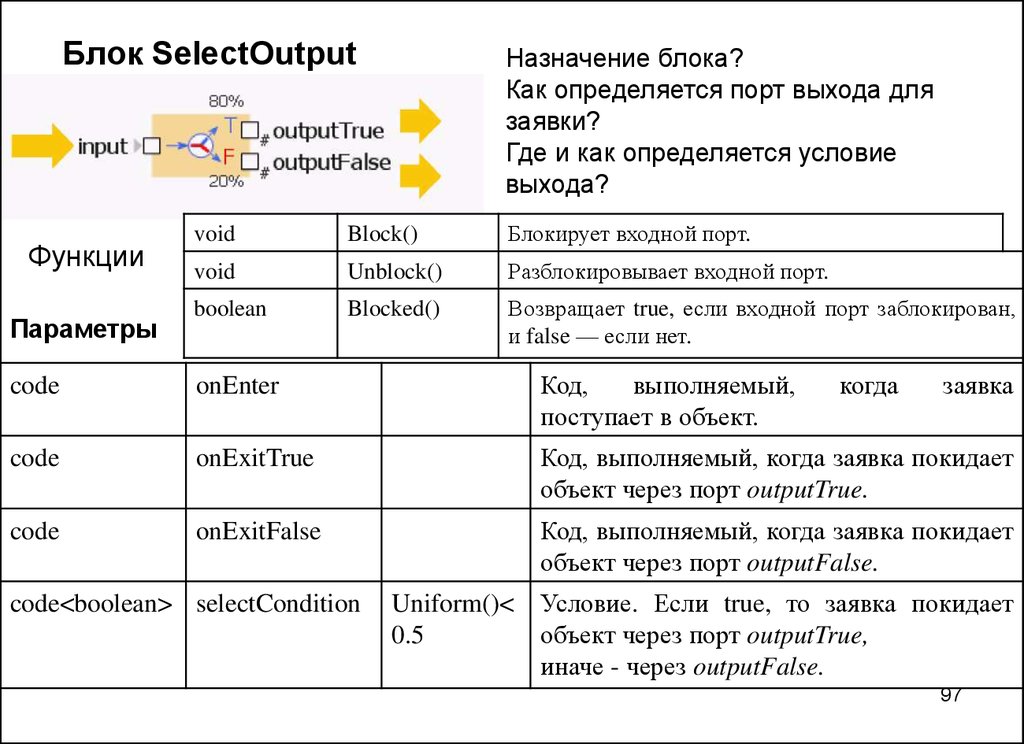
Блок SelectOutputФункции
Параметры
Назначение блока?
Как определяется порт выхода для
заявки?
Где и как определяется условие
выхода?
void
Block()
Блокирует входной порт.
void
Unblock()
Разблокировывает входной порт.
boolean
Blocked()
Возвращает true, если входной порт заблокирован,
и false — если нет.
code
onEnter
Код,
выполняемый,
поступает в объект.
code
onExitTrue
Код, выполняемый, когда заявка покидает
объект через порт outputTrue.
code
onExitFalse
Код, выполняемый, когда заявка покидает
объект через порт outputFalse.
code<boolean> selectCondition
когда
заявка
Uniform()< Условие. Если true, то заявка покидает
0.5
объект через порт outputTrue,
иначе - через outputFalse.
97
98.
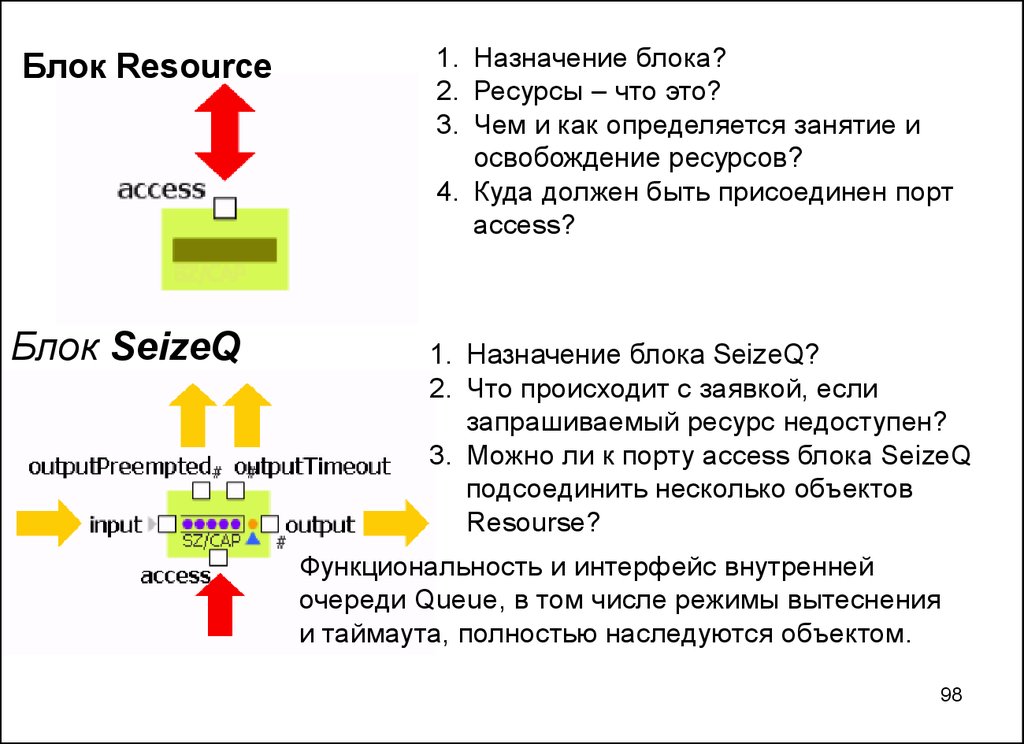
Блок ResourceБлок SeizeQ
1. Назначение блока?
2. Ресурсы – что это?
3. Чем и как определяется занятие и
освобождение ресурсов?
4. Куда должен быть присоединен порт
access?
1. Назначение блока SeizeQ?
2. Что происходит с заявкой, если
запрашиваемый ресурс недоступен?
3. Можно ли к порту access блока SeizeQ
подсоединить несколько объектов
Resourse?
Функциональность и интерфейс внутренней
очереди Queue, в том числе режимы вытеснения
и таймаута, полностью наследуются объектом.
98
99.
Блок ReleaseБлок ProcessQ
1. Назначение блока Release?
2. Можно ли к порту access объекта
Release подсоединить сразу
несколько объектов Resource?
Какой ресурс будет задействован в
этом случае?
3. Какое время занимает процедура
занятия и освобождения?
- Назначение блока?
-Какова внутренняя структура блока?
-Сколько объектов Resource можно
подсоединить к порту access объекта
ProcessQ?
-Функциональность и интерфейс каких
объектов наследуются объектом
ProcessQ
99
100.
Контрольные вопросы :На какую предметную область ориентирован класс моделей
СМО.
2. Основные подсистемы класса СМО? Какие свойства СМО
позволяет найти моделирование СМО?
3. Что такое заявка в СМО? Какие параметры необходимы для
конкретизации заявки? Потока заявок?
4. Что такое дисциплина обслуживания? Какие дисциплины Вы
знаете?
5. Основные события в СМО и действия, которые они
вызывают?
6. Дайте характеристику основных блоков библиотеки СМО?
7. Что собой представляет заявка? Как имитируется процесс
генерации заявок? Какие параметры необходимо задать для
блока source?
8. Как имитируется процесс обработки заявок? Параметры
блока delay?
9. Как удаляются заявки из системы? Параметры блока sink?
10. Регистратор очереди? Его особенности и параметры?
11. Как реализуется ветвление потока заявок?
12. Как строится модель СМО?
1.
100
101.
ЛитератураОСНОВНАЯ:
1.
2.
Кумунжиев К.В. Теория систем и системный анализ. Учебное пособие,
части 1,2. Ульяновск, 2003.
Карпов Ю.Г. Имитационное моделирование систем. – СПб.: БХВПетербург, 2005.-400 с.
ДОПОЛНИТЕЛЬНАЯ:
1.
2.
3.
4.
5.
6.
7.
Бенькович Е.С, Колесов Ю.Б., Сениченков Ю.Б. Практическое
моделирование динамических систем – СПб.:БХВ-Петербург, 2002.
Дубров А.М., Лагоша Б.А., Хрусталев Е.Ю. Моделирование рисковых
ситуаций в экономике и бизнесе. Учебное пособие. М., 2000.
Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное
моделирование экономических процессов: Учебное пособие. – М.:
Финансы и статистика, 2002.
Ослин Б.Г. Имитационное моделирование систем массового
обслуживания. Томск, 2003.
Питерсон Дж. Теория сетей Петри и моделирование систем. М.: Мир,
1984.
Советов Б.Я., Яковлев С.А. Моделирование систем. Учебник для вузов.
М., 1998.
Трояновский В.М. Математическое моделирование в менеджменте.
Учебное пособие. М., 2000.
101
102.
Оглавление:1. Принципы построения языков и систем моделирования……………3
2. Алгебро-дифференциальные уравнения как класс моделей……...11
3. Потоковые схемы…………………………………………………… ……16
4. Сигнальные схемы…………………………………………………….…...22
5. Операторный метод и структурные схемы………………….………....28
6. Сигналы в частотной области…………………………………..……..…36
7. Системы в частотной области…………………………………………....41
8. Идентификация моделей по экспериментальным данным……… ...49
9. Моделирование асинхронных дискретных систем……..……………..58
10. Асинхронные дискретно-событийные процессы……………………..71
11. Системы массового обслуживания………………………………….....86
Литература………………………………………….………………………....102
102































































 Программирование
Программирование Информатика
Информатика








