Похожие презентации:
Пара сил. (Лекция 3)
1. Лекция №3
2. 2.4. Пара сил.
Определение. Система из 2 равных по величинеи противоположных по направлению сил,
действующих на одно и то же твердое тело,
называется парой сил.
F2
F1
А
В
- пара сил,
АВ - образующая.
F1 , F2
3.
Свойства:1. Проекция пары сил на любую координатную
ось равна 0.
2. Алгебраическим (векторным) моментом пары
сил называется алгебраический (векторный)
момент одной из сил пары, вычисленный
относительно точки приложения другой силы
из
этой
пары,
т.е.
M (F , F ) M (F ) M (F )
1
2
B
1
A
2
4.
Следствие. Любую совокупность пар сил можнозаменить одной парой сил.
Замечание. Пара сил задается не при помощи сил
и образующих, а при помощи ее векторного
(алгебраического) момента.
5. 3. Статика
Статика изучает равновесие тел.6. 3.1. Основная теорема статики (теорема Пуансо)
Рассмотрим совокупность сил, действующихn
на ТТ
F-
k
k 1
F1
A1
B
A2
An
Fn
F2
7.
Определение. Главным вектором системы силназывают вектор R n F
, который
k
k 1
приложен в центре приведения.
Определение. Главным моментом системы
сил относительно точки В называют вектор
n
M B M B ( Fk )
k 1
8.
Основная теорема статики. Любую системусил, действующих на одно твердое тело,
можно заменить на эквивалентную ей по
действию систему сил, составленную из
силы, равной главному вектору этой
системы сил, и пары сил, векторный момент
которой равен главному моменту этой
системы сил, т. е.
F
n
k
k 1
~ R, M B
9. 3.2. Условие равновесия системы сил (уравнения равновесия)
Определение. Система сил находится вравновесии, если выполнено условие:
RA 0,
M A 0.
10.
Плоская система сил:n
RA Fk
k 1
n
M A M A ( Fk )
k 1
Fkx 0,
k 1
n
k 1Fky 0.
n
k 1M A ( Fk ) 0
n
т. А xy
11. 3.6. Внешние и внутренние силы.
Определение. Сила взаимодействия междуточками, входящими в одну механическую
систему, называются внутренними и
обозначаются(i ) .
Определение. Сила взаимодействия между
точками, не входящими в одну
механическую систему, называются
(e) внешними и обозначаются
.
12.
Свойства:1. Главный вектор внутренних сил равен 0.
2. Главный момент внутренних сил равен 0.
13. 4. Динамика механических систем.
4.1. Основные теоремы динамикиТеорема 1 (об изменении количества
движения
механической системы).
dQ (e ) - дифференц. форма записи
F
dt
Скорость изменения количества движения
механической системы равна главному
вектору внешних сил, действующих на
данную механическую систему.
14.
Определение. Количеством движения МТqk mk vk
называется вектор МТ, равный
.
Определение. Количеством движения МС
называется свободный вектор, равный
геометрической сумме количеств движения
n
n
материальных точек, т.е.
Q q k mk v k
k 1
k 1
15.
Определение. Полным импульсомвнешних
t
(e)
(e)
сил
S F dt
0
называется выражение:
.
(e)
Q Q0 S
записи
- интегральная форма
Изменение количества движения
механической системы за конечный
промежуток времени равно полному
импульсу внешних сил, вычисленных за тот
же самый промежуток времени.
16.
Законы сохранения:(e)
0 Q const
1. Если F
(e)
2. Если Fx 0 Qx const
( e)
F M
3. Если t 0
.
.
Q const
17.
Теорема 2 (о движении центра масс).(e )
MwC F
Центр масс хоть и является
геометрической точкой, но движется по
закону материальной точки,
обладающих массой всей механической
системы, под действием внешних сил,
приложенных к точкам механической
системы.
18.
Определение. Центром масс называетсягеометрическая точка, радиус-вектор
которой определяется согласно формуле:
mk rk
n
rC
k 1
n
m
k 1
k
19.
Если движение задано в декартовойпрямоугольной системе координат, то
координаты центра масс определяются по
формуле:
n
mk x k
k 1
x
,
n
C
mk
k 1
n
mk y k
k 1
,
yC n
mk
k 1
n
mk z k
k 1
zC n
mk
k 1
20.
Замечание: хотя внутренние силы явно вформуле не участвуют, они вызывают
изменение внешних сил, которые в свою
очередь влияют на движение
механической системы.
Законы сохранения:
(e)
1. Если F
0 wC 0
2. Если F ( e ) 0 wCx 0
x
3. Если t 0 F ( e) M
.
.
wC 0
21.
Теорема об изменении кинетического моментаМС
(e )
dK O
MO
dt
Скорость изменения кинетического момента
механической системы относительно какойлибо точки равна главному моменту
внешних сил, вычисленного относительно
той же самой точки.
Эта теорема справедлива и для координатных
осей:
22.
dK Ox(e)
M
,
Ox
dt
dK Oy
(e)
M Oy ,
dt
dK Oz
(e)
dt M Oz .
Рассмотрим случай, когда ТТ совершает
вращательное движение относительно оси
z:
K Oz I z
23.
Определение. Кинетическим моментом МТотносительно точки (оси) называют момент
количества движения данной точки,
вычисленный относительно точки (оси), т.
е.
K O M O (q ) M O (mv )
K x M x (q ) M x (mv ),
K y M y (q ) M y (mv ),
K M (q ) M (mv ).
z
z
z
24.
Определение. Моментом инерциимеханической системы относительно т. О
n
называютI величину,
.
m r 2 равную
O
k 1
k k
Определение. Моментом инерции
механической системы относительно
координатных осей называют величины,
n
равные
2
I x mk dxk ,
k 1
n
2
I
m
dy
y k k ,
k 1
I n m dz 2 ,
k
k
z
k 1
25.
Определение. Радиусом инерциимеханической системы относительно точки
(осей) называют величины, равные
IO
iO
M
Ix
и i x M ,
Ix
,
i x
M
Ix
i x M .
26.
Законы сохранения:(e)
1. Если M O 0 K O const
(e)
K Ox const
M
0
Ox
2. Если
(е)
3. Если t 0 М О M
.
.
K O const
.









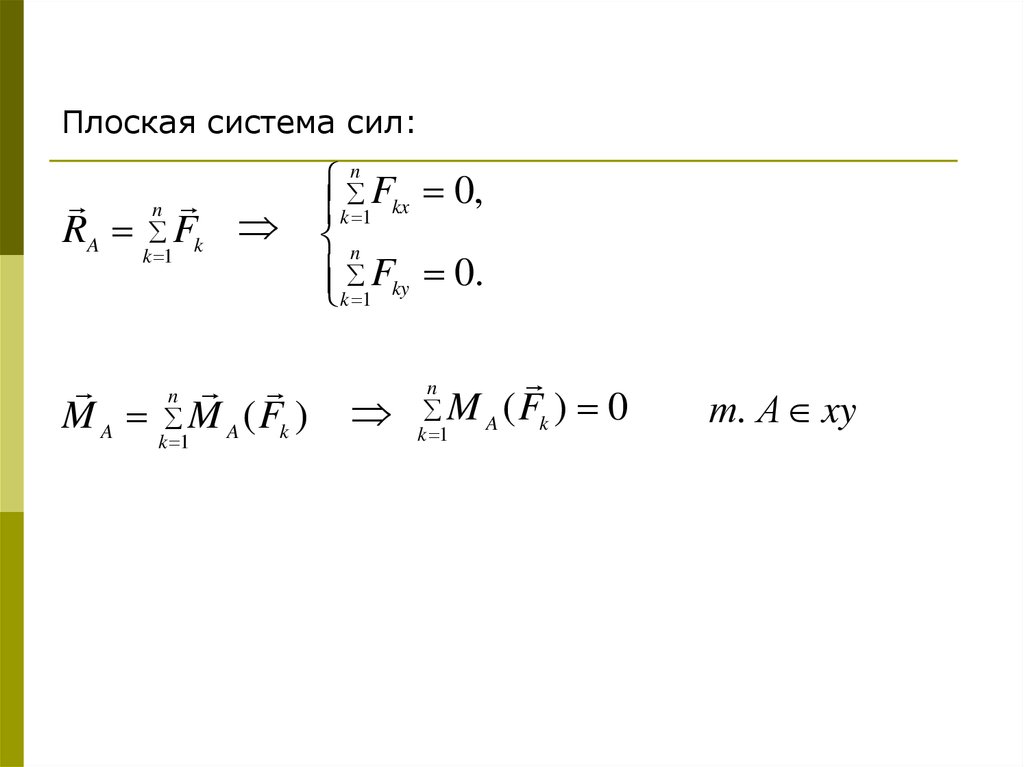
















 Физика
Физика








