Распределения Стьюдента и Пирсона

1.

Распределения Стьюдента и Пирсона.

2.

Распределение Пирсона (хи-квадрат)
Определение. Распределением Пирсона с k степенями свободы называется
распределение суммы квадратов k независимых случайных величин, распределённых по стандартному нормальному закону, т.е.
где Zi (i=1,2,…,k) имеет нормальное распределение N(0;1).
Его плотность вероятности имеет вид:
Для целых положительных
значений:

3.

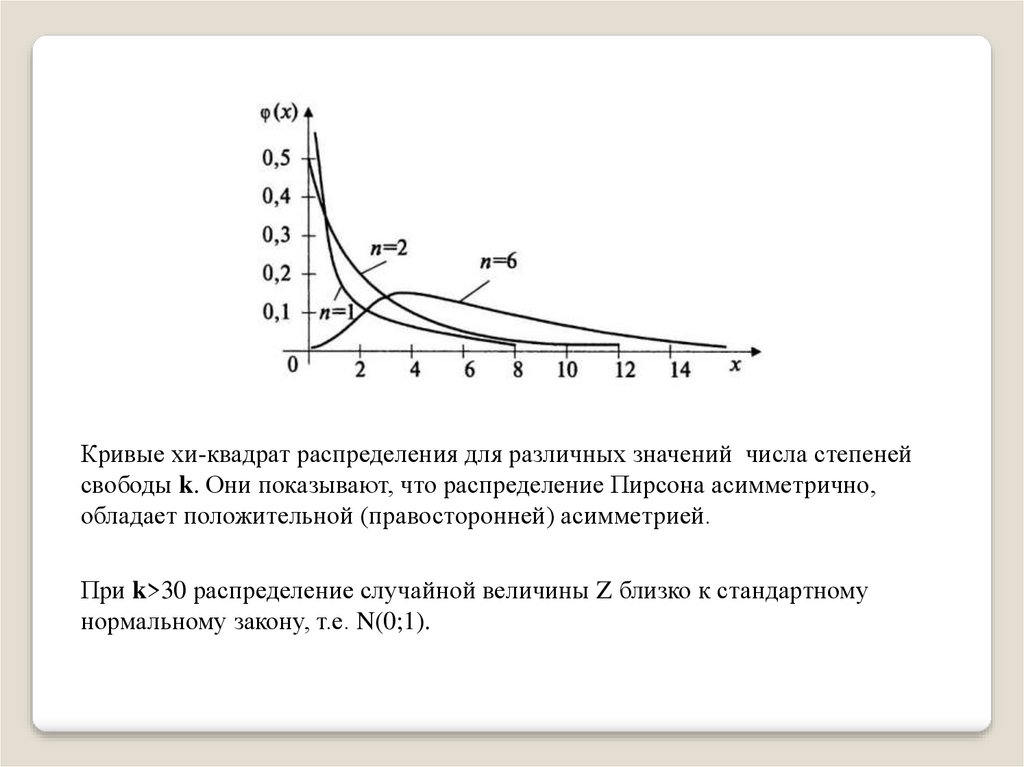
Кривые хи-квадрат распределения для различных значений числа степеней
свободы k. Они показывают, что распределение Пирсона асимметрично,
обладает положительной (правосторонней) асимметрией.
При k>30 распределение случайной величины Z близко к стандартному
нормальному закону, т.е. N(0;1).

4.

Распределение Стьюдента.
Определение. Распределением Стьюдента (или t-распределением) называется
распределение случайной величины
где Z – случайная величина, распределённая по стандартному нормальному
закону, т.е. N(0;1).
-независимая от Z случайная величина, имеющая распределение Пирсона с
k степенями свободы.
Плотность вероятности распределения Стьюдента имеет вид:

5.

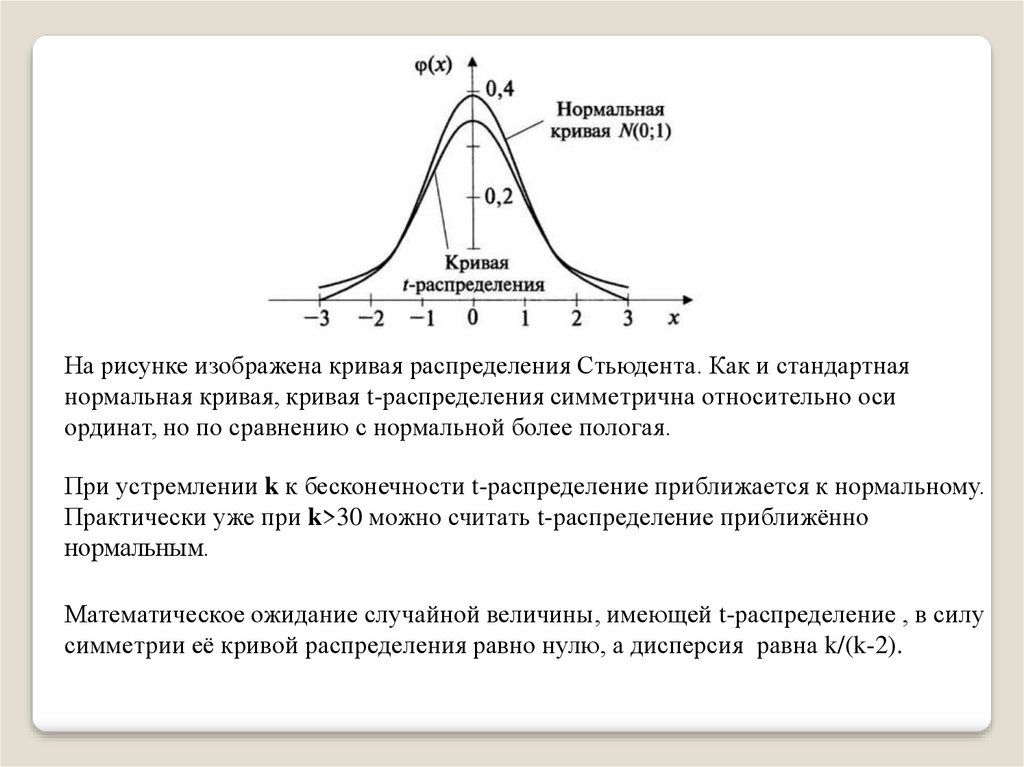
На рисунке изображена кривая распределения Стьюдента. Как и стандартная
нормальная кривая, кривая t-распределения симметрична относительно оси
ординат, но по сравнению с нормальной более пологая.
При устремлении k к бесконечности t-распределение приближается к нормальному.
Практически уже при k>30 можно считать t-распределение приближённо
нормальным.
Математическое ожидание случайной величины, имеющей t-распределение , в силу
симметрии её кривой распределения равно нулю, а дисперсия равна k/(k-2).

6.

Построение доверительного интервала для генеральной средней по малой выборке
(рассматриваемый признак имеет нормальное распределение).
Формула доверительной вероятности для малой выборки:
- предельная ошибка малой выборки
Доверительный интервал для генеральной средней:

7.

Задачка. Из большой партии счётчиков частиц отобрали 20 приборов.
Среднеквадратичное отклонение числа зарегистрированных частиц среди
отобранных приборов составило 30. Найти вероятность того, что среднее
число регистраций во всей партии отличается от среднего числа регистраций
среди отобранных счётчиков не более, чем на 15.

8.

9.

Построение доверительного интервала для генеральной дисперсии.
Формула доверительной вероятности для генеральной дисперсии:
Для среднеквадратичного отклонения:

10.

Задачка. Производилось наблюдение 20 радиоактивных образцов в течение часа.
Среднеквадратичное отклонение числа распадов этих образцов составило 15.
Предполагая, что количество распадов подчинено нормальному распределению,
найти границы, в которых с вероятностью 0,9 заключена генеральная дисперсия
числа распадов в час.