Похожие презентации:
Теория вероятностей. Основные законы распределения случайных величин
1. Теория вероятностей
Основные законы распределенияслучайных величин
2.
Нормальный закон распределенияНСВ Х имеет нормальный закон распределения
(закон Гаусса) с параметрами а и σ2 (Х~N(а; σ2)), если
ее плотность вероятности имеет вид:
f N ( x)
1
2
e
( x a )2
2 2
Кривую нормального закона распределения
называют нормальной или гауссовой кривой.
3.
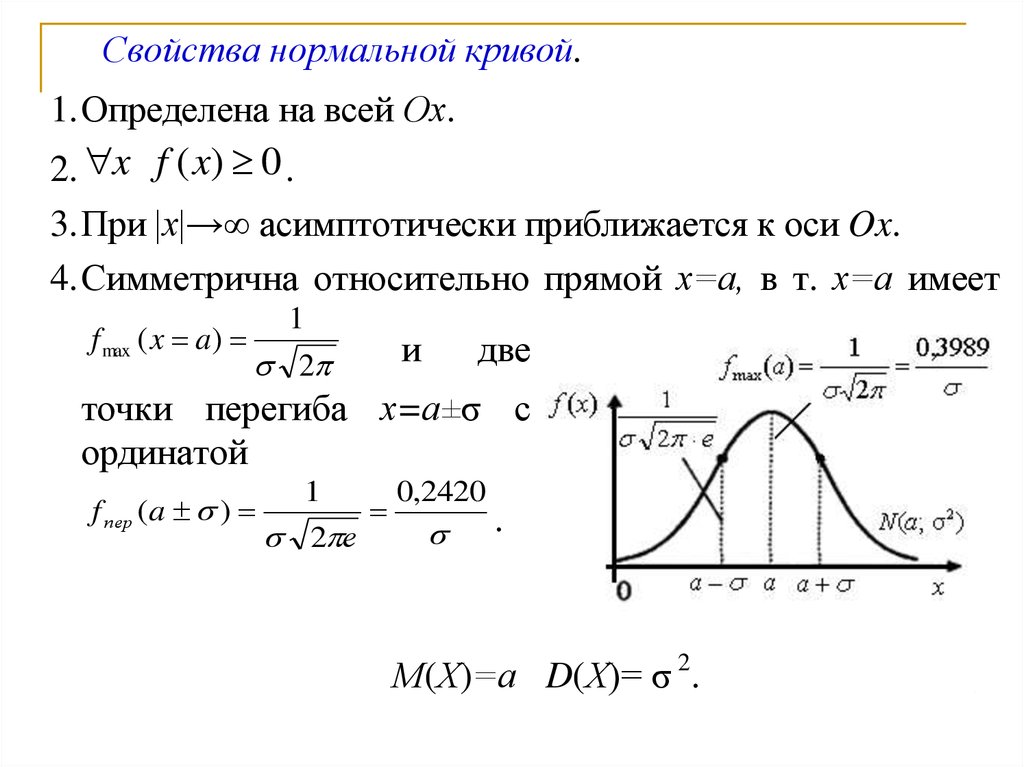
Свойства нормальной кривой.1. Определена на всей Ох.
2. x f ( x) 0 .
3. При |х|→∞ асимптотически приближается к оси Ox.
4. Симметрична относительно прямой х=а, в т. х=а имеет
1
f max ( x a)
2
и
две
точки перегиба х=а±σ с
ординатой
f пер (a )
1
2 е
0,2420
.
М(Х)=а D(Х)= σ 2.
4.
x aНормальный закон распределения СВ Z
с
параметрами а=0, σ2=1, т.е. N(0;1), называется стандартным
x a
Z
или нормированным, а соответствующая СВ
называется стандартной или нормированной
z
1
f N ( z)
e 2
2
Функция распределения:
2
1 1 x a
FN ( x) Ф
2 2
5.
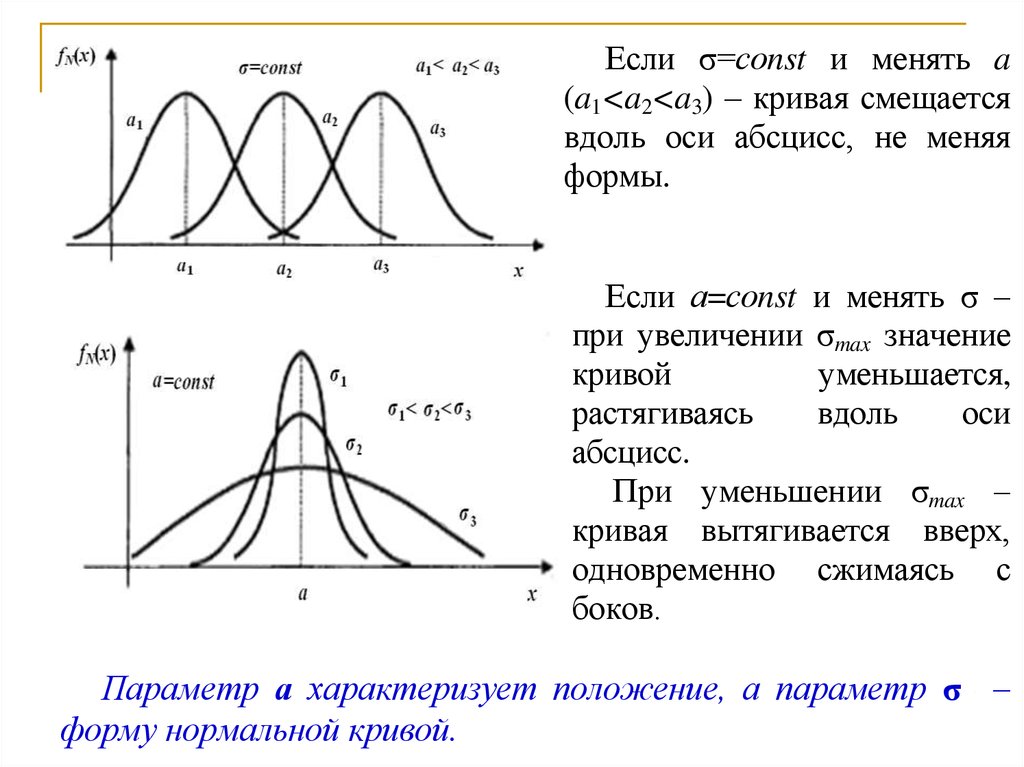
Если σ=соnst и менять a(a1<a2<a3) – кривая смещается
вдоль оси абсцисс, не меняя
формы.
Если а=соnst и менять σ –
при увеличении σmax значение
кривой
уменьшается,
растягиваясь
вдоль
оси
абсцисс.
При уменьшении σmax –
кривая вытягивается вверх,
одновременно сжимаясь с
боков.
Параметр а характеризует положение, а параметр σ –
форму нормальной кривой.
6.
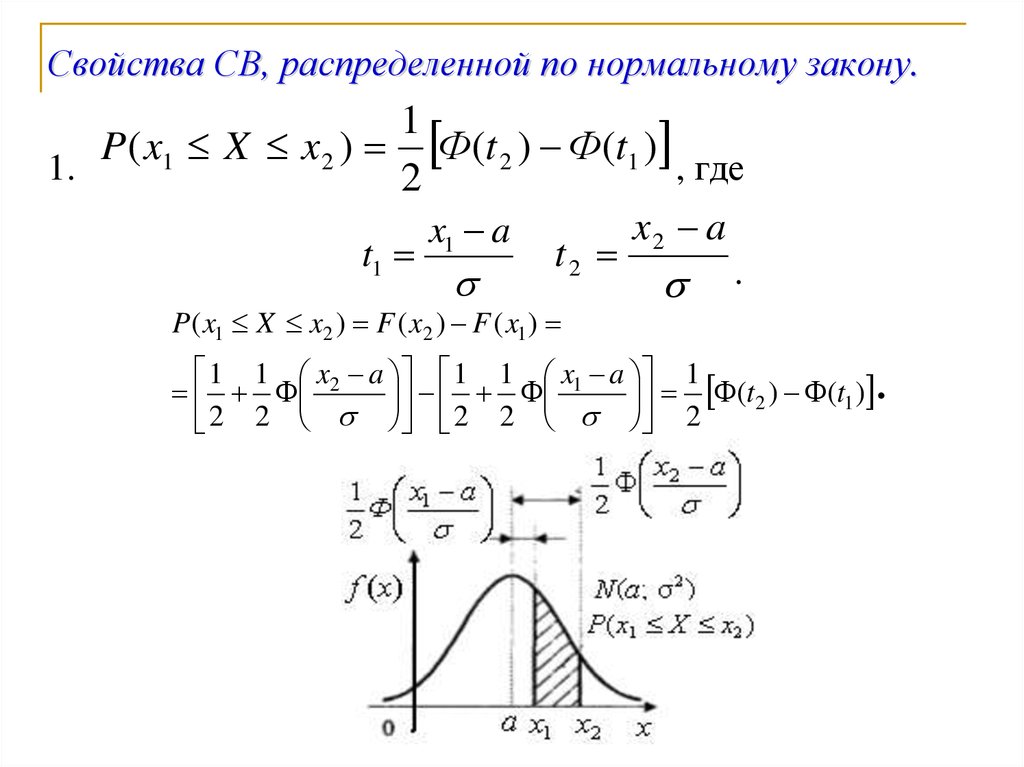
Свойства СВ, распределенной по нормальному закону.1
P( x1 X x 2 ) Ф(t 2 ) Ф(t1 )
1.
, где
2
x2 a
x1 a
t1
t2
.
P( x1 X x2 ) F ( x2 ) F ( x1 )
1 1 x a 1 1 x1 a 1
2
(t2 ) (t1 ) .
2 2 2 2 2
7.
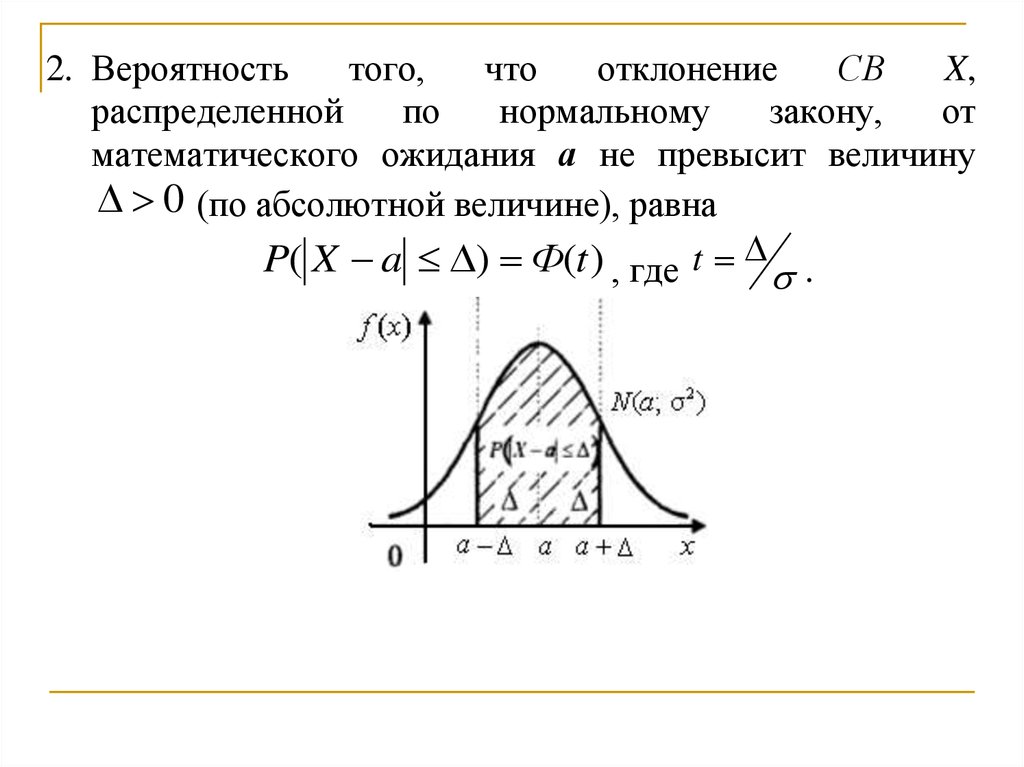
2. Вероятностьтого,
что
отклонение
СВ
X,
распределенной
по
нормальному
закону,
от
математического ожидания а не превысит величину
0 (по абсолютной величине), равна
P( X a ) Ф(t ) , где t .
8.
Вычисляя при различных значениях Δ вероятностиP( X a ) (t ) ,
получим
Δ=
P( X a ) Ф(1) 0,6827 ,
Δ=2
P( X a 2 ) Ф(2) 0,9545 ,
Δ=3
P( X a 3 ) Ф(3) 0,9973 .
«Правило трех сигм»:
Если СВ Х~N(а, 2), то практически достоверно, что ее
значения заключены в интервале (а–3 , а+3 ).
9.
Распределения, связанные с нормальнымраспределением
Число степеней свободы определяется как
разность между числом суммируемых CВ и
числом линейных связей, ограничивающих
свободу изменения этих величин.
10.
χ2-распределение (распределение Пирсона).Распределением χ2 (хи-квадрат) с k степенями свободы
называется распределение суммы квадратов k независимых СВ,
распределенных по стандартному нормальному закону, т.е.
k
2 Z i2
i 1
,
где Zi (i 1,k ) ~ N (0; 1) .
Плотность вероятности χ2 - распределения имеет вид:
k
x
1
1
x2 e 2,
k
k
f ( x) 2 2
2
0,
при х 0
при х 0
где
( y ) e t t y 1dt
0
– гамма-функция Эйлера (для целых
положительных значений Г(у)=(у-1)!).
11.
2Кривые χ – асимметричны, обладают положительной
(правосторонней) асимметрией.
Распределение
χ2(k)
определяется
одним
параметром – числом
степеней свободы k.
С увеличением числа степеней свободы распределение
медленно приближается к нормальному.
2
Z
2
2k близко к
При k>30 распределение СВ
N(0;1).
12.
Распределение Стьюдента.Распределением Стьюдента (или t-распределением)
называется
распределение
СВ,
равное
отношению
нормированной СВ к корню квадратному из независимой СВ,
распределенной по закону χ2.
t Z
1 2
k
где Z ~ N(0;1);
χ2 ~ χ2(k),независимая от Z.
Плотность вероятности распределения Стьюдента:
k 1
k 1
x2 2
2
f ( x)
1
n
k
k
2
где Г(y) — гамма-функция в точке у.
13.
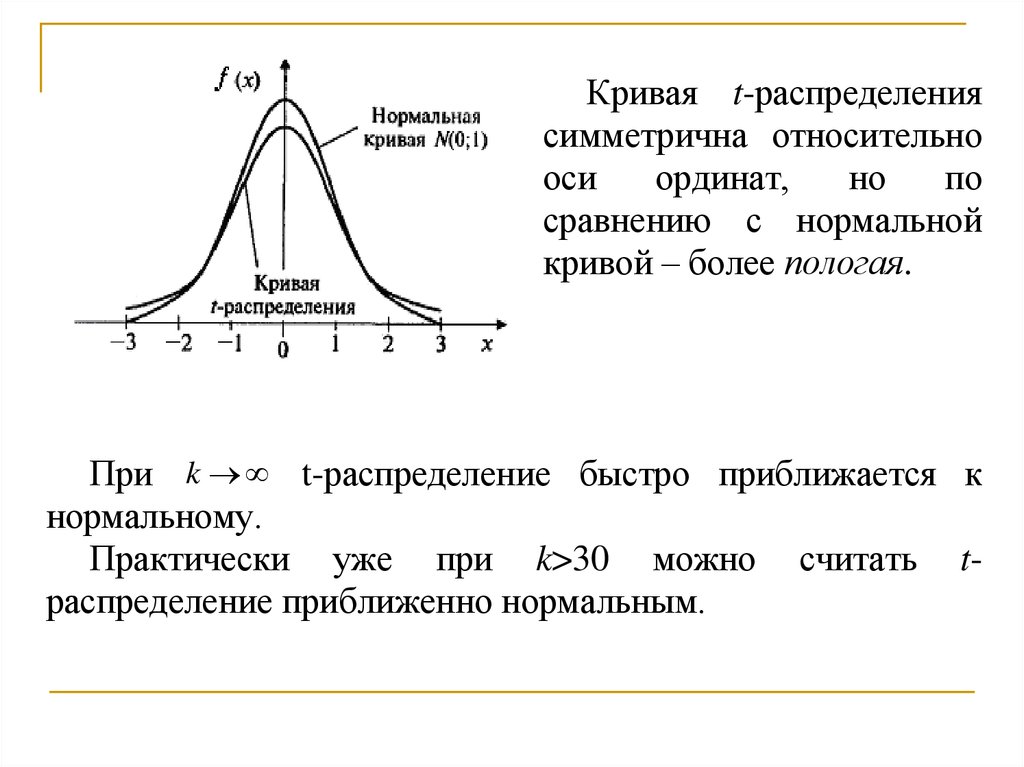
Кривая t-распределениясимметрична относительно
оси
ординат,
но
по
сравнению с нормальной
кривой – более пологая.
При k t-распределение быстро приближается к
нормальному.
Практически уже при k>30 можно считать tраспределение приближенно нормальным.
14.
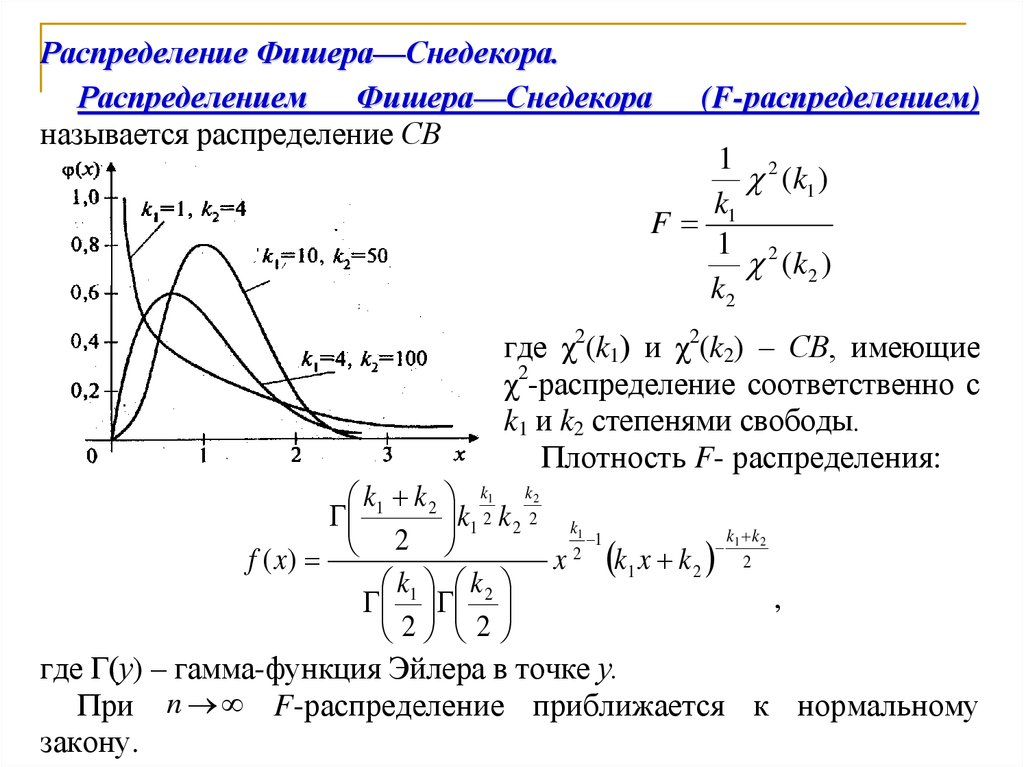
Распределение Фишера—Снедекора.Распределением
Фишера—Снедекора
называется распределение СВ
(F-распределением)
1 2
(k1 )
k1
F
1 2
(k 2 )
k2
где χ2(k1) и χ2(k2) – СВ, имеющие
χ2-распределение соответственно с
k1 и k2 степенями свободы.
Плотность F- распределения:
k1 k 2 k1 k2
k1 2 k 2 2 k1
k k
1
2
1 2
2
f ( x)
x k1 x k 2 2
k k
,
1 2
2 2
где Г(у) – гамма-функция Эйлера в точке у.
При n F-распределение приближается к нормальному
закону.
15. Математическая статистика
Проверка статистическихгипотез
16.
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗСтатистическая гипотеза – некоторое предположение,
формулируемое на основе выборки, о законе распределения СВ
или о параметрах этого закона.
Проверяемую гипотезу, утверждающую, что различие между
сравниваемыми характеристиками отсутствует, а наблюдаемые
отклонения объясняются лишь случайными колебаниями в
выборках называют нулевой (основной) гипотезой и обозначают
Н0.
Гипотезу Н1, являющуюся логическим отрицанием Н0,
называют альтернативной (конкурирующей), т.е. если гипотеза
Н0 будет отвергнута, то будет иметь место альтернативная
гипотеза Н1.
Замечание. Н0 часто специально подбирается так, чтобы
отвергнуть ее и принять тем самым альтернативную.
17.
ОШИБКИ ПЕРВОГО И ВТОРОГО РОДАПринятие или отклонение выдвинутой гипотезы
соответствует истине с некоторой вероятностью.
Н0
Ошибка первого рода возникает с вероятностью тогда,
когда отвергается верная гипотеза Н0 и принимается
конкурирующая гипотеза Н1:
PH 0 ( H1 ) .
Вероятность называется уровнем значимости.
Ошибка второго рода возникает с вероятностью в том
случае, когда принимается неверная гипотеза Н0, в то время
как справедлива конкурирующая гипотеза Н1:
PH1 ( H 0 ) .
18.
Кроме совершения ошибок может быть принято иверное решение.
Доверительная вероятность – это вероятность не
совершить ошибку первого рода и принять верную
гипотезу Н0:
PH0 ( H 0 ) 1 .
Вероятность отвергнуть ложную
называется мощностью критерия:
гипотезу
Н0
PH1 ( H1 ) 1 .
Исключить ошибки первого и второго рода
невозможно в силу ограниченности выборки.
Единственный способ уменьшения вероятности
ошибок – увеличение объема выборки.
19.
Правило, по которому гипотеза Н0 принимается илиотвергается, называется статистическим критерием
(
x
,...,
x
)
1
n
(статистика):
.
( x1 ,..., xn )
Статистика
–
специально
подобранная выборочная характеристика, точное или
приближенное распределение которой известно.
Статистику обозначают
u или z, если она распределена нормально,
F – по закону Фишера-Снедекора,
t – по закону Стьюдента,
χ2– по закону χ – квадрат.
Вычисленное по выборке значение критерия
*
называют наблюдаемым значением φнабл= .
20.
КРИТИЧЕСКАЯ ОБЛАСТЬ.ОБЛАСТЬ ПРИНЯТИЯ ГИПОТЕЗЫ
Множество W возможных значений критерия, при
которых Н0 не отклоняется, называется областью
принятия гипотезы, а множество W возможных
значений критерия, при которых Н0 отклоняется,
называется критической областью.
Основной принцип проверки статистической
гипотезы:
Если значение критерия φ попадает в область W, то
гипотеза принимается, а если в область W – гипотеза
отклоняется.
Точки, отделяющие критическую область от области
принятия гипотезы, называются критическими φкр.
21.
Заранее задается α, считая, что в одном отдельновзятом испытании событие с вероятностью меньшей
α, практически не происходит.
По α находим такое число ( ) кр , чтобы
вероятность P( набл кр ) .
кр
находят по таблицам критических точек
соответствующих распределений.
Основная идея: если набл кр , то это означает,
что произошло «практически невозможное» событие
и поэтому с вероятностью 1 гипотезу Н0 следует
отвергнуть и принять Н1.
В противном случае можно считать, что
наблюдения не противоречат гипотезе Н0.
22.
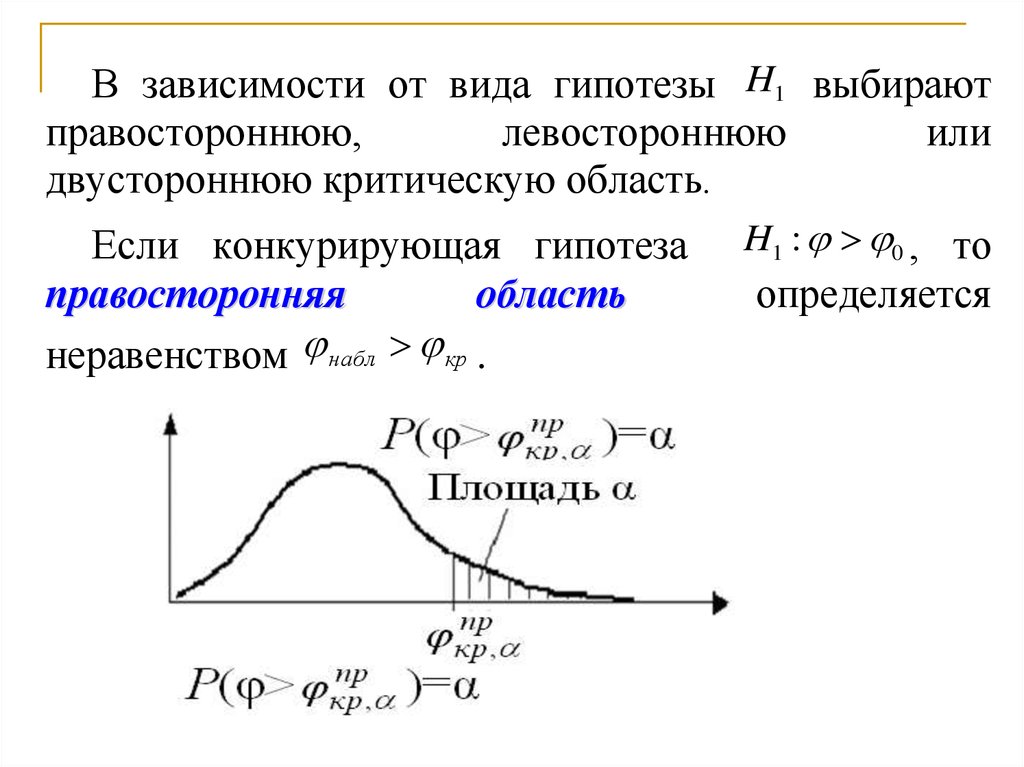
В зависимости от вида гипотезы H1 выбираютправостороннюю,
левостороннюю
или
двустороннюю критическую область.
Если конкурирующая гипотеза H1 : 0 , то
правосторонняя
область
определяется
неравенством набл кр .
23.
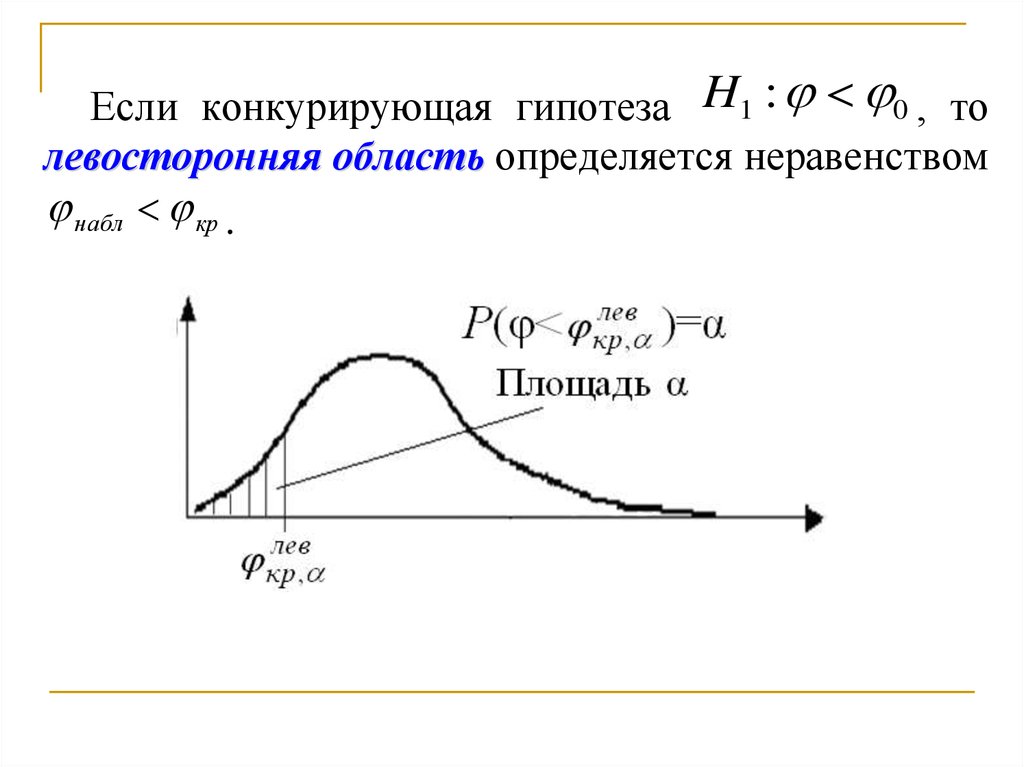
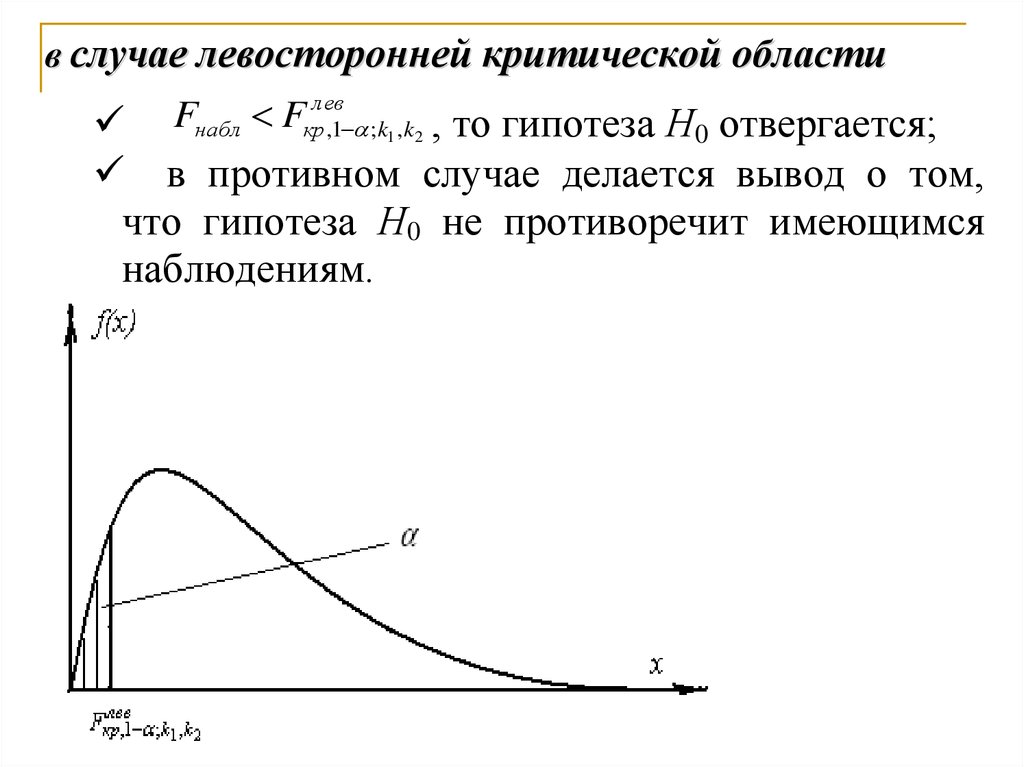
Если конкурирующая гипотеза H1 : 0 , толевосторонняя область определяется неравенством
набл кр .
24.
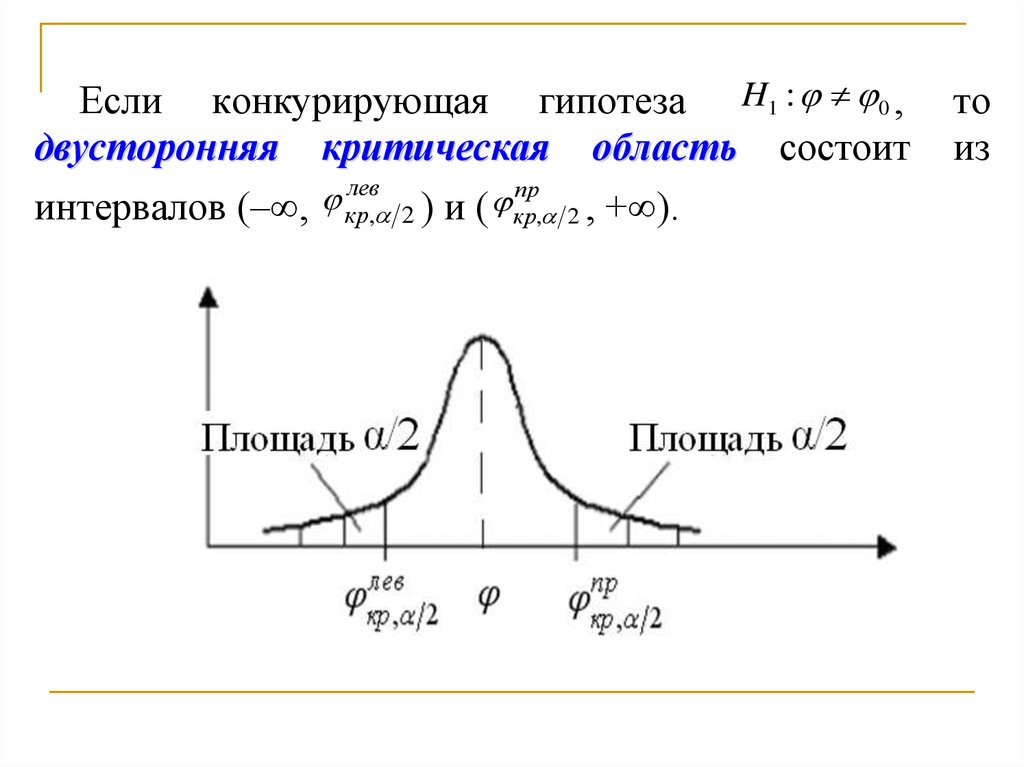
Если конкурирующая гипотеза H1 : 0 ,двусторонняя критическая область состоит
лев
пр
интервалов (–∞, кр, 2 ) и ( кр, 2 , +∞).
то
из
25.
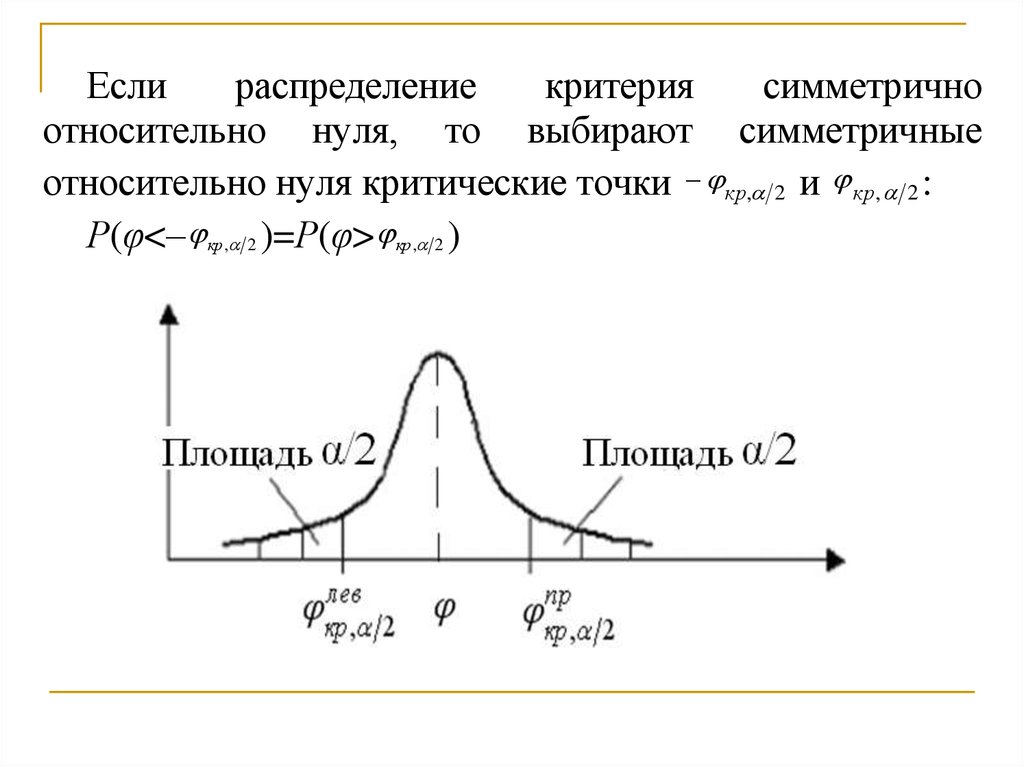
Еслираспределение
критерия
симметрично
относительно нуля, то выбирают симметричные
относительно нуля критические точки кр, 2 и кр, 2 :
Р(φ<– кр , 2 )=Р(φ> кр , 2 )
26.
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗОбщая схема проверки гипотез:
1. Формулировка проверяемой (нулевой – Н0) и
альтернативной (H1) гипотез.
2. Выбор соответствующего уровня значимости α.
3. Определение объема выборки n.
4. Выбор критерия φ для проверки Н0.
5. Определение критической области и области
принятия гипотезы.
6. Вычисление наблюдаемого значения критерия φнабл
7. Принятие статистического решения.
27. Математическая статистика
Примерыпроверки гипотез
Проверка гипотез о равенстве
числовых характеристик
генеральных совокупностей
28.
СРАВНЕНИЕ СРЕДНИХ ДВУХ ГЕНЕРАЛЬНЫХСОВОКУПНОСТЕЙ ПРИ ИЗВЕСТНЫХ ДИСПЕРСИЯХ
Имеются 2 совокупности, характеризуемые
неизвестными средними a х и a у и известными
2
2
дисперсиями
и
Необходимо проверить
х
у.
H 0 : ax a y .
H1(1) : a x a y
или
H1( 2) : a x a y
или
H1(3) : a x a y .
Для проверки Н0 взяты две независимые выборки
объемом n х и n у , по которым найдены х и у .
В случае справедливости гипотезы Н0 статистика
x y
Z
~ N (0,1)
2
2
х nx у n у
29.
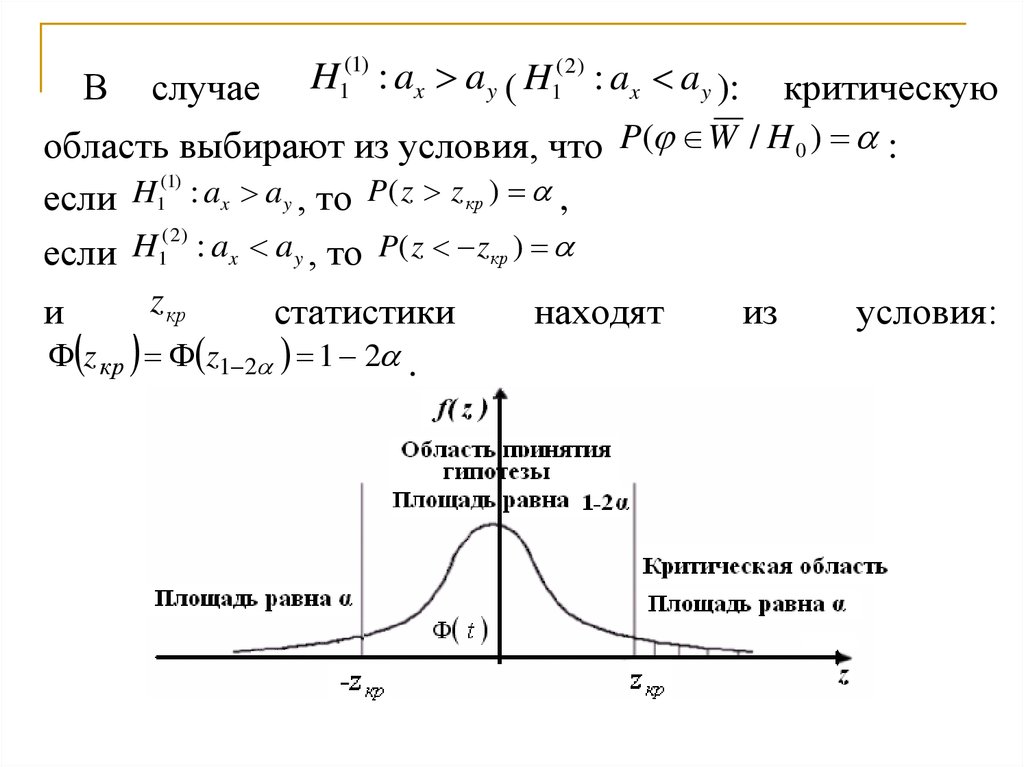
Вкритическую
область выбирают из условия, что P( W / H 0 ) :
(1)
H
если 1 : ax ay , то P( z z кр ) ,
( 2)
H
если 1 : ax ay , то P( z zкр )
z кр
и
статистики
находят
из
условия:
случае
H1(1) : ax ay ( H1( 2) : ax a y ):
z кр z1 2 1 2 .
30.
При гипотезе Н1: ax a y – двусторонняя критическаяобласть
(zкр;+∞)∩(–∞;zкр) так, чтобы
P ( z z кр )
2 и
P( z z кр )
.
Критическое значение статистики находят из условия:
z кр z1 1 .
2
Подсчитывают zнабл. Если на уровне значимости α:
|zнабл|> zкр, то гипотеза Н0 отвергается;
|zнабл|≤ zкр, то делается вывод о том, что гипотеза Н0 не
противоречит имеющимся наблюдениям.
31.
СРАВНЕНИЕСРЕДНИХ ДВУХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ
ПРИ НЕИЗВЕСТНЫХ ДИСПЕРСИЯХ
Имеются 2 совокупности, характеризуемые
неизвестными средними ах и ау.
2
2
2
Дисперсии х и у неизвестны, но равны ( х = у2 =σ2).
Необходимо проверить гипотезу
H 0 : ax a y
(1)
1
( 2)
H
: a x a y или 1 : a x a y или H1(3) : a x a y
H
В качестве неизвестной σ2 берем «исправленную»
выборочную дисперсию «смешанной» совокупности
объема nx n y
2
s
2
2
nx s x n y s y
nx n y 2 .
32.
В случае справедливости гипотезы Н0 статистикаt
Z
k
2
х у
~t (γ 1 ; k nx n y 2)
2
2
nx s x n у s у 1
1
nx n y 2 nx n y
t кр находится по таблице Стьюдента в зависимости от
критической области: односторонняя критическая область
P(t t кр ) 1 2 ,
строится
из
предположения,
что
двусторонняя – P(t t кр ) 1 .
Если наблюдаемой значение статистики на уровне
значимости α:
t набл t кр |, то гипотеза Н0 отвергается;
t набл t кр , то делается вывод о том, что гипотеза Н0 не
противоречит имеющимся наблюдениям.
33.
ПРОВЕРКА ГИПОТЕЗО РАВЕНСТВЕ ДИСПЕРСИЙ ДВУХ
СОВОКУПНОСТЕЙ
Имеются
2
нормально
распределенные
2
2
совокупности, дисперсии которых
и
у
х
неизвестны. Необходимо проверить гипотезу
H 0 : х2 y2 2
Взяты две независимые выборки объемом nx и ny.
Для
оценки
дисперсий
используются
2
2
«исправленные» выборочные дисперсии s х и s y .
2
2
Задача сводится к сравнению дисперсий s х и s y .
34.
В случае справедливости гипотезы Н0 статистика1
nx 1 s x2 2 2
n 1
s
F x
x2 ~F ( ; k1 nx 1; k 2 n y 1)
1
sy
n y 1 s y2 2
ny 1
т.к. F-распределение является несимметричным, то
2
2
H
:
1
х
y
если
– выбирают критическую область
пр
( Fкрпр, ; ) , где точка Fкр, определяется из условия
P( F (k1 nx 1; k2 ny 1) Fêðïð, ) .
если
H1 : õ2 y2
– выбирают критическую область
лев
(0; Fêðëåâ
, ) , где точка Fкр, определяется из условия
P( F (k1 ny 1; k2 nx 1) Fêðëåâ
,1 ) 1
35.
еслиH1 : õ2 y2
– выбирают двустороннюю
ëåâ
ïð
(
0
;
F
)
(
F
êð ,1 2
критическую область
и êð , 2 ; ) , где
точки
Fкрлев,1 2
пр
F
и кр,
находят из условия
P( F (k1 ny 1; k2 nx 1) Fêðëåâ
,1 2 ) 1 2
2
P( F (k1 nx 1; k2 ny 1) Fêðïð, 2 ) 2
Правую критическую точку (большую единицы)
находят
по
таблице
критических
точек
ïð
F
распределения Фишера – Снедекора êð , 2 .
Левую же границу находят из соотношения,
доказанного для критерия Фишера:
1
лев
Fкр,1 2;k ,k
1 2
F пр2;k ,k
2 1
36.
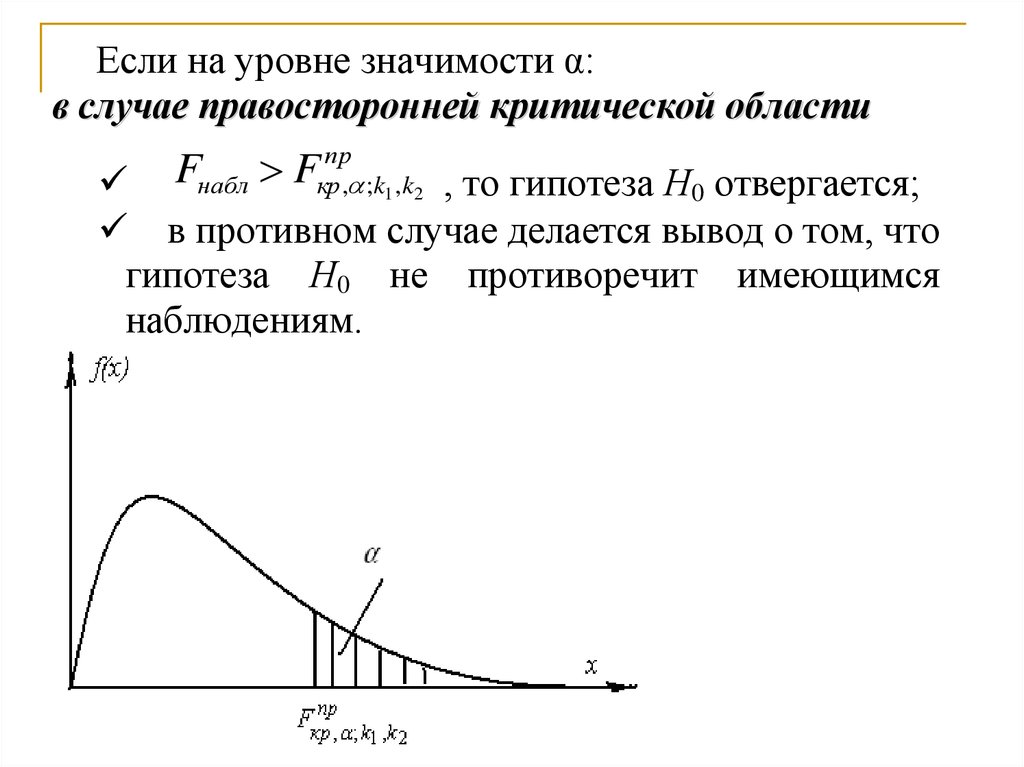
Если на уровне значимости α:в случае правосторонней критической области
Fнабл F
, то гипотеза Н0 отвергается;
в противном случае делается вывод о том, что
гипотеза Н0 не противоречит имеющимся
наблюдениям.
пр
кр , ;k1 ,k2
37.
в случае левосторонней критической областиFнабл Fкрлев,1 ;k1 ,k2 , то гипотеза Н0 отвергается;
в противном случае делается вывод о том,
что гипотеза Н0 не противоречит имеющимся
наблюдениям.
38.
в случае двусторонней критической областиFнабл F
или Fíàáë F
, то гипотеза
Н0 отвергается;
в противном случае делается вывод о том, что
гипотеза Н0 не противоречит имеющимся
наблюдениям.
лев
кр ,1 ;k1 , k2
ïð
êð , ;k1 ,k2
39.
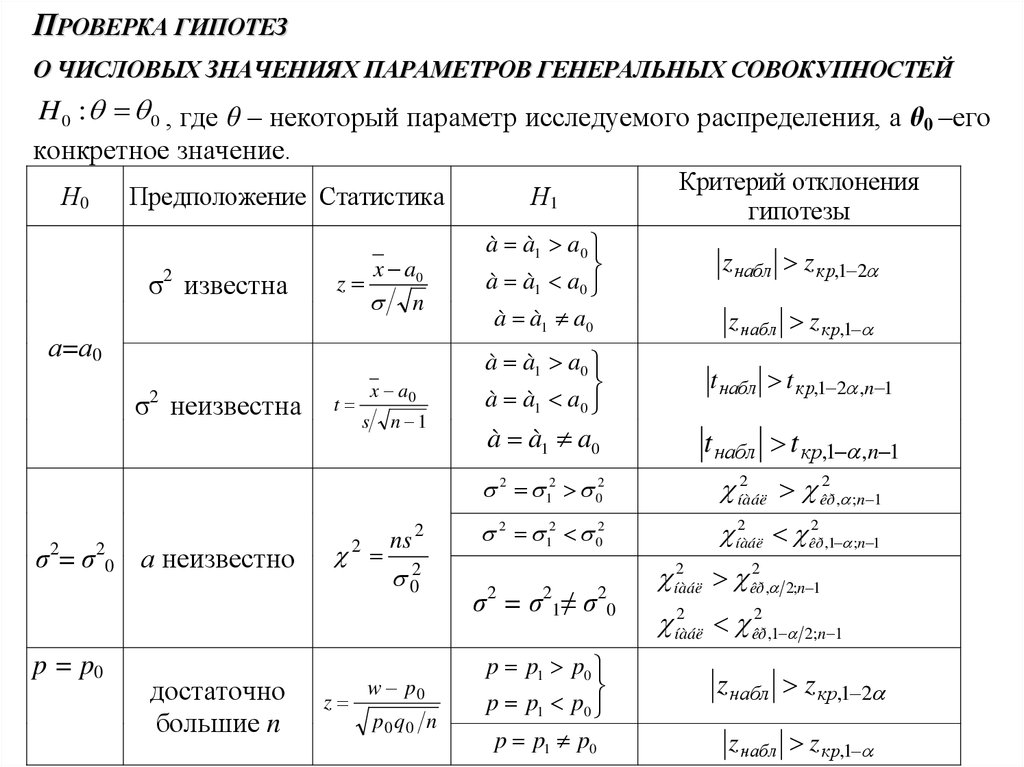
ПРОВЕРКА ГИПОТЕЗО ЧИСЛОВЫХ ЗНАЧЕНИЯХ ПАРАМЕТРОВ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ
H 0 : 0 , где θ – некоторый параметр исследуемого распределения, а θ0 –его
конкретное значение.
Н0
Предположение Статистика
2
σ известна
x a0
z
n
а=а0
2
σ неизвестна
σ2= σ20 а неизвестно
p = p0
достаточно
большие n
x a0
t
n 1
s
2
z
ns 2
02
w p0
p0 q0 n
Н1
à à1 a0
à à1 a0
à à1 a0
Критерий отклонения
гипотезы
z набл z кр,1 2
z набл z кр,1
à à1 a0
à à1 a0
t набл t кр,1 2 ,n 1
à à1 a0
t набл t кр,1 ,n 1
2 12 02
2
íàáë
êð2 , ;n 1
2 12 02
2
íàáë
êð2 ,1 ;n 1
σ2 = σ21≠ σ20
p p1 p0
p p1 p0
p p1 p0
2
íàáë
êð2 , 2;n 1
2
íàáë
êð2 ,1 2;n 1
z набл z кр,1 2
z набл z кр,1

























 Математика
Математика








