Похожие презентации:
Производственные функции. Гипотеза максимизирующего поведения производителя
1. Производственные функции
2. ПФ
q f ( x1 , x2 ,..., xn ).• функциональная зависимость между
количеством используемых в
производстве ресурсов и объемом
выпускаемой продукции
3. Гипотеза максимизирующего поведения производителя:
производитель из всего множествапланов производства выбирает тот,
который принесет ему максимальную
прибыль.
4. Гипотезы
• Гипотеза Н1 (гипотеза измеримости): каждыйресурс является количественно измеримым.
• Гипотеза H2 (гипотеза однородности): каждая точка
пространства Rn+ может быть отождествлена с
некоторым планом производства, (все ресурсы могут
использоваться в количестве, измеряемом любым
неотрицательным действительным числом).
• Гипотеза Н3 (гипотеза однозначности): при
одинаковых затратах ресурсов производитель
выпускает одно и то же количество продукции.
5. пространство ресурсов
- множество n-мерных векторов снеотрицательными координатами
Rn x ( x1, x2 ,..., xn ) xi 0, i 1,2,..., n .
• точки этого множества – планы
производства по ресурсам.
6. Основные типы производственных функций
Линейная
Кобба-Дугласа
Леонтьева
…
7. Поверхность (линия) уровня
– множество значений аргумента, в которыхфункция принимает одно и то же значение
Геометрически линия уровня (уровень)
функции двух переменных - плоская кривая,
получаемая при пересечении графика этой
функции плоскостью, параллельной
координатной плоскости XOY
Z=C, где C=const
Изобразить поверхность на плоскости можно,
проектируя линии уровня на плоскость XOY.
Семейство полученных кривых задается
уравнениями вида
F(x,y)=C
8.
Линии уровняфункции двух переменных
9. Частные производные
• Частная производная функции f ( x1 , x2 ,..., xn )в точке по переменной x k
f
u
lim
x k
xk 0 x k
- обыкновенная производная функции одной
переменной x k при фиксированных
значениях других переменных
- она характеризует скорость изменения ФНП в
направлении данной координатной оси x k при
фиксированных значениях других координат.
10. Предельный продукт
• =предельная эффективность ресурса,=предельная производительность
ресурса,
=предельная отдача ресурса при
плане x ( x1 , x2 )
f ( x1 , x2 )
MP1
x1
f
f ( x1 , x2 ) df ( x1 , x2 )
x1
x1
f ( x1 , x2 )
MP2
x2
x1 1 MP1 q
11. средний продукт
• средний продукт первого ресурса(средняя производительность ресурса,
средняя отдача ресурса)
f ( x1 , x2 ) q
AP1
x1
x1
- отношение объема выпущенной
продукции к количеству затраченного
переменного ресурса
12. Производственная функция (ПФ) типа Кобба – Дугласа где Q – объем производства, a0 > 0 , 0 < a < 1, 0 < b < 1 K – капитал, L – рабочая сила,
Производственная функция(ПФ) типа Кобба – Дугласа
Q f ( K , L) a0 K L ,
a b
где Q – объем производства,
a0 > 0 , 0 < a < 1, 0 < b < 1
K – капитал,
L – рабочая сила,
f (1,1) a0 ,
f (0, L) f ( K ,0) 0.
Пример:
ПФ небольшого цеха, изготавливающего рамы для
картин, имеет вид:
q f ( x1 , x2 ) 4 x
1/ 2 1/ 4
1
2
x
где x1 – отработанные человеко-часы,
x2 – отработанные машино-часы,
q – число изготовленных рам.
Найти количество продукции при плане x* = (64, 81).
13. ПРИМЕР:
q f ( x1 , x 2 ) 4 x1/ 2
1
x2
1/ 4
Вычислим частные производные ПФ, т.е. первый и
второй предельный продукты (предельную отдачу
первого и второго ресурса) для плана x*=(64, 81):
1/ 4
f
2
81
3
1 / 2 1 / 4
2 x1 x2
,
1/ 2
64
,
81
x1
64
4
1/ 2
f
64
8
1 / 2 3 / 4
x1 x2
3/ 4
.
64,81
x2
81
27
• значение 3/4 первого предельного продукта означает,
что при увеличении затрат первого ресурса на
единицу и неизменных затратах второго выпуск
продукции увеличится примерно на 3/4 ед.
• Каков экономический смысл второго предельного
продукта?
14. Уровень ПФ – изокванта
• Построить изокванту, проходящую через точку х*q f ( x ) 4 64
*
1/ 2
81
1/ 4
96
• затраты первого и второго ресурсов для всех планов
производства, обеспечивающих выпуск 96 единиц
продукции, связаны уравнением:
1/ 2 1/ 4
1
2
4x
x
96
x2
24
x1
4
2
331776
x1
• Графиком полученной функции в пространстве
ресурсов является изокванта, соответствующая
выпуску 96 единиц продукции
2
15. Изокванта производственной функции, соответствующая выпуску 96 единиц продукции – линия уровня ПФ
x2x*
x*
81
q=96
O
64
x1
Построить изокванты q=60, q=80 на том же рис.
16. Градиент
• Градиент ФНП в точке – вектор, координатыкоторого равны частным производным
функции в этой точке
F x
F x
.
grad F F x
, ,
xn
x1
• Градиент указывает направление и
величину максимальной скорости
возрастания функции в точке
17. Свойства градиента
• Градиент функции в точке перпендикулярен(ортогонален) поверхности уровня,
проходящей через данную точку.
• Если приращения аргумента достаточно
малы, функция возрастает (убывает)
только для тех из них, которые составляют
острый (тупой) угол с градиентом
• Функция практически не меняется для
приращений, ортогональных градиенту.
• Градиент ПФ называют вектором
предельного продукта
18. Экономическая область ПФ
• область, в которой увеличение затратлюбого ресурса не приводит к
уменьшению выпуска продукции.
• План ( x1 , x2 ) лежит в экономической
области ПФ
MP1 ( x1, x2 ) 0
MP2 ( x1, x2 ) 0
19. Закон убывающей отдачи ресурса
• если последовательное равномерное увеличениезатрат этого ресурса при фиксированных значениях
остальных приводит к последовательно
уменьшающемуся приросту выпуска продукции.
• Теорема. Для того, чтобы в некоторой области
выполнялся Закон убывающей отдачи ресурса,
необходимо и достаточно, чтобы в этой области
вторая частная производная ПФ по соответствующей
переменной была отрицательна:
2
f ( x1 , x2 ,..., xn )
0
2
xi
20. Коэффициенты эластичности выпуска по затратам ресурсов
• определяются следующими формулами:x1
f ( x1 , x2 )
x2
f ( x1 , x2 )
e x (q)
e x (q)
2
1
f ( x1 , x2 )
x2
f ( x1 , x2 )
x1
• Коэффициенты эластичности равны отношению
предельной отдачи ресурса к средней отдаче
ресурса:
MPi
e xi (q)
APi
• Экономический смысл: коэффициент эластичности
выпуска по затратам первого ресурса показывает, на
сколько примерно процентов изменится выпуск
продукции, если затраты первого ресурса увеличить
на 1%.
21. Эффект масштаба
q0 f ( x1 , x2 )- объем выпускаемой
продукции при плане ( x1 , x2 ).
• При увеличении затрат ресурсов в k раз
(k > 1) выпуск составит
q f (kx , kx
1
тоже в k раз
q1 kq0
выпуск
продукции
более, чем в k раз
увеличился
менее, чем в k раз
q1 kq0
q1 kq0
1
2
)
постоянный
возрастающий
убывающий
эффект от расширения
масштабов производства
22. Однородные функции
• Функция нескольких переменных называетсяоднородной порядка m, если для всех х из
некоторой области Х
f (kx1 , kx2 ,..., kxn ) k f ( x1 , x 2 ,..., x n )
m
• Если ПФ является однородной
порядка m, то
• при m=1 ПФ обладает постоянным;
• при m>1 ПФ обладает возрастающим
• при m<1 ПФ обладает убывающим
эффектом
масштаба
23. Эффект масштаба
X2X2
X2
3x2
3q
2x2
2x2
2q
2x2
2q
x1
2x1
q
q
q
0
2q
x2
x2
x2
3x1
постоянный
X1
0
x1
2x1
убывающий
X1
0
x1
2x1
X1
возрастающий
24. Поиск точки равновесия производителя
25. Планирование производства
• Долговременное• Кратковременное
Long-run
• возможны изменения всех
ресурсов
short-run
• Есть ограничения на ресурсы
• Все ресурсы
переменные
• Эффект от расширения
масштаба производства
• Ресурсы
постоянные и
переменные
• Закон убывающей отдачи
переменного ресурса
26. Приращение ФНП
f f (M ) f (M 0 ) f ( x dx, y dy) f ( x, y)функция f(x,y) имеет в точке М0 непрерывные частные
производные, то
по известным приращениям аргументов Δx, Δy,
приближенно вычислим
полное приращение функции
f
f
f d f
x
y
x
y
27. Дифференциал ФНП
полным дифференциалом функцииназывается линейная по приращениям
аргументов часть приращения функции
f
f
df
dx1
dx2
x1
x2
xi dxi
28. Замещение ресурсов
без изменения объёма выпускаf ( x1 , x2 )
f ( x1 , x2 )
0 q
dx1
dx2
x1
x2
0 MP1 ( x1 , x2 ) x1 MP2 ( x1 , x2 ) x2
MP1 ( x1 , x2 )
x2
x1
MP2 ( x1 , x2 )
29. Предельная норма технологического замещения второго ресурса первым
MP1 ( x1 , x2 )MRTS12 ( x1 , x2 )
q
const
MP2 ( x1 , x2 )
MRTS – marginal rate of technical substitution.
• Экономический смысл предельной нормы
замещения - это примерное количество второго
ресурса, которое можно сэкономить, увеличив
затраты первого ресурса на 1 единицу, при этом
объем выпуска не изменится.
MRTS 12 ( x1 , x2 ) x2
30. Геометрический смысл предельной нормы замещения второго ресурса первым:
MRTS 12 ( x1 , x2 )численно равна тангенсу угла наклона
касательной к изокванте в точке (x1,x2),
взятому с обратным знаком.
• мы будем рассматривать тангенс
смежного острого угла, поскольку
тангенсы этих углов отличаются
только знаком.
31. Основные свойства
MRTS 1, 2 ( x1 , x 2 )MRTS 12 ( x1 , x2 )
численно равна тангенсу острого угла tg
наклона касательной к изокванте в
точке (x1,x2).
x2
MRTS12 ( x1 , x2 )
x1
x2 MRTS 12 ( x1 , x2 ) x1
f ( x1, x2 ) f ( x1 x1; x2 MRTS12 ( x1 , x2 )) const.
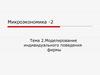
32. Закон убывания у ПФ типа Кобба-Дугласа
Закон убывания MRTS 1, 2у ПФ типа Кобба-Дугласа
MRTS 1, 2
X2
1
0
непрерывно убывает
(tg 2 tg 1 )
2
X1
возможна замещаемость ресурсов в определенных границах
33. Линейная производственная функция
q f ( x1, x2 ) a1x1 a2 x2 ,• применяется при моделировании таких производственных
процессов, где выпуск однородной продукции является
результатом одновременного функционирования нескольких
технологий,
• выпуск линейно зависит от затрат,
• ресурсы полностью взаимозаменяемы, т.е.
для выпуска достаточно наличия хотя бы одного ресурса.
X2
MRTS 1, 2
MRTS 2,1
a1
;
a2
(a1,a2)
a1
a2
a1
0
a2
X1
34. ПРИМЕРЫ применения линейной ПФ:
• производство однотипных деталейрабочими различных разрядов,
• выемка грунта рабочими или
экскаваторами,
• выручка дистрибьюторов однородного
товара,
• сегмент рынка, крупная отрасль,
• народное хозяйство в целом.
35. Ресурсы
постоянныепеременные
• x = (x1, x2, ..., xn) - план по
затратам переменных
ресурсов
• вектор w = (w1, w2, ..., wn)
задает цены переменных
ресурсов.
• Стоимость переменных
ресурсов = переменные
• стоимость затраченных
постоянных ресурсов С0 =
постоянные
издержки,
издержки
G(x) =
w x
•общая стоимость затраченных ресурсов = общие издержки
C0 w x
36. Изокоста
- множество планов производства содинаковыми переменными издержками
• Уравнение изокосты
G ( x) w1 x1 w2 x2 c
• Семейство изокост на плоскости –
множество отрезков параллельных
прямых с нормалью w (w1 , w2 )
• Угол наклона изокосты к оси Оx1
определяется отношением цен на
ресурсы:
tg = – w1/ w2.
37. Поиск оптимального плана – точки равновесия х*
• выпуск заданногоколичества
продукции q с
наименьшими
переменными
издержками
G ( x) w x min,
при условии
q( x) const
x 0.
• выпуск
максимального
количества
продукции при
наличии бюджетного
ограничения
q( x) max
при условии
G ( x) w x const
x 0.




































 Экономика
Экономика