Похожие презентации:
Методи вирішення нелінійних рівнянь. (Лекція 3)
1. Чисельні методи
ЛЕКЦІЯ 3«Наближене рішення нелінійних рівнянь»
2. Наближене рішення нелінійних рівнянь.
Групи методів:Метод половинного ділення, хорд,
метод дотичних, комбінований
метод
Метод ітерації
Методи відділення ізольованих
коренів рівняння
3. Метод половинного ділення
Постановка задачі. Дано нелінійне рівнянняF ( x) 0 , де функція y F ( x) визначена і
неперервна для всіх , при чому функція
змінює знак на кінцях цього відрізку, тобто
F (a) F (b) 0
Знайти наближений розв'язок даного рівняння
F ( x) 0 з точністю 10 3 , а так само необхідне
для цього число розбиття відрізка [a, b] .
Наближене рішення і похибка наближення
знаходяться за наступною схемою:
an bn
2
bn an
2
n 0,1, 2,
; a0 a, b0 b
4. Метод половинного ділення (продовження)
Деbn an
bn 1 an 1 b a
n
2
2
F (an ) F (bn ) 0
задовольняє умовам:
(bn an )
з останнього визначається число розбиття
відрізка
b a
n log 2
5. Метод ітерації
Постановка задачі. Дано нелінейне рівняння,де функція y F ( x) визначена та неперервнодиференціюєма для всіх x [a, b], при чому
функція змінює знак на кінцях цього
відрізку, тобто F (a) F (b) 0
Знайти наближене рішення даного
рівняння F ( x) 0
з точністю 10 3 .
Наближене рішення та похибка наближення
знаходяться за наступною схемою:
Рівняння F ( x) 0 приводиться до виду x ( x),
де функція y ( x) задовольняє умовам:
xn xn 1
1 q
q
6. Метод ітерації (продовження)
диферинцюєма на даному відрізку та0 ( x) q 1
При вирішенні нелінійного рівняння методом
ітерацій скористуємся записом рівняння в
вигляді x=f(x). Задаються початкове
значення аргумента x0 та точність ε. Перше
наближення рішення x1 знаходимо з выразу
x1=f(x0), друге - x2=f(x1) і т.д. В загальному
випадку (i+1)-е наближання знайдемо за
формулою xi+1 =f(xi). Цю процедуру
повторюємо поки |f(xi)|>ε. Умова сходимості
метода ітерацій |f'(x)|<1.
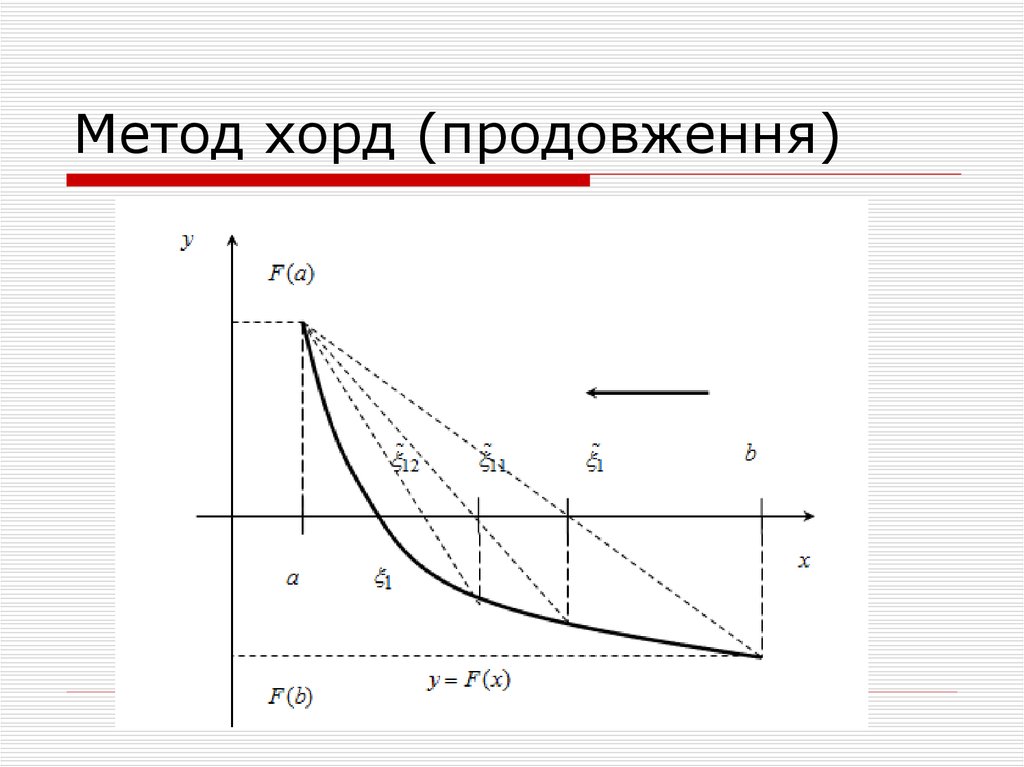
7. Метод хорд
При вирішенні нелінійного рівняння методом хордзадається інтервал [a,b], на якому існує тільки одно
рішення і точність ε. Потім через дві точки з
координатами (a,F(a)) і (b,F(b)) проводимо відрізок
прямої лінії (хорду) та визначити точку перетину
цієї лінії з віссю абсцис (точка c). Якщо при цьому
F(a)∙F(c)<0, то праву межу інтервалу переносимо в
точку с (b=c). Якщо указана умова не виконується,
то в точку c переноситься ліва межа інтервалу
(а=с). Пошук рішення припиняється при досягненні
заданої точності |F(c)|< ε. Для визначення точки
перетину хорди з віссю абсцис скористуємося
наступною формулою
8. Метод хорд (продовження)
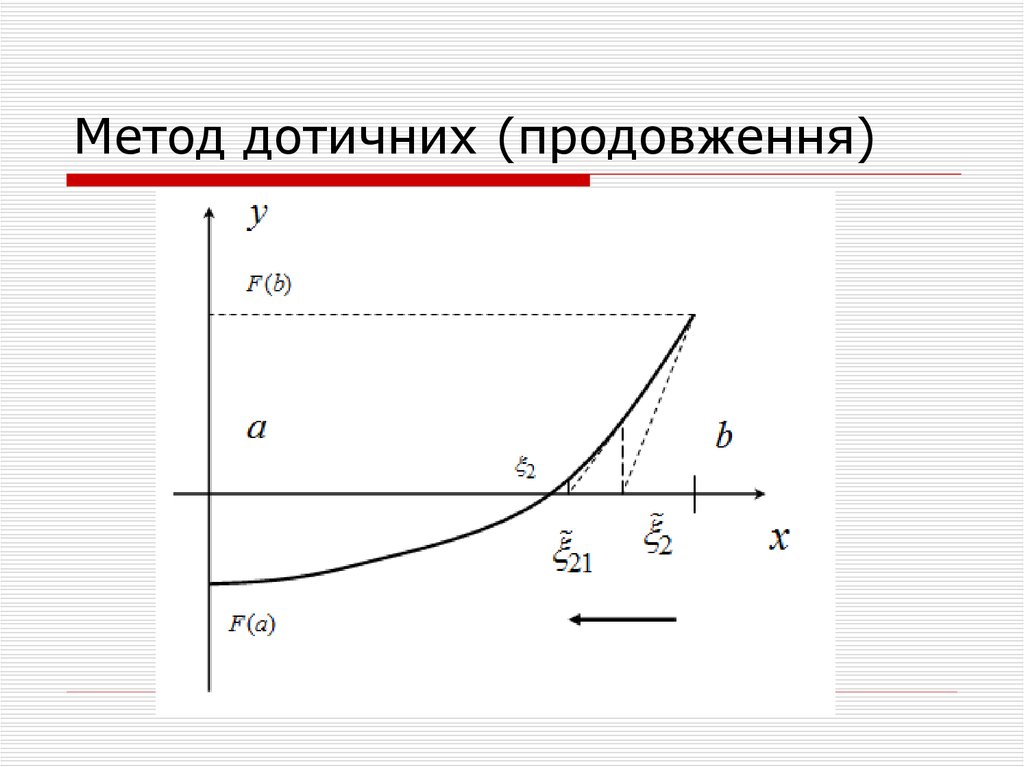
9. Метод дотичних
При вирішенні нелінійного рівняння методомдотичних задаються початковее значення
аргументу x0 та точність ε. Потім в точці (x0,F(x0))
проводимо дотичну до графіку F(x) і визначимо
точку перетину дотичну з віссю абсцис x1. В точці
(x1,F(x1)) знову будуємо дотичну, знаходимо
наступне наближення шукомого рішення x2 та ін.
Вказану процедуру повторюємо доки |F(xi)| > ε.
Для визначення точки перетину (i+1) дотичної з
віссю абсцис скористуємося наступною формулою.
Умова сходимості методу дотичних F(x0)∙F''(x0)>0.








 Математика
Математика








