Проекционное черчение

1.

© Терехова Н.В. «Проекционное черчение» Графика
«Сопряжения».
Сопряжение – это плавный переход из одной линии в другую.
Все из вас обязательно получали травмы об угол мебели, проходя между рядами столов в
классе, тем более, если проход оказывался узким. Обратите внимание, что новая мебель,
выпускаемая промышленностью, имеет обтекаемые углы (скругления). Вспомните форму
стиральной машины, музыкального центра – они тоже имеют обтекаемые формы, которые
воспринимаются глазами лучше, и позволяют избежать травмы. На обтекаемые формы
приятнее смотреть, они успокаивающе воздействуют на психику человека.
Познакомимся с построением касательной к окружности.
Касательная – это прямая, имеющая с окружностью одну
общую точку.
Помни! Касательная к окружности всегда лежит на
перпендикуляре к ее радиусу.
Ì
R
à
L
Рассмотрим построение касательной к окружности из заданной точки.
Î
À
Ä à í î : î ê ð ó æí î ñ òü è òî ÷ ê à
1
Î
À
Ñ î å ä è í è ò ü ò î ÷ ê ó À è ö å í ò ð î ê ð ó æí î ñ ò è î ò ð å ç ê î ì ï ð ÿ ì î é
2
1

2.

© Терехова Н.В. «Проекционное черчение» Графика
Î
À
Ê
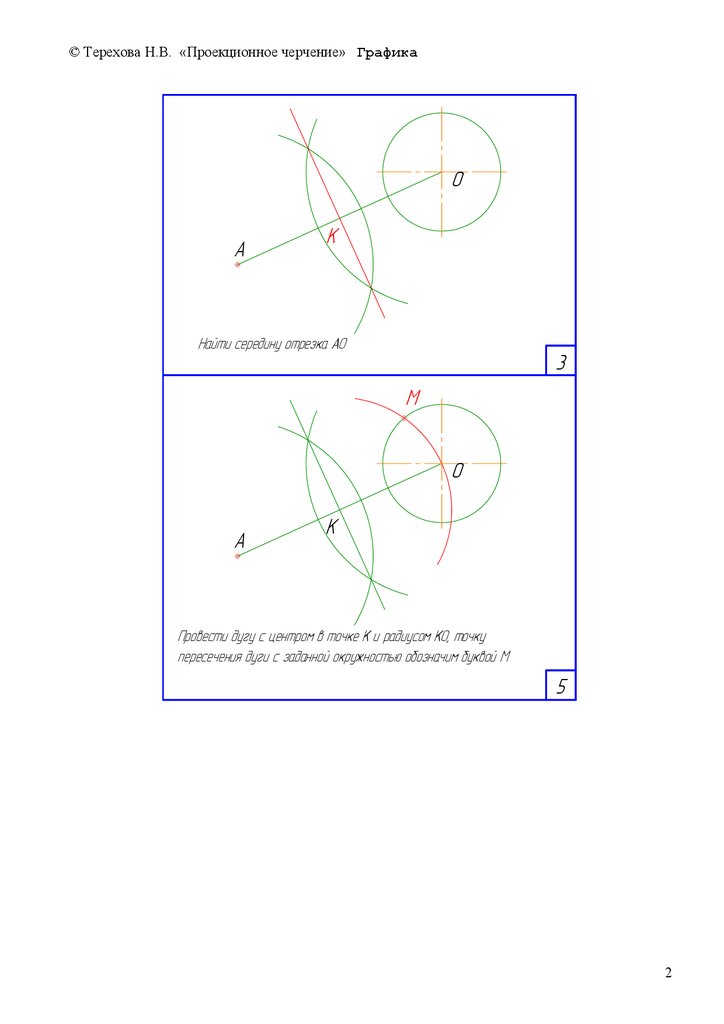
Íàéòè ñåðåäèíó îòðåçêà ÀÎ
3
Ì
Î
À
Ê
Ïðîâåñòè äóãó ñ öåíòðîì â òî÷êå Ê è ðàäèóñîì ÊÎ, òî÷êó
ïåðåñå÷åíèÿ äóãè ñ çàäàííîé îêðóæíîñòüþ îáîçíà÷èì áóêâîé Ì
5
2

3.

© Терехова Н.В. «Проекционное черчение» Графика
Ì
Î
Ê
À
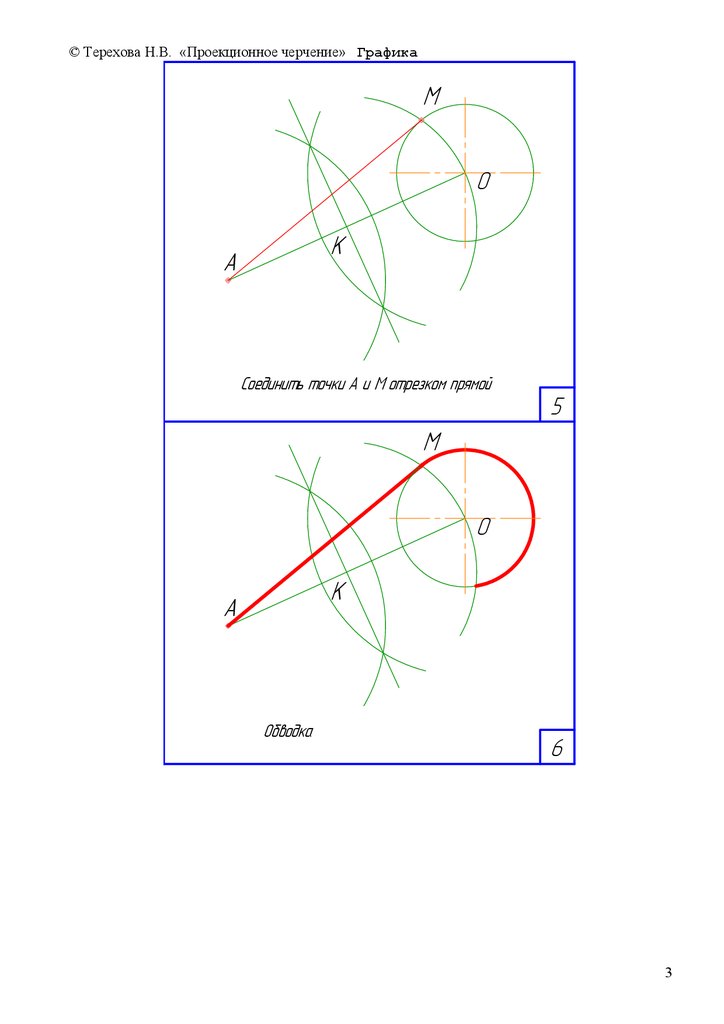
Ñîåäèíèòü òî÷êè À è Ì îòðåçêîì ïðÿìîé
5
Ì
Î
Ê
À
Îáâîäêà
6
3

4.

© Терехова Н.В. «Проекционное черчение» Графика
Построение касательной к двум дугам окружностей.
Внешнее касание.
Шаг 1. Дано: окружности с заданным радиусом, на заданном расстоянии друг от друга.
R2
O2
R1
O1
Шаг 2. Начертить окружность (окружность разности ∆L) с центром в точке О2 и радиусом
равным разности значений заданных радиусов.
R2 - R1
O2
L
O1
Шаг 3. Построим касательную из точки О1 к окружности разности. Это построение для нас уже
знакомо (построение касательной к окружности из заданной точки). Соединим центры
окружностей отрезком прямой.
O2
O1
4

5.

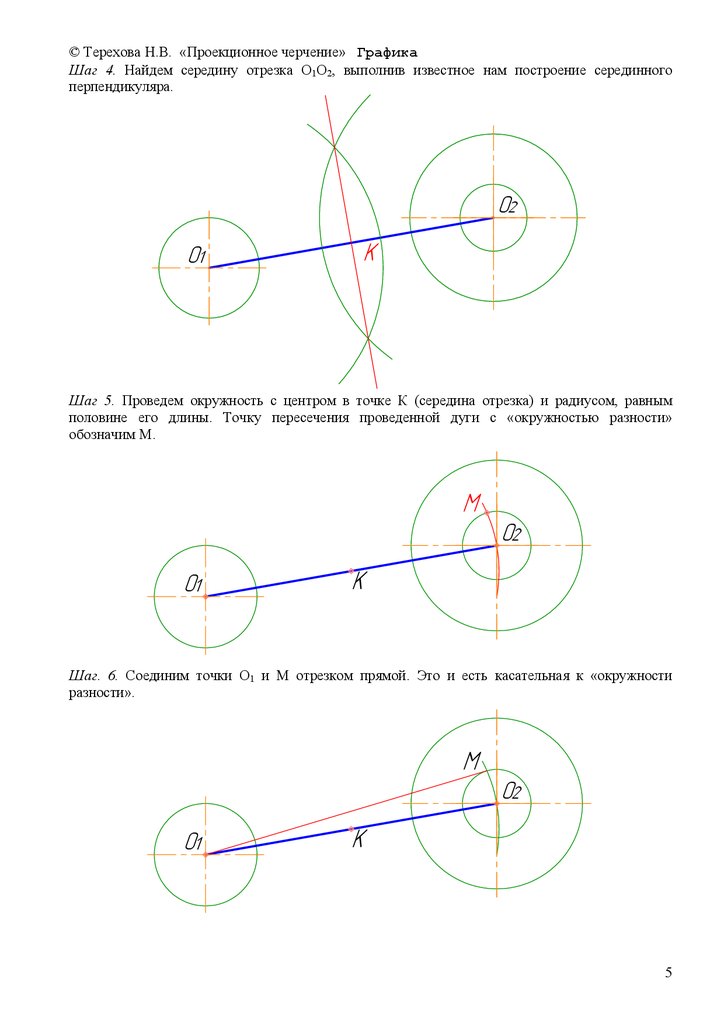
© Терехова Н.В. «Проекционное черчение» Графика
Шаг 4. Найдем середину отрезка О1О2, выполнив известное нам построение серединного
перпендикуляра.
O2
Ê
O1
Шаг 5. Проведем окружность с центром в точке К (середина отрезка) и радиусом, равным
половине его длины. Точку пересечения проведенной дуги с «окружностью разности»
обозначим М.
M
O2
O1
Ê
Шаг. 6. Соединим точки О1 и М отрезком прямой. Это и есть касательная к «окружности
разности».
M
O2
O1
Ê
5

6.

© Терехова Н.В. «Проекционное черчение» Графика
Шаг 7. Найдем точку касания на заданной окружности (касательная к окружности всегда лежит
на перпендикуляре к ее радиусу). Для этого проведем прямую через центр заданной
окружности и точку М. Точку пересечения прямой с заданной окружностью обозначим N.
N
M
O2
O1
Ê
Шаг 8. Искомая касательная будет параллельна О1М и пройдет через точку N. Следовательно,
необходимо выполнить построение параллельной прямой через заданную точку. Для этого мы
строим окружность с центром в точке N и радиусом, равным длине отрезка О1М.
R = |Î1; Ì|
N
M
O2
N1
O1
Ê
Шаг 9. Соединим точки N1и N отрезком прямой. Построение завершено.
N
M
N1
O2
O1
Ê
6

7.

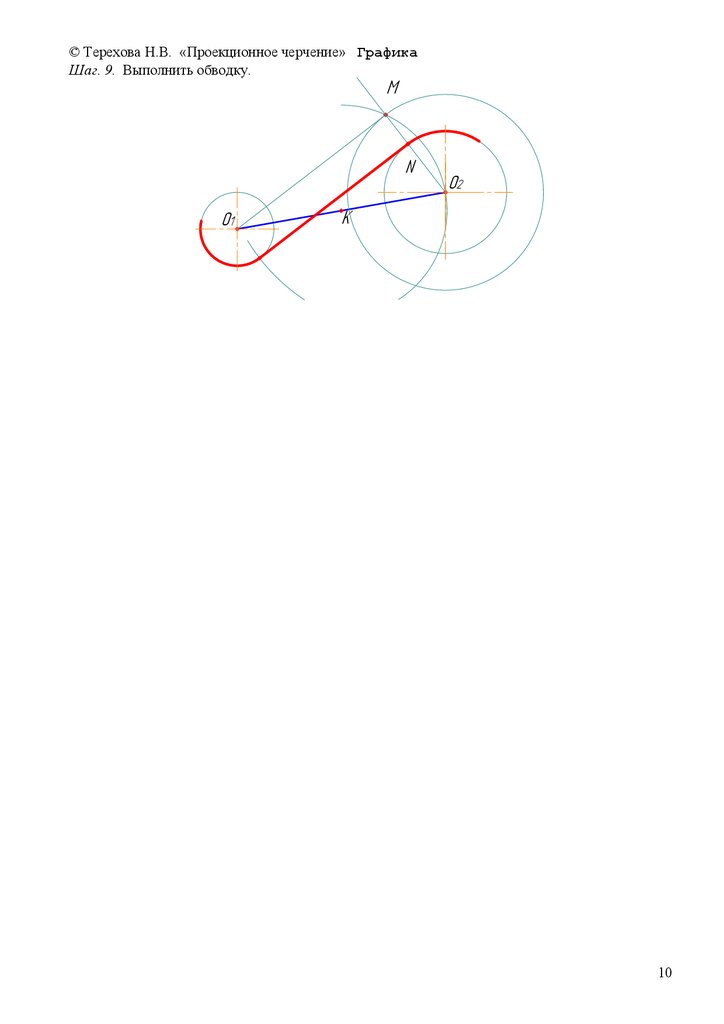
© Терехова Н.В. «Проекционное черчение» Графика
Шаг 9. Выполняем обводку с кривых линий строго до точек касания, затем обводим прямую
линию строго от точки касания до точки касания.
N
M
O2
Ê
O1
Внутреннее касание.
Шаг 1. Построить окружность с центром в точке О2, радиусом равным сумме значений
заданных радиусов ( «окружность суммы»)
R2
+
1
R
SL
O1
O2
Шаг 2. Построить касательную к «окружности суммы» из точки О1. Построение для нас
знакомо. Для этого соединим центры заданных окружностей отрезком прямой.
O2
O1
7

8.

© Терехова Н.В. «Проекционное черчение» Графика
Шаг 3. Найдем середину полученного отрезка , построив серединный перпендикуляр.
O2
O1
Ê
Шаг 4. Проведем окружность с центром в точке К и радиусом, равным половине длины отрезка
О1О2. Точку пересечения дуги с «окружностью суммы» обозначим М.
M
O2
O1
Ê
Шаг 5. Соединим отрезком прямой точки О1 и М – это и есть касательная к «окружности
суммы», проведенная из заданной точки О1.
M
O2
O1
Ê
8

9.

© Терехова Н.В. «Проекционное черчение» Графика
Шаг 6. Проведем прямую через точки М и О2, точку пересечения этой прямой с заданной
окружностью обозначим N – точка касания.
M
N
O2
Ê
O1
Шаг 7. Искомая касательная параллельна проведенной, поэтому дальнейшее построение
сводится к построению параллельной прямой через заданную точку. Для этого проводим
окружность с центром в точке N радиусом равным О1М.Точку пересечения обозначим N1.
M
N
R
O1
1
=O
M
O2
Ê
N1
Шаг 8. Соединить отрезком прямой точки N и N1.
M
N
O1
O2
Ê
9

10.

© Терехова Н.В. «Проекционное черчение» Графика
Шаг. 9. Выполнить обводку.
M
N
O1
O2
Ê
10