Похожие презентации:
Тела Архимеда
1. Тела Архимеда
Работу выполнилУченик 10-11 класса
Самохвалов Андрей
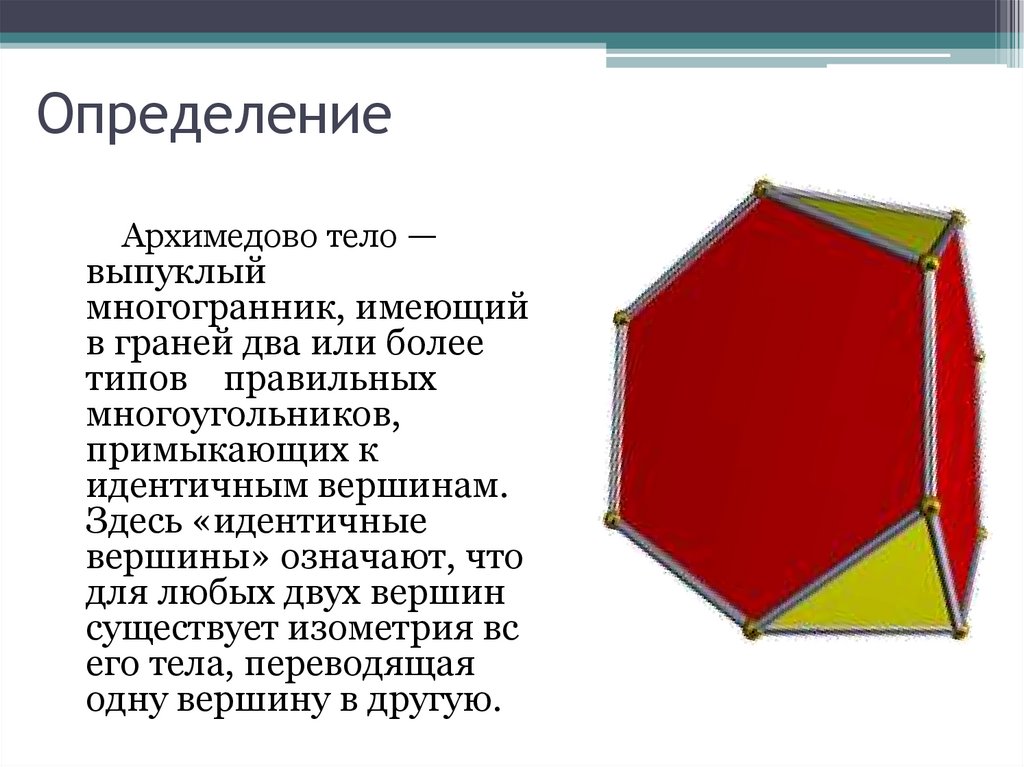
2. Определение
Архимедово тело —выпуклый
многогранник, имеющий
в граней два или более
типов правильных
многоугольников,
примыкающих к
идентичным вершинам.
Здесь «идентичные
вершины» означают, что
для любых двух вершин
существует изометрия вс
его тела, переводящая
одну вершину в другую.
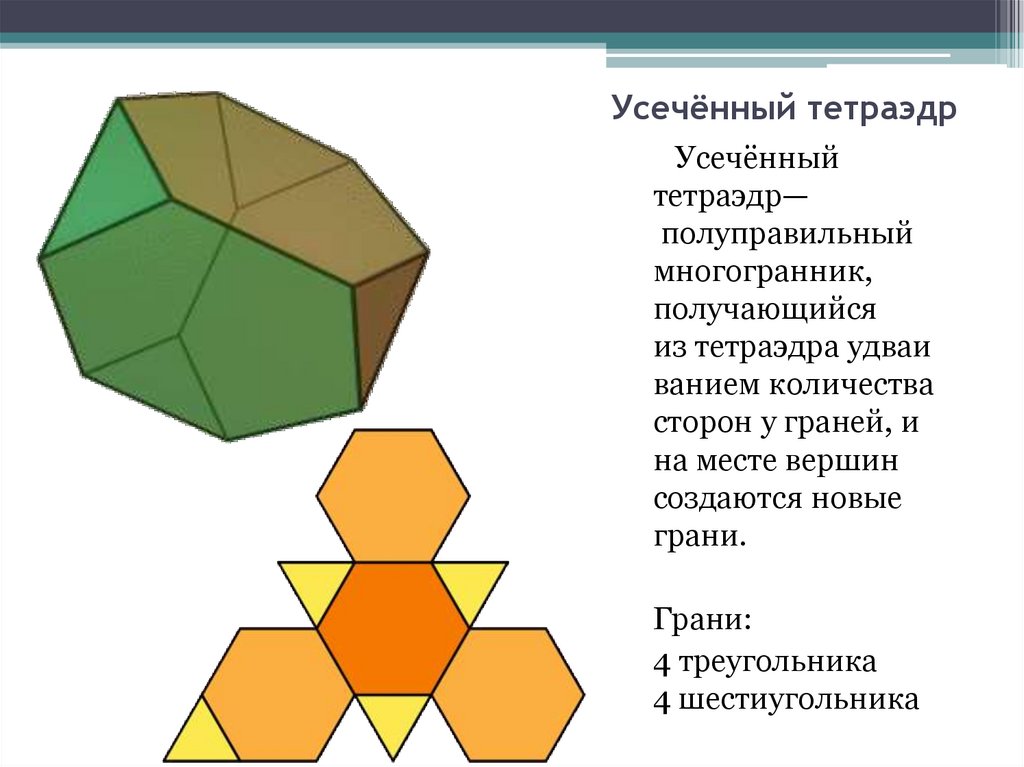
3. Усечённый тетраэдр
Усечённыйтетраэдр—
полуправильный
многогранник,
получающийся
из тетраэдра удваи
ванием количества
сторон у граней, и
на месте вершин
создаются новые
грани.
Грани:
4 треугольника
4 шестиугольника
4. Кубоктаэдр
Полуправильныймногогранник, состоящий из
14 граней (8 правильных
треугольников
и
6
квадратов). В кубоктаэдре 12
одинаковых
вершин,
в
которых
сходятся
два
треугольника и два квадрата,
а также 24 одинаковых
ребра, каждое из которых
разделяет треугольник и
квадрат.
5. Усечённый куб
Усечённый куб—полуправильный
многогранник (архимедов
о тело) с 14 гранями,
составленный из
8 правильных
треугольников и
6 правильных
восьмиугольников.
В каждой из его 24
одинаковых вершин
сходятся две
восьмиугольных грани и
одна треугольная.
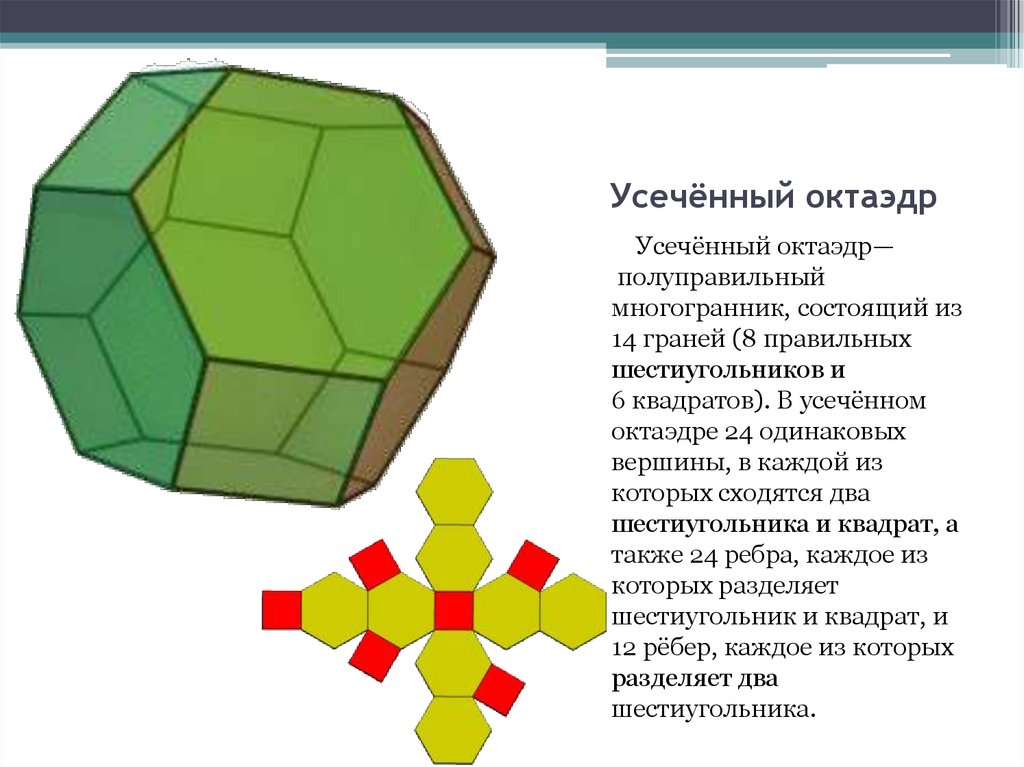
6. Усечённый октаэдр
Усечённый октаэдр—полуправильный
многогранник, состоящий из
14 граней (8 правильных
шестиугольников и
6 квадратов). В усечённом
октаэдре 24 одинаковых
вершины, в каждой из
которых сходятся два
шестиугольника и квадрат, а
также 24 ребра, каждое из
которых разделяет
шестиугольник и квадрат, и
12 рёбер, каждое из которых
разделяет два
шестиугольника.
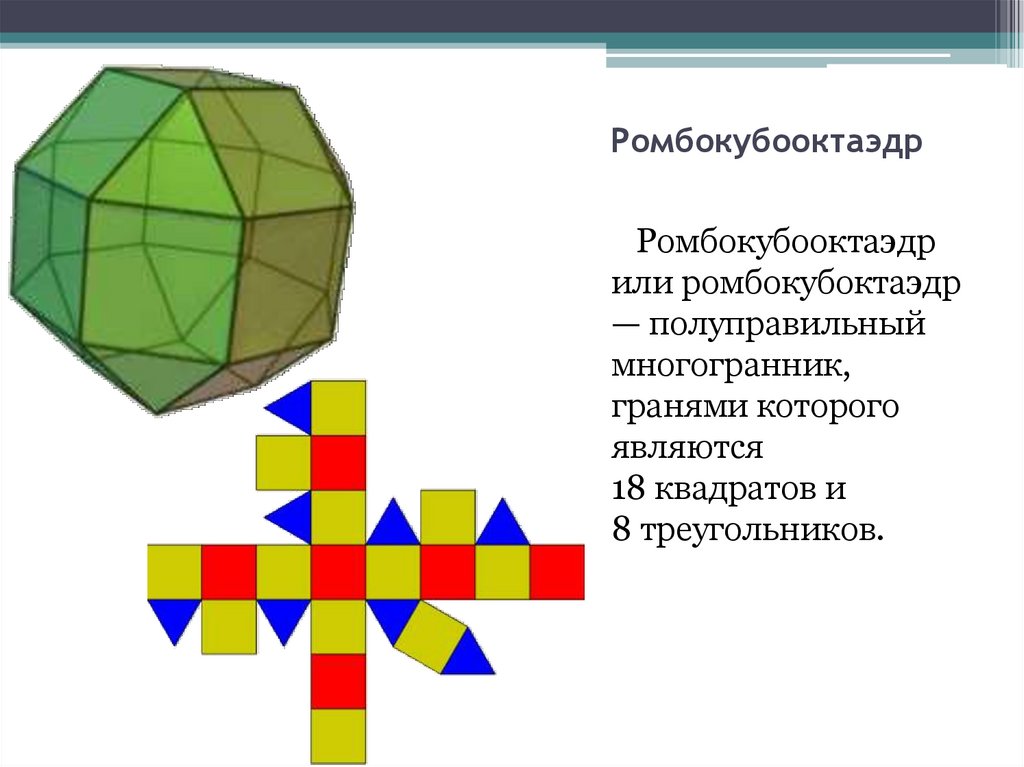
7. Ромбокубооктаэдр
Ромбокубооктаэдрили ромбокубоктаэдр
— полуправильный
многогранник,
гранями которого
являются
18 квадратов и
8 треугольников.
8. Усечённый кубооктаэдр
Усечённыйкубооктаэдр усечённый
кубоктаэдр—
полуправильный
многогранник (архимедово
тело) с
12 квадратными гранями, 8
гранями в виде
правильного шестиугольник
а, 6 гранями в виде
правильного восьмиугольник
а, 48 вершинами и 72
рёбрами. Поскольку каждая
из граней многогранника
имеет центральную
симметрию (что
эквивалентно повороту на
180°), усечённый
кубооктаэдр
является зоноэдром.
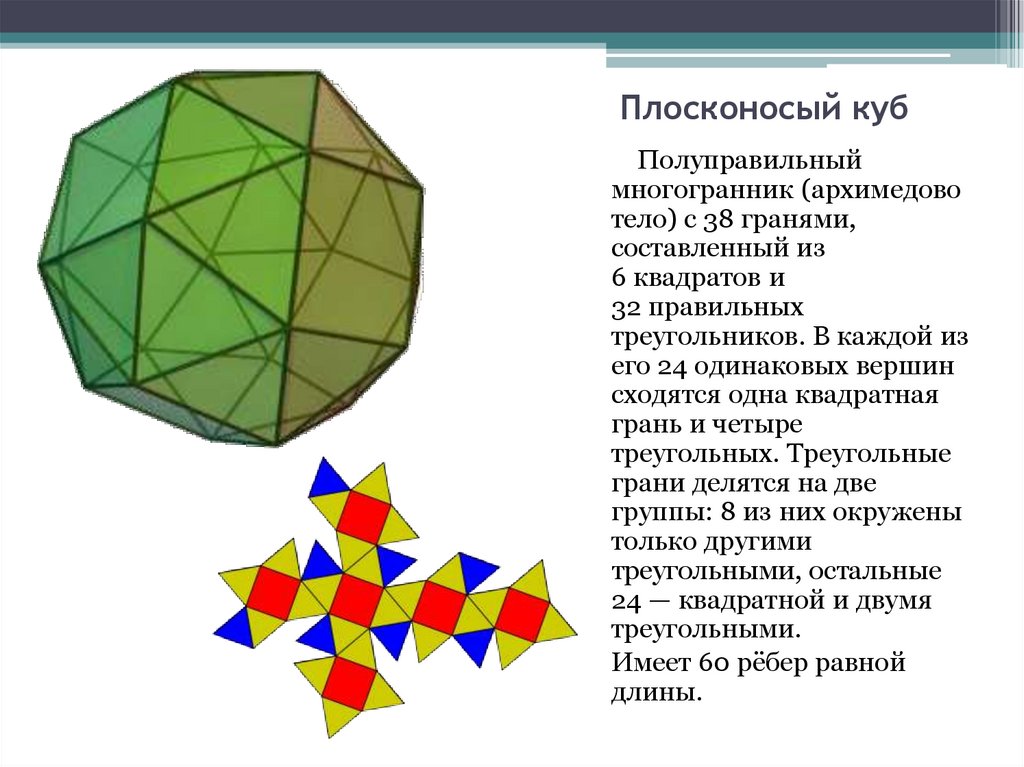
9. Плосконосый куб
Плосконосый кубПолуправильный
многогранник (архимедово
тело) с 38 гранями,
составленный из
6 квадратов и
32 правильных
треугольников. В каждой из
его 24 одинаковых вершин
сходятся одна квадратная
грань и четыре
треугольных. Треугольные
грани делятся на две
группы: 8 из них окружены
только другими
треугольными, остальные
24 — квадратной и двумя
треугольными.
Имеет 60 рёбер равной
длины.
10. Икосододекаэдр
Полуправильныймногогранник, состоящий
из 32 граней
(12 правильных
пятиугольников и
20 правильных
треугольников). В
икосододекаэдре 30
одинаковых вершин, в
которых сходятся два
треугольника и два
пятиугольника, а также 60
одинаковых рёбер, каждое
из которых разделяет
треугольник и
пятиугольник.
11. Усечённый додекаэдр
Усечённый додекаэдрУсечённый
додекаэдр —
полуправильный
многогранник (архимед
ово тело) с 32 гранями,
составленный из
20 правильных
треугольников и
12 правильных
десятиугольников В
каждой из его 60
одинаковых вершин
сходятся две
десятиугольных грани и
одна треугольная.
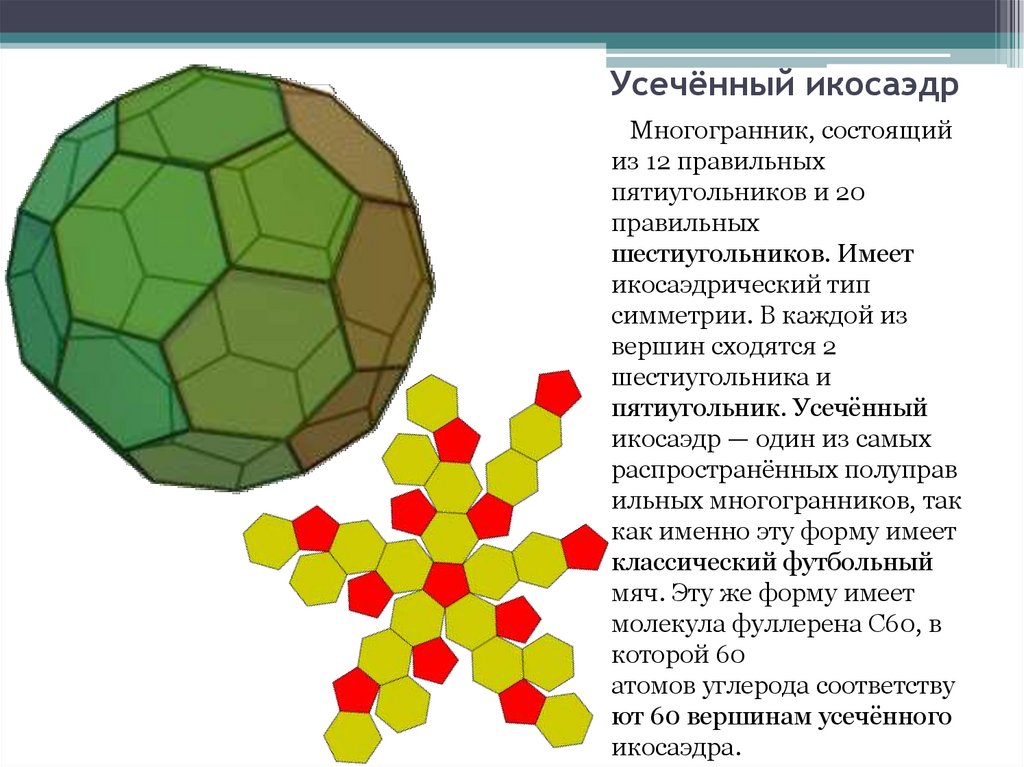
12. Усечённый икосаэдр
Усечённый икосаэдрМногогранник, состоящий
из 12 правильных
пятиугольников и 20
правильных
шестиугольников. Имеет
икосаэдрический тип
симметрии. В каждой из
вершин сходятся 2
шестиугольника и
пятиугольник. Усечённый
икосаэдр — один из самых
распространённых полуправ
ильных многогранников, так
как именно эту форму имеет
классический футбольный
мяч. Эту же форму имеет
молекула фуллерена C60, в
которой 60
атомов углерода соответству
ют 60 вершинам усечённого
икосаэдра.
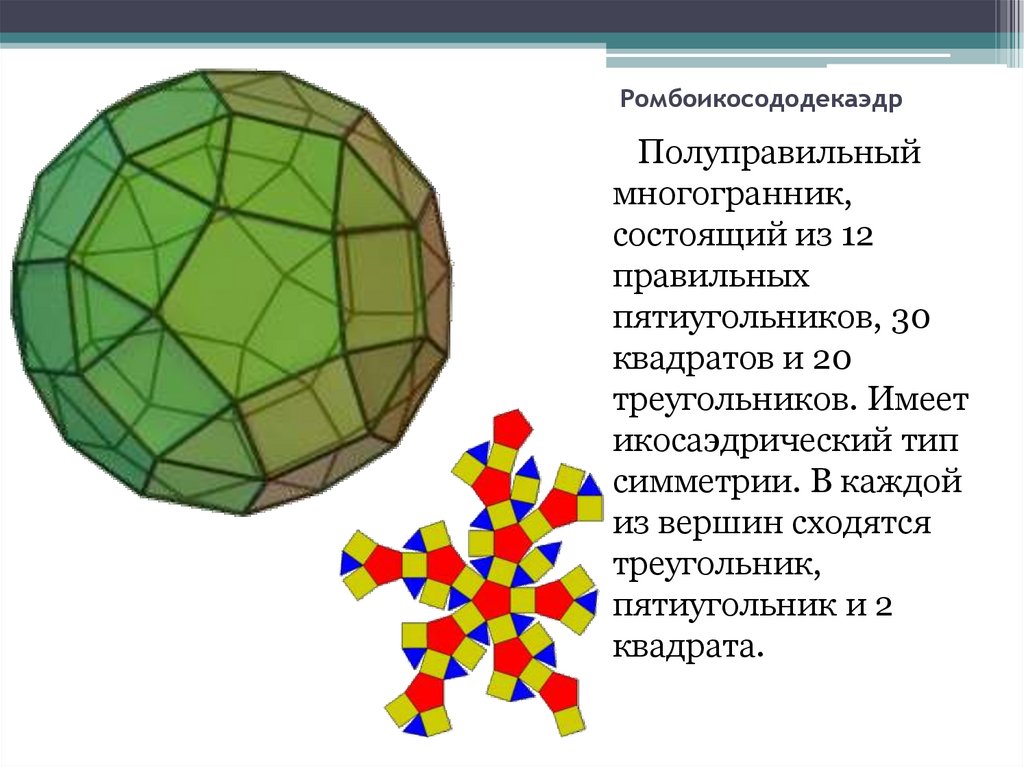
13. Ромбоикосододекаэдр
Полуправильныймногогранник,
состоящий из 12
правильных
пятиугольников, 30
квадратов и 20
треугольников. Имеет
икосаэдрический тип
симметрии. В каждой
из вершин сходятся
треугольник,
пятиугольник и 2
квадрата.
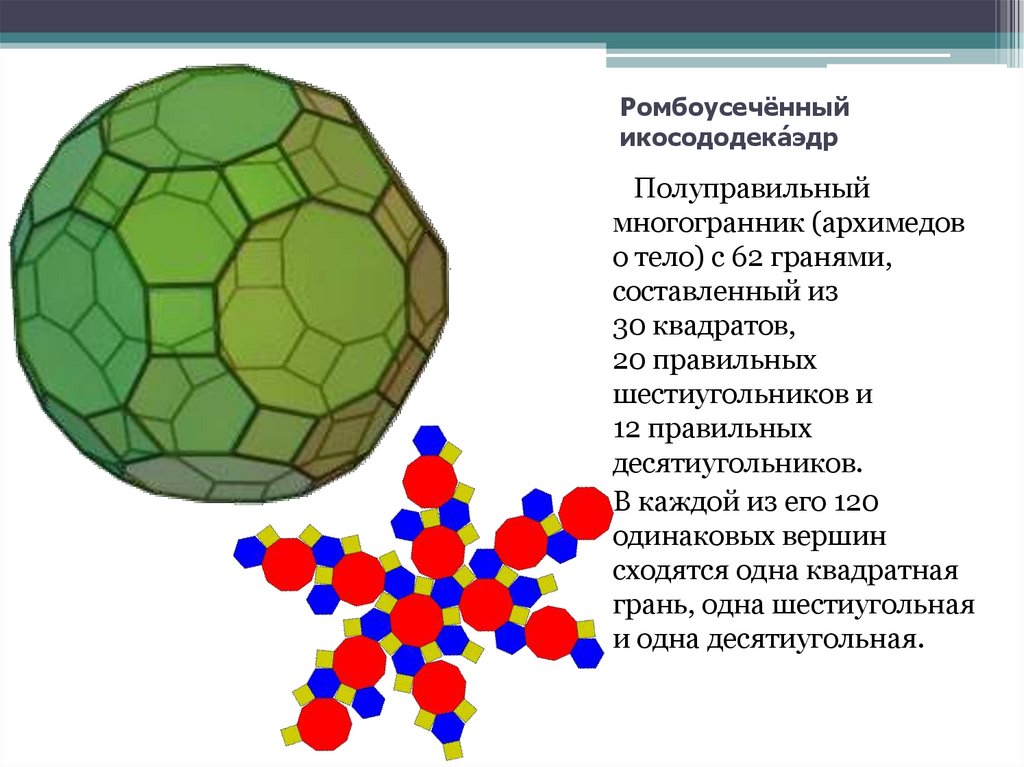
14. Ромбоусечённый икосододека́эдр
Ромбоусечённыйикосододека́ эдр
Полуправильный
многогранник (архимедов
о тело) с 62 гранями,
составленный из
30 квадратов,
20 правильных
шестиугольников и
12 правильных
десятиугольников.
В каждой из его 120
одинаковых вершин
сходятся одна квадратная
грань, одна шестиугольная
и одна десятиугольная.
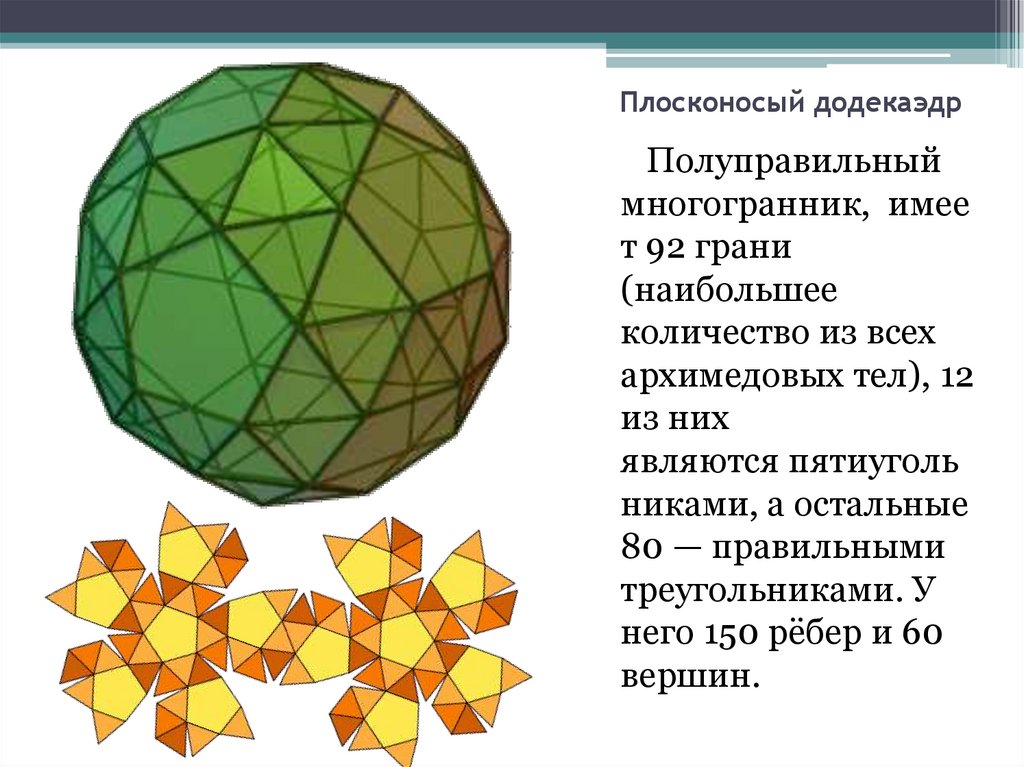
15. Плосконосый додекаэдр
Полуправильныймногогранник, имее
т 92 грани
(наибольшее
количество из всех
архимедовых тел), 12
из них
являются пятиуголь
никами, а остальные
80 — правильными
треугольниками. У
него 150 рёбер и 60
вершин.
16. Вывод
Всего существует 13 тел Архимеда и все они представленыполуправильными многогранниками.








 Математика
Математика








