Оптимальное решение задач бережливого производства в процессе деревообработки

1. Оптимальное решение задач бережливого производства в процессе деревообработки

ГАПОУ КК «Краснодарский гуманитарно-технологический колледж»
Оптимальное решение задач
бережливого производства в
процессе деревообработки
Автор работы: Хомяков Кирилл
студент 1 курса ГАПОУ КК КГТК
Руководитель: Андрюхина Марина Ильинична
преподаватель математики ГАПОУ КК КГТК
Краснодар, 2022 г

2.

ВВЕДЕНИЕ
В научно-исследовательской работе рассматриваются
вопросы бережливого производства, в частности, вопрос
ресурсосбережения за счет минимизации потерь сырья в
процессе деревообработки. В работе представлено
оптимальное решение задач ресурсосбережения с
помощью методов математического анализа.

3.

ДЕРЕВООБРАБОТКА
Деревообработка – это технологические
процессы, применяемые при обработке
древесины и древесных материалов для
придания им определённых размеров,
формы и качества, а также для получения
готовых изделий. Включает: резание,
гнутьё, склеивание, сборку и отделку.

4.

ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
История развития деревообрабатывающей
промышленности началась в начале XVIII
века, но интенсивности достигла только к
середине XIX века. Создавались комбинаты и
заводы, которые занимались не только
распилом материала, но и изготовление
мебели, спичек и клееной фанеры. Объемы
производства росли, но отрасль находилась на
низком уровне технического развития по
сравнению с зарубежными странами. До
революции 1917 года основной продукцией
данной отрасли были пиломатериалы. Перед
Первой Мировой войной стали открываться
крупные
и
оснащенные
заводы
деревообрабатывающей промышленности в
Архангельске, Онеге.

5.

ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
В период с 1929 по 1940 годы отмечался рост
капстроительства, мебельного и прочего
производства. Предприятия стали выпускать
продукцию для массового потребителя (окна,
двери и др.). Многие комбинаты и заводы
автоматизировали
свои
производственные
процессы. Вторая Мировая война, финансовые
и экономические кризисы в стране негативно
сказывались на развитии отрасли. Многие
предприятия закрывались из-за убытков.
Работники становились безработными и
вынуждены были искать новое место работы,
даже не по специальности. Происходило и
сокращение экспорта продукции, снижение
объемов производства и скопление запасов
невостребованной продукции на складах.

6.

СОВРЕМЕННЫЕ ТЕНДЕНЦИИ В ДЕРЕВООБРАБАТЫВАЮЩЕЙ ПРОМЫШЛЕННОСТИ
В настоящее время деревообрабатывающая промышленность
активно развивается. Доля России в мировых запасов леса составляет
¼ часть и занимает, согласно мировой статистике, одно из первых
мест по динамике развития. За последние 10 лет увеличились объемы
международной торговли продуктами деревообрабатывающей
промышленности.
Это
объясняется
экологичностью,
универсальностью и энергоемкостью материалов из древесины.
По данным Федеральной службы государственной статистики на
2020 г, обработкой древесины и производством изделий из нее в
России занимается более 19 300 предприятий, на которых работает
около 217 тыс. человек, обеспечивающих сегодня, по разным оценкам,
от 0,9 до 1,2 % ВВП страны.
Мировым
трендом
выступает
активное
внедрение
инновационных технологий на уровне организации предприятия,
производства и сбыта. Инновации в деревообработке несут
прогрессивный характер и укрепляют взаимосвязи с другими
отраслями. Гиганты лесной промышленности стремятся снизить
затраты сырья, оптимизировать организацию управления и привлечь
бизнес-инвестиции.

7.

ПРИНЦИПЫ БЕРЕЖЛИВОГО ПРОИЗВОДСТВА
Бережливое производство – это концепция
управления производственным предприятием, которая
основана на постоянном стремлении предприятия к
устранению всех видов потерь. Одной из задач
«бережливого производства» является ресурсосбережение.
Под термином «ресурсосбережение» нужно понимать
комплекс
мер
по
обеспечению
рационального,
экономически верного использования ресурсов.
Целью мероприятий, направленных на ресурсосбережение,
является: поиск потенциальных и реальных источников
экономии и способов рационального использования
материальных и нематериальных ресурсов; повышение
прибыли с помощью ресурсосберегающих процессов;
сокращение энерго- и материалоемкости производства.
Ключевыми задачами можно назвать: снижение затрат
материальных ресурсов при производстве востребованных
товаров; увеличение объемов производства за счет
экономии и рационального использования ресурсов.

8.

АКТУАЛЬНОСТЬ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ
Тема бережливого производства, ресурсосбережения
обосновывает актуальность научно-исследовательской
работы, поскольку во все времена человек непременно
ищет такой путь, который помог бы ему достигнуть
наибольшей выгоды. Например, как из круглого бревна
выпилить прямоугольную балку с наименьшим
количеством отходов? Ответы на этот и другие вопросы
минимизации потерь сырья в процессе деревообработки
может быть получен путем решения задач на
оптимизацию методами математического анализа.

9.

ЦЕЛЬ И ЗАДАЧИ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ
Целью научно-исследовательской работы является
поиск наилучшего решения задач минимизации потерь
сырья в процессе деревообработки и получения готовых
изделий из дерева.
Для достижения цели необходимо решить задачи:
построить геометрическую модель;
составить алгебраическую модель – функцию,
выражающую зависимости между переменными
величинами;
исследовать алгебраическую модель на экстремумы с
помощью производной;
сформулировать наилучшее решение поставленной
задачи.

10.

ОБЪЕКТ, ПРЕДМЕТ И МЕТОДЫ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ
Объектом исследования является продукт, полученный в
процессе деревообработки, а предметом исследования
является минимизация потерь в процессе деревообработки.
В ходе работы использовались методы исследований:
поиск, изучение и анализ информации;
моделирование;
методы математического
анализа;
+
анализ результатов;
обобщение.
Работа является научно-исследовательской и содержит
теоретические исследования, базирующиеся на применении
математических
и
логических
методов
познания.
Результатом
теоретического
исследования
является
установление новых зависимостей, выраженных в
математических соотношениях.

11.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
Еще с античных времен человек сталкивался с необходимостью
решения задач на экстремумы. В Древней Греции до VI века до н.э.
установили факты об экстремальных свойствах круга и шара.
Экстремальными задачами занимались многие античные ученые –
Евклид, Архимед, Аристотель и др.
После гибели античной цивилизации научная жизнь в Европе
стала возрождаться только в XV веке. Задачи на экстремумы
оказались среди тех, которыми интересовались лучшие умы того
времени. Если в античные времена задачи на экстремумы
исследовались только геометрическими методами и каждая задача
для своего решения требовала специфического приема, то в XVII
веке появились общие методы изучения задач на экстремумы,
которые привели к созданию дифференциального и интегрального
исчислений. Первые элементы математического анализа были
созданы И. Кеплером (1615 год) Открытое И. Кеплером основное
свойство экстремумов было затем оформлено в виде теоремы
сначала П. Ферма (для многочленов), потом Исааком Ньютоном и
Г. В. Лейбницем.
Ньютон Исаак (1642 - 1727)
Лейбниц Готфрид Вильгельм
(1646 - 1716)

12.

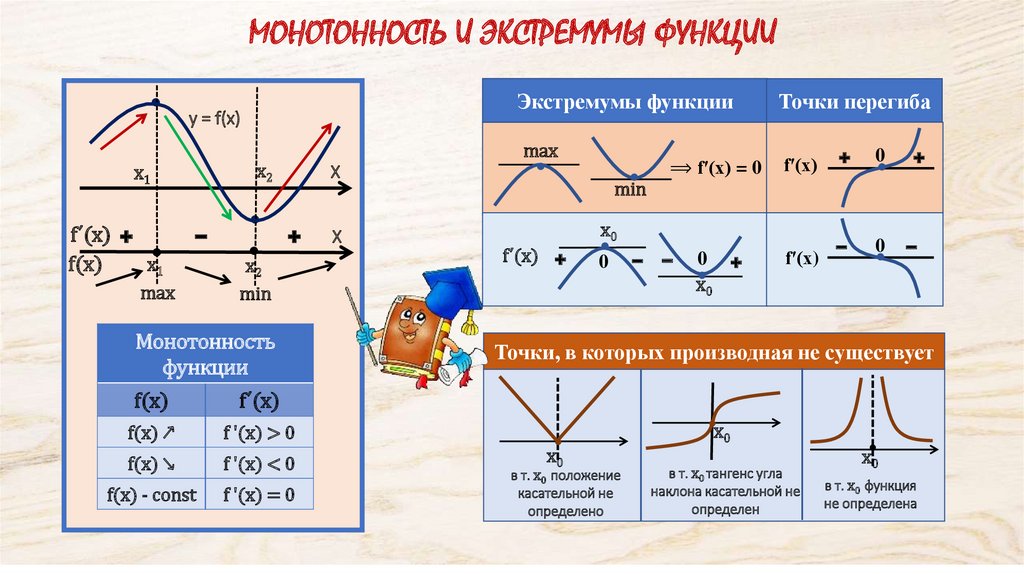
МОНОТОННОСТЬ И ЭКСТРЕМУМЫ ФУНКЦИИ
Экстремумы функции
у = f(x)
max
x2
x1
f΄(x) +
x1
f(x)
−
max
x2
min
Х
+
Монотонность
функции
f(x)
f΄(x)
f(x) ↗
f ʹ(x) > 0
f(x) ↘
f ʹ(x) < 0
f(x) - const
f ʹ(x) = 0
Х
⟹ fʹ(x) = 0
Точки перегиба
fʹ(x)
+
0
−
0
+
min
x0
f΄(x) +
0
− −
0 +
x0
fʹ(x)
−
Точки, в которых производная не существует
x0
в т. x0 положение
касательной не
определено
x0
в т. x0 тангенс угла
наклона касательной не
определен
x0
в т. x0 функция
не определена

13.

АЛГОРИТМ ИССЛЕДОВАНИЯ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
Алгоритм исследования функции
Аналитическая и геометрическая интерпретации
1. Найти производную функции
f'(x).
2. Найти точки в которых
производная равна нулю или не
существует
f'(x) = 0,
x1, x2, x3, … , xn - нули производной.
3. Отметить точки на числовой
прямой и определить знак
производной на получившихся
промежутках
4. По знаку производной
определить характер
монотонности функции и точки
экстремума
5. Записать ответ
точка
перегиба
f΄(x)
f(x)
точки
экстремума
−
−
+ Х
+
↘
↘
↗
↘ x1
x4 ↗
x2
x3
min max
min
−
f(x) ↗ на промежутках (x2; x3) и (x4; +∞),
f(x) ↘ на промежутках (− ∞; x2) и (x3; x4),
x3 − точка максимума функции,
х2 и x4 − точки минимума функции.

14.

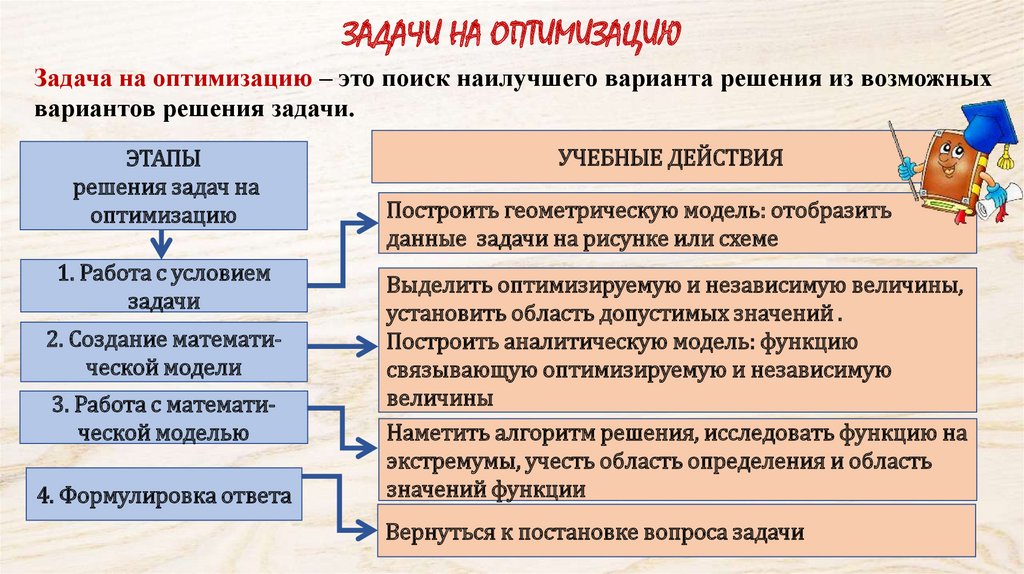
ЗАДАЧИ НА ОПТИМИЗАЦИЮ
Задача на оптимизацию – это поиск наилучшего варианта решения из возможных
вариантов решения задачи.
ЭТАПЫ
решения задач на
оптимизацию
1. Работа с условием
задачи
2. Создание математической модели
3. Работа с математической моделью
4. Формулировка ответа
УЧЕБНЫЕ ДЕЙСТВИЯ
Построить геометрическую модель: отобразить
данные задачи на рисунке или схеме
Выделить оптимизируемую и независимую величины,
установить область допустимых значений .
Построить аналитическую модель: функцию
связывающую оптимизируемую и независимую
величины
Наметить алгоритм решения, исследовать функцию на
экстремумы, учесть область определения и область
значений функции
Вернуться к постановке вопроса задачи

15.

ПРАКТИЧЕСКАЯ ЧАСТЬ. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ
Задача 1. Из заготовок бруса необходимо изготовить
черенки для садового инвентаря. Поперечный срез бруса
R
представляет собой равнобедренную трапецию. Каким
должен
быть
угол
при
основании