Рух тіла під дією декількох сил

1.

2. Рух тіла під дією декількох сил.

РУХ ТІЛА ПІД ДІЄЮ
ДЕКІЛЬКОХ СИЛ.
1
2
3
4
Алгоритм розв’язування задач
Рух тіла по горизонтальній поверхні
Рух тіла по похилій площині
Розв’язування задач

3. Алгоритм розв’язування задач динаміки

АЛГОРИТМ РОЗВ’ЯЗУВАННЯ ЗАДАЧ ДИНАМІКИ
Визначити характер і напрям руху тіла;
Встановити, з якими тілами взаємодіє тіло.
Зробити рисунок, показати всі сили, що діють на
тіло.
Обрати тіло відліку і зв’язати з ним систему
координат.
Записати у векторній формі рівняння другого
закону Ньютона для кожного з тіл.
Спроектувати на координатні осі сили,
прискорення, швидкості.
Записати рівняння другого закону Ньютона в
проекціях на координатні осі, врахувавши знаки
проекцій векторів.

4. Алгоритм розв’язування задач динаміки

АЛГОРИТМ РОЗВ’ЯЗУВАННЯ ЗАДАЧ
ДИНАМІКИ
Якщо в одержаному рівнянні (рівняннях) кількість
невідомих величин дорівнює кількості рівнянь, то
задача може бути розв’язана.
Інакше треба записати додаткові рівняння або
кінематичні формули, виходячи з умови задачі.
Розв’язати рівняння (систему рівнянь) одним з
відомих методів, одержавши остаточну
розрахункову формулу.
Визначити числові значення невідомих величин,
оцінити їх вірогідність; виконати дії над одиницями
вимірювання.
Проаналізувати отриману відповідь.

5. Ковзання тіла по горизонтальній поверхні

КОВЗАННЯ ТІЛА ПО ГОРИЗОНТАЛЬНІЙ
ПОВЕРХНІ
Y
Fтер
N
a
О
mg
F
X
F N mg Fтер ma

6. Ковзання тіла по горизонтальній поверхні. Задача №1.

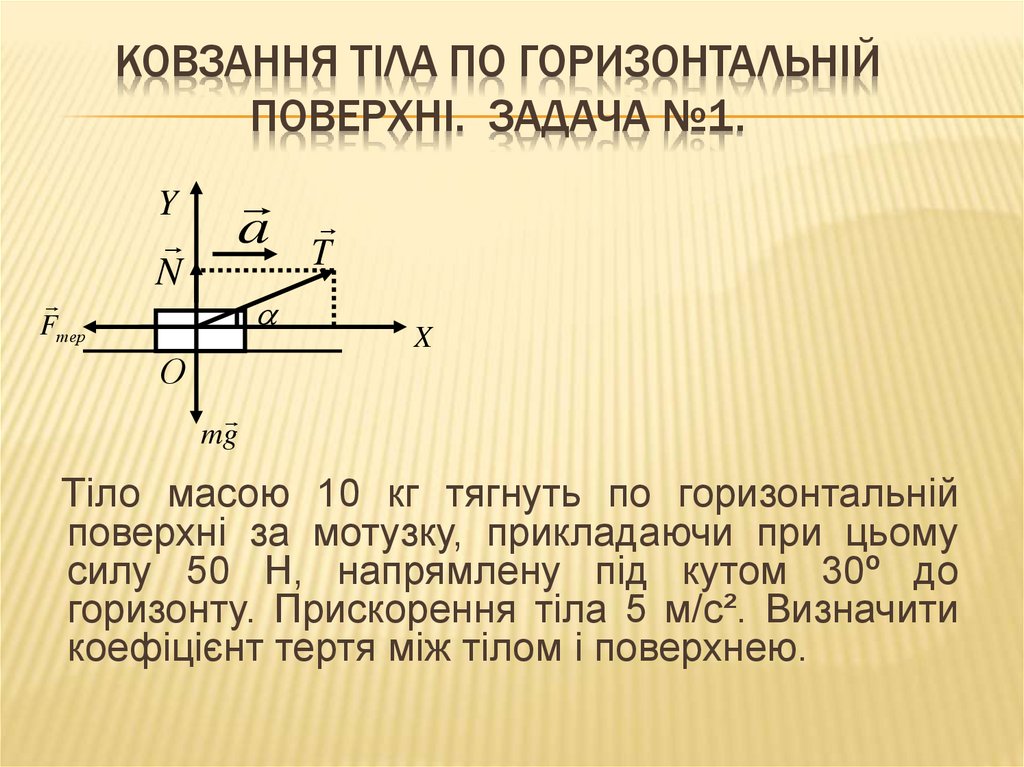
КОВЗАННЯ ТІЛА ПО ГОРИЗОНТАЛЬНІЙ
ПОВЕРХНІ. ЗАДАЧА №1.
Y
Fтер
N
a
О
T
X
mg
Тіло масою 10 кг тягнуть по горизонтальній
поверхні за мотузку, прикладаючи при цьому
силу 50 Н, напрямлену під кутом 30º до
горизонту. Прискорення тіла 5 м/с². Визначити
коефіцієнт тертя між тілом і поверхнею.

7. Пов’яжемо систему координат із тілом на поверхні Землі, спрямуємо вісь ОY вертикально вгору, вісь ОX – горизонтально. Запишемо

ПОВ’ЯЖЕМО СИСТЕМУ КООРДИНАТ ІЗ ТІЛОМ НА ПОВЕРХНІ ЗЕМЛІ,
СПРЯМУЄМО ВІСЬ ОY ВЕРТИКАЛЬНО ВГОРУ, ВІСЬ ОX – ГОРИЗОНТАЛЬНО.
ЗАПИШЕМО ДРУГИЙ ЗАКОН НЬЮТОНА У ВЕКТОРНОМУ ВИГЛЯДІ:
T N mg Fтер ma
ОX:
T cos Fтер ma
ОY:
T sin N mg 0
Fтер N
Спроектуємо рівняння
на осі координат:
N mg T sin
Fтер N (mg T sin )
T cos (mg T sin ) ma
T cos ma
Н кг м / с 2 Н
1
2
mg T sin
кг м / с Н Н

8. Рівномірний рух тіла по похилій площині.

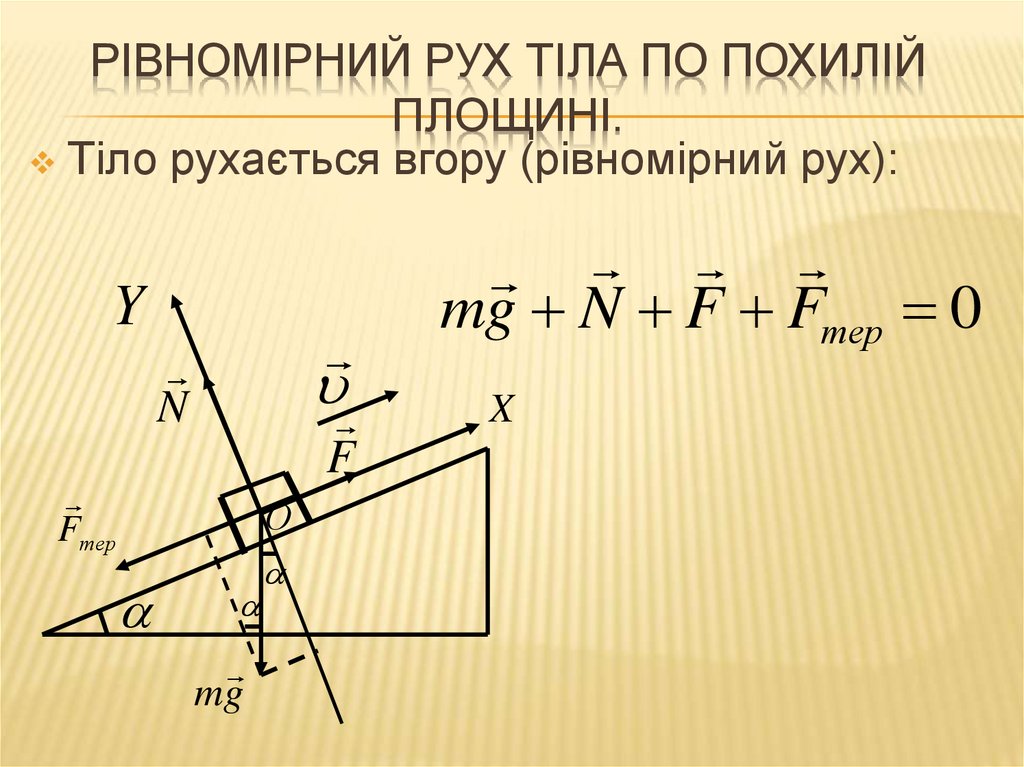
РІВНОМІРНИЙ РУХ ТІЛА ПО ПОХИЛІЙ
ПЛОЩИНІ.
Тіло рухається вгору (рівномірний рух):
Y
N
F
Fтер
О
mg
mg N F Fтер 0
X

9. Рівноприскорений рух по похилій площині.

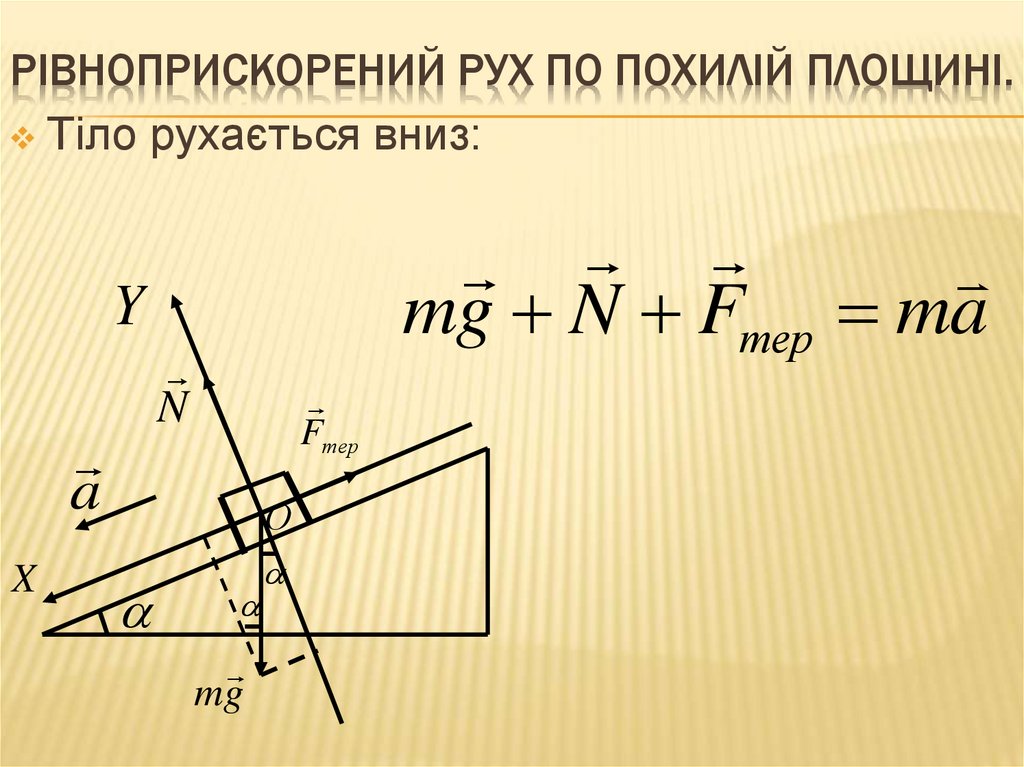
РІВНОПРИСКОРЕНИЙ РУХ ПО ПОХИЛІЙ ПЛОЩИНІ.
Тіло рухається вниз:
mg N Fтер ma
Y
N
a
X
Fтер
О
mg

10. Рівноприскорений рух по похилій площині. Задача №2.

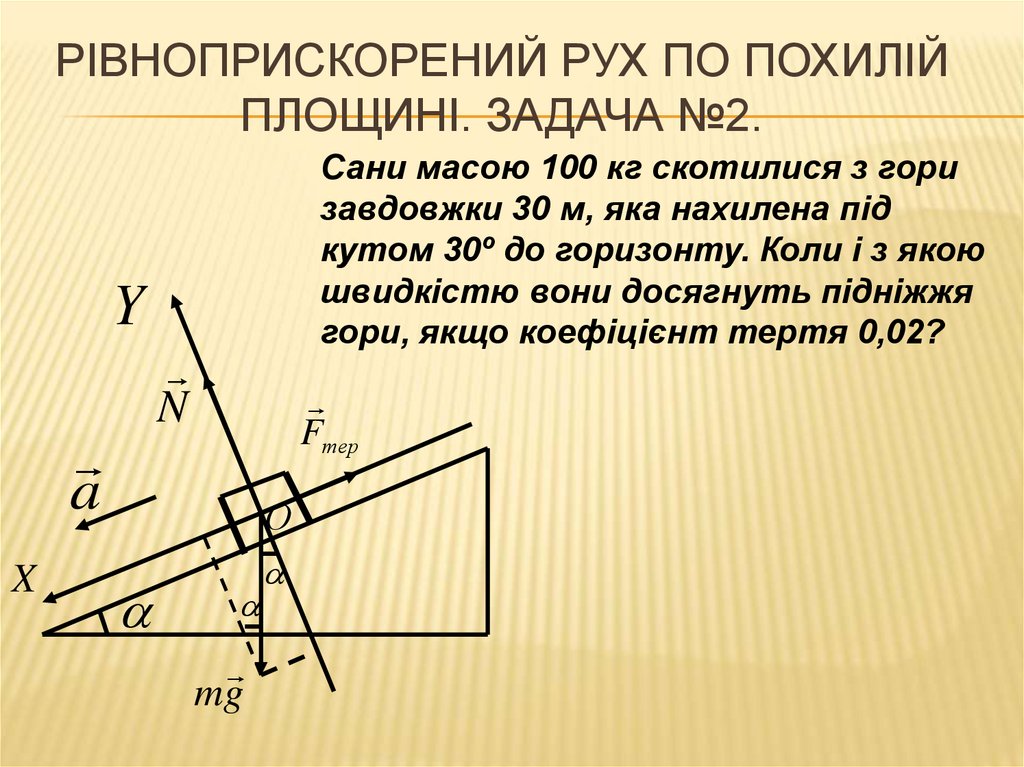
РІВНОПРИСКОРЕНИЙ РУХ ПО ПОХИЛІЙ
ПЛОЩИНІ. ЗАДАЧА №2.
Сани масою 100 кг скотилися з гори
завдовжки 30 м, яка нахилена під
кутом 30º до горизонту. Коли і з якою
швидкістю вони досягнуть підніжжя
гори, якщо коефіцієнт тертя 0,02?
Y
N
a
X
Fтер
О
mg

11. На сани діють сила тяжіння, сила реакції опори і сила тертя.

НА САНИ ДІЮТЬ СИЛА ТЯЖІННЯ, СИЛА
РЕАКЦІЇ ОПОРИ І СИЛА ТЕРТЯ.
Äàíî :
l 30 ì
30
0,02
0
m 100êã
t ?
?
mg N Fтер ma
О : mg sin Fтер ma; a
mg sin Fтер
m
О : N mg cos 0; N mg cos
Fтер N mg cos
mg sin mg cos
a
g (sin cos )
m
При рівноприскореному русі без початкової швидкості шлях:
at 2
2l
l
t
2
a
2l
g (sin cos )
at g (sin cos ) t
t
2 30 ì
3,56ñ
2
9,8 ì / ñ (0,5 0,02 0,866)
9,8 ì / ñ2 (0,5 0,02 0,866) 3,56ñ 16,85 ì / ñ

12. Рух зв’язаних систем. Задача №3.

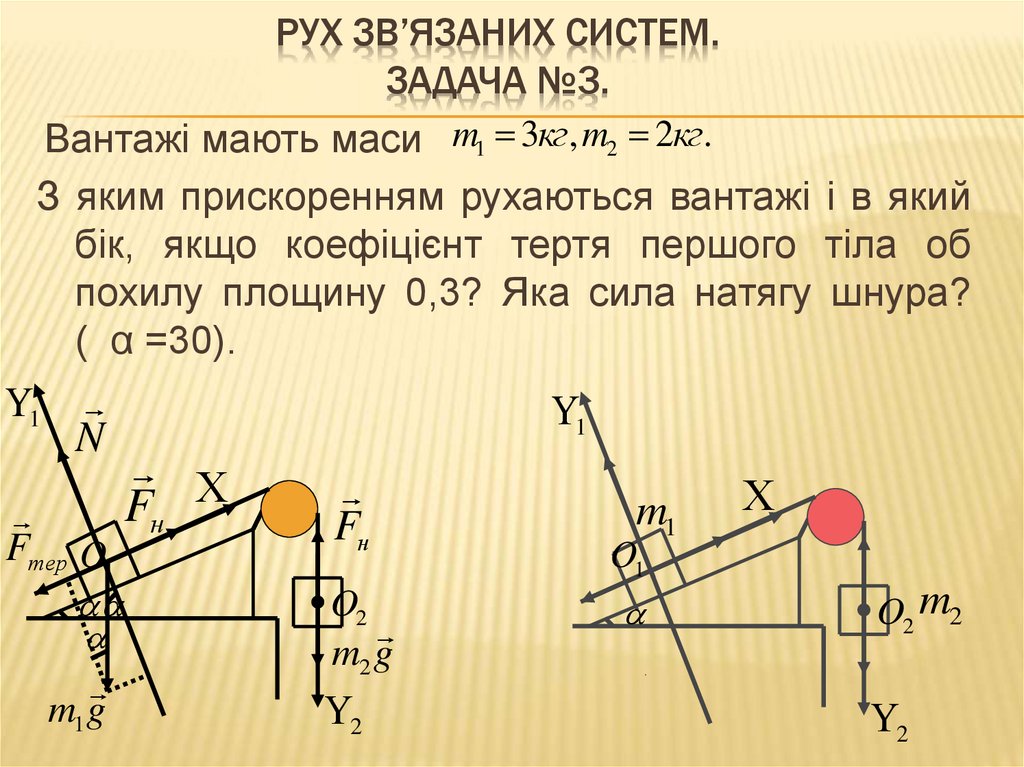
РУХ ЗВ’ЯЗАНИХ СИСТЕМ.
ЗАДАЧА №3.
Вантажі мають маси m1 3кг , m2 2кг.
З яким прискоренням рухаються вантажі і в який
бік, якщо коефіцієнт тертя першого тіла об
похилу площину 0,3? Яка сила натягу шнура?
( α =30).
1
N
Fтер O1
m1 g
1
Fн
Fн
O2
m2 g
2
m1
O1
O2 m2
2

13. Припустимо, що перший вантаж піднімається по похилій площині, а другий опускається.

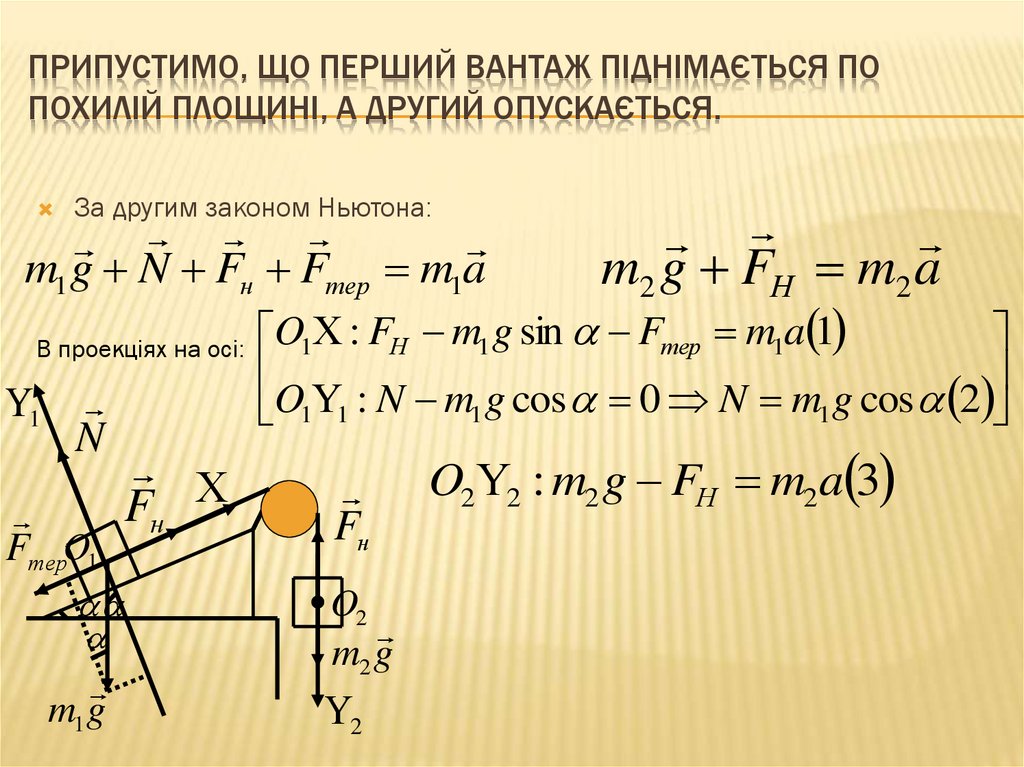
ПРИПУСТИМО, ЩО ПЕРШИЙ ВАНТАЖ ПІДНІМАЄТЬСЯ ПО
ПОХИЛІЙ ПЛОЩИНІ, А ДРУГИЙ ОПУСКАЄТЬСЯ.
За другим законом Ньютона:
m2 g FН m2 a
В проекціях на осі: O1 : FН m1 g sin Fтер m1a 1
m1 g N Fн Fтер m1a
1
N
FтерO1
m1 g
O1 1 : N m1 g cos 0 N m1 g cos 2
Fн
Fн
O2
m2 g
2
O2 2 : m2 g FН m2a 3

14. Додамо два рівняння:

ДОДАМО ДВА РІВНЯННЯ:
FН m1 g sin m1 g cos m1a
m g F m a
Н
2
2
g m2 m1 (sin cos ) m1 m2 a
g (m2 m1 (sin cos ))
a
m1 m2
м кг
а 2 м / с 2
с кг
9,8(2 3(0,5 0,3 0,866))
a
0,56 м / с 2
3 2
FН m2 ( g a)
FН 20,72 Н

15. Рівноприскорений рух по похилій площині.

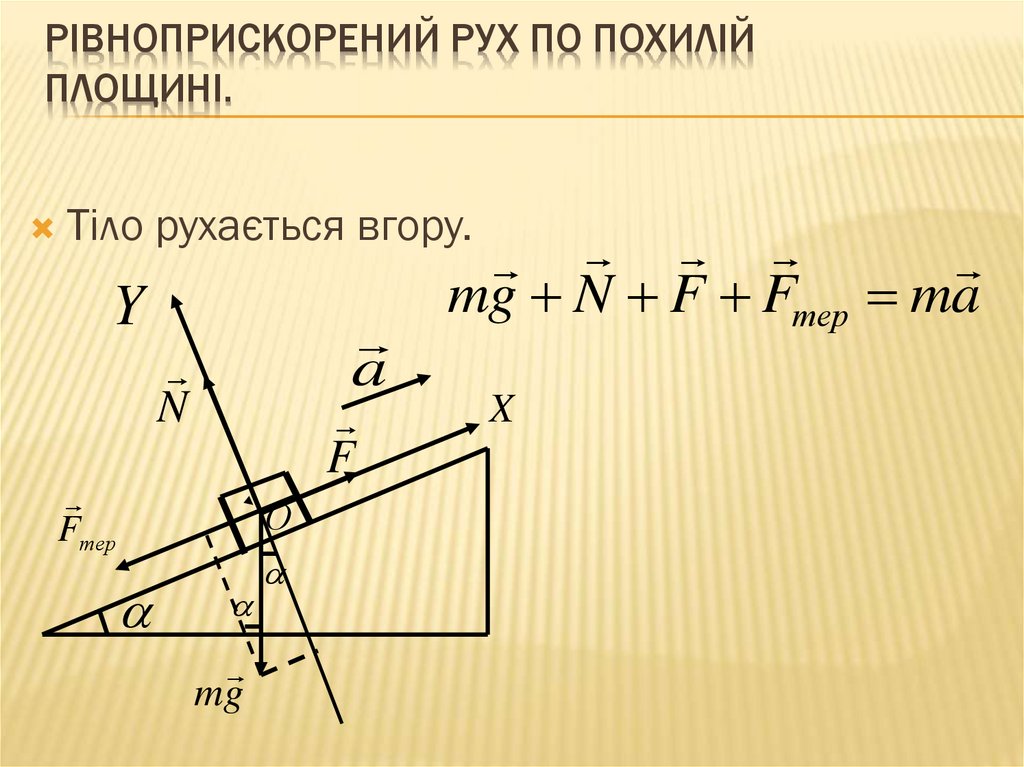
РІВНОПРИСКОРЕНИЙ РУХ ПО ПОХИЛІЙ
ПЛОЩИНІ.
Тіло рухається вгору.
Y
a
N
F
Fтер
О
mg
mg N F Fтер ma
X

16. Задача №4.

ЗАДАЧА №4.
На похилій площині, довжиною 13 м і
висотою 5 м, знаходиться вантаж,
маса якого 26 кг. Коефіцієнт тертя між
вантажем і дошкою 0,5.
Яку силу потрібно прикласти до
вантажу вздовж похилої площини, щоб
його витягнути? Рух вважати
рівноприскореним із прискоренням
0,5 м/с².

17. Виконати рисунок, зобразити сили, координатні вісі.

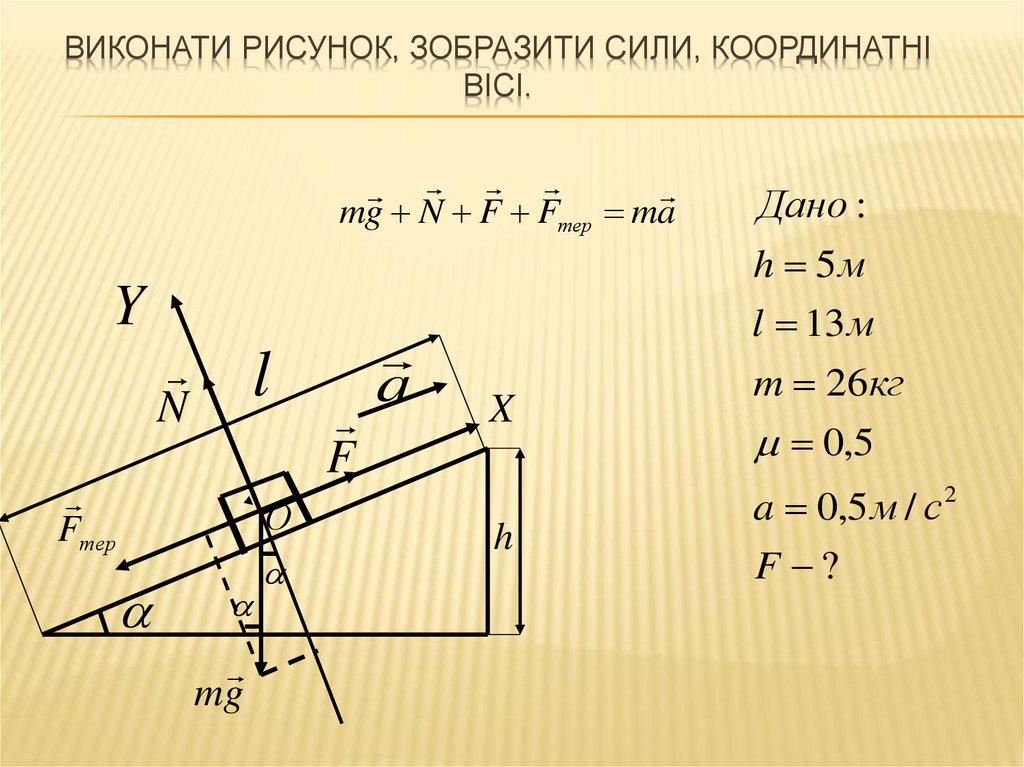
ВИКОНАТИ РИСУНОК, ЗОБРАЗИТИ СИЛИ, КООРДИНАТНІ
ВІСІ.
mg N F Fтер ma
h 5м
Y
N
l
Fтер
О
Дано :
mg
F
a
l 13 м
X
h
m 26кг
0,5
a 0,5 м / с 2
F ?

18. Розв’язок задачі.

РОЗВ’ЯЗОК ЗАДАЧІ.
mg N F Fтер ma
Врахувавши, що
Fтер
О : F Fтер mg sin ma
О : N mg cos 0
2
h
h
2
N ;
cos
1
sin
1
sin ;
l
l
h
F N mg ma
l
2
h
N mg 1 0
l
h
N mg 1
l
2
2
h
h
F mg 1 mg ma
l
l
2
h
h
F ma mg 1 mg
l
l
Відповідь: F=132 Н

19. «Якщо не знаєш, як розв’язувати задачу, почни її розв’язувати».

«ЯКЩО НЕ ЗНАЄШ, ЯК РОЗВ’ЯЗУВАТИ ЗАДАЧУ,
ПОЧНИ ЇЇ РОЗВ’ЯЗУВАТИ».
Отже, розв’язуючи будь-яку задачу з динаміки,
необхідно:
1) виконати пояснювальний рисунок,
2) вказати сили, та записати рівняння другого
закону Ньютона,
3) обрати систему відліку, знайти проекції ( слід
знати, як напрямлені сили, коли вони виникають і
за якими формулами визначаються.
Головне: «Якщо не знаєш, як розв’язувати задачу,
почни її розв’язувати».
Не потрібно боятися зробити хибний крок.
Навчитися розв’язувати задачі з фізики може кожен,
потрібно тільки їх розв’язувати.

20.

Ви познайомились із
розв’язуванням деяких типових
задач із динаміки.
Звичайно, розглянути всі типи задач
неможливо.
Але головне – у вас є алгоритм
розв’язування й приклади роботи
з цим алгоритмом.
Решта за вами.
Бажаю Удачі !!!