Похожие презентации:
Обобщенная модель нейрона. Персептрон (структура, алгоритмы обучения). Решение задачи распознавания образов с помощью НС
1.
Лекция 5Обобщенная модель нейрона.
Персептрон (структура, алгоритмы обучения).
Решение задачи распознавания образов с помощью НС.
2.
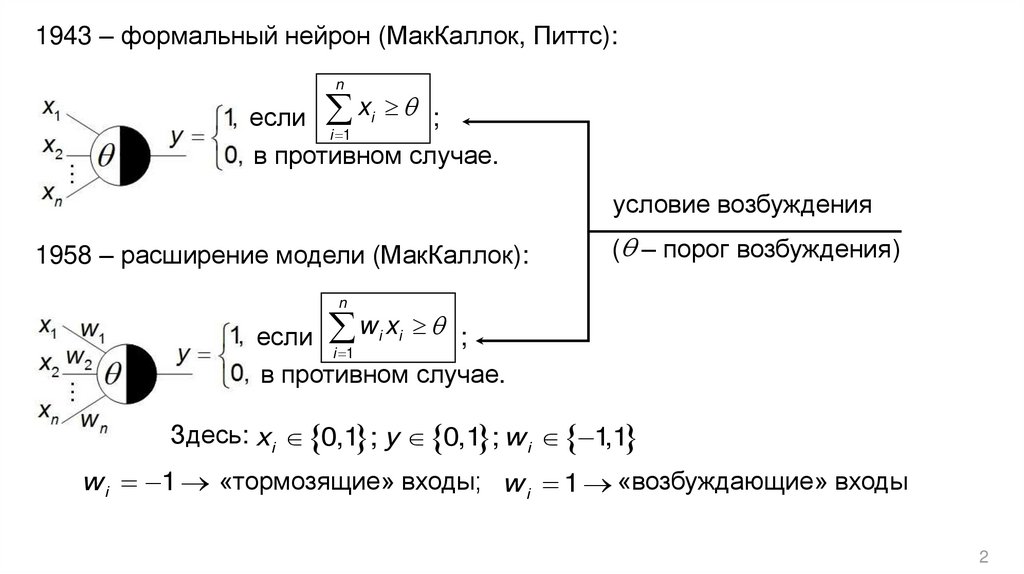
1943 – формальный нейрон (МакКаллок, Питтс):n
если xi ;
i 1
в противном случае.
условие возбуждения
1958 – расширение модели (МакКаллок):
( – порог возбуждения)
n
если w i xi ;
i 1
в противном случае.
Здесь: xi 0,1 ; y 0,1 ; w i 1,1
w i 1 «тормозящие» входы; w i 1 «возбуждающие» входы
2
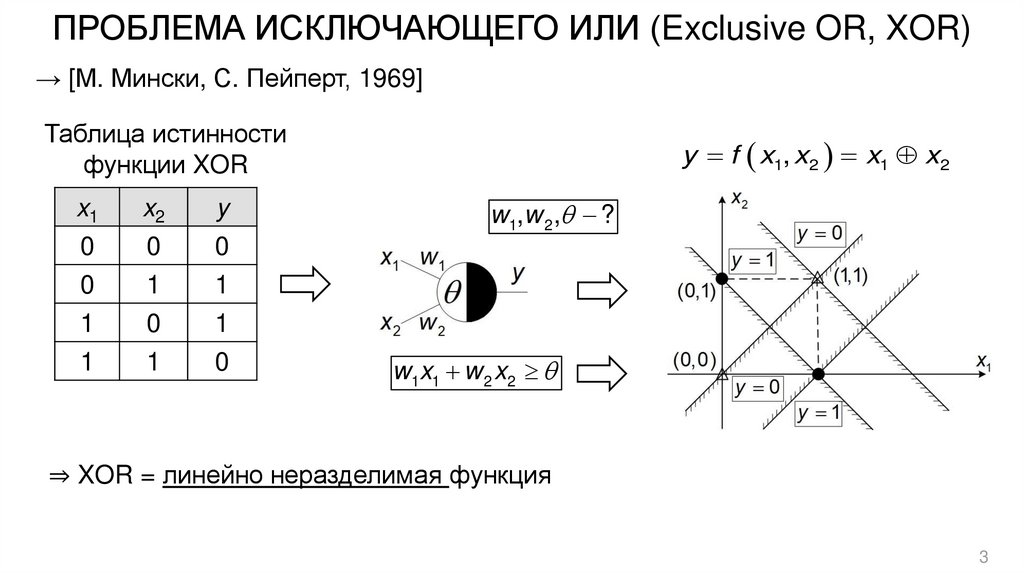
3. ПРОБЛЕМА ИСКЛЮЧАЮЩЕГО ИЛИ (Exclusive OR, XOR)
→ [М. Мински, С. Пейперт, 1969]Таблица истинности
функции XOR
x1
0
0
1
1
x2
0
1
0
1
y
0
1
1
0
y f x1, x2 x1 x2
w1,w 2 , ?
w1x1 w 2 x2
⇒ XOR = линейно неразделимая функция
3
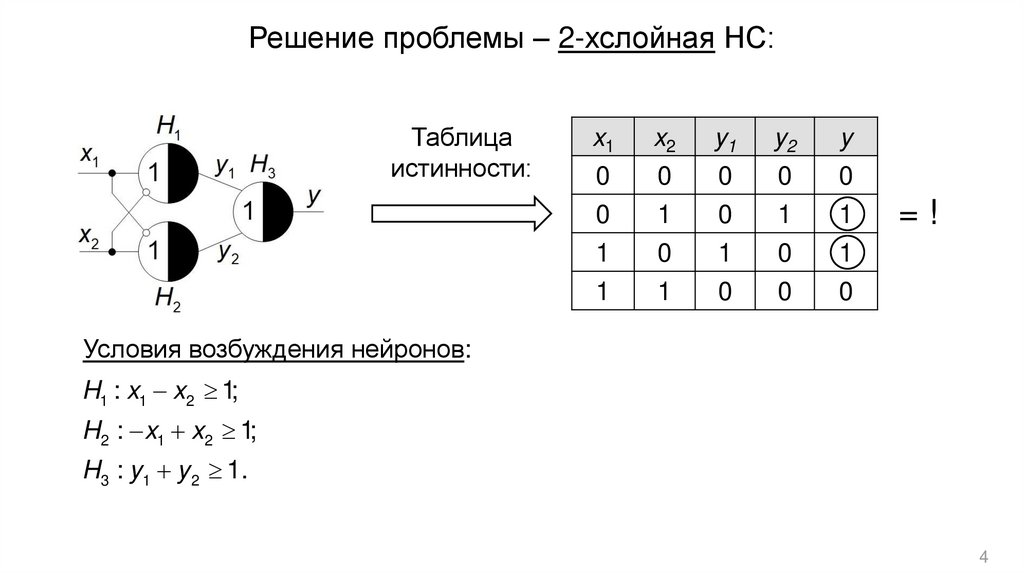
4.
Решение проблемы – 2-хслойная НС:Таблица
истинности:
x1
0
0
1
1
x2
0
1
0
1
y1
0
0
1
0
y2
0
1
0
0
y
0
1
1
0
=!
Условия возбуждения нейронов:
H1 : x1 x2 1;
H2 : x1 x2 1;
H3 : y1 y 2 1.
4
5. ОБОБЩЕННАЯ МОДЕЛЬ НЕЙРОНА
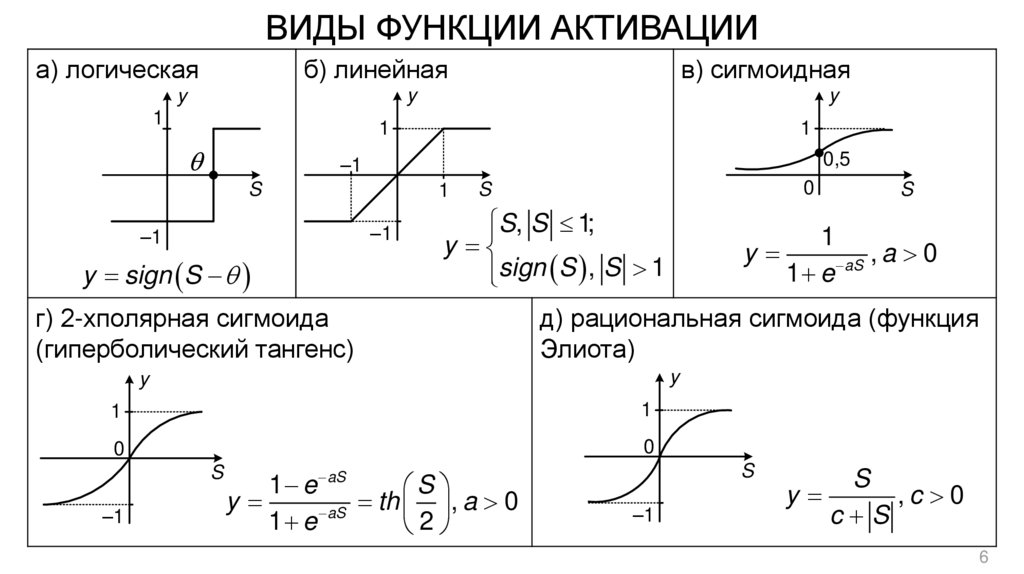
56. ВИДЫ ФУНКЦИИ АКТИВАЦИИ
а) логическаяб) линейная
в) сигмоидная
y
y
y
1
1
1
0,5
–1
S
1
–1
–1
y sign S
0
S
S, S 1;
y
sign S , S 1
г) 2-хполярная сигмоида
(гиперболический тангенс)
1
y
,a 0
aS
1 e
д) рациональная сигмоида (функция
Элиота)
y
y
1
1
0
0
S
–1
S
S
aS
1 e
S
y
th , a 0
aS
1 e
2
–1
S
y
,c 0
c S
6
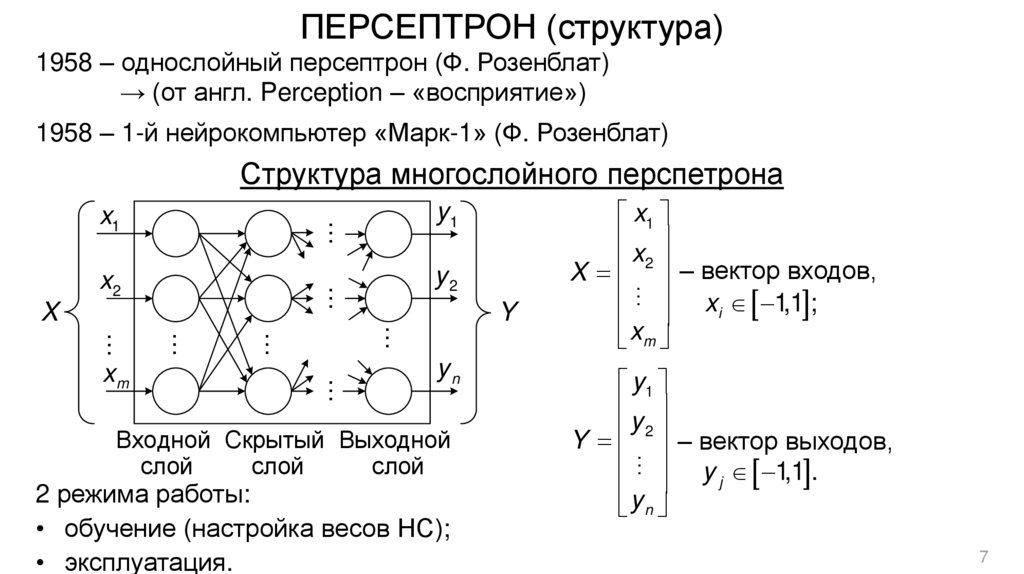
7. ПЕРСЕПТРОН (структура)
1958 – однослойный персептрон (Ф. Розенблат)→ (от англ. Perception – «восприятие»)
1958 – 1-й нейрокомпьютер «Марк-1» (Ф. Розенблат)
Структура многослойного перспетрона
y1
x2
y2
X
Y
xm
yn
2 режима работы:
• обучение (настройка весов НС);
• эксплуатация.
y1
y2
Y
– вектор выходов,
y j 1,1 .
yn
…
Входной Скрытый Выходной
слой
слой
слой
x1
x2
– вектор входов,
X
x 1,1 ;
i
xm
…
x1
7
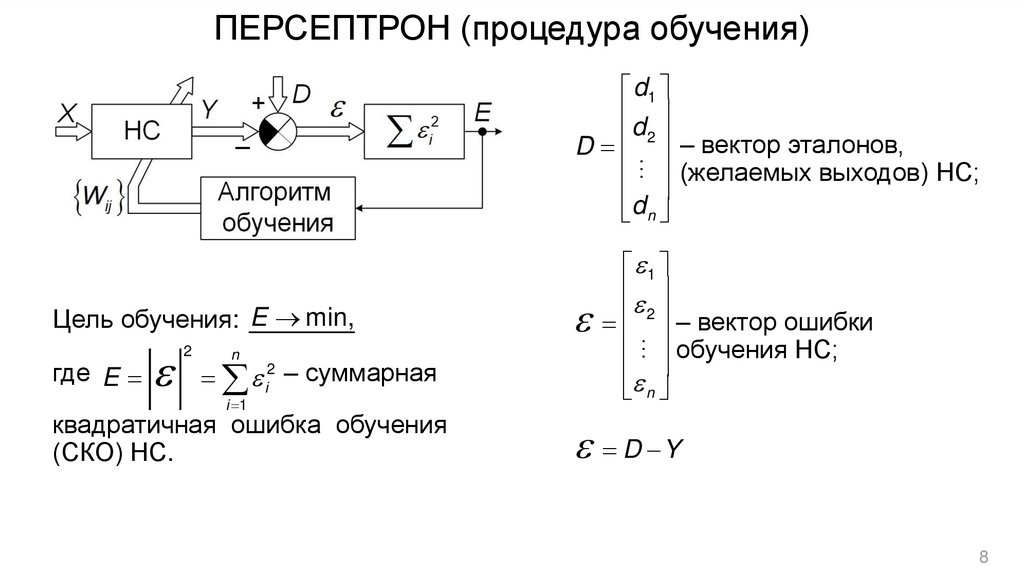
8. ПЕРСЕПТРОН (процедура обучения)
…d1
d2
– вектор эталонов,
D
(желаемых выходов) НС;
d n
Цель обучения: E min,
n
i2 – суммарная
i 1
квадратичная ошибка обучения
(СКО) НС.
…
где E
2
1
2
– вектор ошибки
обучения НС;
n
D Y
8
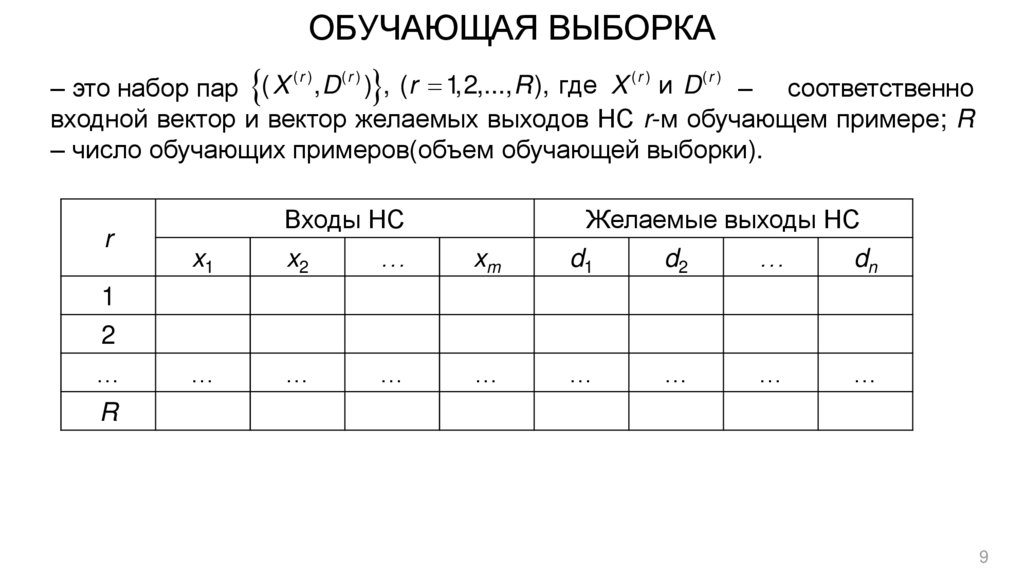
9. ОБУЧАЮЩАЯ ВЫБОРКА
(r )(r )
(r )
(r )
– это набор пар ( X , D ) , (r 1,2,..., R ), где X и D – соответственно
входной вектор и вектор желаемых выходов НС r-м обучающем примере; R
– число обучающих примеров(объем обучающей выборки).
r
Входы НС
Желаемые выходы НС
x1
x2
…
xm
d1
d2
…
dn
…
…
…
…
…
…
…
…
1
2
…
R
9
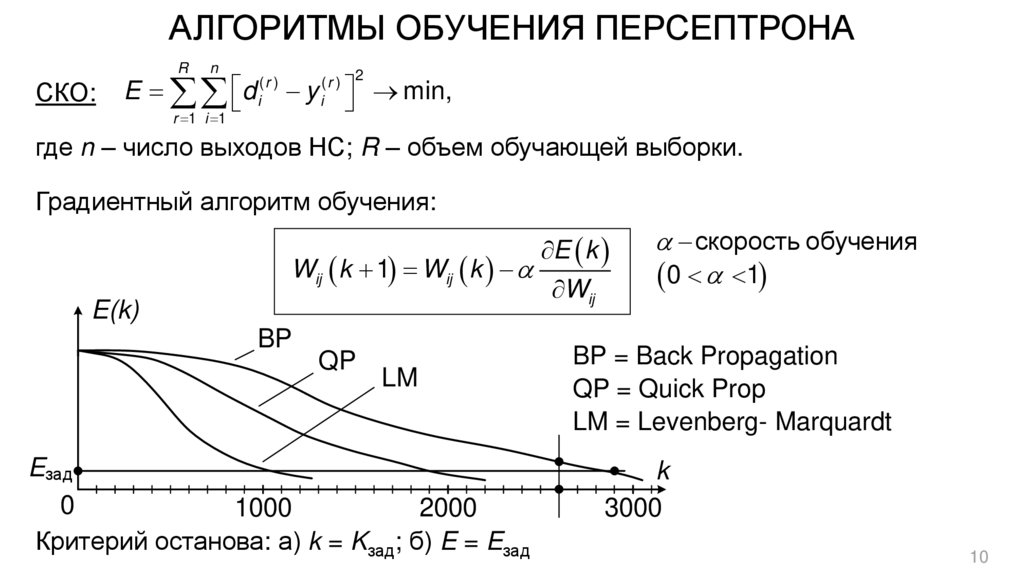
10. АЛГОРИТМЫ ОБУЧЕНИЯ ПЕРСЕПТРОНА
RСКО:
n
E d
r 1 i 1
(r )
i
y
(r ) 2
i
min,
где n – число выходов НС; R – объем обучающей выборки.
Градиентный алгоритм обучения:
Wij k 1 Wij k
E(k)
BP
QP
LM
Eзад
0
1000
2000
Критерий останова: а) k = Kзад; б) E = Eзад
E k
Wij
скорость обучения
0 1
BP = Back Propagation
QP = Quick Prop
LM = Levenberg- Marquardt
k
3000
10
11. СЛОЖНОСТИ ПРОЦЕССА ОБУЧЕНИЯ
1) «зависание» в локальных минимумах→ метод «тяжелого» шарика:
Wij k 1 Wij k Wij k Wij k 1
где Wij k
E k
; 0 1 момент;
Wij
2) регуляризация процесса обучения:
n
n
E d
r 1 i 1
где
(r )
i
y
Wij2 min
(r ) 2
i
i, j
– коэффициент «штрафа» весов НС;
3) эффект «переобучения» (over-learning) НС
→ выбор оптимальной сложности НС (количества нейронов в скрытом
слое); тестирование / валидация НС.
11
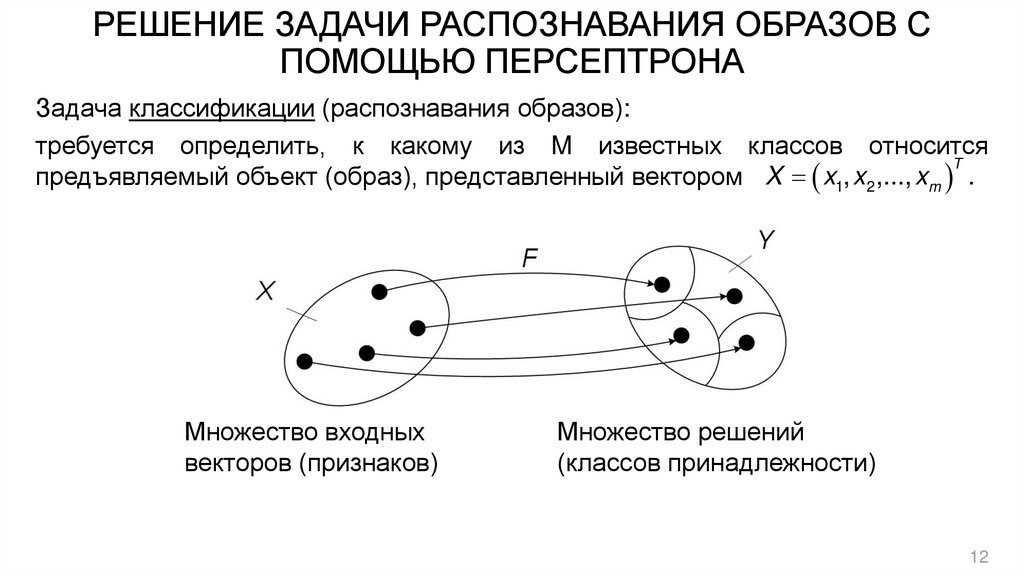
12. РЕШЕНИЕ ЗАДАЧИ РАСПОЗНАВАНИЯ ОБРАЗОВ С ПОМОЩЬЮ ПЕРСЕПТРОНА
Задача классификации (распознавания образов):требуется определить, к какому из M известных классов относится
T
предъявляемый объект (образ), представленный вектором X x1, x2 ,..., xm .
Множество входных
векторов (признаков)
Множество решений
(классов принадлежности)
12
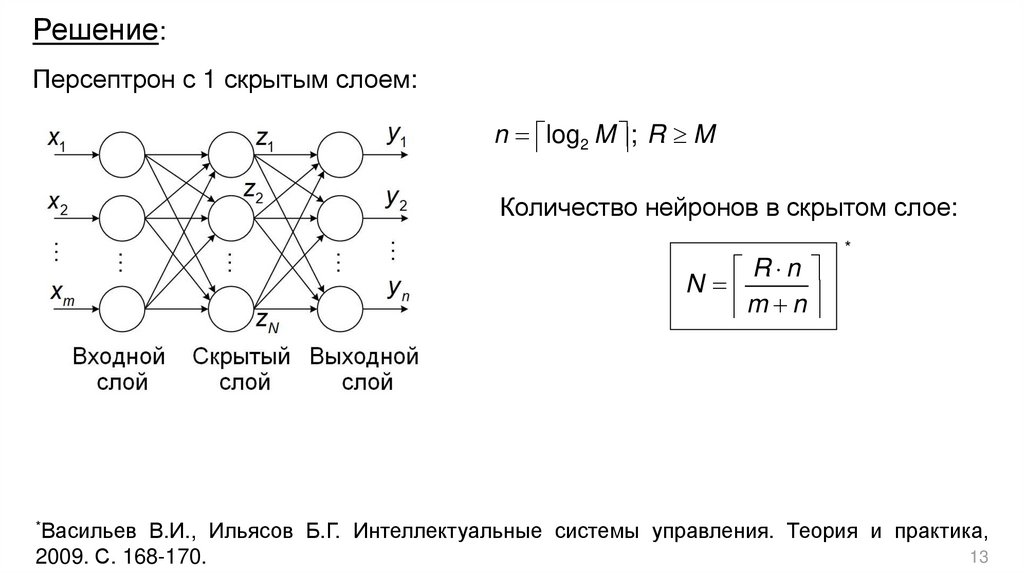
13.
Решение:Персептрон с 1 скрытым слоем:
n log2 M ; R M
Количество нейронов в скрытом слое:
R n
N
m n
*Васильев
*
В.И., Ильясов Б.Г. Интеллектуальные системы управления. Теория и практика,
13
2009. С. 168-170.
14. ПРИМЕР
Дано: 7х5 матрица входных образов (изображений):M = 64 (буквы, цифры, символы); входы xi 1,1 ;
вектор желаемых реакций НС: D d1, d 2 ,..., d n – двоичный
T
код / номер образа (класса изображений).
7
5
Решение: m 7 5 35; R M 64;
R n 64 6
n log2 64 6; N
10.
m n 35 6
Структура НС: 35 – 10 – 6:
w1 w ij(1)
35 10
, w 2 w ij(2)
10 6
– матрицы
весов синаптических связей;
F1( ), F2 ( ) – сигмоидные функции
активации
Количество настраиваемых параметров (весов) НС: КП 35 10 10 6 410.
14




 Информатика
Информатика








