Похожие презентации:
Случайные процессы (Лекция 8)
1. Лекция 8
Случайные процессыЛекция 8
Случайные процессы
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
1
2. Классификация процессов
Случайные процессыКлассификация процессов
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
2
3. Классификация процессов
Случайные процессыКлассификация процессов
С практической точки зрения решение о
случайности или детерминированности процесса
основывается на способности воспроизвести
процесс в ходе контролируемого эксперимента.
Если это приводит к одним и тем же
результатам, то процесс считается детерминированным.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
3
4. Классификация процессов
Случайные процессыКлассификация процессов
Детерминированные процессы – это процессы,
которые можно описать математическими
формулами (т.е. мы можем определить
положение системы в любой момент времени с
разумной точностью).
► Движение спутника на околоземной
орбите, измерение температуры воды при
нагревании.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
4
5. Классификация процессов
Случайные процессыКлассификация процессов
Процессы,
такие
как
высота
волн,
напряжение в нашей электросети, изменение
численности жителей в Харькове с течением
времени, не являются детерминированными –
положение системы в таких процессах точно
определить невозможно. Для описания этих
процессов требуются вероятностные понятия и
статистические характеристики.
Теорией случайных процессов называется
математическая наука, изучающая случайные
явления в динамике их развития.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
5
6. Марков Андрей Андреевич Марков Андрей Андреевич Марков Андрей Андреевич
Случайные процессыМарков Андрей Андреевич
1856-1922
Русский математик.
Написал около 70 работ по
теории
чисел,
теории
приближения функций, теории
вероятностей. Существенно расширил сферу применения закона
больших чисел и центральной
предельной теоремы. Является
основоположником теории случайных процессов.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
6
7. Классификация процессов
Случайные процессыКлассификация процессов
Третий вид процессов - хаотические. С одной
стороны – детерминированные. Но очень
нелинейные, с сильной зависимостью от
начальных условий. В реальности начальные
условия точно повторить нельзя, и поведение
системы через некоторое время становится
непредсказуемым. На выходе такие системы
имеют случайные траектории и к ним требуются
вероятностные подходы.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
7
8. Определение случайного процесса
Случайные процессыОпределение случайного процесса
Случайные процессы являются математическими моделями для описания случайных
явлений, развивающихся во времени. При этом
предполагается, что состояние в текущий
момент времени есть случайная величина (t , w)
На пространстве элементарных событий
определена -алгебра его подмножеств F и для
его
определена
события
любого
A F
вероятность P ( A) . Таким образом задано
вероятностное пространство , F , P .
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
8
9. Определение случайного процесса
Случайные процессыОпределение случайного процесса
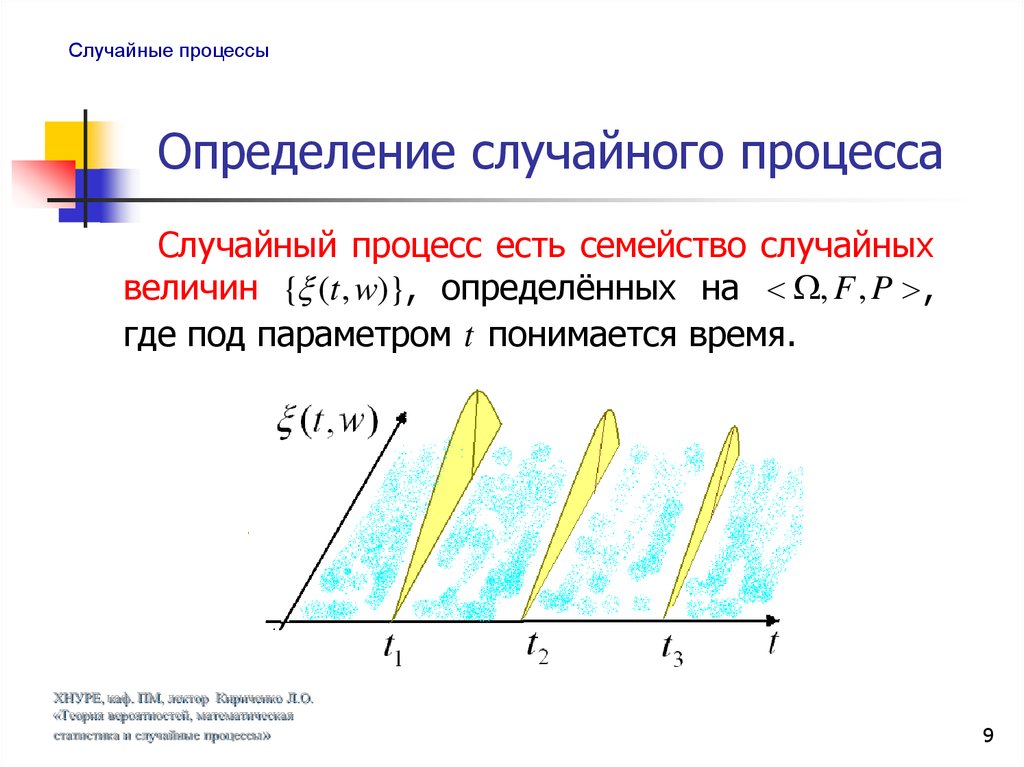
Случайный процесс есть семейство случайных
величин { (t , w)}, определённых на , F , P ,
где под параметром t понимается время.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
9
10. Определение случайного процесса
Случайные процессыОпределение случайного процесса
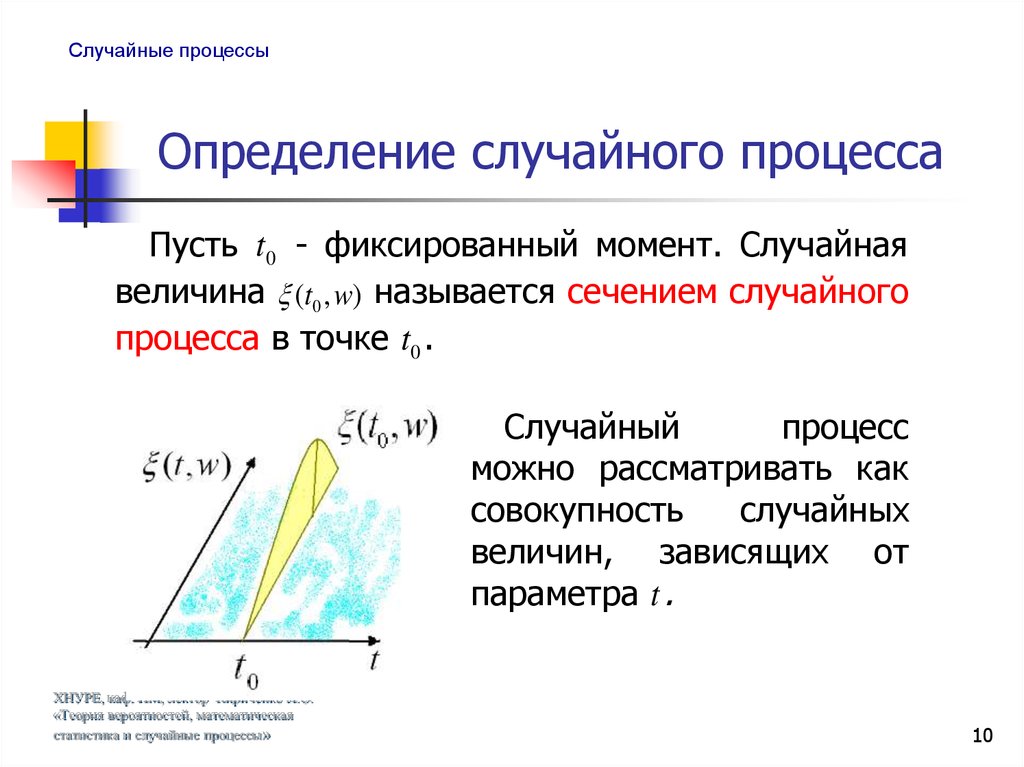
Пусть t0 - фиксированный момент. Случайная
величина (t0 , w) называется сечением случайного
процесса в точке t0 .
процесс
Случайный
можно рассматривать как
случайных
совокупность
величин, зависящих от
параметра t .
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
10
11. Определение случайного процесса
Случайные процессыОпределение случайного процесса
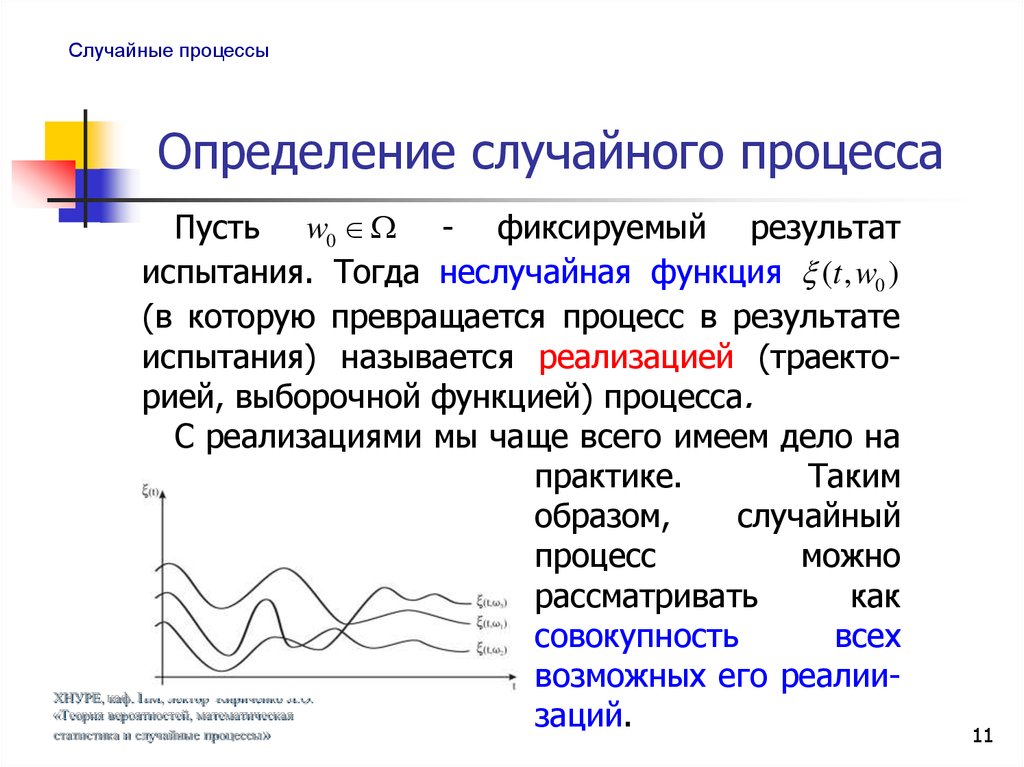
Пусть w0 - фиксируемый результат
испытания. Тогда неслучайная функция (t , w0 )
(в которую превращается процесс в результате
испытания) называется реализацией (траекторией, выборочной функцией) процесса.
С реализациями мы чаще всего имеем дело на
практике.
Таким
образом,
случайный
процесс
можно
рассматривать
как
совокупность
всех
возможных его реалииХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
заций.
статистика и случайные процессы»
11
12. Определение случайного процесса
Случайные процессыОпределение случайного процесса
Случайный процесс можно рассматривать как
совокупность случайных величин, зависящих от
параметра t .
Случайный процесс
можно
рассматривать как
совокупность всех
возможных реализаций.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
12
13. Непрерывность и дискретность случайных процессов
Случайные процессыНепрерывность и дискретность
случайных процессов
Случайный процесс называется процессом с
дискретным
временем
(или
случайной
последовательностью) если система, в которой
он протекает, может менять своё состояние
только в дискретные моменты времени.
► Некто накупил всяких лотерейных билетов.
Выигрыши происходят в определённые дни.
Случайный процесс (t ) - число билетов,
выигравших до момента времени t .
Случайный процесс называется процессом с
непрерывным временем, если переходы системы
могут происходить в любой момент t .
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
13
14. Непрерывность и дискретность случайных процессов
Случайные процессыНепрерывность и дискретность
случайных процессов
Случайный процесс называется процессом с
дискретными состояниями, если в любой момент
времени множество его состояний конечно или
счётно (если любое его сечение – дискретная
случайная величина ).
► Техническое устройство может иметь три
состояния: работает нормально, работает с
перебоями, ремонтируется. Случайный процесс
(t ) - состояние устройства в момент времени t
Случайный процесс называется процессом с
непрерывными состояниями, если множество его
состояний несчётно (если любое его сечение –
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей,
математическая
непрерывная
случайная величина ).
статистика и случайные процессы»
14
15. Законы распределения случайного процесса
Случайные процессыЗаконы распределения
случайного процесса
Универсальной, исчерпывающей характеристикой случайной величины является её функция
распределения F ( x) P( x) .
При любом фиксированном t получим сечение
случайного процесса. Это случайная величина,
которая имеет закон распределения.
F ( x, t ) P( (t ) x)
одномерный закон распределения. Функция зависит от
двух аргументов (t и x ) и
характеризует свойства одного
отдельного сечения.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
15
16. Законы распределения случайного процесса
Случайные процессыЗаконы распределения
случайного процесса
Двумерный закон распределения
F ( x1 , t1 , x2 , t2 ) P( (t1 ) x1 , (t2 ) x2 ) - функция 4-х
аргументов.
Это
уже
неприятно.
Далее – трехмерные и
т.д. Теоретически число
сечений можно увеличивать неограниченно.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
16
17. Законы распределения случайного процесса
Случайные процессыЗаконы распределения
случайного процесса
Однако на практике очень часто вполне можно
ограничиться двумерным законом. Например,
огромный класс марковских процессов (процессы
без последствия), гауссовские процессы (очень
широкий класс процессов, которые являются
моделями сигналов и помех в радиотехнике), для
которых двумерный закон распределения является
исчерпывающей характеристикой.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
17
18. Законы распределения случайного процесса
Случайные процессыЗаконы распределения
случайного процесса
Пусть (t ) - случайный процесс и задано
некоторое произвольное множество моментов
времени.
Соответствующая
совокупность
случайных величин (t1 ),..., (tn ) имеет n – мерную
функцию распределения
F ( x1 ,..., xn , t1 ,..., tn ) P{ (t1 ) x1 ,..., (tn ) xn }.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
18
19. Законы распределения случайного процесса
Случайные процессыЗаконы распределения
случайного процесса
Семейство конечномерных распределений
случайного процесса – это совокупность n мерных функций распределения для различных
n и моментов t .
Семейство конечномерных распределений
является основной характеристикой случайного
его
определяющей
полностью
процесса,
свойства. Говорят, что случайный процесс,
семейство
его
задано
если
задан,
конечномерных распределений.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
19
20. Колмогоров Андрей Николаевич
Случайные процессыКолмогоров Андрей Николаевич
1903-1987
Великий русский
математик.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
20
21. Моментные характеристики
Случайные процессыМоментные характеристики
Для характеристики случайной величины
были
определены
неслучайные
числовые
характеристики – математическое ожидание
M [ ] - среднее значение случайной величины;
дисперсия D[ ] - разброс значений относительно
корреляционный
момент
M [ ];
COV [ , ] M ( M )( M ) , который характеризует степень линейной зависимости между
случайными величинами и .
Так как сечения случайного процесса
представляют собой случайные величины , мы
можем
определить
основные
моментные
характеристики случайного процесса.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
21
22. Моментные характеристики
Случайные процессыМоментные характеристики
Неслучайная функция m (t ) , которая t равна
математическому ожиданию соответствующего
сечения случайного процесса m (t ) M [ (t )],
называется
математическим
ожиданием
случайного процесса.
Его можно найти
через
одномерный
закон распределения:
m (t )
xp ( x, t )dx
.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
22
23. Моментные характеристики
Случайные процессыМоментные характеристики
Дисперсия случайного процесса – это
неслучайная функция, которая t равна
дисперсии
соответствующего
сечения.
D (t ) D[ (t )] M [( (t ) M (t )) 2 ] - можно найти
через одномерный закон
распределения.
D (t )
x 2 p ( x, t )dx m 2 (t )
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
23
24. Моментные характеристики. Пример.
Случайные процессыМоментные характеристики. Пример.
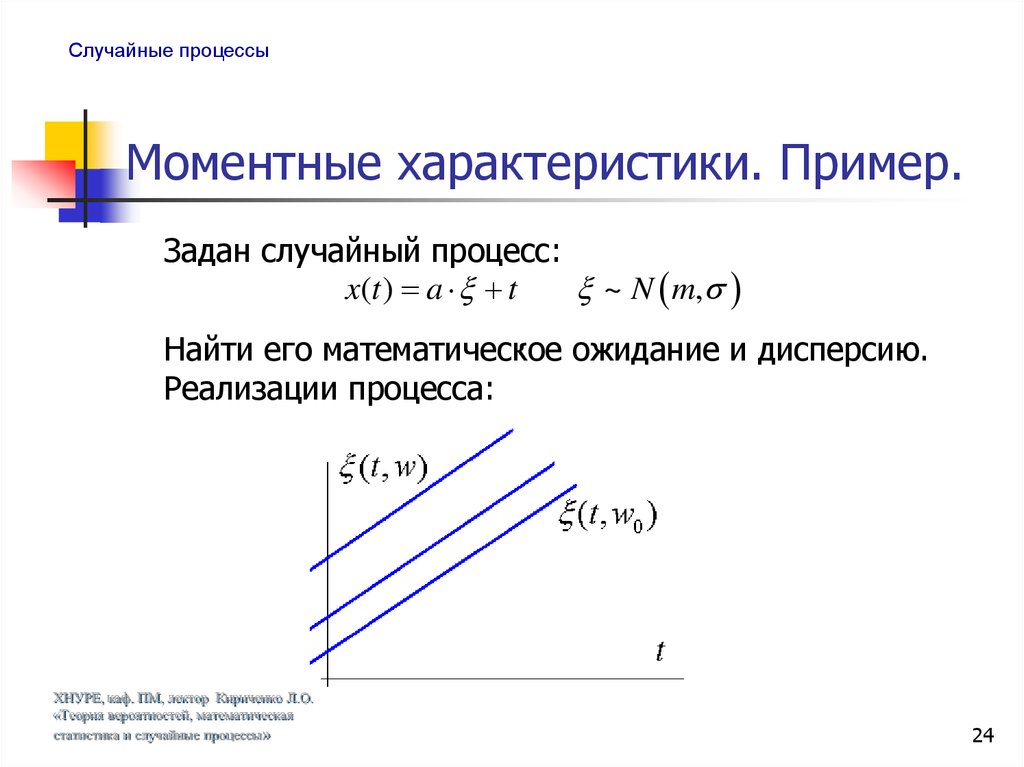
Задан случайный процесс:
x(t ) a t
~ N m,
Найти его математическое ожидание и дисперсию.
Реализации процесса:
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
24
25. Моментные характеристики. Пример.
Случайные процессыМоментные характеристики. Пример.
mx t M a t am t
Dx t D a t D a D t a 2 2
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
25
26. Корреляционная функция
Случайные процессыКорреляционная функция
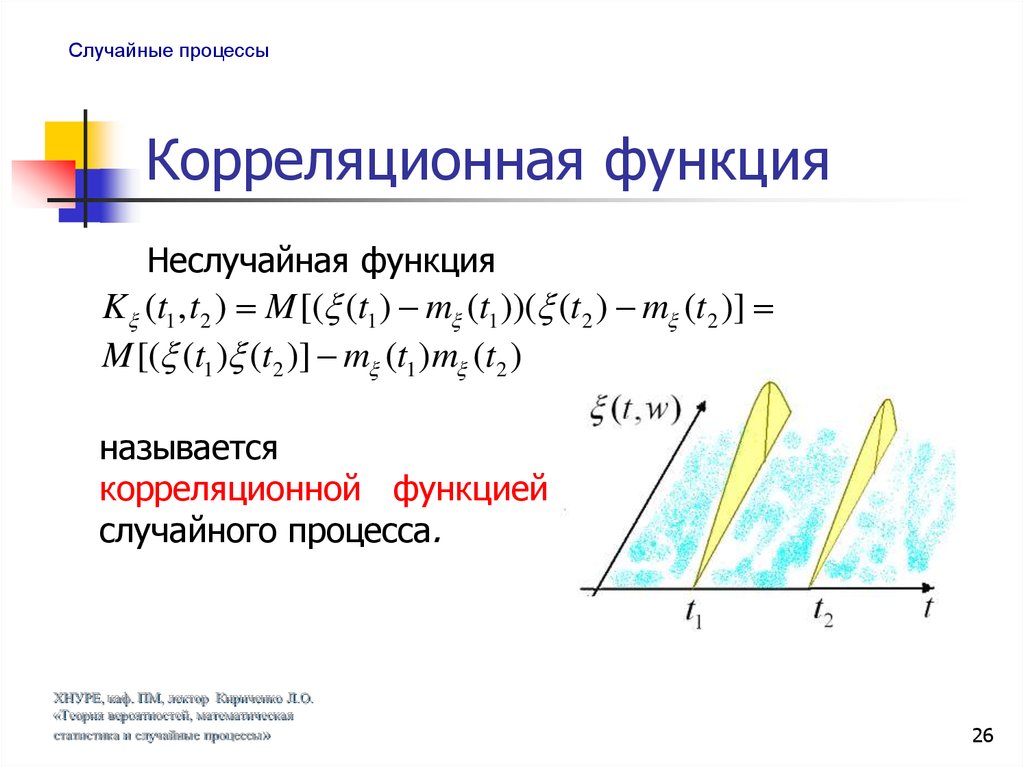
Неслучайная функция
K (t1 , t2 ) M [( (t1 ) m (t1 ))( (t2 ) m (t2 )]
M [( (t1 ) (t2 )] m (t1 )m (t2 )
называется
корреляционной функцией
случайного процесса.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
26
27. Корреляционная функция
Случайные процессыКорреляционная функция
Корреляционная функция для каждой пары чисел t1
и t2 равна корреляционному моменту соответствующих
сечений и характеризует степень их линейной
зависимости. Для расчёта корреляционной функции
необходимо знать двумерное распределение:
.
K (t1 , t2 )
(x
1
m (t1 ))( x2 m (t2 )) p ( x1 , x2 , t1 , t2 )dx1 , dx2
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
27
28. Корреляционная функция. Пример.
Случайные процессыКорреляционная функция. Пример.
x(t ) a t
~ N m,
K x t1 , t2 M x t1 mx t1 x t2 mx t2
M a t1 am t1 a t2 am t2
2
a 2 M m a 2 2
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
28
29. Свойства корреляционной функции
Случайные процессыСвойства корреляционной функции
1. При равенстве аргументов t1 t2 t K (t , t ) D (t ) .
симметрична
функция
2. Корреляционная
относительно своих аргументов K (t1 , t2 ) K (t2 , t1 )
корреляционной
3. Модуль
превосходит
не
функции
среднеквадрапроизведение
тичных отклонений соответствующих сечений
K (t1 , t2 ) D (t1 ) D (t2 )
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
29
30. Свойства корреляционной функции
Случайные процессыСвойства корреляционной функции
Нормированная корреляционная функция
K (t1 , t2 )
r (t1 , t2 )
(t1 ) (t2 )
(аналог - коэффициент корреляции
COV ( X , Y )
x y
).
Свойства нормированной корреляционной функции
следуют из свойств корреляционной функции.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
30
31. Свойства корреляционной функции
Случайные процессыСвойства корреляционной функции
1) При равенстве аргументов t1 t2
D (t )
r (t )
1.
(t ) (t )
2) r (t1 , t2 ) r (t2 , t1 ) .
3) r (t1, t2 ) 1.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
31
32. Стационарные процессы
Случайные процессыСтационарные процессы
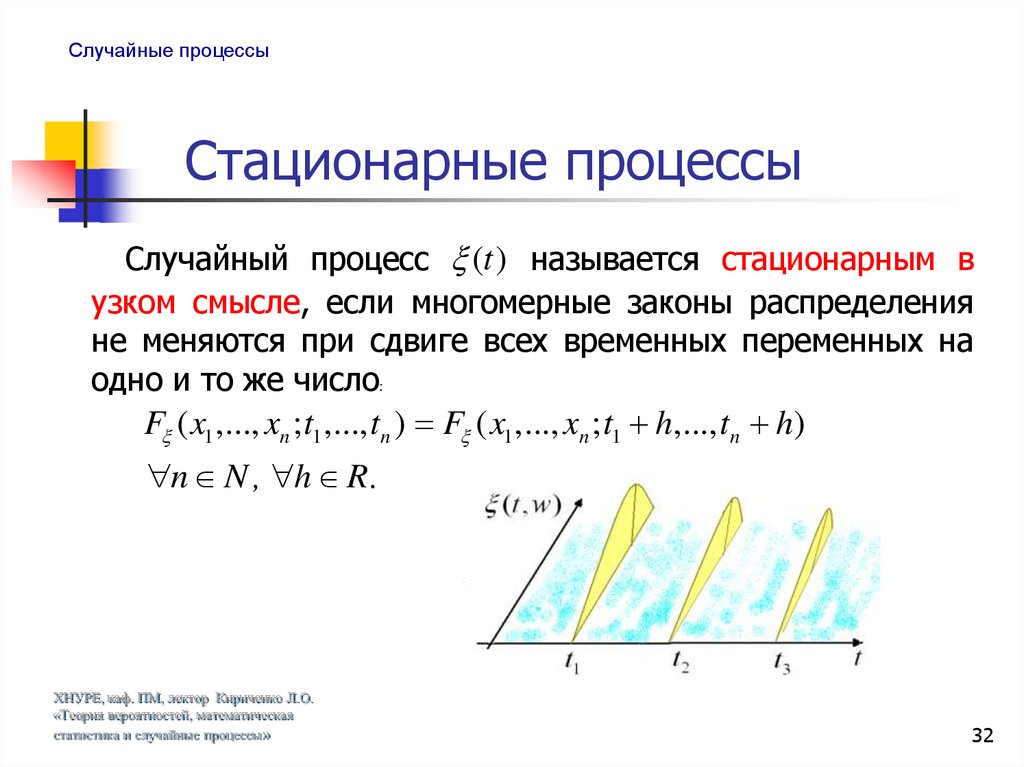
Случайный процесс (t ) называется стационарным в
узком смысле, если многомерные законы распределения
не меняются при сдвиге всех временных переменных на
одно и то же число:
F ( x1 ,..., xn ; t1 ,..., tn ) F ( x1 ,..., xn ; t1 h,..., tn h)
n N , h R .
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
32
33. Стационарные процессы
Случайные процессыСтационарные процессы
Более обширный класс - процессы, стационарные в
широком смысле. Чаще всего под стационарностью
понимается стационарность в широком смысле.
Случайный процесс называется стационарным в
широком смысле если:
m (t ) m const ,
D (t ) D const ,
K (t1 , t2 ) K (t2 t1 ) K ( ) .
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
33
34. Стационарные процессы
Случайные процессыСтационарные процессы
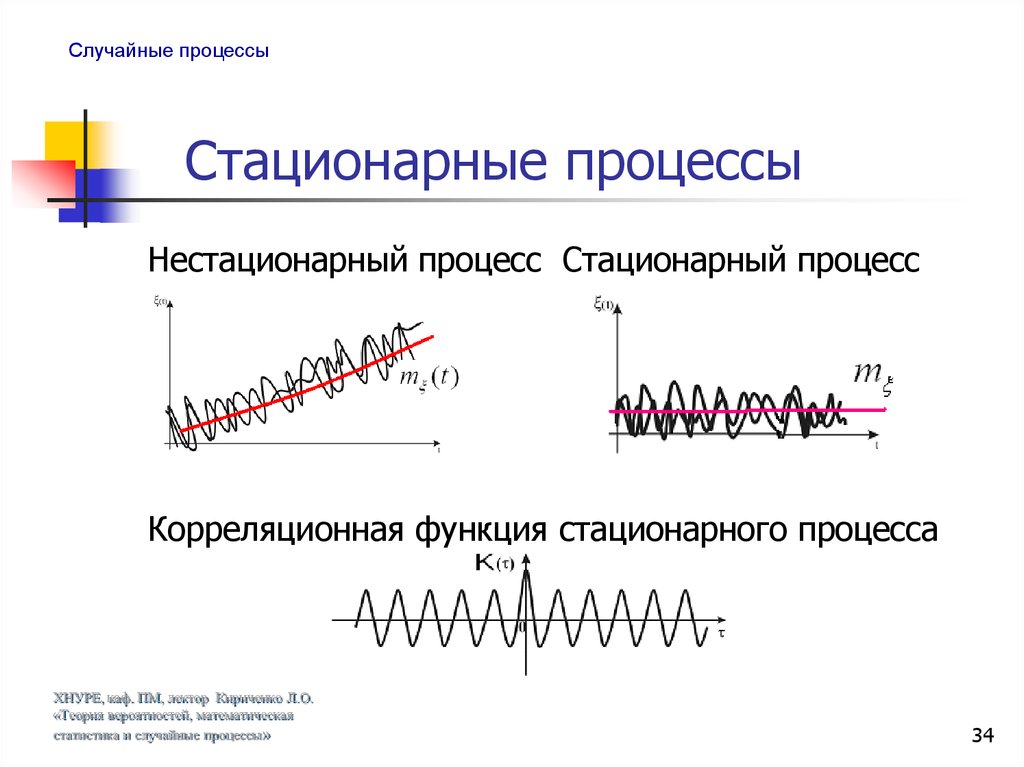
Нестационарный процесс Стационарный процесс
Корреляционная функция стационарного процесса
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
34
35. Стационарные процессы. Пример.
Случайные процессыСтационарные процессы. Пример.
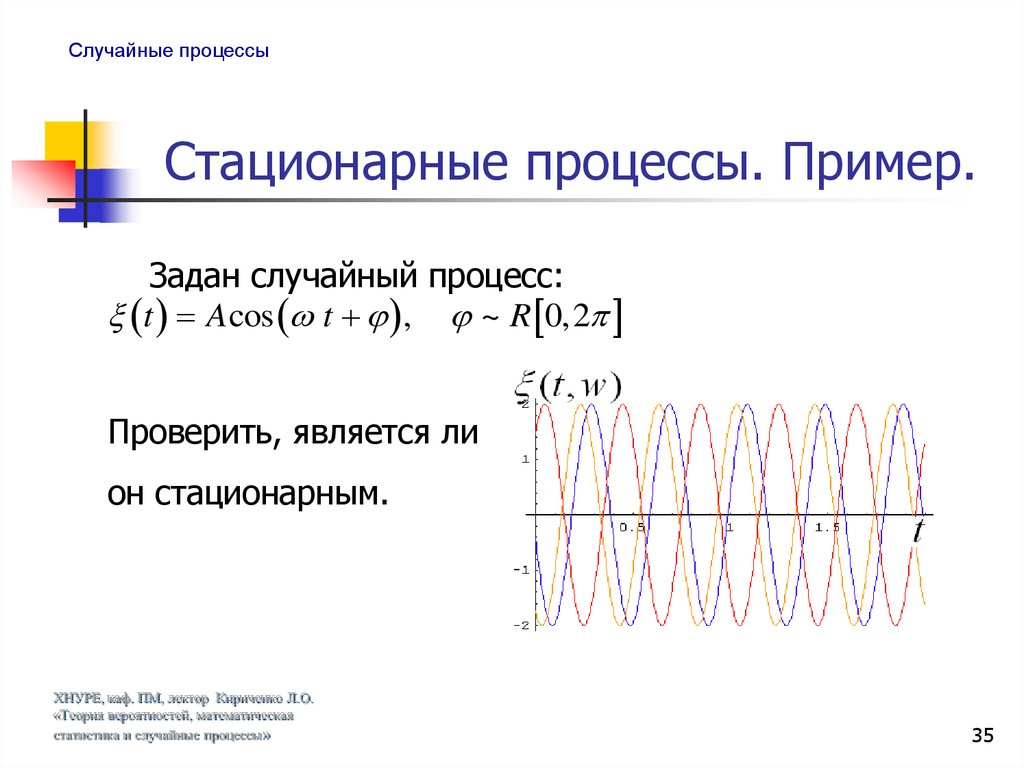
Задан случайный процесс:
t A cos t , ~ R 0,2
Проверить, является ли
он стационарным.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
35
36. Стационарные процессы. Пример.
Случайные процессыСтационарные процессы. Пример.
Плотность распределения случайной величины :
1
.
2
Математическое ожидание процесса:
p ( x)
M t
2
0
1
A cos t x dx
2
2
A
sin t x
0
0
2
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
36
37. Стационарные процессы. Пример.
Случайные процессыСтационарные процессы. Пример.
Корреляционная функция процесса:
K t1 , t2 M t1 m t1 t2 m t2 M t1 t2
2
A cos t1 x A cos t2 x
0
1
dx
2
2
2
A2
x cos t1 t2 dx cos t1 t2 2 x dx
2 2 0
0
A2
A2
2 A2
cos ( t1 t2 )
cos t1 t2
cos t1 t2
2
2
4
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
37
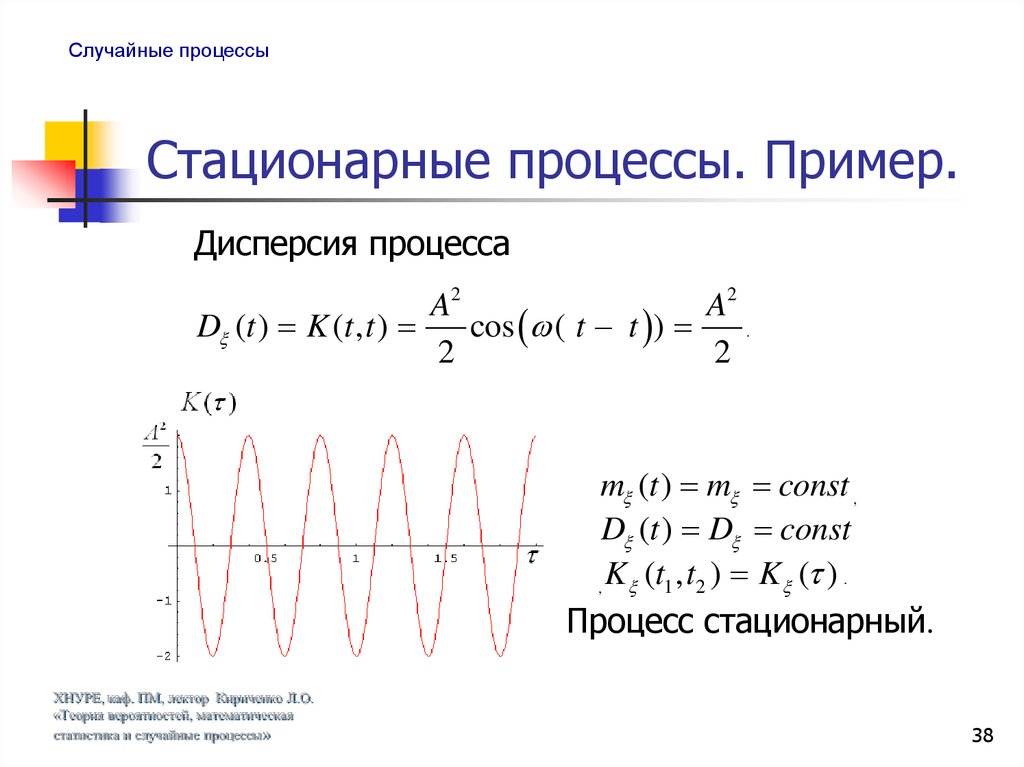
38. Стационарные процессы. Пример.
Случайные процессыСтационарные процессы. Пример.
Дисперсия процесса
A2
A2
D (t ) K (t , t )
cos ( t t )
.
2
2
m (t ) m const ,
D (t ) D const
K (t1 , t2 ) K ( ) .
,
Процесс стационарный.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
38
39. Эргодические процессы
Случайные процессыЭргодические процессы
Самыми важными (по прикладному значению) из
стационарных процессов для нас являются эргодические.
называется
процесс
случайный
Стационарный
эргодическим, если для него осреднение по ансамблю
реализаций может быть заменено осреднением по времени
по одной реализации.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
39
40. Эргодические процессы
Случайные процессыЭргодические процессы
Т.е. по любой одной достаточно длинной реализации
мы можем судить о свойствах всех реализаций случайного
процесса.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
40
41. Эргодические процессы
Случайные процессыЭргодические процессы
Достаточное условие эргодичности:
eсли
lim K ( ) 0 ,
то случайный процесс является эргодическим.
ХНУРЕ, каф. ПМ, лектор Кириченко Л.О.
«Теория вероятностей, математическая
статистика и случайные процессы»
41
42.
СПАСИБОЗА ВНИМАНИЕ !!!
42

































 Математика
Математика








