Похожие презентации:
Рабочая тетрадь по наглядной геометрии как инструмент пропедевтики основного курса геометрии для 5-6 классов
1. Рабочая тетрадь по наглядной геометрии как инструмент пропедевтики основного курса геометрии для 5-6 классов
РАБОЧАЯ ТЕТРАДЬ ПОНАГЛЯДНОЙ ГЕОМЕТРИИ
КАК ИНСТРУМЕНТ ПРОПЕДЕВТИКИ
ОСНОВНОГО КУРСА ГЕОМЕТРИИ
ДЛЯ 5-6 КЛАССОВ
ВОЛКОВА
А.А.
МАШКОВЦЕВА
ПЕРМЯКОВА
ФИЛИМОНОВА
А.А.
А.Д.
С.А
ПОД РУКОВОДСТВОМ ЛУНЕЕВОЙ ОЛЬГИ ЛЕОНИДОВНЫ
2. Актуальность: проблема усвоения геометрических знаний
АКТУАЛЬНОСТЬ: ПРОБЛЕМА УСВОЕНИЯГЕОМЕТРИЧЕСКИХ ЗНАНИЙ
3. Данную проблему можно связать с:
ДАННУЮ ПРОБЛЕМУ МОЖНО СВЯЗАТЬ С:• недостаточно развитыми геометрическими представлениями
• отсутствием пространственного мышления
• отсутствием навыков представления
• изображения геометрических фигур
ВЫВОД:
Работать с геометрическим материалом нужно
начинать как можно раньше – в 5-6 классах – и
усложнять его по мере приближения к
основному курсу геометрии в 7 классе.
4. Смирнова И.М., Смирнов В.А. Наглядная геометрия 5-6 классы
СМИРНОВА И.М., СМИРНОВ В.А.НАГЛЯДНАЯ ГЕОМЕТРИЯ 5-6 КЛАССЫ
Данной проблемой занимались разные педагоги и дидакты. Разработано
довольно много курсов, учебников, пособий по наглядной геометрии.
5. Стандарты нового поколения требуют:
СТАНДАРТЫ НОВОГО ПОКОЛЕНИЯ ТРЕБУЮТ:• реализации деятельностного подхода в образовании
• активного включения школьников в работу на уроке
Помимо этого, при анализе материалов различных конкурсов и олимпиад, мы пришли к
выводу, что многие из них содержат много задачного материала, доступного для 5-6
классов, развивающих пространственное воображение, поэтому использование их мы
считаем очень уместным и полезным.
Например, следующее задание из игры-конкурса «Кенгуру» см. на следующем слайде.
6. задание из игры-конкурса «Кенгуру»
ЗАДАНИЕ ИЗ ИГРЫ-КОНКУРСА«КЕНГУРУ»
Прогуливаясь по парку, Бетти сделала 4 фотографии газона с
фигурно подстриженными кустами. В каком порядке сделаны эти
фотографии, если Бетти обошла газон один раз, двигаясь из
отмеченной точки в направлении, указанном стрелочкой?
Использование таких заданий позволяет развивать пространственное воображение,
они привлекают своей нестандартностью и необычностью.
7.
Необходимость в созданиипособия, позволяющего
развить геометрические
представления, культуру (в
частности культуру чертежа),
привлечь к изучению
геометрии, показать её
красоту и применимость в
жизни.
*в максимально
интерактивной форме.
8. Рабочая программа 5 класса
РАБОЧАЯ ПРОГРАММА 5 КЛАССАГлава 1. Общие представления о геометрии
Первые шаги в геометрии
Пространство и размерность
Простейшие геометрические фигуры
Глава 2. Отрезки и ломаные
Действия с отрезками
Задачи со спичками
Ломаная. Ломаная на узорах
Рисунки из отрезков. Понятие огибающей
Глава 3. Плоские фигуры
Углы. Смежные и вертикальные углы
Построение с помощью циркуля и линейки биссектрисы угла и угла, равного данному.
Задача о трисекции угла
Часы
10
Треугольники. Сумма углов треугольника. Виды и свойства треугольников
1
11
12
Многоугольники
Геометрические головоломки (танграм, стомахион)
1
13
Правильные многоугольники. Узоры из правильных многоугольников
1
114
Построение правильных многоугольников с помощью циркуля и линейки
1
1
2
3
4
5
6
7
8
9
15
16
Паркеты
Глава 4. Площади
Конструирование из Т
1
1
1
4
1
1
1
1
8
1
1
1
1
5
1
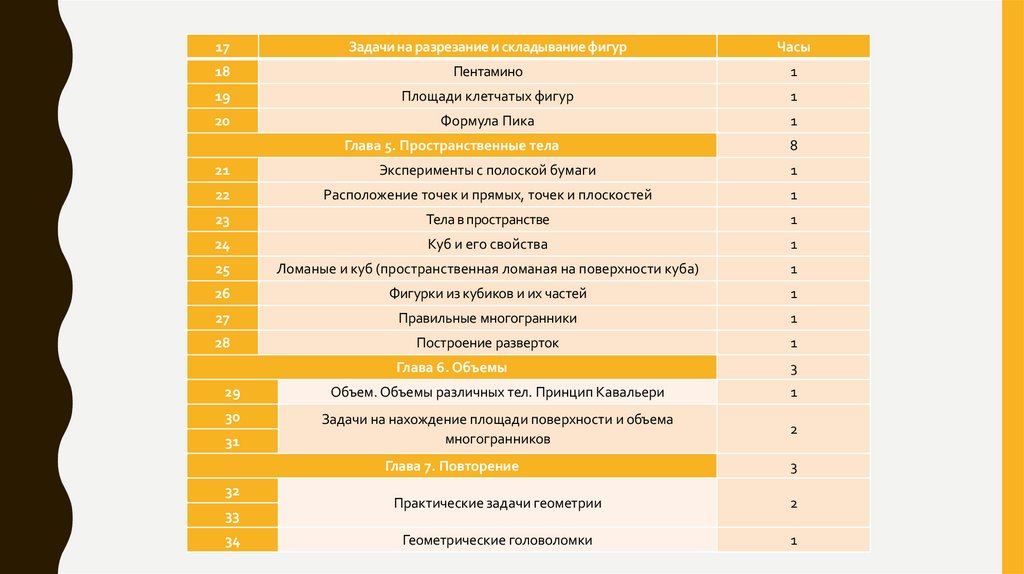
9.
17Задачи на разрезание и складывание фигур
Часы
18
Пентамино
1
19
Площади клетчатых фигур
1
20
Формула Пика
1
Глава 5. Пространственные тела
8
21
Эксперименты с полоской бумаги
1
22
Расположение точек и прямых, точек и плоскостей
1
23
Тела в пространстве
1
24
Куб и его свойства
1
25
Ломаные и куб (пространственная ломаная на поверхности куба)
1
26
Фигурки из кубиков и их частей
1
27
Правильные многогранники
1
28
Построение разверток
1
Глава 6. Объемы
3
29
Объем. Объемы различных тел. Принцип Кавальери
1
30
Задачи на нахождение площади поверхности и объема
многогранников
2
31
Глава 7. Повторение
32
33
34
3
Практические задачи геометрии
2
Геометрические головоломки
1
10. Рабочая программа 6 класса
РАБОЧАЯ ПРОГРАММА 6 КЛАССА№
Тема
Глава 1. Занимательная геометрия
Кол-во
часов
4
1
Лабиринты
1
2
Оригами
1
3
Кривые Дракона
1
4
Топологические головоломки
1
Глава 2. Параллельность и перпендикулярность
5
5
Параллельность и перпендикулярность
1
Взаимное расположение прямых и плоскостей
2
8
Конструкции из параллельных прямых
1
9
Деление отрезка в данном отношении
1
6
7
Глава 3. Четырехугольники
10
4
Четырехугольники, их частные случаи и свойства. Геометрия клетчатой бумаги
2
12
Площади четырехугольников
1
13
Геометрические головоломки, задачи и игры
1
11
Глава 4. Окружность и круг
6
14
Окружность, элементы окружности. Круг, части круга
1
15
Геометрические конструкции из точек, отрезков, окружностей
1
16
Кружево и вышивка на уроках геометрии. Спирограф
1
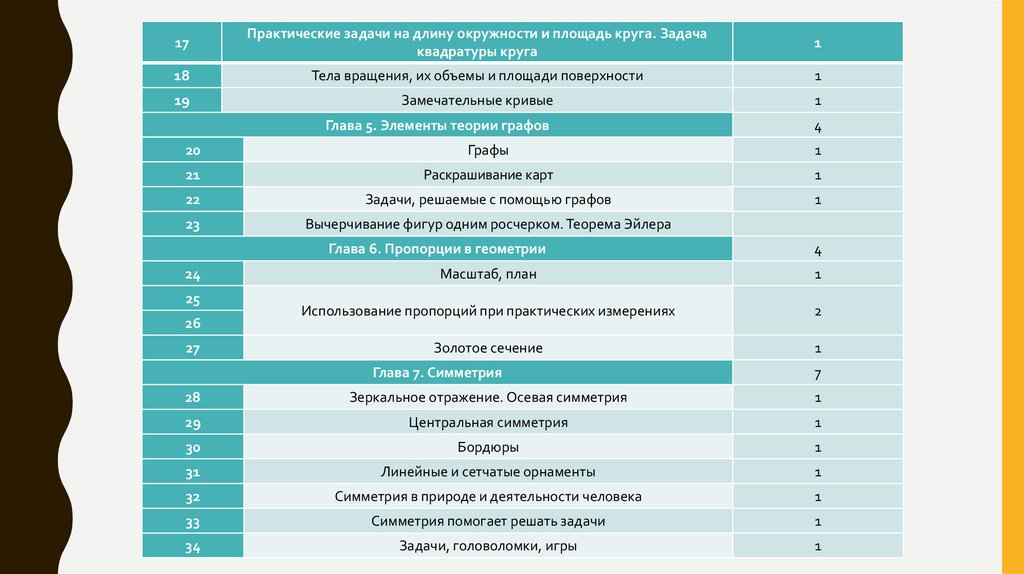
11.
17Практические задачи на длину окружности и площадь круга. Задача
квадратуры круга
1
18
Тела вращения, их объемы и площади поверхности
1
19
Замечательные кривые
1
Глава 5. Элементы теории графов
4
20
Графы
1
21
Раскрашивание карт
1
22
Задачи, решаемые с помощью графов
1
23
Вычерчивание фигур одним росчерком. Теорема Эйлера
Глава 6. Пропорции в геометрии
24
25
26
27
4
Масштаб, план
1
Использование пропорций при практических измерениях
2
Золотое сечение
1
Глава 7. Симметрия
7
28
Зеркальное отражение. Осевая симметрия
1
29
Центральная симметрия
1
30
Бордюры
1
31
Линейные и сетчатые орнаменты
1
32
Симметрия в природе и деятельности человека
1
33
Симметрия помогает решать задачи
1
34
Задачи, головоломки, игры
1
12. Уровни сложности:
УРОВНИ СЛОЖНОСТИ:Простой уровень сложности:
Повышенный уровень:
Конкурсные задачи:
13. Внеклассное чтение Факты о кубике рубика
ВНЕКЛАССНОЕ ЧТЕНИЕФАКТЫ О КУБИКЕ РУБИКА
• 1. Кубик Рубика изобрел венгерский скульптор и
преподаватель архитектуры Эрнё Рубик. Последние
годы автор головоломки занимается разработкой
видеоигр.
• 2. Эрнё Рубик потратил целый месяц, когда сам
впервые пытался собрать кубик Рубика.
• 3. Кубик Рубика имеет 6 граней, 12 рёбер, 8 углов и
образован из 26 мелких деталей. Игрок ориентируется
по цвету центрального элемента на каждой грани.
• 4. Любая цветовая комбинация в классическом кубике
Рубика может быть достигнута менее чем за 20 ходов.
• 5. Кубик Рубика имеет 43 252 003 274 489 856 000
возможных перестановок. В рамках человеческого
мышления такая величина — практически
бесконечность.
14. Подводим итоги
ПОДВОДИМ ИТОГИИтак, представленный в рабочей
тетради материал позволяет
подготовить учащихся 5-6 классов к
основному курсу геометрии. Он дает
возможность представить красоту
этого предмета, его вездесущность
в окружающем нас мире.
БЛАГОДАРИМ ВАС ЗА ВНИМАНИЕ!












 Математика
Математика


