Моделирование деформирования упругопластических многослойных пластин

1. Выпускная квалификационная работа бакалавра на тему: «Моделирование деформирования упругопластических многослойных пластин на

Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский государственный технический университет имени Н.Э. Баумана
(национальный исследовательский университет)»
(МГТУ им. Н.Э. Баумана)
ФАКУЛЬТЕТ «Фундаментальные науки»
КАФЕДРА «Вычислительная математика и математическая физика»
Направление подготовки «Математика и компьютерные науки» 02.03.01
Выпускная квалификационная работа бакалавра на тему:
«Моделирование деформирования
упругопластических многослойных пластин
на основе асимптотической теории»
Выполнила: студент группы АК3-81Б Шайхлисламова А.Р.
Научный руководитель: доцент кафедры ФН-11, к.ф.-м.н. Губарева Е.А.
Консультант: заведующий кафедрой ФН-11, д.ф.-м.н. Димитриенко Ю.И.

2. Концептуальная постановка задачи

• Моделирование тонких упругопластических композиционных
материалов играет важную роль в современном мире. Одним из
приоритетных
направлений
является
аэрокосмическая
промышленность.
• АО УНИИКМ, входящий в состав АО ВПК НПО
«Машиностроения» занимается производством составных
материалов для аэрокосмической техники из углерод-углеродных
композиционных материалов.
• ОНПП «Технология» им. А. Г. Ромашина за 2019 год приняло
участие в реализации пяти космических программ и выпустило
более 200 единиц высокотехнологичной продукции из
полимерных композиционных материалов для российской
космической отрасли.
Заготовка насадки из УУКМ «Граурис»
для ЖРД 11Д58-М
Обечайка ракеты-носителя
Кожух задней подвески реверсазвукопоглащающей конструкции.
Материал: стеклопластик СТ-69Н. Снижение массы на 11,2 кг (20%)

3. Цели и задачи

• линеаризация общей постановки задачи теории течения (трехмерной)
• формулировка локальных задач нулевого, первого, второго, третьего и n-го
приближения для линеаризованной постановки трехмерной задачи теории
течения для изотропных упругопластических сред при малых деформациях
• решение локальных задач нулевого, первого, второго и третьего
приближения для линеаризованной постановки трехмерной задачи теории
течения для изотропных упругопластических сред при малых деформациях
• решение задачи об изгибе многослойной упругопластической симметричной
пластины

4. Математическая постановка задачи (1)

Мы рассматриваем изотропную упругопластическую среду при малых деформациях. Модель
теории пластического течения имеет вид:
ij cijkl kl klp
f
p
h
kl
kl
f f I H p 0, 1, 2
ij
ij
H H I p
2 ij
(1)
Где - тензор напряжений, - тензор деформаций (полных),
деформаций, - тензор скоростей пластических деформаций,
индикатор пластического деформирования:
- тензор пластических
- параметр нагружения, -

5. Математическая постановка задачи (2)

Далее путем линеаризации мы получаем линейную постановку трехмерной задачи теории
течения в скоростях для изотропных упругопластических сред при малых деформациях:
• где k – номер итерации, - тензор
скоростей полных деформаций, - тензор
скоростей пластических деформаций, тензор скоростей упругих деформаций, тензор скоростей напряжений, С приведенный тензор упругости, зависящий от
деформаций и напряжений на k-1
итерации, а V - вектор скорости.
(k )
kl
( k ) 0
i ij
( k 1) ( k )
ij( k ) Сijkl
kl
(k ) 1
(k )
(k )
V
V
kl
k l
l k
2
Vi Vei ; ij( k ) n j Si
T
Vi 0; ij n j 0
(k )e
kl
(k ) p
kl
p
kl
e
kl
(k )
ij
( k 1)
ijkl
(2)
( k 1)
kl
( k 1)
ij
i
• В данной системе первое уравнение равновесия, второе – линеаризованное
уравнение теории пластического течения,
третье – закон для деформации в скоростях,
четвертое – граничные условия, пятое –
условия идеального контакта.

6. Метод решения

Решать задачу будем с помощью асимптотической теории.
Введем малый параметр h / L 1, как отношение общей толщины пластины h к характерному
размеру всей пластины L (её максимальной длине). Введём также глобальные xk и локальную
координаты:
xk xk / L, x3 / , k 1, 2, 3,
где xk - обычные декартовы координаты, ориентированные таким образом, что ось Ox3
направлена по нормали к внешней и внутренней плоскостям пластины, а оси Ox1 , Ox2
принадлежат срединной поверхности пластины. Полагаем, что существуют два масштаба
изменения перемещений uk : один по направлениям Ox1 , Ox2 , а второй по направлению Ox3 .
Координаты x3 и в методе асимптотического осреднения рассматриваются как независимые
переменные. Координата по толщине пластины изменяется в диапазоне 0,5 0,5 .
Решение задачи нам нужно искать в виде асимптотических разложений по параметру в виде
функций, зависящих от глобальных и локальной координат
Vk( k ) Vk(0)( k ) xI Vk(1)( k ) xI , 2Vk(2)( k ) xI , 3Vk(3)( k ) xI , ...

7. Асимптотические разложения

Асимптотические разложения для скоростей полных деформаций:
ij( k ) ij(0)( k ) ij(1)( k ) 2 ij(2)( k ) ...
где
и так далее.
IJ(0)( k )
1 (0)( k )
k)
VI , J VJ(0)(
,
,I
2
IJ(1)( k )
1 (1)( k )
k)
VI , J VJ(1)(
,
,I
2
IJ(2)( k )
1 (2)( k )
k)
VI , J VJ(2)(
,I
2
k)
I(0)(
3
1 (0)( k )
k)
V3, I VI(1)(
,
/3
2
k)
I(1)(
3
1 (1)( k )
k)
V3, I VI(2)(
,
/3
2
k)
I(2)(
3
1 (2)( k )
k)
V3, I VI(3)(
/3
2
(1)( k )
33(0)( k ) V3/3
;
(2)( k )
33(1)( k ) V3/3
;
(3)( k )
33(2)( k ) V3/3
Асимптотические разложения для скоростей напряжений
ij{k} ij(0){k} ij(1){k} 2 ij(2){k} ...
где
( k 1) (0)( k )
( k 1) (0)( k )
IJ(0)( k ) сIJKL
KL сIJk
,
3 k3
( k 1) (1)( k )
( k 1) (1)( k )
IJ(1)( k ) сIJKL
KL сIJk
3 k3
( k 1) (2)( k )
( k 1) (2)( k )
IJ(2)( k ) сIJKL
KL сIJk
,
3 k3
k)
1) (0)( k )
k)
i(0)(
сi(3kKL
KL сi(3kk 31) k(0)(
3
3
k)
1) (1)( k )
k)
i(1)(
сi(3kKL
KL сi(3kk 31) k(1)(
,
3
3
и так далее.
k)
1) (2)( k )
k)
i(2)(
сi(3kKL
KL сi(3kk 31) k(2)(
3
3

8. Формулировка локальных задач 0, 1, 2 приближения

i(0)
3/3 0,
Для нулевого приближения:
IJ(0)( k )
k)
1) (0)( k )
k)
i(0)(
сi(3kKL
KL сi(3kk 31) k(0)(
3
3
1 (0)( k )
k)
VI , J VJ(0)(
,
,I
2
3 : i(0)
3 0;
S : i(0)
3 0,
(0)
(0)
i(1)
3/3 iJ , J hi ,
Для первого приближения:
IJ(1)( k )
Для второго приближения:
IJ(2)( k )
(1)( k )
33(0)( k ) V3/3
(3)
Vi (1) 0;
1 (1)( k )
k)
V3,I VI(2)(
,
/3
2
Vi (2) 0,
(2)( k )
33(1)( k ) V3/3
(4)
Vi (2) 0;
k)
1) (2)( k )
k)
i(2)(
сi(3kKL
KL сi(3kk 31) k(2)(
3
3
1 (2)( k )
k)
VI , J VJ(2)(
,
,I
2
3 : i(2)
3 0;
Vi (1) 0,
k)
I(1)(
3
S : i(1)
3 0,
(1)
(1)
i(2)
3/3 iJ , J hi ,
1 (0)( k )
k)
V3, I VI(1)(
,
/3
2
k)
1) (1)( k )
k)
i(1)(
сi(3kKL
KL сi(3kk 31) k(1)(
3
3
1 (1)( k )
VI , J VJ(1)(,I k ) ,
2
3 : i(1)
3 0;
k)
I(0)(
3
k)
I(2)(
3
S : i(2)
3 0,
1 (2)( k )
k)
V3, I VI(3)(
,
/3
2
Vi (3) 0,
Vi (3) 0;
(3)( k )
33(2)( k ) V3/3
(5)

9. Формулировка локальных задач 3 и более высших приближений

(2)
(2)
i(3)
3/3 iJ , J hi ,
Для третьего приближения:
IJ(3)( k )
k)
1) (3)( k )
k)
i(3)(
сi(3kKL
KL сi(3kk 31) k(3)(
3
3
1 (3)( k )
k)
VI , J VJ(3)(
,
,I
2
k)
I(3)(
3
1 (3)( k )
k)
V3, I VI(4)(
,
/3
2
(6)
(4)( k )
33(3)( k ) V3/3
3 : Si(1)(2)
3 p i 3
n)
i(3/3
iJ( n, J1) hi( n 1) ,
Для n-го приближения:
( k 1) ( n )( k )
ij( n )( k ) сijKL
KL сijk( k 3 1) k( n3)( k )
1) ( n )( k )
i(3n )( k ) сi(3kKL
KL сi(3kk 31) k( n3)( k ) ,
( n )( k )
IJ
1
VI(,nJ)( k ) VJ(,nI)( k ) ,
2
3 : i(3n ) p n 3 i 3 ;
1) ( n )( k )
( k 1) ( n )( k )
33( n )( k ) с33( kKL
KL с3333
k3
( n )( k )
I3
1
V3,( nI )( k ) VI(/3n 1)( k ) ,
2
S : i(3n ) 0,
Vi ( n 1) 0,
( n )( k )
33
(7)
( n 1)( k )
3/3
V
Vi ( n 1) 0;
,

10. Решение задачи нулевого приближения

Решение уравнений равновесия с граничными условиями в локальной задаче для нулевого
(0)
приближения имеет вид: i 3 0, : 0,5 0,5
Подставляя сюда вторую и третью группу определяющих (3) соотношений для компонент
(0)
( k 1) (0)( k )
( k 1) (0)( k )
скоростей напряжения i 3 , получаем, что сi 3 KL KL сi 3k 3 k 3 0
(1)( k )
(0)( k )
(0)( k )
Далее получаем следующие дифференциальные уравнения: VI /3 V3,I 2 I 3 ,
Интегрируем с учетом начальных условий и получаем:
k)
(0){ k }
VI(1)( k ) V3,(0)(
2U IKL KL
I
(0)( k )
V3(1)( k ) U 3 KL KL
Находим компоненты скоростей тензора напряжений:
(0)( k 1) (0)( k )
IJ(0)( k ) сIJKL
KL
где
k 1)
( k 1)
( k 1) ( k 1) 1 ( k 1)
сi(0)(
сIJKL
сIJk
сi 3 KL
3 KL
3 сk 3i 3
(1)( k )
(0)( k )
V3/3
33

11. Решение задачи изгиба многослойной упругопластической пластины

Рассмотрим задачу изгиба прямоугольной упругопластической пластины, притом на нее
действует давление, равномерно распределенное по ее длине. В случае симметричного
расположения слоев пластины относительно плоскости 0 , имеем следующие начальные
данные:
(0)( k )
k)
VI(0)( k ) 0, KL
0, TIJ( k ) 0, I(0)(
0,
3
k)
I(1)(
0
3
Пусть пластина шарнирно закреплена на торцах, тогда этому условию соответствуют
следующие граничные условия:
(0)( k )
x 0, x 1: V3(0)( k ) 0,V3,11
0

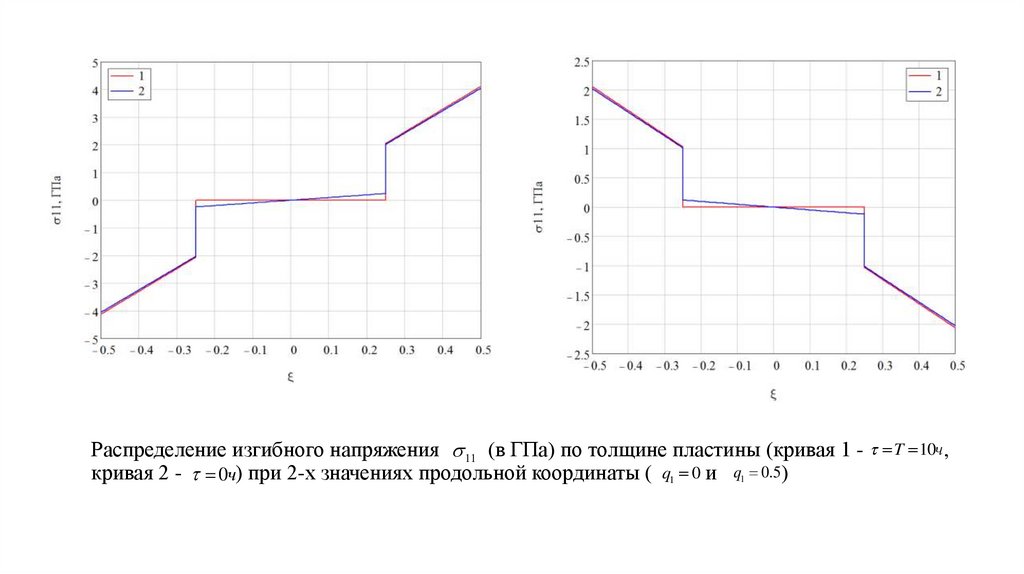
12. Распределение изгибного напряжения (в ГПа) по толщине пластины (кривая 1 - , кривая 2 - ) при 2-х значениях продольной

Распределение изгибного напряжения 11 (в ГПа) по толщине пластины (кривая 1 - T 10ч,
кривая 2 - 0ч) при 2-х значениях продольной координаты ( q1 0 и q1 0.5)

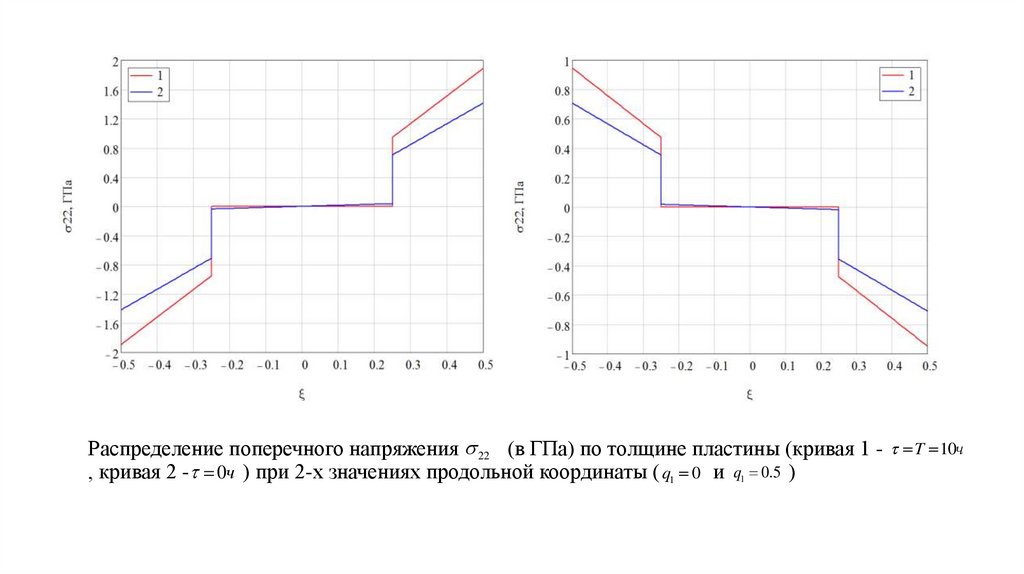
13. Распределение поперечного напряжения (в ГПа) по толщине пластины (кривая 1 - , кривая 2 - ) при 2-х значениях продольной

Распределение поперечного напряжения 22 (в ГПа) по толщине пластины (кривая 1 - T 10ч
, кривая 2 - 0ч ) при 2-х значениях продольной координаты ( q1 0 и q1 0.5 )

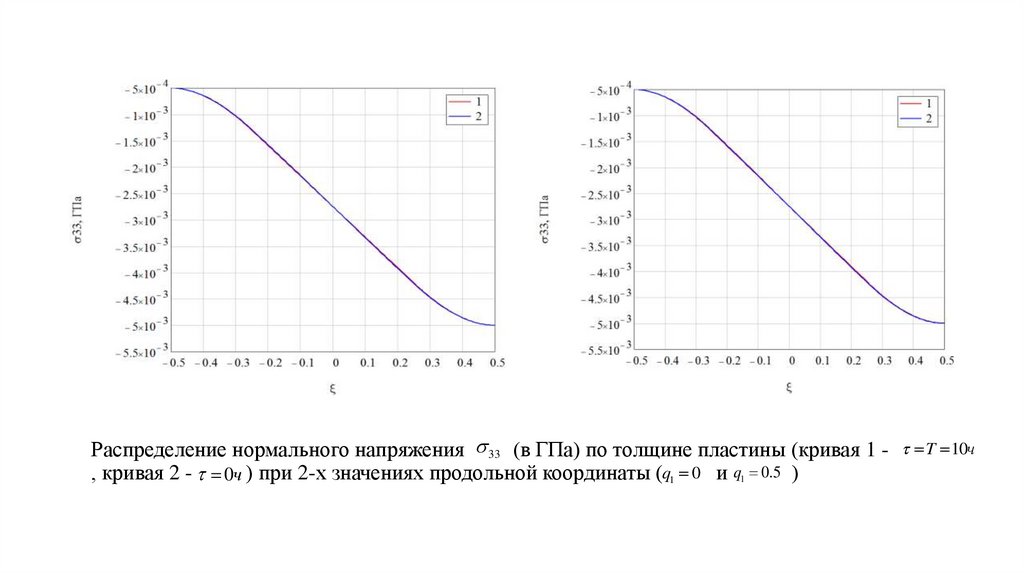
14. Распределение нормального напряжения (в ГПа) по толщине пластины (кривая 1 - , кривая 2 - ) при 2-х значениях продольной

Распределение нормального напряжения 33 (в ГПа) по толщине пластины (кривая 1 - T 10ч
, кривая 2 - 0ч ) при 2-х значениях продольной координаты (q1 0 и q1 0.5 )

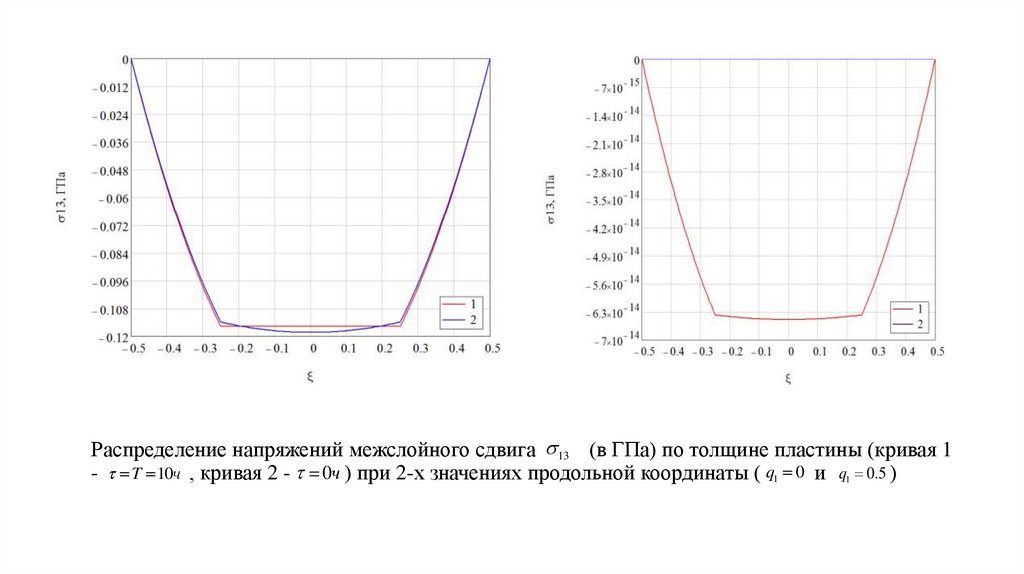
15. Распределение напряжений межслойного сдвига (в ГПа) по толщине пластины (кривая 1 - , кривая 2 - ) при 2-х значениях продольной

Распределение напряжений межслойного сдвига 13 (в ГПа) по толщине пластины (кривая 1
- T 10ч , кривая 2 - 0ч ) при 2-х значениях продольной координаты ( q1 0 и q1 0.5 )

16.

Выводы
В результате проделанной работы были осуществлены следующие задачи:
• линеаризована общая постановка задачи теории течения (трехмерная);
• сформулированы локальные задачи нулевого, первого, второго, третьего и n-го
приближения для линеаризованной постановки трехмерной задачи теории течения для
изотропных упругопластических сред при малых деформациях;
• решены локальные задачи нулевого, первого, второго и третьего приближения для
линеаризованной постановки трехмерной задачи теории течения для изотропных
упругопластических сред при малых деформациях;
• получено решение задачи изгиба многослойной упругопластической пластины под
действием равномерно распределенного давления.

17. Хочу выразить слова благодарности своим научным руководителям Димитриенко Юрию Ивановичу, Губаревой Елене Александровне, всему

преподавательскому составу
кафедры ФН-11 и нашему нормоконтролеру Кудрявцевой
Светлане Сергеевне!

18. Спасибо за внимание!