Похожие презентации:
Преобразования Галилея. Лекция 2
1. Лекция 2
2. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ
3.
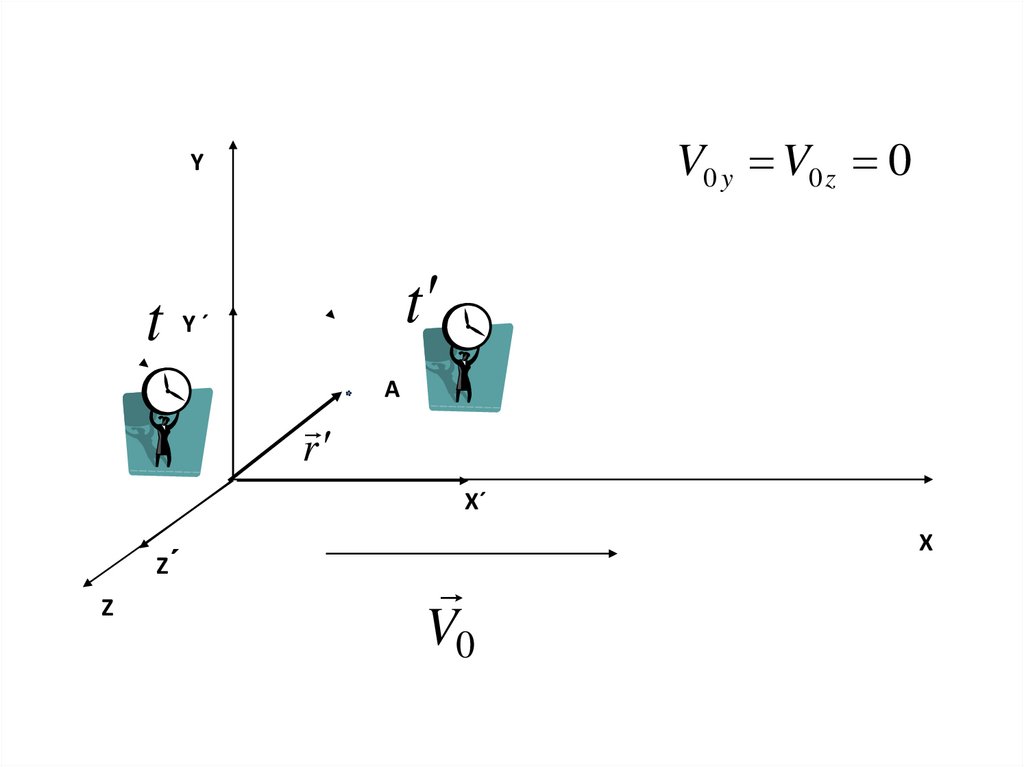
V0 y V0 z 0Y
t
t
Y´
r
A
X´
Z´
Z
V0
X
4.
x x V0ty y
z z
t t
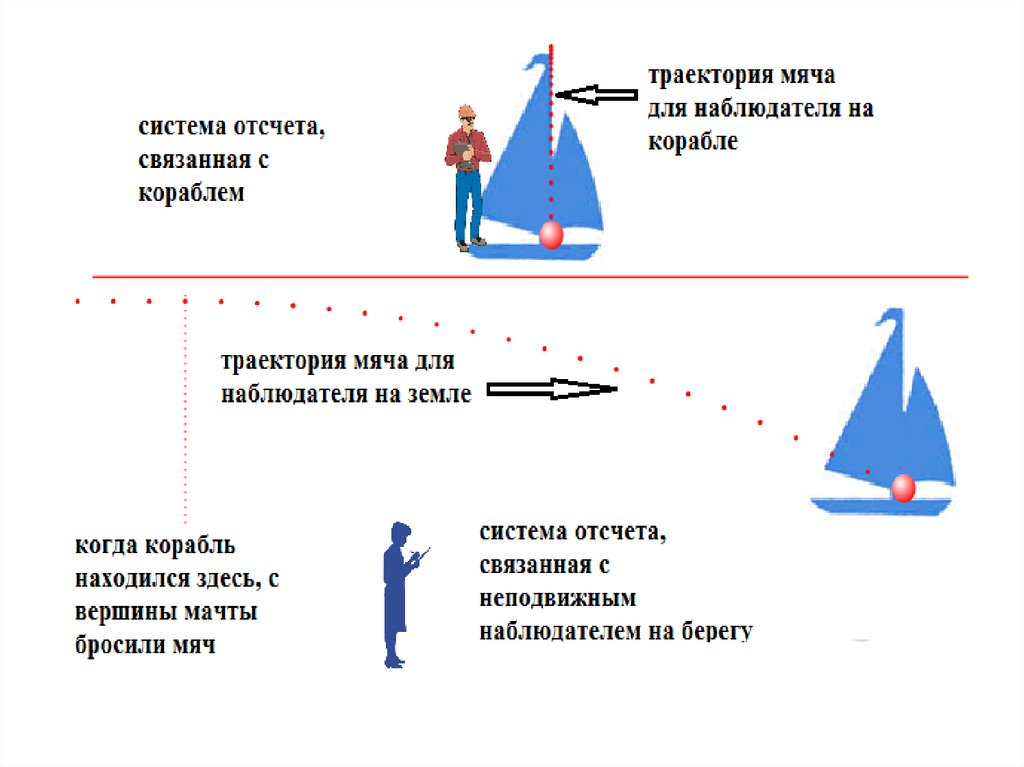
Преобразования Галилея
5.
V V0 VdV dV0 dV
dt
dt
dt
dV
a
dt
dV
a
dt
a a
V0 const
t t
dV0
0
dt
6. Принцип относительности Галилея
• Все законы механики имеют одинаковуюформу во всех инерциальных системах
отсчета
7.
8. ИМПУЛЬС СИСТЕМЫ ЧАСТИЦ И ЗАКОН ЕГО СОХРАНЕНИЯ
9.
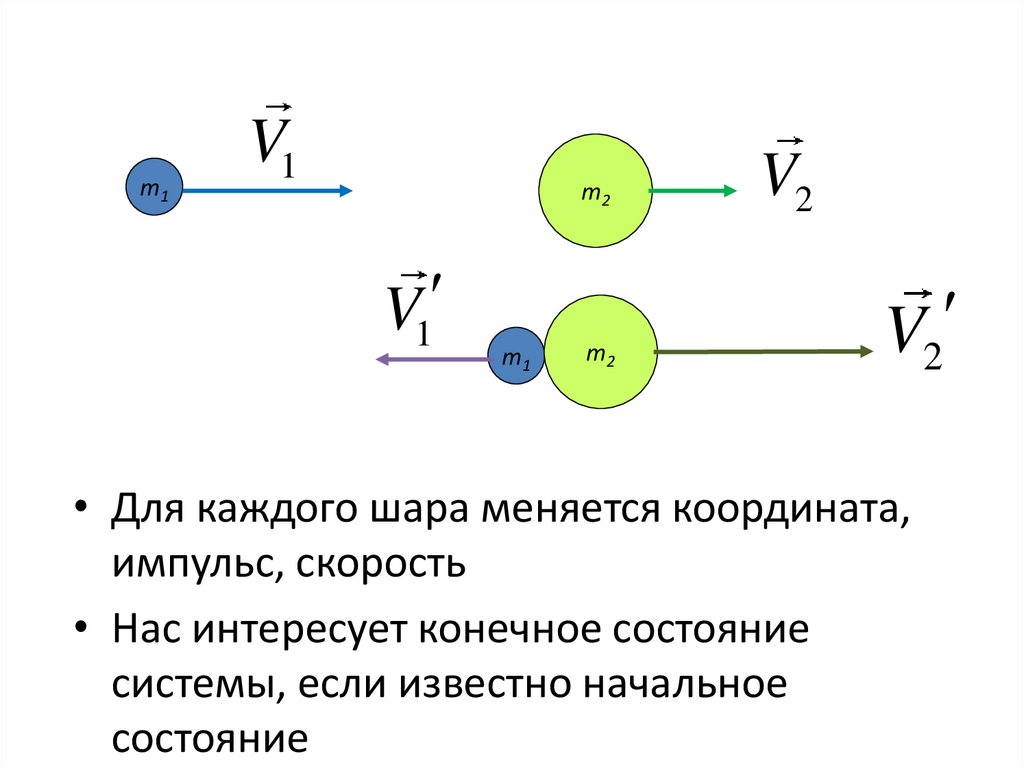
m1V1
m2
V1
m1
m2
V2
V2
• Для каждого шара меняется координата,
импульс, скорость
• Нас интересует конечное состояние
системы, если известно начальное
состояние
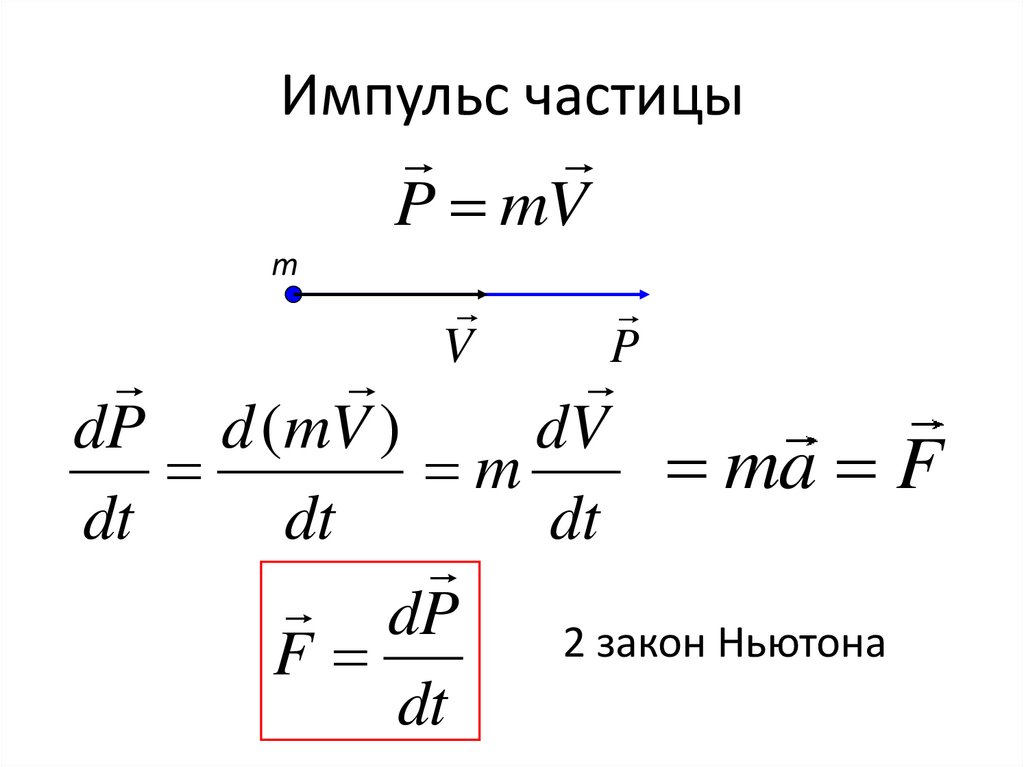
10. Импульс частицы
P mVm
V
P
dV
dP d (mV )
ma F
m
dt
dt
dt
dP
2 закон Ньютона
F
dt
11.
Fdt• Импульс силы
F 0, P const
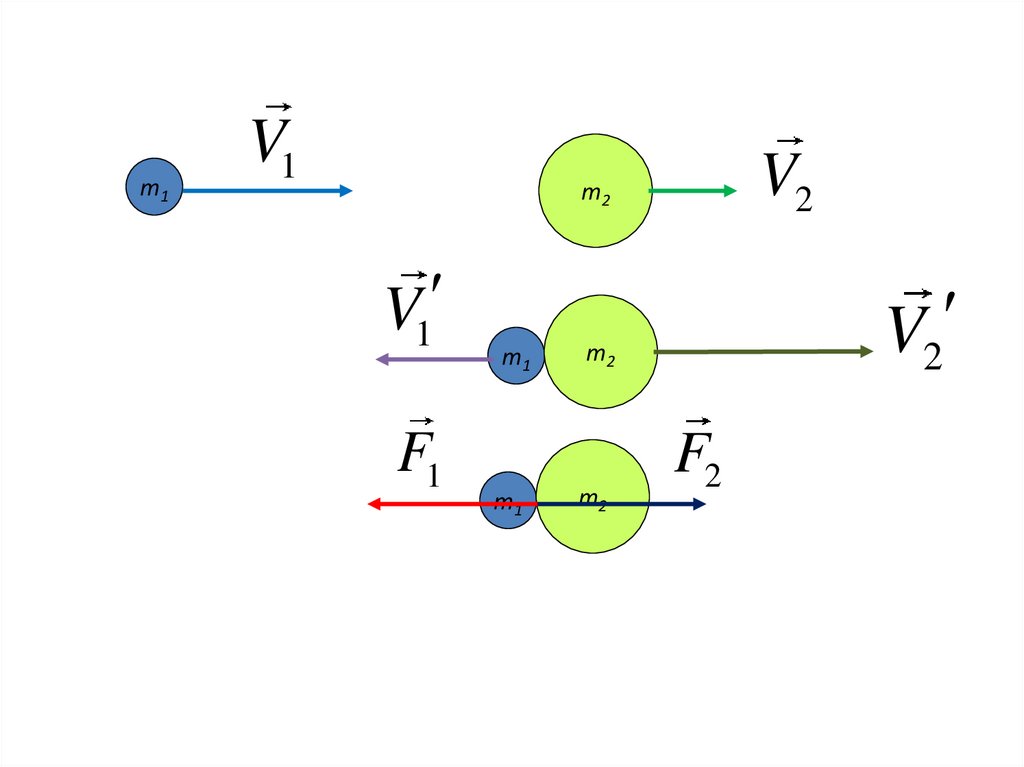
12.
m1V1
V2
m2
V1
F1
m1
m1
V2
m2
m2
F2
13.
F1 t P1• Для 1 шара
F2 t P2
• Для 2 шара
F F t P P
F F 0
1
1
2
2
F1 F2
1
2
• По 3 закону Ньютона
F1 F2
14.
• Для любого промежутка времениP1 P2 0
P1 P1 P1
P2 P2 P2
P1 P1 P2 P2 0
P1 P2 P1 P2
15.
• В системе двух шаров действовали тольковнутренние силы
• Если на систему не действуют внешние силы, то
она называется замкнутой
• В замкнутой системе тела взаимодействуют
только между собой и не взаимодействуют с
другими внешними телами
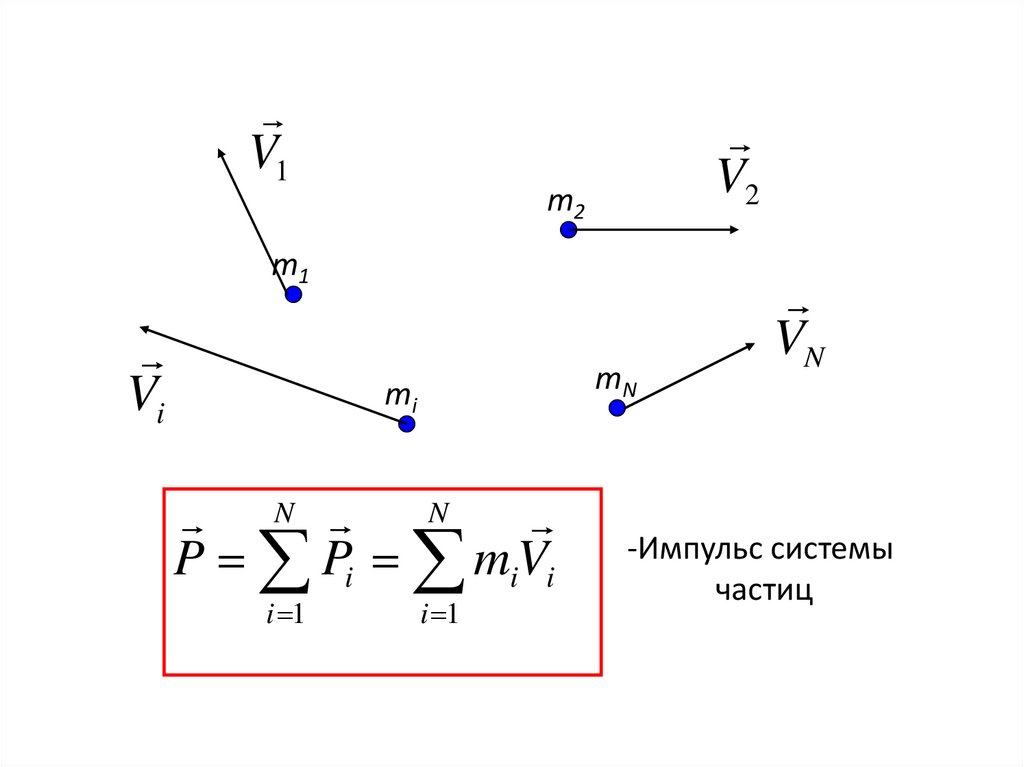
16. Импульс системы частиц
• Частицы могут взаимодействовать междусобой – внутренние силы
• Частицы могут взаимодействовать с
внешними телами- внешние силы
17.
V1V2
m2
m1
Vi
mN
mi
N
N
P Pi miVi
i 1
i 1
VN
-Импульс системы
частиц
18.
NdPi
dP d N
( Pi )
dt dt i 1
i 1 dt
N
dPi
Fik Fi (out)
dt k 1,k i
N
- Равнодействующая внутренних сил, которые
F
ik
k 1, k i
Fi (out)
действуют на i материальную точку
со стороны остальных
- Равнодействующая внешних сил, которые
действуют на i материальную точку
19.
NdPi
dP
dt
i 1 dt
N N
N
dP
Fik Fi ( out)
dt i 1 k 1,k i
i 1
N
Fik 0
N
i 1 k 1, k i
dP
dt
- Сумма всех внутренних
сил
По третьему закону Ньютона равна 0
Fi (out)
N
i 1
20.
• Если на систему не действуют внешниесилы, то она называется замкнутой
• Для замкнутой системы
P const
dP
0
dt
- Закон сохранения импульса
21. Закон сохранения импульса
• Импульс замкнутой системы сохраняется,т.е. не меняется с течением времени
• Связан с однородностью пространства
• Фундаментальный закон природы
22.
• http://www.walterfendt.de/html5/phen/newtoncradle_en.htm• https://www.youtube.com/watch?v=rBD3rLFb
fsQ
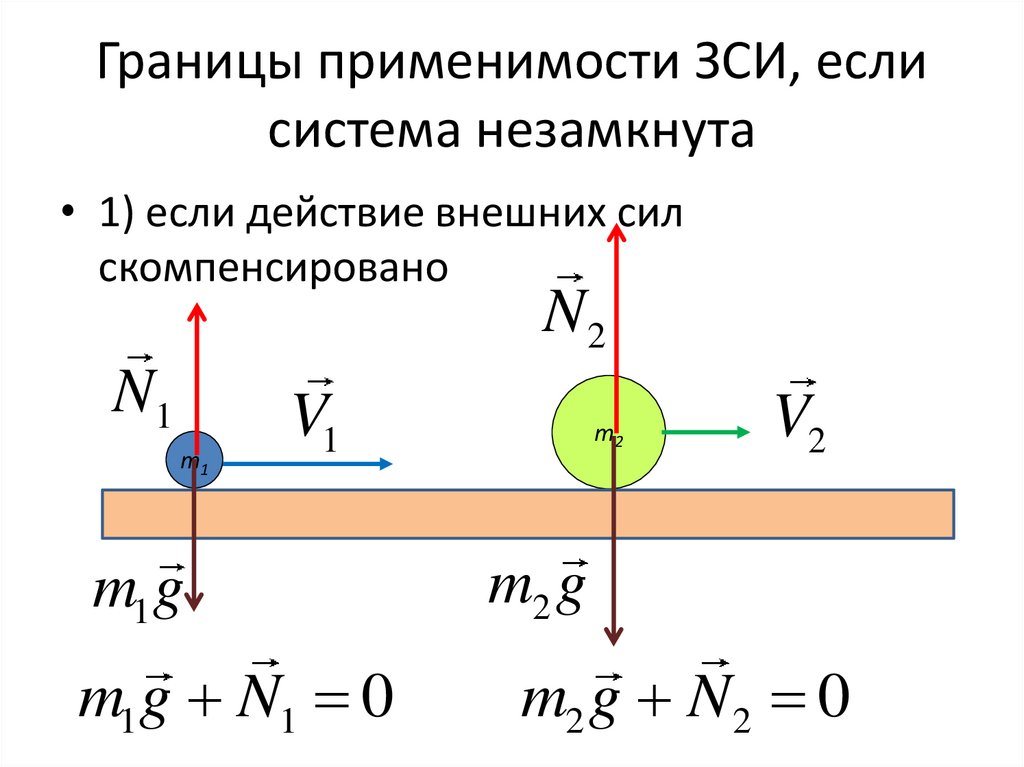
23. Границы применимости ЗСИ, если система незамкнута
• 1) если действие внешних силскомпенсировано
N2
N1
m1
V1
m1 g
m1g N1 0
m2
V2
m2 g
m2 g N 2 0
24.
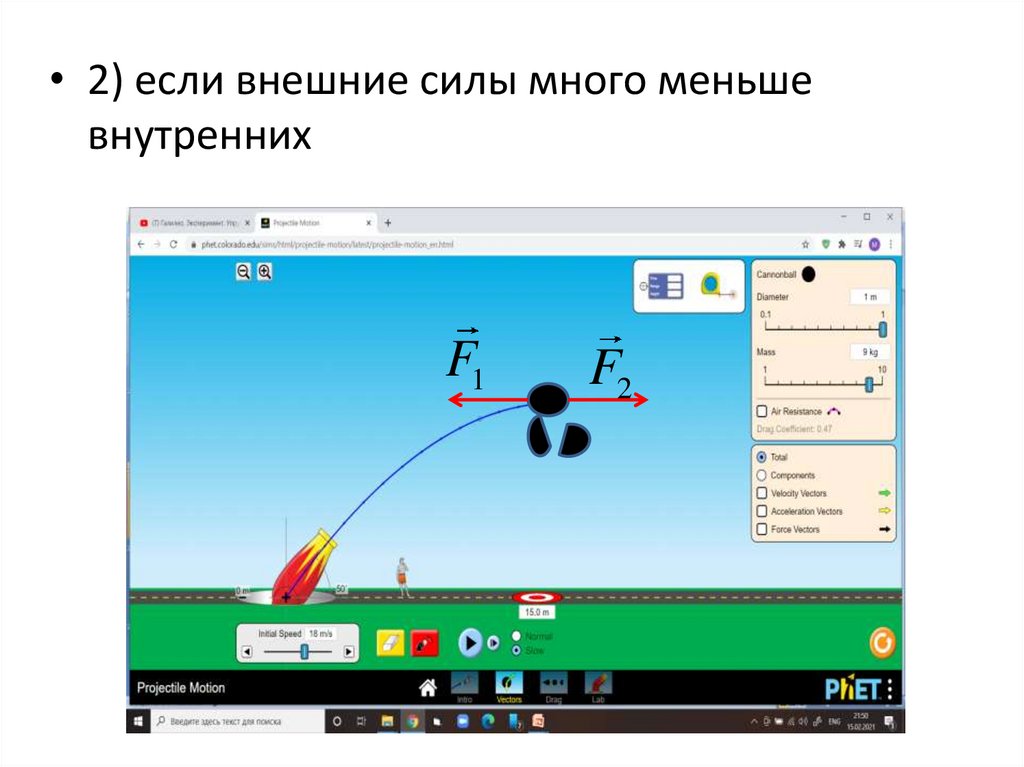
• 2) если внешние силы много меньшевнутренних
F1
F2
25.
F1m1g
F2
m2 g
mg tполета P
F tвз P
• Изменение импульса при полете до верхней
точки траектории и при разрыве снаряда
примерно одинаковое
• Время полета много меньше времени
взрыва t
t
вз
полета
• Закон сохранения импульса можно применять во
всех быстропротекающих процессах
• ( стрельба, взрывы, удары)
26.
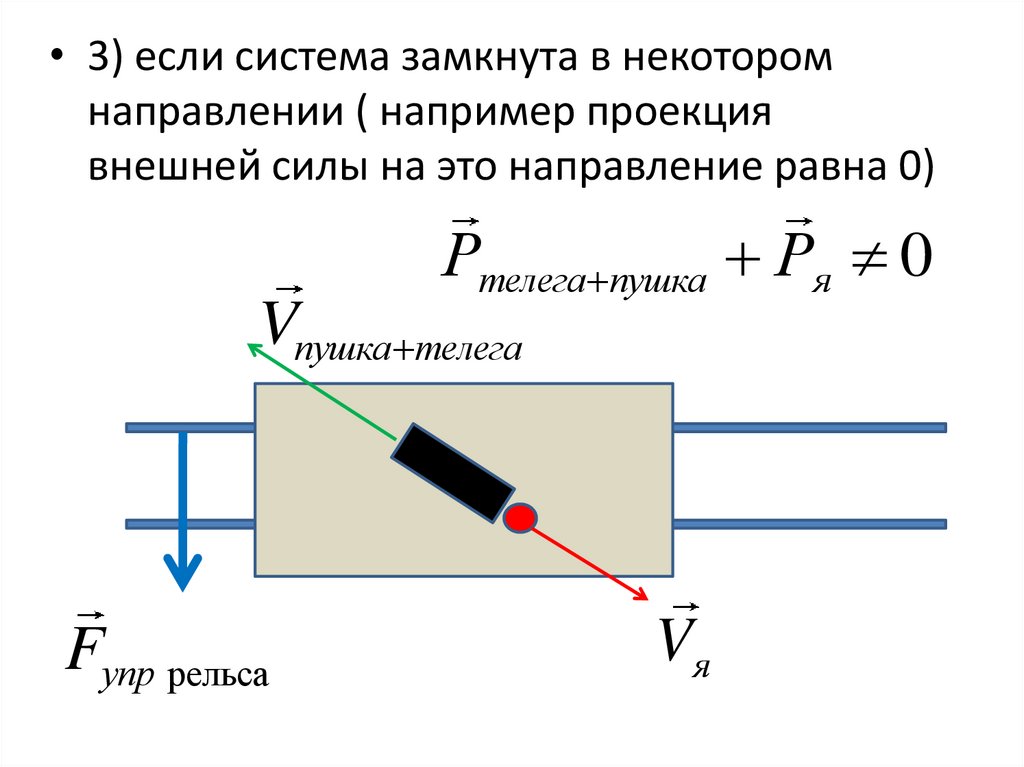
• 3) если система замкнута в некоторомнаправлении ( например проекция
внешней силы на это направление равна 0)
Ртелега пушка Ря 0
Vпушка телега
Fупр рельса
Vя
27.
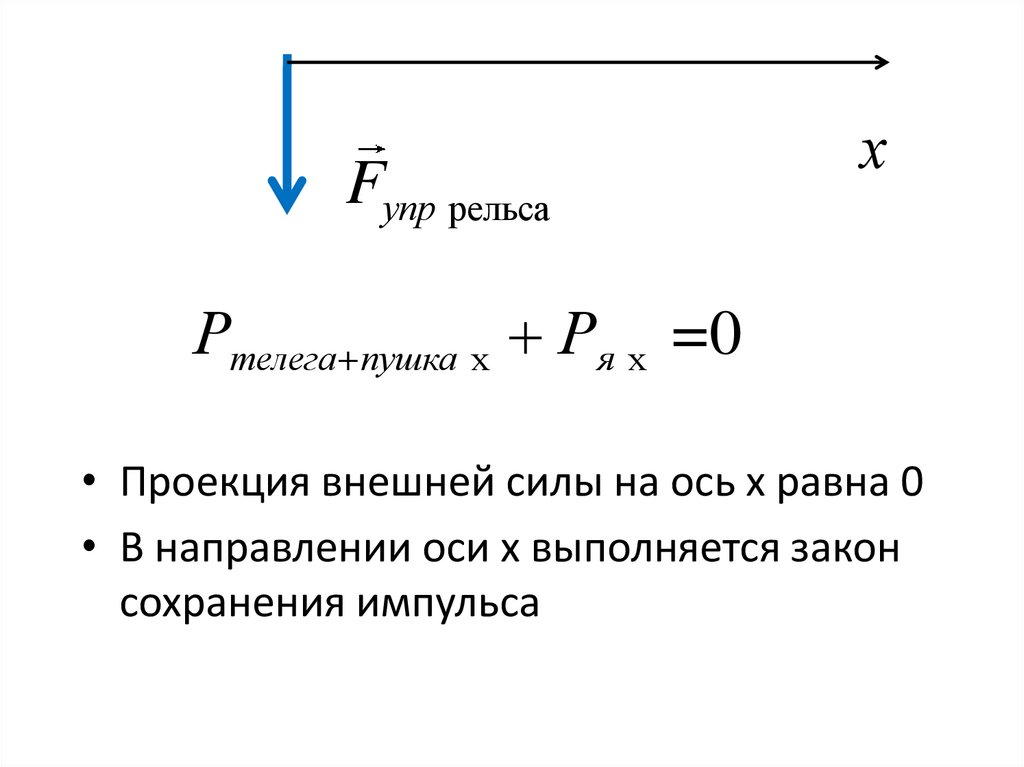
Fупр рельсах
Ртелега пушка х Ря х =0
• Проекция внешней силы на ось х равна 0
• В направлении оси х выполняется закон
сохранения импульса
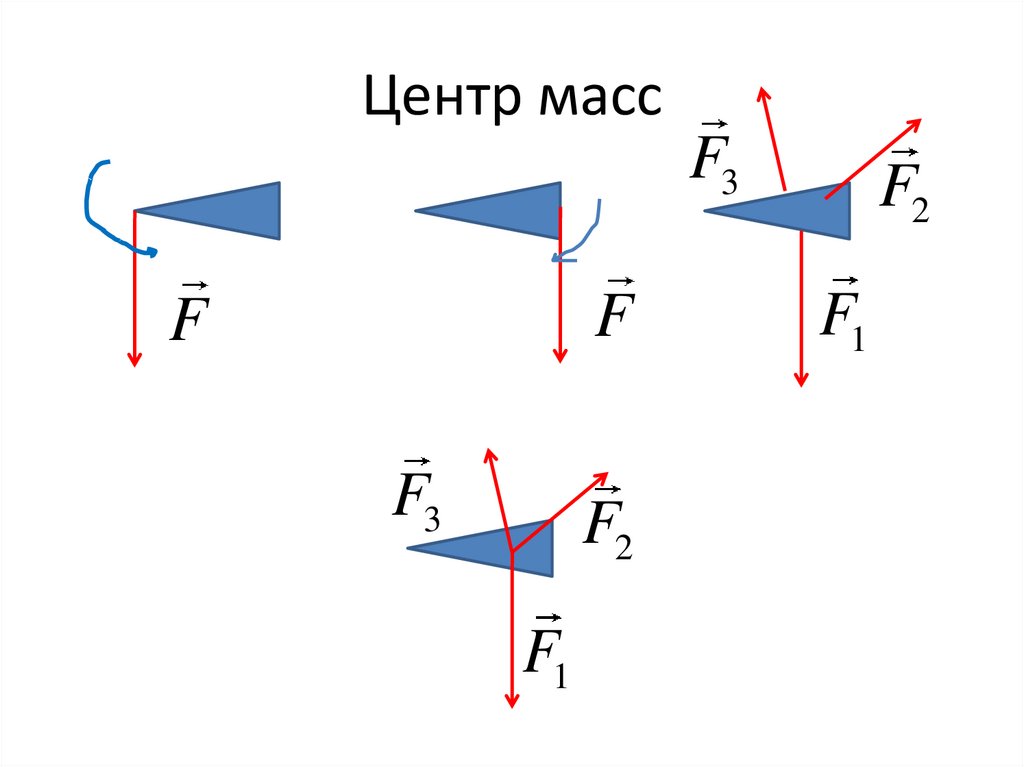
28. Центр масс
F3F
F
F3
F2
F1
F2
F1
29.
• Центр масс- точка пересечения линийдействия сил, которые вызывают только
поступательное движение
30. ЦЕНТР МАСС СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
m1r1
О
rC
ri
mi
r2
rN
m2
mN
mi ri
N
rC
i 1
N
m
i 1
- Радиус –вектор, определяющий положение центра масс
i
31.
NxC
m x
i 1
N
i i
m
i 1
i
N
yC
m y
i 1
N
i
m
i 1
N
i
zC
i
2
2
2
rC xC yC zC
m z
i 1
N
i i
m
i 1
i
32. Скорость центра масс
Nm
i 1
i
M
- Масса системы материальных точек
N
1 N
drC
dri
1
rC
m
r
i i
m
i
M i 1
dt
M
dt
i
1
drC
d
r
i
VC -скорость центра масс
Vi
dt
dt
N
1
VC
miVi
M i 1
33.
• Если скорость центра масс равна 0, тосистема как целое покоится
• Однако, ее части могут двигаться
относительно друг друга
34.
miVi PN
i 1
P MVC
• Импульс системы равен произведению
массы системы на скорость ее центра масс
35. Уравнение движения центра масс
P MVCdVC
dP
M
dt
dt
dP
Fout - Результирующая внешних сил
dt
dVC
-Уравнение движения
M
Fout центра масс
dt
36. Закон движения центра масс
• Центр масс системы материальных точекдвижется так, как двигалась бы
материальная точка, в которой
сосредоточена масса системы и к ней бы
были приложены все внешние силы
37.
Fout 0dVC
0
dt
VC const
P const
• Если центр масс системы материальных
точек движется равномерно и
прямолинейно, то ее импульс сохраняется
38. Система центра масс
• Если нас интересует движение частицвнутри системы, а не ее движение как
целого, целесообразно пользоваться той
системой отсчета, где центр масс покоится
• Систему отсчета, жестко связанную с
центром масс называют СИСТЕМОЙ
ЦЕНТРА ИНЕРЦИИ (центра масс)- СЦИ
39.
VC 0P MVC 0
P 0
• В СЦИ полный импульс системы частиц
равен 0
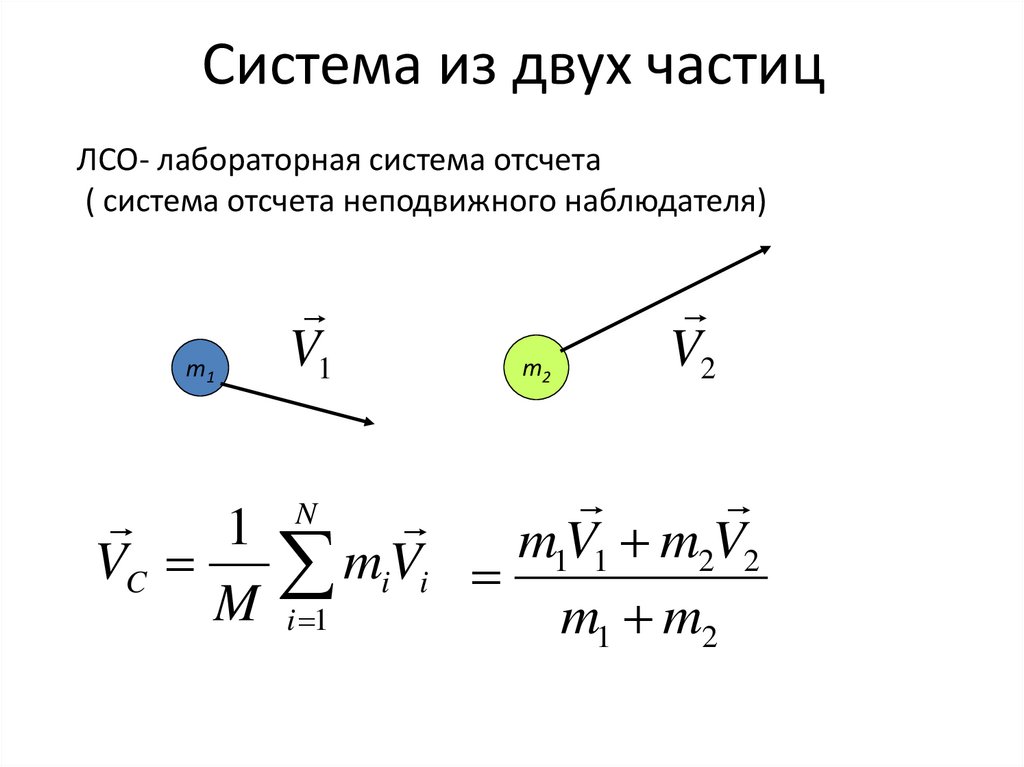
40. Система из двух частиц
ЛСО- лабораторная система отсчета( система отсчета неподвижного наблюдателя)
m1
V1
m2
V2
1
m
V
m
V
1
1
2
2
VC
miVi
M i 1
m1 m2
N
41.
Найдем скорости частиц в СЦИ- (системе центра инерции)V1
и
V2
По закону сложения скоростей
V1 V1 VC
V2 V2 VC
m1V1 m2V2
V1 V1 VC V1
m1 m2
m (V V )
V1 2 1 2
m1 m2
42.
V2 V2 VCm1V1 m2V2
V2 V2 VC V2
m1 m2
m1 (V2 V1 )
V2
m1 m2
43. Найдем суммарный импульс частиц в СЦИ
P m1V1 m2V2m2 (V1 V2 )
m1 (V2 V1 )
P m1
m2
m1 m2
m1 m2
P 0
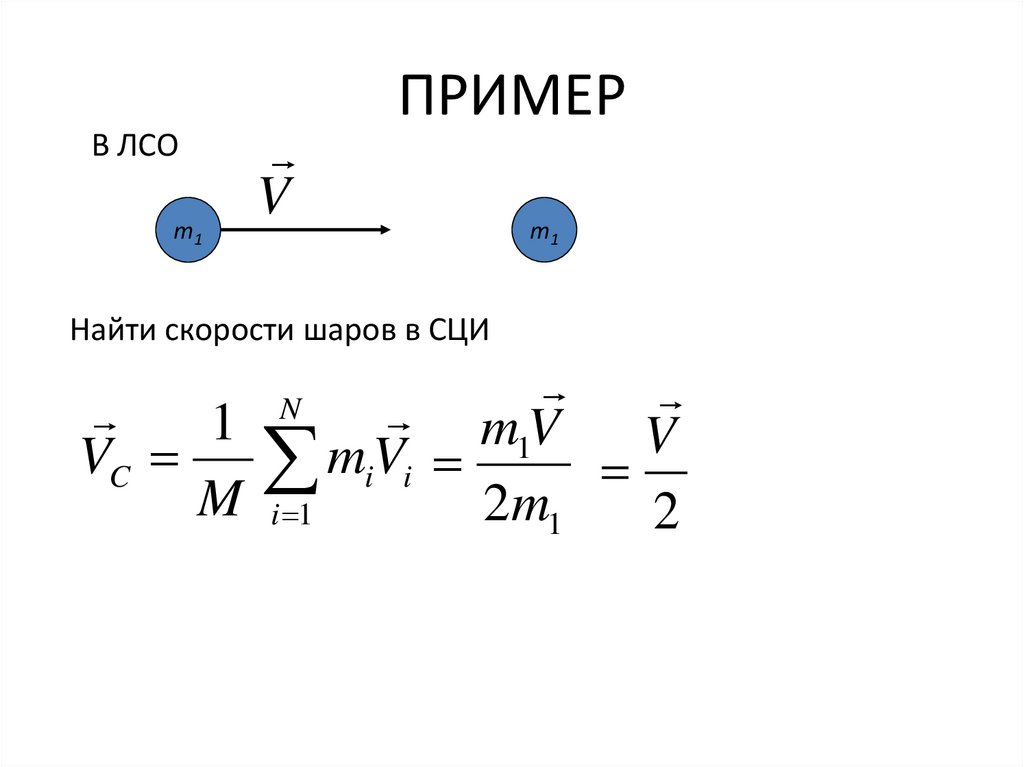
44. ПРИМЕР
В ЛСОm1
V
ПРИМЕР
m1
Найти скорости шаров в СЦИ
N
mV
1
V
1
VC
miVi
M i 1
2m1
2
45.
По закону сложения скоростейV1 V1 VC
V1 V1 VC
V
V
V1 V
2
2
V2 V2 VC
V
V2 0
2
V2 V2 VC
V
2
46.
m1V
2
V
2
m1



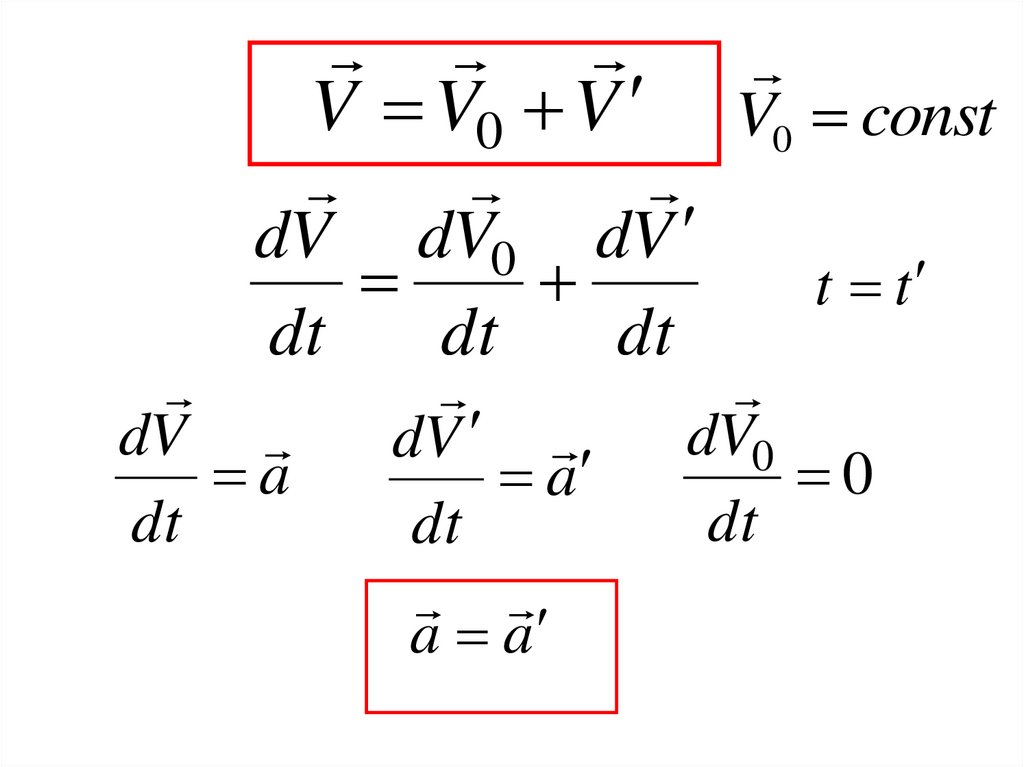

























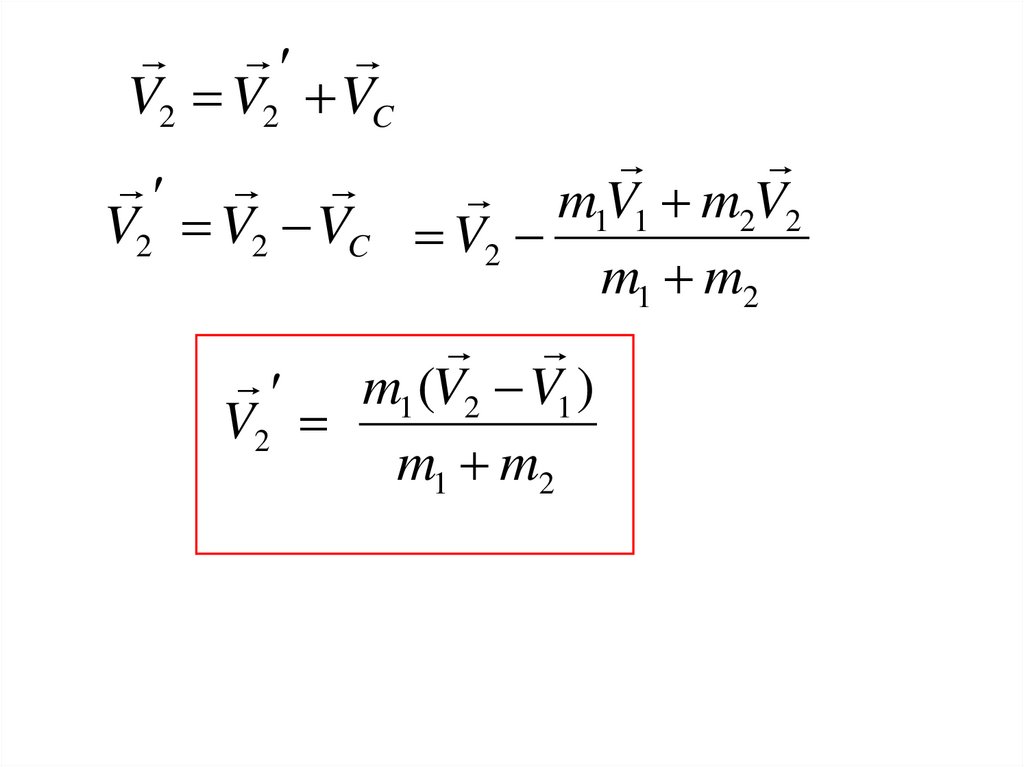



 Физика
Физика








