Похожие презентации:
Компланарные векторы
1.
2.
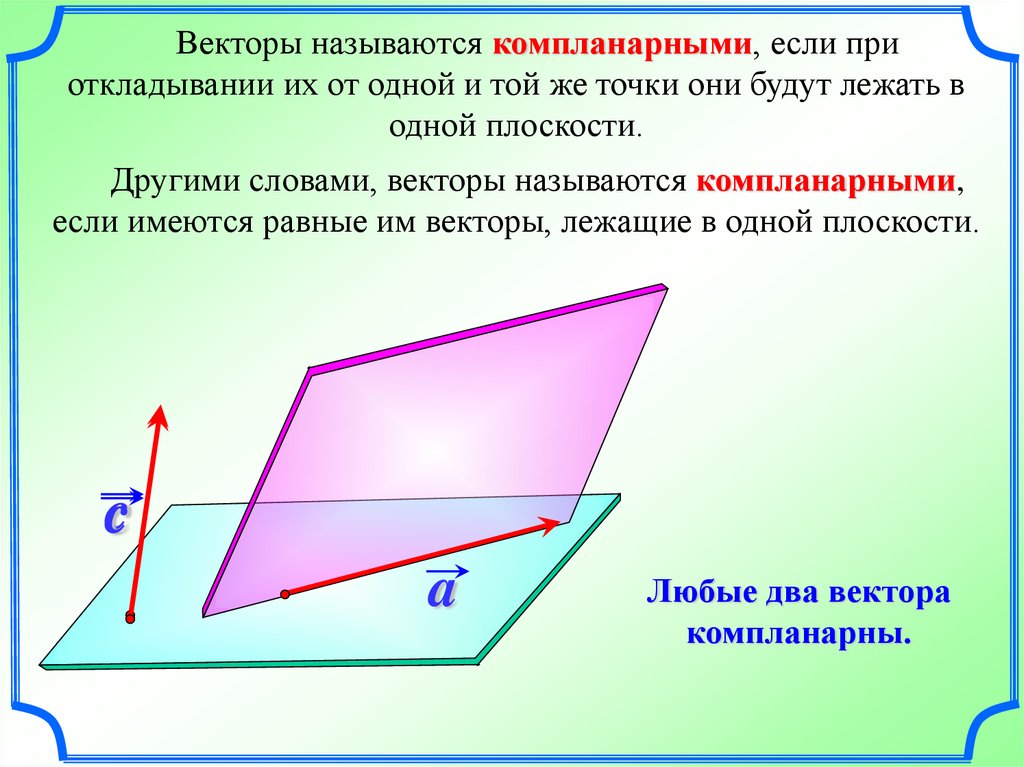
Векторы называются компланарными, если приоткладывании их от одной и той же точки они будут лежать в
одной плоскости.
Другими словами, векторы называются компланарными,
если имеются равные им векторы, лежащие в одной плоскости.
c
a
Любые два вектора
компланарны.
3.
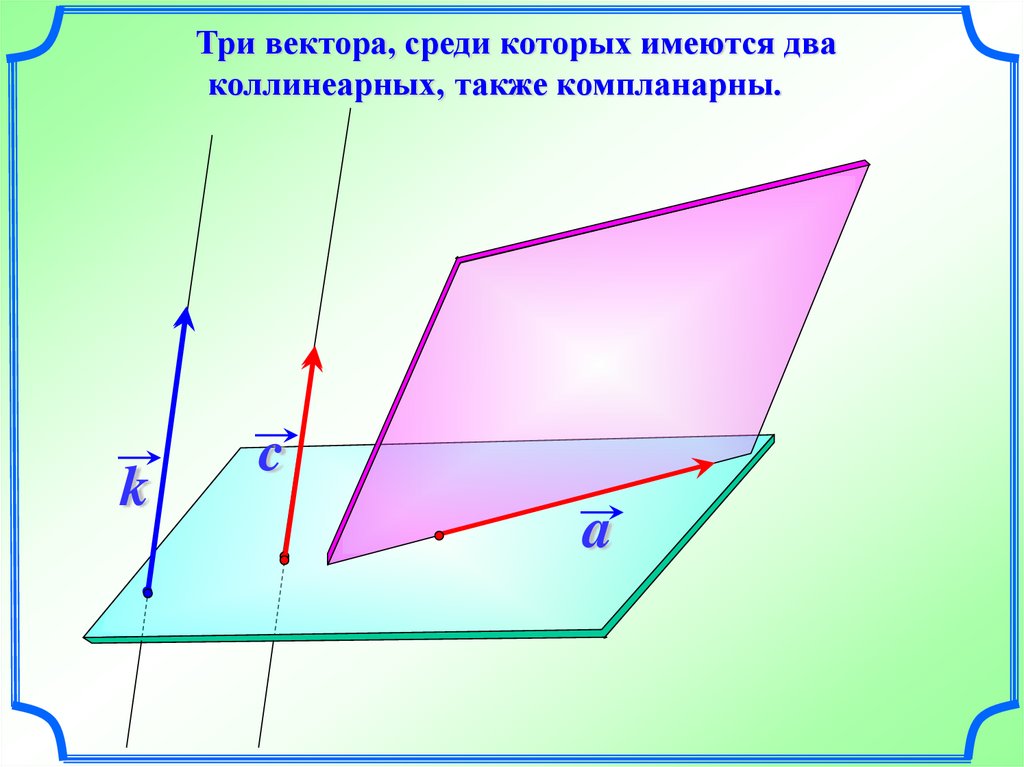
Три вектора, среди которых имеются дваколлинеарных, также компланарны.
k
c
a
4.
Разложение вектора по трем некомпланарным векторам.Если вектор представлен в виде
p = xa + yb + zc
x , y иz
где
- некоторые числа, то говорят, что вектор
разложен по векторам
a,b
и
c.
Числа
p
x, y и z
называются коэффициентами разложения.
Теорема о разложении вектора по трем некомпланарным
векорам.
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
5.
6. Умножение вектора на число
Произведением ненулевог о вектора a на число kназывается такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3
7.
Умножение вектора на число.b
a
1
a
2
2b
ka
2b b
2b = 2 b
1
a
2
1
a
2
a
=
1
2
a
8.
Умножение вектора на число.Произведение нулевого вектора на любое число считается
нулевой вектор.
k o=o
Произведение любого вектора на число нуль есть нулевой
вектор.
a b,
Для любых
o a=o
и любых чисел k ,l справедливы
равенства:
(kl)a = k (l a)
Сочетательный закон
k (a + b) = ka + kb
Первый распределительный
закон
(k+l)a = ka + la
Второй распределительный
закон
9. Сложение векторов
Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
10. Правило треугольника
Для сложения двух векторов необходимо :1. отложить от какой нибудь точки А вектор
AB, равный а
2. от точки В отложить вектор BC , равный b
3. вектор AC называется суммой векторов a и b
B
a
a
b
А
b
a b
C
11.
Сложение векторов.Правило треугольника.
a+b
b
a
b
a
12.
По правилу треугольника складываются иколлинеарные векторы, хотя при их сложении
треугольника и не получается
b
a+b
a
b
a
13. Правило параллелограмма
Для сложения двух векторов необходимо :1. отложить от какой нибудь точки А
вектор AB, равный а
2. от точки А отложить вектор AC, равный b
3. достроить фигуру до параллелограмма , проведя
дополнительные линии параллельно данным
векторам
4. диагональ параллелограмма сумма векторов
B
a
a
b
А
с
b
с a b
C
14.
Сложение векторов. Правило параллелограмма.a+b
b
b
a+b
a
a
15. Правило параллелограмма
16. Правило многоугольника
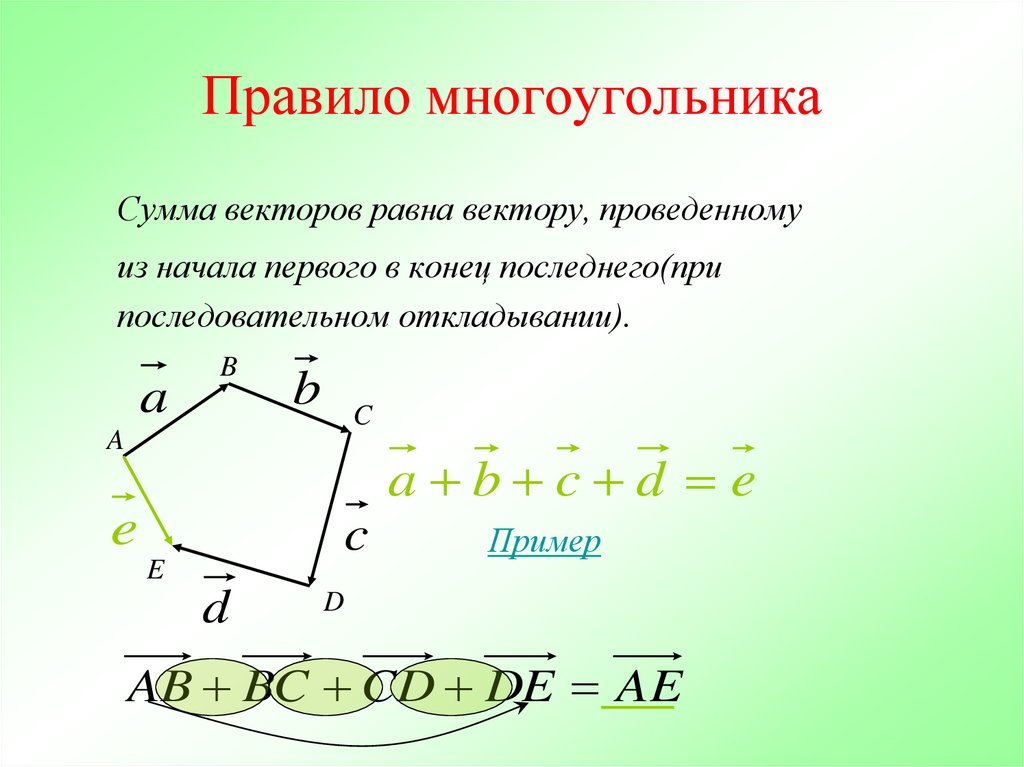
Сумма векторов равна вектору, проведенномуиз начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
a b c d e
e
c
E
d
Пример
D
AB BC CD DE AE
17.
Сложение векторов.Правило многоугольника.
АВ + ВС + СD + DO = АO
n
m
a
m
c
c
a
n
18. Правило сложения нескольких векторов
са
b
a+b+c+d
b
d
а
d
с
19. Правило параллелепипеда
Вектор, лежащий на диагонали параллелепипеда,равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B
A1
C1
1
d
AB b
D1
с bB
C
А
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d
20. Свойства сложения
Для любых векторов a , b и c справедливыравенства :
a b b a
a b с а b с
переместительный закон
сочетательный закон
21.
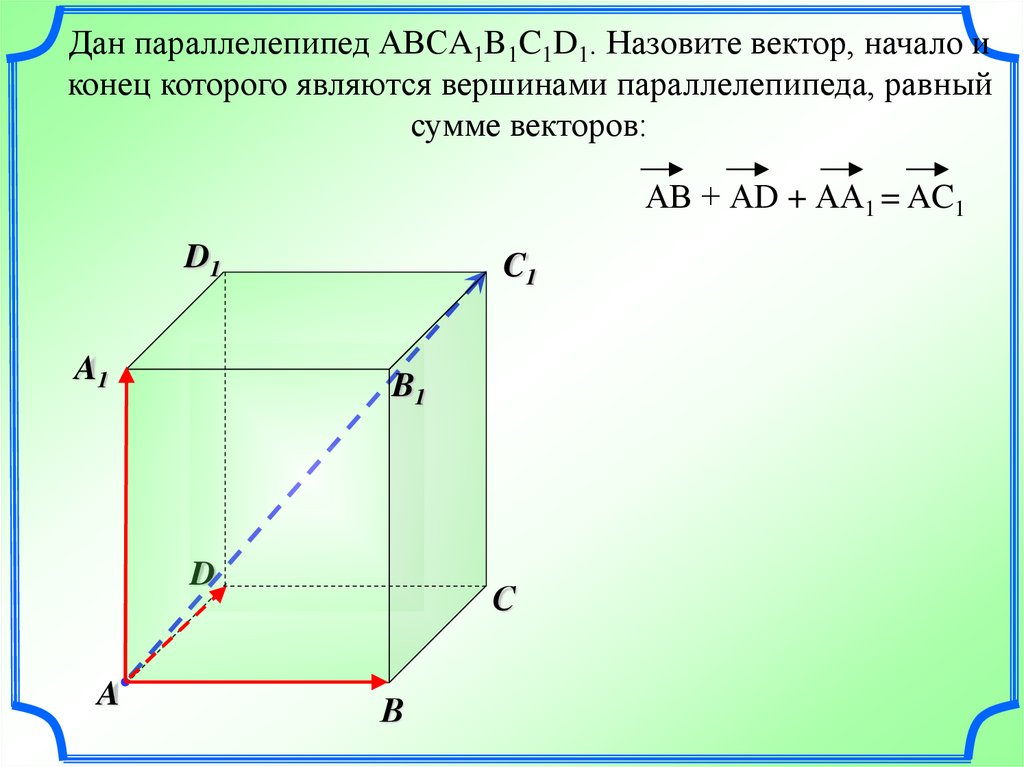
Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало иконец которого являются вершинами параллелепипеда, равный
сумме векторов:
АВ + АD + АА1 = AC1
D1
A1
C1
B1
D
A
С
В
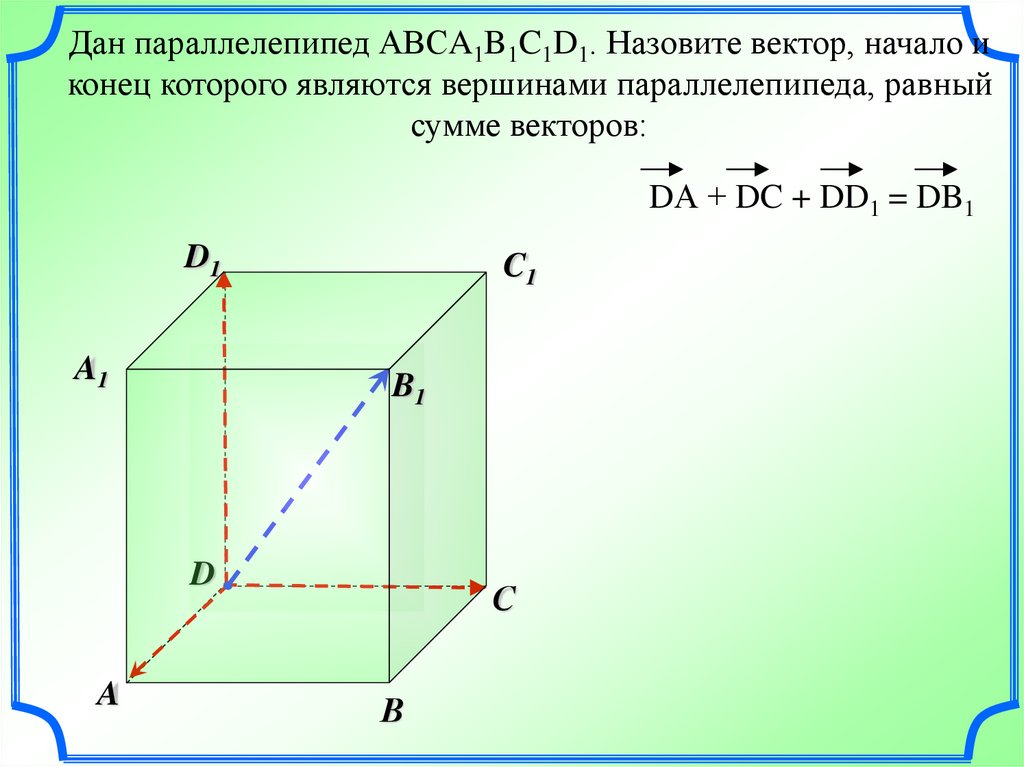
22.
Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало иконец которого являются вершинами параллелепипеда, равный
сумме векторов:
DА + DC + DD1 = DB1
D1
A1
C1
B1
D
A
С
В
23. Вычитание
Разностью векторов a и b называется такойвектор, сумма которого с вектором b равна
вектору a .
24. Вычитание
Для вычитания одного вектора из другого необходимо :1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
a
a b
A
b
C
25. Сложение с противоположным
Разность векторовкак сумму вектора
a
a
и
b можно представить
и вектора,
противоположного вектору
b.
a b a b
a
B
b
a b
b
O
А
a
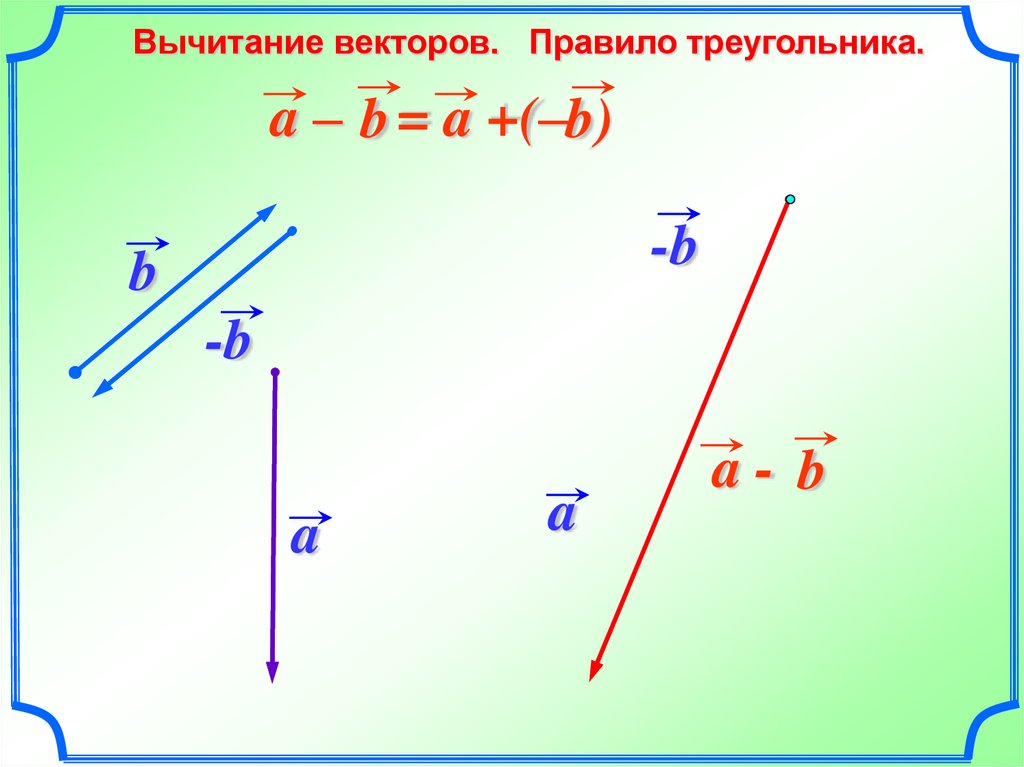
26.
Вычитание векторов. Правило треугольника.a – b = a +(–b)
-b
b
-b
a
a
a- b
27. Самостоятельная работа
Постройте вектораа; в ; с ; m; n
I вариант
II вариант
Постройте вектора
Постройте вектора
1.
1.
2.
3.
4.
5.
k a b
t c m
d 3n k
e 3d b
s e 3t
2.
3.
4.
5.
k a b
t 2c m
d n 3k
e 2d b
s e 2t





















 Математика
Математика








