векторы в пространстве

1.

2.

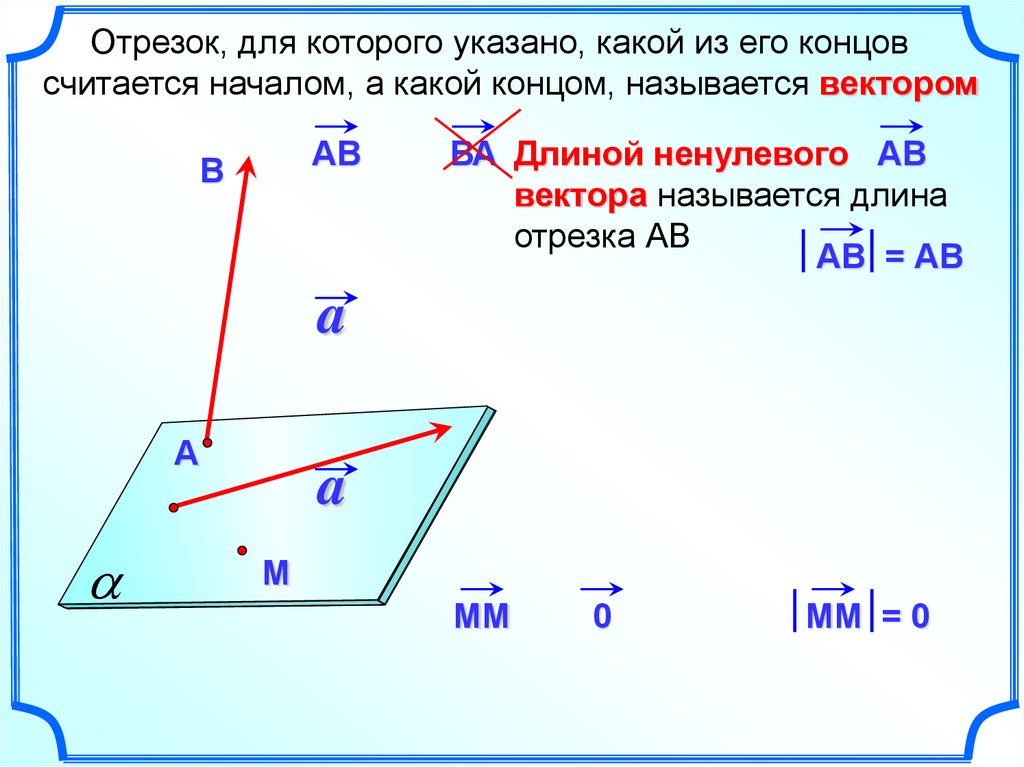
Отрезок, для которого указано, какой из его концов
считается началом, а какой концом, называется вектором
АВ
В
ВА Длиной ненулевого АВ
вектора называется длина
отрезка АВ
АВ = АВ
a
А
a
M
MM
0
MM = 0

3.

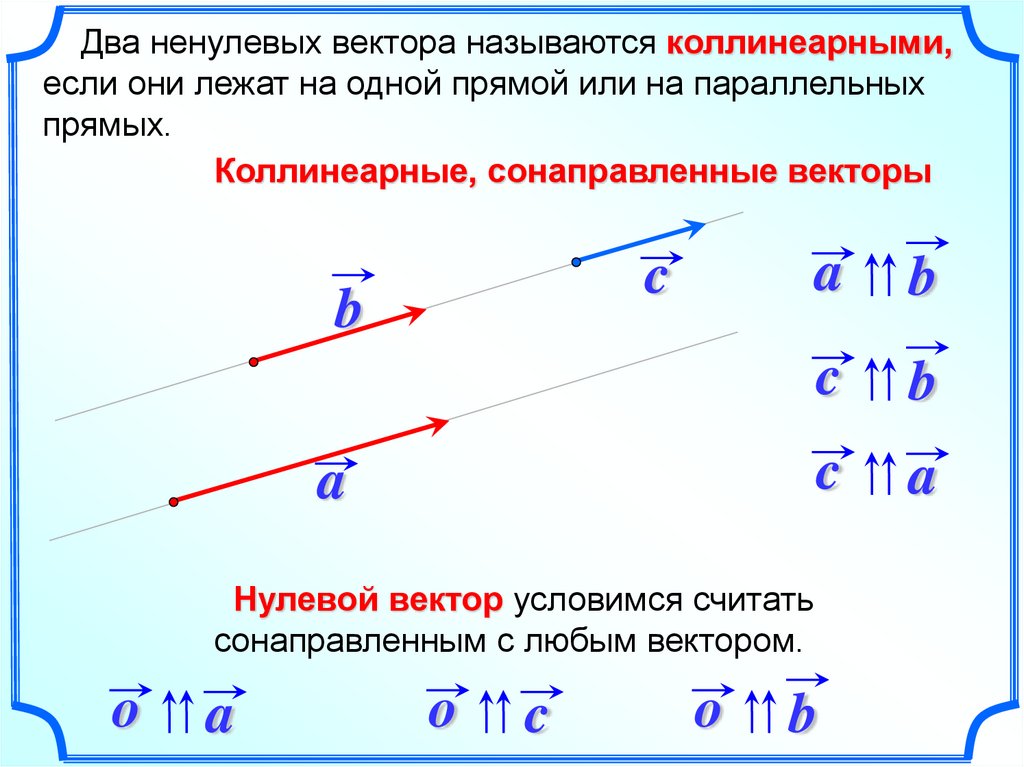
Два ненулевых вектора называются коллинеарными,
если они лежат на одной прямой или на параллельных
прямых.
Коллинеарные, сонаправленные векторы
c
b
a
a
b
c
b
c
a
Нулевой вектор условимся считать
сонаправленным с любым вектором.
o
a
o
c
o
b

4.

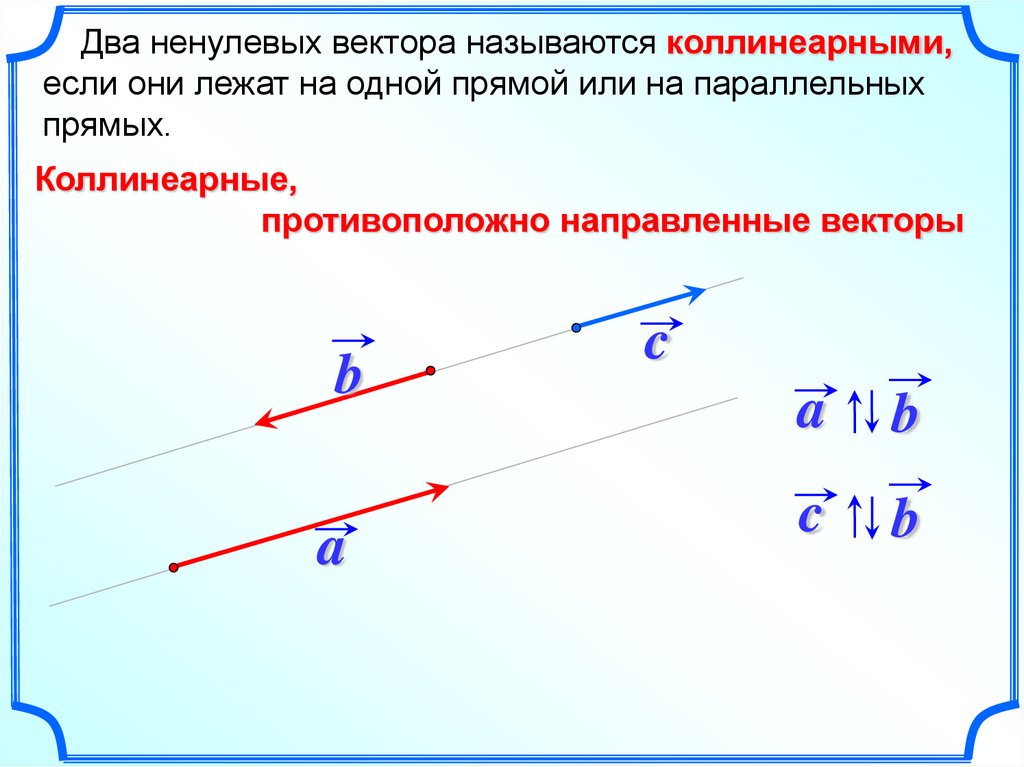
Два ненулевых вектора называются коллинеарными,
если они лежат на одной прямой или на параллельных
прямых.
Коллинеарные,
противоположно направленные векторы
b
a
c
a
b
c
b

5.

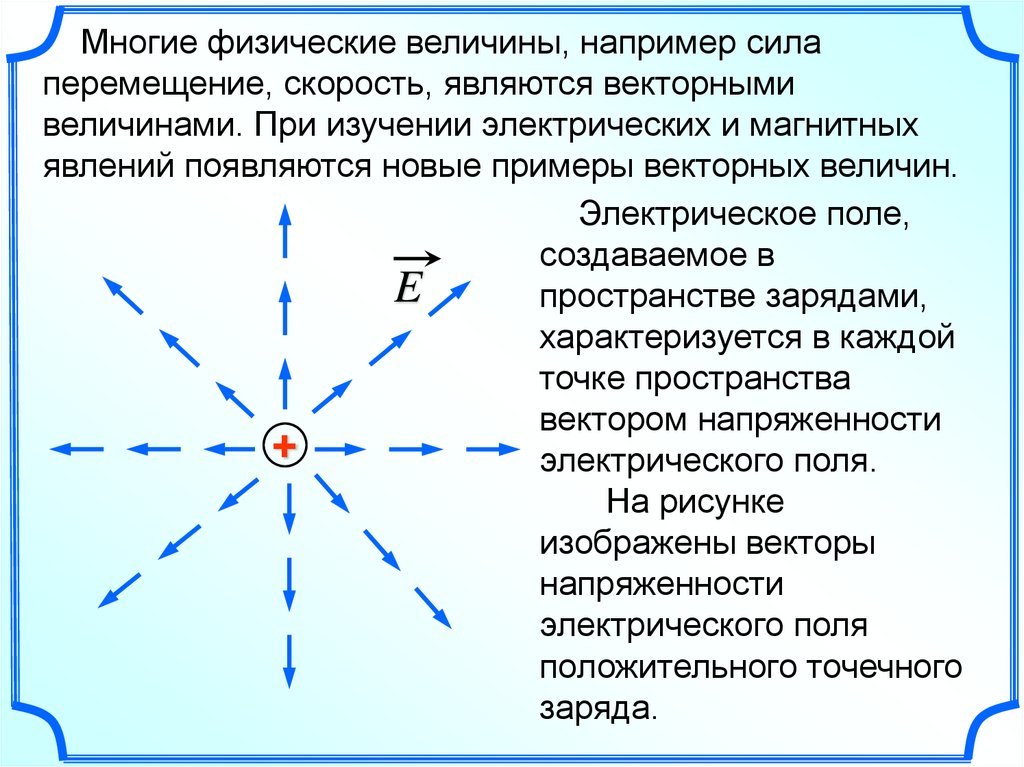
Многие физические величины, например сила
перемещение, скорость, являются векторными
величинами. При изучении электрических и магнитных
явлений появляются новые примеры векторных величин.
Электрическое поле,
создаваемое в
E
пространстве зарядами,
характеризуется в каждой
точке пространства
вектором напряженности
+
электрического поля.
На рисунке
изображены векторы
напряженности
электрического поля
положительного точечного
заряда.

6.

Направление тока
B
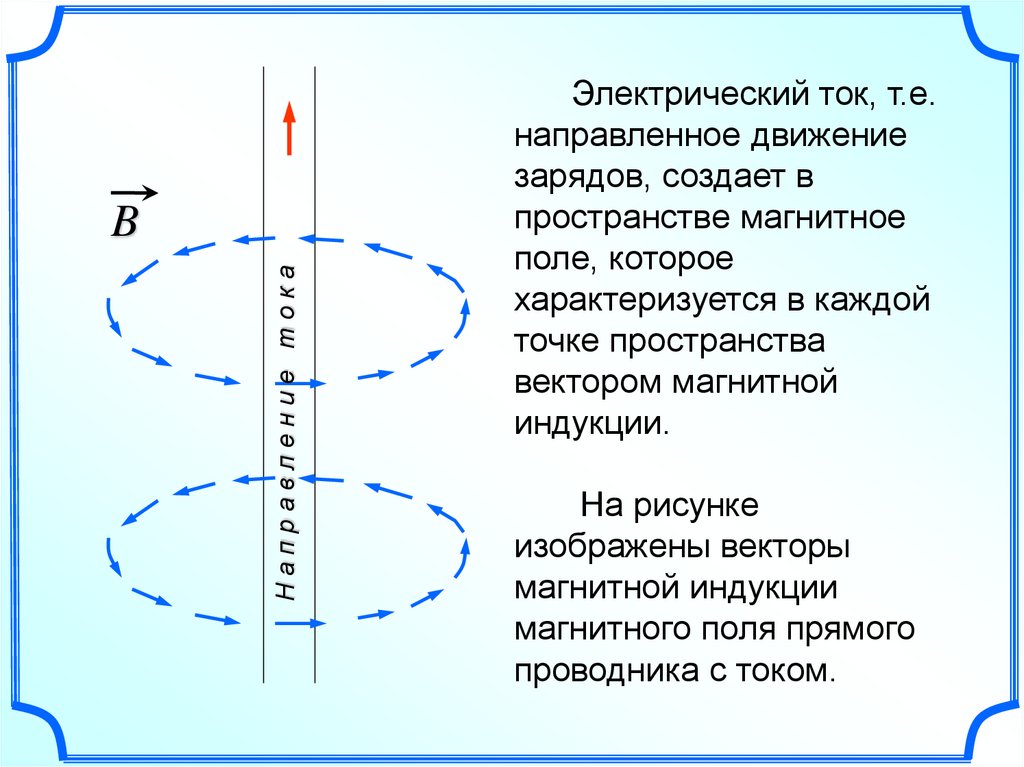
Электрический ток, т.е.
направленное движение
зарядов, создает в
пространстве магнитное
поле, которое
характеризуется в каждой
точке пространства
вектором магнитной
индукции.
На рисунке
изображены векторы
магнитной индукции
магнитного поля прямого
проводника с током.

7.

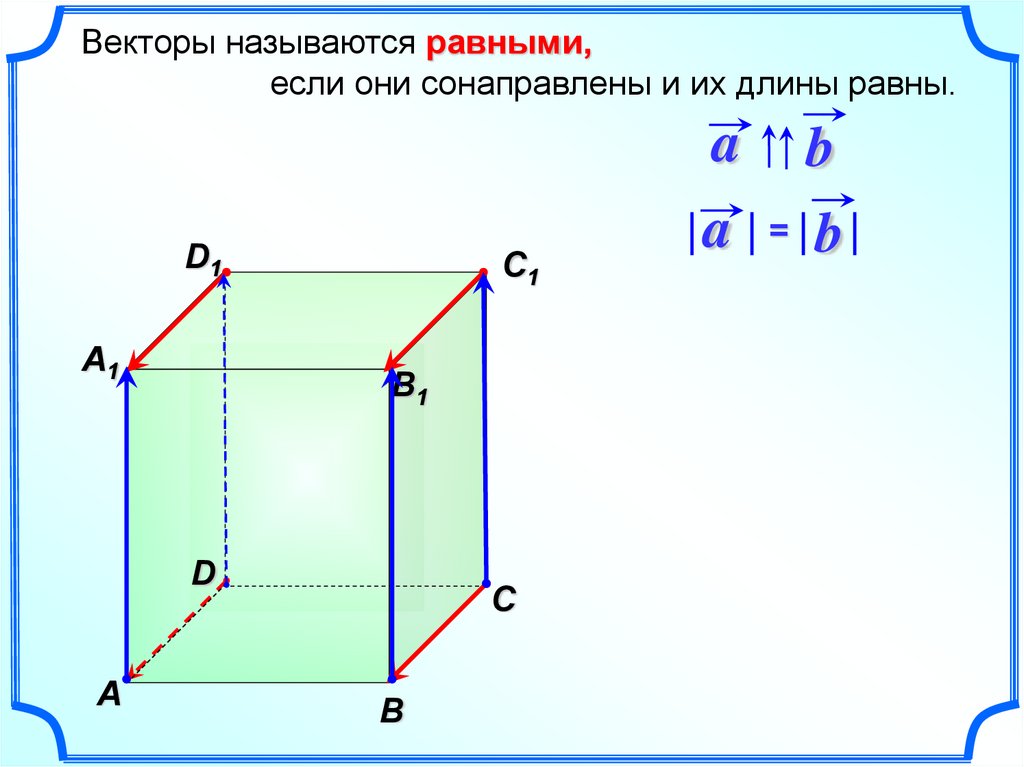
Векторы называются равными,
если они сонаправлены и их длины равны.
a
D1
A1
C1
B1
D
A
C
B
b
a = b

8.

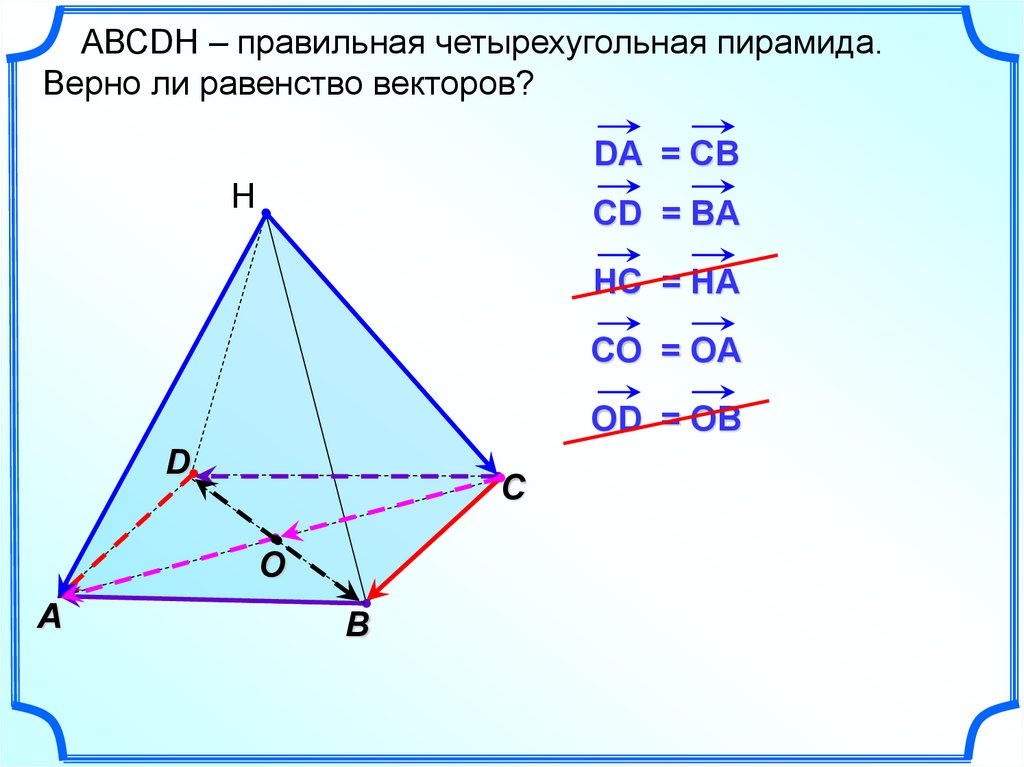
АВСDH – правильная четырехугольная пирамида.
Верно ли равенство векторов?
DA = CB
Н
CD = BA
HC = HA
CO = OA
OD = OB
D
С
O
А
В

9.

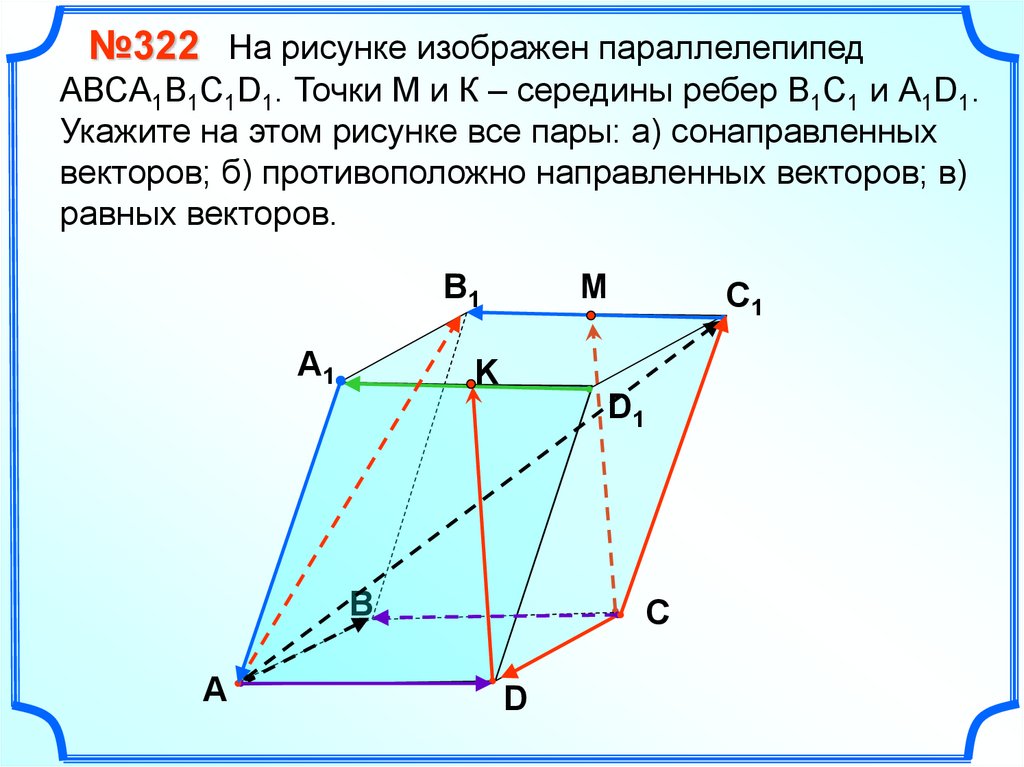
№322 На рисунке изображен параллелепипед
АВСA1B1C1D1. Точки М и К – середины ребер В1С1 и А1D1.
Укажите на этом рисунке все пары: а) сонаправленных
векторов; б) противоположно направленных векторов; в)
равных векторов.
В1
А1
M
С1
K
D1
В
А
С
D

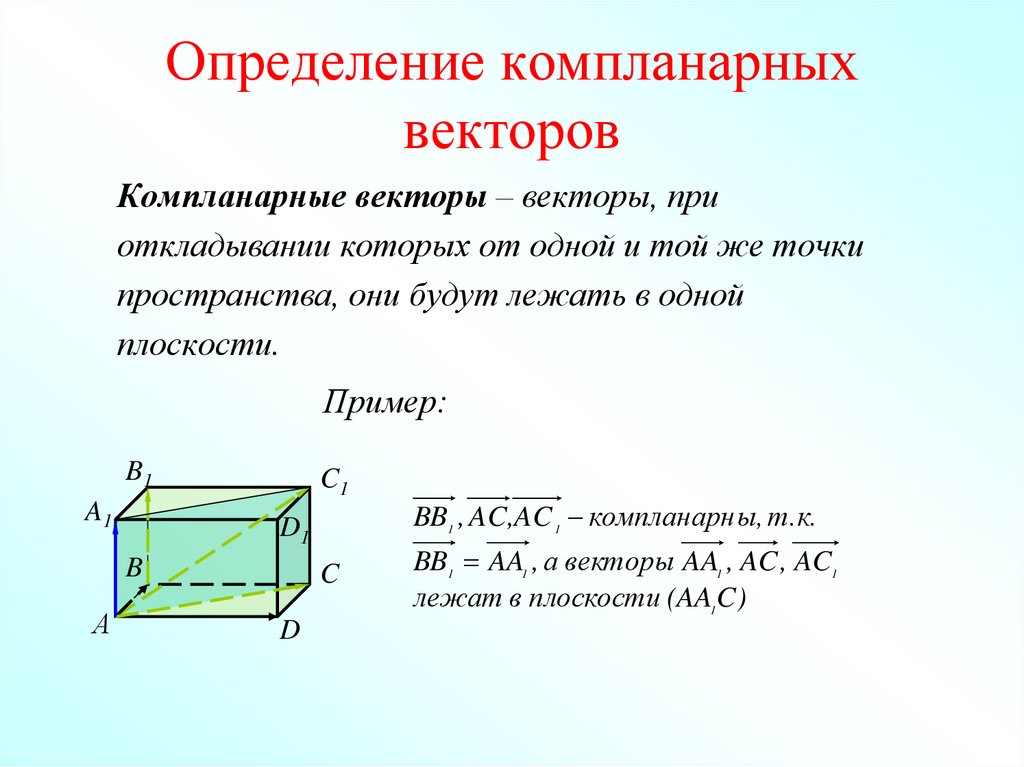
10. Определение компланарных векторов

Компланарные векторы – векторы, при
откладывании которых от одной и той же точки
пространства, они будут лежать в одной
плоскости.
Пример:
B1
A1
C1
D1
B
А
C
D
BB1 , AC,AC 1 компланарн ы, т.к.
BB1 AA1 , а векторы AA1 , AC , AC1
лежат в плоскости (AA1C)

11. О компланарных векторах

Любые два вектора всегда компланарны.
α
a
b
a
b
a
b
a и b компланарн ы
Три вектора, среди которых имеются два
коллинеарных, компланарны.
a, b и c
компланарн ы
если
a, b, c
a kb

12. Признак компланарности

Если вектор c можно разложить по векторам
а и b, т.е. представить в виде
с xa yb
где х и у некоторые числа, то векторы a, b
и c компланарн ы.

13. Разложение вектора по трем некомпланарным векторам

Если вектор p представлен в виде
p xa yb z c
где x, y, z – некоторые числа, то говорят, что вектор
p разложен по векторам a , b и c .
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.

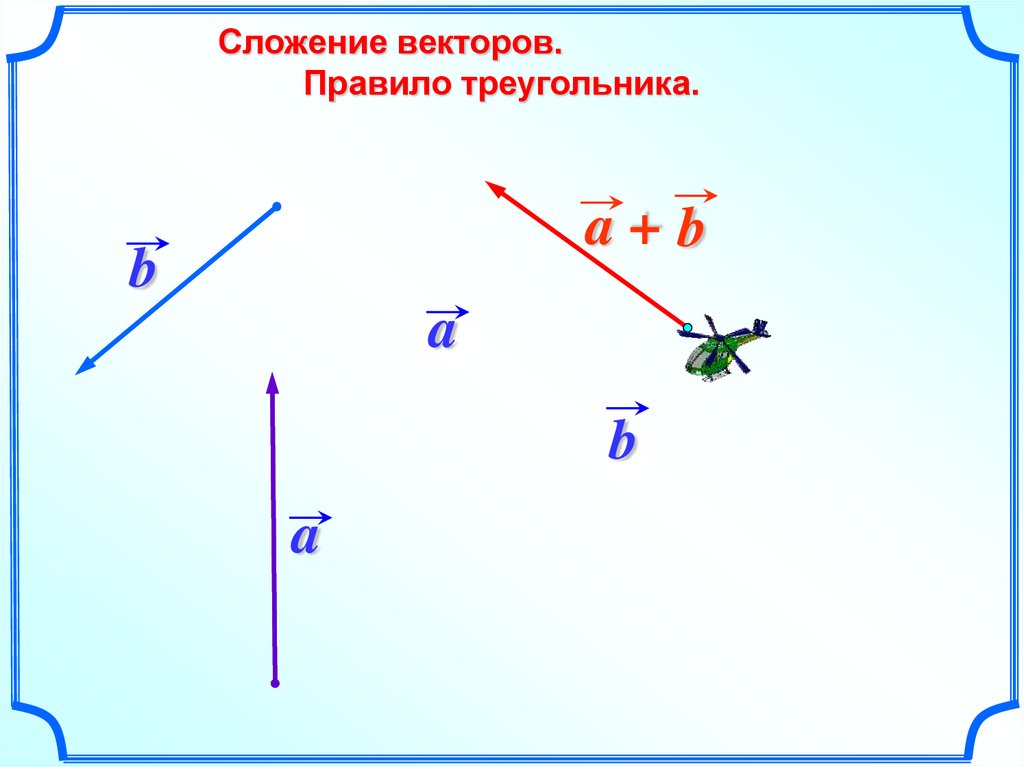
14.

Сложение векторов.
Правило треугольника.
a+b
b
a
b
a

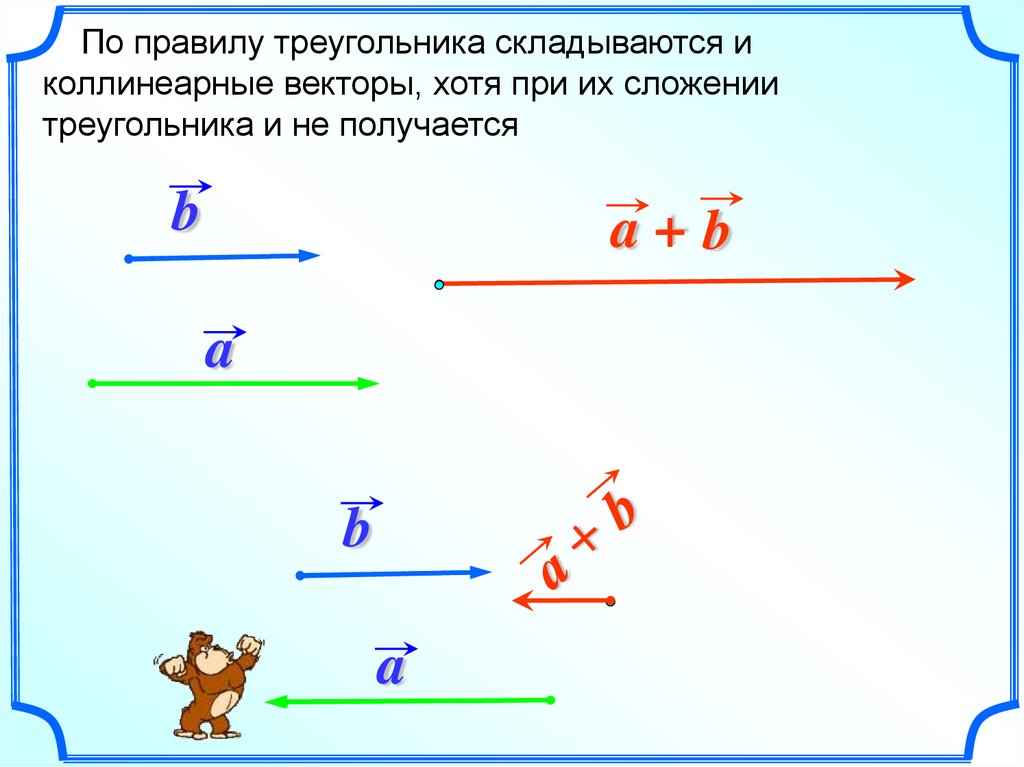
15.

По правилу треугольника складываются и
коллинеарные векторы, хотя при их сложении
треугольника и не получается
b
a+b
a
b
a

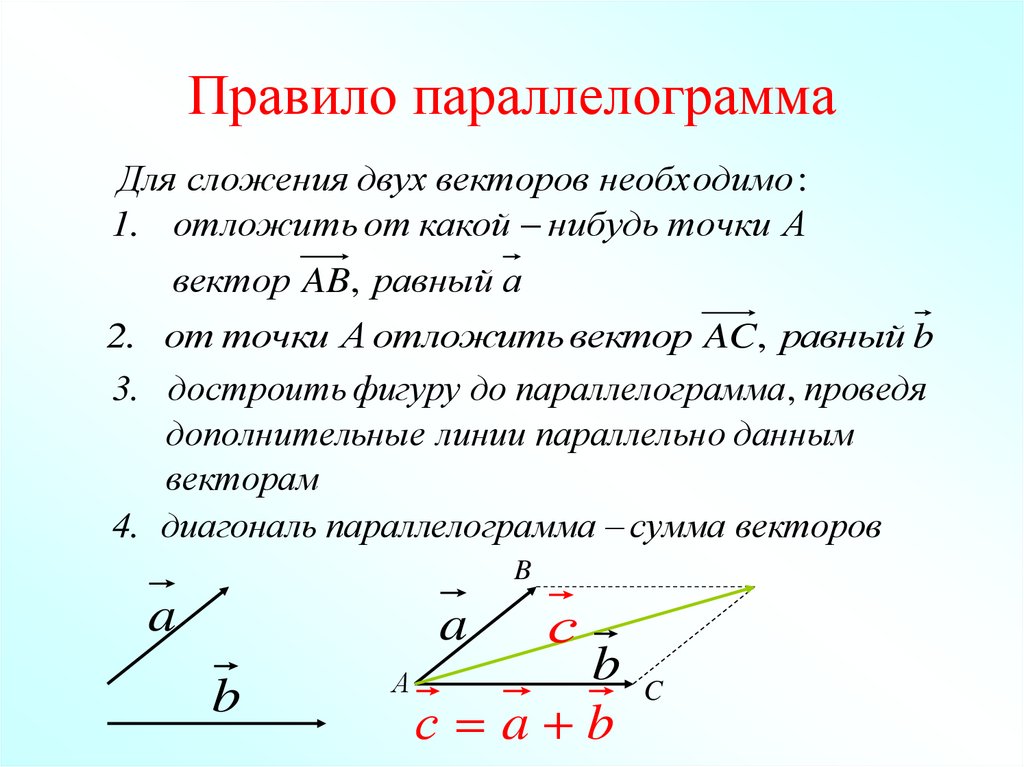
16. Правило параллелограмма

Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от точки А отложить вектор AC, равный b
3. достроить фигуру до параллелограмма , проведя
дополнительные линии параллельно данным
векторам
4. диагональ параллелограмма сумма векторов
B
a
a
b
А
с
b C
с a b

17. Свойства сложения

Для любых векторов a , b и c справедливы
равенства :
a b b a
переместительный закон
a b с а b с сочетательный закон

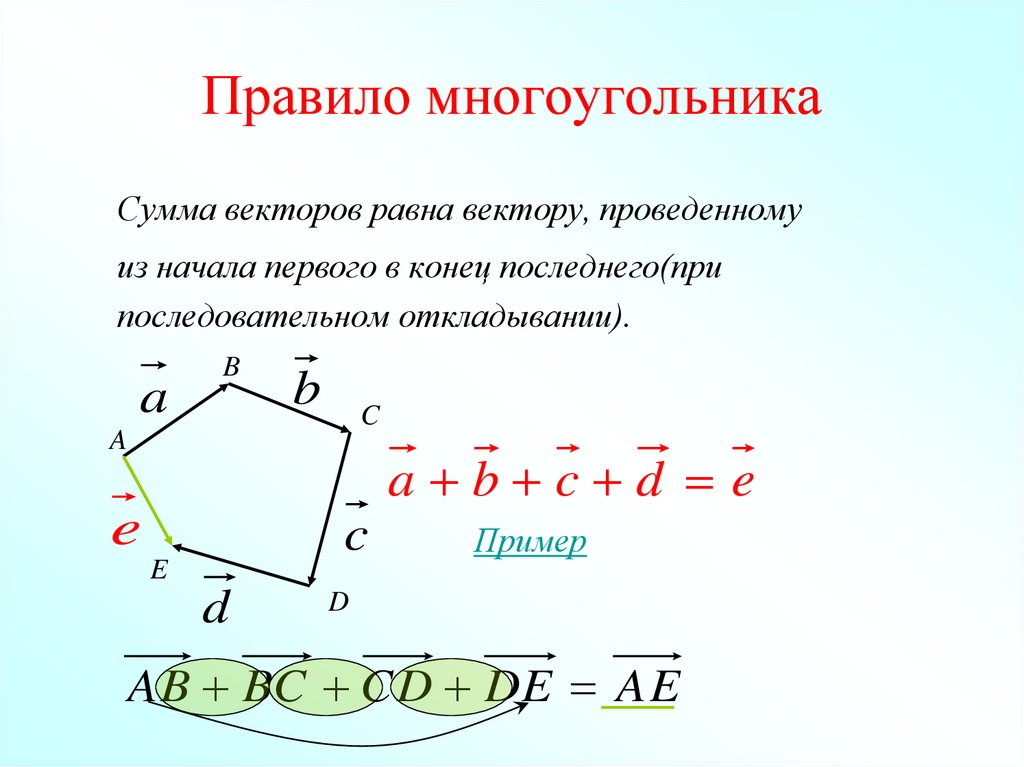
18. Правило многоугольника

Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
a b c d e
e
c
E
d
Пример
D
AB BC CD DE AE

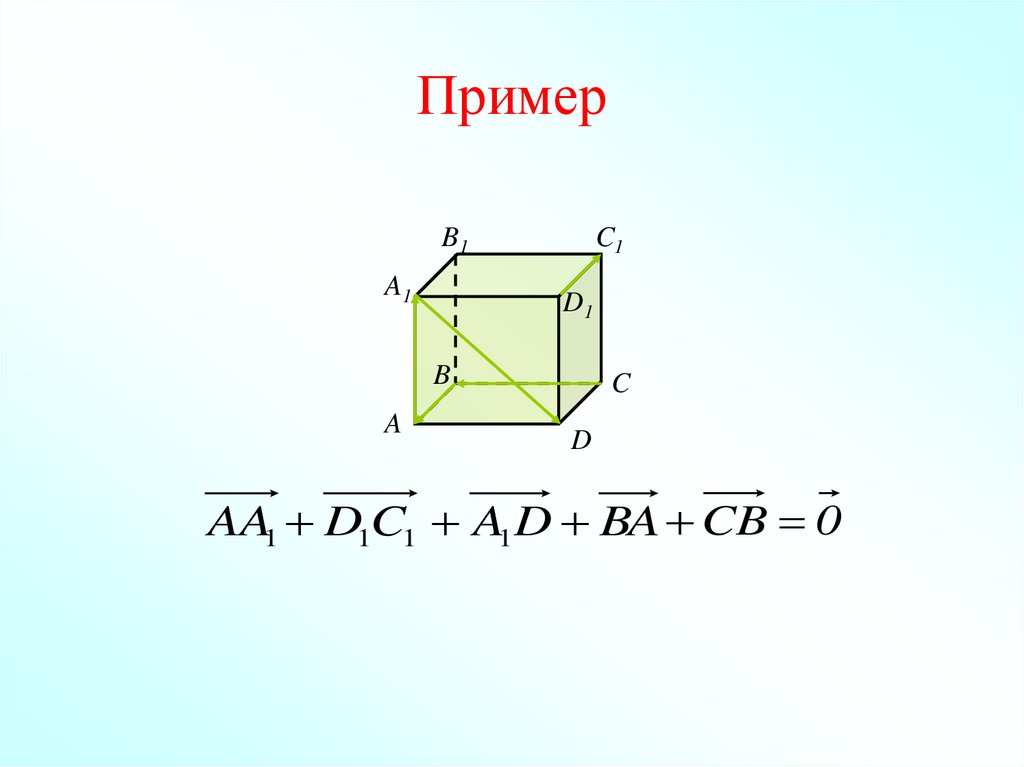
19. Пример

B1
A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0

20. Правило параллелепипеда

Вектор, лежащий на диагонали параллелепипеда,
равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B
A1 1
C1
d
AB b
D1
с bB
C
А
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d

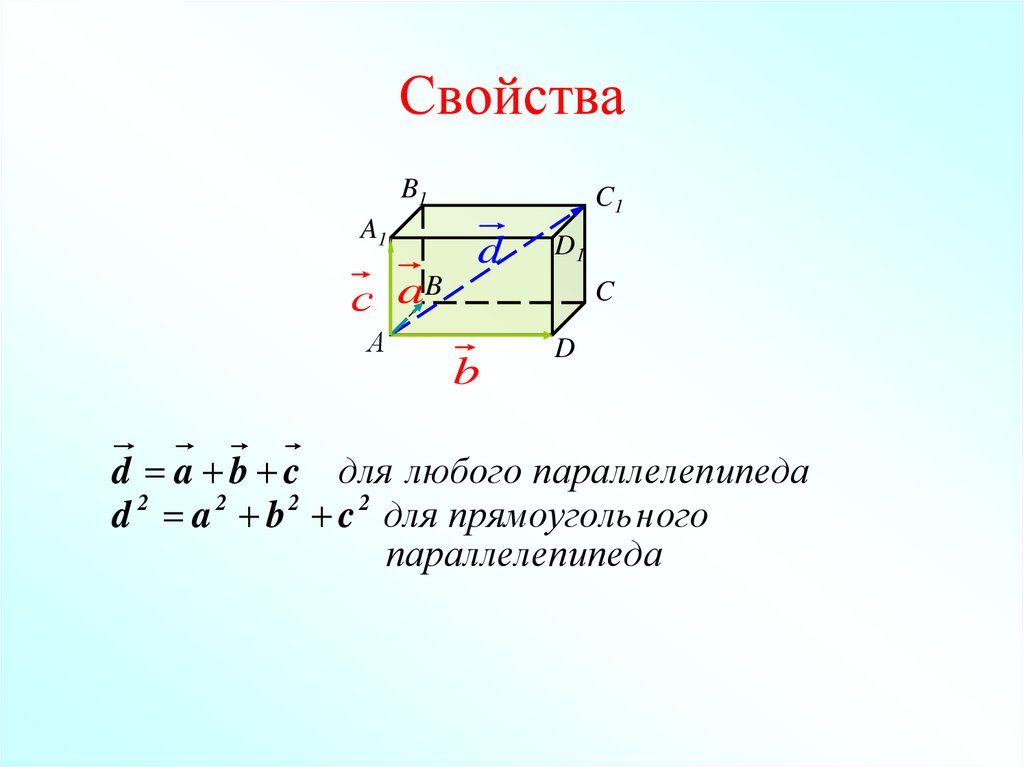
21. Свойства

B1
A1
C1
d
D1
с aB
А
C
b
D
d a b c для любого параллелеп ипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелеп ипеда

22. Вычитание

Для вычитания одного вектора из другого необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
a
a b
A
b
C

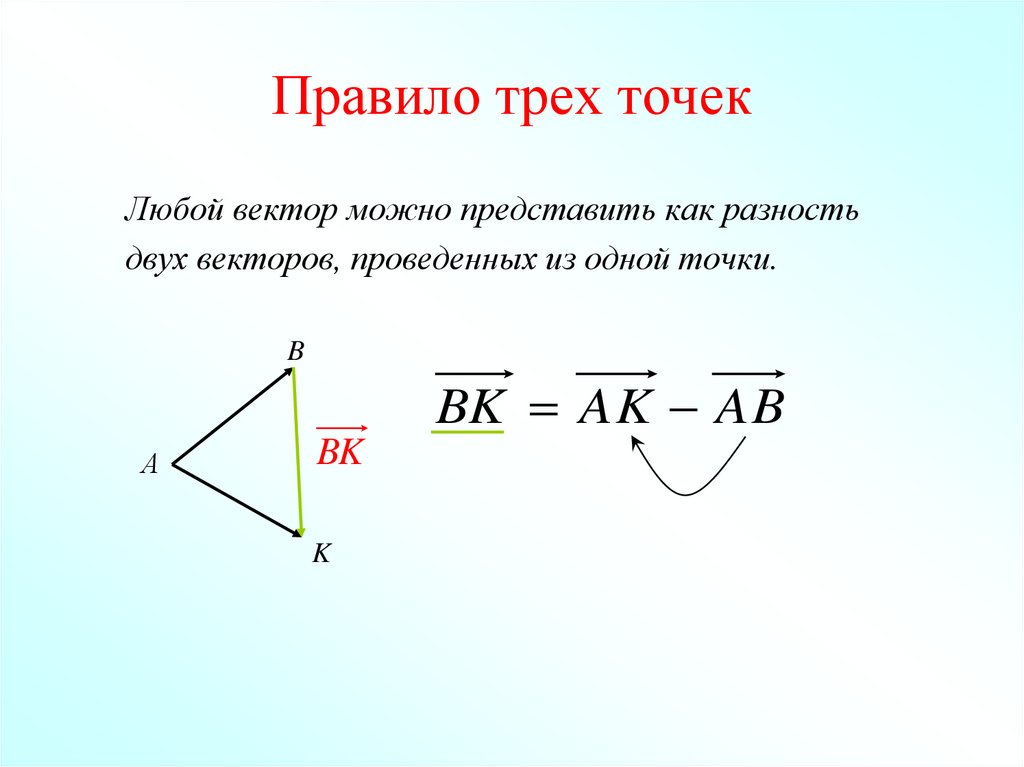
23. Правило трех точек

Любой вектор можно представить как разность
двух векторов, проведенных из одной точки.
B
BK AK AB
А
BK
K

24. Сложение с противоположным

Разность векторов a и b можно представить
как сумму вектора a и вектора,
противоположного вектору b.
a b a b
a
B
b
a b
b
O
А
a

25. Умножение вектора на число

Произведением ненулевог о вектора a на число k
называется такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3

26. Свойства

• Произведением нулевого вектора на любое число
считается нулевой вектор.
0 n 0
• Произведение любого вектора на число нуль есть
нулевой вектор.
n 0 0

27. Свойства

Для любыхвект оровa и b и любых
чисел k, l справедливы равенст ва:
(kl)a k(la )
сочет ат ельный закон
k( a b ) k a k b
1 ый распределит ельный
закон
(k l)a k a l a
2 ой распределит ельный
закон

28. Скалярное произведение

Скалярным произведением двух векторов
называется произведение их длин на косинус угла
между ними.
ab a b cos( a ; b )

29. Справедливые утверждения

• скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти
векторы перпендикулярны
a b 0 a 0 b 0 a b
• скалярный квадрат вектора (т.е. скалярное
произведение вектора на себя) равен квадрату
его длины
2
a
а
2
а
2

30. Вычисление скалярного произведения в координатах

Скалярное произведение векторов a x1 ; y1 ; z1
и b x 2 ; y2 ; z 2 выражается формулой
a b x 1 x 2 y1 y 2 z 1 z 2

31. Свойства скалярного произведения

Для любых векторов a , b и с и любого
числа k справедливы равенства :
10.
2
a 0 причем a 0 при a 0
20. a b ba (переместительный закон)
(распределительный
0
a
b
c
a
c
b
c
3.
закон)
40. k a b k a b (сочетательный закон)

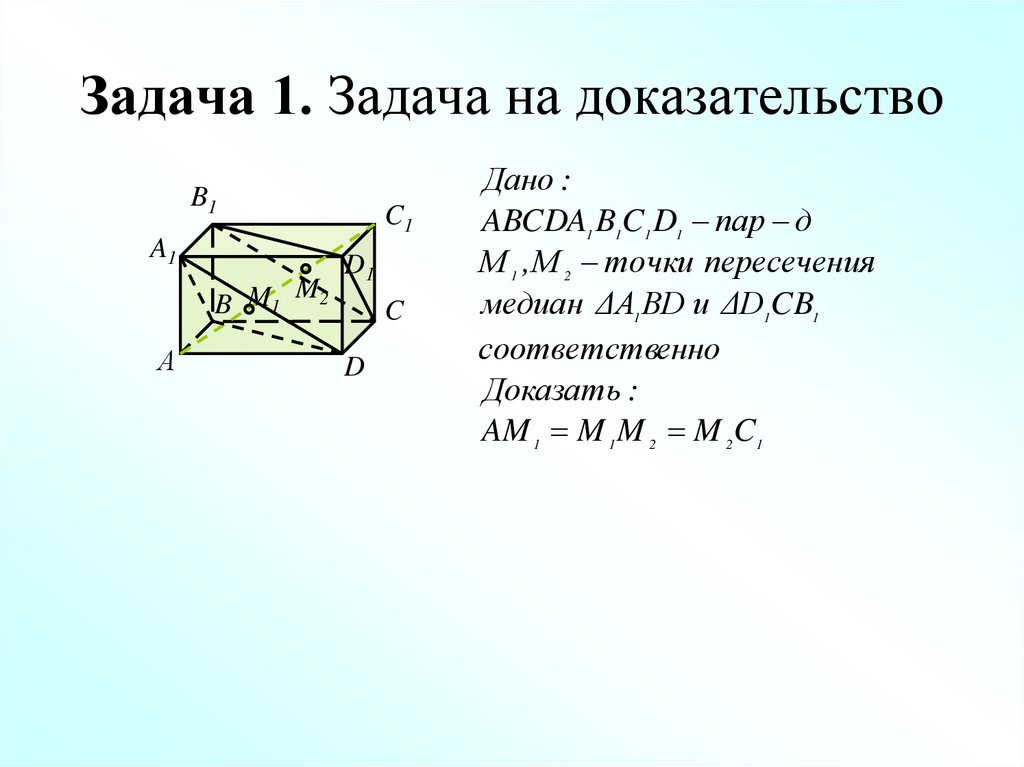
32. Задача 1. Задача на доказательство

B1
C1
A1
B M1
А
M2
D1
C
D
Дано :
ABCDA1 B1C1 D1 пар д
М 1 , М 2 точки пересечения
медиан ΔА1 ВD и ΔD1CB1
соответственно
Доказать :
AM 1 M 1 M 2 M 2 C1

33. Решение

B1
C1
A1
B M1
M2
D1
C
Дано :
ABCDA1 B1C1 D1 пар д
М 1 , М 2 точки пересечения
медиан ΔА1 ВD и ΔD1CB1
соответственно
Доказать :
AM 1 M 1 M 2 M 2 C1
А
D
Доказательство :
Рассм. тетраэдр AA1 BD
M 1 центроид ΔA1 M 1 B
1
AM 1 ( AA1 AB AD )
3
AC1 AA1 AB AD по правилу пар да
1
AM 1 AC1
3
1
M AC1 AM 1 AC1
3
1
аналогично M 2 AC1 C1 M 2 AC1
3
следовательно AM 1 M 1 M 2 M 2 C1 ч.т.д.

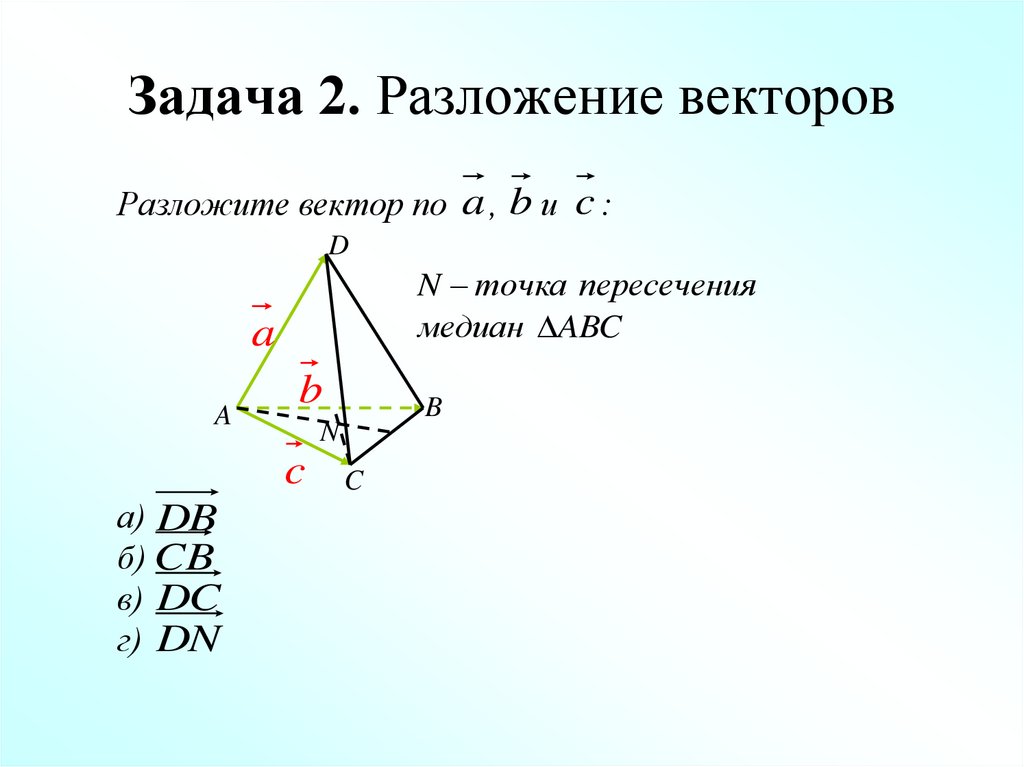
34. Задача 2. Разложение векторов

Разложите вектор по a , b и c :
D
N точка пересечения
медиан ABC
a
A
b
N
c
а) DB
б) CB
в) DC
г) DN
B
C

35. Решение

а) DB b a
б) CB b c
в) DC c a
г) DN a 1 AN a 1 ( 1 ( b c ))
3
1
1
a b c
6
6
3 2

36. Задача 3. Сложение и вычитание

Упростите выражения:
а) CM MK
б) DM MA
в) SD ST
г) PL PK
д) AC BC PM AP BM
е) AD MP EK EP MD

37. Решение

а) CM MK CK
б) DM MA DA
в) SD ST TD
г) PL PK KL
д) AC BC PM AP BM
AC CB MP PA BM
AB MA BM AM MA 0
е) AD MP EK EP MD
AD DM MP PE EK
AK

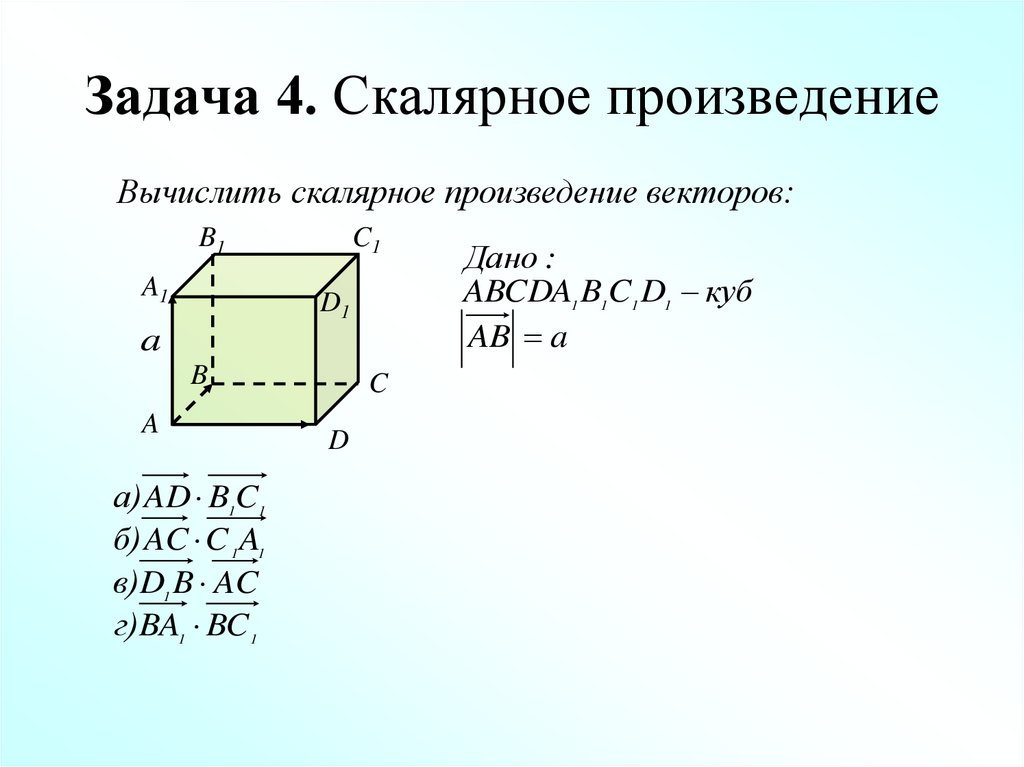
38. Задача 4. Скалярное произведение

Вычислить скалярное произведение векторов:
C1
B1
A1
D1
a
B
A
а) AD B1C1
б) AC C 1 A1
в)D1 B AC
г)BA1 BC 1
C
D
Дано :
ABCDA1 B1C1 D1 куб
AB a

39. Решение

2
а) AD B1C1 AD AD 2 a 2
б)AC диагональ квадрата
AC A1C1 C1 A1
AC C 1 A1 AC ( A1C1 ) AC A1C1 (a 2 )2 2a 2
в)D1 B диагональ куба
D1 B a 2 (a 2 )2 3a(п( т.Пифагора из ΔDD1 B)
2
a3 3
D1 B AC 3a 2 a 2 cos45 a 3 6
2
г)BA1 , BC 1 диагонали квадратов
ΔA1 BC 1 равносторонний, A1 BC 1 60
1 2a 2
a2
BA1 BC 1 a 2 a 2
2
2

40.

УСПЕХОВ!!!