Молекулярные массы и гибкость полимеров

1. КУРС ЛЕКЦИЙ «ХИМИЯ ВЫСОКОМОЛЕКУЛЯРНЫХ СОЕДИНЕНИЙ»

ЛЕКЦИЯ 3. МОЛЕКУЛЯРНЫЕ МАССЫ И ГИБКОСТЬ
ПОЛИМЕРОВ

2.

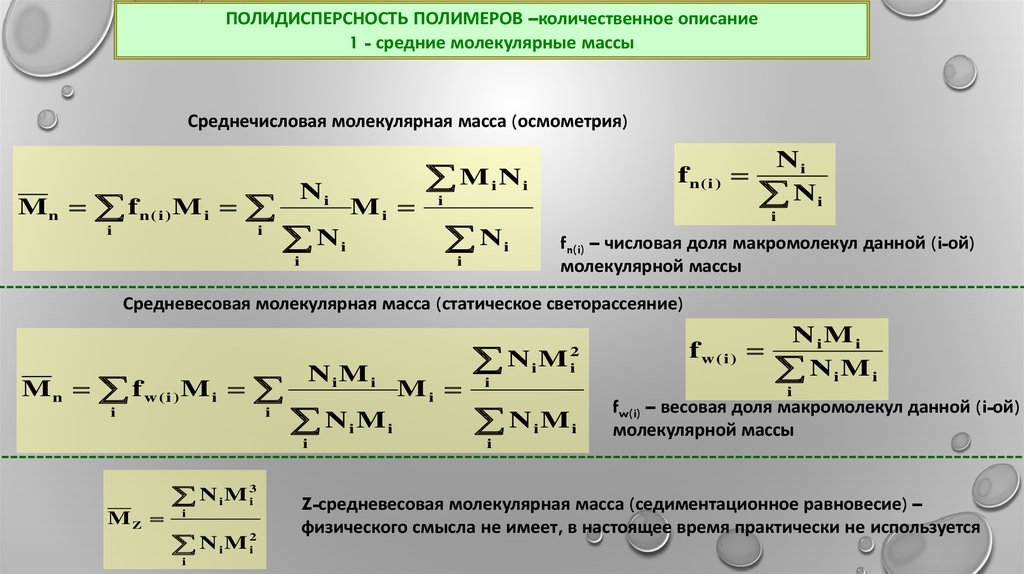
ПОЛИДИСПЕРСНОСТЬ ПОЛИМЕРОВ –количественное описание
1 - средние молекулярные массы
Среднечисловая молекулярная масса (осмометрия)
Mn
fn ( i )M i
i
i
Ni
Ni
Mi
i
Mi Ni
fn( i )
i
Ni
i
Ni
Ni
i
fn(i) – числовая доля макромолекул данной (i-ой)
молекулярной массы
Средневесовая молекулярная масса (статическое светорассеяние)
Mn
f w ( i )M i
i
i
NiMi
NiMi
i
MZ
N i M i3
i
N i M i2
i
Mi
NiM
2
i
i
NiMi
i
fw(i )
NiMi
NiMi
i
fw(i) – весовая доля макромолекул данной (i-ой)
молекулярной массы
Z-средневесовая молекулярная масса (седиментационное равновесие) –
физического смысла не имеет, в настоящее время практически не используется

3.

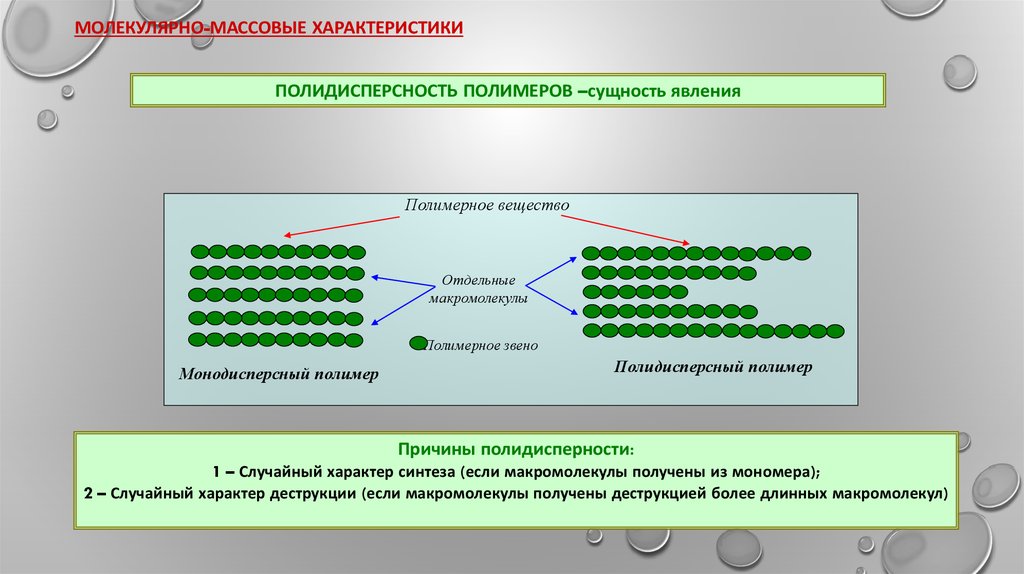
МОЛЕКУЛЯРНО-МАССОВЫЕ ХАРАКТЕРИСТИКИ
ПОЛИДИСПЕРСНОСТЬ ПОЛИМЕРОВ –сущность явления
Полимерное вещество
Отдельные
макромолекулы
Полимерное звено
Монодисперсный полимер
Полидисперсный полимер
Причины полидисперности:
1 – Случайный характер синтеза (если макромолекулы получены из мономера);
2 – Случайный характер деструкции (если макромолекулы получены деструкцией более длинных макромолекул)

4.

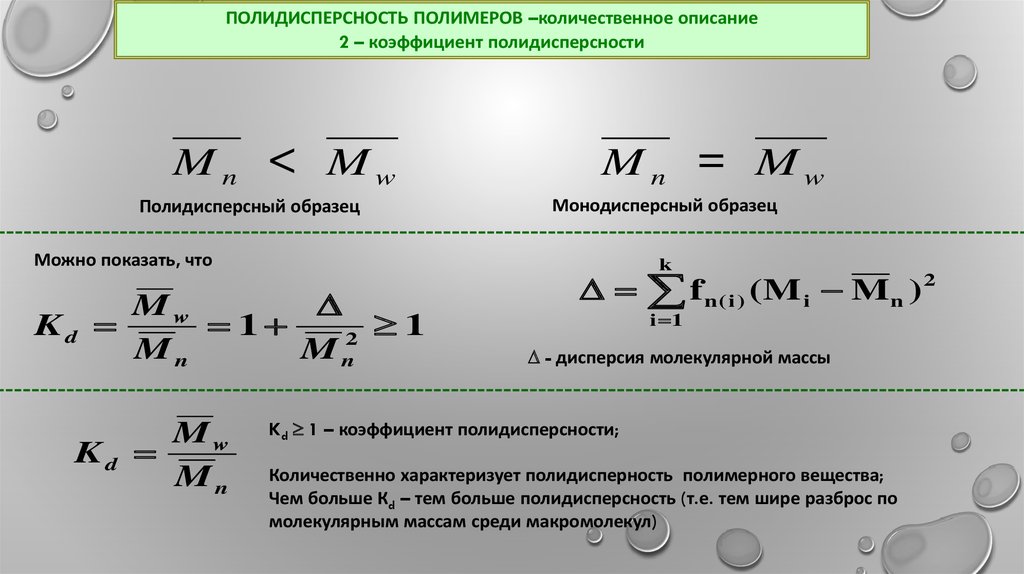
ПОЛИДИСПЕРСНОСТЬ ПОЛИМЕРОВ –количественное описание
2 – коэффициент полидисперсности
Mn
< Mw
Полидисперсный образец
Можно показать, что
Kd
Mw
1
1
2
Mn
Mn
Kd
Mw
Mn
Mn
= Mw
Монодисперсный образец
k
2
f
(
M
M
)
n( i ) i
n
i 1
- дисперсия молекулярной массы
Kd 1 – коэффициент полидисперсности;
Количественно характеризует полидисперность полимерного вещества;
Чем больше Кd – тем больше полидисперсность (т.е. тем шире разброс по
молекулярным массам среди макромолекул)

5.

Задача №1
Вычислите среднечисловую и средневесовую молекулярные массы, а также коэффициент
полидисперсности полимера, представляющего собой смесь двух равных по молям фракций
макромолекул с молекулярными массами 100 и 1000.
Ответ:
Mn
Pn
M0
Mw
Pw
M0
M n 550
M w 918 K d 1.67
Среднечисловая степень полимеризации, М0 – масса
мономерного звена
Kd
Средневесовая степень полимеризации,
М0 – масса мономерного звена
Mw
Pw
Mn
Pn

6.

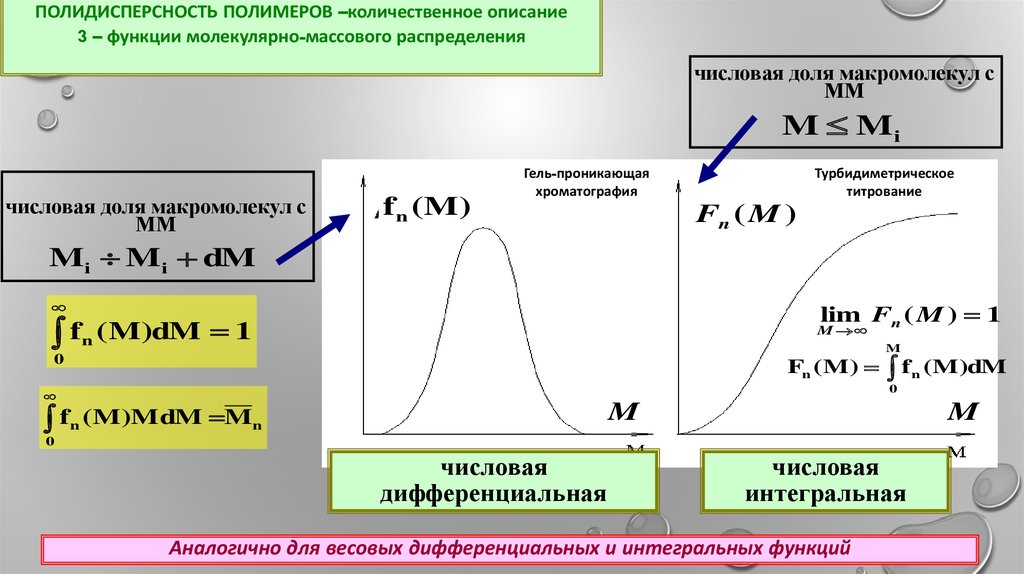
ПОЛИДИСПЕРСНОСТЬ ПОЛИМЕРОВ –количественное описание
3 – функции молекулярно-массового распределения
числовая доля макромолекул с
ММ
M Mi
числовая доля макромолекул с
ММ
f n (M)
Гель-проникающая
хроматография
Турбидиметрическое
титрование
Fn ( M )
Mi Mi dM
lim Fn ( M ) 1
fn (M)dM 1
M
Fn (M )
0
M
fn (M)dM
0
fn (M)MdM Mn
M
M
0
числовая
дифференциальная
числовая
интегральная
Аналогично для весовых дифференциальных и интегральных функций

7.

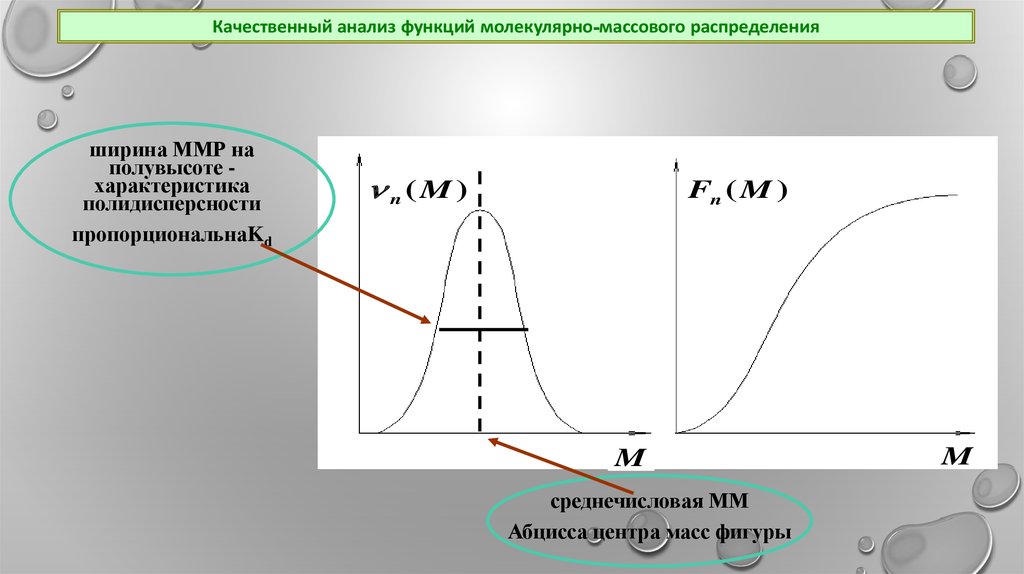
Качественный анализ функций молекулярно-массового распределения
ширина ММР на
полувысоте характеристика
полидисперсности
пропорциональнаKd
n(M )
Fn ( M )
M
среднечисловая ММ
Абцисса центра масс фигуры
M

8.

Задача №2
На рисунке приведены весовые функции молекулярно-массового распределения для двух полимеров 1 и 2.
Сравните (>, <, =, «нельзя ответить однозначно») среднечисловые и средневесовые молекулярные массы
данных полимеров, а также их коэффициенты полидисперсности.
fw (M)
Ответ:
1
M w (1) M w ( 2)
K d ( 2) K d (1)
2
M n (1) M n ( 2)
M

9.

КОНФИГУРАЦИОННАЯ ИЗОМЕРИЯ
КОНФИГУРАЦИЯ
относительное взаимное расположение атомов и атомных групп в макромолекуле,
которое задается в процессе синтеза и не может быть
изменено без разрыва связей основной цепи
1. Топологическая изомерия
2. Изомерия положения:
«голова-голова», «голова-хвост», «хвост-хвост», изомерия положения двойной связи
3. Цис-транс изомерия: цис- и транс-изомеры
4. Стереоизомерия: изо-, синдио- и атактические изомеры

10.

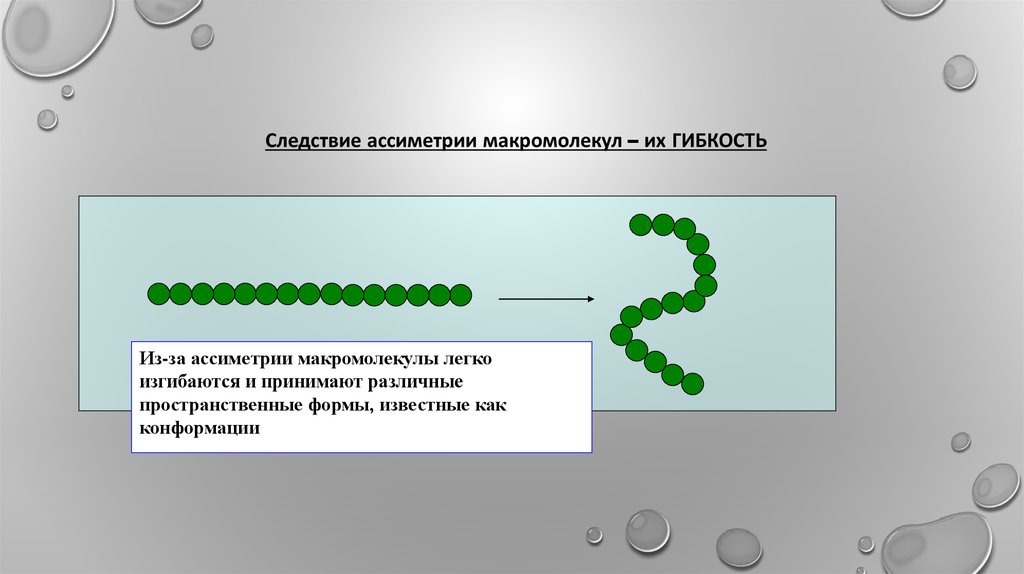
Следствие ассиметрии макромолекул – их ГИБКОСТЬ
Из-за ассиметрии макромолекулы легко
изгибаются и принимают различные
пространственные формы, известные как
конформации

11.

КОНФОРМАЦИЯ
Взаимное расположение атомов и атомных групп,
которое может быть изменено без разрыва связей
основной цепи за счет внутреннего вращения вокруг
химических связей
Конформация - это пространственная форма макромолекулы,
которую она принимает в результате теплового движения.

12.

Потеря фиксированной формы при образовании углеродной цепи
метан
этан
пропан

13.

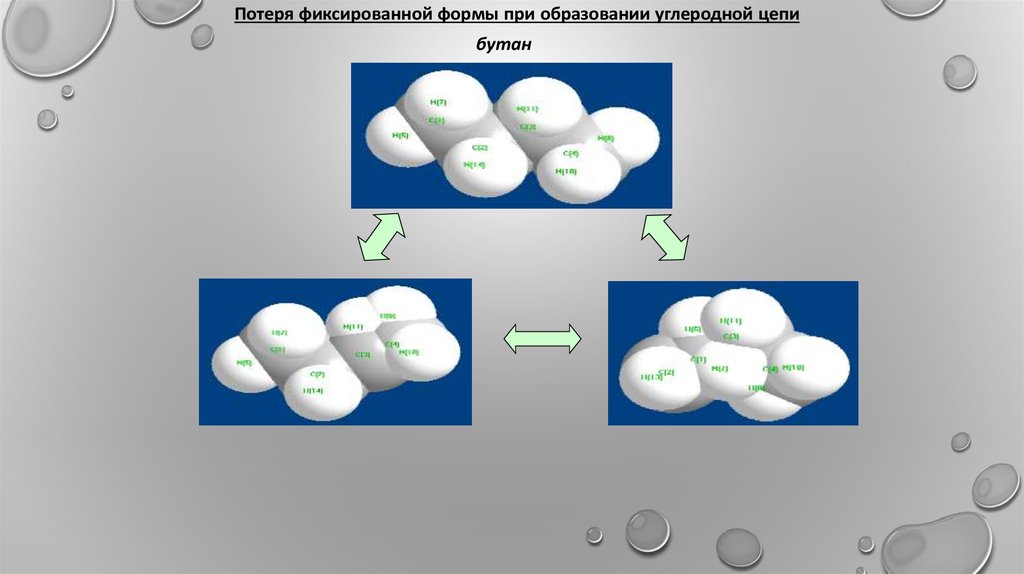
Потеря фиксированной формы при образовании углеродной цепи
бутан

14.

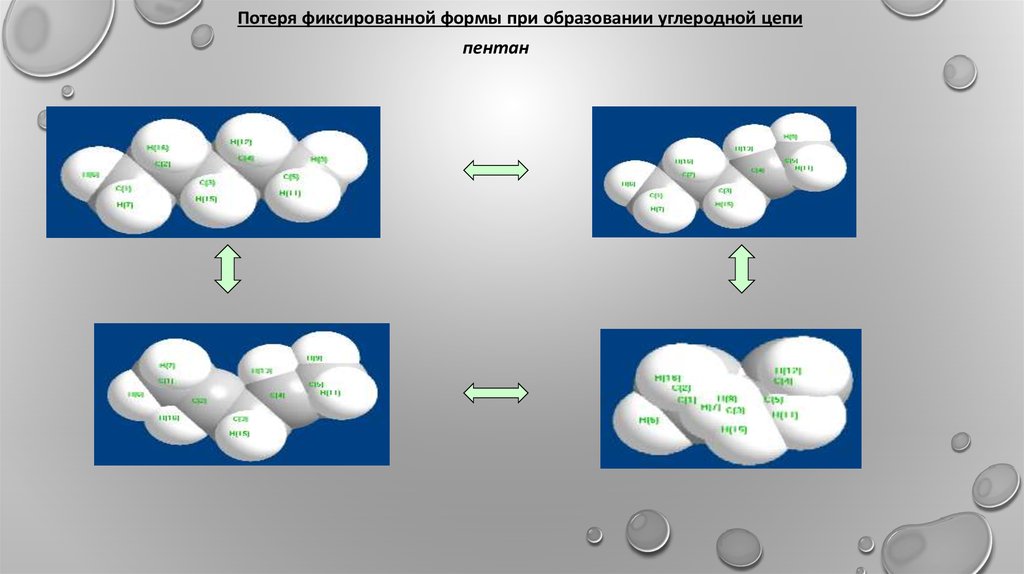
Потеря фиксированной формы при образовании углеродной цепи
пентан

15.

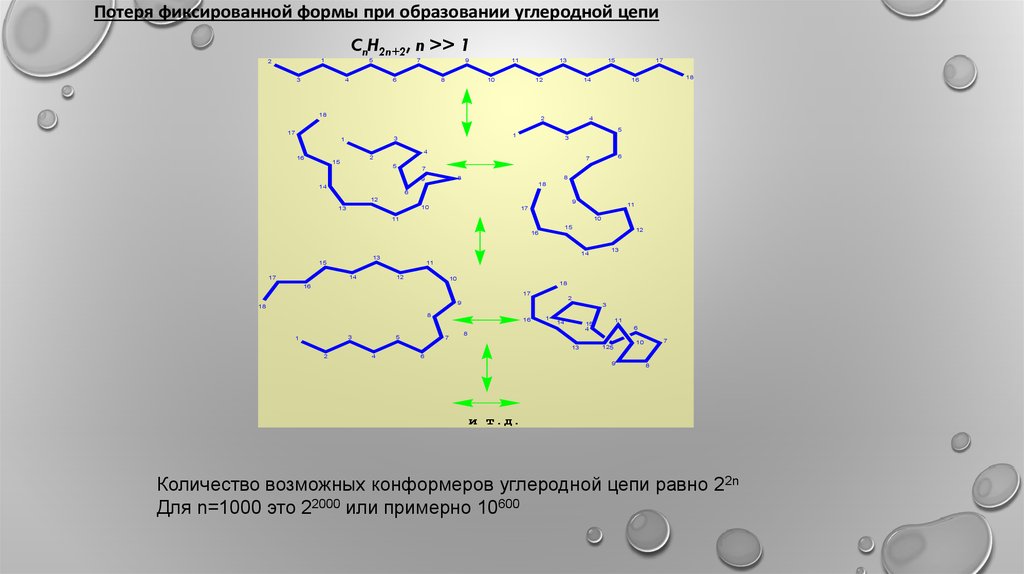
Потеря фиксированной формы при образовании углеродной цепи
CnH2n+2, n >> 1
1
2
5
3
4
7
9
6
8
11
13
10
15
12
18
17
14
2
18
16
4
5
17
1
3
1
3
4
16
2
15
6
7
5
7
8
8
9
18
14
6
12
9
10
13
11
17
10
11
15
12
16
11
14
17
12
10
18
16
17
2
9
18
3
8
3
1
5
16
7
1
14
4
11
15
4
8
13
2
13
14
13
15
6
125
7
10
6
9
8
и т.д.
Количество возможных конформеров углеродной цепи равно 22n
Для n=1000 это 22000 или примерно 10600

16.

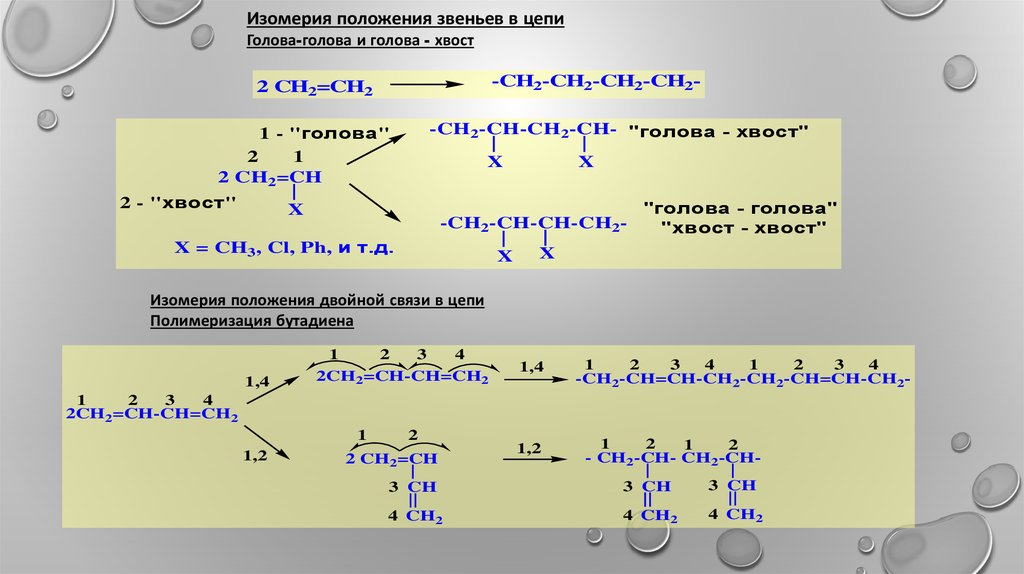
Изомерия положения звеньев в цепи
Голова-голова и голова - хвост
-CH2-CH2-CH2-CH2-
2 CH2=CH2
-CH2-CH-CH2-CH- "голова - хвост"
1 - "голова"
2
1
2 CH2=CH
2 - "хвост"
X
X
X
-CH2-CH-CH-CH2-
X = CH3, Cl, Ph, и т.д.
X
"голова - голова"
"хвост - хвост"
X
Изомерия положения двойной связи в цепи
Полимеризация бутадиена
1,4
1
2
3
4
2CH2=CH-CH=CH2
1,4
1
2
3
4
1
2
3
4
-CH2-CH=CH-CH2-CH2-CH=CH-CH2-
1
2
3
4
2CH2=CH-CH=CH2
1
1,2
2
2 CH2=CH
1,2
1
2
1
2
- CH2-CH- CH2-CH-
3 CH
3 CH
3 CH
4 CH2
4 CH2
4 CH2

17.

Цис- Транс- изомерия
1
CH2
C
3
2
H
4
CH2
C
1
CH2
120o
H
3
2
C
H
4
CH2
C
120o
H
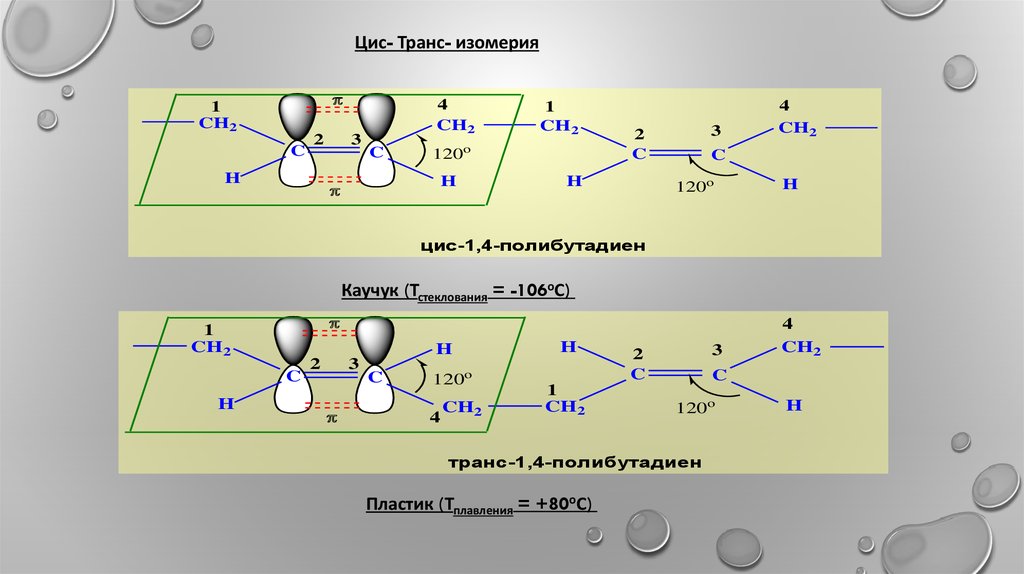
цис-1,4-полибутадиен
Каучук (Тстеклования = -106оС)
1
CH2
H
C
H
2
3
C
120o
4
CH2
H
1
CH2
3
2
C
C
120o
транс-1,4-полибутадиен
Пластик (Тплавления = +80оС)
4
CH2
H

18.

КОНФИГУРАЦИОННАЯ ИЗОМЕРИЯ
3. цис- и транс-изомеры
CH2
CH2
CH
CH2
CH
CH
CH
CH2
CH2
CH
CH2
CH2
цис - 1,4-полибутадиен
CH
CH
CH
CH2
транс - 1,4-полибутадиен

19.

Стереоизомерия
2
2
3
C
1
4
(L) или (-) энантиомер
H
4
3 C
X
3
C
4
1
(D) или (+) энантиомер
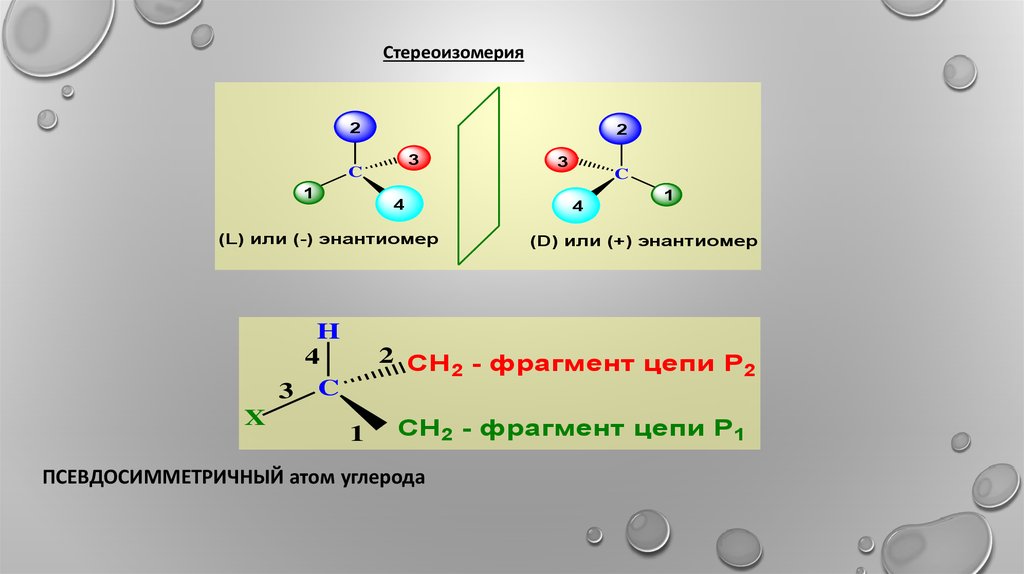
2 CH - фрагмент цепи P
2
2
1
CH2 - фрагмент цепи P1
ПСЕВДОСИММЕТРИЧНЫЙ атом углерода

20.

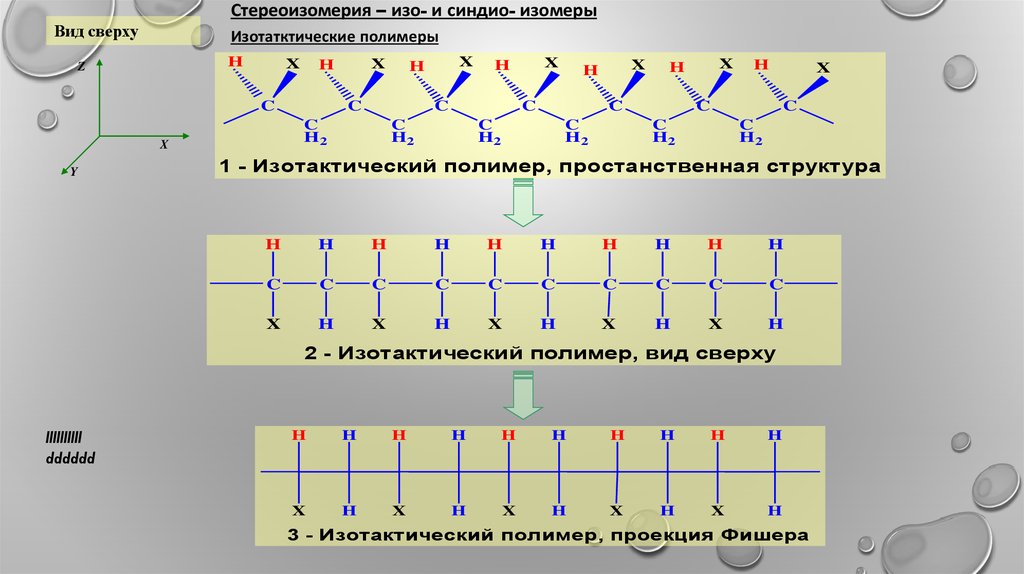
Стереоизомерия – изо- и синдио- изомеры
Вид сверху
Изотатктические полимеры
H
Z
X
C
X
H
C
X
H
C
C
H2
X
Y
X
H
C
C
H2
X
H
C
C
H2
C
H2
X
H
H
C
X
C
C
H2
C
H2
1 - Изотактический полимер, простанственная структура
H
H
H
H
H
H
H
H
H
H
C
C
C
C
C
C
C
C
C
C
X
H
X
H
X
H
X
H
X
H
2 - Изотактический полимер, вид сверху
llllllllll
dddddd
H
H
H
H
H
H
H
H
H
H
X
H
X
H
X
H
X
H
X
H
3 - Изотактический полимер, проекция Фишера

21.

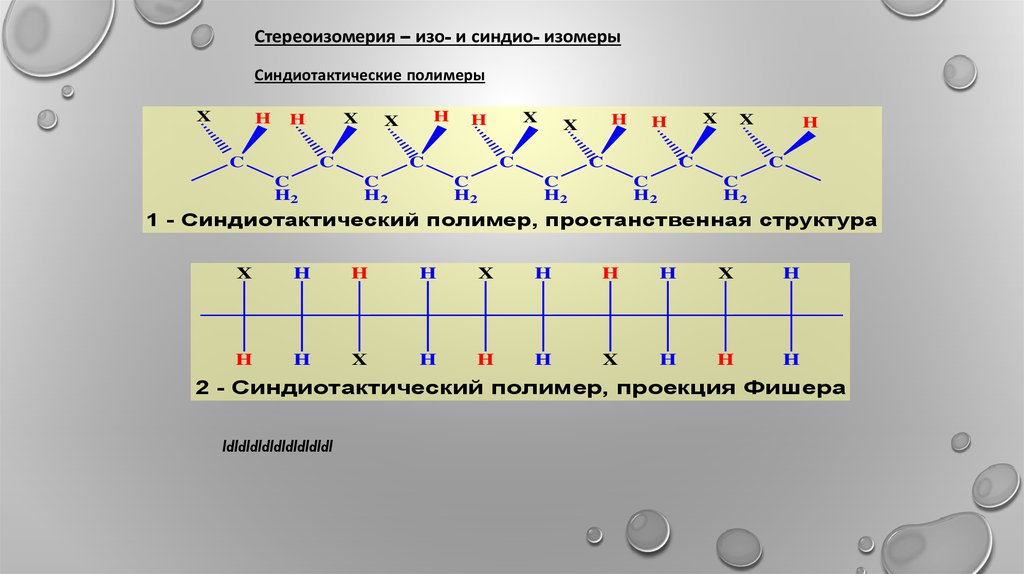
Стереоизомерия – изо- и синдио- изомеры
Синдиотактические полимеры
X
H
X
H
C
C
C
H2
H
X
C
C
H2
X
H
C
C
H2
H
X
C
C
H2
X
H
X
C
C
H2
H
C
C
H2
1 - Синдиотактический полимер, простанственная структура
X
H
H
H
X
H
H
H
X
H
H
H
X
H
H
H
X
H
H
H
2 - Синдиотактический полимер, проекция Фишера
ldldldldldldldldldl

22.

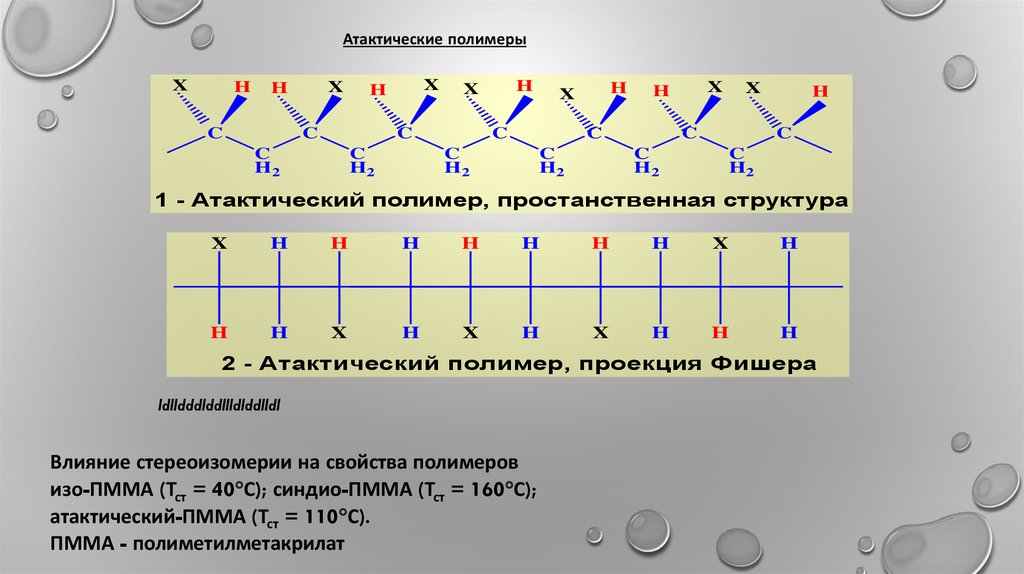
Атактические полимеры
X
H
X
H
C
X
H
C
C
C
H2
C
H2
H
X
H
X
C
C
C
H2
C
H2
X
H
X
C
C
H2
H
C
C
H2
1 - Атактический полимер, простанственная структура
X
H
H
H
H
H
H
H
X
H
H
H
X
H
X
H
X
H
H
H
2 - Атактический полимер, проекция Фишера
ldlldddlddllldlddlldl
Влияние стереоизомерии на свойства полимеров
изо-ПММА (Тст = 40 С); синдио-ПММА (Тст = 160 С);
атактический-ПММА (Тст = 110 С).
ПММА - полиметилметакрилат

23.

23

24.

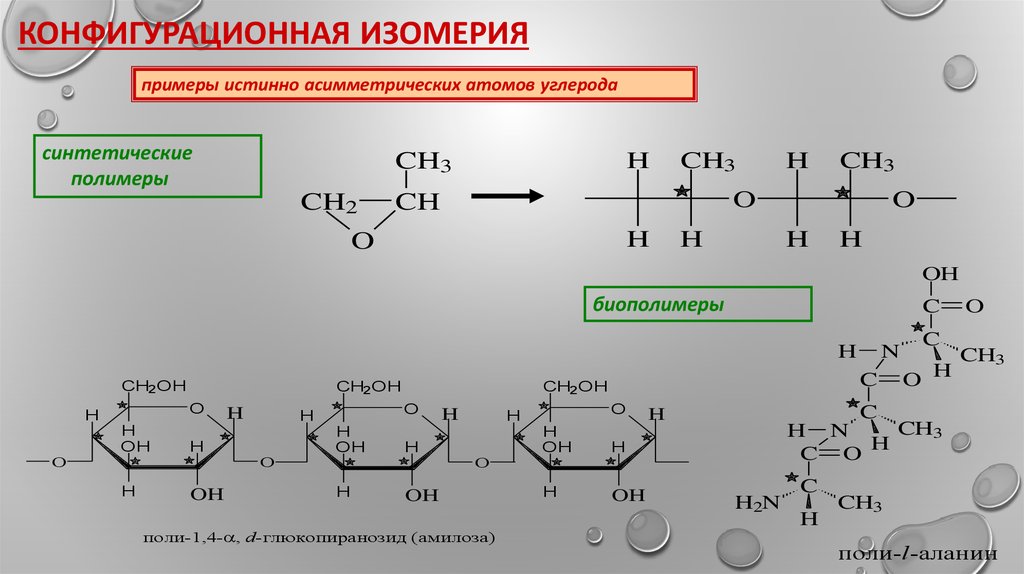
КОНФИГУРАЦИОННАЯ ИЗОМЕРИЯ
примеры истинно асимметрических атомов углерода
синтетические
полимеры
H
CH3
CH2
CH3
H
CH3
O
CH
H
O
H
O
H
H
OH
биополимеры
C
H
CH2OH
O
H
O
CH2OH
H
OH
H
H
OH
H
O
C
CH2OH
O
H
H
OH
H
H
OH
H
O
H
O
поли-1,4- , d-глюкопиранозид (амилоза)
N
H
OH
H
H
OH
C
O H
O
CH3
C
H
CH3
H N
H
C O
H2N
C
H
CH3
поли-l-аланин

25.

Задача № 3
Перечислите все возможные изомеры для полиизопрена
Ответ:
1
CH2
1
2
1
CH2
2
C
3
CH
,
CH3
1
,
3
CH
1
4
CH2 CH2
2
C
CH3
4
3
4
CH2
2
C
,
4
3
CH
CH3
4
CH2
4
CH2
Цис-, транс-изомерия
4
CH2
3
CH
H2C
C
C
CH3
CH3Изомерия
3
CH
2
CH3
CH3
CH2
C
C
H2C
CH
CH2
CH
CH2
«голова-голова»,
«голова-хвост»,
изо-, синдио- и
атактичность
CH2

26.

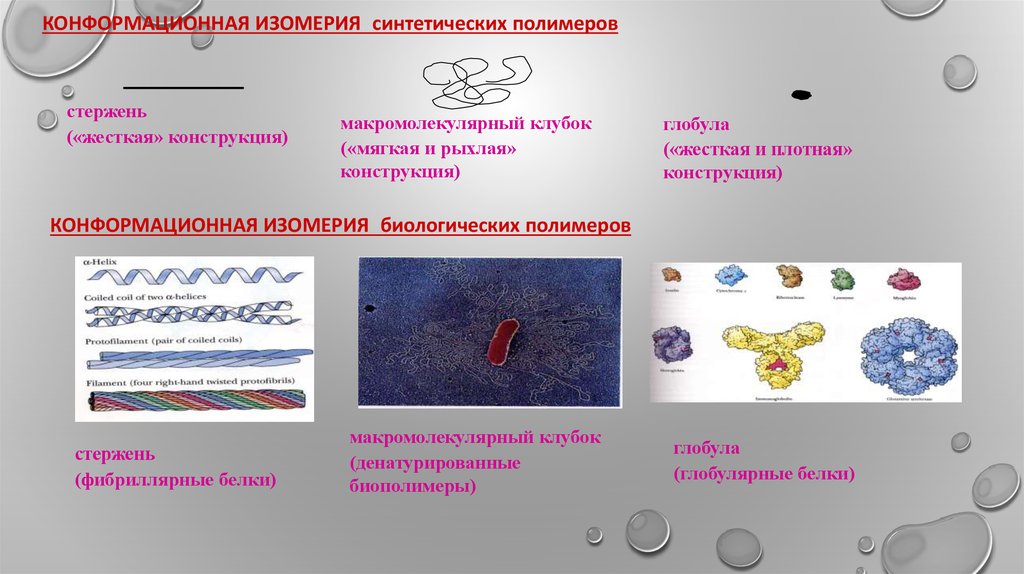
КОНФОРМАЦИОННАЯ ИЗОМЕРИЯ синтетических полимеров
стержень
(«жесткая» конструкция)
макромолекулярный клубок
(«мягкая и рыхлая»
конструкция)
глобула
(«жесткая и плотная»
конструкция)
КОНФОРМАЦИОННАЯ ИЗОМЕРИЯ биологических полимеров
стержень
(фибриллярные белки)
макромолекулярный клубок
(денатурированные
биополимеры)
глобула
(глобулярные белки)

27.

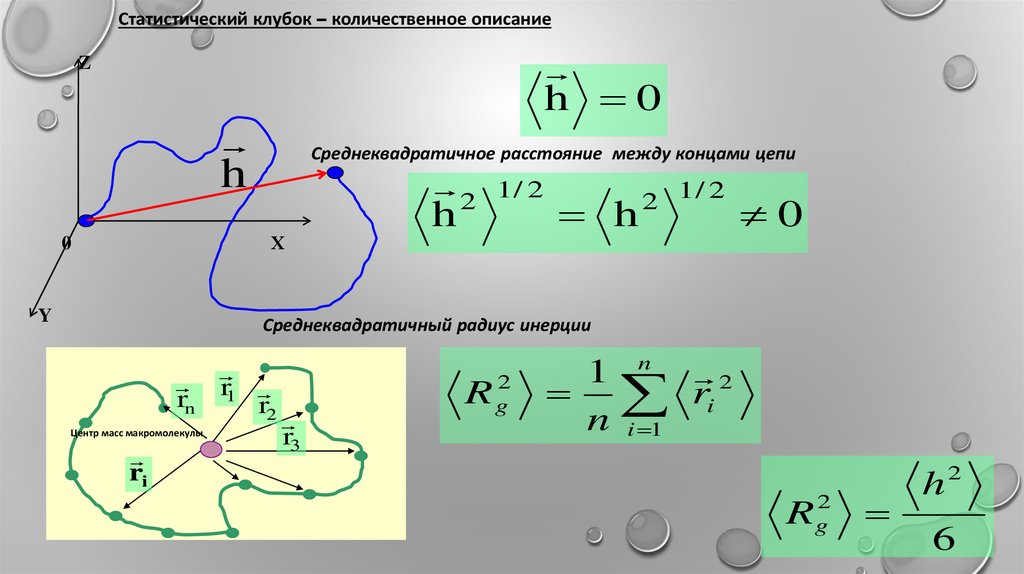
Статистический клубок – количественное описание
h 0
Z
h
Среднеквадратичное расстояние между концами цепи
Х
0
Y
2
h
1/ 2
h
2 1/ 2
0
Среднеквадратичный радиус инерции
rn
Центр масс макромолекулы
ri
r1
r2
r3
R g2
1 n 2
ri
n i 1
Rg2
h2
6

28.

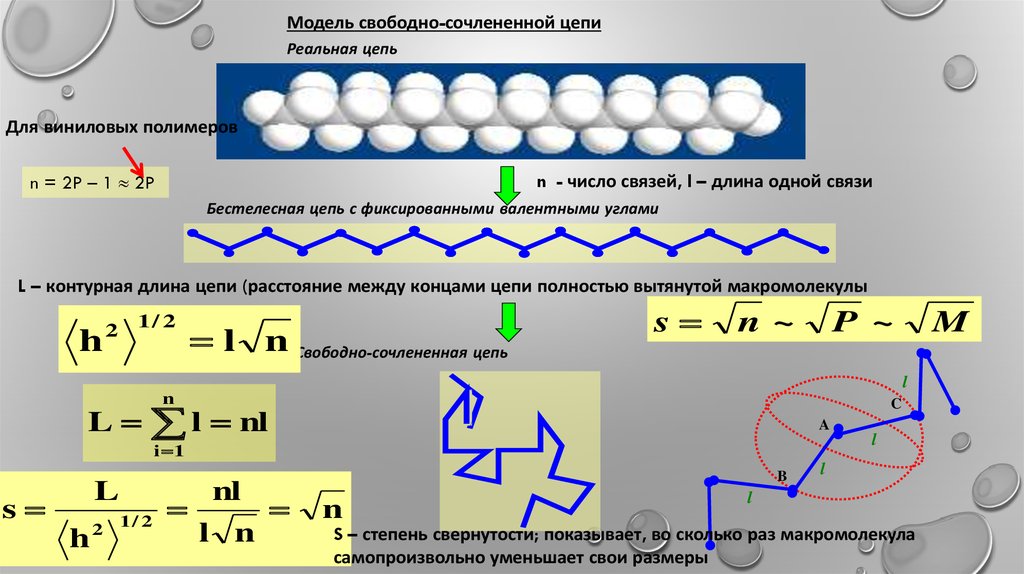
Модель свободно-сочлененной цепи
Реальная цепь
Для виниловых полимеров
n = 2P – 1 2P
n - число связей, l – длина одной связи
Бестелесная цепь с фиксированными валентными углами
L – контурная длина цепи (расстояние между концами цепи полностью вытянутой макромолекулы
h
2
1/ 2
l n Свободно-сочлененная цепь
s
n~
P ~
M
l
L
n
l nl
C
A
l
i 1
s
L
h2
1/ 2
nl
l n
B
n
l
l
S – степень свернутости; показывает, во сколько раз макромолекула
самопроизвольно уменьшает свои размеры

29.

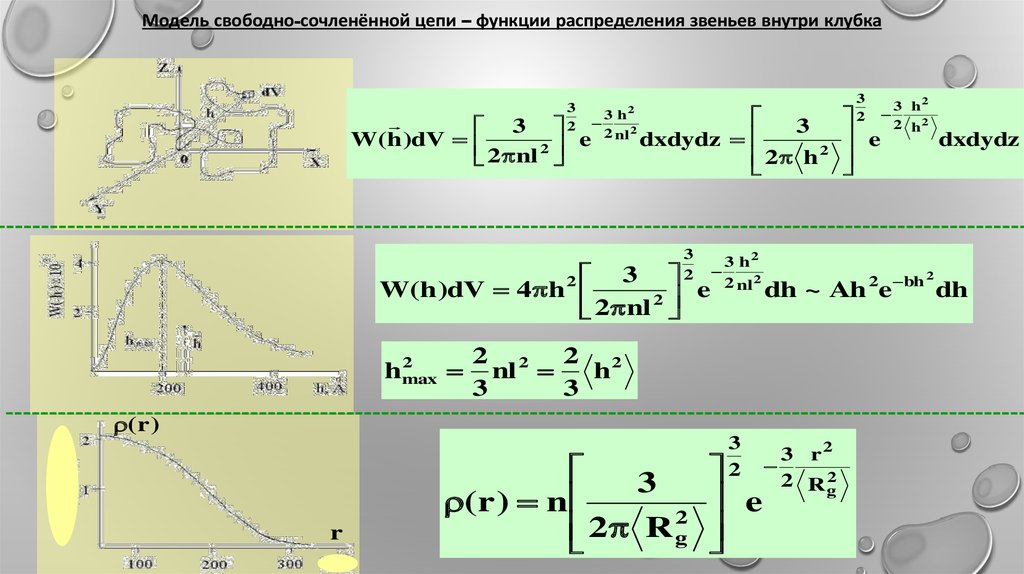
Модель свободно-сочленённой цепи – функции распределения звеньев внутри клубка
3
2
3
2
3h
3
3
2 nl 2
e
W(h )dV
e
dxdydz
2
2
2 nl
2 h
2
2
3
2
3
W(h )dV 4 h
e
2
2 nl
2
hmax
3 h2
2 nl 2
2 bh 2
dh ~ Ah e
2 2 2 2
nl
h
3
3
(r )
3
2
r
3
e
(r ) n
2
2
R
g
3 h2
2 h2
3 r2
2 R g2
dxdydz
dh

30.

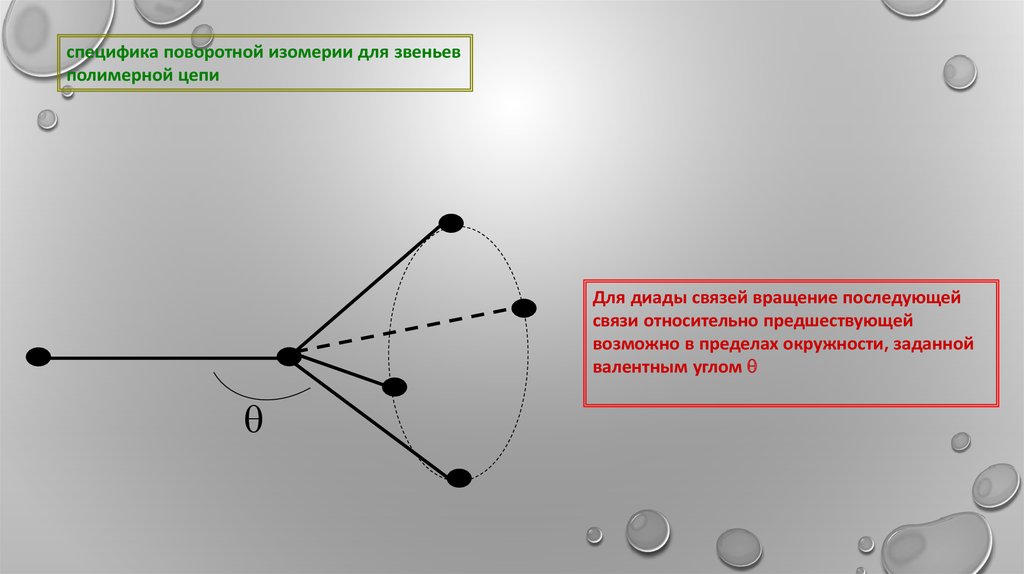
специфика поворотной изомерии для звеньев
полимерной цепи
Для диады связей вращение последующей
связи относительно предшествующей
возможно в пределах окружности, заданной
валентным углом

31.

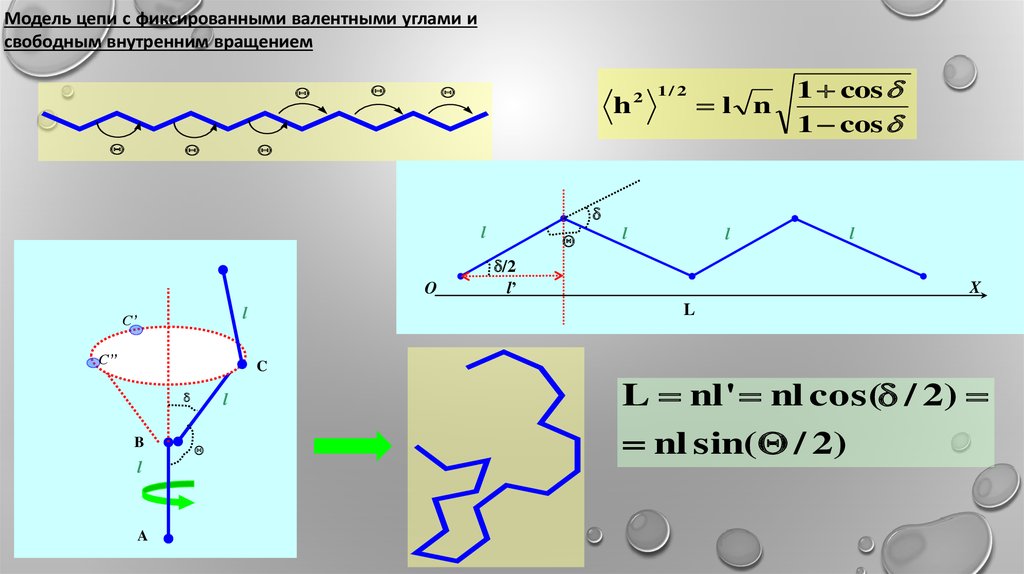
Модель цепи с фиксированными валентными углами и
свободным внутренним вращением
h
2
1/ 2
l n
1 cos
1 cos
l
O
C’’
C
B
l
A
l
l
l
/2
l’
l
X
L
l
C’
L nl ' nl cos( / 2)
nl sin( / 2)

32.

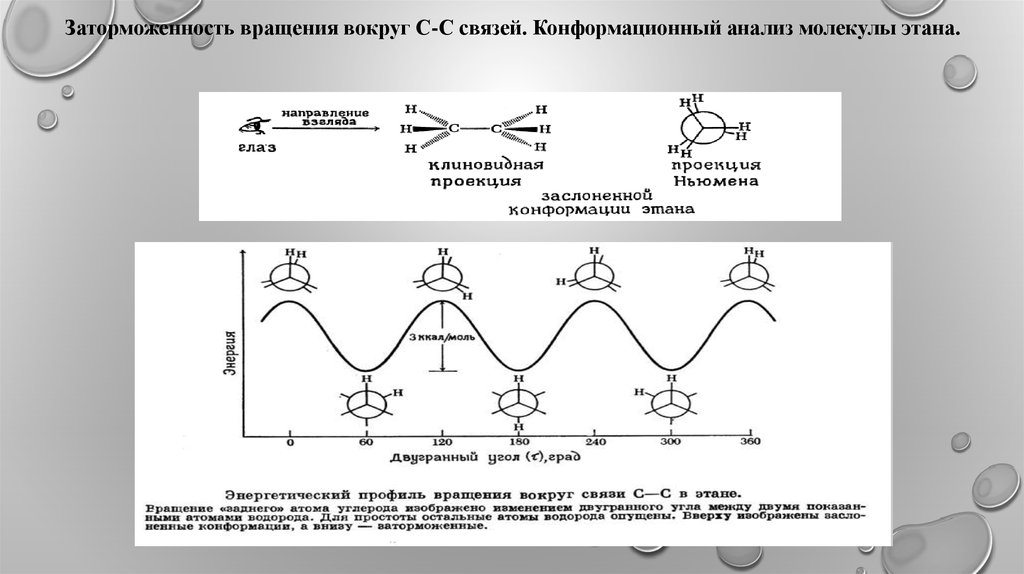
Заторможенность вращения вокруг С-С связей. Конформационный анализ молекулы этана.

33.

поворотная изомерия на примере
дихлорэтана

34.

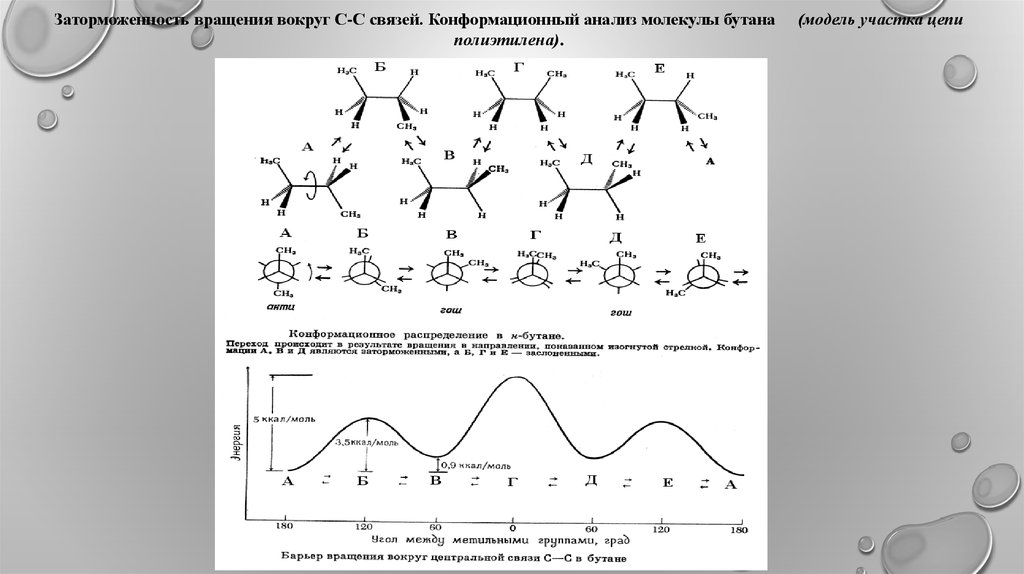
Заторможенность вращения вокруг С-С связей. Конформационный анализ молекулы бутана
полиэтилена).
(модель участка цепи

35.

Понятие персистентной длины возникает при рассмотрении модели свободносочленённой цепи с некоторыми усложнениями, а именно при учете корреляции
направлений отдельных участков цепи, разделённых некоторым расстоянием. В данной
модели рассматривается цепь, представляющая собой последовательность N шарнирно
соединенных жестких сегментов длины l каждый (если не учитывать взаимодействие
между непосредственно не связанными звеньями, то мы будем иметь дело с
идеальной цепью).
Для описания данной цепи вводится вектор R, соединяющий концы нашей цепи.
Наиболее удобной величиной является среднеквадратичное (усредненное по всем
конформациям) расстояние между концами — это простейшая характеристика
среднего размера макромолекулы. Вектор R представляет собой сумму векторов,
соединяющих между собой точки-бусинки. Вопрос о разбиении полимерной цепи на
подобные участки, когда систему можно было бы считать идеальной, и приводит к
понятию персистентной длины и связанному с ним критерию идеальности.
35

36.

Свободное вращение звеньев вокруг валентных связей ограничивается взаимодействием
функциональных групп, входящих в состав этих звеньев. Интенсивность такого ограничения
свободного вращения звеньев характеризуется величиной потенциального барьера U0. Значения
U0 пропорциональны kT, где k - константа Больцмана. Если U0 << kT, то гибкость макромолекулы
оказывается близкой к идеальной. Для многих волокнообразующих полимеров U0 < kT. Если же
U0 >> kT, то полимерная цепь обретает форму жесткого стержня.
Для характеристики гибкости реальных макромолекул часто используют понятие
"статистического сегмента".
36

37.

Вращение отдельных групп и звеньев в полимерной цепи не свободно, а заторможенно. Можно представить
себе такую модель полимерной цепи, в которой ее отдельные участки, состоящие из нескольких звеньев,
могли бы свободно вращаться. Очевидно, что величина такого участка будет больше, чём размер реального
звена. Однако в обоих случаях число возможных конформаций макромолекул будет одинаковым. Иными
словами, для удобства математического описания гибкости макромолекулы реальная полимерная цепь с
заторможенным вращением звеньев заменяется гипотетической моделью, способной принимать такое же
количество конформаций, что и реальная цепь, но построенной из свободносочлененных жестких участков сегментов.
Таким образом, статистический сегмент Куна - это математическая абстракция, мера гибкости
макромолекул, введенная для описания физических свойств полимеров законами идеальных
систем.
Чем жестче макромолекула, тем больше размер сегмента. Предельно жесткая макромолекула представляет
собой один сегмент, который включает в себя все звенья полимерной цепи. Если в результате элементарного
акта теплового движения в перемещении участвуют nK звеньев цепи макромолекулы,
37

38.

специфика поворотной изомерии для звеньев
полимерной цепи
В полимерной цепи вращение
последующей связи
относительно предшествующей
возможно в пределах сегмента
окружности, заданного углом
заторможенного внутреннего
вращения φ
φ
Вращение каждой последующей связи
относительно предшествующей определяет
гибкость макромолекулы
Макромолекула сворачивается в
макромолекулярный клубок

39.

Модель цепи с фиксированными валентными углами
и заторможенным внутренним вращением
l
C’
C
B
l
l
A
h
2
1/ 2
l n
1 cos
1 cos
Эффект кооперативности
h2
1/ 2
l n
1 cos
1 cos
1 cos
1 cos
1
1 cos
1 cos

40.

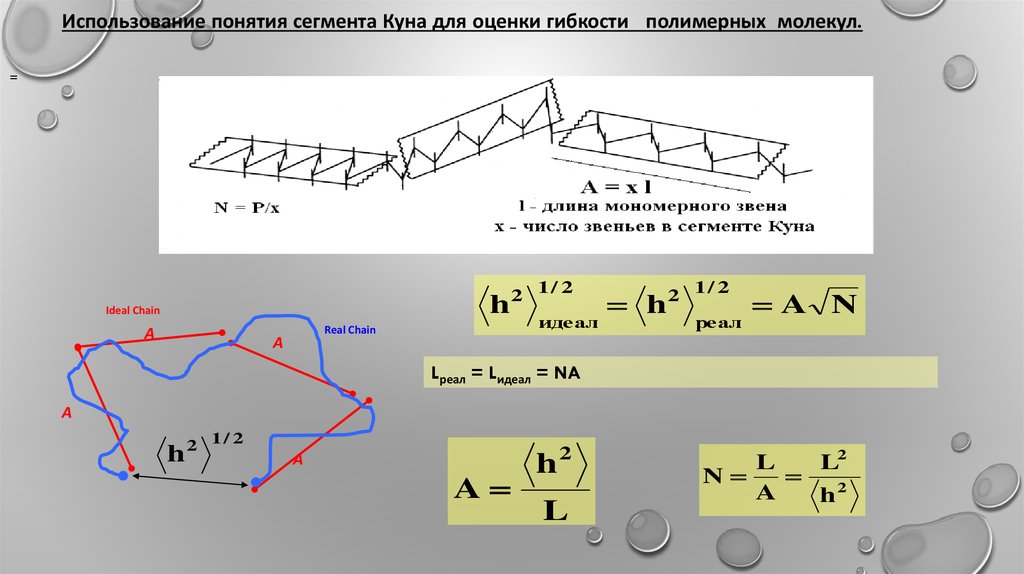
Использование понятия сегмента Куна для оценки гибкости полимерных молекул.
=
h
Ideal Chain
A
Real Chain
A
2 1/ 2
идеал
h
2 1/ 2
реал
A N
Lреал = Lидеал = NA
A
h
2 1/ 2
A
A
h2
L
L
L2
N
A
h2

41.

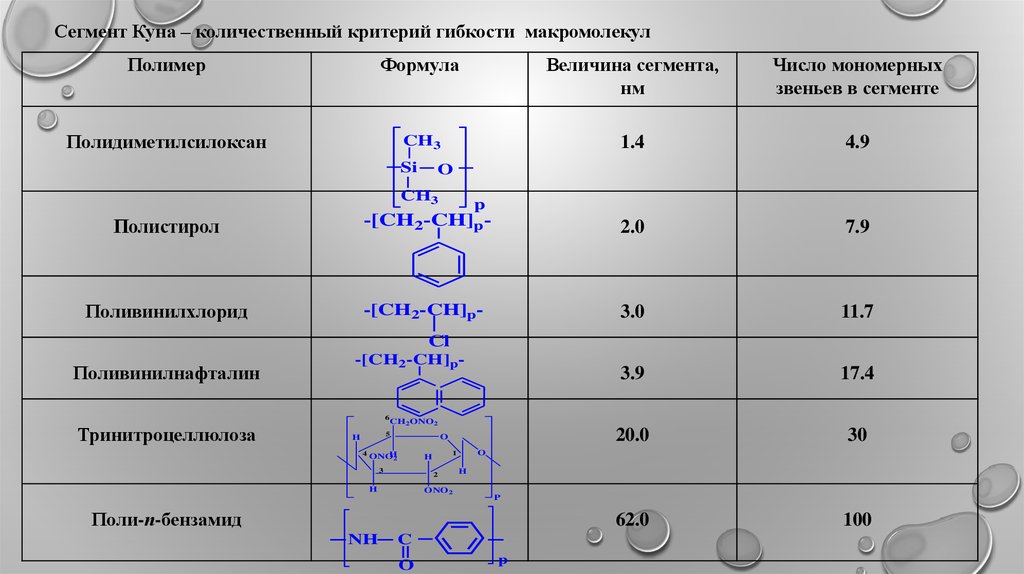
Сегмент Куна – количественный критерий гибкости макромолекул
Полимер
Формула
Величина сегмента,
нм
Число мономерных
звеньев в сегменте
Полидиметилсилоксан
CH3
1.4
4.9
Si
O
CH3
p
Полистирол
-[CH2-CH]p-
2.0
7.9
Поливинилхлорид
-[CH2-CH]p-
3.0
11.7
3.9
17.4
20.0
30
62.0
100
Cl
Поливинилнафталин
-[CH2-CH]p-
6
Тринитроцеллюлоза
CH2ONO2
5
H
O
4 ONO
H2
H
3
2
H
O
1
ONO2
H
P
Поли-п-бензамид
NH
C
O
p

42.

Задача №4
Дана макромолекула полиэтилена степени полимеризации 800. Рассчитайте:
(1) контурную длину макромолекулы;
(2) среднеквадратичное расстояние между концами цепи;
(3) степень свёрнутости исходя из:
(а) модели свободно-сочлененной цепи (длина С-С связи - 0.154 нм);
(б) модели цепи с фиксированными валентными углами и свободным внутренним врашением
(длина С-С связи – 0.154 нм; валентный угол С-С-С = 109.5о; cos(180-109.5)о = 0.334;
sin(109.5о/2) = 0.817 ;
(в) используя экспериментально установленное значения статистического сегмента Куна для
полиэтилена (длина сегмента - 2 нм, количество мономерных звеньев в сегменте - 8). Какой из
этих расчётов наиболее близок к реальности?
Ответ:
(а) L = 246. 4 нм; <h> = 6.2 нм; S = 40;
(б) L = 201. 3 нм; <h> = 8.7 нм; S = 23;
(а) L = 200 нм; <h> = 200 нм; S = 10;

43.

Кинетическая и термодинамическая гибкость
Величина U определяет
термодинамическую гибкость Чем меньше
U, тем больше термодинамическая
гибкость макромолекулы
Величина U0 определяет кинетическую
гибкость. Чем меньше U0, тем больше
кинетическая гибкость макромолекулы