Контактные явления

1. Твердотельная электроника

Электронный учебно-методический
комплекс
Твердотельная электроника
Презентации к лекционному курсу
Контактные явления
МОСКВА
2016
НИУ «МЭИ»

2. Барьер на границе металла с полупроводником (барьер Шоттки)

qX S Eвак Ec
Eвак F

3.

Работа выхода равна разности между энергией
покоящегося электрона в вакууме у поверхности
образца полупроводника и уровнем Ферми в данном
полупроводнике.

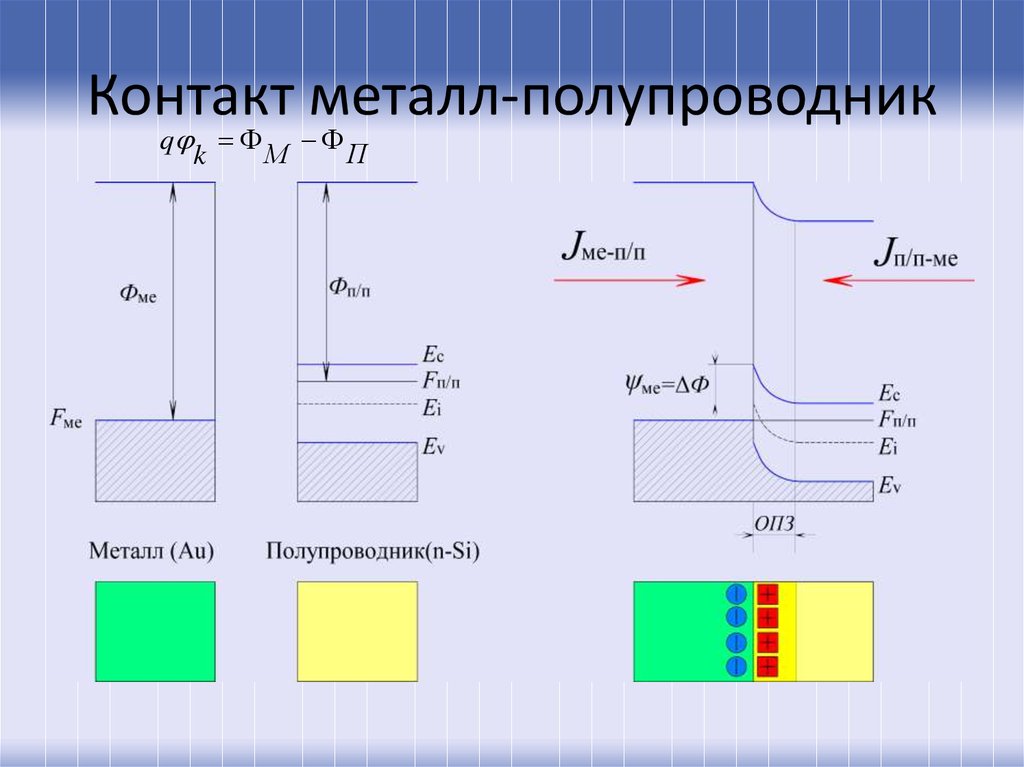
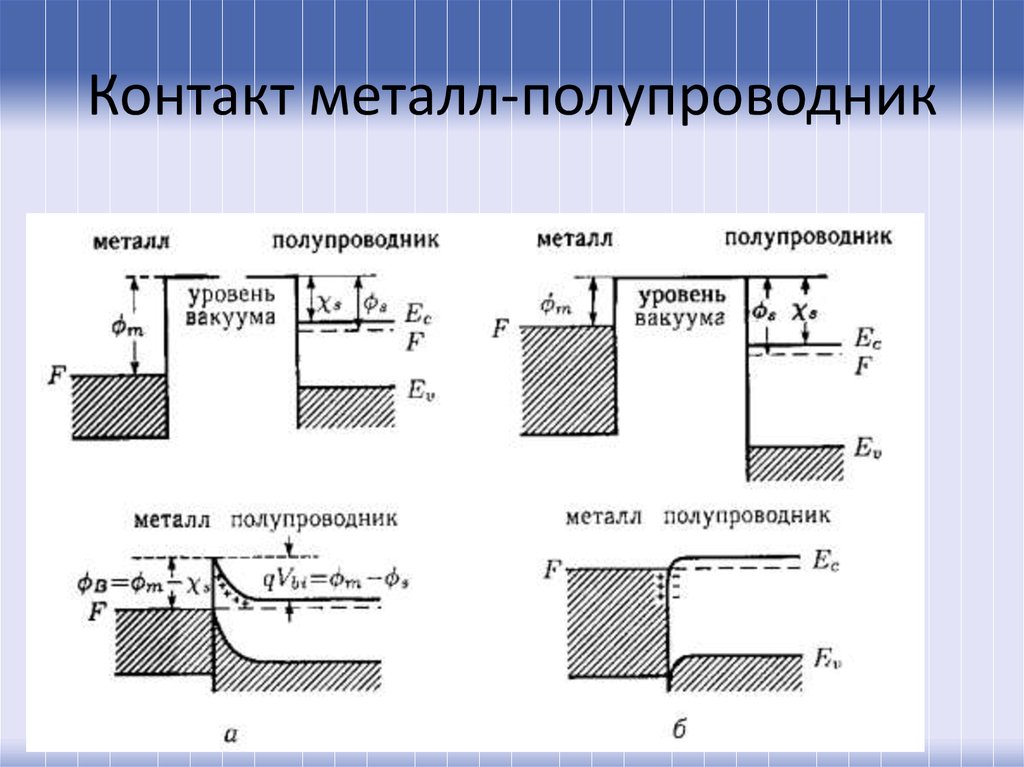
4. Контакт металл-полупроводник

q
М
П
k

5. Контакт металл-полупроводник

6. Контакт металл-собственный полупроводник

ФП ФМ
ФП ФМ

7. Контакт металл-электронный полупроводник

ФП ФМ
ФП ФМ

8. Контакт металл-дырочный полупроводник

ФП ФМ
ФП ФМ

9.

Без смещения:
W0
2 0 k
q Nd
m
2 q N d k
0

10.

Со смещением:
2 0 k Vсм
W
q Nd
2 q N d k V
m
0

11. Сила изображения

q2
E пот x
16 0 x

12. Сила изображения

• Если теперь вблизи границы раздела металл –
вакуум имеется электрическое поле , то
выражение для энергии электрона на расстояния
х приобретает вид:
2
q
Eпот x
q x x
16 0 x

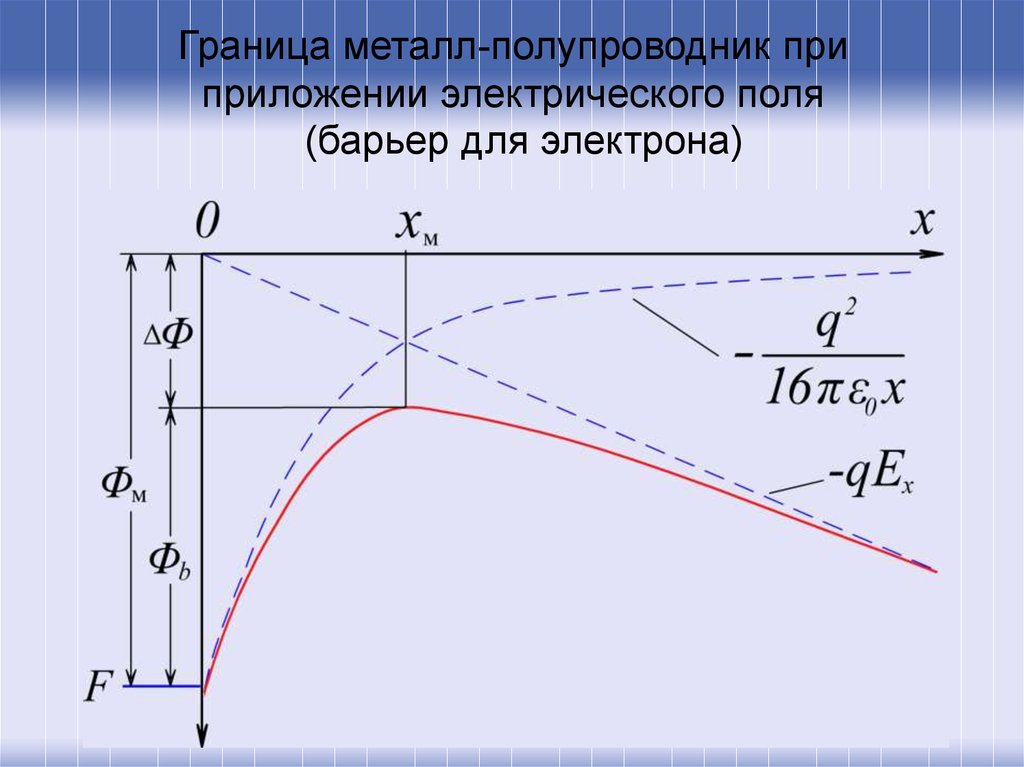
13. Граница металл-полупроводник при приложении электрического поля (барьер для электрона)

14. Граница металл-полупроводник при приложении электрического поля (барьер для электрона)

• Эта функция имеет максимум в точке хm. Его
положение можно определить из условия
d E x
0
dx
q
xm
0
16 0
• где в качестве обычно принимается
максимальное электрическое поле в обедненной
области. Контактное электрическое поле
понижает высоту барьера на величину 0,01-0,04
эВ.

15. Прямое и обратное смещение перехода металл-полупроводник

16.

Важно подчеркнуть, что внешнее напряжение
может только выпрямить границы разрешенных
зон .
Другими словами, при приложении больших
прямых смещений электроны начнут «убегать» от
батареи смещения и все зоны будут наклоняться.

17.

18. Расчет ВАХ барьера Шоттки

При приложении напряжения:
2 0 k Vсм
W
q Nd
где
J J п.п
V
T
Jм Js e
1
Ub
J s A T 2 e T
4 mn* q k 2
mn*
A
120
3
h
m0
А
см 2 K 2 - Постоянная Ричардсона

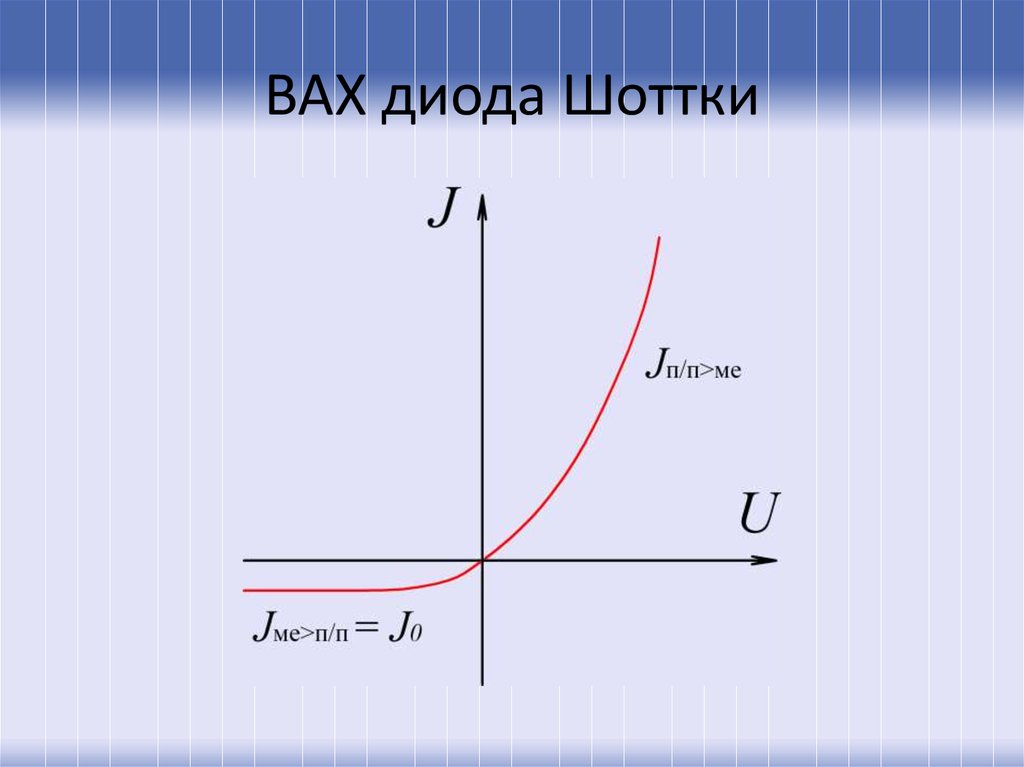
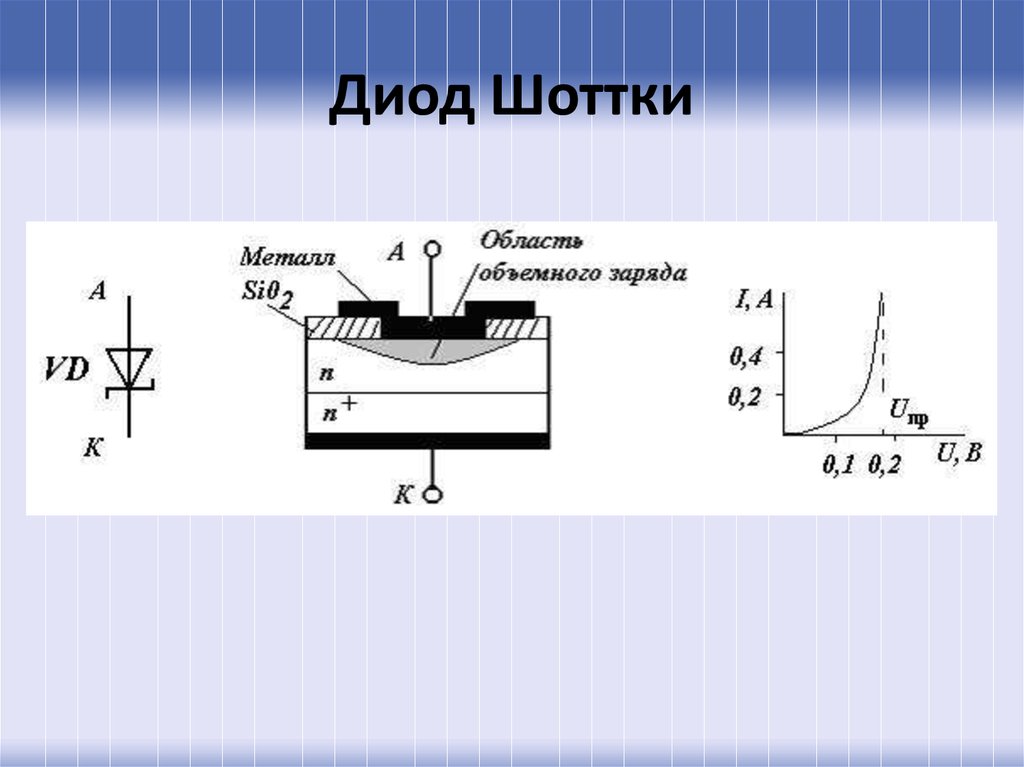
19. ВАХ диода Шоттки

20. Диод Шоттки

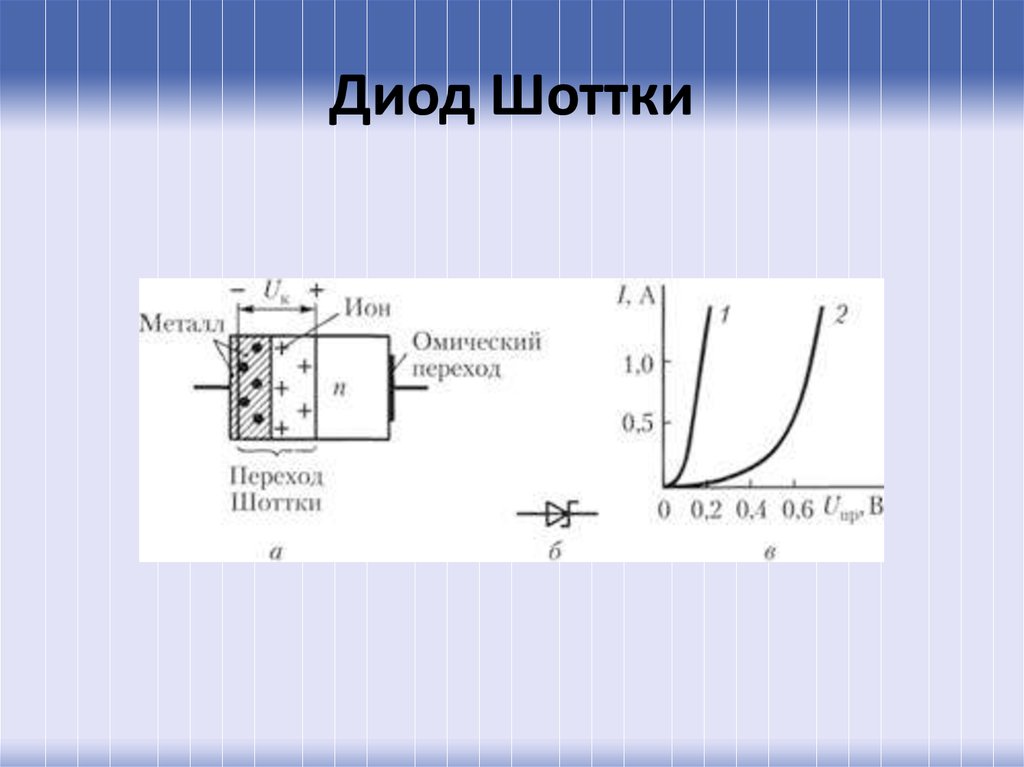
21. Диод Шоттки

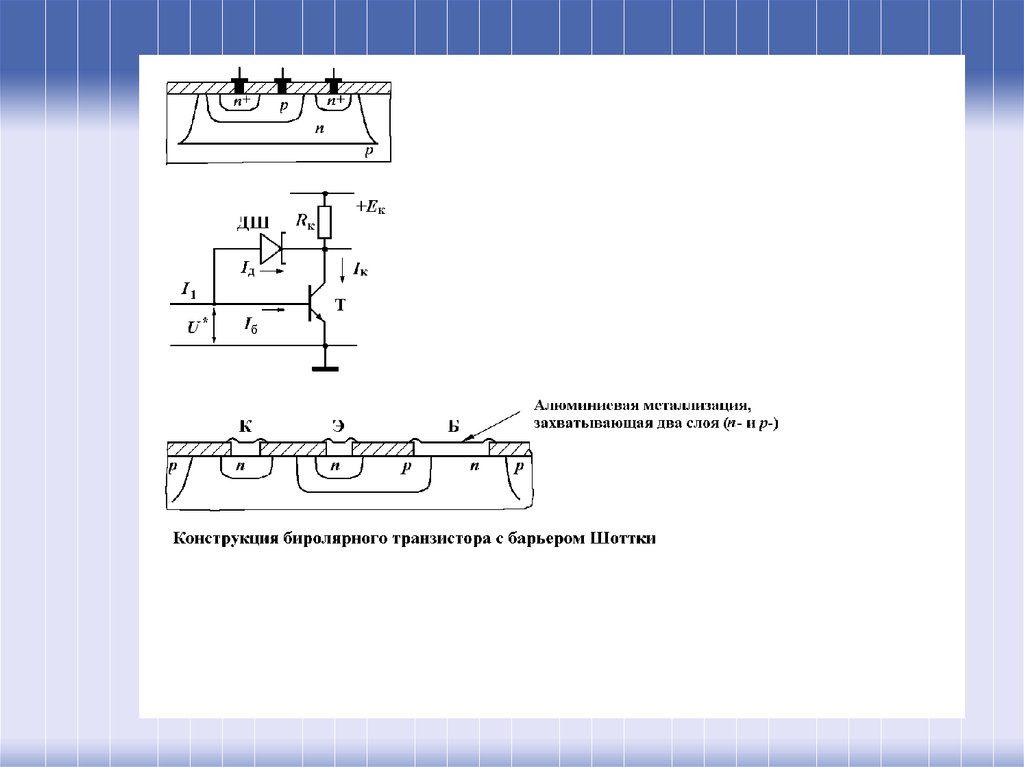
22.

• ДШ характеризуются быстрой
рекомбинацией инжектированных
носителей (время жизни носителей крайне
мало), а значит и высоким
быстродействием. Благодаря
минимальному сопротивлению базы и
отсутствию процессов накопления и
рассасывания избыточных зарядов,
быстродействие получается достаточно
высоким: граничная частота fгр = 1010 Гц.

23.

24.

25.

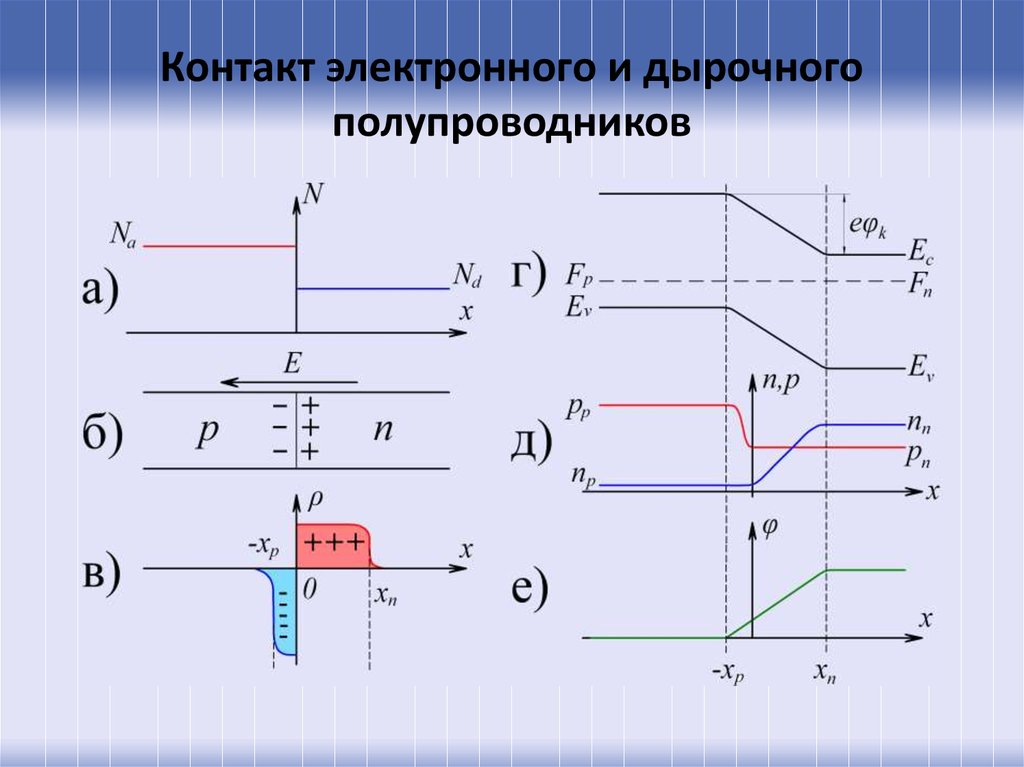
Контакт электронного и дырочного
полупроводников

26. Возникновение потенциального барьера. Контактная разность потенциалов

27. Контакт электронного и дырочного полупроводников

28.

29.

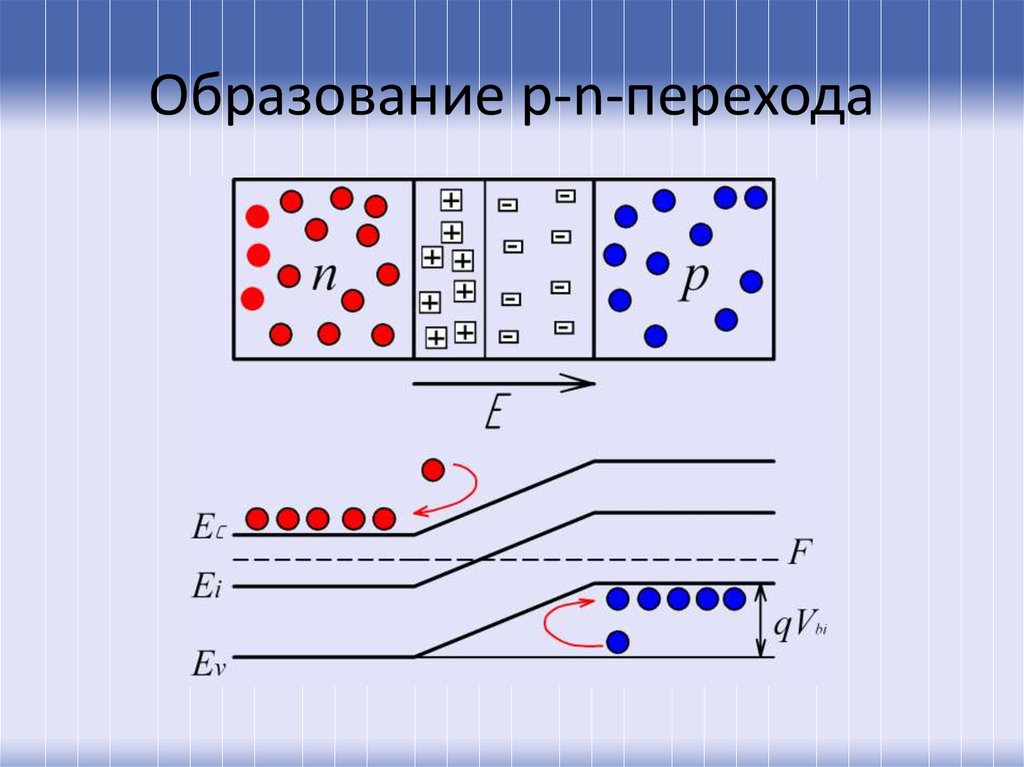
30. Образование p-n-перехода

31.

Перераспределение носителей, образовавшееся при
контакте, и формирование потенциального барьера
высотой q k приводит к тому, что диффузионный
поток основных носителей ( n n и p p ) прекращается.
Энергетический барьер существует именно для
основных носителей, потенциального барьера для
неосновных носителей ( pn и n p ) нет

32.

Для того чтобы рассчитать распределения
концентраций
свободных
носителей
в
приповерхностной области необходимо решить
уравнение Пуассона, устанавливающее связь между
распределением потенциала и пространственного
заряда ρ(x):

33. Решение уравнения Пуассона

34.

Толщина ОПЗ
Wp
Wn
Na
Nd
;
W0 N d N a W0 N d N a
k
q
2 0 s
N W
d
2
n
N aW
2
p
Nd Na
W
2 0 s
Nd Na
2 0 s
Nd Na
W0
k
q
Nd Na
q
2
0

35.

Чем выше степень легирования n- и pобластей полупроводника, тем меньше
толщина ОПЗ. Если одна из областей
легирована значительно сильнее другой, то
большая часть падения потенциала приходится
на высокоомную область

36. Определение контактной разности потенциалов

37.

Потенциальный барьер в pn-переходе тем выше,
чем сильнее легированы p- и n-области. По мере
роста
температуры
величина n 2 возрастает.
i
Выражение под знаком логарифма стремится к
нулю, т.е. контактная разность потенциалов с
ростом температуры уменьшается.
При высоких температурах начинает доминировать
собственная проводимость как в p-, так и в nобласти, при этом в каждой из областей уровень
Ферми стремится к середине запрещенной зоны и q k
стремится к нулю.

38.

Связь концентрации носителей с
pn n p
q k
exp
p p nn
kT
q k
p n p p exp
kT
k
exp
Т
k
p p exp
Т
k
k
q k
n p nn exp
nn exp
kT
Т

39. Рассмотрим теперь pn-переход, к которому приложено прямое смещение Vсм (минус батареи к n-типу, плюс – к p-типу).

Допустим, что все приложенное внешнее напряжение падает
на pn-переходе.
При прямом смещении высота потенциального барьера
понижается на qVсм по сравнению с равновесным
состоянием, соответственно изменяется и толщина ОПЗ:
2 0 s
Nd Na
Wпр
k Vсм
q
Nd Na

40.

Понижение потенциального барьера приводит к
увеличению потока основных носителей заряда по
сравнению с равновесным состоянием. Под действием
диффузионных процессов основные носители ( n n и p p )
перемещаются в соседнюю область, становясь
неосновными носителями ( p n и n p ).
Образовавшийся градиент концентрации неосновных
носителей приводит к появлению диффузионных токов
неосновных носителей заряда, он направлен от ОПЗ
вглубь полупроводника. При этом направления
диффузионных токов, создаваемых p n и n p совпадают,
в то время как их потоки направлены в разные стороны.

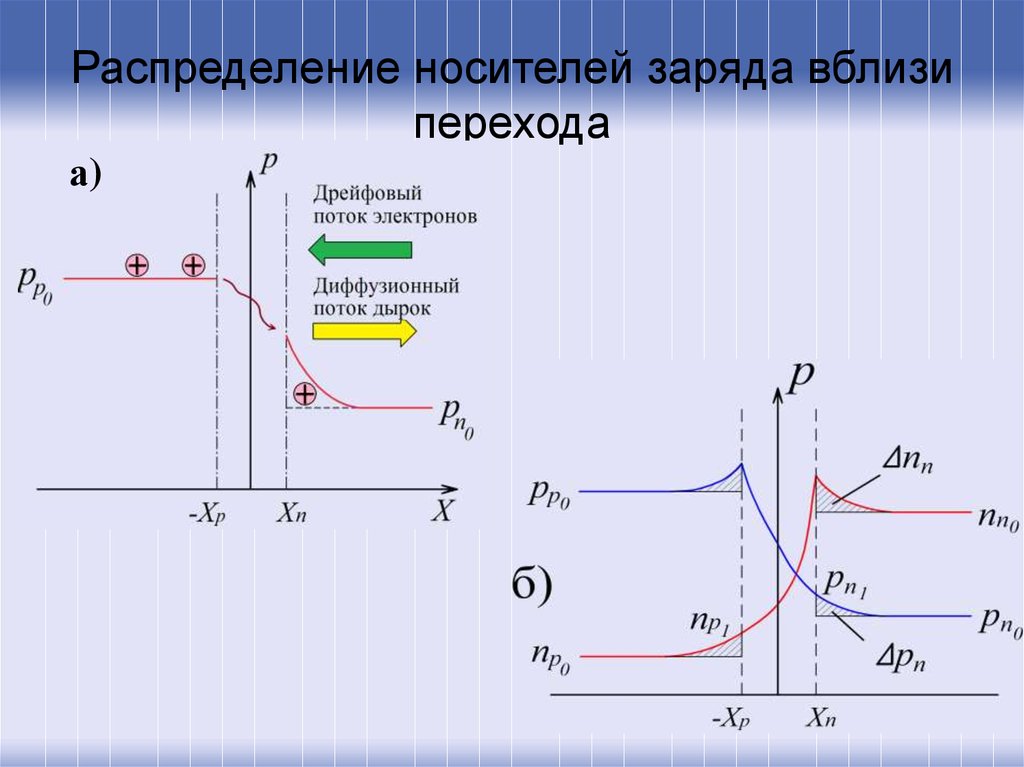
41. Распределение носителей заряда вблизи перехода

а)

42.

Введение в полупроводник носителей заряда с
помощью pn-перехода при подаче на него
прямого смещения в область, где эти носители
заряда являются неосновными, называют
инжекцией.
Концентрация дырок в n-области вблизи контакта
будет равна:
pn p n 0 p

43.

Для ее нахождения в стационарном случае на
границе с ОПЗ (при х Wn ) нужно вместо q k
q k Vсм
использовать значение
( k Vсм )
Vсм
p no exp
p n Wn p p exp
T
T
Концентрация неосновных носителей в
низколегированной области (базе) зависит от
концентрации носителей в высоколегированной
области (эмиттере) и от напряжения
смещения, приложенного к
pn-переходу

44. Распределение неосновных носителей в базе

p n Wn p n p n 0
Vсм
p no exp
1
T

45.

Аналогичные явления происходят в p-области: сюда из nобласти инжектируются электроны и концентрация
избыточных электронов при x=-Wp составит:
Vсм
n p W p n po exp
1
T

46.

Если к pn-переходу приложено обратное смещение
(минус батареи к p-типу, плюс – к n-типу), потенциальный
барьер повышается на q k . Толщина слоя ОПЗ
увеличивается:
2 0 s
Nd Na
Wобр
k Vсм
q
Nd Na

47.

Чем сильнее переход смещен в обратном направлении,
тем выше потенциальный барьер, и тем меньшее
количество основных носителей заряда способно
преодолеть возросший потенциальный барьер. В
соответствии с этим количество неосновных носителей
заряда в приконтактной области уменьшается по
сравнению с равновесным состоянием, следовательно,
уменьшается и количество основных носителей заряда
вследствие соблюдения электронейтральности. Это
явление носит название экстракции носителей заряда

48.

Таким образом, при обратном смещении pn-перехода ток
основных носителей заряда будет меньше, чем при
равновесном состоянии, а ток неосновных носителей
заряда практически не изменится. Поэтому суммарный
ток через pn-переход будет направлен от n-области к pобласти и с увеличением обратного напряжения вначале
будет незначительно расти, а затем стремиться к
некоторой величине, называемой током насыщения Js.

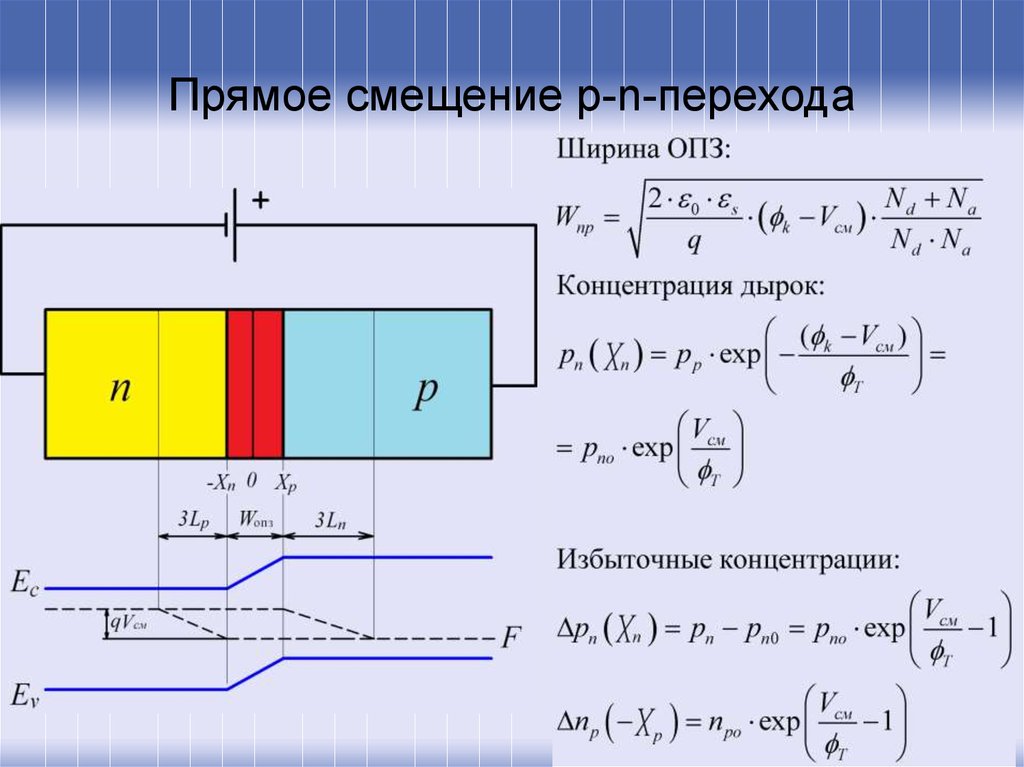
49.

Прямое смещение p-n-перехода

50.

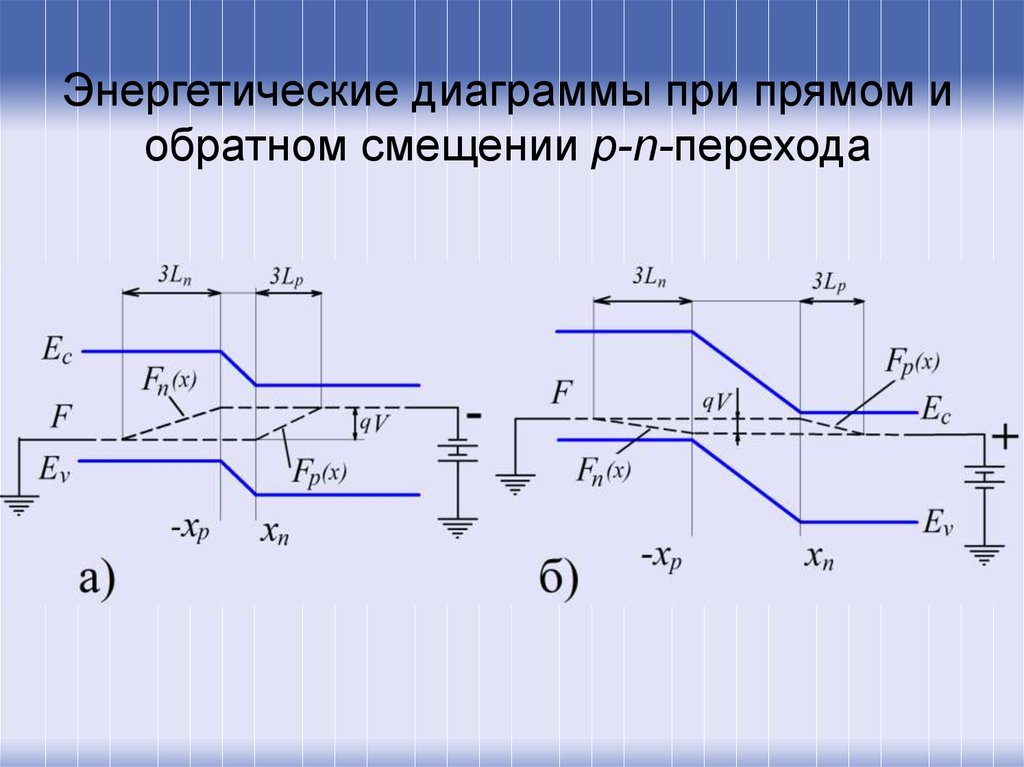
Энергетические диаграммы при прямом и
обратном смещении p-n-перехода

51. Идеальная МДП–структура

Если на окисел, покрывающий поверхность кристалла,
нанести металлический электрод (затвор), то, изменяя его
потенциал относительно объема кристалла, возможно изменять
величину заряда в приповерхностной области полупроводника
и, соответственно, её проводимость.
Этот эффект положен в основу целого ряда
полупроводниковых устройств, среди которых самое
известное – МДП-транзистор.

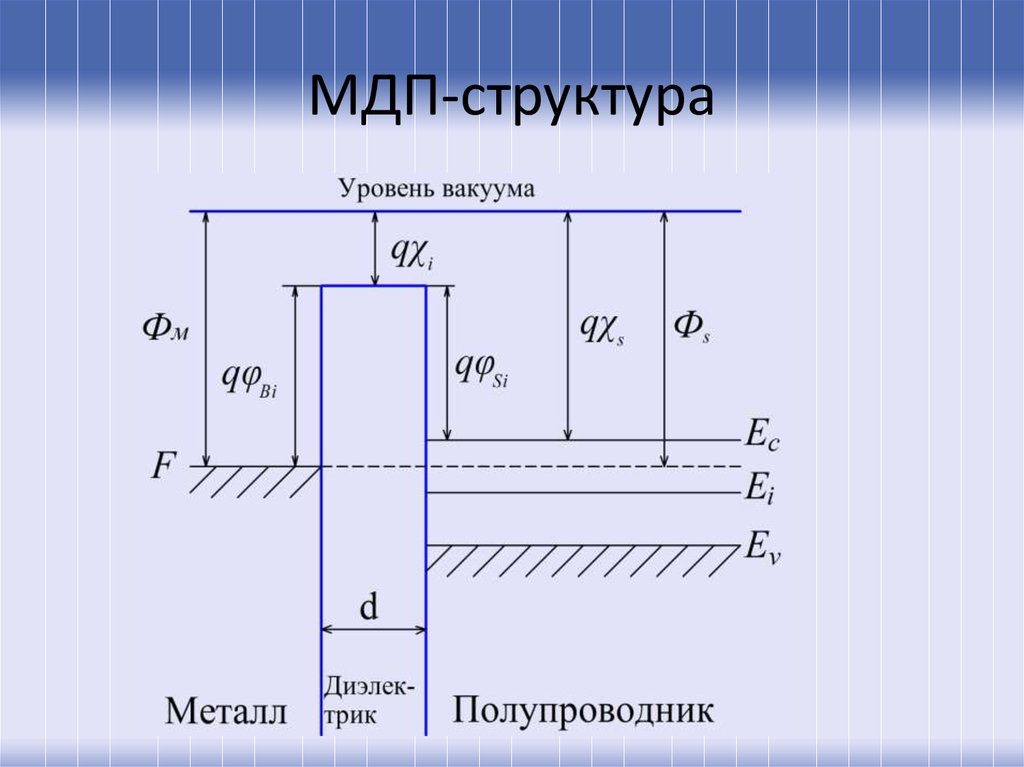
52.

МДП-структура

53. МДП-структура

54.

• На границе металл-диэлектрик,
диэлектрик-полупроводник, а в отсутствии
диэлектрика на границе металлполупроводник возникает контактная
разность потенциалов:
q
1
2
k

55. Обогащение

n-тип

56. Обеднение

p-тип
n-тип

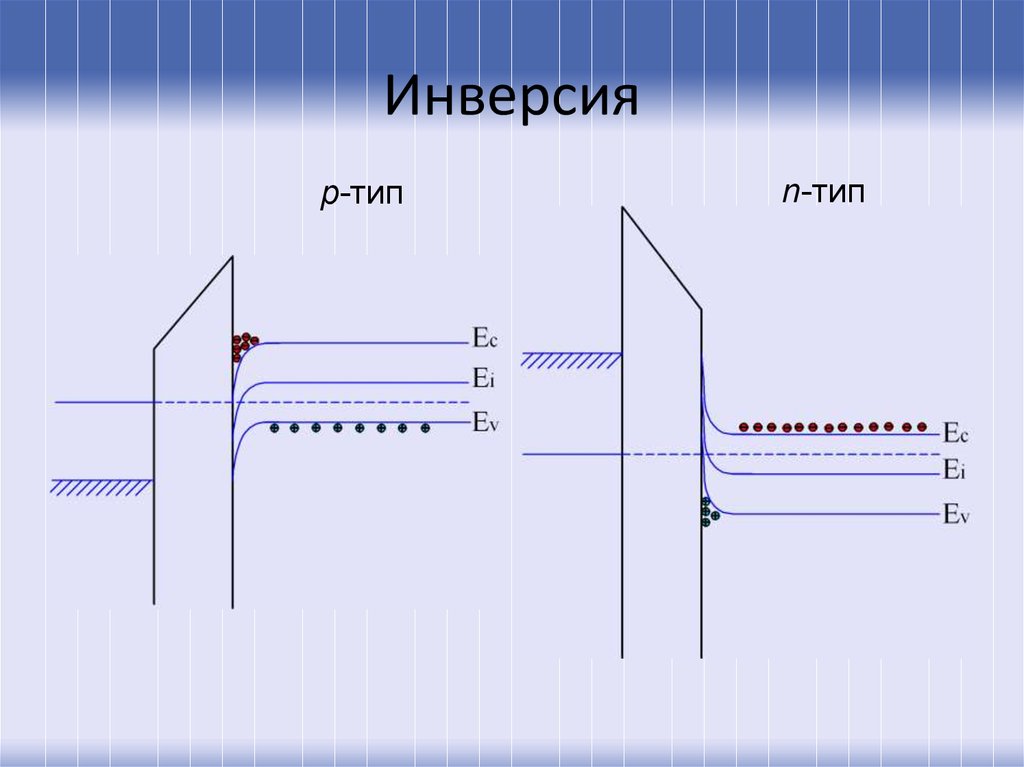
57. Инверсия

p-тип
n-тип

58. Допущения для «идеальной» МДП-структуры

• Разность работ выхода между металлом затвора и
диэлектриком, диэлектриком и полупроводником, равна
нулю.
• Диэлектрик является идеальным изолятором.
• В диэлектрике и на границах раздела металл-диэлектрик и
полупроводник-диэлектрик нет никаких зарядов, т.е.
диэлектрик не имеет дефектов.
При любых смещениях в структуре могут существовать
только заряд в ее полупроводниковой части и равный ему
заряд противоположного знака на металлическом
электроде, отделенном от полупроводника слоем
диэлектрика.

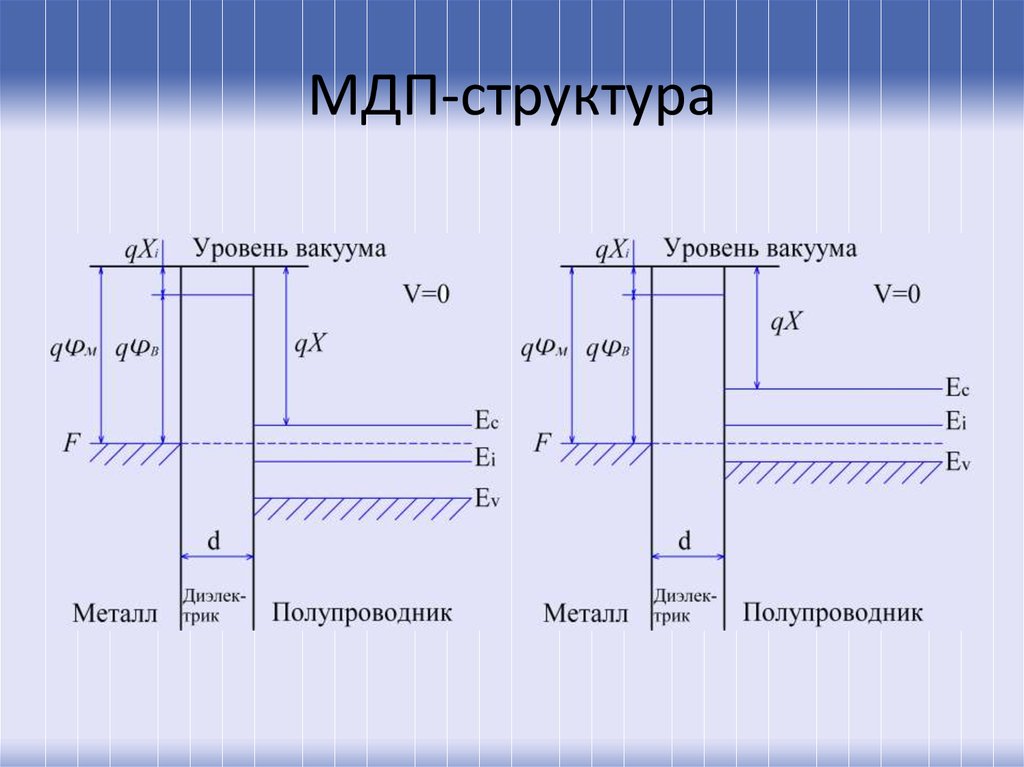
59. МДП-структура

60. Для характеристики изгиба будем использовать понятие поверхностного потенциала φs

ρ x q N a
2 x
E x
2
x
s 0
0 s
x
0
d
0 при х w
dx
q N a
2
x w
2 s 0
q N a w 2
s
2 s 0

61. Расчет параметров

62. К расчету МДП-структуры

(4.6)
(4.7)
(4.8)
(4.9)
(4.10)
(4.11)
(4.12)

63. Емкость барьера Шоттки

0 q Nd 0 S
C S
2 k Vсм
L
k Vсм
q 0 Nd S
2C 2
2

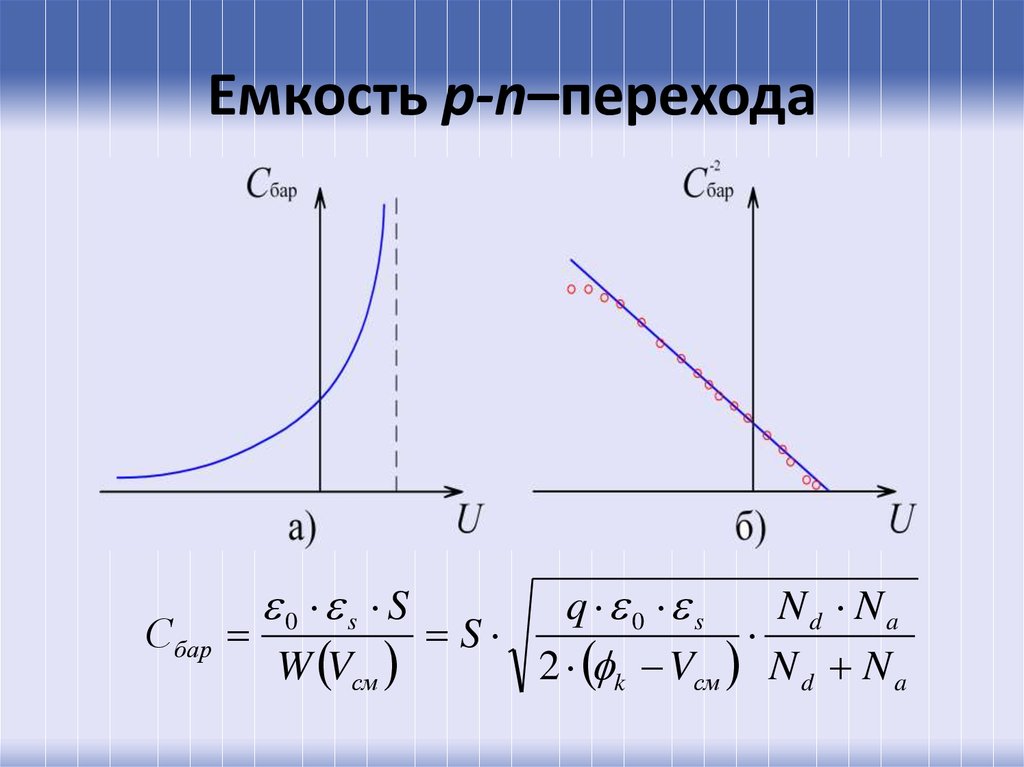
64. Емкость p-n–перехода

Сбар
0 s S
W Vсм
q 0 s
Nd Na
S
2 k Vсм N d N a

65. Диффузионная емкость pn-перехода

Диффузионная емкость pnперехода
C диф
( I p p I n n )
T
S
j p p j n n
T

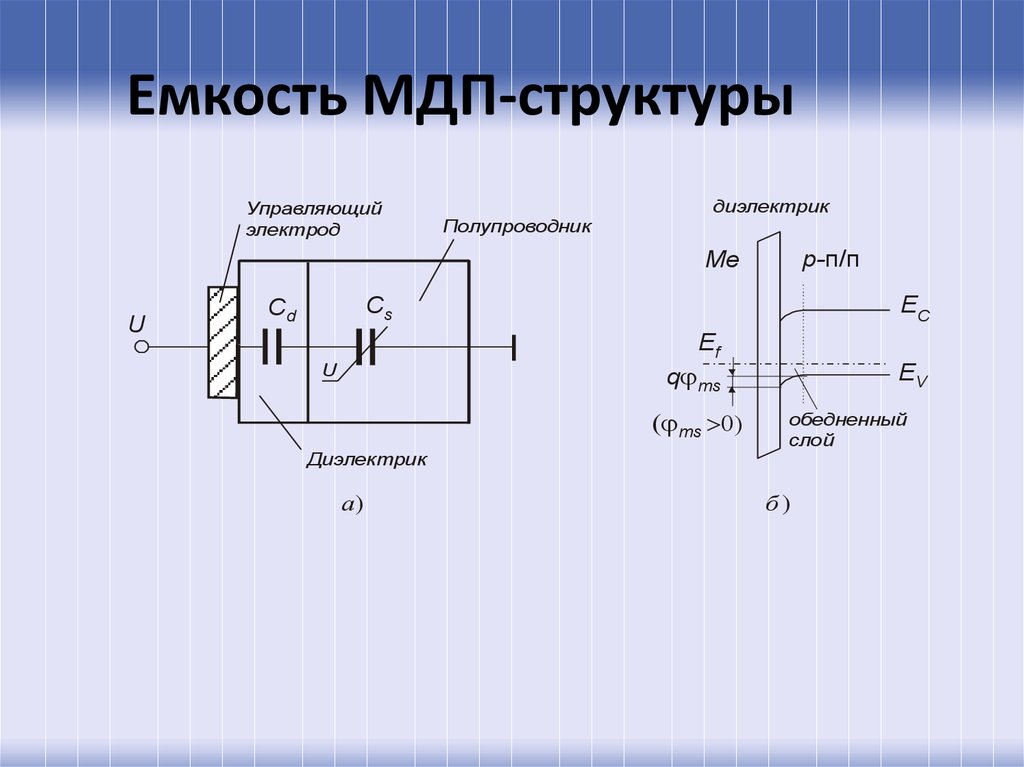
66. Емкость МДП-структуры

Управляющий
электрод
Полупроводник
диэлектрик
p-п/п
Me
U
EС
Cs
Cd
Ef
q ms
U
ms
Диэлектрик
а)
EV
обедненный
слой
б)

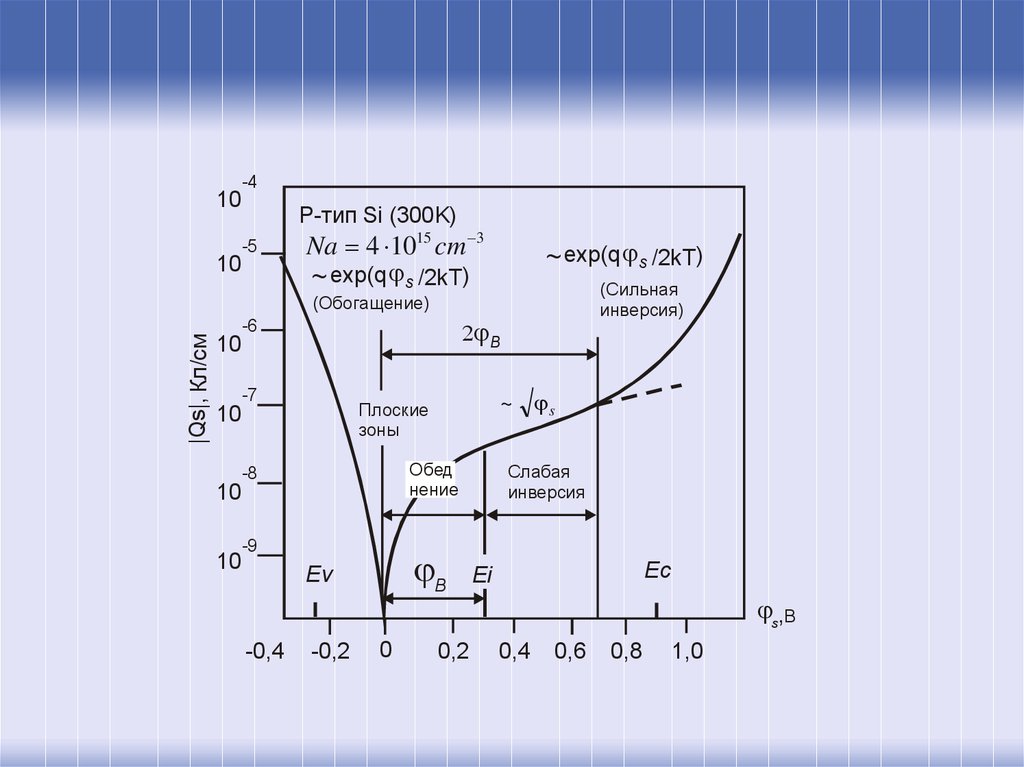
67.

10
10
-4
P-тип Si (300K)
-5
Na 4 1015 cm 3
~ exp(q s /2kT)
|Qs|, Кл/см
(Обогащение)
-7
~ s
Плоские
зоны
10
Обед
нение
-8
10
-9
B
Ev
-0,4
(Сильная
инверсия)
B
-6
10
10
~ exp(q s /2kT)
-0,2
0
0,2
Слабая
инверсия
Ec
Ei
s,B
0,4
0,6
0,8
1,0

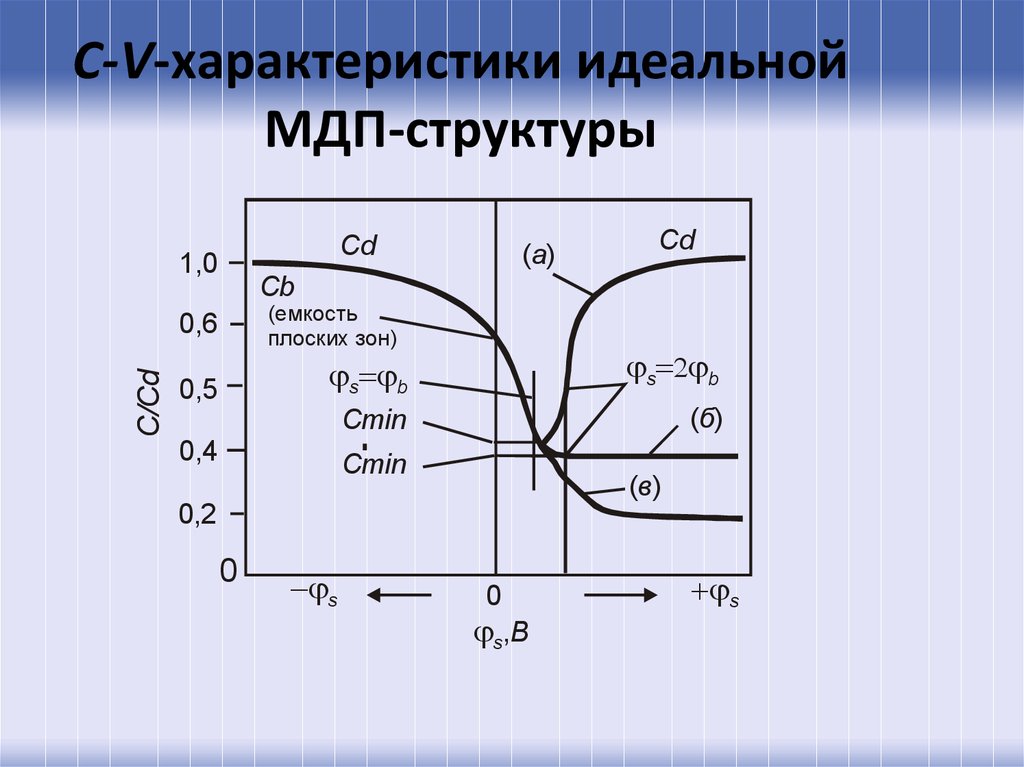
68. С-V-характеристики идеальной МДП-структуры

Cd
1,0
Cd
Cb
(емкость
плоских зон)
0,6
C/Cd
(a)
0,5
s b
s b
Cmin
(б)
0,4
Cmin
(в)
0,2
0
s
0
s,B
s

69. Заряды в окисле

Металл
Na+
заряд подвижных
ионов Q
K+
заряд захваченный
в окисле
Фиксированный
заряд окисла
SiO 2
+++
+
+
SiO к
+
+
+
+
+
+
+
+
+
---
Заряд, захваченный
поверхностными ловушками
Si