Похожие презентации:
Проекционное черчение
1.
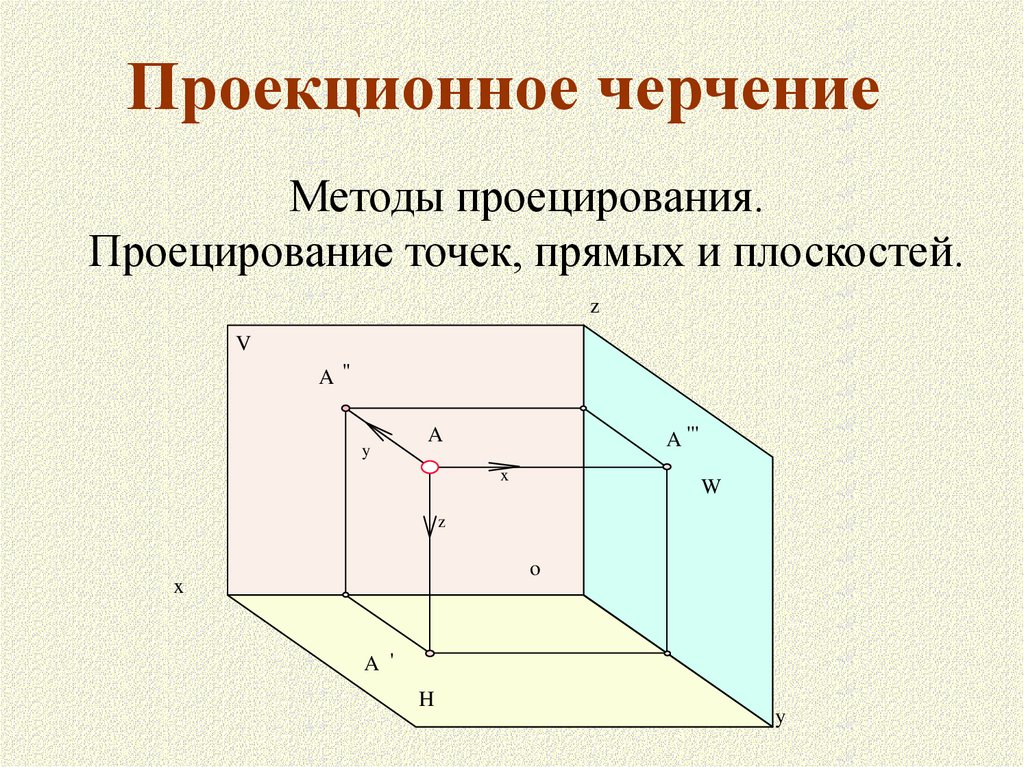
Проекционное черчениеМетоды проецирования.
Проецирование точек, прямых и плоскостей.
z
V
A"
y
A '''
A
x
W
z
o
x
A '
H
y
2.
Для того чтобы чертеж был геометрическиравноценным изображаемой фигуре (оригиналу), он
должен быть построен по определенным геометрическим
законам.
В начертательной геометрии чертеж строится при
помощи Метода проецирования , поэтому чертежи носят
название проекционных чертежей .
При построении этих чертежей широко
используются проекционные свойства фигур, благодаря
чему изображение обладает такими геометрическими
свойствами, по которым можно судить о свойствах самого
оригинала.
3.
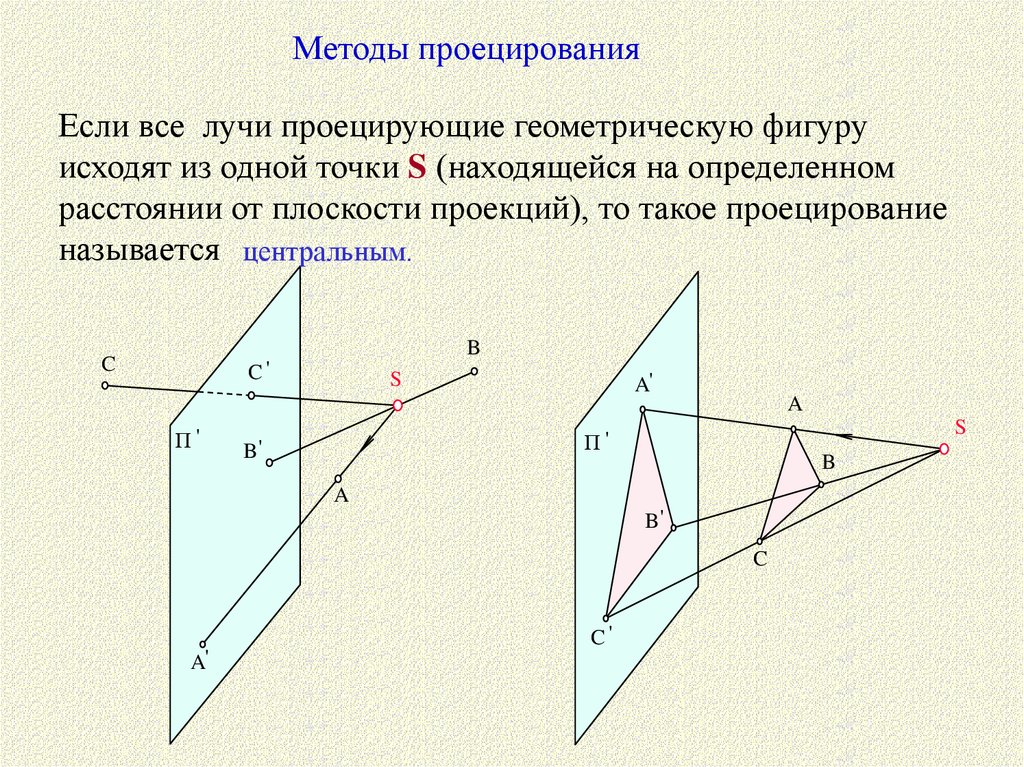
Методы проецированияЕсли все лучи проецирующие геометрическую фигуру
исходят из одной точки S (находящейся на определенном
расстоянии от плоскости проекций), то такое проецирование
называется центральным.
B
C
C'
П'
S
A'
A
S
П'
B'
B
A
B'
C
C'
A'
4.
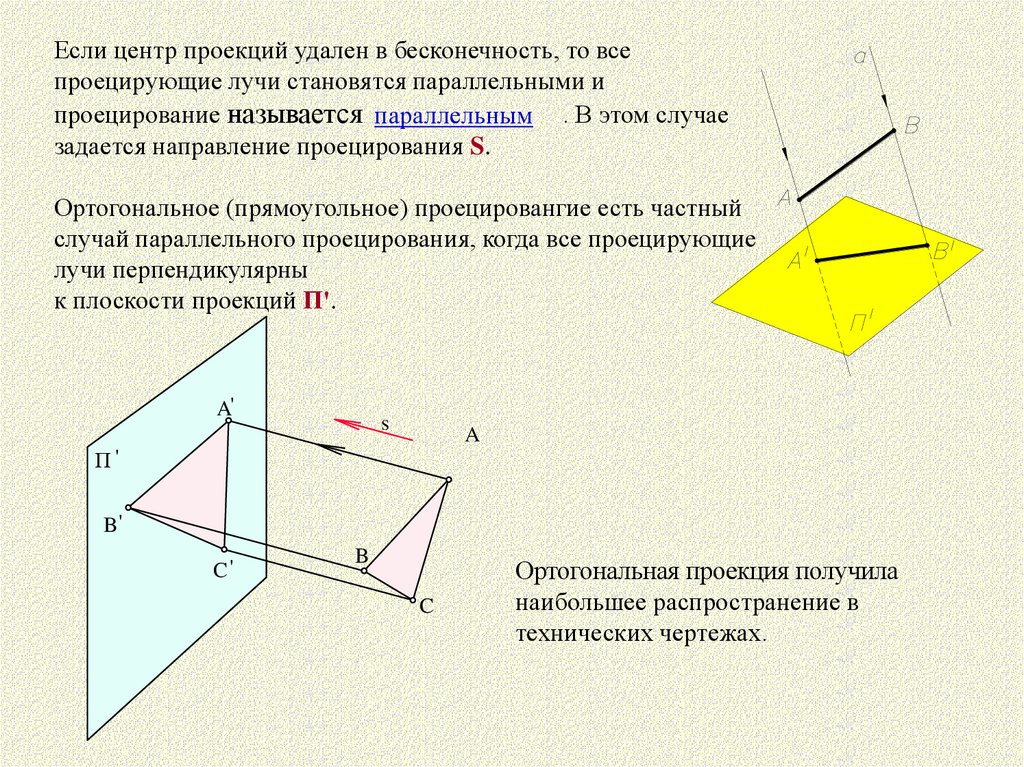
Если центр проекций удален в бесконечность, то всепроецирующие лучи становятся параллельными и
проецирование называется параллельным . В этом случае
задается направление проецирования S.
Ортогональное (прямоугольное) проецировангие есть частный
случай параллельного проецирования, когда все проецирующие
лучи перпендикулярны
к плоскости проекций П'.
A'
s
A
П'
B'
C'
B
C
Ортогональная проекция получила
наибольшее распространение в
технических чертежах.
5.
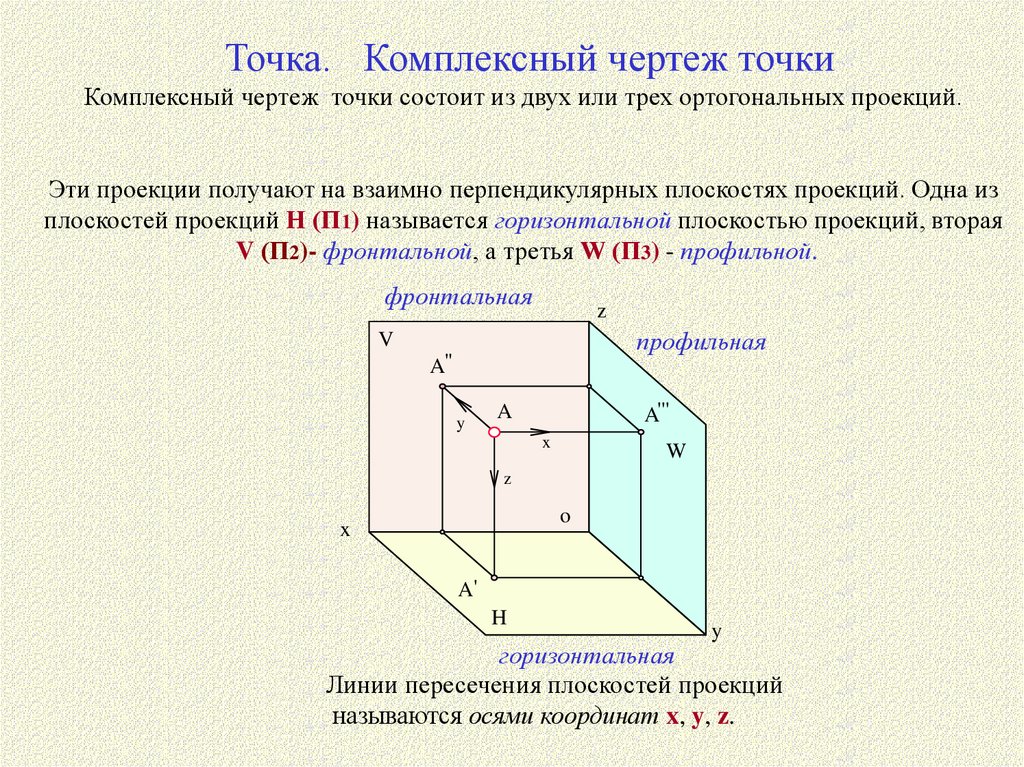
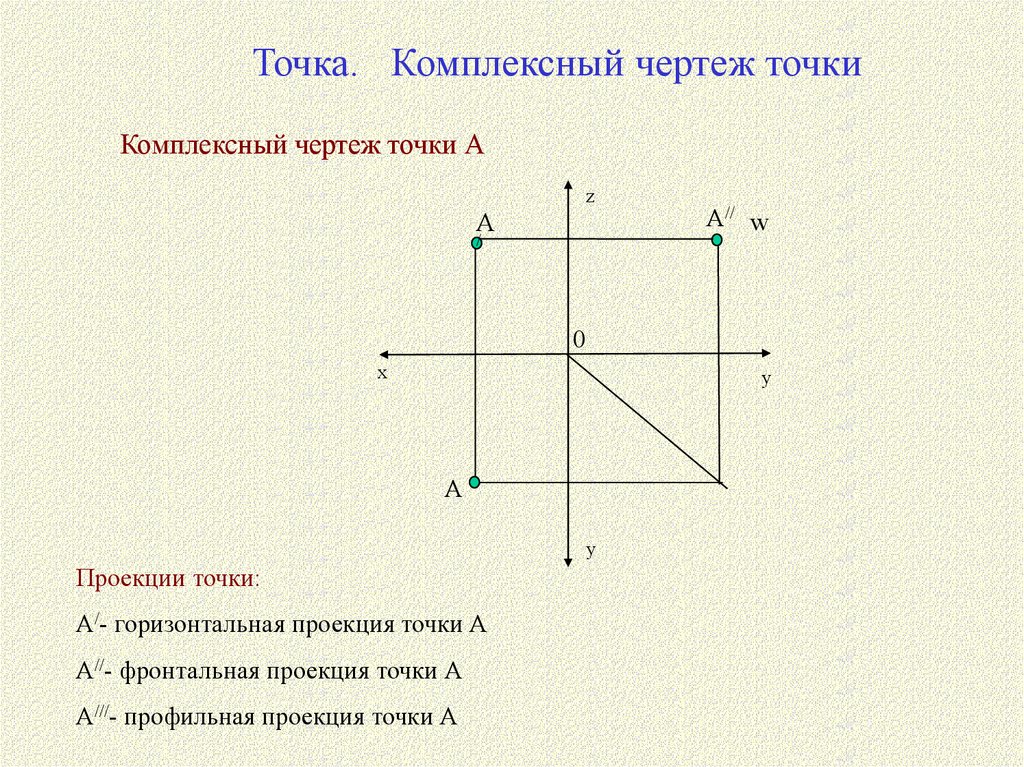
Точка. Комплексный чертеж точкиКомплексный чертеж точки состоит из двух или трех ортогональных проекций.
Эти проекции получают на взаимно перпендикулярных плоскостях проекций. Одна из
плоскостей проекций H (П1) называется горизонтальной плоскостью проекций, вторая
V (П2)- фронтальной, а третья W (П3) - профильной.
фронтальная
z
профильная
V
A"
y
A'''
A
x
W
z
o
x
A'
H
y
горизонтальная
Линии пересечения плоскостей проекций
называются осями координат x, y, z.
6.
Точка. Комплексный чертеж точкиКомплексный чертеж точки А
z
А
/
А// w
0
х
y
А
y
Проекции точки:
А/- горизонтальная проекция точки А
А//- фронтальная проекция точки А
А///- профильная проекция точки А
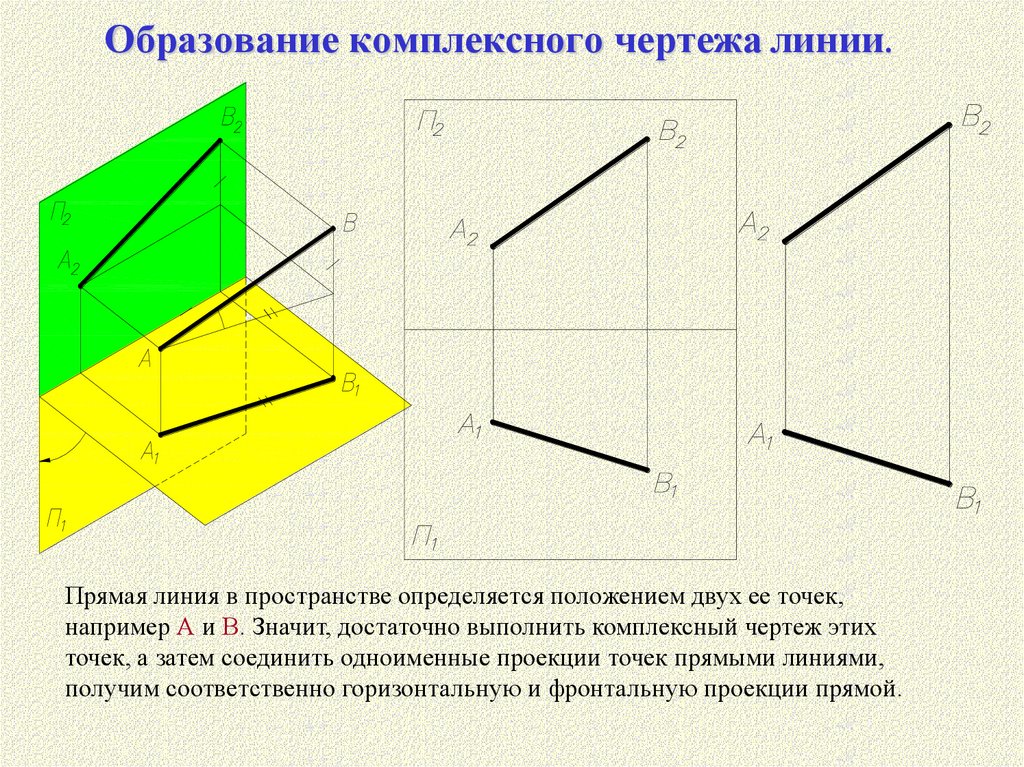
7. Образование комплексного чертежа линии.
Прямая линия в пространстве определяется положением двух ее точек,например А и B. Значит, достаточно выполнить комплексный чертеж этих
точек, а затем соединить одноименные проекции точек прямыми линиями,
получим соответственно горизонтальную и фронтальную проекции прямой.
8.
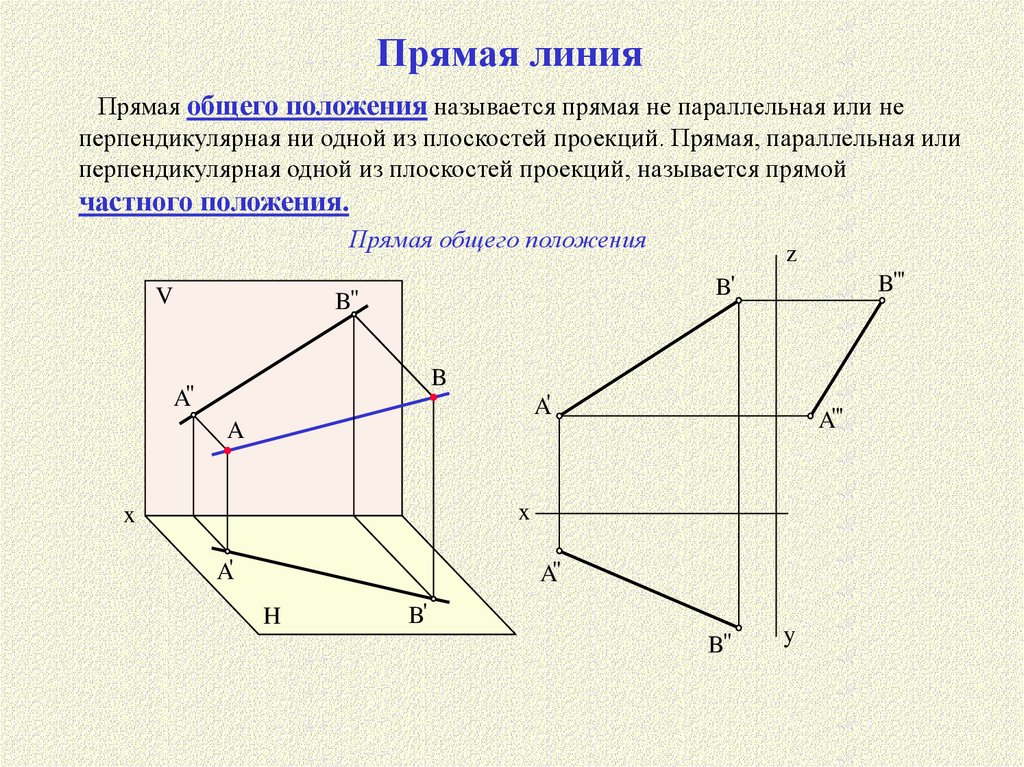
Прямая линияПрямая общего положения называется прямая не параллельная или не
перпендикулярная ни одной из плоскостей проекций. Прямая, параллельная или
перпендикулярная одной из плоскостей проекций, называется прямой
частного положения.
Прямая общего положения
V
z
B"'
B'
B"
B
A"
A'
A"'
A
x
x
A'
A"
H
B'
B"
y
9.
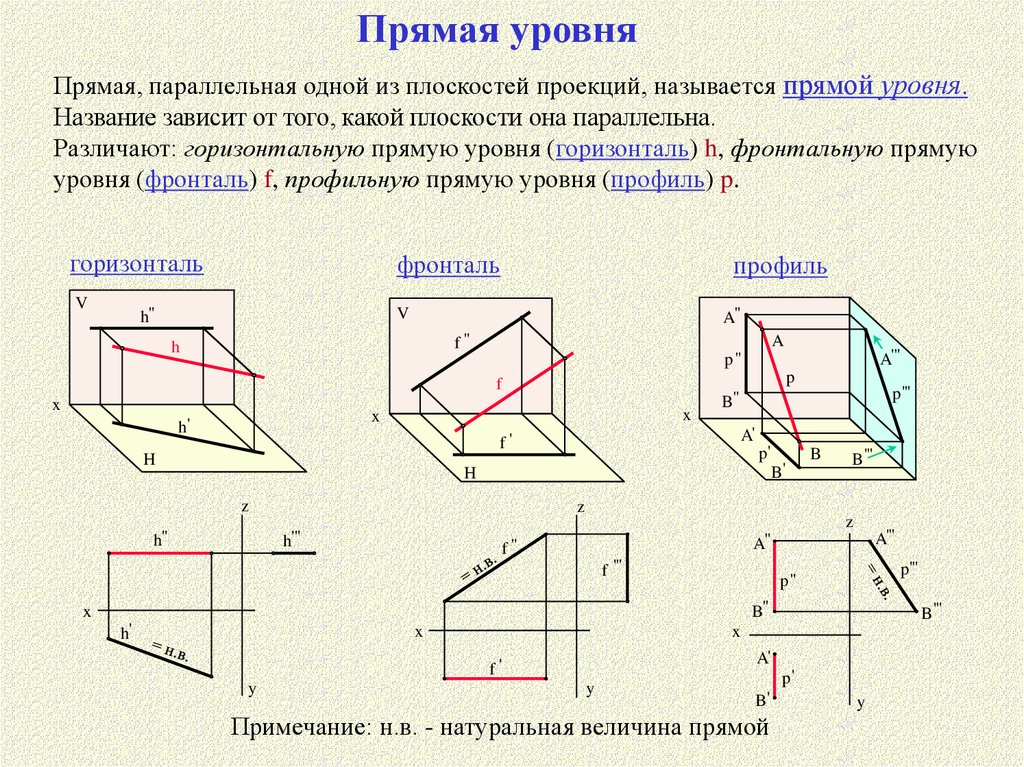
Прямая уровняПрямая, параллельная одной из плоскостей проекций, называется прямой уровня.
Название зависит от того, какой плоскости она параллельна.
Различают: горизонтальную прямую уровня (горизонталь) h, фронтальную прямую
уровня (фронталь) f, профильную прямую уровня (профиль) p.
горизонталь
V
фронталь
h"
профиль
V
A"
f"
h
A
A'"
p"
p
f
x
x
x
h'
A'
f'
H
p'
B'
H
z
h"
z
h'"
p '"
B"
B
B'"
z
A'"
A"
f"
f '"
p '"
p"
B"
x
h'
x
x
A'
f'
y
B'"
y
p'
B'
Примечание: н.в. - натуральная величина прямой
y
10.
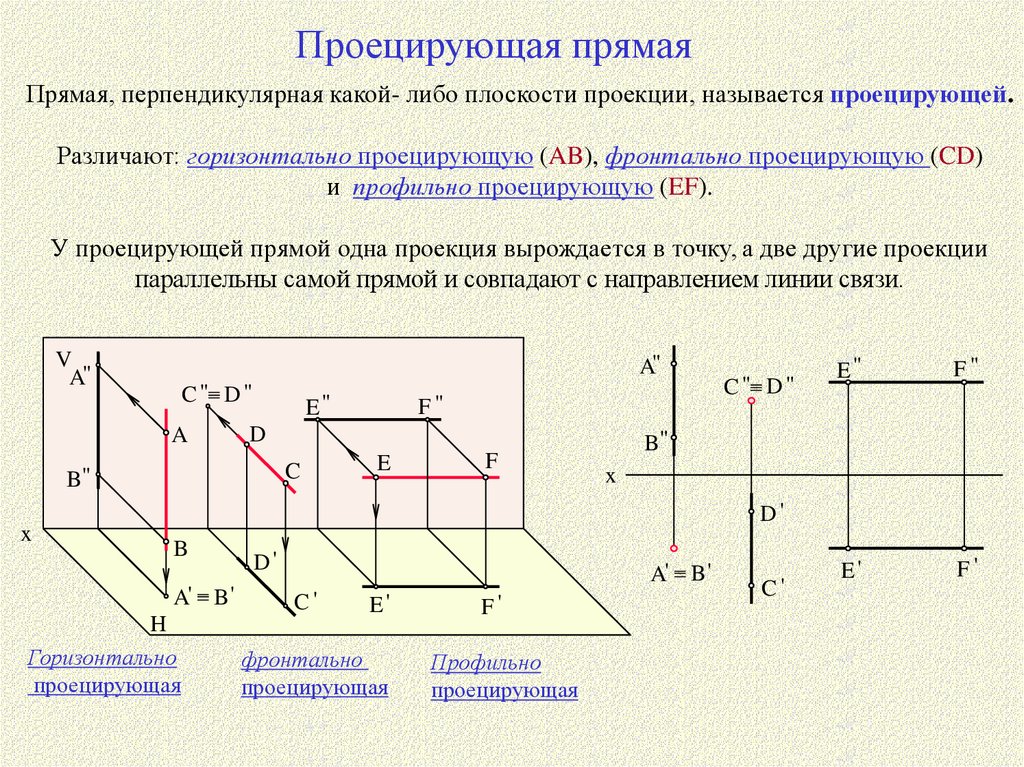
Проецирующая прямаяПрямая, перпендикулярная какой- либо плоскости проекции, называется проецирующей.
Различают: горизонтально проецирующую (AB), фронтально проецирующую (CD)
и профильно проецирующую (EF).
У проецирующей прямой одна проекция вырождается в точку, а две другие проекции
параллельны самой прямой и совпадают с направлением линии связи.
V
A"
A"
_
C "_ D "
A
E"
D
C
B"
x
F"
E
F
_
C "_ D "
E"
F"
E'
F'
B"
x
D'
B
_
A' _ B '
H
Горизонтально
проецирующая
D'
_
A' _ B '
C'
E'
фронтально
проецирующая
F'
Профильно
проецирующая
C'
11.
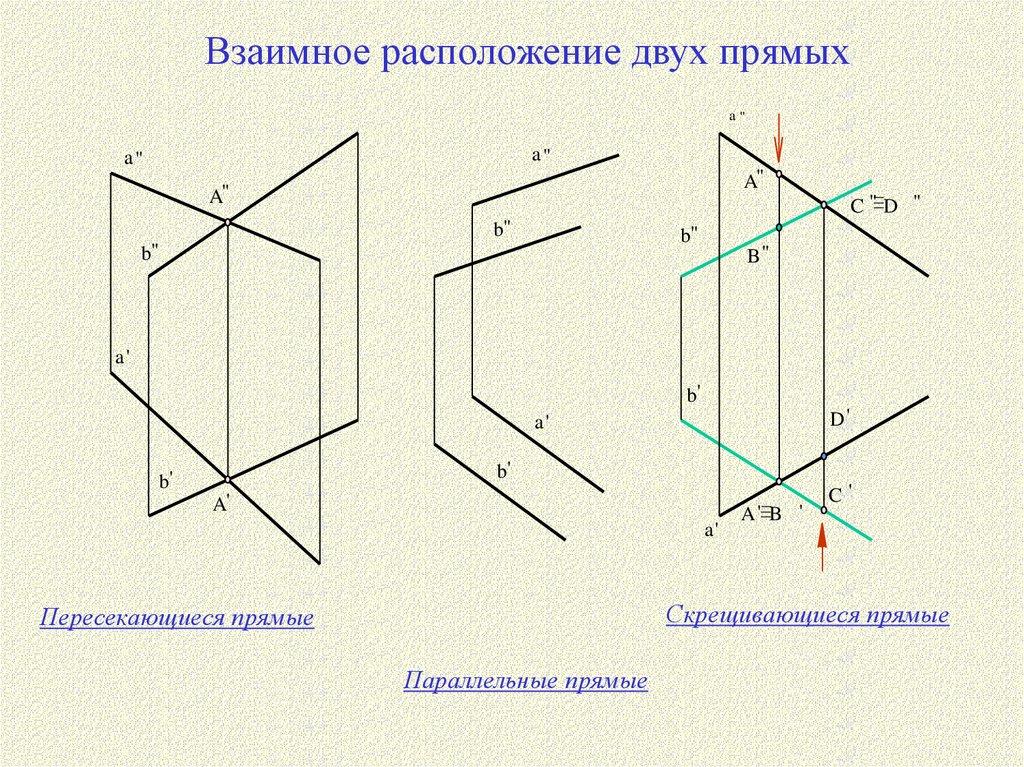
Взаимное расположение двух прямыхa"
a"
a"
A"
A"
b"
b"
b"
__
C "_D "
B"
a'
b'
D'
a'
b'
b'
A'
a'
__
A '_B '
C'
Скрещивающиеся прямые
Пересекающиеся прямые
Параллельные прямые
12.
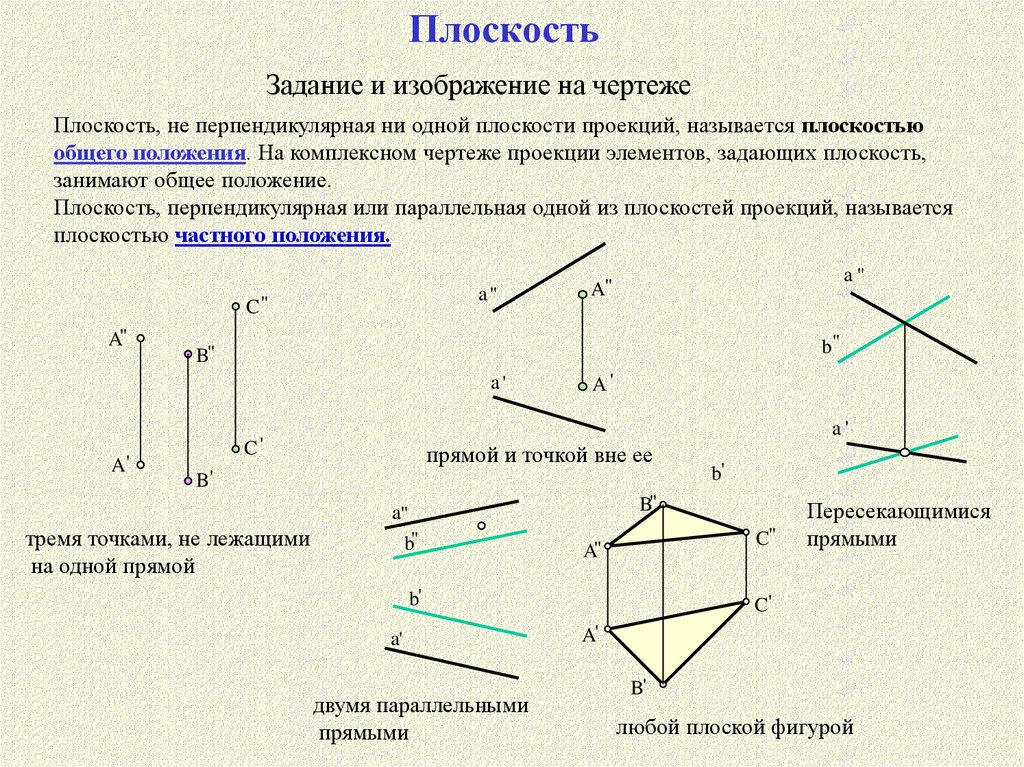
ПлоскостьЗадание и изображение на чертеже
Плоскость, не перпендикулярная ни одной плоскости проекций, называется плоскостью
общего положения. На комплексном чертеже проекции элементов, задающих плоскость,
занимают общее положение.
Плоскость, перпендикулярная или параллельная одной из плоскостей проекций, называется
плоскостью частного положения.
a"
C"
A"
b"
B"
a'
A'
a"
A"
A'
a'
C'
прямой и точкой вне ее
B'
B"
a"
тремя точками, не лежащими
на одной прямой
b'
b"
C"
A"
b'
a'
двумя параллельными
прямыми
Пересекающимися
прямыми
C'
A'
B'
любой плоской фигурой

 Инженерная графика
Инженерная графика








