Похожие презентации:
Математическая статистика, комбинаторика и теория вероятностей
1.
Математическаястатистика, комбинаторика
и теория вероятностей
2.
Содержание• Терминология и историческая справка
• Статистика
• Теория вероятностей
• Комбинаторика
• Бином Ньютона, формула Паскаля
• Применение комбинаторики для
подсчета вероятностей
• Решение вероятностных задач
3.
Терминологияи
историческая справка
4. Терминология
Статистика – это раздел прикладной математики, в которомисследуются количественные характеристики массовых
случайных событий или явлений
Комбинаторика - это раздел математики, в котором
изучаются вопросы о том, сколько различных комбинаций,
подчиненных тем или иным условиям, можно составить из
заданных объектов.
Теория вероятностей - раздел математики, изучающий
закономерности случайных явлений: случайные события,
случайные величины, их свойства и операции над ними.
5. Историческая справка
Математическая статистика возникла в17 веке и развивалась параллельно с
теорией вероятностей. Дальнейшее
развитие математической статистики
(вторая половина 19 начало 20-ых
веков) обязано в первую очередь,
П.Л. Чебышеву, А.А. Маркову,
А.М. Ляпунову, К. Гауссу, А. Кетле,
Ф.Гальтону, К Пирсону, и др.
6. Историческая справка
В 20 –ом веке наиболее существенныйвклад в математическую статистику был
сделан советскими учёными (А.Н.
Колмогоровым, В.И. Романовским, Е.Е.
Слуцким, Н.В. Смирновым, Б.В.
Гнеденко),
а также английскими учёными
(Стъюдентом, Р. Фишером,
Э. Пурсоном)
и американскими учёными
(Ю. Нейман, А Вальд).
7. Историческая справка
Термин «комбинаторика» былвведён в математический
обиход немецким
философом, математиком
Лейбницем, который в 1666
году опубликовал свой труд
«Рассуждения о
комбинаторном искусстве».
Готфрид Вильгельм Лейбниц
8. Историческая справка
Возникновение теориивероятностей как науки относят
к средним векам и первым
попыткам математического
анализа азартных игр.
Основоположниками являются:
Блез Паскаль, Пьер Ферма, Христиан
Гюйгенс, Якоб Бернулли
Блез Паскаль
9.
СТАТИСТИКАэто раздел математики, в котором
исследуются количественные
характеристики массовых случайных
событий или явлений
10. Этапы статистической обработки данных
1) Сначала данные измерений упорядочивают игруппируют
2) Составляют таблицу распределения данных
3) Строят графики распределения данных в виде:
• многоугольника распределения данных (полигон)
• гистограммы (столбчатые диаграммы)
• круговой диаграммы
11. 4) Составляется паспорт данных, который состоит из основных числовых характеристик полученной информации:
• Кратность измерений• Объём измерений (варианты) –
• Размах измерений • Частота варианты• Мода измерений • Среднее арифметическое • Процентная частота
вариантыизмерений • Медиана измерений -
12.
ТЕОРИЯВЕРОЯТНОСТЕЙ
раздел математики, изучающий
закономерности случайных явлений:
случайные события, случайные
величины, их свойства и операции над
ними.
13.
В теории вероятностей изучают различныемодели случайных событий, их свойства и
числовые характеристики.
Классическое определение вероятности.
Вероятностью события А при проведении
некоторого испытания называют отношение
числа тех исходов, в результате которых
наступает событие А, к общему числу всех
(равновозможных между собой) исходов этого
испытания
14. т.е.
N ( A)Р ( А)
N
Где: N - число всех возможных исходов
N(А) - количество тех исходов,
в которых наступает событие А
15. Алгоритм нахождения вероятности случайного события
Для нахождения вероятности случайного события Апри проведении некоторого испытания следует
найти:
1) Число N всех возможных исходов данного испытания
2) Количество N(А) – тех исходов, в которых наступает
событие А
3) Найти частное N(А) / N оно и будет равно
вероятности события А
16. Например
Найти вероятность того, что при одном бросании игральногокубика выпадет: а) пять очков б) четное число очков
в) число, большее четырёх г) число, не кратное 3.
Решение.
а) N(А)=1; N=6 => Р(А)=1\6
б) N(А)=3 (т.к.могло выпасть 2;4;6); N=6 => Р(А)=1\2
в) N(А)=2 (т.к.могло выпасть 5;6); N=6 => Р(А)=1\3
г) N(А)=4 (т.к.могло выпасть 1;2;4;5); N=6 => Р(А)=2\3
17. Виды событий
• Невозможное событие - это событие, которое никогдане наступает при проведении данного испытания.
и его Р(А)=0
• Достоверное событие – это событие, которое
обязательно наступит при проведении данного
испытания.
Значит его Р(А)=1
• Противоположное событие (Ā) – это событие, которое
наступит в том и только том случае, когда не наступит
интересующее нас событие. Р(Ā) = 1 – Р(А)
18. Запомним
Р(А) достоверного события =1Р(А) невозможного события = 0
Р(А) случайного события 0≤ Р(А) ≤1, т.е.
вероятность – это всегда дробь
Р(А) противоположного события = 1 - Р(А)
Сумма противоположных событий всегда равна 1,
т.е.
19. Правило умножения
Для того, чтобы найти число всех возможныхисходов проведения двух независимых
испытаний А и В, следует перемножить число
всех исходов испытания А и число всех исходов
испытания В.
Правило умножения часто используют для вычисления вероятности.
20. Например
Учебник:стр.317 задачи 1,2,3
21.
стр. 319№ 149-152
22.
КОМБИНАТОРИКАэто раздел математики, в котором изучаются
вопросы о том, сколько различных
комбинаций, подчиненных тем или иным
условиям, можно составить из заданных
объектов.
23. Из истории комбинаторики
• С комбинаторными задачами люди столкнулись и вглубокой древности.
• В Древнем Китае увлекались составлением магических
квадратов. В Древней Греции занимались теорией
фигурных чисел.
• Комбинаторные задачи возникли и в связи с такими
играми, как шашки, шахматы, домино, карты, кости и
т.д.
Комбинаторика становится наукой лишь в 18 в. –
в период, когда возникла теория вероятности.
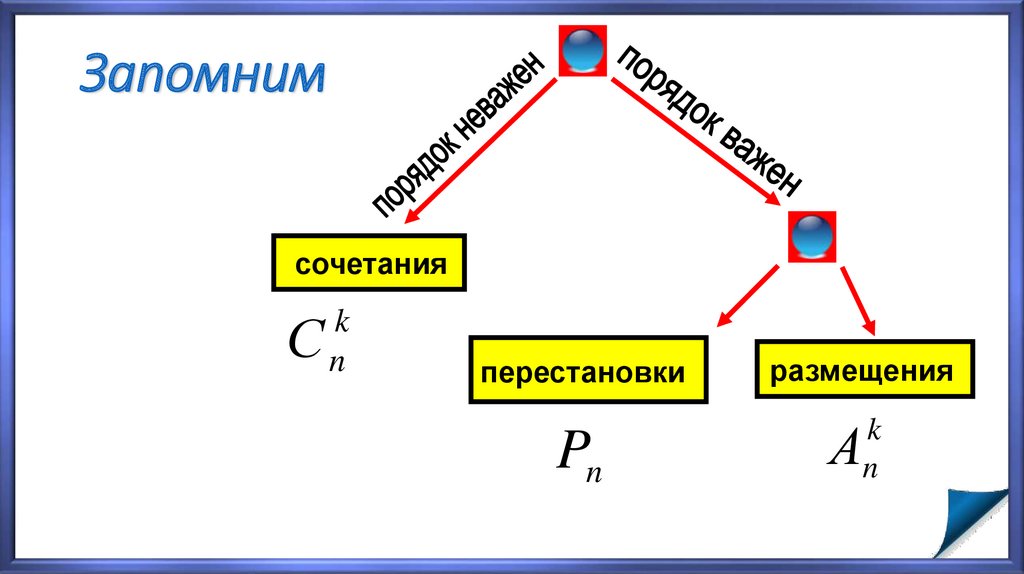
24. Основные понятия комбинаторики
•Перестановки•Сочетания
•Размещения
25. Вспомним
Произведение подряд идущих первых nнатуральных чисел обозначают n! и называют
«эн факториалом».
n! = 1·2·3·…· n
Вычислим: 1! ; 2!; 3!; 4!
Вспомним, что принято считать 0! =1
Часто используется формула: n! = (n-1)! · n
26. Определение
Перестановками без повторений из nэлементов по n называются такие
соединения, которые отличаются друг от
друга только порядком расположения
элементов
Обозначение: Pn
27. Теорема 1 (о перестановке элементов)
n различных элементов можнорасставить по одному на n различных
мест ровно n! способами.
Pn = n!
28. Формула перестановок
Pn = n!29. Пример 1
Сколькими способами 4 человека смогутразместиться на четырехместной
скамейке?
Решение.
P4 = 4! = 1 ·2 ·3 ·4 = 24
Ответ: 24 способами
30. Пример 2
Антон, Борис и Виктор купили3 билета на футбол на 1-е, 2-е, 3-е места
первого ряда стадиона. Сколькими
способами мальчики могут занять эти места?
Решение.
P3 = 3! = 6
31. Определения
• Число всех выборов k элементов из n данных безучета порядка называют числом сочетаний, из n
элементов по k и обозначают
• Число всех выборов k элементов из n данных
с учётом их порядка называют числом
размещений из n элементов по k и обозначают
32. Запомним
Два сочетания из n элементов по k считаютсяразными, если они отличаются друг от друга
хотя бы одним элементом.
В сочетаниях не имеет значения, в каком порядке указаны
элементы.
Два размещения из n элементов по k считаются
разными, если они различаются самими
элементами или порядком их расположения.
33. Типичные вопросы
Сколькими способами можно выбрать 5учеников из 30 для дежурства в столовой;
Актив класса (староста, культорг,
редактор
стенгазеты,
организатор
спортивных мероприятий) – 4 человека
из 30;
7 монет из 10 данных монет;
34.
Используя эти обозначения, нетрудно записатьответы на поставленные выше вопросы:
• Сколькими способами можно выбрать 5
учеников из 30 для дежурства в столовой:
• Актив класса (староста, культорг, редактор
стенгазеты, организатор спортивных
мероприятий) – 4 человека из 30:
• 7 монет из 10 данных монет:
35. Запомним
сочетанияС
k
n
перестановки
Pn
размещения
А
k
n
36. Теорема 4
Для любых натуральных чисел n и k, таких, чтоk< n, справедливы следующие соотношения:
1) А n(n 1)( n 2)....( n k 1)
k
n
n!
2) A
(n k )!
k
n
n!
4)C
k! (n k )!
k
n
k
n
A
3)C
k!
k
n
37. Запомним
n!А
n!
(n n)!
n
n
38. Следствия (из теоремы 4)
Справедливы формулы:С 1
n
n
(для облегчения вычислений)
С 1
C С
k
n
0
n
n k
n
39. Например
Необходимо вычислитьС
13
15
Решение.
С
13
15
С
2
15
n(n 1) 15 14
105
2!
2
40. Применение комбинаторики в реальной жизни
•учебные заведения (составление расписаний);•сфера общественного питания (составление меню);
•лингвистика (рассмотрение вариантов комбинаций букв).
•география (раскраска карт);
•спортивные соревнования (расчёт количества игр между
участниками);
•производство (распределение нескольких видов работ
между рабочими);
•агротехника (размещение посевов на нескольких полях);
41.
•азартные игры (подсчёт частоты выигрышей);•химия (анализ возможных связей между химическими
элементами);
• биология (расшифровка кода ДНК);
•военное дело (расположение подразделений);
•астрология (анализ расположения планет и созвездий);
•экономика (анализ вариантов купли-продажи акций);
•криптография (разработка методов шифрования);
•доставка почты (рассмотрение вариантов пересылки).
42.
Формулабинома Ньютона
43.
Для любого натурального значения n вернаследующая формула:
1 n 1
n
2 n 2 2
n
3 n 3 3
n
(а в) C a C a b C a b C a b ...
n
k n k k
n
0 n
n
n 1 1 n 1
n
C a b ... C a b C a b
n 0 n
n
где числа С называют биноминальными
коэффициентами
44. Т.е.
10 1 0
1 0 1
а в С1 а в С1 а в
а в
С а в С а в С а в
а в
С а в С а в С а в С а в
2
3
0
2
0
3
2 0
3 0
1 1 1
2
1 2 1
3
2
2
0 2
2 1 2
3
3
3
0 3
45. Например
Учебник: стр. 330Пример. Раскрыть скобки в выражениях:
6
а)
(а в )
б) (а 2в)
2
5
46.
Решениевероятностных
задач
47. Теоремы сложения и умножения для двух событий
1) P(A + B) = P(A) + P(B) (для независимыхсобытий)
2) P(A + B) = P(A) + P(B) - P(AB) (для зависимых
событий)
3) P(AB) = P(A)∙P(B),
4) P(AB) = P(A)∙ P(B ׀A)
48. Задача 1
Решение.Число стандартных
подшипников равно 1000 –
На завод привезли партию из
30 = 970. Будем считать, что
1000 подшипников.
каждый подшипник имеет
Случайно в эту партию
одинаковую вероятность
попало 30 подшипников, не
быть выбранным. Тогда
полная группа событий
удовлетворяющих
состоит из N = 1000
стандарту. Определить
равновероятных исходов, из
вероятность Р(А) того, что
которых событию А
взятый наудачу подшипник
благоприятствуют N(A) = 970
исходов.
окажется стандартным.
Ответ: 0,97
49. Задача 2
В ящике лежат 6 красных и Решение.6 синих шаров. Наудачу
Р(А) = 0, т.к. это событие
вынимают 8 шаров.
А - невозможное.
Определите вероятность Ответ: 0.
события А - все
выбранные шары
красные.
50. Задача 3
Научная конференция проводится 3Решение.
дня. Всего запланировано 50
Т.к. в третий день будут
докладов: в первый день – 30
докладов, а остальные распределены слушать (50-30):2=10
поровну между вторым и третьим
докладов, то N(A) = 10.
днями. Порядок докладов
А N=50, тогда
определяется жеребьевкой. Какова
Р(А) = N(A): N = 10:50 =
вероятность, что доклад профессора
М. окажется запланированным на
= 1/5=0,2
последний день конференции?
Ответ: 0,2
51. Задача 4
Перед началом первого турачемпионата по теннису разбивают на
игровые пары случайным образом с
помощью жребия. Всего в
чемпионате участвует 46 теннисистов,
среди которых 19 участников из
России, в том числе Ярослав Исаков.
Найдите вероятность того, что в
первом туре Ярослав Исаков будет
играть с каким – либо теннисистом из
России.
Решение.
Число всех исходов
равно (46-1)=45, т.е.
N=45.
N(A) = (19-1)=18
Тогда
Р(А) = N(A):N =
=18:45 = 2:5 =0,4
Ответ: 0,4
52. Задача 5
Монету бросаютчетыре раза.
Найдите
вероятность того,
что решка не
выпадет ни разу.
Решение. Выписываем все
возможные комбинации орлов и
решек: OOOO; OOOP; OOPO; OOPP;
OPOO; OPOP OPPO; OPPP; POOO;
POOP; POPO; POPP; PPOO; PPOP;
PPPO; PPPP.
Значит N= 16, а N(A) = 1, тогда
Р(А) = N(A):N = 1:16 = 0,0625
Ответ: 0,0625
53. Задача 6
В урне 5 белых, 20красных и 10 черных
шаров, не отличающихся
по размеру. Шары
тщательно
перемешивают и затем
наугад вынимают 1 шар.
Какова вероятность того,
что вынутый шар
окажется белым или
черным?
Решение. Пусть событие А –
появление белого или черного шара.
Разобьем это событие на более
простые. Пусть В1 – появление
белого шара, а В2 – черного. Тогда,
А=В1+В2 по определению суммы
событий. Следовательно
Р(А)=Р(В1+В2). Т.к. В1 и В2 –
несовместные события, то по
теореме о вероятности суммы
несовместных событий
Р(В1+В2) = Р(В1)+Р(В2).
N=35, N(В1)=5 тогда Р(В1)= 5:35=1/7
N(В2)=10 тогда Р(В2)=10:35=2/7
Значит Р(А)= 1/7+2/7=3/7
54. Задача 7
Ведутся поиски двухпреступников. Каждый из них
независимо от другого может
быть обнаружен в течение суток
с вероятностью 0,5. После
поимки одно из них, в связи с
увеличением количества
сотрудников, занятых в
поисках, вероятность найти
второго возрастает до 0,7. Какова
вероятность того, что в течение
суток будет обнаружены оба
преступника.
Решение. Пусть событие А –
“обнаружены два преступника”.
Разобьем это событие на более
простые. Пусть В1 – обнаружен
первый преступник, а В2 –
обнаружен второй преступник,
после того, как пойман первый.
Тогда, А=В1·В2 по определению
произведения событий.
Следовательно Р(А)=Р(В1·В2). Т.к.
В1 и В2 – зависимые события, то по
теореме о вероятности
произведения зависимых событий
Р(В1·В2) = Р(В1)·Р(В2/В1)=0,5·0,7=
= 0,35.
55. Задача 8
Два стрелкастреляют по одной
мишени. У одного
вероятность
попадания 0,8, у
другого – 0,2.
Какова
вероятность
поражения цели?
Решение.
Пусть A – цель поражена, В –
противоположное событие (цель не
поражена). Будем считать, что
стрелки стреляют независимо друг от
друга, тогда вероятность не поразить
мишень равна Р(В)=0,2 · 0,8=0,16
Отсюда, вероятность поразить
мишень (противоположное событие)
Р(А)= 1 - Р(В) =1 - 0,16 = 0,84
Ответ: 0,84
56. Задача 9
Решение. Обозначим через В1,B2, B3– события, заключающиеся в том, что
мы попали в первый, второй и третий
Вам надо купить
магазины соответственно, а событие
определенную книгу. Всего 3
A то , что купленная книга пиратская.
магазина. Вероятность того,
По условию Р(В1) =0,5, P(B2)=0,3, и
что книга будет куплена в
Р(В3)=0,2. События В1, В2, В3 первом магазине – 50%, во
несовместны. Из условия известно
втором – 30%, в третьем –
также, что Р В1(А)=0,4, P В2(A)=0,5,
20%. В первом магазине 40%
книг пиратского издания, во
P В3(A)=0,2.
Тогда полная
втором 50% пиратских книг и
вероятность купить пиратскую книгу
в третьем – 20%. Какова
(не важно в каком магазине) равна
вероятность, что купленная
Р(А)=РВ1(А)·Р(В1)+РВ2(А)·Р(В2)+РВ3(А)·
вами книга окажется
·Р(В3)= 0,5·0,4+0,3·0,5+0,2·0,2=0,39
пиратского издания?
Ответ: 0,39
57. Задача 10
Вгруппе
30
студентов.
Необходимо
выбрать старосту,
заместителя
старосты
и
профорга. Сколько
существует
способов
это
сделать?
Решение.
Старостой может быть выбран
любой
из
30
студентов,
заместителем
любой
из
оставшихся 29, а профоргом –
любой
из
оставшихся
28
студентов, т. е. n1=30, n2=29, n3=28.
По правилу умножения общее
число
N
способов
выбора
старосты, его заместителя и
профорга
равно:
N=n1·n2·n3=30·29·28=24360.



































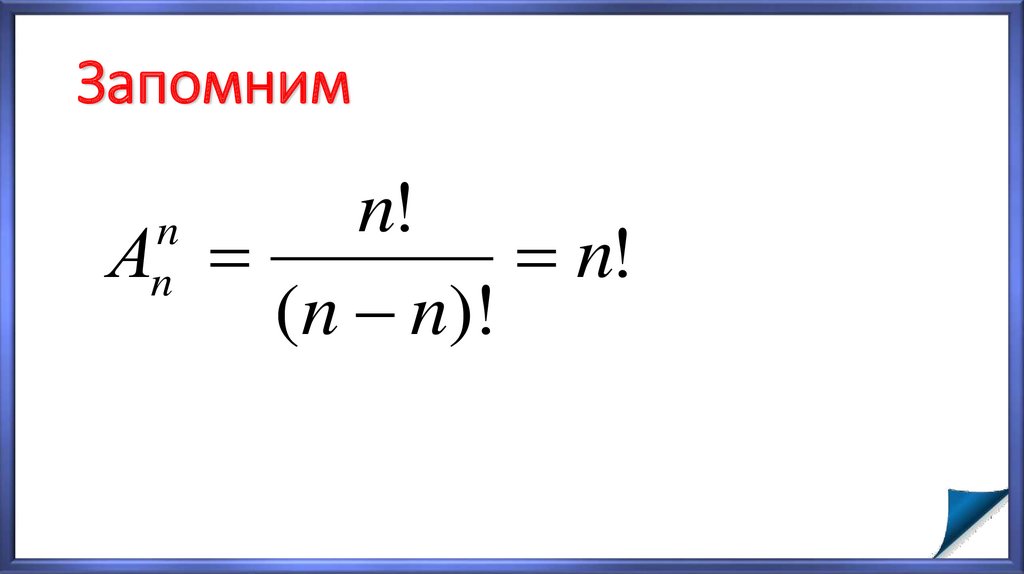






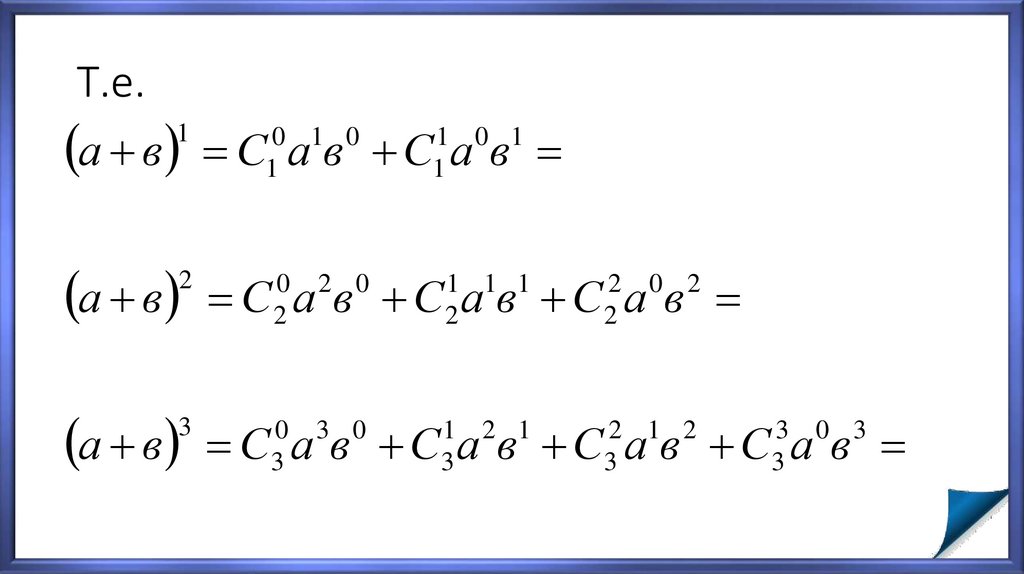













 Математика
Математика








