Теория вероятностей. Математическая статистика

1. Теория вероятностей. Математическая статистика.

1

2.

Теория вероятностей – математическая наука, изучающая
закономерности в случайных явлениях.
Под опытом (экспериментом, испытанием) мы будем понимать
некоторую воспроизводимую совокупность условий, при которых наблюдается
то или иное явление, фиксируется тот или другой результат.
Опыт может протекать независимо от человека, который может выступать
в роли наблюдателя.
Опыт со случайным исходом – это опыт, результат которого варьируется
при его повторении.
Случайным событием называется всякий факт, которой в опыте со случайным
исходом может произойти или не произойти.
События обозначают большими буквами латинского алфавита.
2

3. Примеры

1)Опыт:
бросание монеты.
Событие: появление числа.
2) Опыт:
стрельба по мишени.
Событие: попадание в десятку.
3) Опыт:
изъятие карты из колоды.
Событие: появление короля.
4) Опыт:
измерение температуры у
больных.
Событие: температура равна 39 хотя бы у
одного больного.
3

4. Вероятность

Вероятность – это число, характеризующее
степень возможности события.
Наблюдаемые события делятся на 3 вида:
достоверное – событие, которое в результате
опыта неизбежно произойдет;
невозможное – событие, которое в данном
опыте не может произойти;
случайное – событие, которое в результате
опыта либо происходит, либо не происходит.
4

5. Примеры

1. В корзине три белых шара.
Опыт: извлечение 1 шара.
Событие A: шар белый
( достоверное событие).
Событие B: шар черный шар
(невозможное событие).
2. В корзине два белых и один черный шар.
Опыт: извлечение 1 шара.
Событие C: шар белый
(случайное событие).
Событие D: шар зеленый
(невозможное событие).
? Сформулируйте достоверное событие для данного опыта.
5

6. Полная группа событий

Говорят, что несколько событий в данном опыте
образуют полную группу, если в результате опыта
неизбежно должно появиться хотя бы одно из них.
Примеры:
появление 1, 2,3,…..6 при бросании игральных
костей.
появление карты масти черви, пики, крести, бубны
при вынимании 1 карты из колоды.
при ответе на два вопроса: «хотя бы один не
верный», «хотя бы один верный»
К полной группе можно прибавить еще какие угодно
события.
6

7. Несовместные события

Несколько событий в данном опыте называются
несовместными, если никакие два из них не могут
появиться вместе.
Примеры:
выпадение 1 и 2 при бросании кости;
при измерении температуры воздуха ежедневно
t<20˚, t >20˚;
появление короля, десятки, шестерки при вынимании
1 карты из колоды.
Из несовместных событий можно убрать любые
(пока остаются хотя бы 2) не нарушая свойства
несовместности.
7

8. Равновозможные события

Несколько событий в данном опыте
называются равновозможными, если есть
основания считать, что ни одно из них не
является более возможным, чем другое.
Примеры:
появление определенного числа очков при
бросании кости
появление карты одной масти при изъятии 1
карты из колоды.
8

9. Случаи

Образующие полную группу несовместные и равновозможные
события называются случаями (шансами)
Примеры:
появление «герба», «решки» при бросании монеты
появление карты масти «черви», «бубны», «треф», «пики» при
изъятии из колоды одной карты
вызов одного человека к доске из группы студентов
Случай называется благоприятным событию А, если
появление этого случая влечет за собою появление данного
события.
Примеры:
Появление картинки при изъятии одной карты из колоды в 36
карт: благоприятны 4+4+4=12 случаев и неблагоприятны
остальные 24 случая.
Появление герба при бросании монеты: благоприятны 1 случай,
неблагоприятны – 1 случай.
9

10. Классическое определение вероятности

Определение: Вероятностью события А
называется отношение числа
благоприятных этому событию случаев
к общему числу всех случаев
m
P( A)
n
10

11. Свойства вероятности

1.
P ( A)
m n
1
n n
2.
0
P ( A) 0
n
3.
0≤P(A)≤1
- вероятность достоверного события;
- вероятность невозможного события;
- вероятность любого события.
11

12. Задачи:

1) Из урны, содержащей 3 белых шара и 5 синих шаров, извлекают
1 шар. Найти вероятность того, что шар белый.
Событие A : вытащили белый шар.
P(A)=3/8.
2) Из урны, содержащей 8 шаров: 5 синих и 3 красных, извлекают
2 шара. Найти вероятность того, что вытащили 2 синих шара.
Событие B: изъятые шары синие
С 52
P(B)=
С 82
3) Бросают 2 монеты. Найти вероятность, что выпадет хотя бы
один герб
А= {хотя бы 1 герб},
А1= {1 герб, 1 решка} , А2={1 герб, 1 герб}
А3= {1 решка, 1 решка}, А4={1 решка, 1 герб}
P(A)=3/4
4) Забыто три последние цифры в номере телефона. Найти
вероятность того, что номер угадан с первого раза.
Событие С: номер угадан.
1
P(C)=
3
10
12

13. Относительная частота. Устойчивость относительной частоты

Определение: Относительной частотой
называется отношение числа испытаний, в
которых событие появилось к общему числу
фактически произведенных испытаний
m
P
(
A
)
- относительная частота события А
n
или статистическая вероятность, m- число
появлений события,n – общее число
испытаний.
Отличие вероятности от относительной
частоты: вероятность вычисляют до опыта, а
относительную частоту – после опыта.
13

14.

Пример: При бросании игральной кости A –
появление 1: P(А)=1/6, но P (A) не обязательно
равняется 1/6.
При малом числе опытов частота события
непредсказуема, случайна. Однако при большом
числе опытов n частота все более теряет свой
случайный характер, она проявляет тенденцию
стабилизироваться, приближаясь с незначительными
колебаниями к некоторой средней постоянной
величине. Оказалось, что это постоянная величина
есть вероятность появления события.
14

15. Теоремы сложения и умножения вероятностей

1. Условная вероятность.
2. Теоремы умножения вероятностей.
3. Теоремы сложения вероятностей.
4. Формула полной вероятности.
Формула Байеса.
15

16. 1. УСЛОВНАЯ ВЕРОЯТНОСТЬ

16

17. Условная вероятность

Вероятность события А при условии, что
событие В с вероятностью Р(В) 0 уже
произошло, обозначается Р(А/В) и
называется условной вероятностью
события А при условии, что имело
место событие В.
17

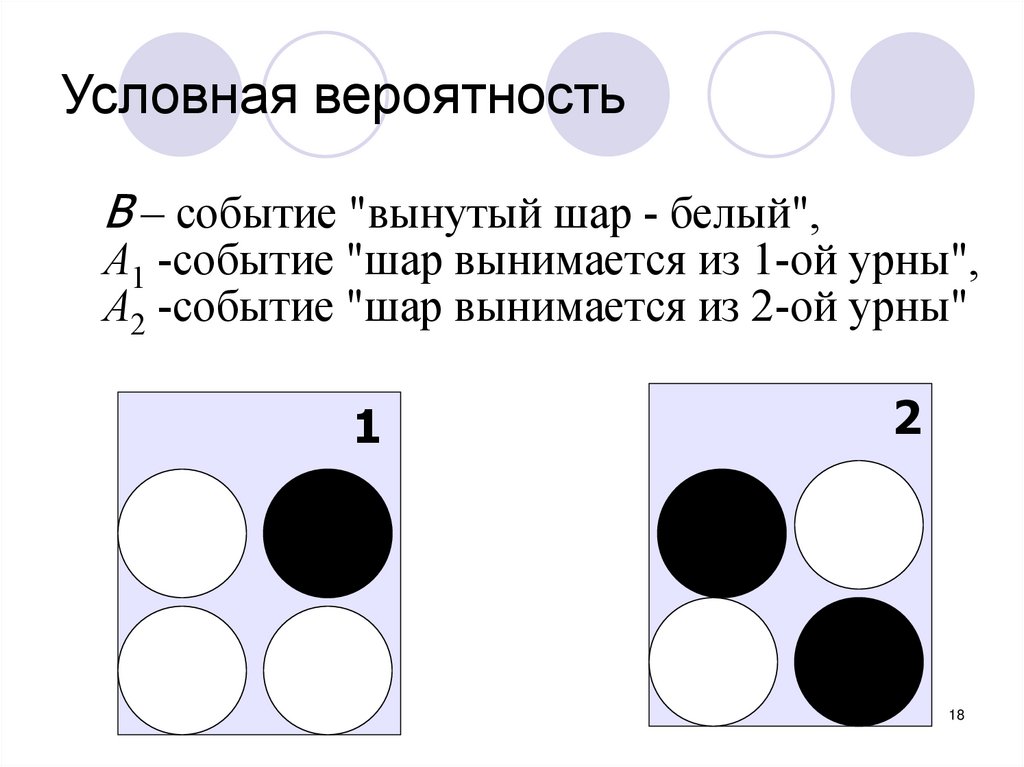
18. Условная вероятность

В – событие "вынутый шар - белый",
А1 -событие "шар вынимается из 1-ой урны",
А2 -событие "шар вынимается из 2-ой урны"
1
2
18

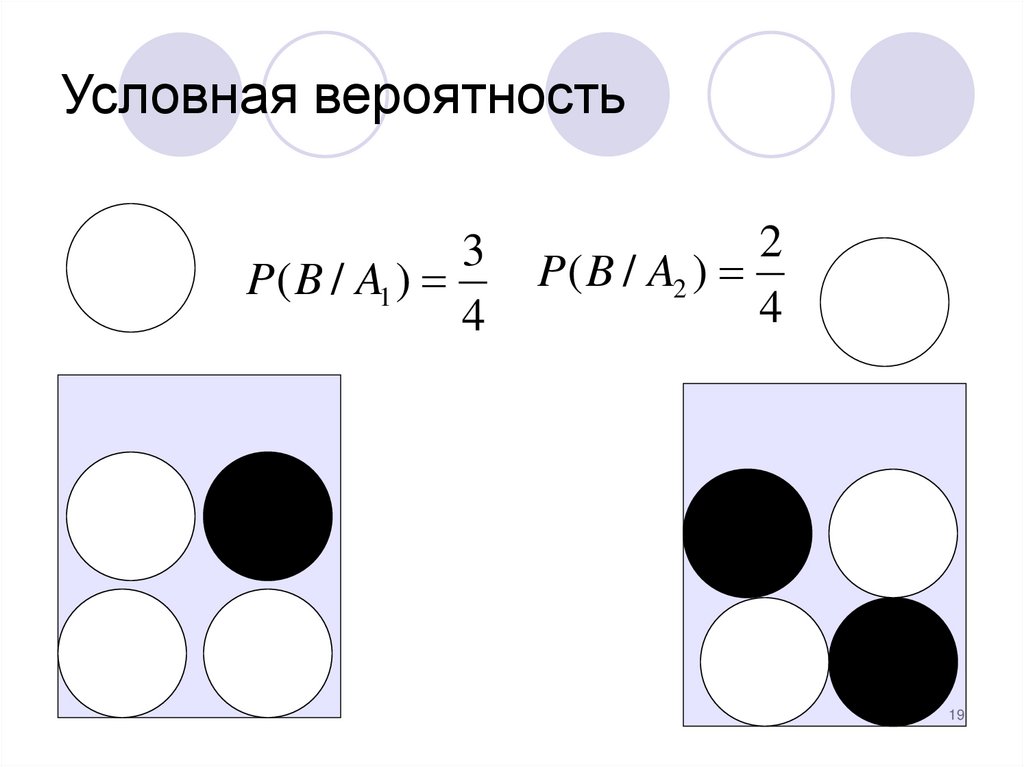
19. Условная вероятность

3
P ( B / A1 )
4
2
P ( B / A2 )
4
19

20. События А и В называются независимыми

если осуществление одного не влияет на
вероятность осуществления другого, т.е.
P( A / B) P( A)
или
P( B / A) P( B)
20

21. 2. ПРОИЗВЕДЕНИЕ ВЕРОЯТНОСТЕЙ

21

22. ТЕОРЕМА 1

Вероятность совместного появления двух
событий равна произведению вероятности
одного из них на условную вероятность
другого, вычисленную в предположении,
что первое событие уже наступило.
P( AB) P( A) P( B / A)
22

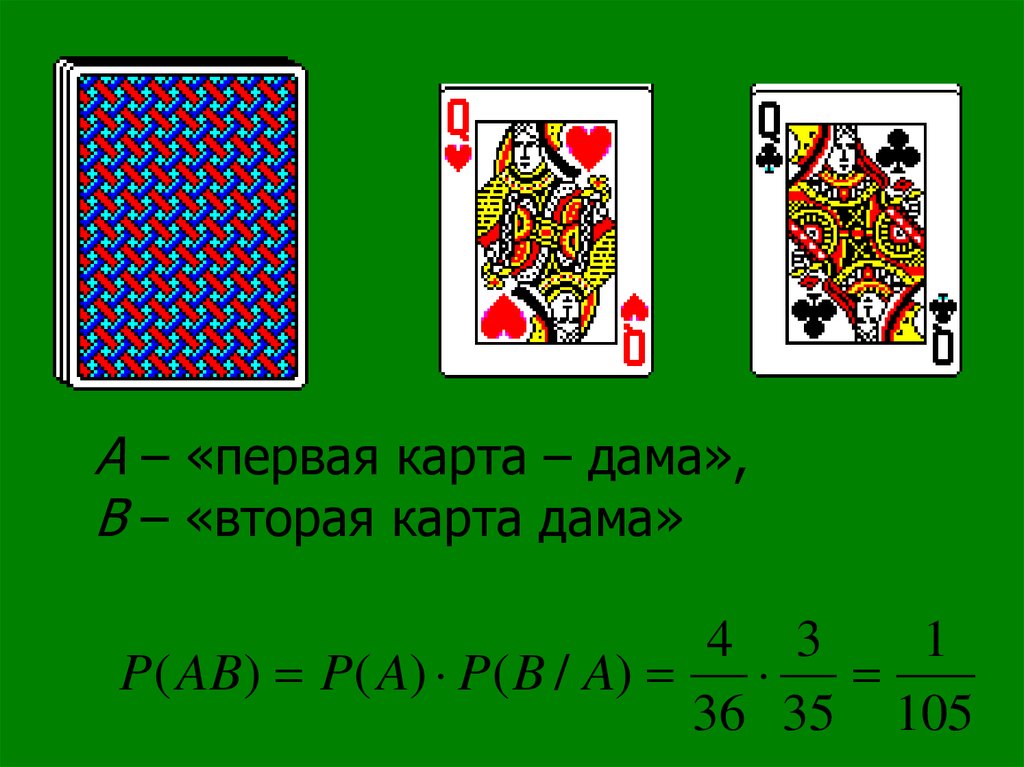
23.

А – «первая карта – дама»,
В – «вторая карта дама»
4 3
1
P( AB) P( A) P( B / A)
36 35 105
23

24. ТЕОРЕМА 2

Вероятность совместного появления
двух независимых событий равна
произведению их вероятностей, т.е.
P( AB) P( A) P( B)
24

25. ТЕОРЕМА 2

Усложненное строение буквы «а» за счет
повторения движения в овале Р(А)=0,06
Буква «д» с надстрочечным элементом
Р(В)=0,29
P( A В) 0,06 0,29 0,0174
25

26. ТЕОРЕМА 3

Если для двух событий выполняется
равенство
P( AB) P( A) P( B)
то эти события независимые.
26

27. ТЕОРЕМА 4

Вероятность совместного наступления
конечного числа событий равна произведению
вероятности одного из них на условные
вероятности всех остальных, причем условная
вероятность каждого последующего события
вычисляется в предположении, что все
предыдущие уже наступили, т.е.
P( A1 A2 ... An ) P( A1 ) P( A2 / A1 ) ... P( An / A1 A2 ... An 1 )
27

28.

Ю
Р
И
С
Т
А1 – первая буква «ю»,
А2 – вторая буква «р»,
А3 – третья буква «и»,
А4 – третья буква «с»,
А5 – пятая буква «т».
В - появится слово «юрист».
28

29.

Ю
Р
И
С
Т
P( B) P( A1 A2 A3 A4 A5 )
1 1 1 1 1
1
33 32 31 30 29 28480320
29

30. ТЕОРЕМА 5

Вероятность совместного появления несколь
событий, независимых в совокупности, равн
произведению вероятностей этих событий, т
P( A1 A2 A3 ... An ) P( A1 ) P( A2 ) P( A3 ) ... P( An )
30

31.

Ю
Р
И
С
Т
P( B) P( A1 A2 A3 A4 A5 )
1
1 1 1 1
33 33 33 33 33
1
39135393
31

32. 3. СУММА ВЕРОЯТНОСТЕЙ

32

33. ТЕОРЕМА 6

Вероятность появления одного из двух
несовместных событий, равна сумме
вероятностей этих событий, т.е.
P( A B) P( A) P( B)
33

34. 25 ЧЕЛОВЕК ИМЕЮТ СЛЕДУЮЩИЕ ОЦЕНКИ

ОТЛИЧНО -
5
ХОРОШО -
10
УДОВЛЕТВОРИТЕЛЬНО - 10
34

35.

Какова вероятность того, что
наугад вызванный курсант
отличник или хорошист?
35

36.

А – наугад вызванный курсант –
отличник,
В – наугад вызванный курсант –
хорошист.
P( A B) P( A) P( B)
5 / 25 10 / 25 0,6
36

37. ТЕОРЕМА 7

Вероятность появления одного из
нескольких попарно несовместных
событий равна сумме вероятностей этих
событий
P( A1 A2 A3 ... An )
P( A1 ) P( A2 ) P( A3 ) ... P( An )
37

38. СЛЕДСТВИЕ

Сумма вероятностей попарно
несовместных событий, образующих
полную группу, равна 1:
P( A1 A2 A3 ... An ) 1
38

39.

Два стрелка стреляют по одной и той же
цели. Вероятности поражения ими цели
соответственно равны 0,8 и 0,7.
Какова вероятность поражения цели?
39

40.

А1 – поражение цели первым стрелком,
А2 – поражение цели вторым стрелком,
В – поражение цели вообще
B A1 A2
Р( B) Р( A1 ) Р( A2 )
0,8 0,7 1,5
1 !!!!
40

41. ТЕОРЕМА 8

Вероятность появления хотя бы одного
из двух совместных событий равна
сумме вероятностей этих событий без
вероятности их совместного
наступления:
P( A B) P( A) P( B) P( AB)
41

42.

P( B) P( A1 ) P( A2 ) P( A1 A2 )
0,7 0,8 0,7 0,8 0,94
42

43. СЛЕДСТВИЕ

В случае трех совместных событий
вероятность их суммы вычисляется по
формуле:
P( A B C ) P( A) P( B) P(C )
P( AB) P( AC ) P( BC ) P( ABC )
43

44. ТЕОРЕМА 9

Вероятность появления хотя бы одного из
событий, независимых в совокупности, равна
разности между единицей и произведением
вероятностей противоположных событий:
P( A1 A2 ... An ) 1 P( A1 ) P( A2 ) ... P( An )
44

45.

P( B) 1 P( A1 ) P( A2 )
1 0,3 0,2 0,94
45

46. 3. Формула полной вероятности. Формула Байеса

46

47. ТЕОРЕМА 10

Вероятность события А, которое может наступить
только при условии появления одного из событий
В1, В2,...,Вn, образующих полную группу попарно
несовместных событий, равна сумме произведений
вероятностей каждого из этих событий на
соответствующую условную вероятность события
А, т.е.
P( A) P( B1 ) P( A / B1 )
P( B2 ) P( A / B2 ) ... P( Bn ) P( A / Bn )
47

48.

Вероятность того, что во время работы ПК произошел
сбой:
в арифметическом устройстве 0,3,
в оперативной памяти – 0,2,
в остальных устройствах – 0,5.
Вероятности обнаружения сбоя в арифметическом
устройстве, в оперативной памяти и в остальных
устройствах соответственно равны 0,8, 0,9, 0,9.
Найти вероятность того, что возникший в ПК сбой
будет обнаружен.
48

49.

Обозначим через А событие – сбой будет обнаружен.
Возможны следующие предположения (гипотезы):
В1 – сбой произошел в арифметическом устройстве,
В2 – сбой произошел в оперативной памяти,
В3 – сбой произошел в остальных устройствах.
Воспользуемся формулой полной вероятности:
P( A) P( B1 ) P( A / B1 ) P( B2 ) P( A / B2 )
P( B3 ) P( A / B3 )
0,3 0,8 0,2 0,9 0,5 0,9 0,87.
49