Похожие презентации:
Экстремумы функции и точки экстремума
1.
Найдите промежутки возрастания и убывания функции:1) у 3 0,5 х
2.
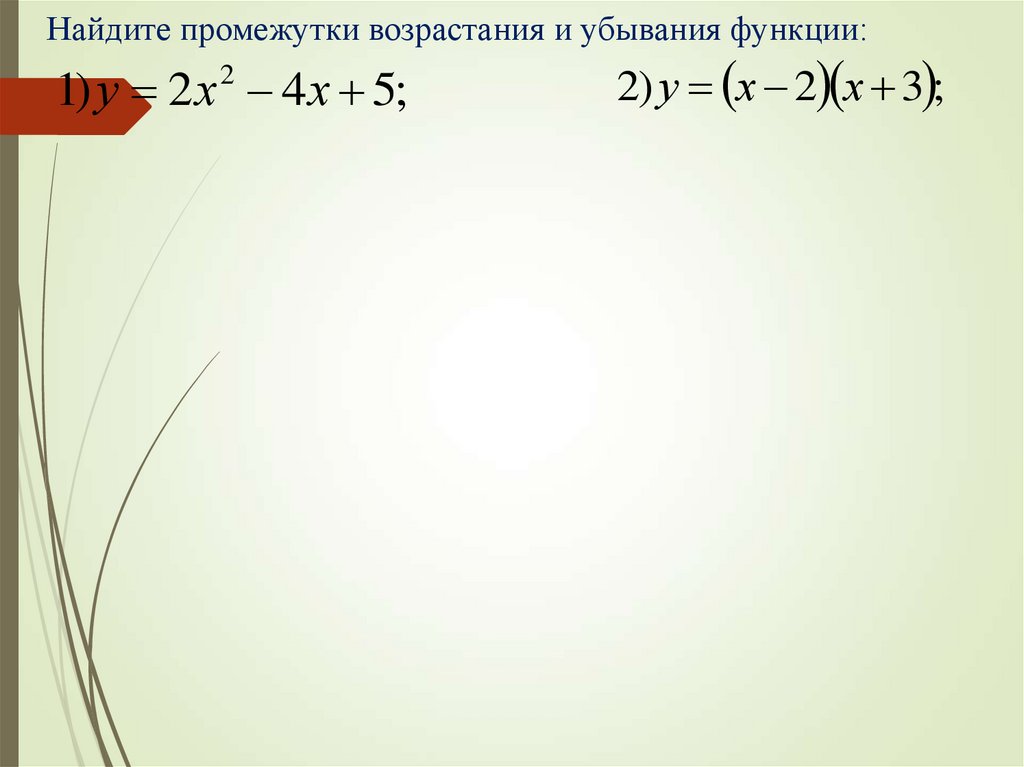
Найдите промежутки возрастания и убывания функции:1) у 2 х 4 х 5;
2
2) у х 2 х 3 ;
3.
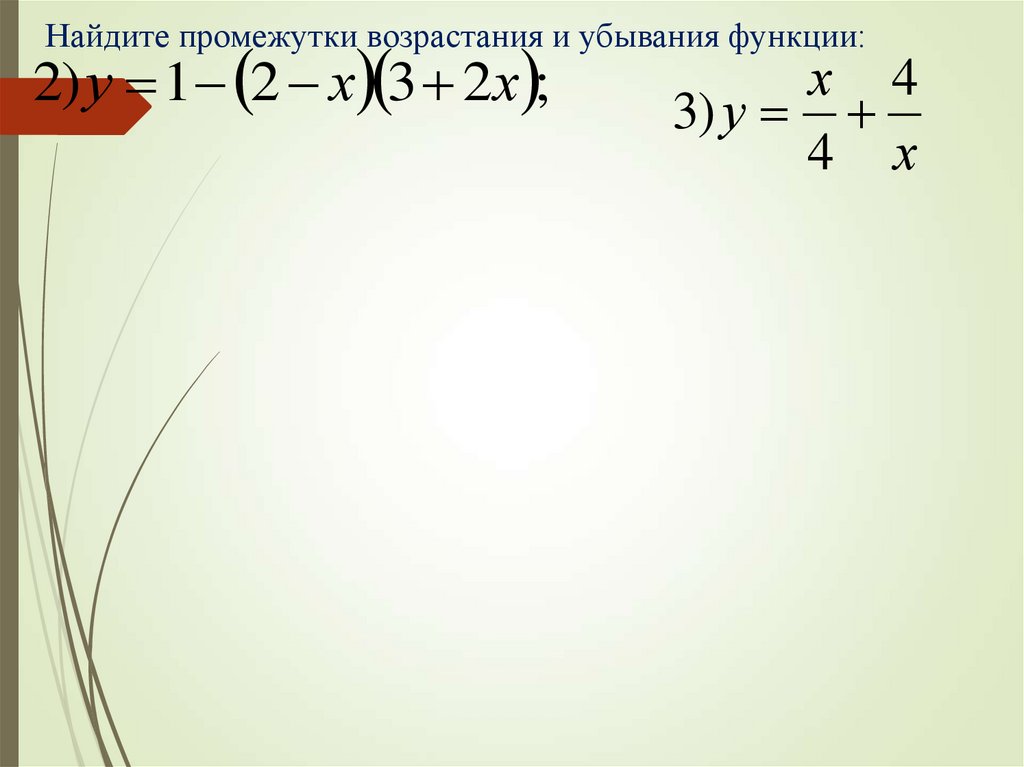
Найдите промежутки возрастания и убывания функции:2) у 1 2 х 3 2х ;
х 4
3) у
4 х
4.
Тема урокаПоведение функции вблизи
критических точек и практическое
применение максимума и минимума
5.
Цель обучения11.5.1.22 знать определения критических
точек и точек экстремума функции
Критерии успеха:
- находит критические точки и точки
экстремума
- умеет по графику данной функции
определять точки экстремума
6.
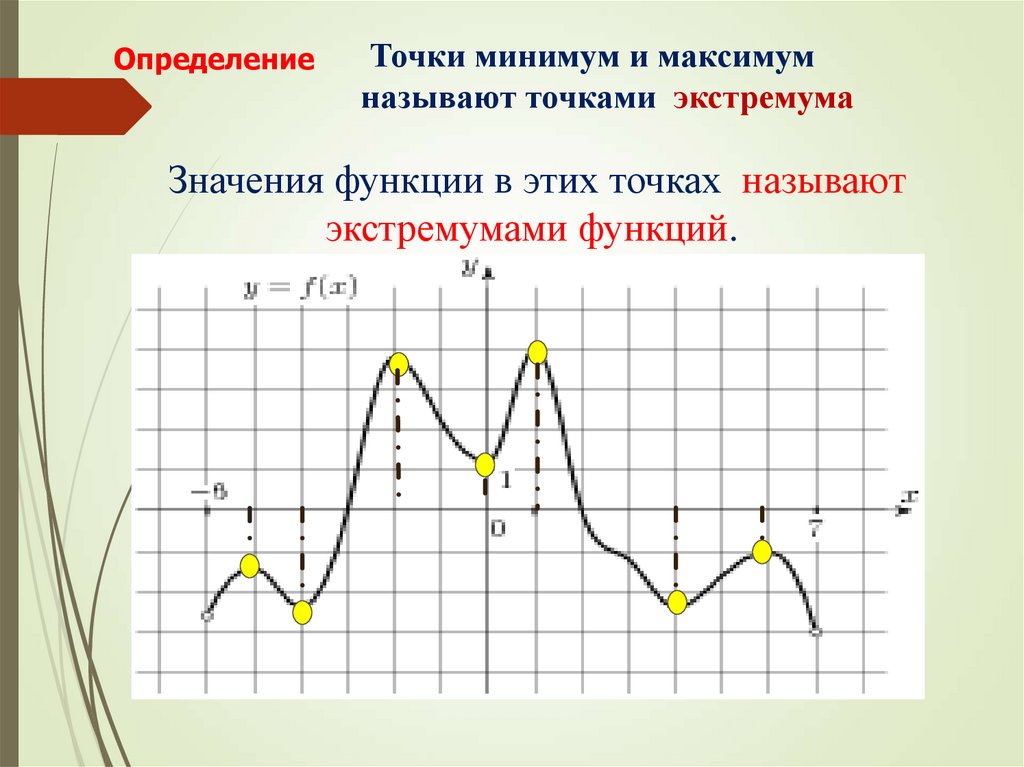
7. Значения функции в этих точках называют экстремумами функций.
Точки минимум и максимумназывают точками экстремума
Определение
Значения функции в этих точках называют
экстремумами функций.
.
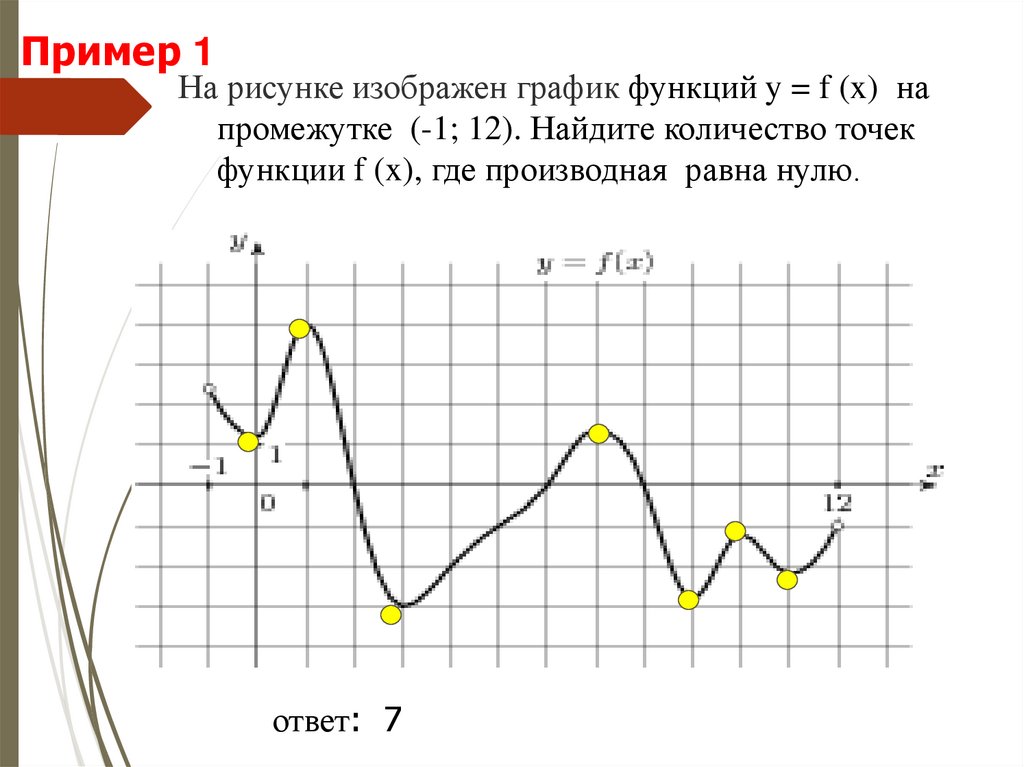
8. На рисунке изображен график функций y = f (x) на промежутке (-1; 12). Найдите количество точек функции f (x), где производная
Пример 1На рисунке изображен график функций y = f (x) на
промежутке (-1; 12). Найдите количество точек
функции f (x), где производная равна нулю.
ответ: 7
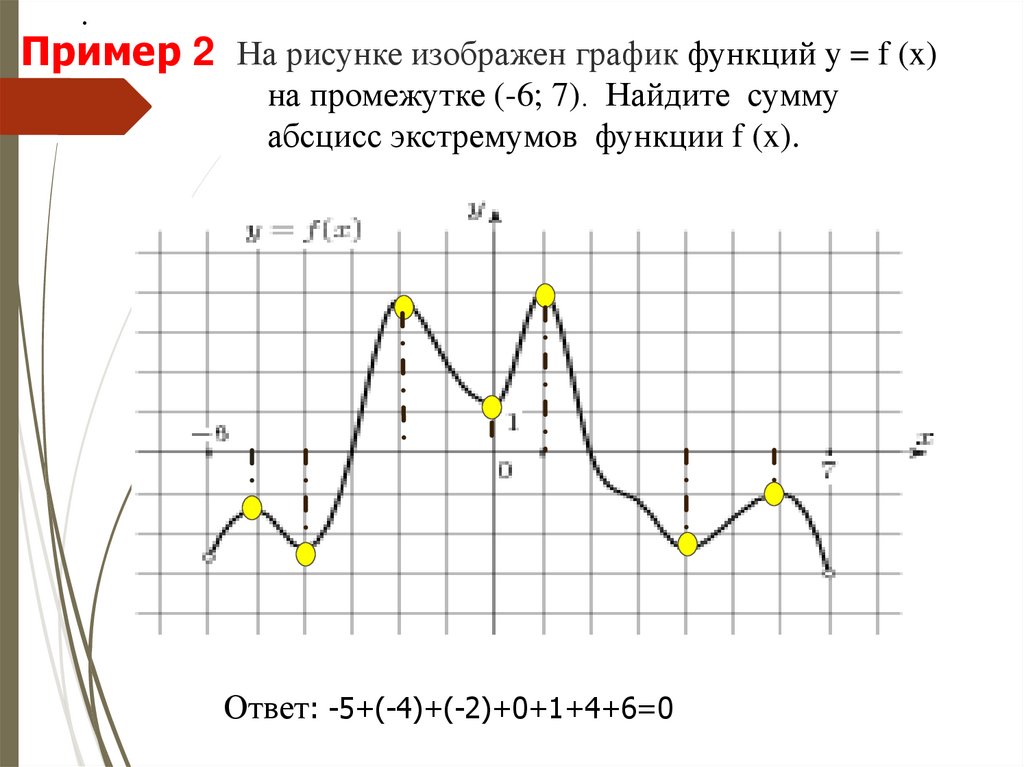
9. На рисунке изображен график функций y = f (x) на промежутке (-6; 7). Найдите сумму абсцисс экстремумов функции f (x).
.Пример 2 На рисунке изображен график функций y = f (x)
на промежутке (-6; 7). Найдите сумму
абсцисс экстремумов функции f (x).
.
Ответ: -5+(-4)+(-2)+0+1+4+6=0
10.
ТЕОРЕМАЕсли точка х0 является точкой
экстремума функции f , и в этой точке
существует производная f ', то она
равняется нулю: f'(x0)=0.
11.
Признак максимума функцииЕсли функция f в точке х0 непрерывна и на интервале
(а, х0) f '(x) > 0 , а на интервале (х0,b) f '(x)< 0, то точка
х0 является точкой максимума функции f.
Признак минимума функции
Если функция f в точке х0 непрерывна и на интервале
(а, х0) f '(x)< 0, а на интервале (х0,b) f '(x) > 0, то точка
х0 является точкой минимума функции f.
f'(x) + х1
f(x)
max
-
х2
min
+
х3
max
-
12.
Признак максимума функции(а;b)
(a; x0)
x0
(x0;b)
f ‘ (x)
+
0
-
f (x)
max
fmax(x) = f (x0)
Признак минимума функции
(а;b)
(a; x0)
x0
(x0;b)
f ‘ (x)
-
0
+
f (x)
min
fmin(x) = f (x0)







 Математика
Математика








