Похожие презентации:
Проводники в электростатическом поле
1. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
2.
• Под действием электрического поля зарядыв проводнике начинают перемещаться
Перемещение зарядов происходит до
тех пор, пока в проводнике не
установится равновесное
распределение зарядов
При равновесном распределении
зарядов поле внутри проводника равно
нулю.
3.
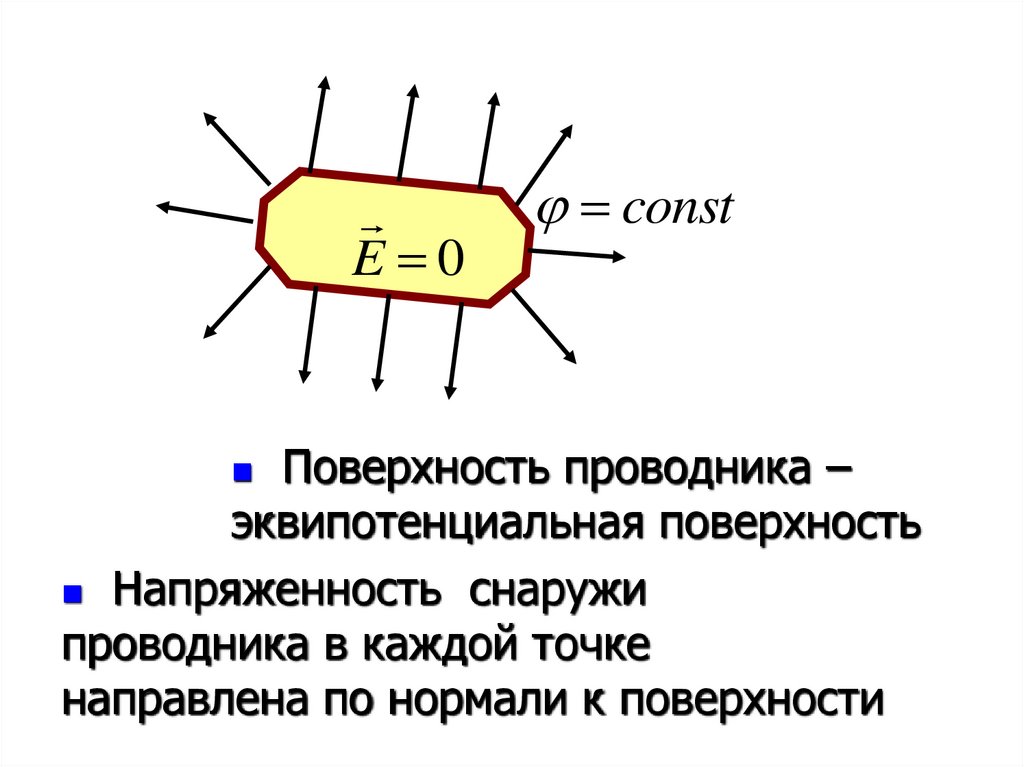
E 0const
Поверхность проводника –
эквипотенциальная поверхность
Напряженность снаружи
проводника в каждой точке
направлена по нормали к поверхности
4.
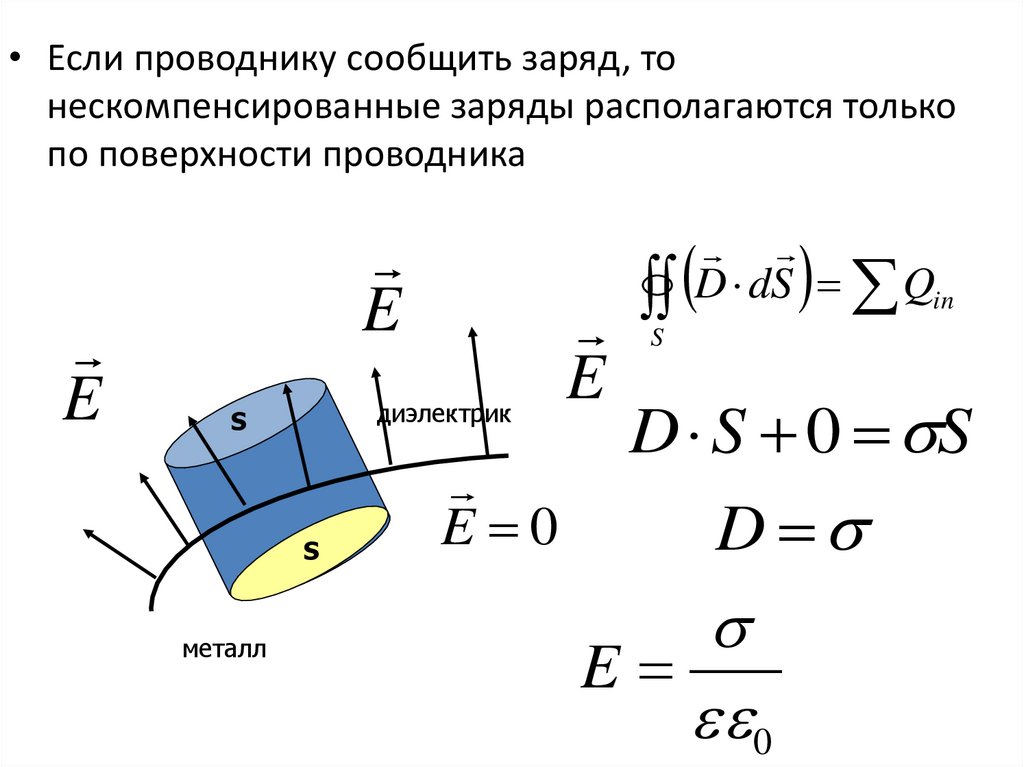
• Если проводнику сообщить заряд, тонескомпенсированные заряды располагаются только
по поверхности проводника
E
E
диэлектрик
S
S
металл
E
D S 0 S
E 0
D
E
0
D dS Qin
S
5.
• Напряженность уповерхности
проводника любой
формы определяется
поверхностной
плотностью
свободных зарядов
E
0
6.
-+
+
+
- +
+
+
-
-
E
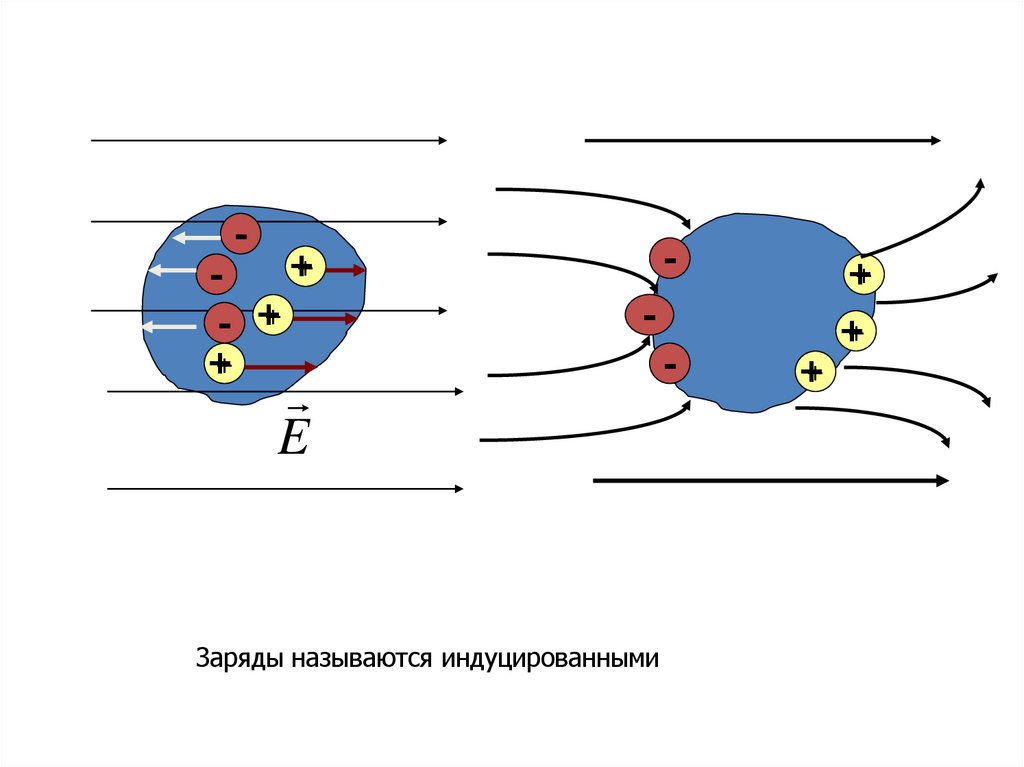
Заряды называются индуцированными
-
E 0
+
+
+
+
+
+
7.
Заряды называются индуцированными ираспределяются по поверхности
проводника
Нейтральный проводник, внесенный в
электростатическре поле, разрывает
линии напряженности: они начинаются
на положительных индуцированных
зарядах и заканчиваются на
отрицательных
8. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ УЕДИНЕННОГО ПРОВОДНИКА
9.
• Емкость уединенногопроводника – это
заряд, который
необходимо сообщить
проводнику, чтобы
изменить его
потенциал на единицу.
C
Q
10.
• Емкость проводника зависит от размеров иформы, но не зависит от типа материала и
агрегатного состояния проводника
• Единица измерения емкости - фарад
11. ПРИМЕР: емкость шара
εC
R
C 1
R 9 10
Емкость Земли 0.6 мкФ
6 км
Q
kQ
R
Q
C k R
12. Конденсаторы
13.
• Конденсаторами называются устройства,обладающие большой емкостью
Конденсаторы, должны иметь такую
форму, чтобы все поле было
сосредоточено между пластинами
Конденсаторы бывают
Плоскими
Сферическими
Цилиндрическими
14. Емкость конденсатора
QC
1 2
1
-разность потенциалов
2 между обкладками
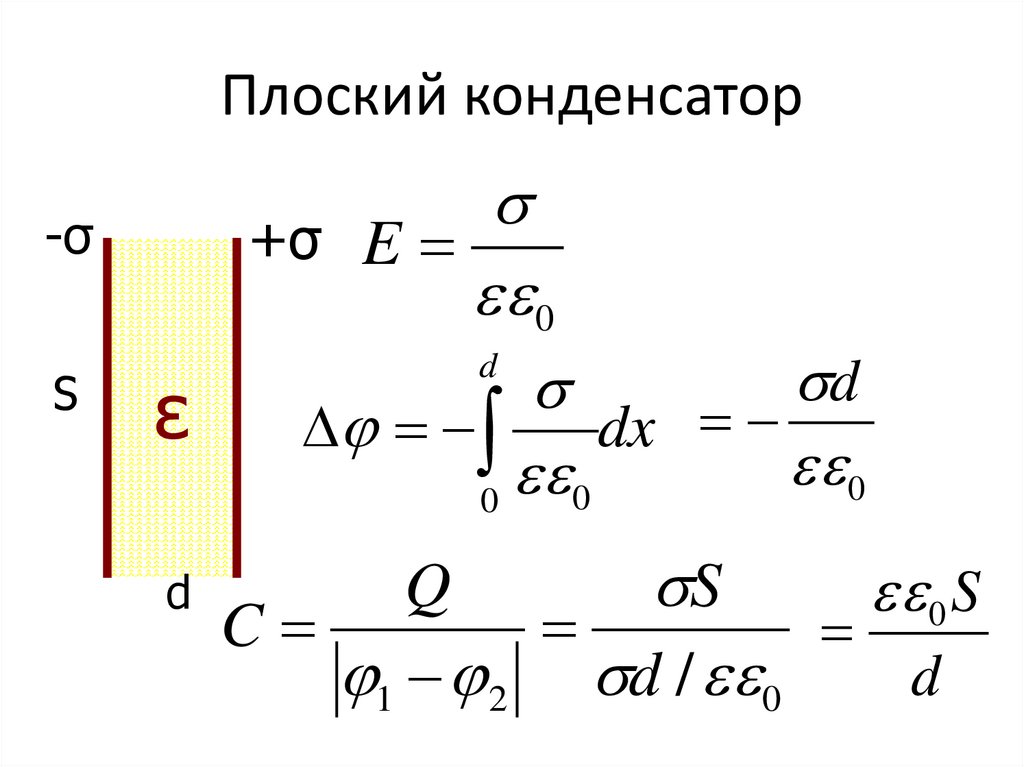
15. Плоский конденсатор
+σ E0
-σ
S
ε
d
d
dx
0
0
0
d
Q
S
0 S
C
d
1 2 d / 0
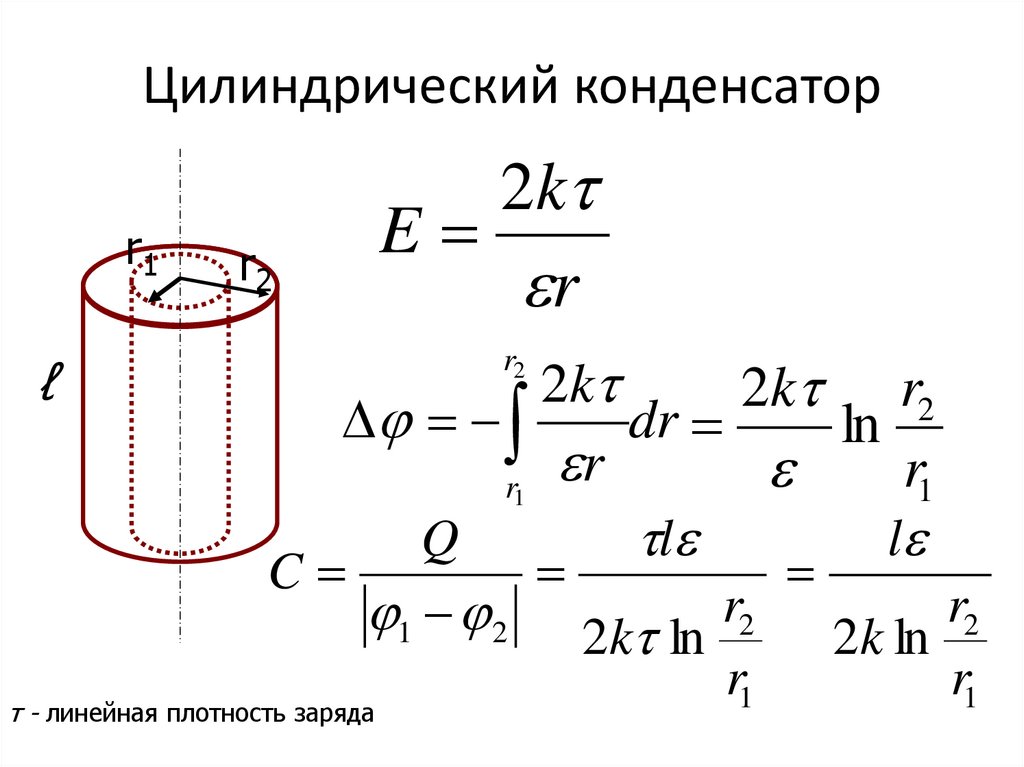
16. Цилиндрический конденсатор
r1ℓ
r2
2k
E
r
2k
2k r2
dr
ln
r
r1
r1
Q
l
l
C
1 2 2k ln r2 2k ln r2
τ - линейная плотность заряда
r2
r1
r1
17. Сферический конденсатор
-Qr1
+Q
r2
kQ kQ
1 2
r1 r2
Q
Q
r
r
1
2
C
1 2 kQ kQ k (r2 r1 )
r1 r2
18. ЭНЕРГИЯ СИСТЕМЫ НЕПОДВИЖНЫХ ТОЧЕЧНЫХ ЗАРЯДОВ
19.
rQ1
Q2
• Найдем энергию, которой обладает 1
заряд в поле второго
W12 Q1 12
kQ2
Q1
r
Энергия 2 заряда в поле первого
W21 Q2 21
kQ1
Q2
r
20.
W12 W21 W1
1
W (W12 W21 ) (Q1 12 Q2 21 )
2
2
1 N
W Qi i
2 i 1
φi – потенциал,
создаваемый в той
точке, где находится
заряд, остальными
зарядами
21. Энергия заряженного уединенного проводника
• Пусть имеется проводник с емкостью CЧтобы увеличить заряд проводника на dq
надо совершить работу
dA dq
dq Cd
C
q
dA C d
22.
CA C d
2
0
2
Энергия проводника – это работа ,
затраченная на его зарядку
C
W
2
2
2
Q
2C
Q
2
23. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
CW
2
2
2
Q
2C
Q
2
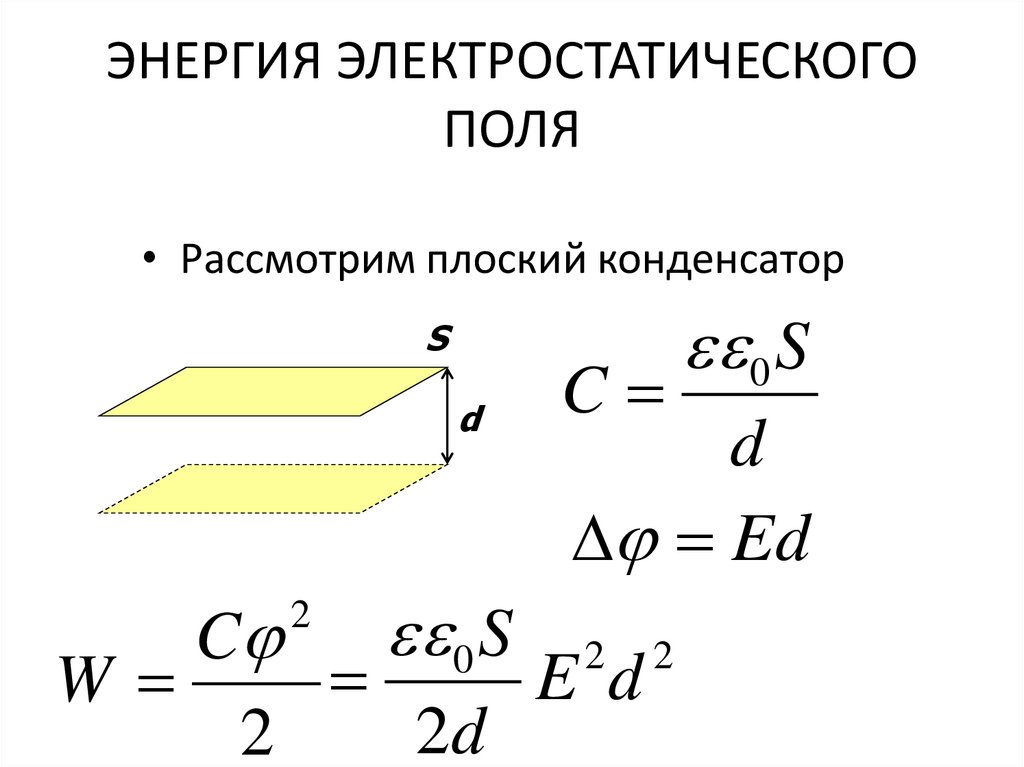
24. ЭНЕРГИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
• Рассмотрим плоский конденсаторS
d
C
d
Ed
0 S 2 2
C
E d
W
2d
2
2
0 S
25.
• Объем конденсатораV Sd
0 Sd 2 0V 2
E
W
E
2
2
26.
Введем объемную плотность энергииW
V
2
Дж
0 E
3
м
2
27.
• В общем случае , чтобы найти энергиюэлектрического поля, надо интегрировать
объемную плотность


















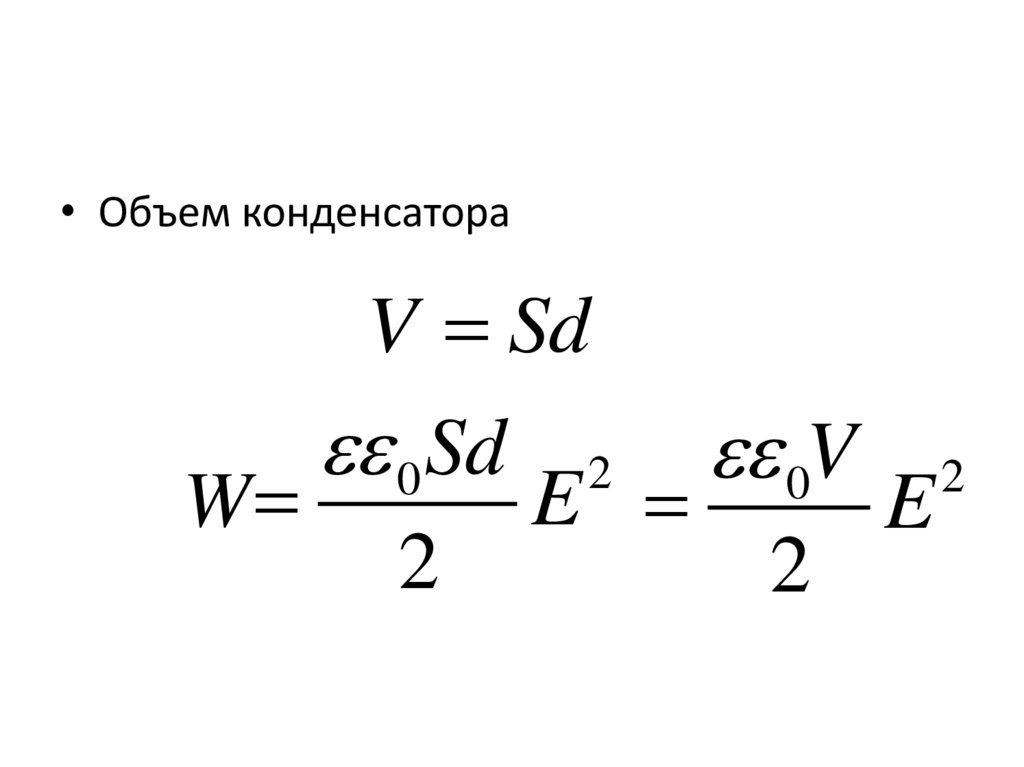
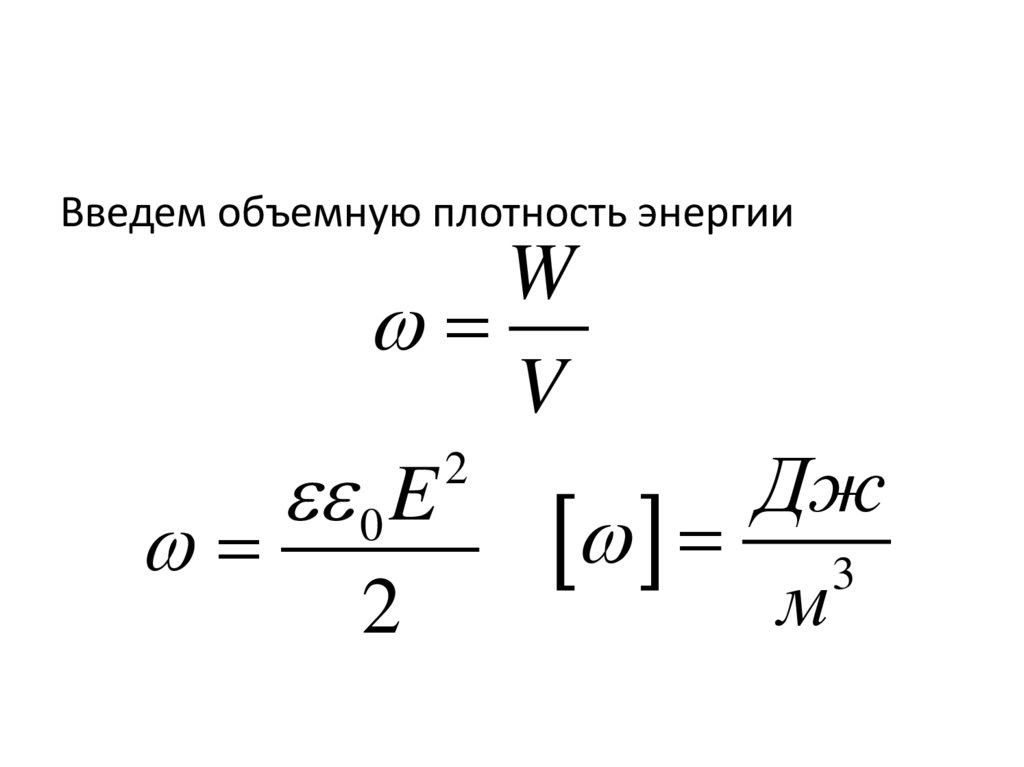

 Физика
Физика








