Электрическое поле заряженных проводников. Энергия электростатического поля. Лекция 4

1. Лекция 4-2020. Электрическое поле заряженных проводников. Энергия электростатического поля.

1 Поле вблизи поверхности проводника
2 Электроемкость проводников и конденсаторов
3 Емкости плоского, цилиндрического и сферического
конденсаторов
4 Энергия системы неподвижных зарядов
5 Энергия заряженного проводника, конденсатора
6 Плотность энергии электростатического поля

2.

Ироничные цитаты
Если бы не было электричества, мы бы
смотрели телевизор в темноте.
Муаммар аль-Каддафи
А.С. Чуев. 2020
2

3.

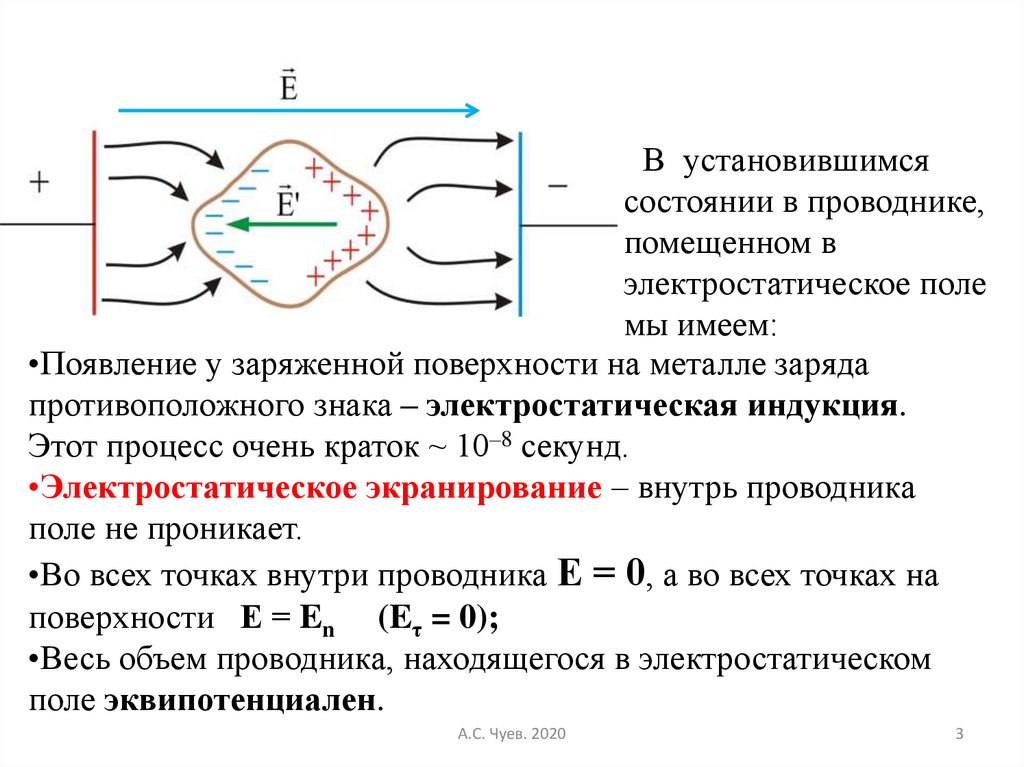
В установившимся
состоянии в проводнике,
помещенном в
электростатическое поле
мы имеем:
•Появление у заряженной поверхности на металле заряда
противоположного знака – электростатическая индукция.
Этот процесс очень краток ~ 10–8 секунд.
•Электростатическое экранирование – внутрь проводника
поле не проникает.
•Во всех точках внутри проводника Е = 0, а во всех точках на
поверхности Е = En (Eτ = 0);
•Весь объем проводника, находящегося в электростатическом
поле эквипотенциален.
А.С. Чуев. 2020
3

4.

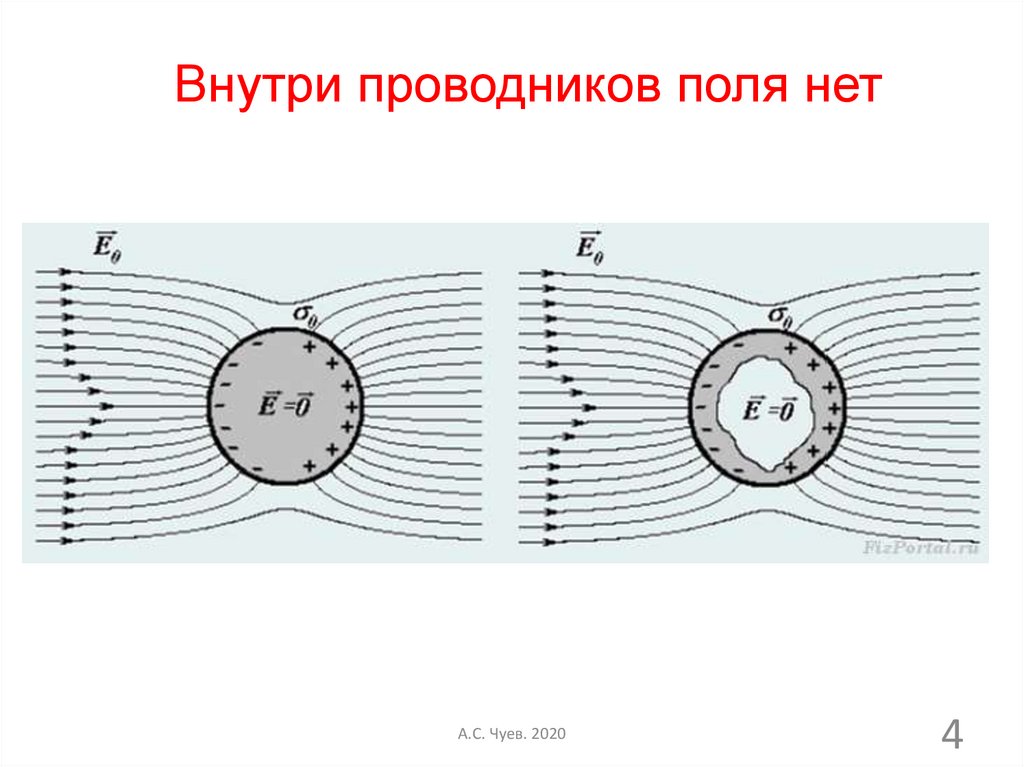
Внутри проводников поля нет
А.С. Чуев. 2020
4

5.

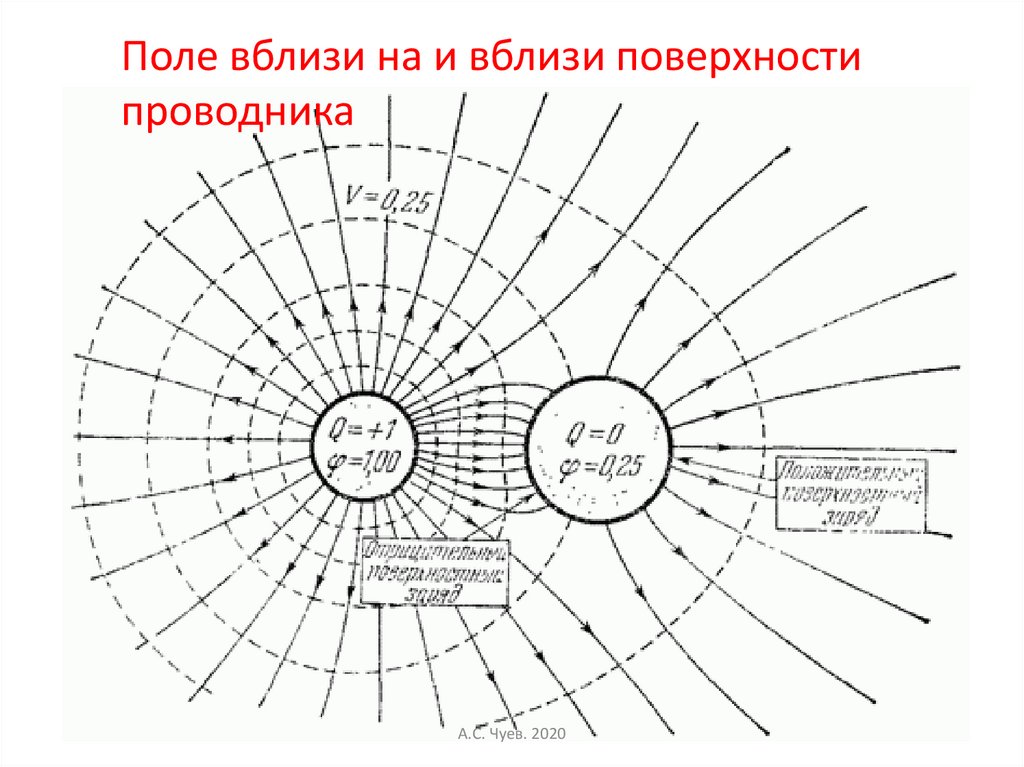
Поле вблизи на и вблизи поверхности
проводника
А.С. Чуев. 2020
5

6.

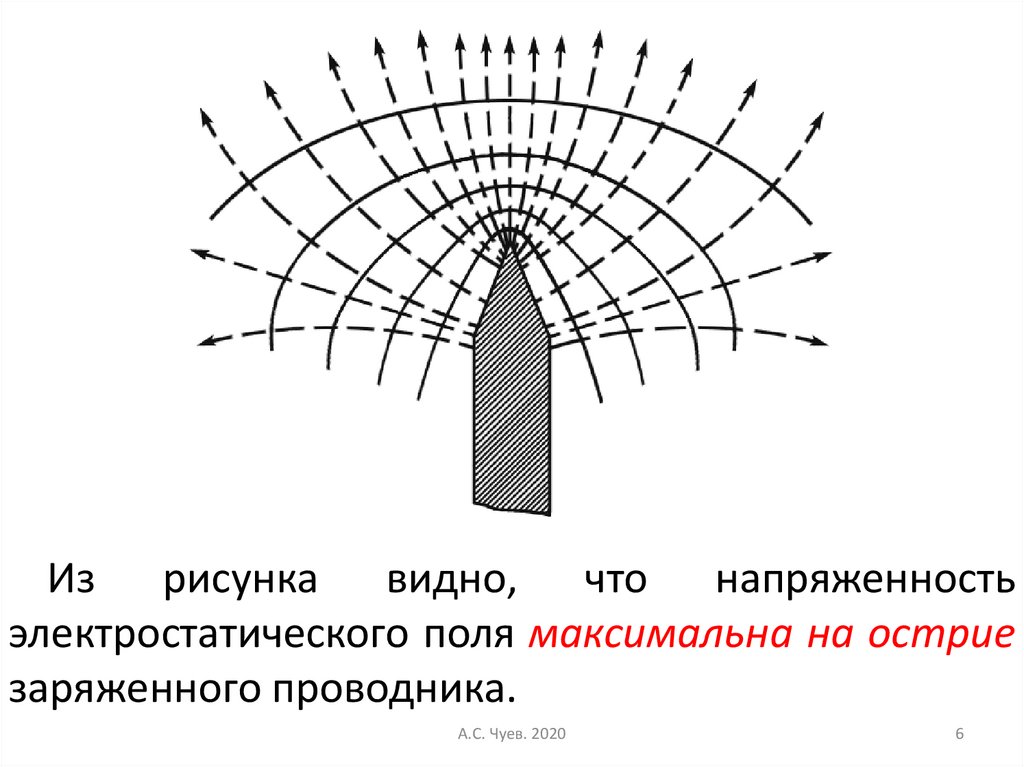
Из рисунка видно, что напряженность
электростатического поля максимальна на острие
заряженного проводника.
А.С. Чуев. 2020
6

7.

А.С. Чуев. 2020
7

8. Электрическая емкость. Конденсаторы.

При сообщении проводнику заряда, на его поверхности
появляется потенциал φ. Если такой же заряд сообщить
другому проводнику, то потенциал будет другой. Это
зависит от геометрических параметров проводника. Но в
любом случае, потенциал φ будет пропорционален заряду
q.
q = Cφ
Коэффициент пропорциональности С есть электроемкость –
физическая величина, численно равная заряду, который
необходимо сообщить проводнику для того, чтобы
изменить его потенциал на единицу.
• Единица измерения емкости в СИ – фарада 1 Ф = 1Кл / 1В.
• Размерность емкости: определить самостоятельно.
А.С. Чуев. 2020
8

9.

А.С. Чуев. 2020
9

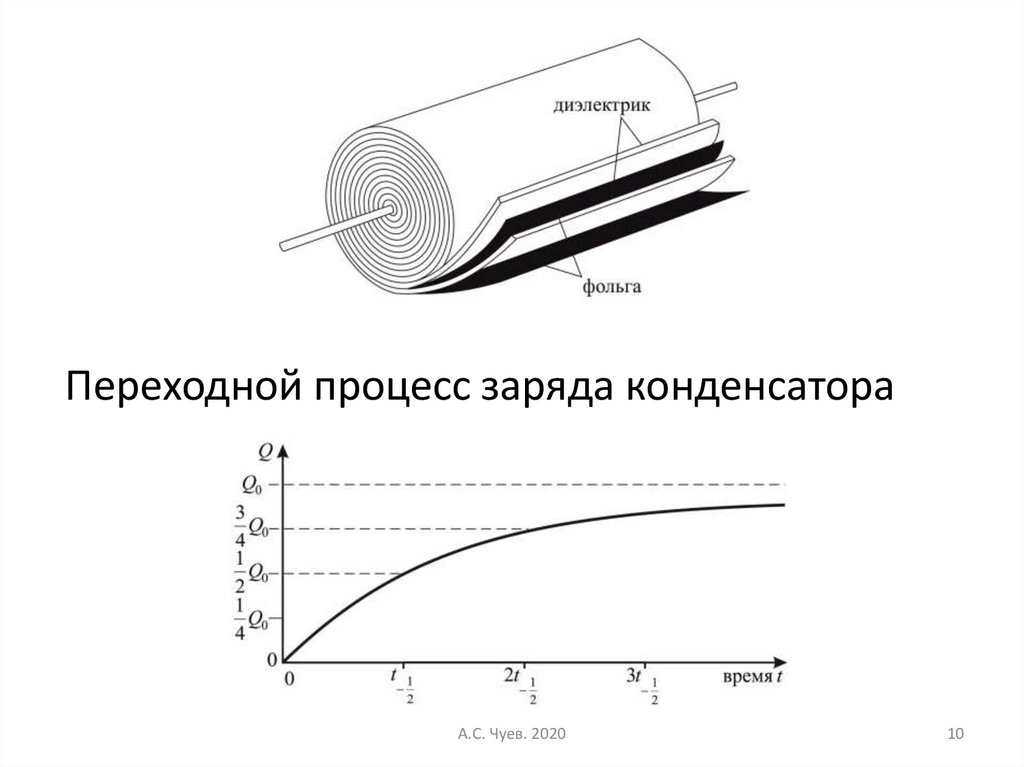
10.

Переходной процесс заряда конденсатора
А.С. Чуев. 2020
10

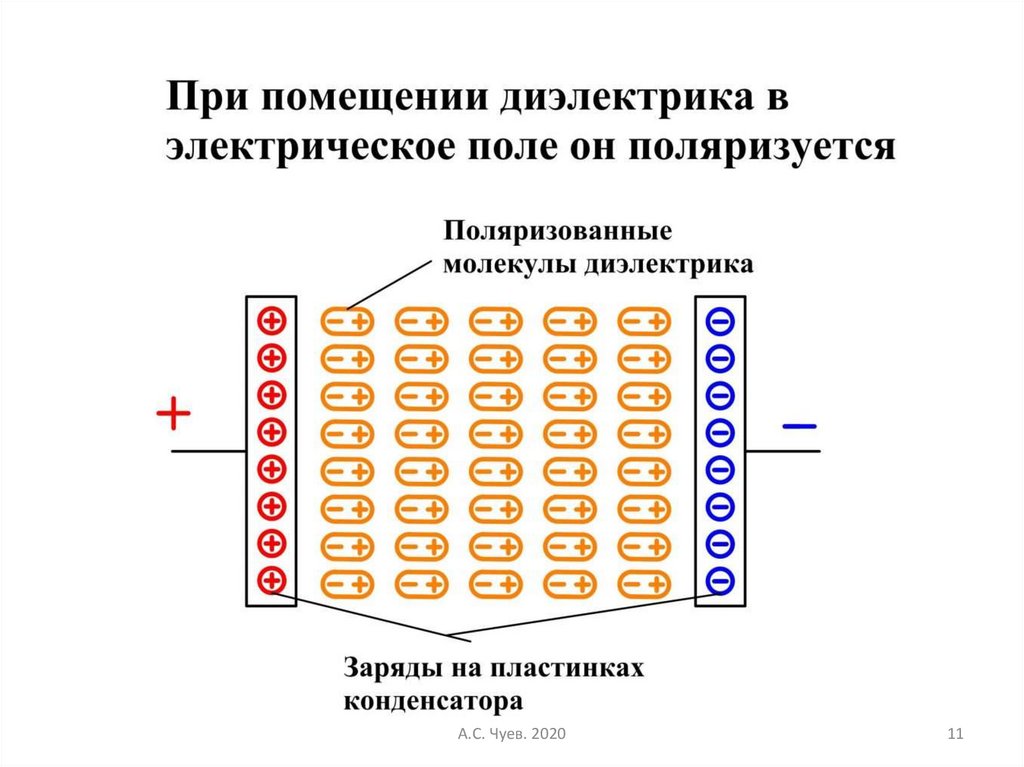
11.

А.С. Чуев. 2020
11

12. Расчет емкости различных конденсаторов

Емкость плоского конденсатора.
σ
1 2 Edx
d
E
;
0
ε 0ε
где
d – расстояние между пластинами.
,
Так как заряд q σS , то
q
S
C
0
1 2
d
А.С. Чуев. 2020
12

13.

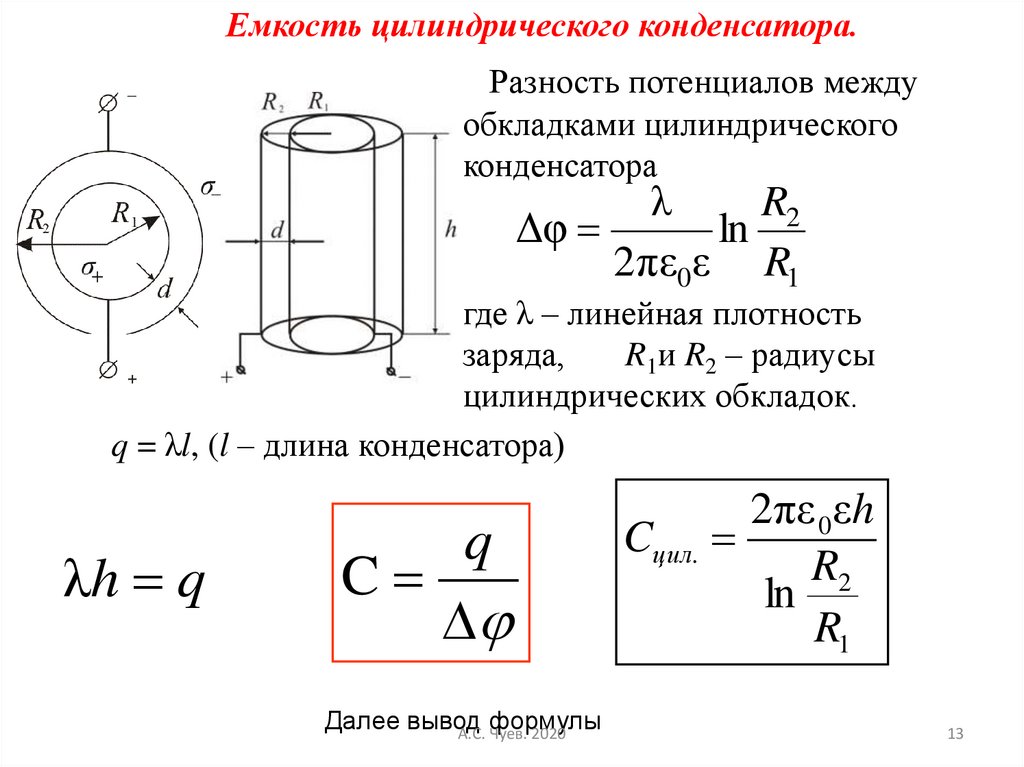
Емкость цилиндрического конденсатора.
Разность потенциалов между
обкладками цилиндрического
конденсатора
λ
R2
Δφ
ln
2πε0ε R1
где λ – линейная плотность
заряда,
R1и R2 – радиусы
цилиндрических обкладок.
q = λl, (l – длина конденсатора)
λh q
q
C
Далее вывод
формулы
А.С. Чуев. 2020
Cцил.
2 πε 0 εh
R2
ln
R1
13

14. Вывод формулы цилиндрического конденсатора

1
Е
0 2 r
q
λ
h
R2
Е
R2
1 q
ε 0 2 πrh
R2
qdr
q
dr
1 2 Edr
;
2πε0 rh 2πε0 h R1 r
R1
R1
q
R2
1 2
ln
2πε 0 h R1
2πε0 h
q
С
1 2 ln R2
R1
Если зазор между обкладками мал: d = R2 – R1, то d << R1, тогда
R2 R2 R1
ln
R1
R1
2 πε 0 hR1
S
Cцил .
ε0
R2 R1
d
А.С. Чуев. 2020
14

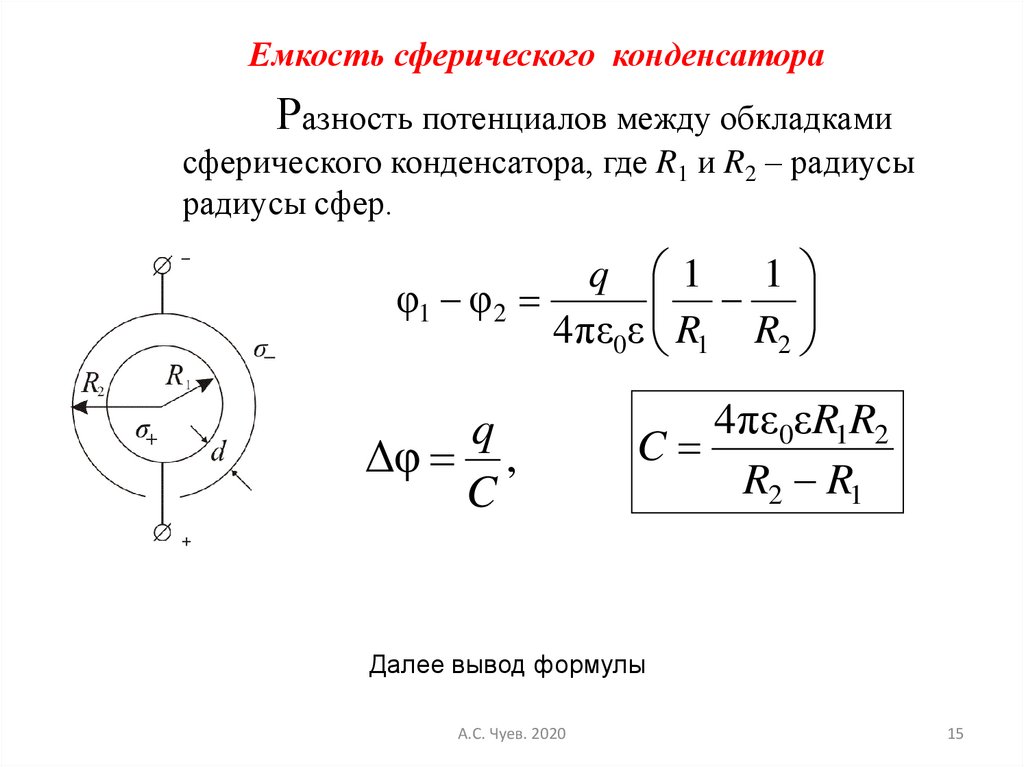
15.

Емкость сферического конденсатора
Разность потенциалов между обкладками
сферического конденсатора, где R1 и R2 – радиусы
радиусы сфер.
q 1
1
φ1 φ 2
4 πε0ε R1 R2
q
Δφ ,
C
4πε0εR1R2
C
R2 R1
Далее вывод формулы
А.С. Чуев. 2020
15

16. Вывод формулы сферического конденсатора (без учета диэлектрика)

R2
R2
qdr
q
1 2 Edr
2
4
πε
r
4πε 0
0
R1
R1
q 1 1
dr
R r 2 4πε0 R1 R2 ;
1
R2
4πε 0
q
С
;
1 2 1 1
R1 R2
А.С. Чуев. 2020
16

17.

В тонком сферическом конденсаторе R1 ≈ R2; S = 4πR2;
R2 – R1 = d – расстояние между обкладками. Тогда
Cсфер .
4πε 0 R 2
S
ε0 .
d
d
Таким образом, емкость тонкого сферического конденсатора,
S
Ссфер . 0 ,
d
совпадает с формулой емкости плоского конденсатора.
А.С. Чуев. 2020
17

18.

А.С. Чуев. 2020
18

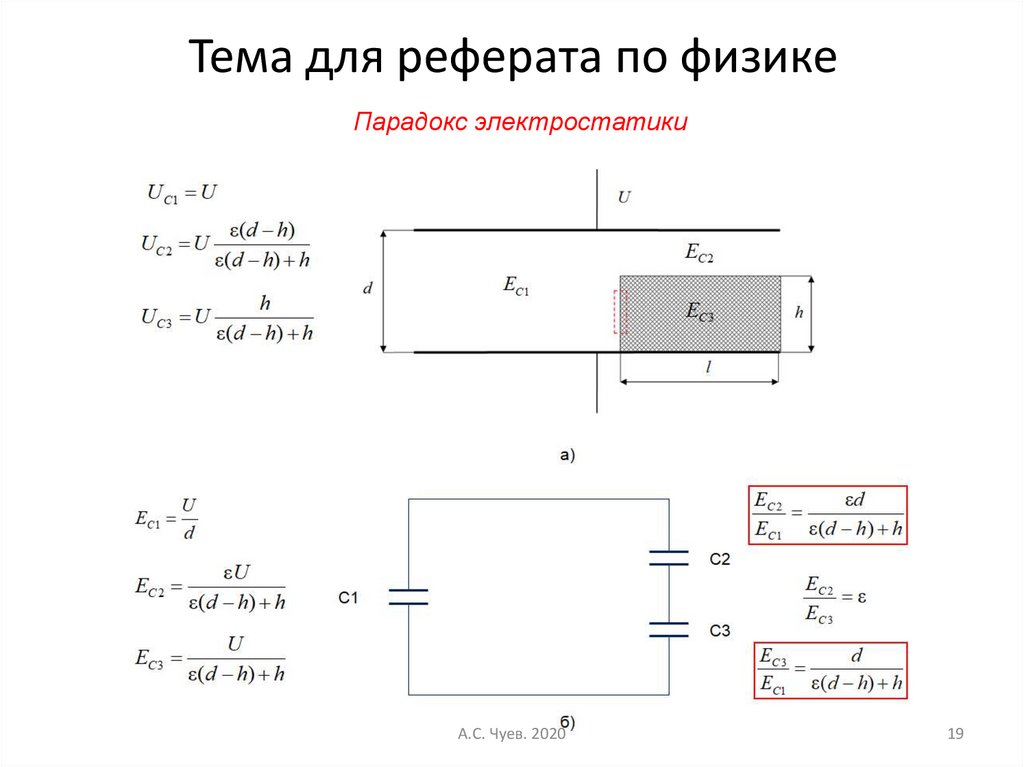
19. Тема для реферата по физике

Парадокс электростатики
А.С. Чуев. 2020
19

20. Энергия заряженного конденсатора

При полном разряде конденсатора, заряженного до напряжения
U, между обкладками проходит заряд dq, при этом работа
dA = Udq.
Работа равна убыли потенциальной энергии конденсатора:
dA = – dW.
Так как q = CU, то dA = CUdU, а полная работа
A dA.
0
1
A W C UdU CU 2
2
U
А.С. Чуев. 2020
20

21.

CU
Wc
2
2
Энергию конденсатора можно определить и по другим
формулам:
2
q
1
Wc
qU
2C 2
А.С. Чуев. 2020
21

22. Энергия электростатического поля (в вакууме)

Носителем энергии в конденсаторе
является электростатическое поле.
CU
0 SU d 0 U
W
Sd
2
2d d 2 d
2
2
2
0 E
W
V
2
2
U
E ; Sd = V – объем. Отсюда:
d
А.С. Чуев. 2020
22

23.

Если поле однородно, то можно посчитать
удельную энергию - w:
0 E
w
2
W
w ;
V
Так как D = ε0εE, то
2
ED
w
2
Формулы справедливы только для
однородного поля.
А.С. Чуев. 2020
23

24. Энергия системы неподвижных зарядов

Если поле создано двумя точечными
зарядами q1 и q2, то
W1 q1φ12
W2 q2φ 21
Здесь φ12 – потенциал поля, создаваемого
зарядом q2 в точке, где расположен заряд q1,
φ21 – потенциал поля от заряда q1 в точке с
зарядом q2.
А.С. Чуев. 2020
24

25.

Для вакуума можно записать
q2
φ12
4πε0r
q1
φ 21
4πε0r
r – расстояние между зарядами.
Из двух последних систем уравнений следует, что
q1q2
W1 W2
W
4πε0r
1
1
1
W W1 W2 (q1φ12 q2φ21 ).
2
2
2
N
1
Энергия системы из N зарядов, : W qi φi
2 i 1
φi φ k
k i
потенциал в точке, где расположен заряд qi,
создаваемый всеми остальными зарядами (кроме qi).
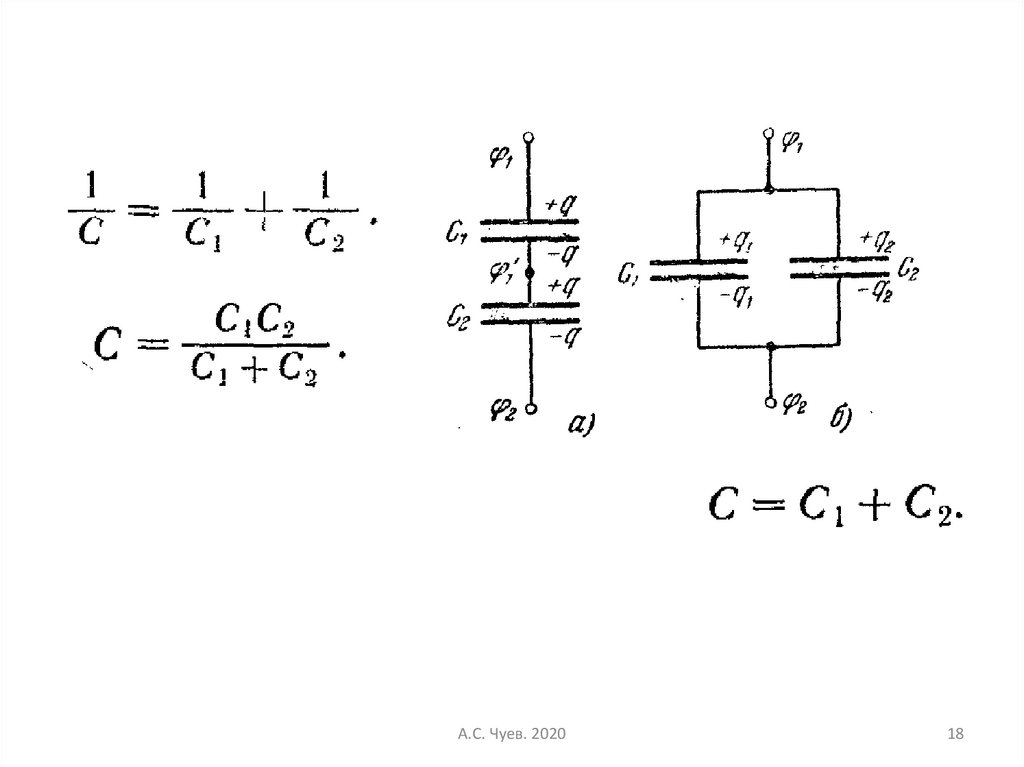
Соединения конденсаторов
- самостоятельно
А.С. Чуев. 2020
25

26.

А.С. Чуев. 2020
26

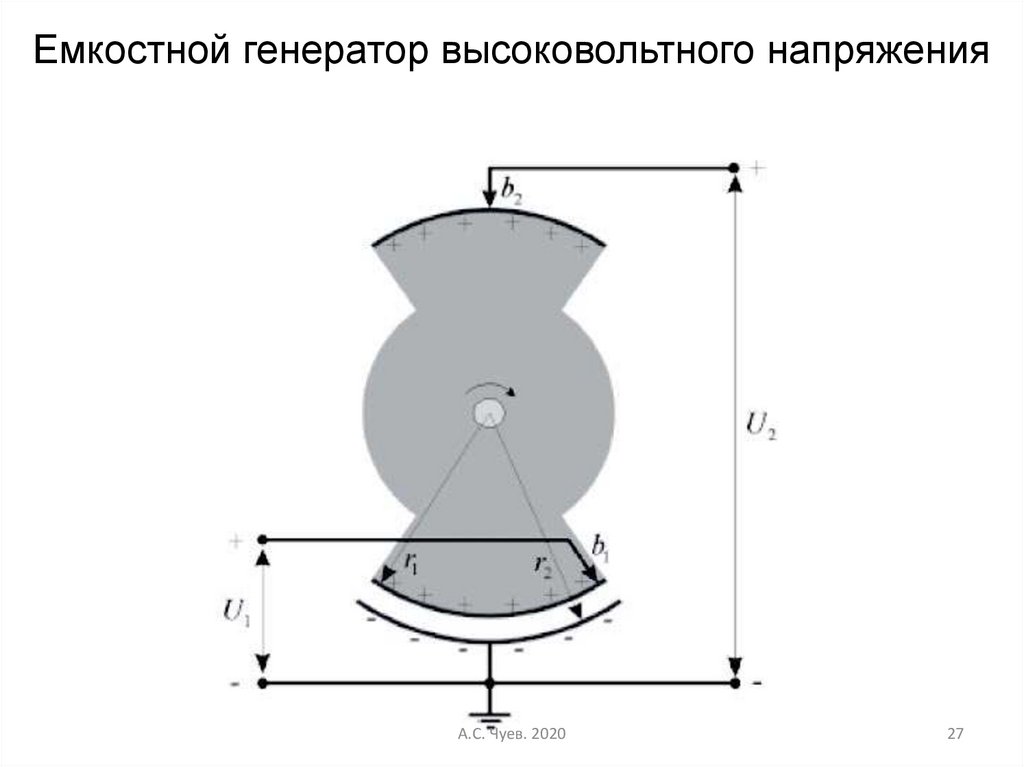
27.

Емкостной генератор высоковольтного напряжения
А.С. Чуев. 2020
27

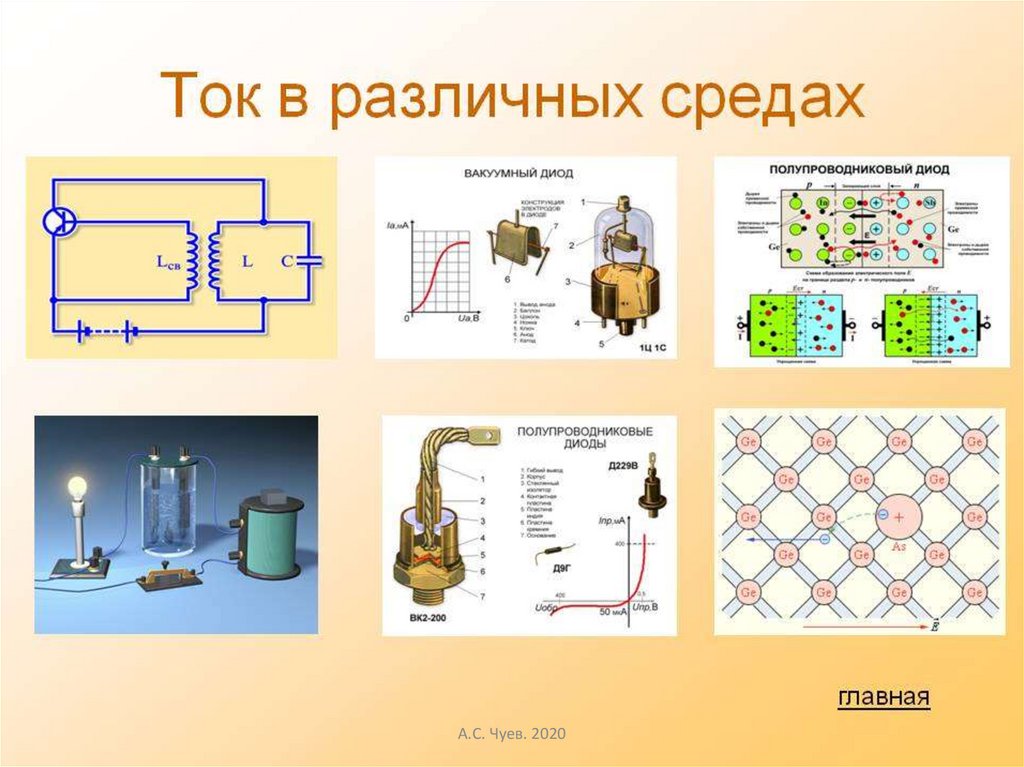
28. Тема «ЭЛЕКТРИЧЕСКИЙ ТОК» (прорабатывается студентами самостоятельно)

Носители тока в средах
Сила и плотность тока
Уравнение непрерывности
Электрическое поле в проводнике с током
Сторонние силы
Закон Ома и Джоуля-Ленца в интегральной
и дифференциальной формах
А.С. Чуев. 2020
28

29.

А.С. Чуев. 2020
29

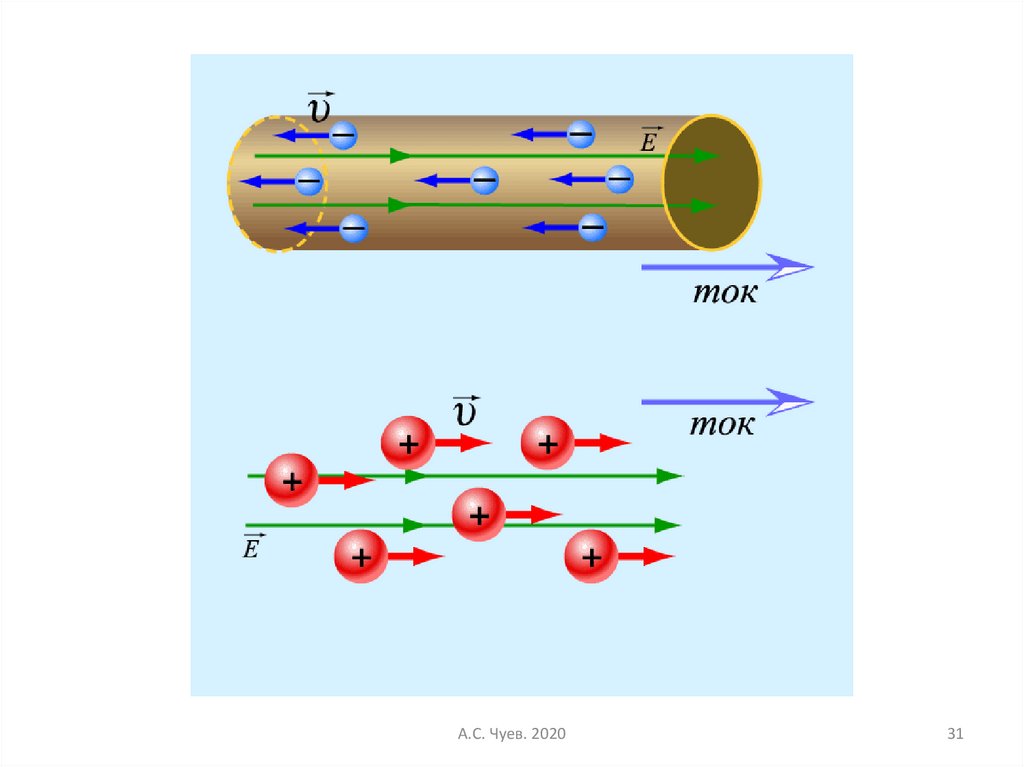
30.

Носители тока в средах.
Сила и плотность тока.
А.С. Чуев. 2020
30

31.

А.С. Чуев. 2020
31

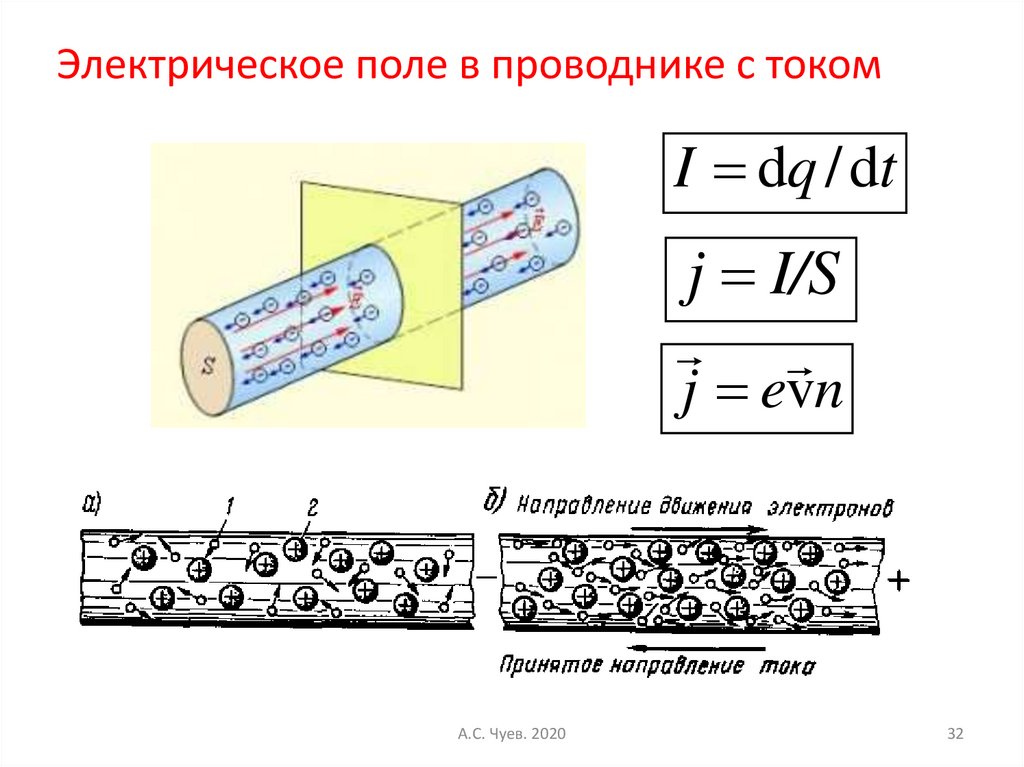
32.

Электрическое поле в проводнике с током
I dq / dt
j I/S
j evn
А.С. Чуев. 2020
32

33.

Уравнение непрерывности
q
S j S t
ρ
divj
t
А.С. Чуев. 2020
Интегральная
форма
Дифференциальная
форма
33

34.

Закон Ома
С учетом, что
Получим
U Ed l Ed S
I
R ρ dl
ρ
dS
dI
1
j
E
dS ρ
j E
Это закон Ома в дифференциальной форме.
Здесь σ 1 / ρ – удельная электрическая
проводимость.
А.С. Чуев. 2020
34

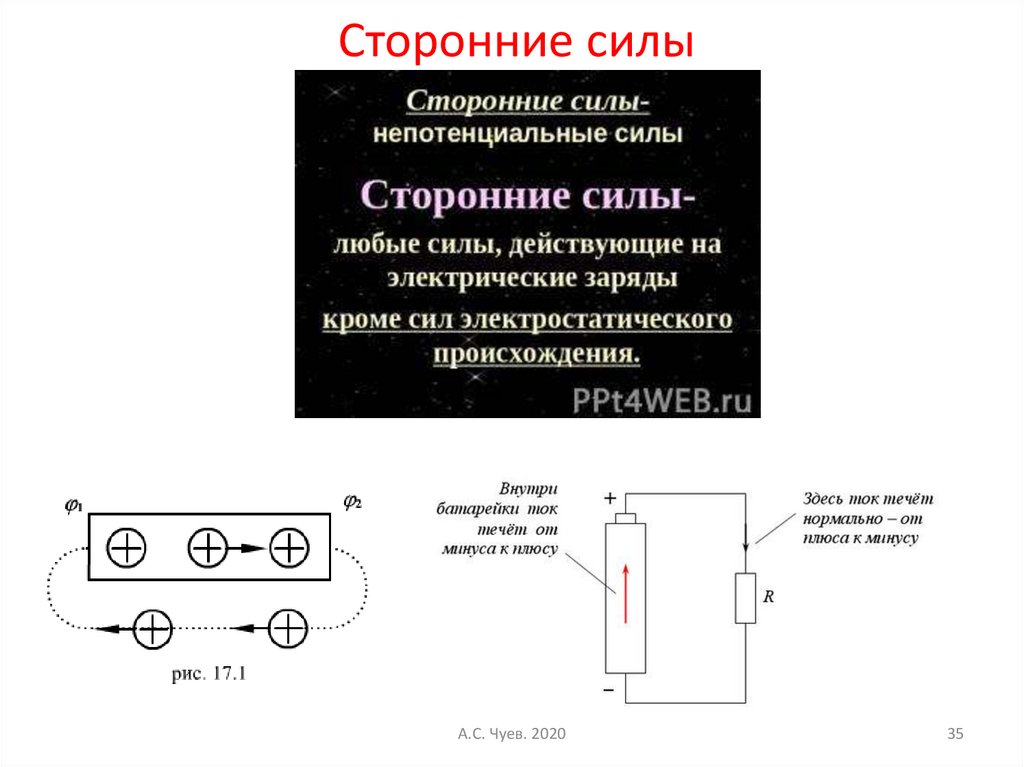
35. Сторонние силы

А.С. Чуев. 2020
35

36. Работа и мощность тока. Закон Джоуля – Ленца

Рассмотрим произвольный участок цепи, к
концам которого приложено напряжение U. За
время dt через каждое сечение проводника
проходит заряд dq Idt.
• При этом силы электрического поля,
действующего на данном участке, совершают
работу:
dA Udq UIdt.
Общая работа:
A IUt IRIt
А.С. Чуев. 2020
36

37.

Тепловая мощность тока в элементе
проводника Δl, сечением ΔS, объемом
ΔV Δl ΔS
равна:
2
N I R I φ j SE l j E V
Тепловая мощность тока N j E V
N
Удельная (по объему) мощность тока n V j E
Используя закон Ома в дифф. форме j E
Получим дифф. форму закона
Джоуля-Ленца
А.С. Чуев. 2020
n σE
2
37

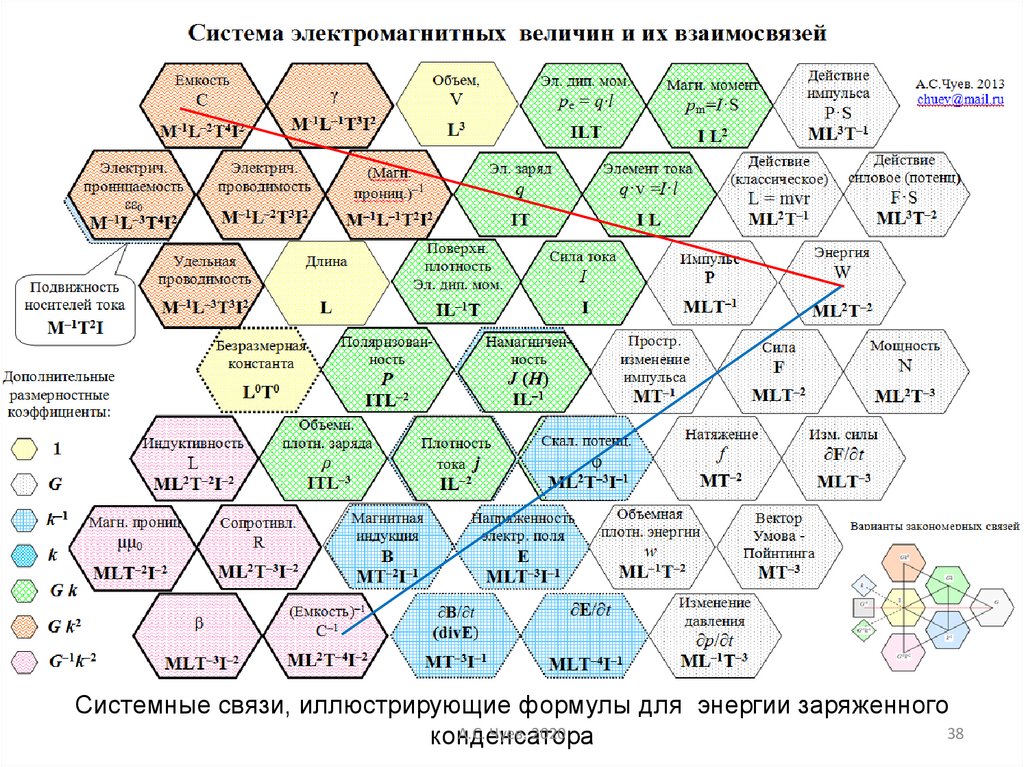
38.

Системные связи, иллюстрирующие формулы для энергии заряженного
А.С. Чуев. 2020
38
конденсатора

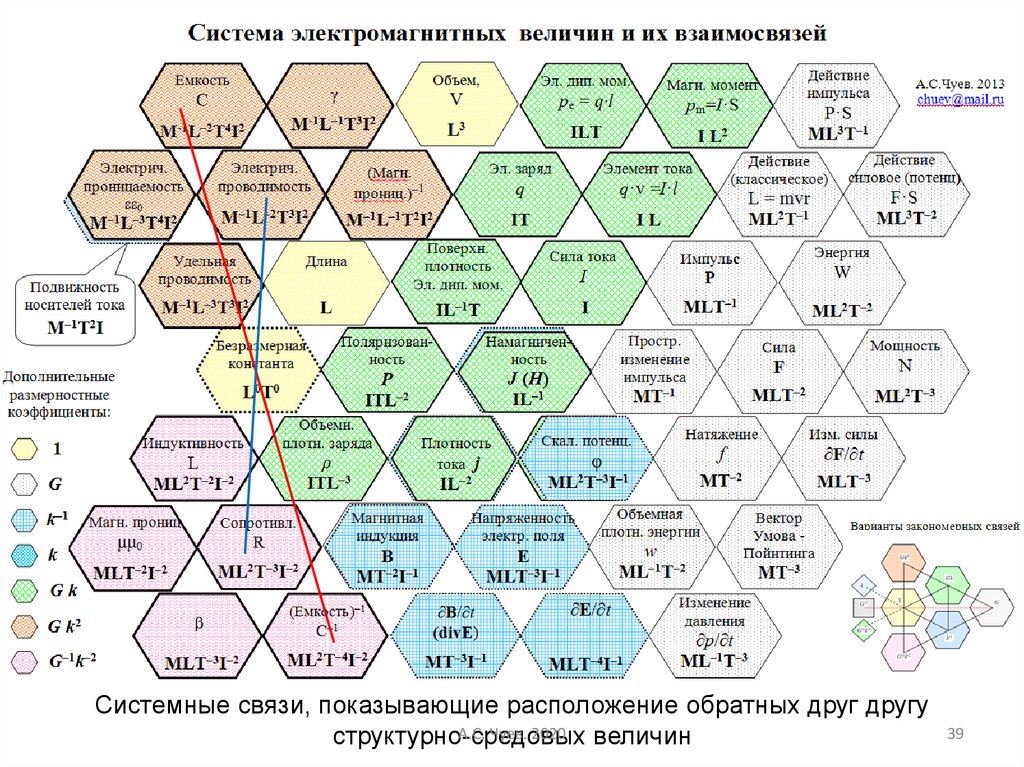
39.

Системные связи, показывающие расположение обратных друг другу
А.С. Чуев. 2020
структурно-средовых
величин
39

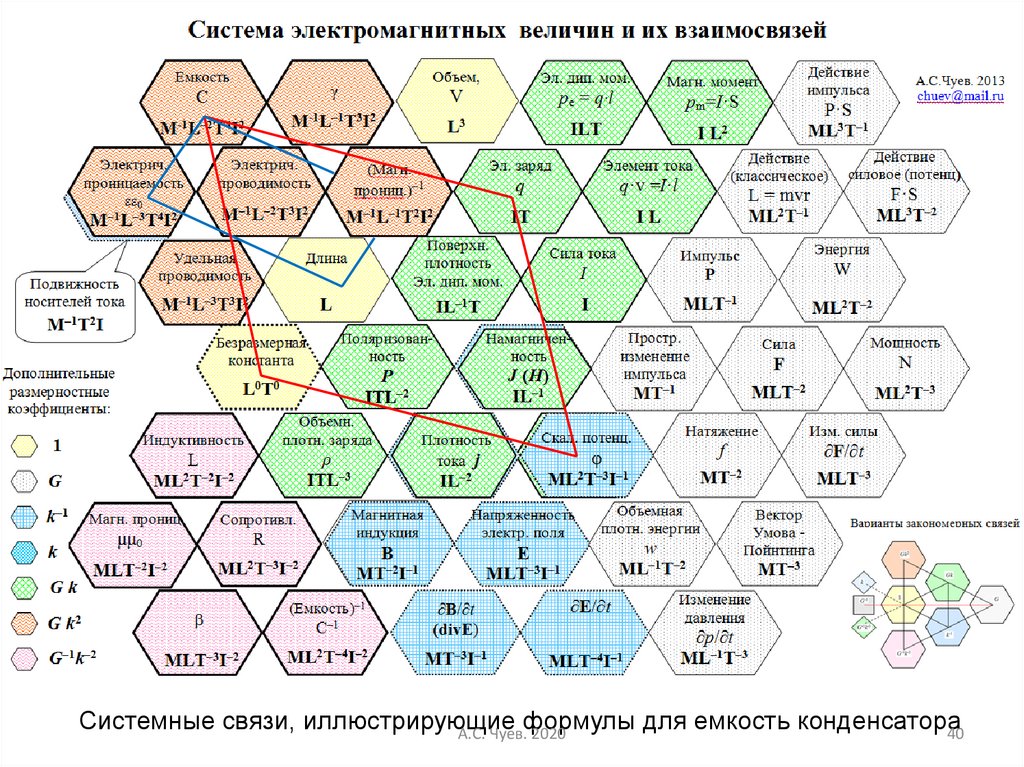
40.

Системные связи, иллюстрирующие
формулы для емкость конденсатора
А.С. Чуев. 2020
40

41.

Системные связи, иллюстрирующие
объемную плотность энергии эл. поля
А.С. Чуев. 2020
41

42.

Системные связи, иллюстрирующие закон Ома в интегральной и
А.С. Чуев. 2020 формах
дифференциальной
42

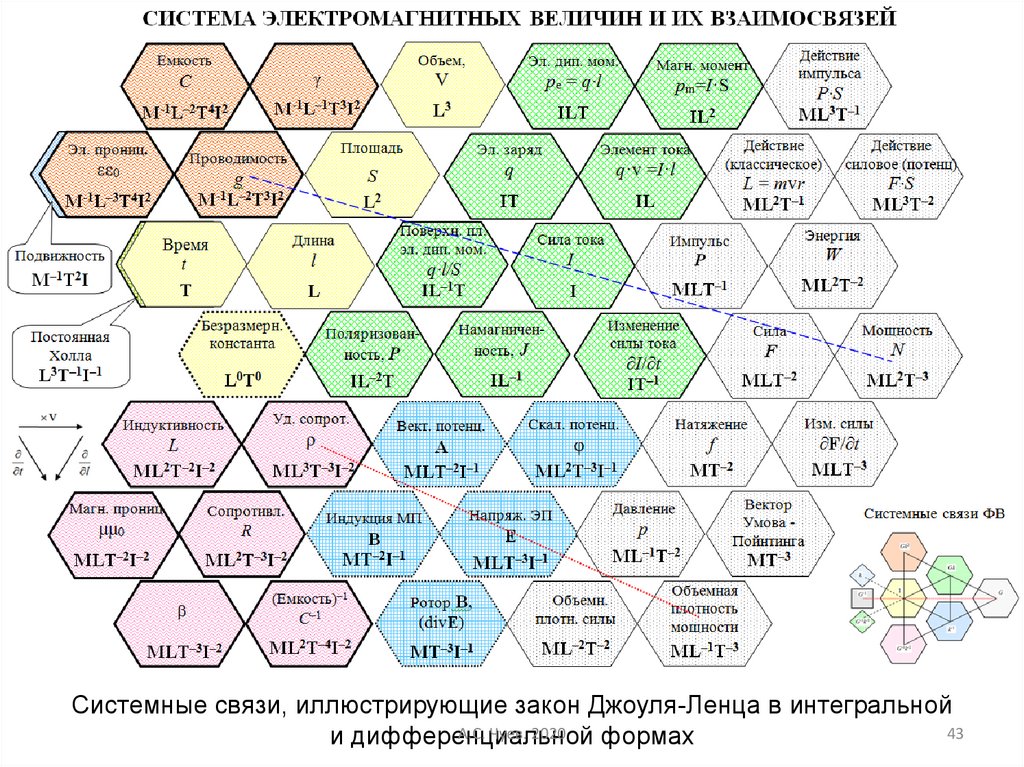
43.

Системные связи, иллюстрирующие закон Джоуля-Ленца в интегральной
А.С. Чуев. 2020
43
и дифференциальной
формах

44.

Презентация по току
и тест
А.С. Чуев. 2020
44

45.

Конец лекции 4
А.С. Чуев. 2020
45