Построение интервального вариационного ряда и гистограммы частот

1. Построение интервального вариационного ряда и гистограммы частот

Соискатель, студент группы ЗПС – 00
Руководитель канд. техн. наук, доцент
Иванов И. П.
Гусаров А. В.
1

2. Исходные данные

Таблица 1.1 – Исходные эмпирические данные
№ п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
xi
1993
2037
2097
2101
2107
2118
2161
2195
2232
2376
2463
2518
2575
2722
2726
1395
1448
1497
1511
1715
1788
1870
1880
1893
1894
2

3. Выражения, по которым выполняются расчеты

Последующие значения верхних xВi и нижних xНi границ интервалов
Размах варьирования R определяется из выражения
R = xmax xmin .
получают из выражений
xВi = xНi 1 xНi + h, где i = 1, 2, ... , k 1 .
(1.1)
Для последнего k -го интервала выражение (1.5) примет вид
xВi = xНi + h, где i = k.
Ширину частичных интервалов h определяют из выражения
R
h= .
k
(1.5)
(1.6)
Построение шкалы интервалов на основе вычисления границ интервалов
(1.2)
продолжается до тех пор, пока величина xВi удовлетворяет соотношению
1
xВi xmax + h .
2
Количество частичных интервалов k определяется с помощью формулы
Г. Стержеса (Старжеса):
(1.10)
Проверка правильности выполнения соотношения (сумма частот должна
k = 1+ 3,32 lg n .
(1.3)
совпадать с объёмом выборки) проводится путем проверки отношения
k
ni = n.
Нижняя граница первого интервала xН1 определяется из выражения
1
xН1 = xmin h .
2
(1.11)
i=1
(1.4)
Для любого i -го интервала (i меняется от 1 до k) выражение для расчета
значения середины частичных интервалов имеет вид
h
xñð.i = xÍ i + .
2
(1.12)
.
3

4. Результаты расчетов

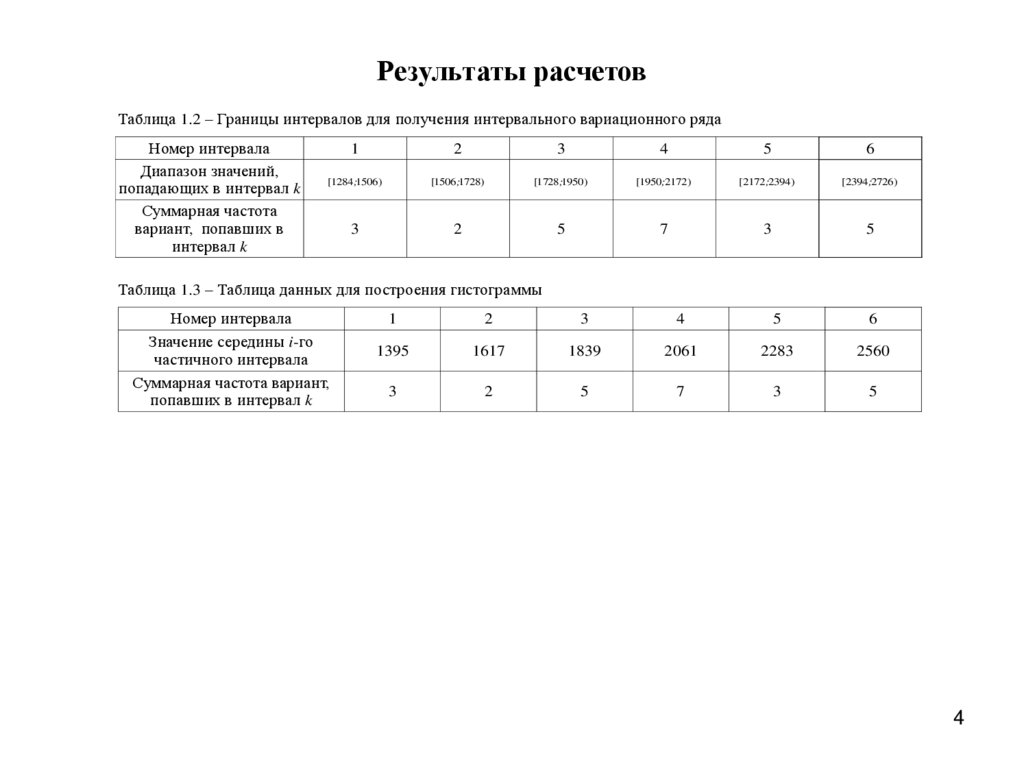
Таблица 1.2 – Границы интервалов для получения интервального вариационного ряда
Номер интервала
Диапазон значений,
попадающих в интервал k
Суммарная частота
вариант, попавших в
интервал k
1
2
3
4
5
6
[1284;1506 )
[1506;1728)
[1728;1950 )
[1950;2172 )
[2172;2394 )
[2394;2726 )
3
2
5
7
3
5
Таблица 1.3 – Таблица данных для построения гистограммы
Номер интервала
1
2
3
4
5
6
Значение середины i-го
частичного интервала
1395
1617
1839
2061
2283
2560
Суммарная частота вариант,
попавших в интервал k
3
2
5
7
3
5
4

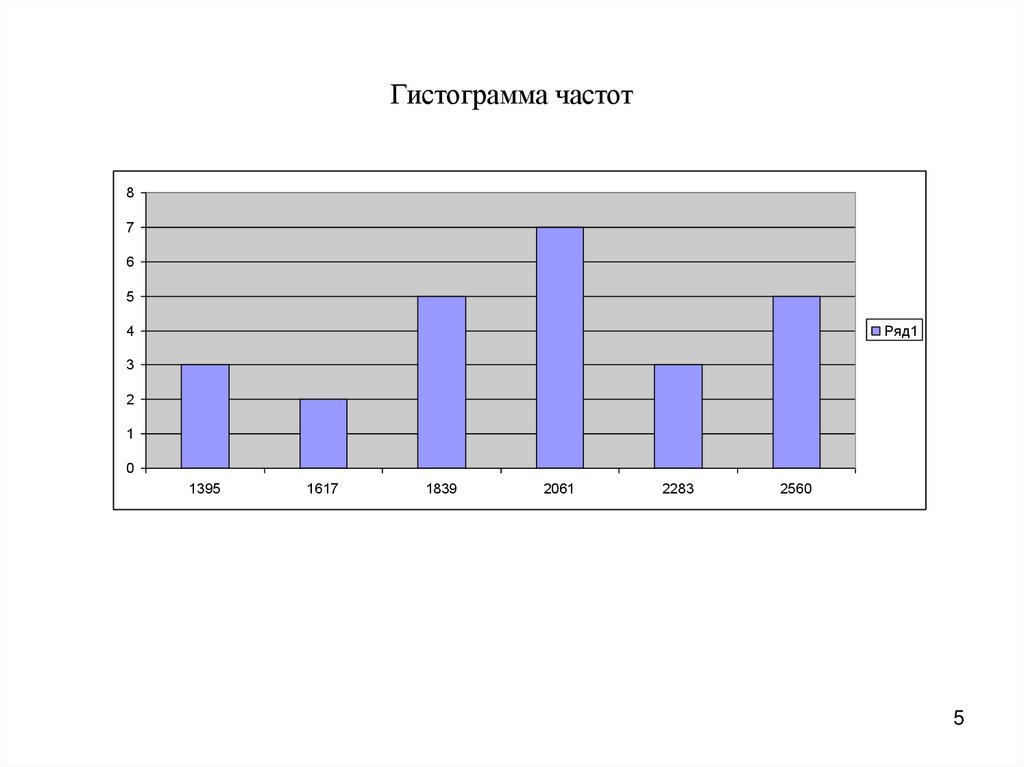
5. Гистограмма частот

8
7
6
5
4
Ряд1
3
2
1
0
1395
1617
1839
2061
2283
2560
5

6. Выводы

В результате выполнения работы были получены следующие результаты:
- ранжированы результаты измерений – получен вариационный ряд;
- определено число групп (6 частичных интервалов) по формуле Старжеса;
- найдена длина частичного интервала и границы каждого интервала;
- результаты измерений были распределены на 6 групп.
По полученным результатам построена гистограмма.
6