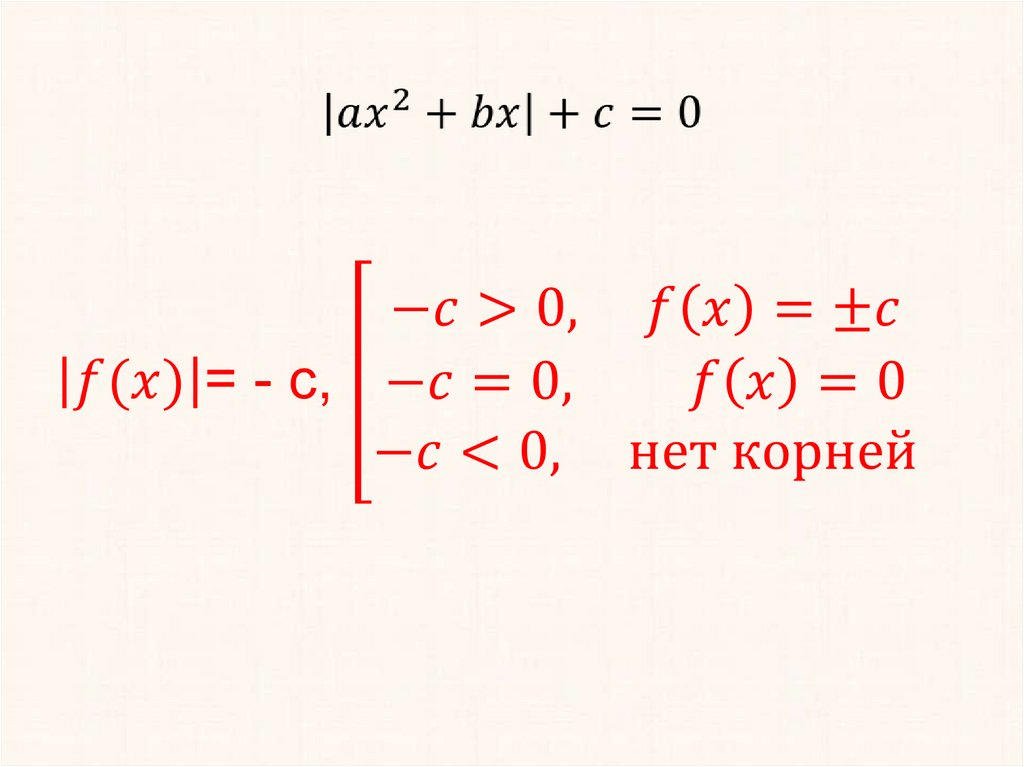Решение квадратных уравнений, содержащих переменную под знаком модуля

1. Решение квадратных уравнений, содержащих переменную под знаком модуля

2. Цели обучения

8.2.2.5 решать уравнения вида
|ax2+bx|+c=0, ax2+b|x|+c=0

3. Критерии оценивания

• знает определение модуля числа
• знает алгоритм решения
квадратных уравнений, содержащих
переменную под знаком модуля
• находит корни квадратных
уравнений, содержащих
переменную под знаком модуля

4. Модуль числа

5.  

6.  

7. Решить уравнение:

х 5х 6
2
1 способ
х 5 х 6,
2
х 5х 6
2
или
х 5 х 6 0 или
2
х1 1, х2 6 ;
Ответ: -6; -3; -2;1
х 5 х 6
2
х 5х 6 0
2
х3 3, х4 2

8. Решить уравнение:

х 5х 6
2

9. Решить уравнение:

х 5 х 8
2
т.к. -8 < 0, то уравнение не
имеет корней

10. Пример 3

2 х 2 х 3 0
Ответ: -1; 1,5

11. Пример 4

х 9 х 16 0
2
Ответ: нет решений

12.

Решить уравнение x² - 2│x │=0
І.Раскрытие модуля по определению
1) Если x ≥ 0, то │x│= x , и уравнение принимает вид
x² - 2x=0, откуда получаем x=0 или x=2; оба значения
удовлетворяют условию x ≥ 0.
2) Если x<0, то │x │= -x , и уравнение принимает вид
x²+2x=0, откуда получаем x=0 или x= -2;
Второе из найденных значений удовлетворяет условию x<0.
Ответ: 0; 2; -2.

13. ІІ Метод замены переменной.

Дано исходное уравнение: x² - 2│x │=0
Замена: │x │= t ≥ 0 , тогда уравнение примет вид
t²-2t=0, откуда получаем t=0 или t=2. Возвращаясь к
исходной переменной, получаем:
│x │=0 , │x │= 2
x = 0 , x = ±2
Ответ: 0; 2; -2.

14. Пример 5

5х 4 х 0
2
Ответ: 0; -0,8; 0,8

15. Пример 6

4х 3 х х 0
2
Ответ: -1; 0; 0,5

16. Домашняя работа

17. Рефлексия