Похожие презентации:
Линейные уравнения с одной переменной, содержащие переменную под знаком модуля
1. Линейные уравнения с одной переменной, содержащие переменную под знаком модуля
2. |х|=4, |5-х|=1, |2х+5|=10, 5|х|=25
3.
Это линейные уравнения с однойпеременной, содержащие
переменную под знаком модуля
4. При решении линейных уравнений с одной переменной, содержащие переменную под знаком модуля, используются:
5. 1. |а-b| ― расстояние между точками А(а) и В(b)на координатной прямой.
6. 2. Определение модуля, записанное формулой: а, если а> или = 0 |а|= -а, если а<0
2. Определение модуля,записанное формулой:
а, если а> или = 0
|а|=
-а, если а<0
7. При вычислениях используются следующие свойства модулей:
8. 1. |а|> или = 0; 2. |-а|=|а| ; 3. |аb|=|a|*|b|; 4. 5. |a|2 = a 2
1. |а|> или = 0;2. |-а|=|а| ;
3. |аb|=|a|*|b|;
4.
5.
2
|a| =
2
a
9. Решить уравнение |x|=3
10. 1 способ. Уравнение |x|=5 запишем в виде |x-0|=5. На координатной прямой имеются две точки, которые удалены от точки с
координатой 0 на расстояние, равное 5 единиц. Это точки скоординатами -5 и 5.
11. Значит, х=-5 или х=5.
12. 2 способ. Решение: 1) Если х >, 0 то х =5. 2) Если х < 0, то –х = 5, х = -5. Тогда, х = 5, или х = -5.
2 способ.Решение: 1) Если х >, 0 то х =5.
2) Если х < 0, то –х = 5, х = -5.
Тогда, х = 5, или х = -5.

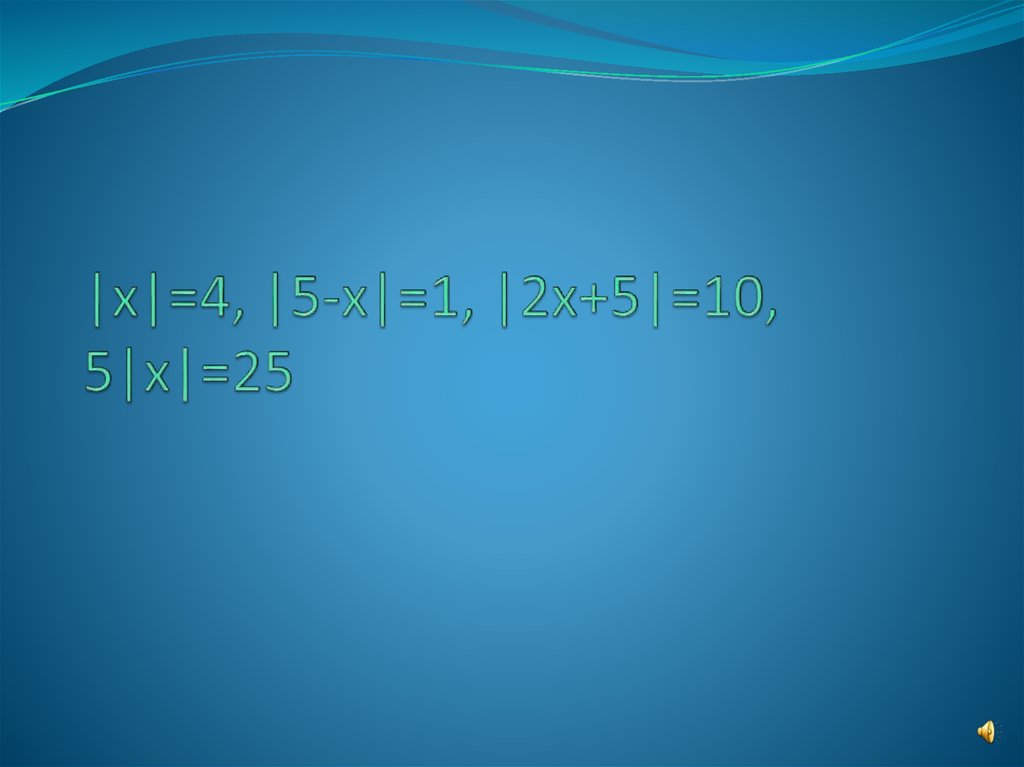













 Математика
Математика








