Елементи механіки суцільних середовищ. (Лекція 6)

1.

Лекція № 6.
Елементи механіки суцільних середовищ
1. Механічні властивості твердих тіл, рідин та
газів
2. Види деформацій, пружність та повзучість.
Закон Гука
3. Ламінарна та турбулентна течії. Циркуляція
4. Сили в’язкого тертя
5. Рівняння неперервності та Бернуллі для
стаціонарної течії ідеальної рідини. Течія
рідин та газів по трубах
6. Рух твердих тіл у рідинах та газах.
Підіймальна сила крила літака

2. Механічні властивості твердих тіл, рідин та газів

1.Механічні властивості твердих тіл, рідин
та газів
Окрім механіки матеріальної точки та механіки
твердого тіла існує ще і механіка суцільних
середовищ.
Суцільним
вважають
середовище,
що
неперервно розповсюджується у просторі (тобто не
враховується
його
дискретна
будова)
і
характеризується пружними властивостями.
Механіка суцільних середовищ – розділ
механіки, присвячений вивченню руху і рівноваги
деформованих твердих тіл, рідин, газів і плазми.

3.

Механіку суцільних середовищ поділяють на:
1) механіку деформованого твердого тіла, включає в себе:
• теорію пружності,
• теорію пластичності,
• механіку руйнування;
2) механіку рідин та газів.

4.

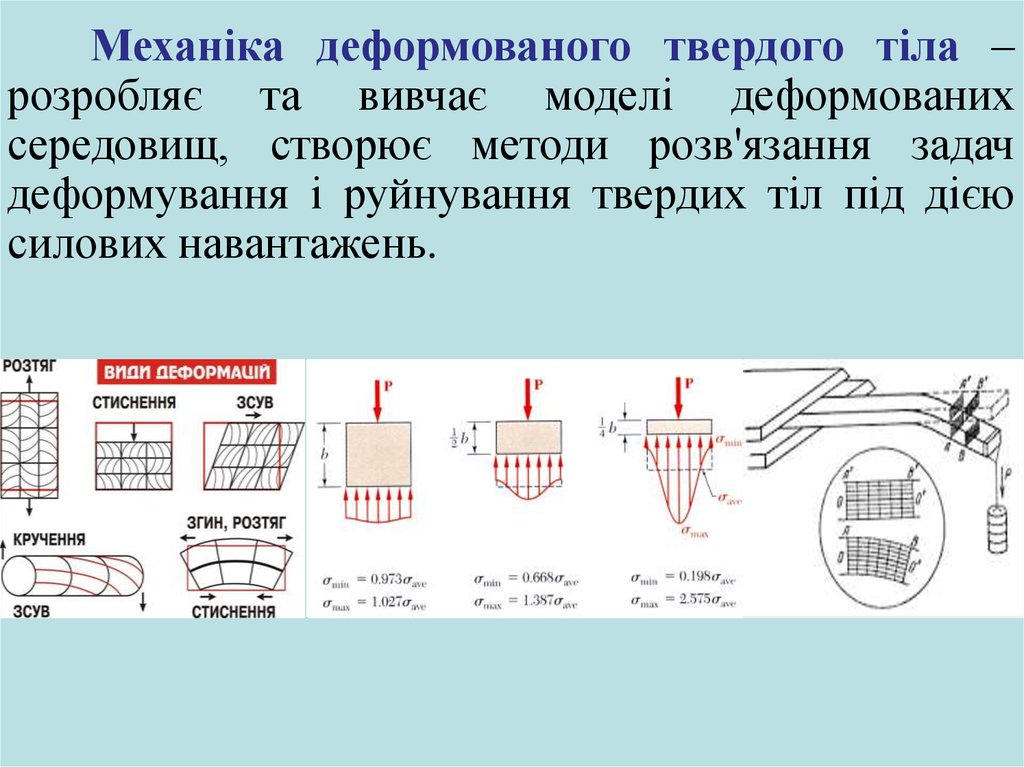
Механіка деформованого твердого тіла –
розробляє та вивчає моделі деформованих
середовищ, створює методи розв'язання задач
деформування і руйнування твердих тіл під дією
силових навантажень.

5.

Теорія пружності – описує матеріали, які
відновлюють свою форму після припинення
силового впливу на них.

6.

Теорія пластичності – описує матеріали (тіла)
що набувають незворотних деформацій під
силовим впливом.

7.

Механіка руйнування – описує закономірності зародження і розвитку неоднорідностей і
дефектів структури матеріалу (тріщин, дислокацій,
пор, включень тощо) при навантаженнях.

8.

Механіка рідин та газів – вивчає рівновагу і
рух рідких і газоподібних середовищ, встановлює
закони розподілу швидкостей і тисків під час руху
рідини, а також вивчає взаємодію рідин та газів
між собою і з твердими тілами, розміщеними в
них.

9. 2. Види деформацій, пружність та повзучість. Закон Гука

Деформація
(від
лат.
deformatio
–
“спотворення”) – зміна розмірів і форми твердого
тіла під дією зовнішніх сил (навантажень) або
інших впливів (температури, електричних чи
магнітних полів тощо).

10.

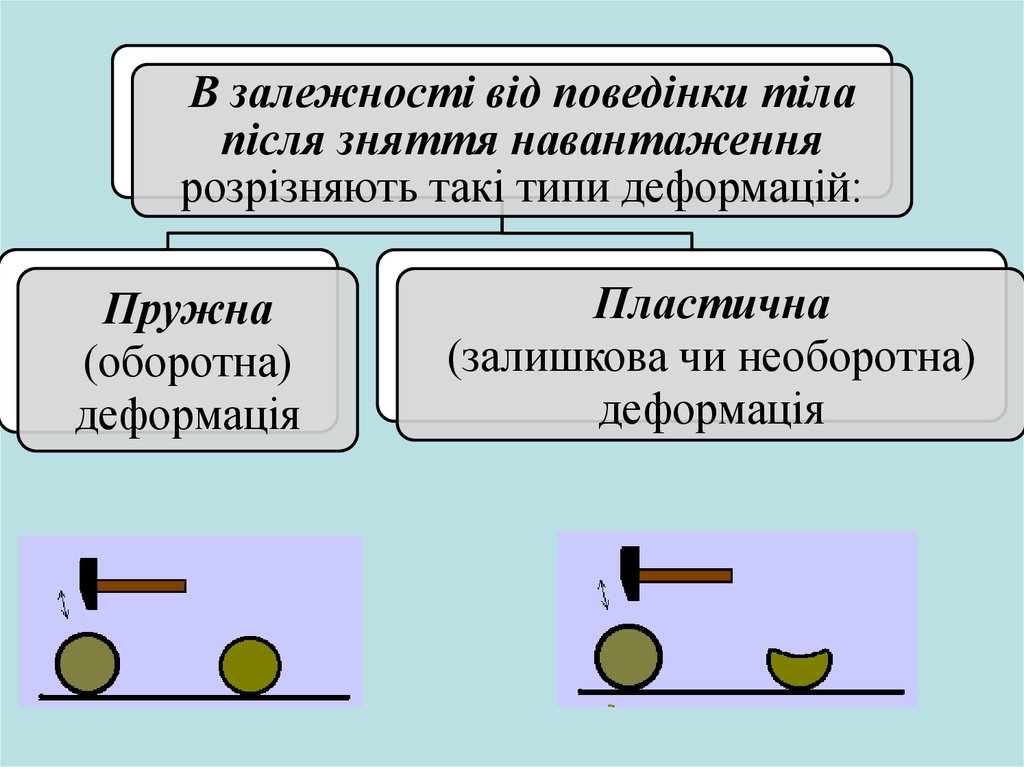
В залежності від поведінки тіла
після зняття навантаження
розрізняють такі типи деформацій:
Пружна
(оборотна)
деформація
Пластична
(залишкова чи необоротна)
деформація

11.

Пружна (або оборотна) деформація – деформація при якій після припинення дії навантаження
тіло повністю відновлює свою початкову форму і
розміри.
Пружні деформації спостерігаються у тому
випадку, коли напруження, що зумовлює
деформацію, не перевищує деяку, визначену для
кожної речовини, межу – межу пружності.
Деякі речовини (метали, каучук) можуть зазнавати значної пружної
деформації, в той час як у
інших (кераміки, пресовані
матеріали)
навіть
незначна
деформація
перестає бути пружною.

12.

Пластична (або залишкова чи необоротна)
деформація – деформація, яка не зникає повністю
після припинення дії навантаження, а отже форма
твердого тіла не відновлюється (робота зовнішніх
сил переходить у теплоту).
Природа пластичної деформації може бути
різною в залежності від температури, тривалості
дії навантаження або швидкості деформації.

13.

Пластичність
–
здатність
матеріалу
незворотньо змінювати свою форму й розміри при
деформації.

14.

Крихкість – відсутність
пластичність матеріалів.
скло
або
незначна

15.

Повзучість – явище зростання деформації
твердого тіла з часом при сталому навантаженні, із
зростанням температури швидкість деформації
збільшується.

16.

На теорії пластичних деформацій засновані
такі технологічні процеси обробки матеріалів, як
“обробка металів тиском” або холодна обробка
металів, а саме: прокатка, пресування, штампування, ковка тощо.

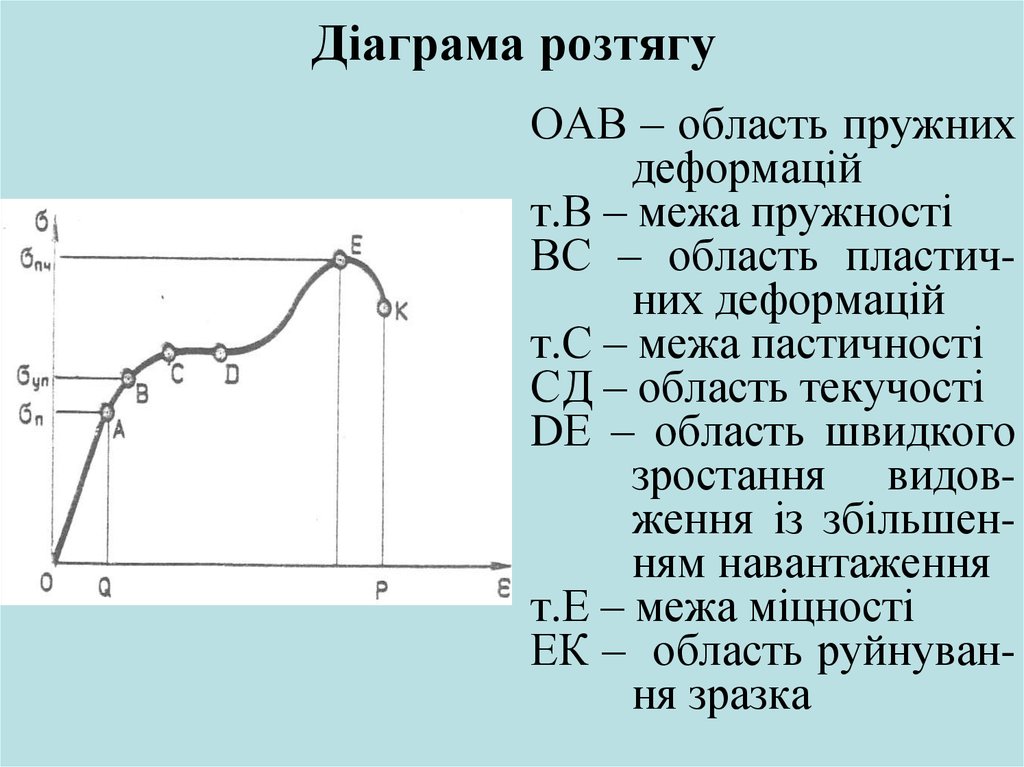
17. Діаграма розтягу

ОАВ – область пружних
деформацій
т.В – межа пружності
ВС – область пластичних деформацій
т.С – межа пастичності
СД – область текучості
DЕ – область швидкого
зростання видовження із збільшенням навантаження
т.Е – межа міцності
ЕК – область руйнування зразка

18.

За зміною форми розрізняють такі основні види
деформацій:

19. Деформація розтягу

Випробують: троси, ціпки…

20. Деформація стиску

Випробують : колоны, стіни…

21. Деформація зсуву

Випробують: болти, заклепки…

22. Деформація кручення

Випробують: гайки, вали, осі…

23. Деформація згину

Випробують: мости, балки…

24.

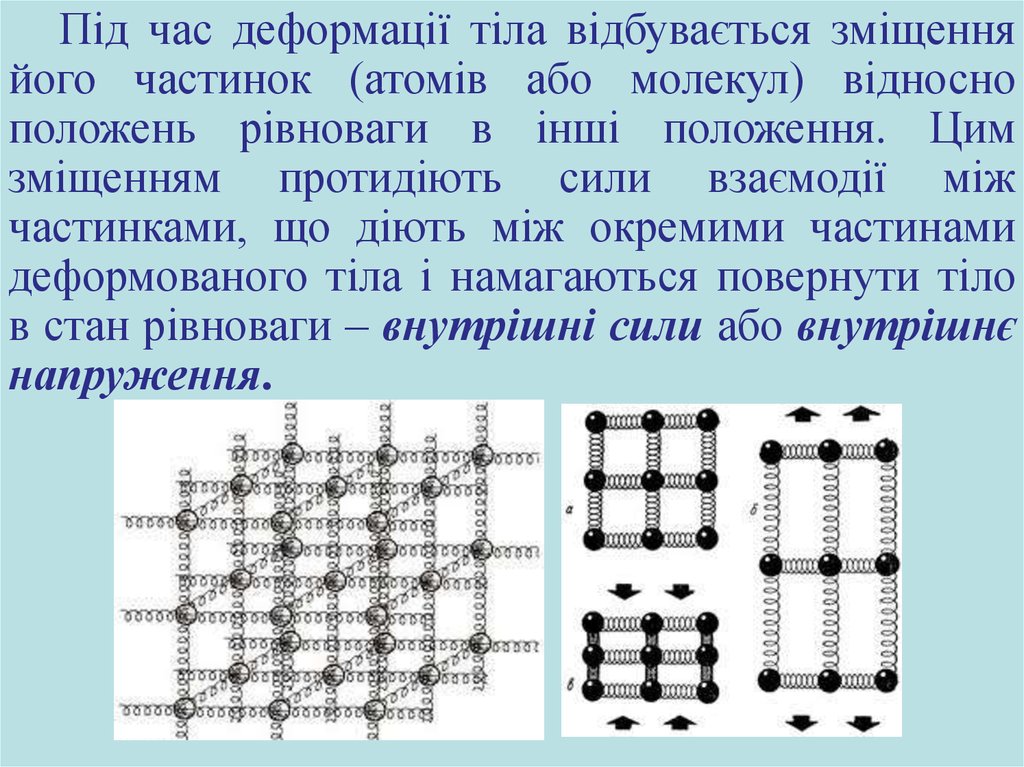
Під час деформації тіла відбувається зміщення
його частинок (атомів або молекул) відносно
положень рівноваги в інші положення. Цим
зміщенням протидіють сили взаємодії між
частинками, що діють між окремими частинами
деформованого тіла і намагаються повернути тіло
в стан рівноваги – внутрішні сили або внутрішнє
напруження.

25.

Внутрішнє (механічне) напруження фізична
величина, що дорівнює відношенню результуючих
пружних сил до площі перерізу тіла:
Fпружн
S
.

26.

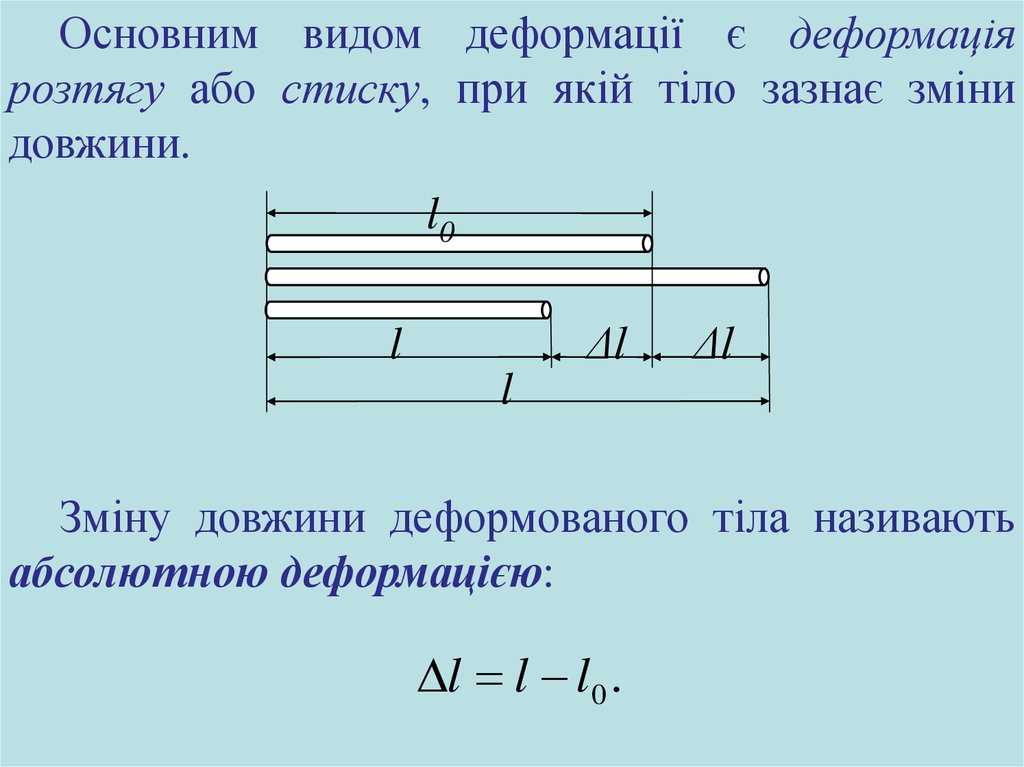
Основним видом деформації є деформація
розтягу або стиску, при якій тіло зазнає зміни
довжини.
l0
Δl
l
Δl
l
Зміну довжини деформованого тіла називають
абсолютною деформацією:
l l l0 .

27.

Оскільки абсолютна деформація не вказує, яку
частину становить зміна довжини від початкової,
то мірою деформації тіла є його відносна
деформація:
l l l0
.
l0
l0
при розтягу ε > 0, а стиску – ε < 0.

28.

Експериментально
встановлено,
що
при
невеликих послідовно зростаючих навантаженнях
механічне напруження пропорційне відносній
деформації – закон Гука:
l
E E ,
l0
де Е – модуль пружності (або модуль Юнга якщо
мова йде про розтяг або стиск), залежить від
матеріалу стержня і його фізичного стану.

29.

При
деформаціях
розтягу
або
стиску
відбувається також зміна поперечних розмірів тіла,
яку характеризують відносним поперечним
стиском або розтягом:
d d d 0
.
d0
d0

30.

Відношення відносної поперечної деформації
тіла до відносної повздовжньої деформації
називають коефіцієнтом Пуассона, який залежить
тільки від матеріалу тіла і є однією із сталих, що
характеризує пружні властивості тіла:
.

31.

Числове значення коефіцієнта Пуассона лежить
у межах: 0 < μ ≤ 0,5.
Для ізотропних матеріалів, що мають однакові
механічні властивості за всіма напрямками
0,25 < μ ≤ 0,33, зокрема, для металів μ = 0,3; для
гуми μ = 0,5; для пористих матеріалів (наприклад,
коркової винної пробки) μ ≈ 0.
Але навіть незначного
зменшення діаметру при
видовженні
пробки
достатньо, щоб більш-менш
легко вийняти її штопором із
пляшки.

32. 3. Ламінарна та турбулентна течії

Рух рідин називають течією, а сукупність
частинок рідини, які рухаються – потоком.
Для графічного зображення руху рідини вводять
поняття ліній течії – ліній, дотичні до яких у
кожній точці співпадають з вектором швидкості
потоку.
Лінії проводять таким чином, щоб густина їх
була пропорційною до швидкості потоку.
Частину рідини, яка обмежена лініями течії
називають трубкою потоку.

33.

Ламінарною течією називають течію в якій
лінії потоку не перетинаються, турбулентною
течією називають течію в якій лінії потоку
перетинаються, тобто є завихрення.

34.

35.

Число Рейнольдса – безрозмірна фізична
величина, що визначає характер течії, визначається
відношенням кінетичної енергії руху рідини до
втрат енергії, зумовлених роботою сил в'язкості.
Визначає відносну роль інерції і в'язкості рідини
під час течії:
d d
Re
де ν=η/ρ – кінематична в'язкість,
ρ – густина рідини,
<υ> – середня по перерізу труби швидкість
рідини,
d – характерний лінійний розмір, наприклад,
діаметр труби

36.

При малих значеннях числа Рейнольдса
(Re≤1000) спостерігається ламінарна течія, перехід
від ламінарної течії до турбулентної здійснюється
в області 1000≤Re≤2000, а при Re=2300 (для
гладких труб) течія – турбулентна.
Якщо число Рейнольдса однакове, то режим
течії різних рідин або газів в трубах різних
перерізів буде однаковим.

37. 4. Сили в’язкого тертя

В’язкість (внутрішнє
тертя) – явище переносу
імпульсу, яке полягає у
властивості
реальних
рідин та газів чинити опір
переміщенню
однієї
частини рідини (газу)
відносно іншої.

38.

Механізм виникнення в’язкості зумовлений
переносом імпульсу ( m ) направленого руху від
одного шару рідини чи газу до іншого.
В реальних рідинах і газах між
молекулами
існують
сили
взаємного притягання і відштовхування.
При
взаємному
зміщенні
одного шару речовини відносно
іншого відстані між молекулами
шарів
збільшуються,
тобто
починають діяти сили взаємного
притягання.
З боку більш швидкого шару починає діяти сила,
що прискорює менш швидкий шар, а з боку
повільних шарів рідини або газу діють сили, що
гальмують рух швидких шарів.

39.

Під час переміщення одних шарів
реальної рідини (газу) відносно
інших виникають сили внутрішнього
тертя, спрямовані вздовж дотичної
до поверхні цих шарів, які
визначають законом Ньютона для
в’язких рідин:
d
F
dy
S,
де F – сила внутрішнього тертя;
d
dy − градієнт швидкості, який показує зміну величини
швидкості потоку при переході від шару до шару у
напрямку осі Оy, перпендикулярному до напрямку
руху рідини (газу);
S – площа поверхні шарів;
− коефіцієнт динамічної в’язкості рідини (газу),
залежить від природи рідини (газу) та температури.

40. 5. Рівняння неперервності та Бернуллі для стаціонарної течії ідеальної рідини. Течія рідин та газів по трубах

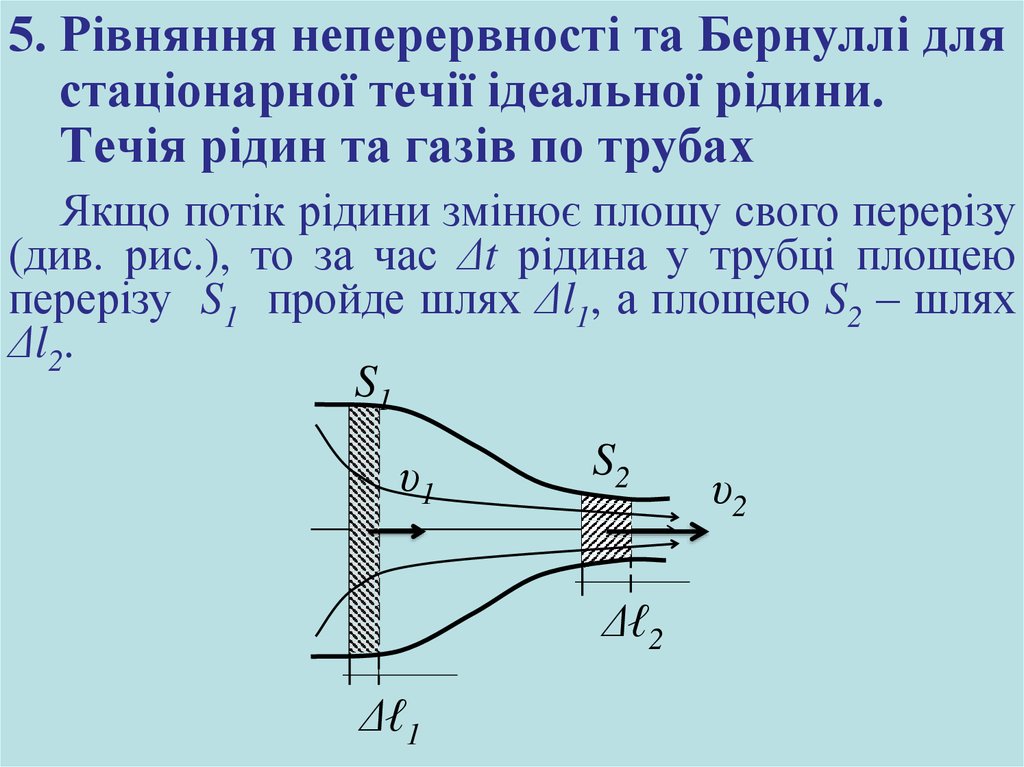
Якщо потік рідини змінює площу свого перерізу
(див. рис.), то за час Δt рідина у трубці площею
перерізу S1 пройде шлях Δl1, а площею S2 – шлях
Δl2.
S1
υ1
S2
Δℓ2
Δℓ1
υ2

41.

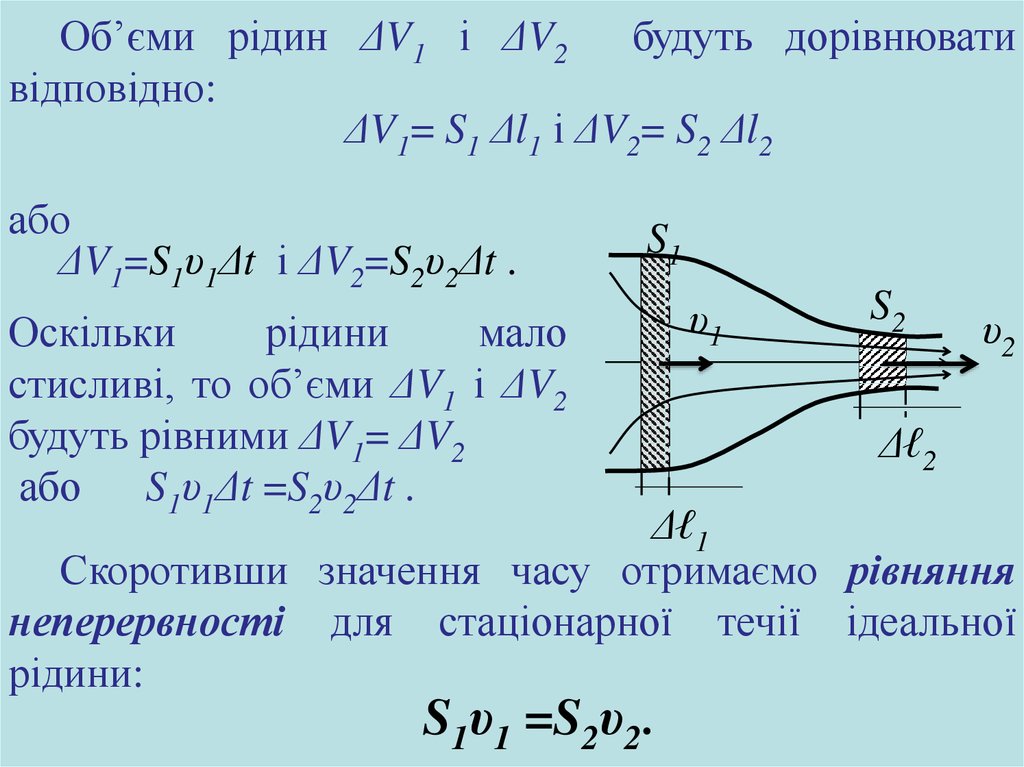
Об’єми рідин ΔV1 і ΔV2
будуть дорівнювати
відповідно:
ΔV1= S1 Δl1 і ΔV2= S2 Δl2
або
ΔV1=S1υ1Δt і ΔV2=S2υ2Δt .
Оскільки
рідини
мало
стисливі, то об’єми ΔV1 і ΔV2
будуть рівними ΔV1= ΔV2
або
S1υ1Δt =S2υ2Δt .
S1
υ1
S2
υ2
Δℓ2
Δℓ1
Скоротивши значення часу отримаємо рівняння
неперервності для стаціонарної течії ідеальної
рідини:
S1υ1 =S2υ2.

42.

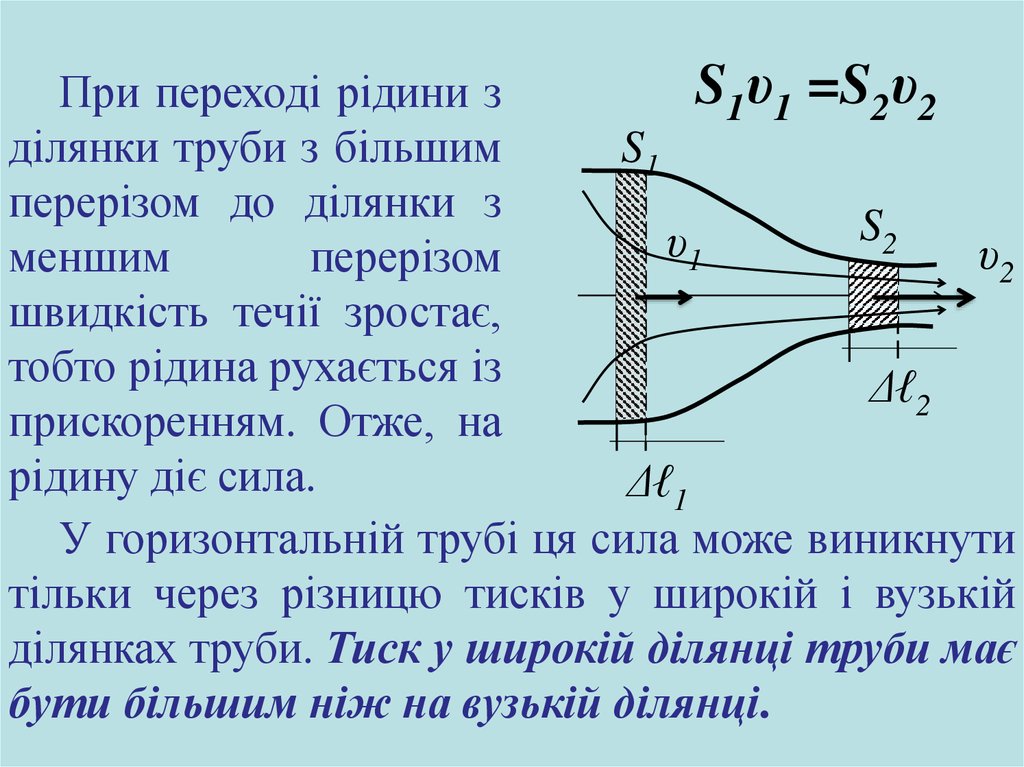
S1υ1 =S2υ2
При переході рідини з
ділянки труби з більшим
S1
перерізом до ділянки з
S2
υ
υ2
1
меншим
перерізом
швидкість течії зростає,
тобто рідина рухається із
Δℓ2
прискоренням. Отже, на
рідину діє сила.
Δℓ1
У горизонтальній трубі ця сила може виникнути
тільки через різницю тисків у широкій і вузькій
ділянках труби. Тиск у широкій ділянці труби має
бути більшим ніж на вузькій ділянці.

43.

З рівняння неперервності для стаціонарної течії
ідеальної рідини випливає, що швидкість потоку
рідини обернено пропорційно залежить від площі його
перерізу.
S1υ1 =S2υ2
Цю залежність широко використовують для
отримання сильного та далекобійного струменя
рідини, наприклад, у брандспойтах для гасіння пожеж;
у гідрорізаках для видобування, розрізування та
обробки будівельних матеріалів; у системах поливу
або пристроях для розпилення рідин (у зволожувачах
повітря, розпилювачах фарб) тощо.

44.

Якщо ділянки труби p m
u
розташовані на різних
S
l S
1
висотах, то прискорення
p
h
l
D m
рідини виникає завдяки
u
h
2
суспільній дії сили
тиску та сили тяжіння.
Оскільки рідина є ідеальною, тобто вона тече по
трубі без тертя, то до її течії можна застосувати
закон збереження механічної енергії.
При переміщенні рідини сили тиску виконують
роботу:
1
1
2
2
2
1
1
2
A F1l1 F2l2 p1S1l1 p2 S 2l2 p1V1 p2V2 ,

45.

При стаціонарній течії зміни, що відбулися за
час Δt у виділеній частині рідини зводяться до
переміщення маси рідини Δm з однієї частини
труби перерізом S1 в іншу частину перерізом S2
(заштриховані об’єми на рис.). Закон збереження
механічної енергії для цієї маси має вигляд:
E1 E2 A,
де E1 і E2 – повні механічні енергії рідини масою
Δm у полі тяжіння Землі:
2
m
m 2
E1
mgh1 , E 2
mgh2 .
2
2
2
1

46.

Оскільки робота сил тиску призводить до зміни
повної механічної енергії, то із попередніх рівнянь
можна отримати співвідношення, яке називають
рівнянням Бернуллі:
2
1
2
gh1 p1
2
2
2
gh2 p2
де ρ – густина рідини,
υ1 і υ1 –швидкості у різних точках потоку,
h1 і2 h2 – висоти, на яких знаходяться точки
– динамічний тиск – є кінетичною енергією
одиниці об’єму рідини,
2
ρgh – гідростатичний тиск – є потенціальною
енергією одиничного об’єму рідини в полі сили
тяжіння Землі,
p – статичний тиск – є роботою сил тиску, що
здійснюється над одиничним об’ємом рідини.

47.

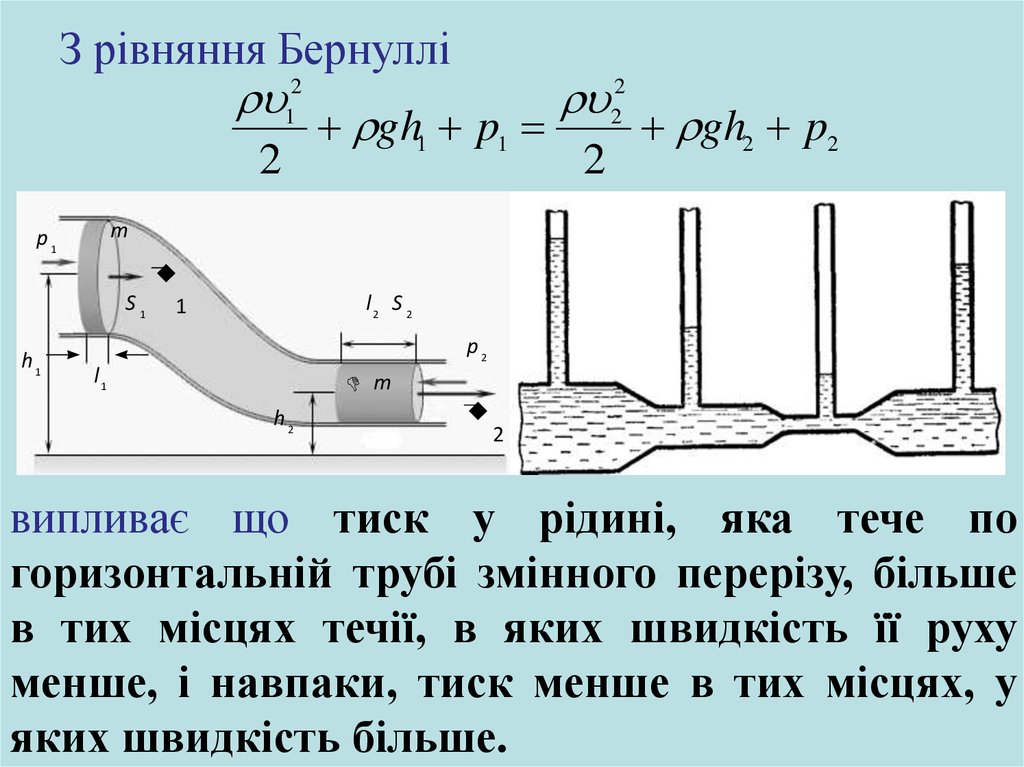
З рівняння Бернуллі
2
2
1
2
gh1 p1
gh2 p2
2
2
m
p1
u
S1 1
h1
l2 S 2
p2
l1
D m
h2
u
2
випливає що тиск у рідині, яка тече по
горизонтальній трубі змінного перерізу, більше
в тих місцях течії, в яких швидкість її руху
менше, і навпаки, тиск менше в тих місцях, у
яких швидкість більше.

48. 6. Рух твердих тіл у рідинах та газах. Підіймальна сила крила літака

Під час руху тіла у рідині або газі, на нього з
боку середовища діє сила лобового опору – сила
зумовлена
в’язкістю
рідини,
а
також
турбулентністю позаду тіла (при великих
швидкостях).

49.

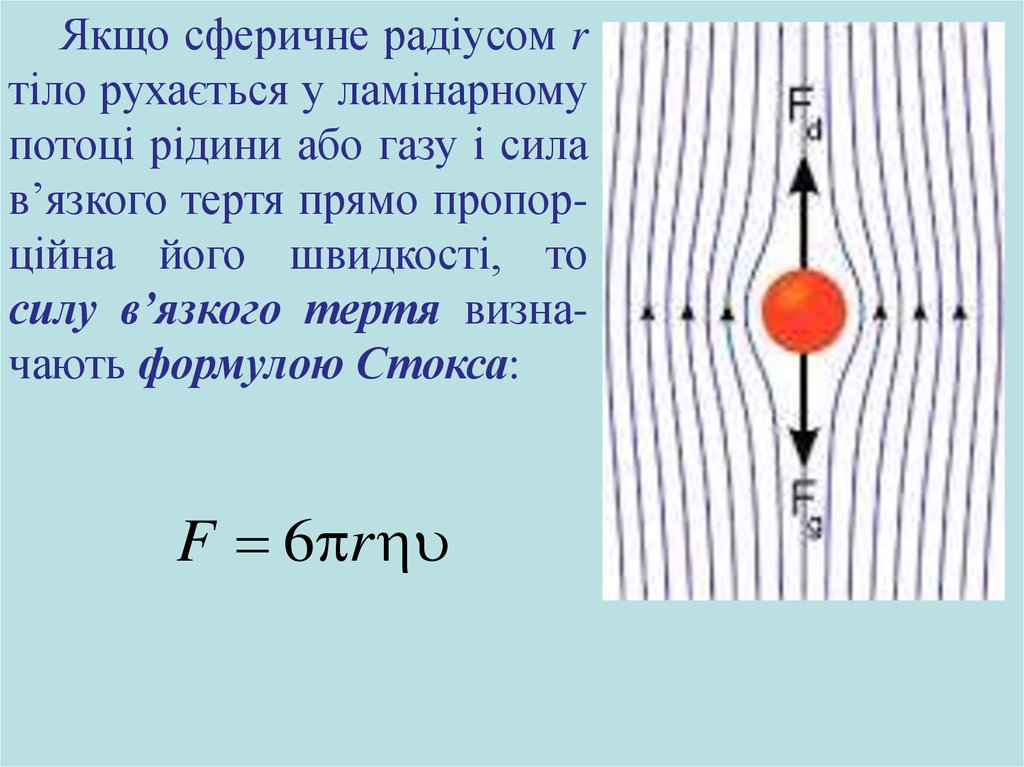
Якщо сферичне радіусом r
тіло рухається у ламінарному
потоці рідини або газу і сила
в’язкого тертя прямо пропорційна його швидкості, то
силу в’язкого тертя визначають формулою Стокса:
F 6 r

50.

При великих швидкостях руху тіл у потоці
рідини або газу, позаду тіла, відбувається відрив
ліній течії, виникають вихрі, що призводить до
інтенсивних турбулентних рухів.
Для тіла сферичної форми
силу лобового опору визначають за формулою:
F Cx S / 2
2
Рис. 1.83
де Cx – коефіцієнт лобового опору для тіла даної
форми;
S – площа поперечного перерізу тіла.
При обтіканні такого тіла потік добре
замикається позаду нього, заважаючи, тим самим,
падінню тиску за тілом.

51.

Розглянемо приклад застосування рівняння
Бернуллі для визначення підйомної сили крила
літака. На рис. показано потік повітря навколо
крила літака. Запишемо рівняння Бернуллі для
нижньої і верхньої точок крила 1 і 2:
12
22
2
gh1 p1
gh2 p2
2
2
2
Р2
Fn
1
1
Р1
Так як h1 h2 (товщина крила невелика), то
рівняння набуває вигляду:
2
1
2
p1
2
2
2
р2

52.

Оскільки 2 1 , то p1 p2 і результуюча сила,
яка діє на крило, буде направлена вгору. Цю силу
називають підйомною силою.

53.

Лекція № 6.
Елементи механіки суцільних середовищ
1. Механічні властивості твердих тіл, рідин та
газів
2. Види деформацій, пружність та повзучість.
Закон Гука
3. Ламінарна та турбулентна течії. Циркуляція
4. Сили в’язкого тертя
5. Рівняння неперервності та Бернуллі для
стаціонарної течії ідеальної рідини. Течія
рідин та газів по трубах
6. Рух твердих тіл у рідинах та газах.
Підіймальна сила крила літака