Теоретична механіка

1. ТЕОРЕТИЧНА МЕХАНІКА

Рекомендована література:
1)
2)
3)
Тарг С.М. Краткий курс теоретической механики.
Яблонский А.А. Сборник заданий для курсовых
работ по теоретической механике.
Бухгольц Н.Н. Основной курс теоретической
механики в 2-х частях.

2.

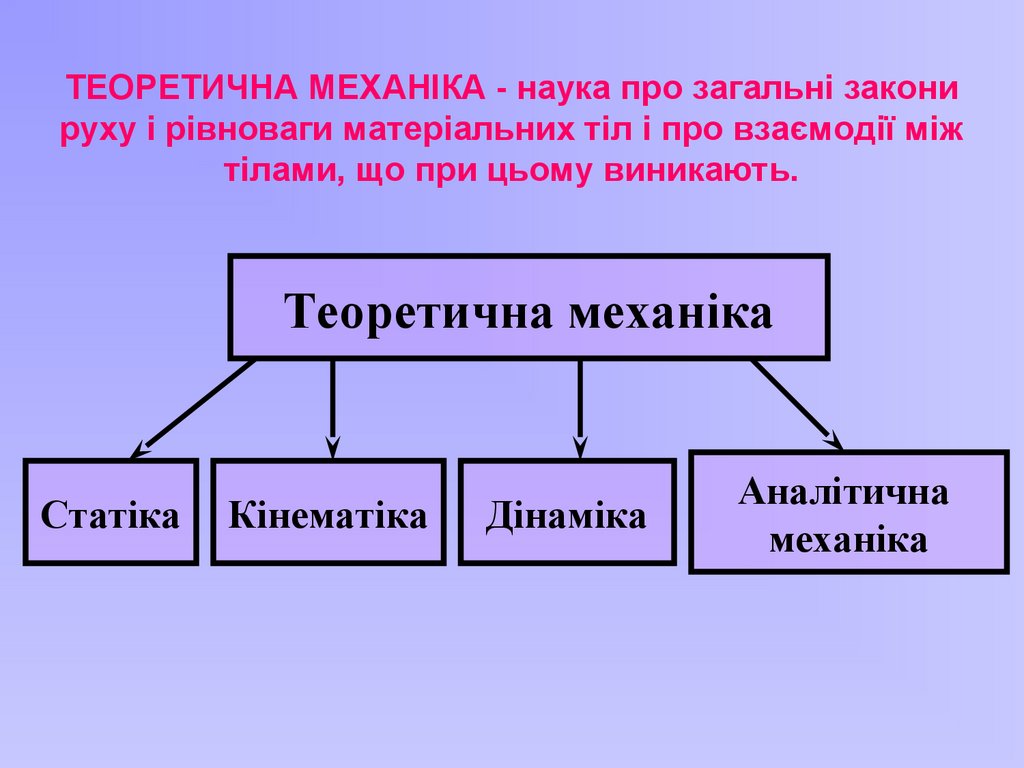
ТЕОРЕТИЧНА МЕХАНІКА - наука про загальні закони
руху і рівноваги матеріальних тіл і про взаємодії між
тілами, що при цьому виникають.
Теоретична механіка
Статіка
Кінематіка
Дінаміка
Аналітична
механіка

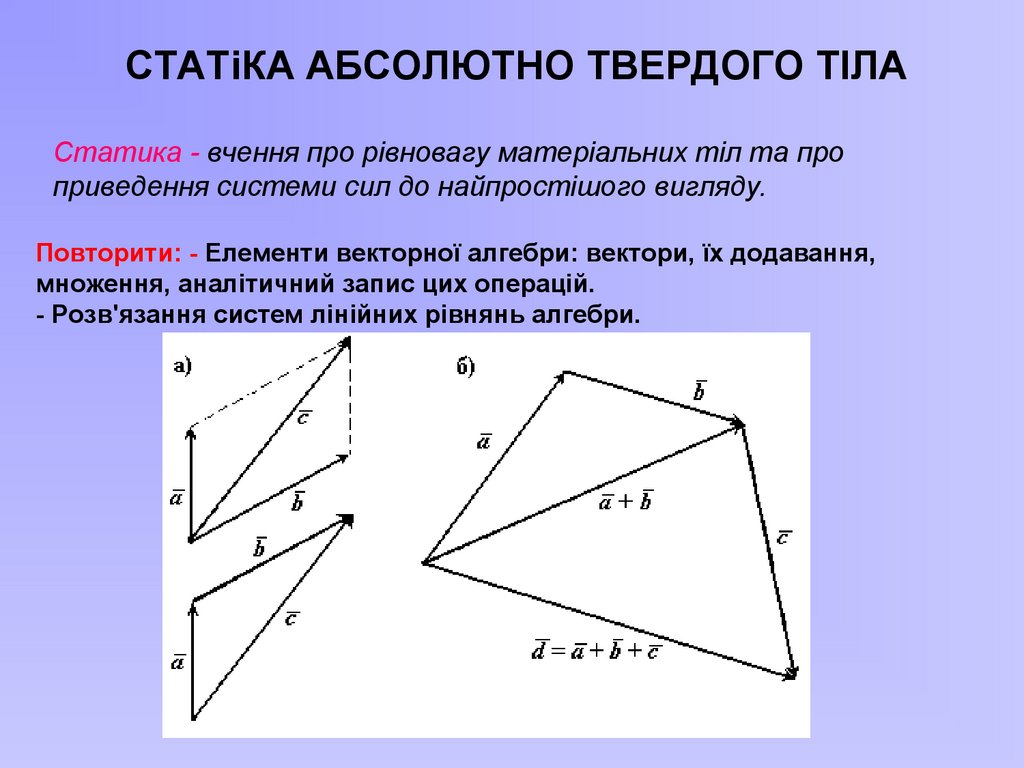
3.

СТАТіКА АБСОЛЮТНО ТВЕРДОГО ТІЛА
Статика - вчення про рівновагу матеріальних тіл та про
приведення системи сил до найпростішого вигляду.
Повторити: - Елементи векторної алгебри: вектори, їх додавання,
множення, аналітичний запис цих операцій.
- Розв'язання систем лінійних рівнянь алгебри.

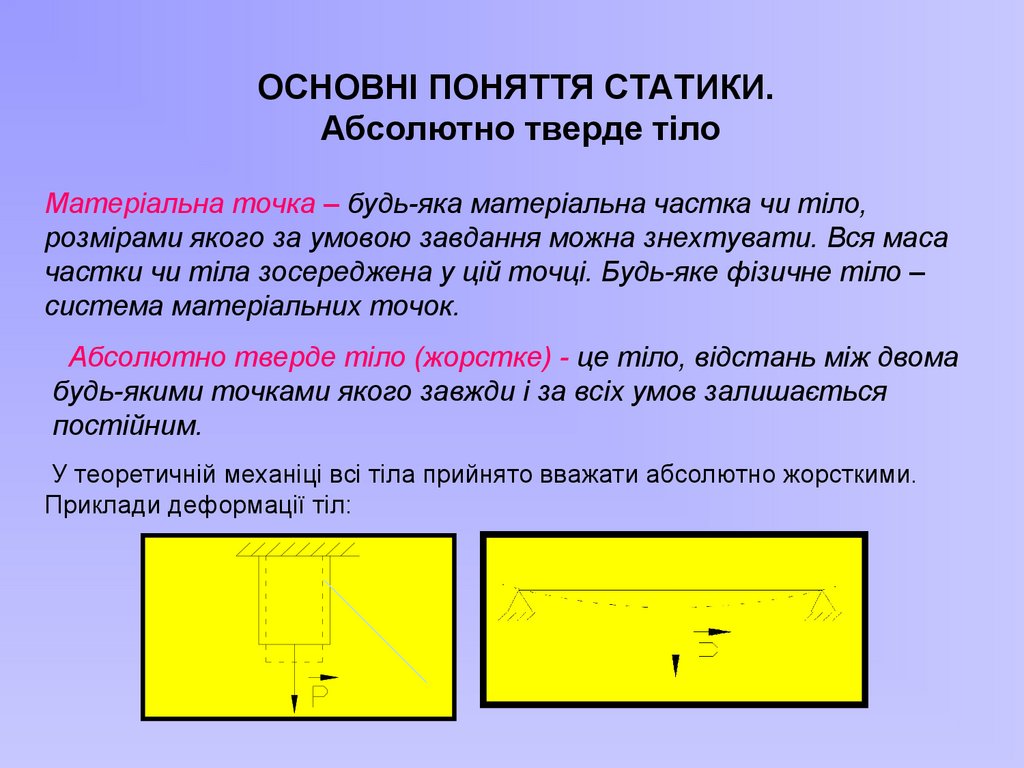
4.

ОСНОВНІ ПОНЯТТЯ СТАТИКИ.
Абсолютно тверде тіло
Матеріальна точка – будь-яка матеріальна частка чи тіло,
розмірами якого за умовою завдання можна знехтувати. Вся маса
частки чи тіла зосереджена у цій точці. Будь-яке фізичне тіло –
система матеріальних точок.
Абсолютно тверде тіло (жорстке) - це тіло, відстань між двома
будь-якими точками якого завжди і за всіх умов залишається
постійним.
У теоретичній механіці всі тіла прийнято вважати абсолютно жорсткими.
Приклади деформації тіл:

5.

Сила - векторна величина, що є кількісним виміром механічної
взаємодії матеріальних тіл і забезпечує рух тіла або його
рівновагу.
Дія сили на тіло визначається:
- чисельною величиною або модулем сили,
- напрямом сили,
- точкою докладання сили,
- лінією дії сили.
Основні одиниці вимірювання силы:
1 ньютон (1 Н) або 1 килограмм (1 кГ). 1кГ = 9,81Н;
1 Н = 0.102 кГ.
Система сил – сукупність сил, які прикладенні до даного тіла.
Система сил, під впливом якої вільне
тверде тіло знаходиться у рівновазі,
називається врівноваженою.
Равнодіюча - це сила, яка одна замінює дію даної системи сил на
тверде тіло.

6.

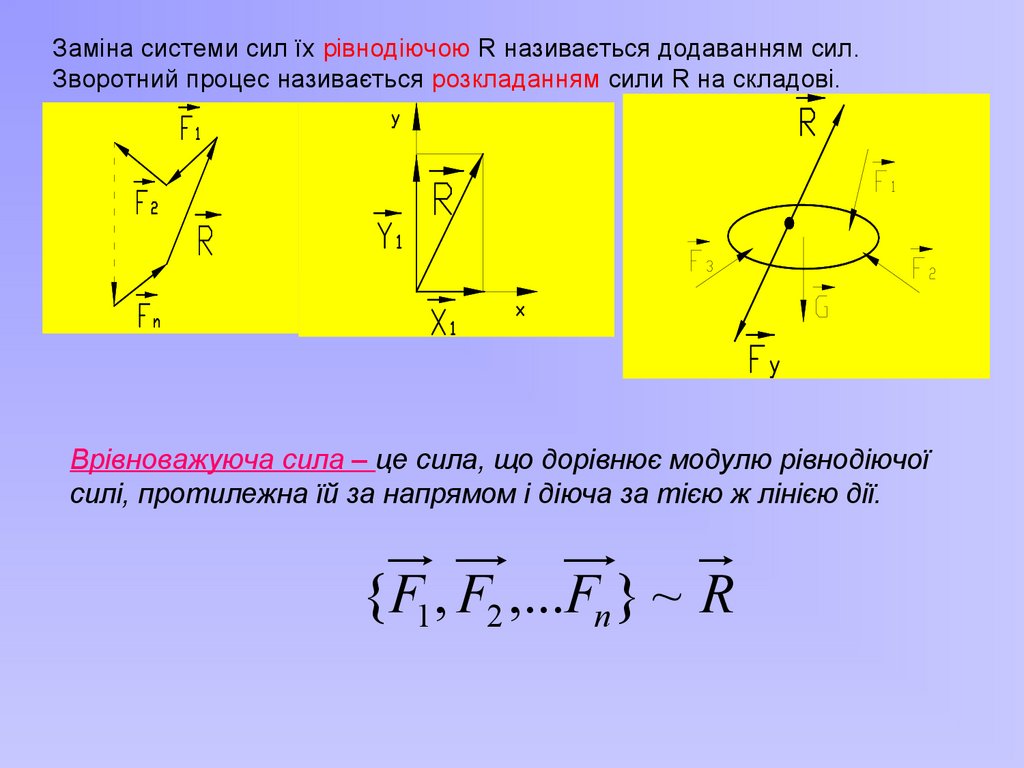
Заміна системи сил їх рівнодіючою R називається додаванням сил.
Зворотний процес називається розкладанням сили R на складові.
Врівноважуюча сила – це сила, що дорівнює модулю рівнодіючої
силі, протилежна їй за напрямом і діюча за тією ж лінією дії.
{F1 , F2 ,...Fn } ~ R

7.

Сили, що діють на тіло, можна розділити на зовнішні та внутрішні.
Зовнішні сили – прикладені до точок твердого тіла із боку інших
тіл.
Внутрішні сили це сили взаємодії між матеріальними точками
даного тіла.(Вивчаються в Опорі матеріалів)
Внутрішні сили, що діють у даному абсолютно твердому тілі, утворюють
врівноважену систему сил і на умови рівноваги тіла не впливають.
Зосередженою силою називається сила, умовно прикладена до
тіла в якійсь одній його точці.
Розподіленими називаються сили, що діють на всі точки
даного тіла або даної частини поверхні.
Плоска система розподілених сил характеризується інтенсивністю q [Н/м]
або [кГ/м] і може бути замінена рівнодіючою Q, яка буде проходити через
центр тяжіння S.

8.

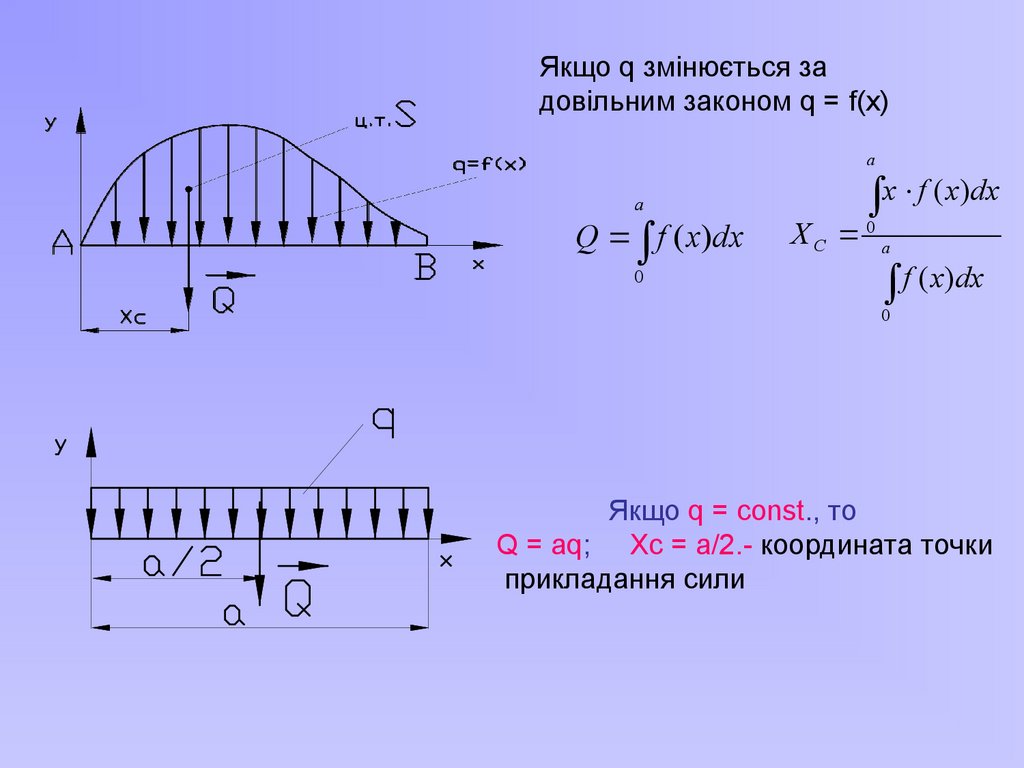
Якщо q змінюється за
довільним законом q = f(x)
a
a
Q f ( x)dx
0
x f ( x)dx
XC 0 a
f ( x)dx
0
Якщо q = const., то
Q = aq; Xc = a/2.- координата точки
прикладання сили

9.

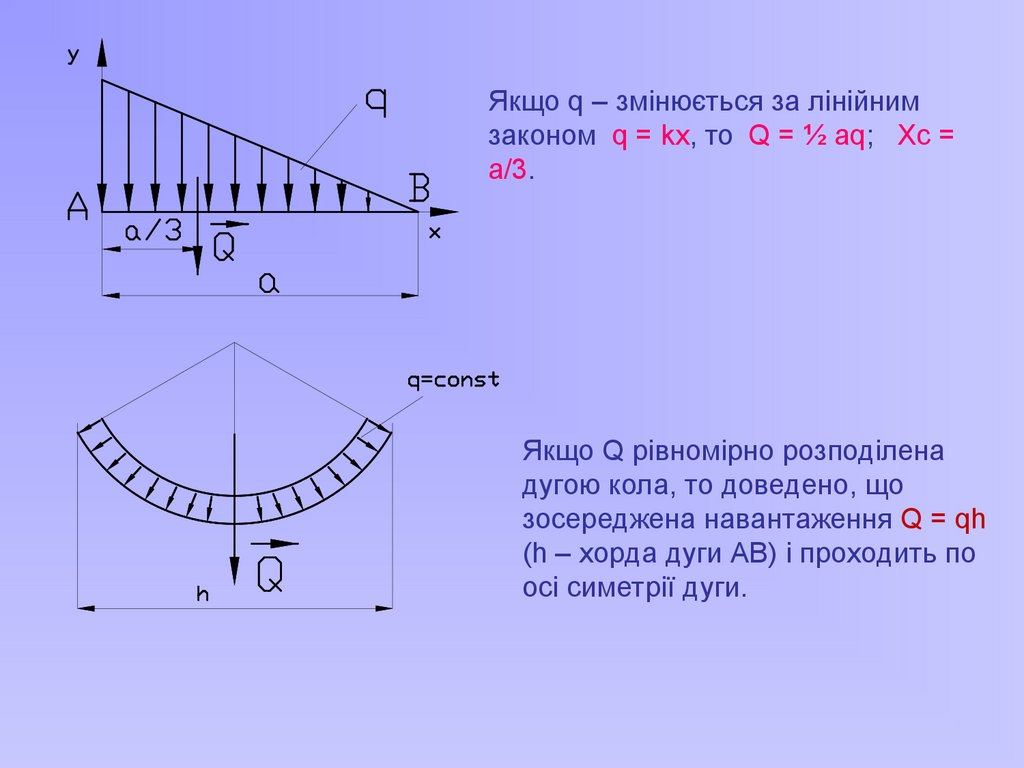
Якщо q – змінюється за лінійним
законом q = kx, то Q = ½ aq; Xc =
a/3.
Якщо Q рівномірно розподілена
дугою кола, то доведено, що
зосереджена навантаження Q = qh
(h – хорда дуги АВ) і проходить по
осі симетрії дуги.

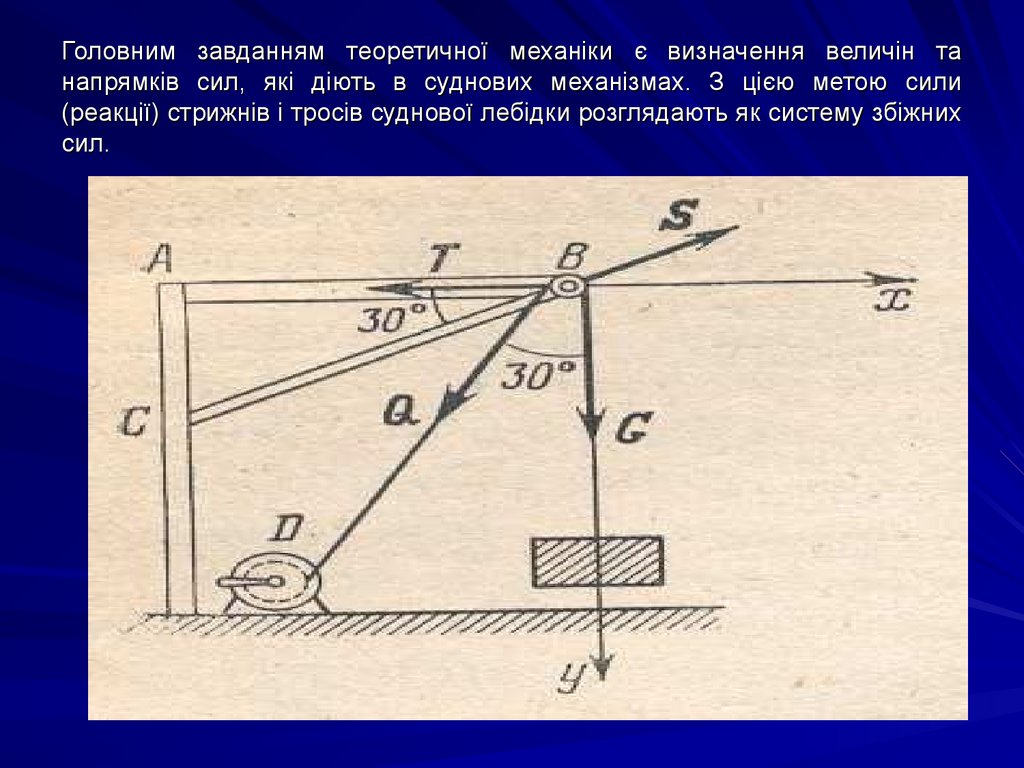
10. Головним завданням теоретичної механіки є визначення величін та напрямків сил, які діють в суднових механізмах. З цією метою

сили
(реакції) стрижнів і тросів суднової лебідки розглядають як систему збіжних
сил.

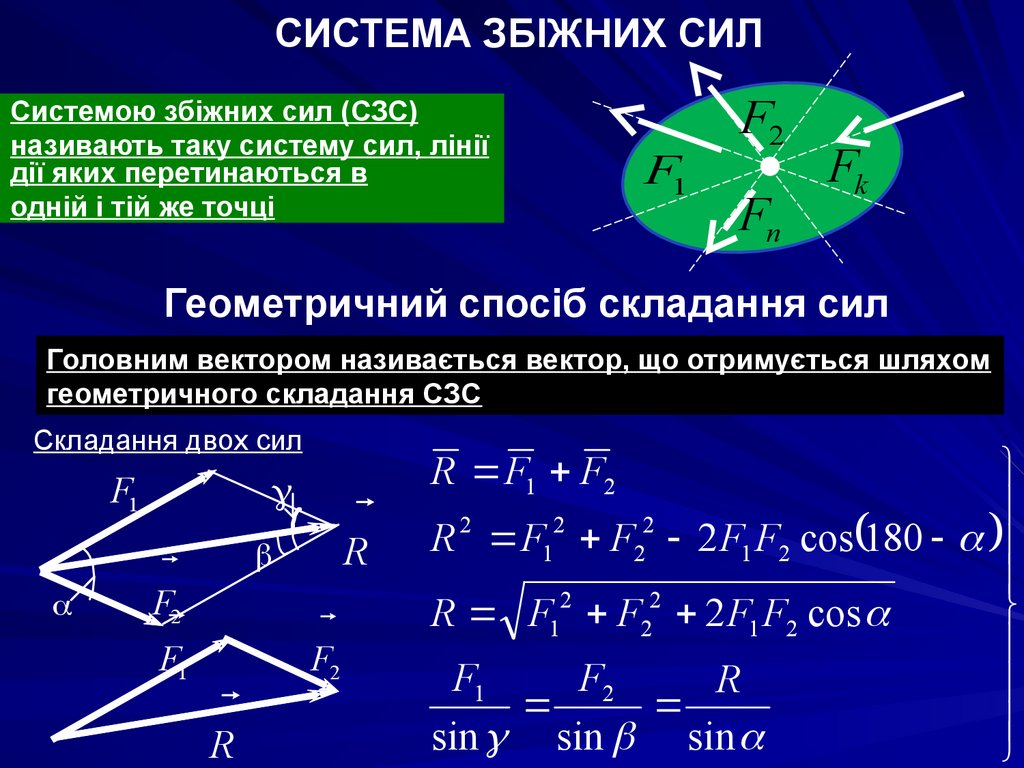
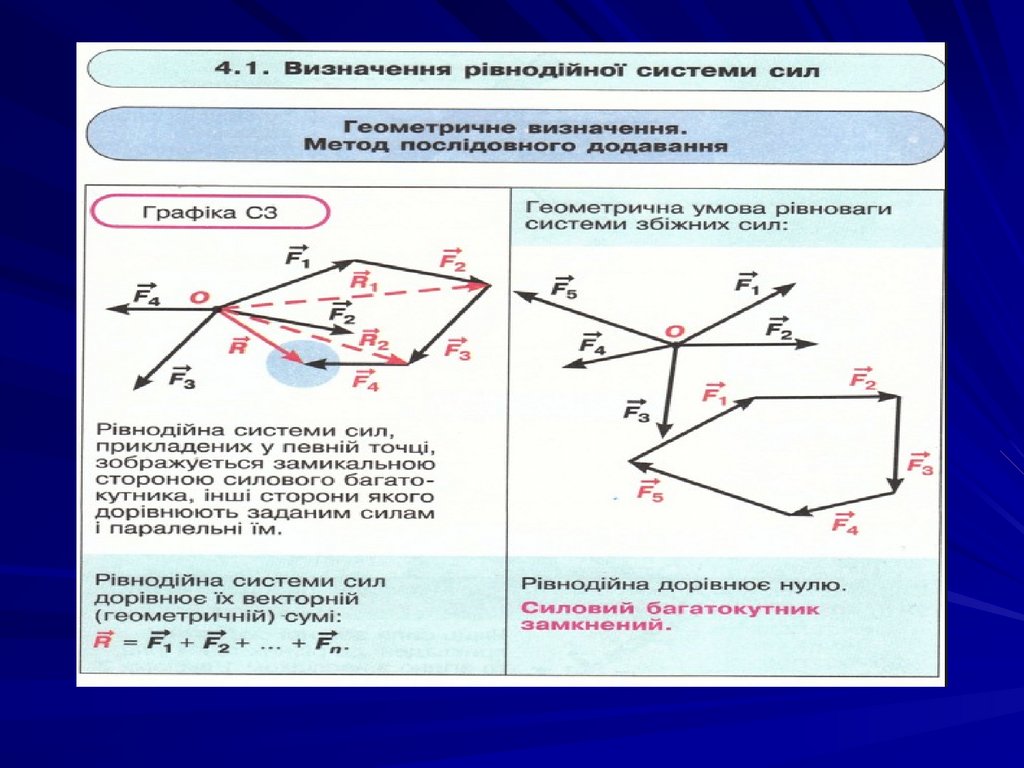
11. СИСТЕМА ЗБІЖНИХ СИЛ

Системою збіжних сил (СЗС)
називають таку систему сил, лінії
дії яких перетинаються в
одній і тій же точці
F1
F2
Fk
Fn
Геометричний спосіб складання сил
Головним вектором називається вектор, що отримується шляхом
геометричного складання СЗС
Складання двох сил
F1
F2
F1
R
R
F2
2
2
2
R F1 F2 2 F1 F2 cos 180
2
2
R F1 F2 2 F1 F2 cos
F1
F2
R
sin sin sin
R F1 F2

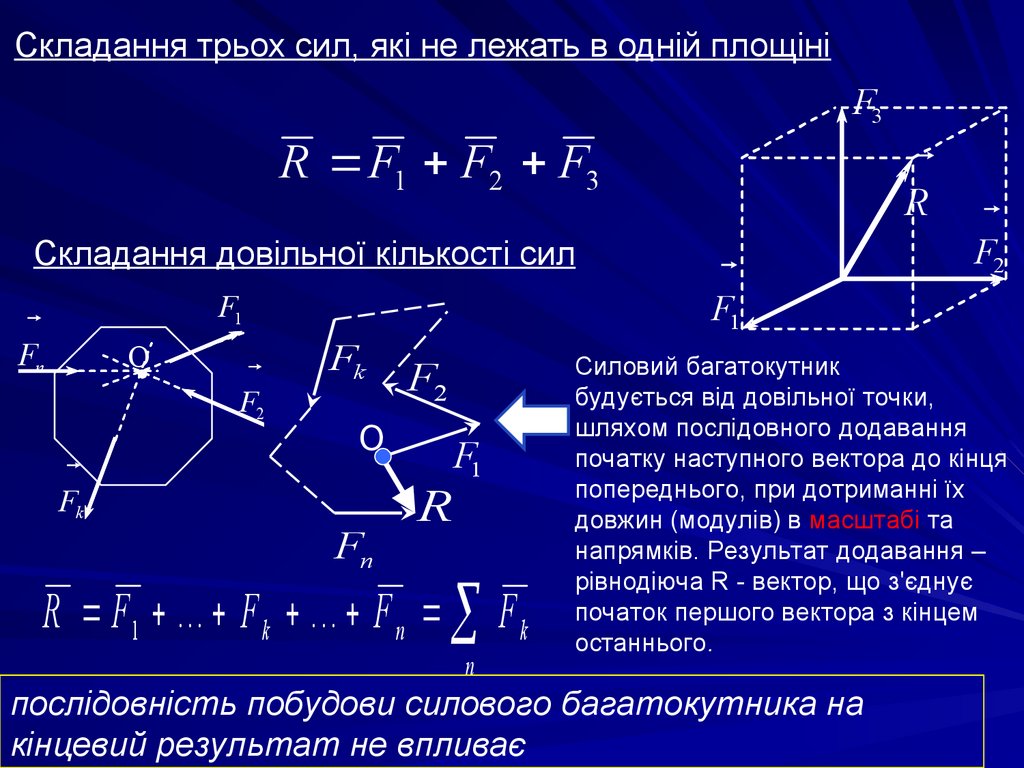
12. Складання трьох сил, які не лежать в одній площіні

F3
R F1 F2 F3
Складання довільної кількості сил
Fn
F1
O
F2
Fk
Fk
O
F 2
F2
F1
О R
F
1
F n
Fk
R
Рис.2.3. Силовой многоугольник
F
n
R F 1 ... F k ... F n F k
n
R
F1
F2
Силовий багатокутник
будується від довільної точки,
шляхом послідовного додавання
початку наступного вектора до кінця
попереднього, при дотриманні їх
довжин (модулів) в масштабі та
напрямків. Результат додавання –
рівнодіюча R - вектор, що з'єднує
початок першого вектора з кінцем
останнього.
послідовність побудови силового багатокутника на
кінцевий результат не впливає

13. Розкладання сил

Проекцією сили на вісь називається
скалярна величина, що дорівнює довжині
відрізка, з відповідним знаком,
укладеного між проекціями початку та
кінця вектора сили на ту ж вісь
F
D
A
a
Fx
З формули видно, що проекція сили має
знак "+", коли α<90о і знак "-", коли α>90о.
Кут утворюється позитивними напрямками вектора і осі,
на яку проектується вектор.
y
Розкласти силу на складові
- це означає знайти таку систему
Збіжних сил, головним вектором якої є
вихідна сила
B
b d Tx
C
c x
Fx F cos
F
Fy
Складова сили – це вектор, який отримується
шляхом множення модуля проекції сили на
одиничний вектор відповідної осі:
T
Fx
x
F x F x i , F y F y j , F z F z k

14. Аналітичний способ складання сил

Теорема про проекцію вектора суми декількох сил:
проекція вектора суми сил на якусь вісь дорівнює алгебраїчній сумі
проекцій доданків векторів цих сил на ту ж вісь
Під “вектором суми”, розуміється вектор, наприклад: R, який
отриманий результаті підсумовування інших векторів, тобто.
R Fk ,
Відповідно до теореми проекції R на координатні осі будуть рівні:
n
R x Fkx , R y Fky , R z Fkz .
n
n
n
Ця теорема дозволяє запропонувати алгоритм розв'язання задачі про
складання системи збіжних сил, тобто. знаходження рівнодіючої R:
R R 2 R 2 R 2
R
F
x
y
z
x kx
F1 проекции F1 x , ..., Fnx
n
сил на оси
cos R x R
... F1 y ,..., Fny R y Fky
n
F ,..., F
cos R y R
Fn
nz
1z
R z Fkz
cos R R
z
n

15. Рівновага системи збіжних сил

Для рівноваги СЗС необхідно і достатньо, щоб
рівнодіюча цих сил дорівнювала нулю, тобто. R=0
Геометрична інтерпретація:
силовий багатокутник, побудований із
цих сил, має бути замкнутим
Це означає, що при побудові силового багатокутника кінець останнього
вектора, який відкладається припадає на початок першого вектора, тобто.
довжина замикаючого вектора (модуль) дорівнодіє R =0.
Аналітична інтерпретація:
для рівноваги СЗС необхідно і
достатньо, щоб суми проекцій цих сил
щодо координатних осей дорівнювали
нулю
Справді, R=0 у разі, якщо її проекції по осях дорівнюють нулю, тобто. Rx = Ry
= Rz = 0. Використовуючи теорему про проекцію вектора суми на вісь,
перейдемо до проекцій сил цієї ССС, тобто.
F 0, F 0, F 0
n
kx
n
ky
n
kz

16.

17. Момент сили відносно центра (або точки)- забезпечує обертальний рух тіла

Момент сили відносно центра (або точки)забезпечує обертальний рух тіла
Моментом сили F щодо центру називається
величина, що дорівнює взятому з відповідним знаком
добутку модуля сили F на довжину плеча h:
mO ( F ) F h
Размірність момента: [Н м] или [кГ м].
Плече сили F щодо центру О – це найкоротша
відстань від центру О до лінії дії сили
(перпендикуляр h, опущений із центру О на лінію дії
сили).
Надалі вважатимемо, що момент має знак «+», якщо сила
прагне повернути тіло проти годинникової стрілки, і знак «-»,
якщо по ходу годинникової стрілки
Властивості момента сили:
1) момент не змінюється при перенесенні сили F вздовж лінії дії;
2) момент дорівнює нулю, якщо F = 0 або h = 0.

18.

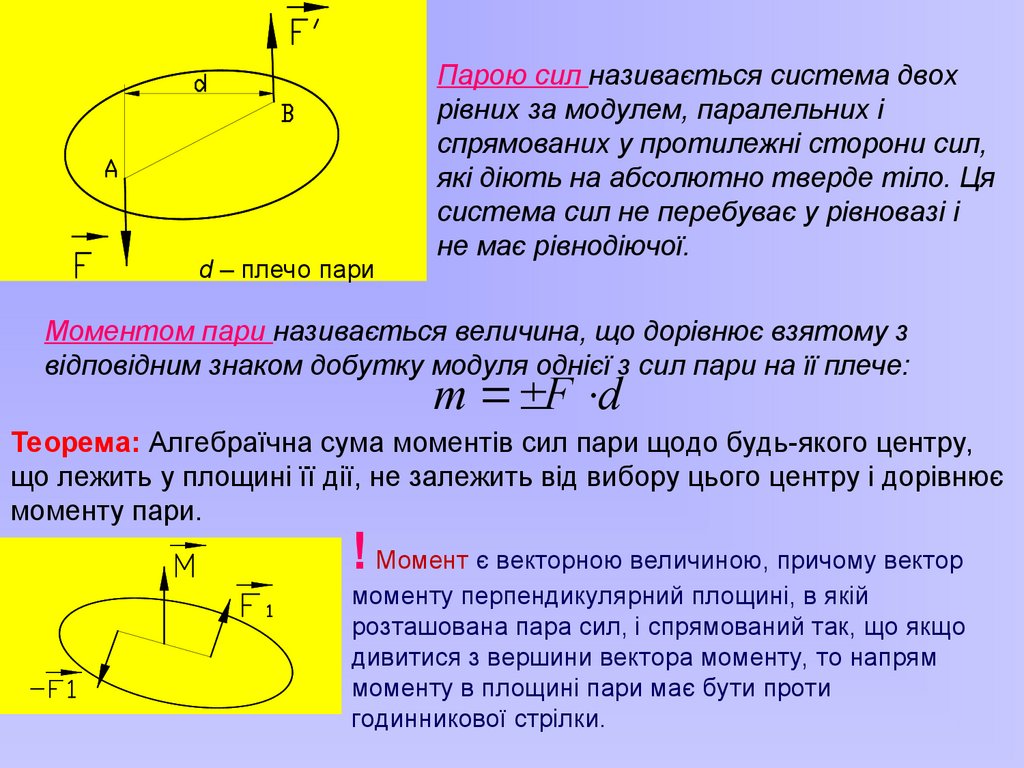
d – плечо пари
Парою сил називається система двох
рівних за модулем, паралельних і
спрямованих у протилежні сторони сил,
які діють на абсолютно тверде тіло. Ця
система сил не перебуває у рівновазі і
не має рівнодіючої.
Моментом пари називається величина, що дорівнює взятому з
відповідним знаком добутку модуля однієї з сил пари на її плече:
m F d
Теорема: Алгебраїчна сума моментів сил пари щодо будь-якого центру,
що лежить у площині її дії, не залежить від вибору цього центру і дорівнює
моменту пари.
! Момент є векторною величиною, причому вектор
моменту перпендикулярний площині, в якій
розташована пара сил, і спрямований так, що якщо
дивитися з вершини вектора моменту, то напрям
моменту в площині пари має бути проти
годинникової стрілки.

19. Складання пар. Умови рівноваги пар

система пар, що лежать в одній площині, еквівалентна одній парі, що
лежить у тій же площині і має момент, що дорівнює алгебраїчній сумі
моментів пар системи
Fk M k d
R R Fk
m1
n
M ( R , R ) R d M k
mk
Fn
mn
Fk
F1
А
R
Fk
d
В
Fn
F1
R
n
щоб скласти систему пар, що лежать в одній площині,
необхідно зробити алгебраїчне складання моментів цих пар
умова рівноваги плоскої системи пар
M 0
n
k
для рівноваги плоскої системи пар необхідно і достатньо, щоб
алгебраїчна сума моментів цих пар дорівнювала нулю

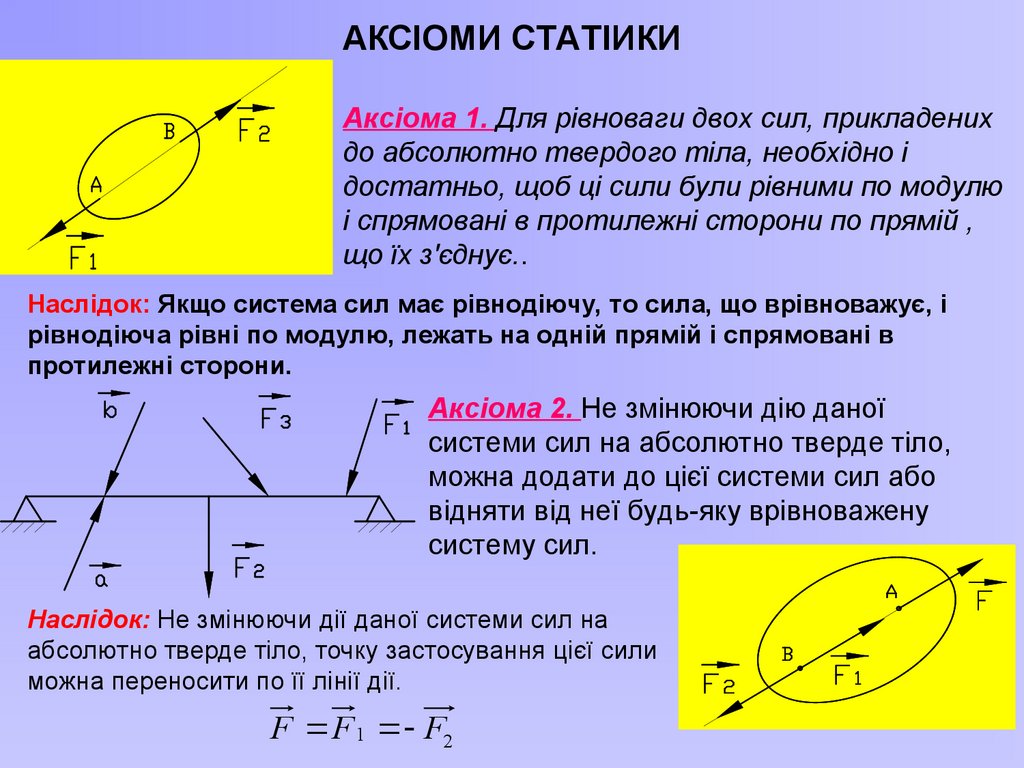
20. АКСІОМИ СТАТІИКИ

Аксіома 1. Для рівноваги двох сил, прикладених
до абсолютно твердого тіла, необхідно і
достатньо, щоб ці сили були рівними по модулю
і спрямовані в протилежні сторони по прямій ,
що їх з'єднує..
Наслідок: Якщо система сил має рівнодіючу, то сила, що врівноважує, і
рівнодіюча рівні по модулю, лежать на одній прямій і спрямовані в
протилежні сторони.
Аксіома 2. Не змінюючи дію даної
системи сил на абсолютно тверде тіло,
можна додати до цієї системи сил або
відняти від неї будь-яку врівноважену
систему сил.
Наслідок: Не змінюючи дії даної системи сил на
абсолютно тверде тіло, точку застосування цієї сили
можна переносити по її лінії дії.
F F 1 F2

21.

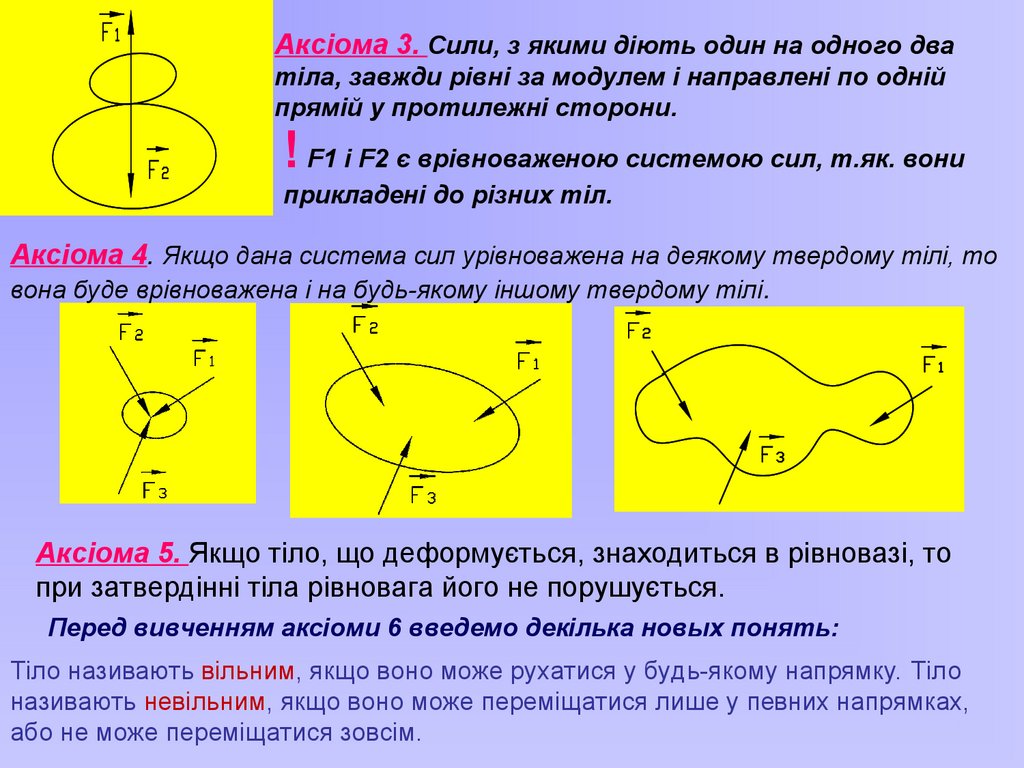
Аксіома 3. Сили, з якими діють один на одного два
тіла, завжди рівні за модулем і направлені по одній
прямій у протилежні сторони.
! F1 і F2 є врівноваженою системою сил, т.як. вони
прикладені до різних тіл.
Аксіома 4. Якщо дана система сил урівноважена на деякому твердому тілі, то
вона буде врівноважена і на будь-якому іншому твердому тілі.
Аксіома 5. Якщо тіло, що деформується, знаходиться в рівновазі, то
при затвердінні тіла рівновага його не порушується.
Перед вивченням аксіоми 6 введемо декілька новых понять:
Тіло називають вільним, якщо воно може рухатися у будь-якому напрямку. Тіло
називають невільним, якщо воно може переміщатися лише у певних напрямках,
або не може переміщатися зовсім.

22.

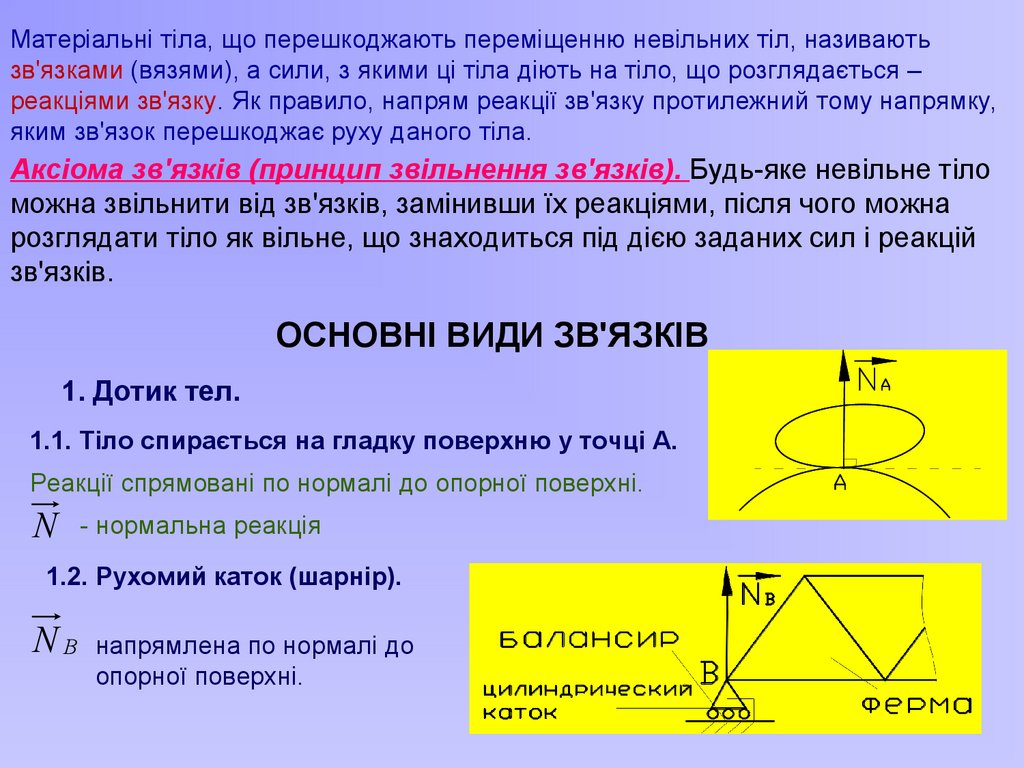
Матеріальні тіла, що перешкоджають переміщенню невільних тіл, називають
зв'язками (вязями), а сили, з якими ці тіла діють на тіло, що розглядається –
реакціями зв'язку. Як правило, напрям реакції зв'язку протилежний тому напрямку,
яким зв'язок перешкоджає руху даного тіла.
Аксіома зв'язків (принцип звільнення зв'язків). Будь-яке невільне тіло
можна звільнити від зв'язків, замінивши їх реакціями, після чого можна
розглядати тіло як вільне, що знаходиться під дією заданих сил і реакцій
зв'язків.
ОСНОВНІ ВИДИ ЗВ'ЯЗКІВ
1. Дотик тел.
1.1. Тіло спирається на гладку поверхню у точці А.
Реакції спрямовані по нормалі до опорної поверхні.
N - нормальна реакція
1.2. Рухомий каток (шарнір).
N B напрямлена по нормалі до
опорної поверхні.

23.

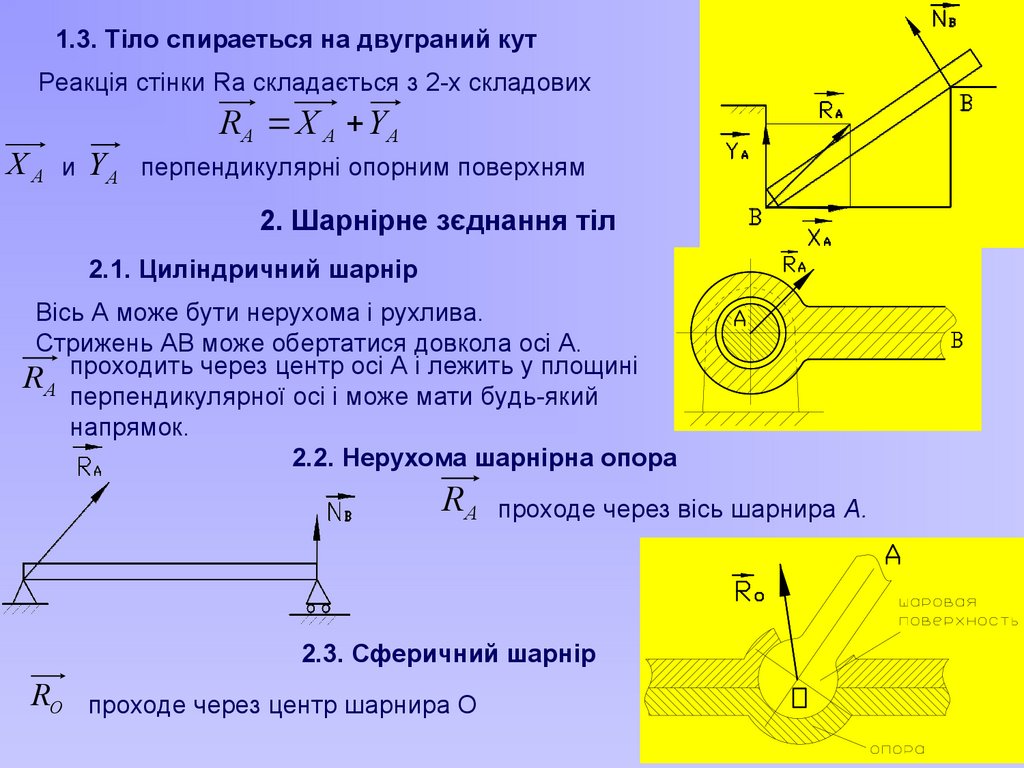
1.3. Тіло спираеться на двуграний кут
Реакція стінки Ra складається з 2-х складових
R A X A YA
X A и YA перпендикулярні опорним поверхням
2. Шарнірне зєднання тіл
2.1. Циліндричний шарнір
Вісь А може бути нерухома і рухлива.
Стрижень АВ може обертатися довкола осі А.
RA проходить через центр осі А і лежить у площині
перпендикулярної осі і може мати будь-який
напрямок.
2.2. Нерухома шарнірна опора
RA проходе через вісь шарнира А.
2.3. Сферичний шарнір
RO проходе через центр шарнира О

24.

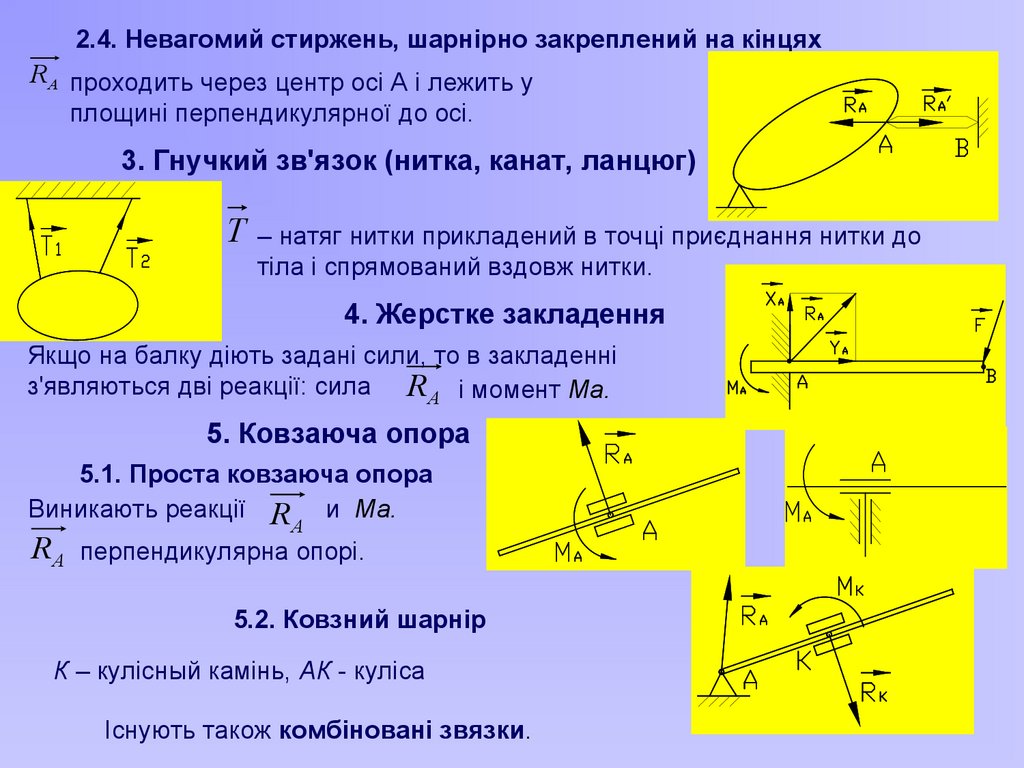
2.4. Невагомий стиржень, шарнірно закреплений на кінцях
RA проходить через центр осі А і лежить у
площині перпендикулярної до осі.
3. Гнучкий зв'язок (нитка, канат, ланцюг)
T – натяг нитки прикладений в точці приєднання нитки до
тіла і спрямований вздовж нитки.
4. Жерстке закладення
Якщо на балку діють задані сили, то в закладенні
з'являються дві реакції: сила R A і момент Ма.
5. Ковзаюча опора
5.1. Проста ковзаюча опора
Виникають реакції R и Ма.
A
RA перпендикулярна опорі.
5.2. Ковзний шарнір
К – кулісный камінь, АК - куліса
Існують також комбіновані звязки.

25. УМОВИ РІВНОВАГИ ДОВІЛЬНОЇ ПЛОСКОЇ СИСТЕМИ СИЛ

Для рівноваги будь-якої плоскої системи сил необхідно та достатньо, щоб
виконувались умови:
R 0
Mо = 0
(1)
Аналітичні (координатні) умови рівноваги (1) можна отримати у 3-х різних
скалярних формах::
1) Основна форма.
2) Друга форма умов
З (1) безпосередньо випливає:
рівноваги:
F 0
F 0
m ( F ) 0
m ( F ) 0
m ( F ) 0
iY
O
i
A
iX
(2)
B
(3)
i
F 0
iY
i
Причому АВ не перпендикулярні Ох,
А і В – будь-які дві точки, що не збігаються на тілі.
3) Третя форма умов рівноваги:
точки А, В, С не лежать на одній прямій.
m ( F ) 0
mB ( Fi ) 0
m ( F ) 0
A
i
С
i
(4)

26.

! Якщо на тіло діє ще й система пар сил з моментами m1, m2… mn, то в
умовах (2), (3), (4) вирази для моментів набудуть вигляду:
m ( F ) m 0
О
i
j
СИСТЕМА ЗБІЖНИХ СИЛ (СЗС)
!Збіжною - називається система сил, лінії дії якої перетинаються в одній
точці. У системі збіжних сил не складають рівняння моментів, оскільки плечі
цих сил дорівнюють 0.
Умови рівноваги:
1) У геометричній формі:
F , F ,...F ~ 0
1
2) У векторній формі:
2
F 0
i
3) У координатній (аналітичній) формі:
n
Fi Fix , Fiy , Fiz
F F F .... F
F F F .... F
ix
1x
2x
nx
iy
1y
2y
ny
iz
1z
2z
nz
F F F .... F

27.

УМОВИ РІВНОВАГИ ДОВІЛЬНОЇ ПРОСТОРОВОЇ
СИСТЕМИ СИЛ
F 0
F 0
F 0
m ( F ) 0
m ( F ) 0
m ( F ) 0
iX
iY
iZ
OX
i
OY
i
OZ
i

28.

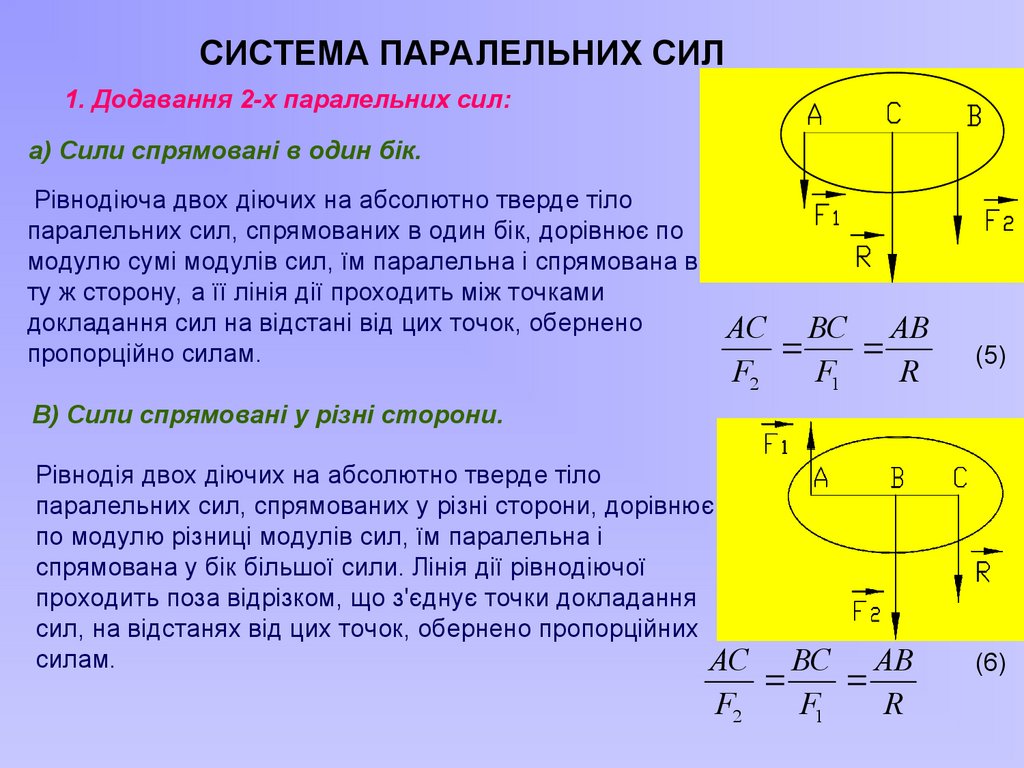
СИСТЕМА ПАРАЛЕЛЬНИХ СИЛ
1. Додавання 2-х паралельних сил:
а) Сили спрямовані в один бік.
Рівнодіюча двох діючих на абсолютно тверде тіло
паралельних сил, спрямованих в один бік, дорівнює по
модулю сумі модулів сил, їм паралельна і спрямована в
ту ж сторону, а її лінія дії проходить між точками
докладання сил на відстані від цих точок, обернено
пропорційно силам.
АС ВС АВ
F2
F1
R
(5)
В) Сили спрямовані у різні сторони.
Рівнодія двох діючих на абсолютно тверде тіло
паралельних сил, спрямованих у різні сторони, дорівнює
по модулю різниці модулів сил, їм паралельна і
спрямована у бік більшої сили. Лінія дії рівнодіючої
проходить поза відрізком, що з'єднує точки докладання
сил, на відстанях від цих точок, обернено пропорційних
силам.
АС
ВС АВ
F2
F1
R
(6)

29. Приведення ПЛАСКОЇ ДОВІЛЬНОЇ СИСТЕМИ СИЛ ДО ЗАДАНОГО ЦЕНТРУ

Паралельний перенос силы
Теорема 1
не змінюючи дії сили на тіло, силу,
прикладену до тіла, можна
перенести паралельно їй самій в
будь-яку точку тіла, прикладаючи,
при цьому, пару з моментом, рівним
моменту сили щодо точки, куди
сила переноситься
М = Fd = Fh
a
F
B
h
A
F
б
B
F
d
А
F
в
B
M
A
F

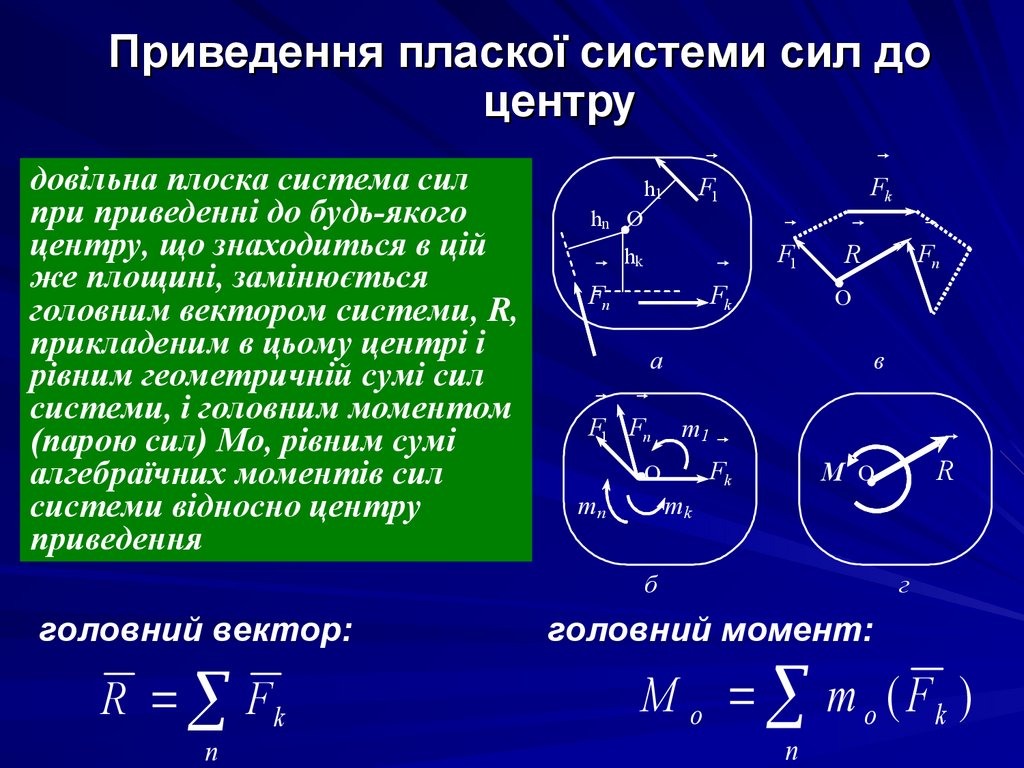
30. Приведення пласкої системи сил до центру

довільна плоска система сил
при приведенні до будь-якого
центру, що знаходиться в цій
же площині, замінюється
головним вектором системи, R,
прикладеним в цьому центрі і
рівним геометричній сумі сил
системи, і головним моментом
(парою сил) Мо, рівним сумі
алгебраїчних моментів сил
системи відносно центру
приведення
F1
h1
hn O
Fn
hk
Fk
Fk
F1
O
a
F1 Fn
в
m1
О
mn
mk
Fk
R Fk
n
R
M O
б
головний вектор:
Fn
R
г
головний момент:
M o m o ( Fk )
n

31. Окремі випадки приведення

1) R=0, Mо=0 - система сил перебуває у рівновазі; ( тіло нерухоме)
2) R=0, Mо 0 - система сил приводиться до однієї пари з
моментом Мо, а результат приведення системи залежить від
вибору центру приведення; (тіло здійснює обертальний рух)
3) R 0:
а) Мо=0 - система приводиться до головного вектора R, який у
цьому випадку виконує функції рівнодіючої;
б) Мо 0 - систему можна привести до головного вектора R,
віддаленого від центру приведення ( )Про на відстані d.
R
R
О
Мо
а
R
О
R
б
О
R
d
в

32.

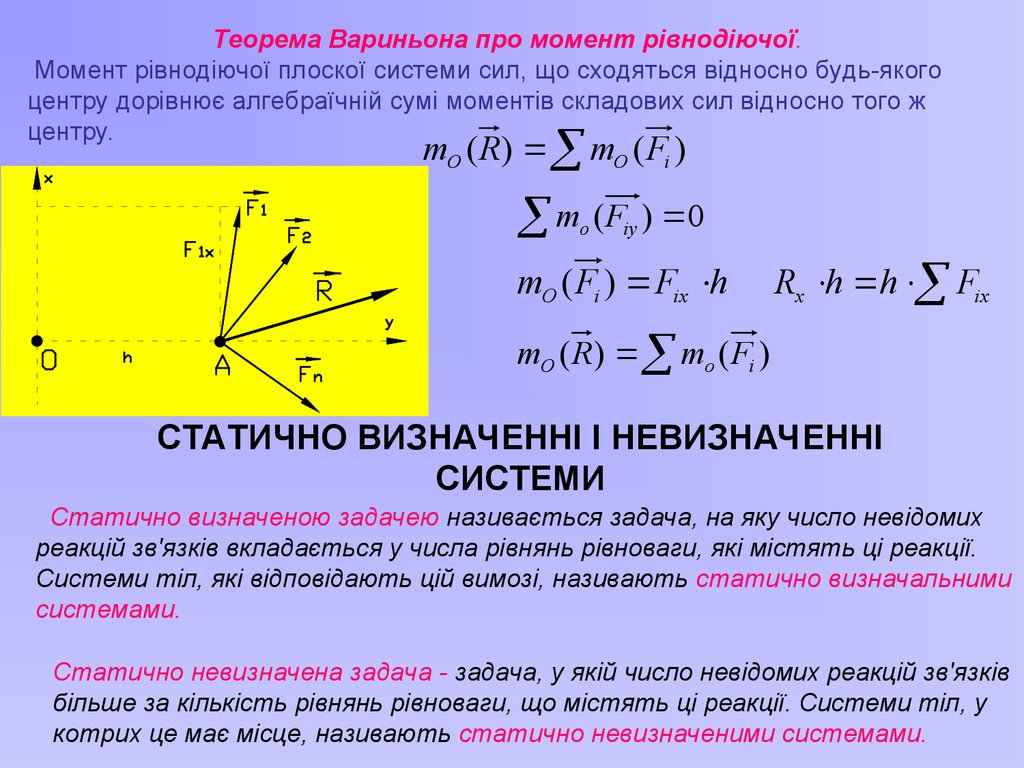
Теорема Вариньона про момент рівнодіючої.
Момент рівнодіючої плоскої системи сил, що сходяться відносно будь-якого
центру дорівнює алгебраїчній сумі моментів складових сил відносно того ж
центру.
mO ( R) mO ( Fi )
m ( F ) 0
o
iy
mO ( Fi ) Fix h
Rx h h Fix
mO ( R ) mo ( Fi )
СТАТИЧНО ВИЗНАЧЕННІ І НЕВИЗНАЧЕННІ
СИСТЕМИ
Статично визначеною задачею називається задача, на яку число невідомих
реакцій зв'язків вкладається у числа рівнянь рівноваги, які містять ці реакції.
Системи тіл, які відповідають цій вимозі, називають статично визначальними
системами.
Статично невизначена задача - задача, у якій число невідомих реакцій зв'язків
більше за кількість рівнянь рівноваги, що містять ці реакції. Системи тіл, у
котрих це має місце, називають статично невизначеними системами.

33.

РІВНОВАГА СИСТЕМИ ТІЛ
Внутрішні зв'язки з'єднують частини даної конструкції.
Зв'язки зовнішні з'єднують конструкцію з тілами, які до неї не входять,
в т.ч. із опорами.
Приклад. Знайти реакції опор тришарнірної арки.
F X X P 0
F Y Y 0
mА ( F i ) YB l P h 0
iX
A
iY
B
A
B
F X X P 0
iX
A
C
F Y Y 0
l
m
(
F
)
P
h
X
h
Y
0
2
iY
А
A
i
C
C
C

34.

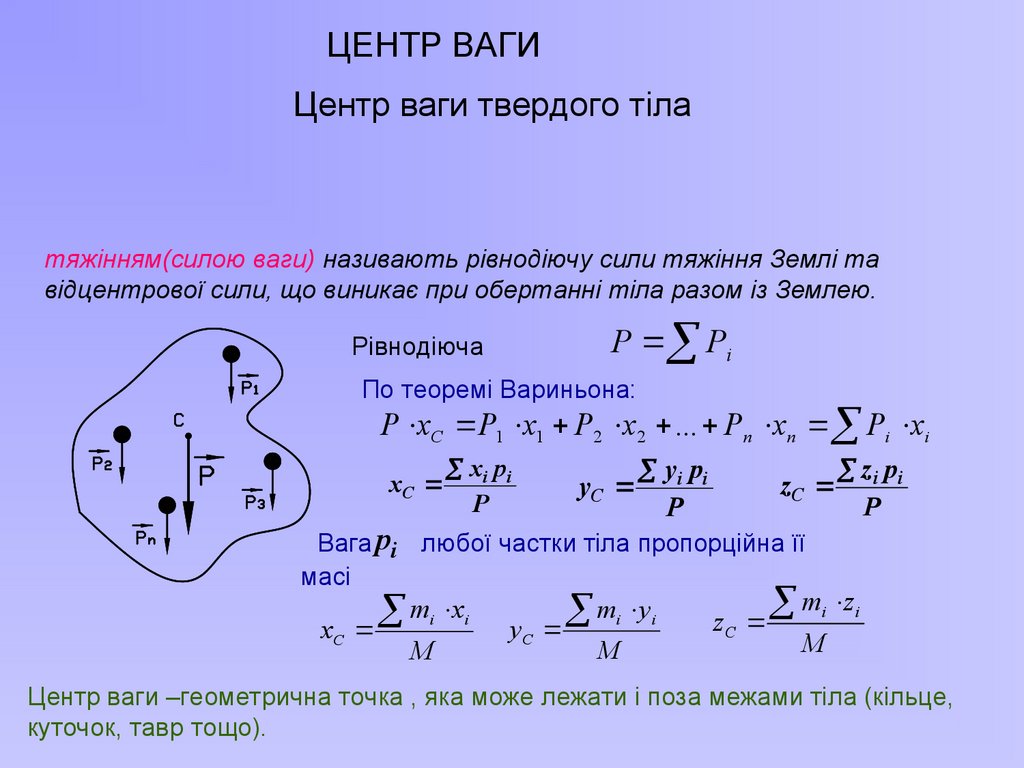
ЦЕНТР ВАГИ
Центр ваги твердого тіла
тяжінням(силою ваги) називають рівнодіючу сили тяжіння Землі та
відцентрової сили, що виникає при обертанні тіла разом із Землею.
Рівнодіюча
Р Рi
По теоремі Вариньона:
Р хС Р1 х1 Р2 х2 ... Рn xn Рi xi
xC
x i pi
P
yi pi
yC
P
zC
z i pi
P
Вага pi любої частки тіла пропорційна її
масі
mi zi
mi yi
mi хi
z
С
yС
хС
M
M
M
Центр ваги –геометрична точка , яка може лежати і поза межами тіла (кільце,
куточок, тавр тощо).

35.

Способи визначення центру тяжіння тіл
1) Симетрія. Якщо однорідне тіло має площину (вісь, центр) симетрії,
то ц. лежить у площині (на осі, у центрі) симетрії..
2) Розбиття. Тіло розбивається на певне
число елементів, ц.т. яких відомий.
загальний ц.т. знаходимо за формулами:
S х S 2 х2
хС 1 1
S
S1 y1 S 2 y2
yС
S
3) Доповнення. Окремий випадок. Якщо
тіло має вирізи, знаходимо ц.т. тіла без
вирізів та ц.т. вирізаної фігури.
S1 х1 S 2 х2
хС
S
S y S 2 y2
yС 1 1
S
4) Інтегрування. Застосовується якщо тіло
неоднорідне.

36.

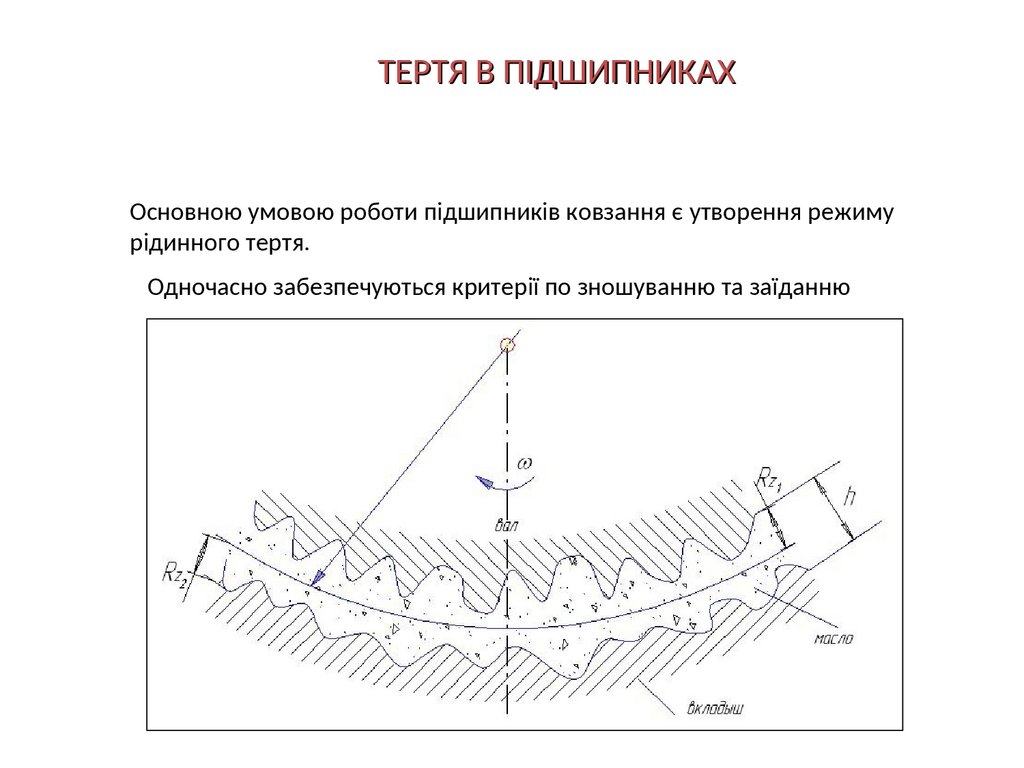
ТЕРТЯ В ПІДШИПНИКАХ
Основною умовою роботи підшипників ковзання є утворення режиму
рідинного тертя.
Одночасно забезпечуються критерії по зношуванню та заїданню

37.

ТЕРТЯ
Тертя ковзання. Кут тертя.
Експериментально встановлено такі закони тертя ковзання:
1) При прагненні зрушити одне тіло
поверхнею іншого в площині зіткнення тіл
виникає сила тертя, спрямована в
протилежний бік.
2) Гранична сила тертя дорівнює добутку статичного
коефіцієнта тертя fo на нормальний тиск (нормальну
реакцію):
F
f N
тр . пр
0
fo – визначається дослідним шляхом:
Дерево по дереву
fo = 0.4 – 0.7; (дуб по дубу fo = 0.54 –
0.62)
Металл по металлу
fo = 0.15 – 0.25; (сталь по стали – 0.15)
3) При рівновазі сила тертя спокою
F F
тр .
тр .пр
4) Величина Fтр.пр. в широких межах не залежить від розмірів
поверхонь, що стикаються при терті.
При русі тіла Fтр. залежить від динамічного коефіцієнта тертя f, який, як
правило, залежить від швидкості руху тіла та визначається дослідним шляхом.
З урахуванням тертя, реакція зв'язку отримує другу складову Fтр., яка відхиляє
повну реакцію зв'язку від нормалі до поверхні на деякий кут.

38.

0 0 - граничне значення (кут тертя)
Fтр
tg 0
или tg 0 f 0
N
Зазвичай розглядається граничне положення
рівноваги, коли сила тертя досягає
найбільшого значення Fтр. і вона
сприймається як зовнішня сила.
Тертя кочення
Тертя кочення - особливий вид опору, що виникає, коли одне з тіл котиться
поверхнею іншого тіла без прослизання
k
F N
R
Розглянемо циліндричний каток. На нього діють
дві сили, що врівноважують: сила тяжіння mg і
нормальна реакція площини N = –mg. Якщо під
дією горизонтальної сили F, прикладеної до
центру котка, він котиться по площині без
ковзання, то сили mg і N утворюють пару сил, що
перешкоджає коченню катка. Плечо пари к
називається коефіцієнтом тертя кочення.

39.

40.

41.

Для работы с подшипником цапфы вала необходимо подвергать
термической или, а шероховатость поверхности Ra – 2,5…0,25 мкм. Более
высокая гладкость поверхности цапфы нежелательна (хуже удерживает смазку).
Види тертя в залежності від кількості мастильного матеріалу в
підшипнику ковзання:
1) рідинне тертя характеризується повним поділом шаром
змащення поверхонь цапфи та підшипника (коефіцієнт тертя та
коефіцієнт втрат енергії в підшипнику при цьому виді тертя
мінімальні);
2) напіврідинне тертя – основна частина взаємодіючих
поверхонь розділена шаром мастильної рідини, а поверхні
підшипника та цапфи контактують вершинами мікронерівностей;
3) напівсухе (граничне) тертя – поверхні цапфи валу та
підшипника майже постійно контактують між собою, проте між
ними є деяка кількість мастильного матеріалу;
4) сухе тертя – у зазорі між поверхнями цапфи валу та
підшипника мастильний матеріал відсутній повністю, внаслідок
чого ці поверхні перебувають у стані безперервного контакту.

42.

Матеріали, що застосовуються для змащування підшипників
ковзання, за рівнем консистентності (за густотою, твердістю) можна
умовно розділити на:
тверді - графіт, дисульфід молібдену, деякі обволікаючі метали,
наприклад, індій;
пластичні (консистентні, що не володіють властивістю краплепадіння) солідол, консталін, літол, деякі мастила ЦИАТИМ;
рідкі – органічні та мінеральні олії, іноді вода та інші рідини,
газоподібні – повітря, азот, інертні гази (аргон).
Чим вище в'язкість мастильного матеріалу, тим важче він видавлюєтеся з
робочого зазору підшипника і, отже, тим товстішим може бути його шар
між цапфою та поверхнею підшипника у процесі їхньої спільної роботи.
Найбільшого поширення у суднових умовах набули рідке та консистентне
мастило.
При використанні рідинного мастила в залежності від способу подачі
мастила в робочий зазор підшипника та розділення твердих поверхонь
шаром рідкого мастила розрізняють гідростатичний та гідродинамічний
способи змащування.

43.

Рис. 10.4. Гідростатичне
змащування підшипника
ковзання.
Гідростатичний спосіб заснований на
розділенні тертьових поверхонь за рахунок
статичного напору мастильної рідини, що
підводиться до підшипника, тобто за рахунок
тиску, створюваного зовнішнім джерелом
(насосом). Тому при гідростатичному способі
змащування мастильна рідина подається
назустріч основним навантаженням (рис.
10.4), що діють на цапфу валу, а тиск насоса
вибирається таким, щоб цапфа валу
спливала на шарі мастила. Застосовується
цей спосіб подачі мастила для змащування
підшипників важко навантажених тихохідних
валів
(наприклад,
для
змащування
підшипників валів суднових двигунів), для
гідростатичного
центрування
валів
у
прецизійних машинах, а також у періоди
розгону до досягнення гідродинамічного
режиму змащування.

44.

Гідродинамічний
змащування
реалізується тільки в процесі обертання
цапфи в підшипнику після досягнення
критичної швидкості обертання (рис. 10.5).
Спочатку цапфа нерухомого валу лежить
на поверхні підшипника (рис. 10.5.а), і
тому початковий період обертання валу
характеризується режимом граничного
змащування.
У міру збільшення кутової швидкості
цапфи частинки мастила за рахунок
налипання на її
Рис. 10.5. Гидродинамическая смазка
подшипника скольжения.
поверхню втягуються в клиновий зазор між цапфою та підшипником. Тиск масла в
ньому підвищується і при досягненні критичної швидкості обертання цапфа валу,
спливаючи, відірветься від поверхні підшипника - відбудеться повний поділ
поверхонь, що труться. Тиск, що розвивається в клиновому зазорі, прямо
пропорційний динамічній в'язкості масла, частоті обертання валу і обернено
пропорційний
товщині
масляного
шару.
Товщина
мастильного
шару
саморегулюється відповідно до навантаження, що діє на цапфу валу – при
збільшенні навантаження товщина шару мастила знижується і навпаки. Тиск у
клиновому шарі може бути більшим, і тому подача масла проводиться в зону
розрідження, що не вимагає великих витрат потужності на змащування та системи
змащення високого тиску (насоси, фільтри, радіатори, трубопроводи тощо).