Определение арксинуса, арккосинуса, арктангенса и арккотангенса числа а

1.

Определение
арксинуса,
арккосинуса,
арктангенса и
арккотангенса
числа а

2.

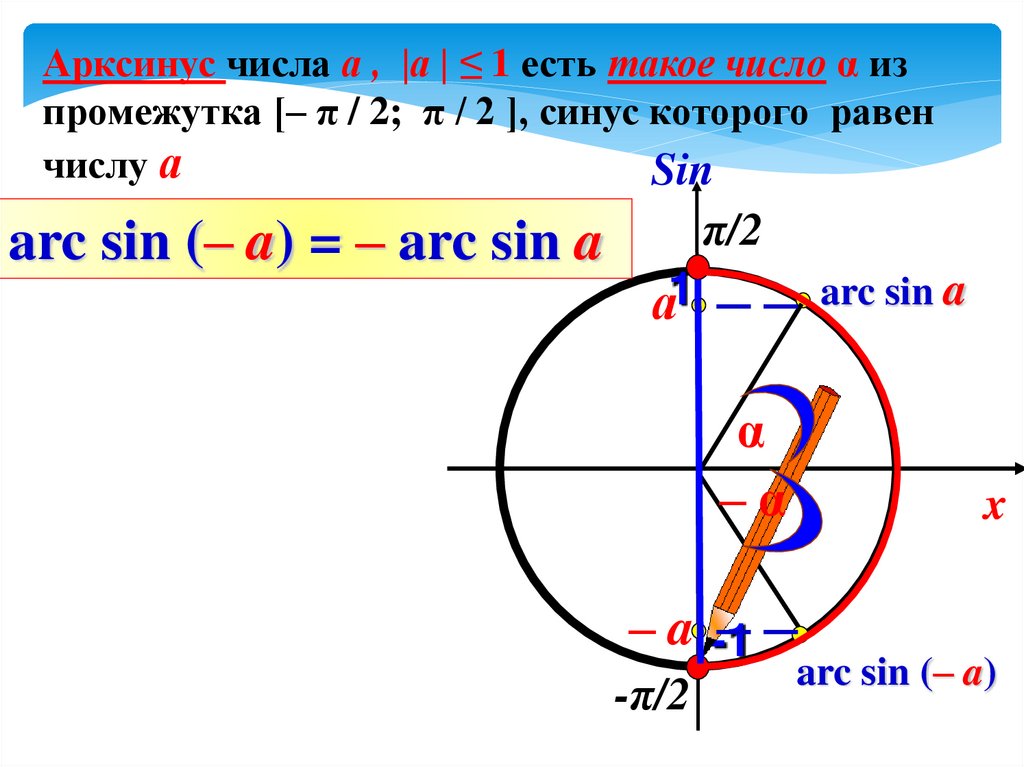
Арксинус числа а , |а | ≤ 1 есть такое число α из
промежутка [– π / 2; π / 2 ], синус которого равен
числу а
Sin
π/2
arc sin (– a) = – arc sin a
а1
arc sin a
α
–α
– a -1
-π/2
x
arc sin (– a)

3.

Sin
Вычислите:
1
arcsin
2 6
2
12
2
2
arcsin
4
2
3
arcsin
2
3
arcsin ( 1)
π/2
2
1
arcsin
2
6
-π/2
1
23
12
Ищу число из отрезка
[-π/2; π/2], синус
которого равен …

4.

Арккосинус числа а , |а | ≤ 1 есть такое число α из
промежутка [ 0; π ], косинус которого равен а
arc cos (– a) = π – arc cos a
Sin
arc cos a
arc соs (– a)
π -1
–a
α
а
1 0 Cos

5.

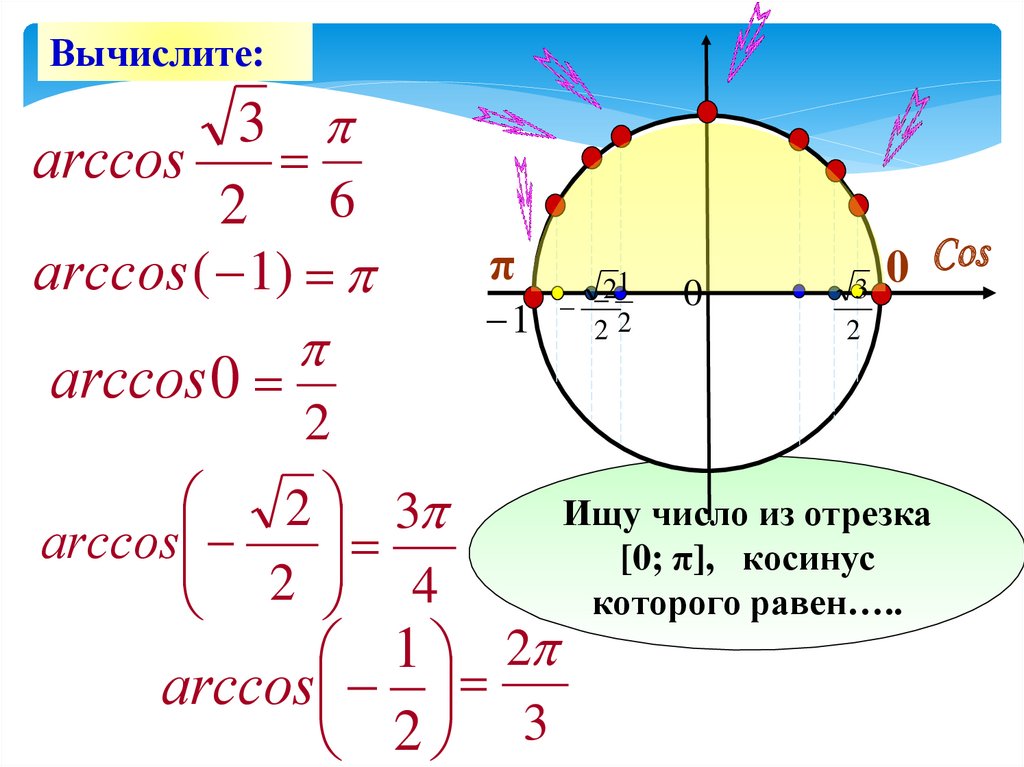
Вычислите:
3
arcсos
2 6
arcсos ( 1)
arcсos 0
π
1
21
22
0
3
2
0 Cos
2
2 3
arcсos
4
2
1 2
arcсos
2 3
Ищу число из отрезка
[0; π], косинус
которого равен…..

6. Имеет ли смысл выражение?

аrcsin (-1/2)
да
аrcsin 1,5
нет
arccos
нет
arccos
да
5
arcsin 3 20
нет
3 1
arccos
5
да

7.

π
1
= 6
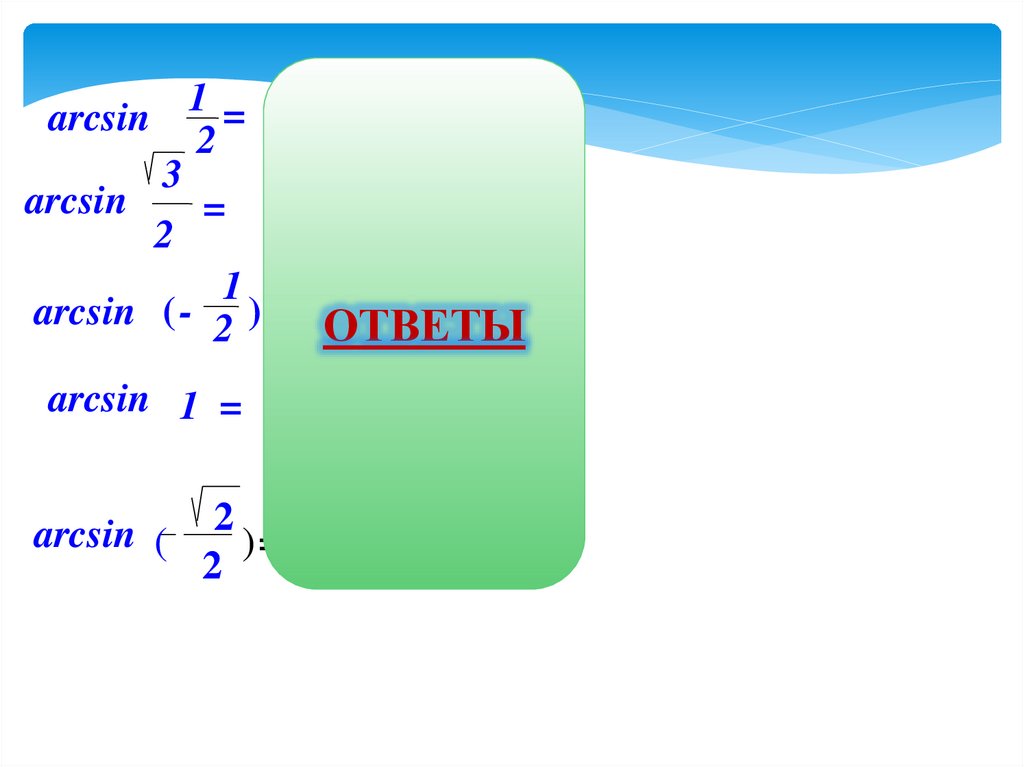
arcsin
2
3
π
arcsin
=
2
3
π
1
arcsin ( - 2 ) = - ОТВЕТЫ
6
π
arcsin 1 =
2
π
2
arcsin (
)= - 4
2

8.

arccos
1 = π
2
3
π
3
arccos
2 = 6
1 2π
arccos (− 1 ) = π ̶ ОТВЕТЫ
arccos =
2
2
3
2 ) 3π
(
arccos
=
2
4
arccos 0 =
π
2

9.

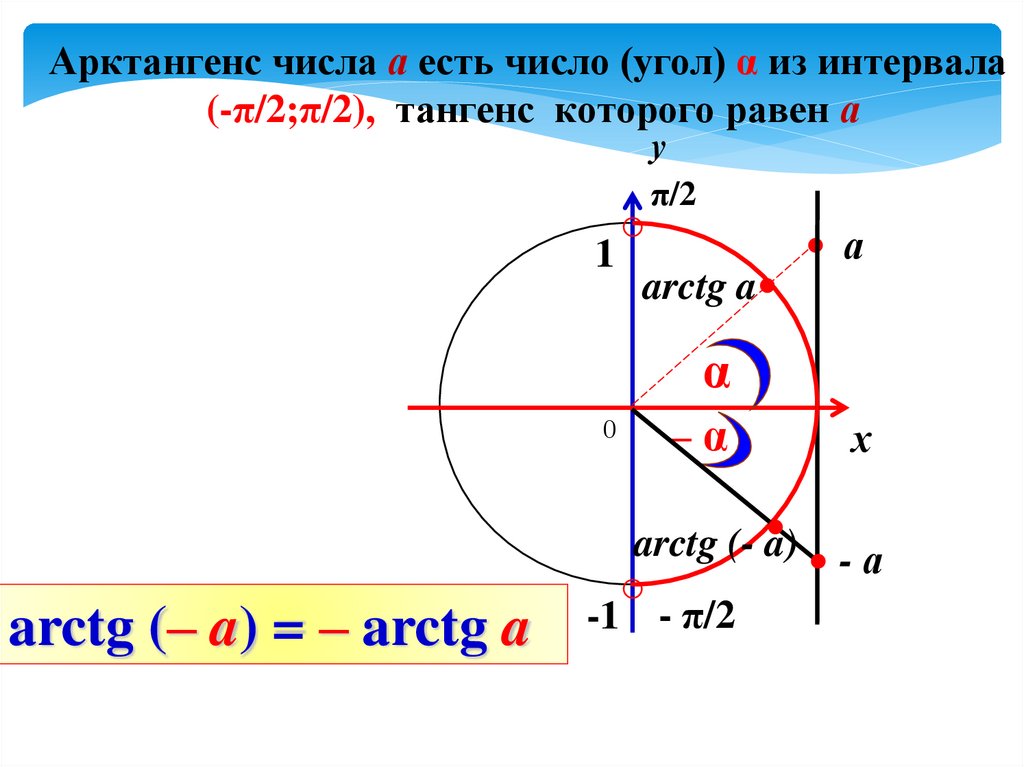
Арктангенс числа а есть число (угол) α из интервала
(-π/2;π/2), тангенс которого равен а
1
○
у
π/2
а
arctg a
α
–α
0
arctg (- a)
arctg (– a) = – arctg a
○
-1 - π/2
х
-а

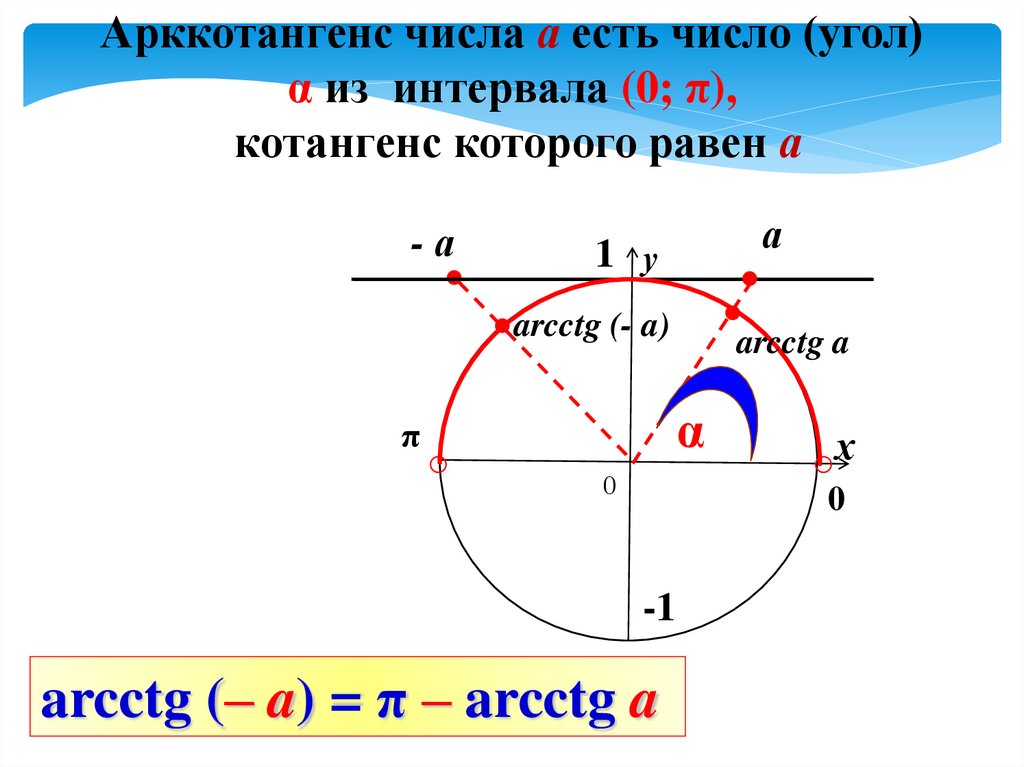
10.

Арккотангенс числа а есть число (угол)
α из интервала (0; π),
котангенс которого равен а
-а
а
1 у
arcctg (- a)
π
○
arcctg a
α
0
○х
0
-1
arcctg (– a) = π – arcctg a

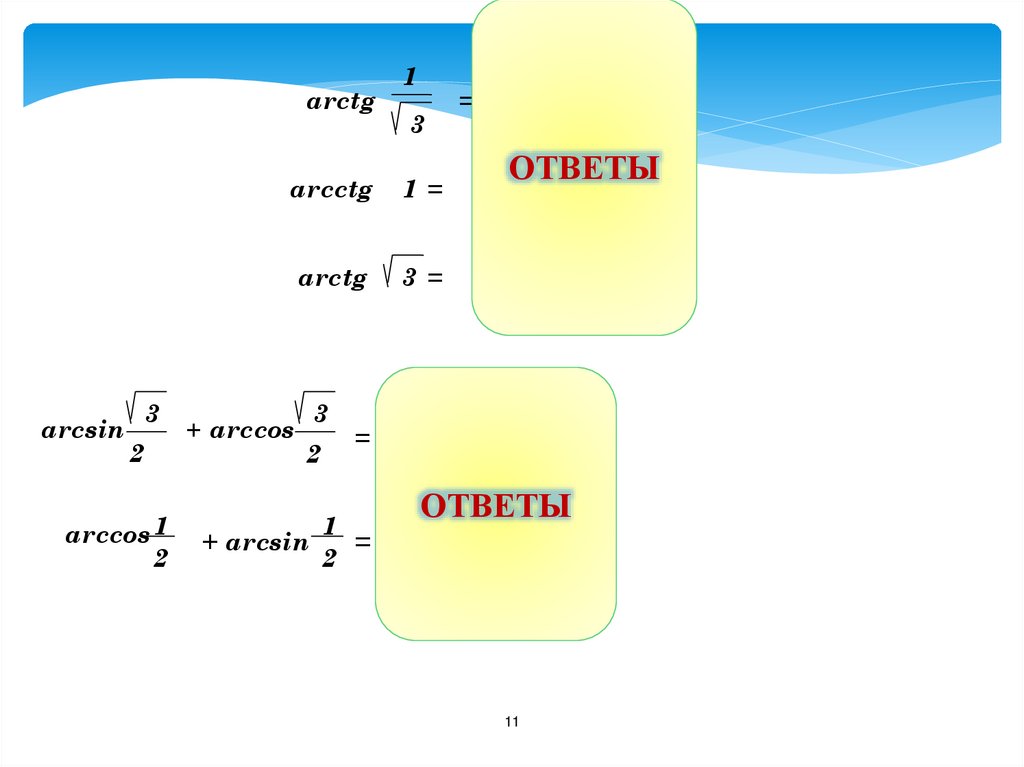
11.

arсtg
arcsin
3
2
arccos 1
2
1
3
arсctg
1=
arсtg
3=
+ arccos
3
2
=
=
П
6
ОТВЕТЫ
П
4
П
3
П
П
П
+ 6 =
2
3
ОТВЕТЫ
1
+ arcsin
= П + П = П
2
6
2
3
11