Похожие презентации:
Электромагнитная природа света. Интерференция света
1. Лекция № 12-13
ЭЛЕКТРОМАГНИТНАЯПРИРОДА СВЕТА.
ИНТЕРФЕРЕНЦИЯ СВЕТА
Литература: Павлов К.Б. Волновые
свойства света. Учебное пособие. – М.:
МВТУ, 1986, Иродов И.Е. Волновые
процессы. Основные законы. – М. – С.-П.:
Физматлит, 1999.
2.
Волновая оптика изучает широкий кругзакономерностей, связанных с процессами
распространения света в материальных
средах с учетом его волновой природы.
К ней относятся: интерференция света,
дифракция света, голография, поляризация
света, дисперсия света.
Вопросы, рассматриваемые в волновой
оптике,
вместе
с
вопросами,
рассматриваемыми в квантовой оптике, в
которой изучаются механизмы процессов
испускания и поглощения света, составляют
содержание физической оптики.
3.
Физическая оптика – наука о природесвета и световых явлений.
Геометрическая оптика рассматривает
распространение
света
на
основе
представлений о световых лучах, исходя из
эмпирически установленных законов. Ее
методы широко используются при расчетах и
проектировании самых сложных оптических
систем и устройств.
Геометрическая и физическая оптики
являются частями единой и многосторонней
науки о свете – оптики.
4. Шкала электромагнитных излучений
В 60-х г.г. 19 века Максвелл теоретическиоткрыл э/м волны. Экспериментальные
данные измерений скорости света в вакууме и
в воздухе совпали с расчетными значениями
скорости распространения э/м волн:
v 1
0 0 c
c n ,
где c – скорость света в вакууме, n –
показатель преломления среды.
5.
Поэтому предположили, что светпредставляет собой э/м волны. Подтвердили
э/м природу света опыты Г.Герца (в 1888 г.),
показавшего, что для э/м волн имеют место те
же законы отражения и преломления, что и
для света.
В разное время были открыты
различные
излучения,
как
и
свет
представляющие собой э/м волны и
отличающиеся от света значениями длин
соответствующих э/м волн.
6.
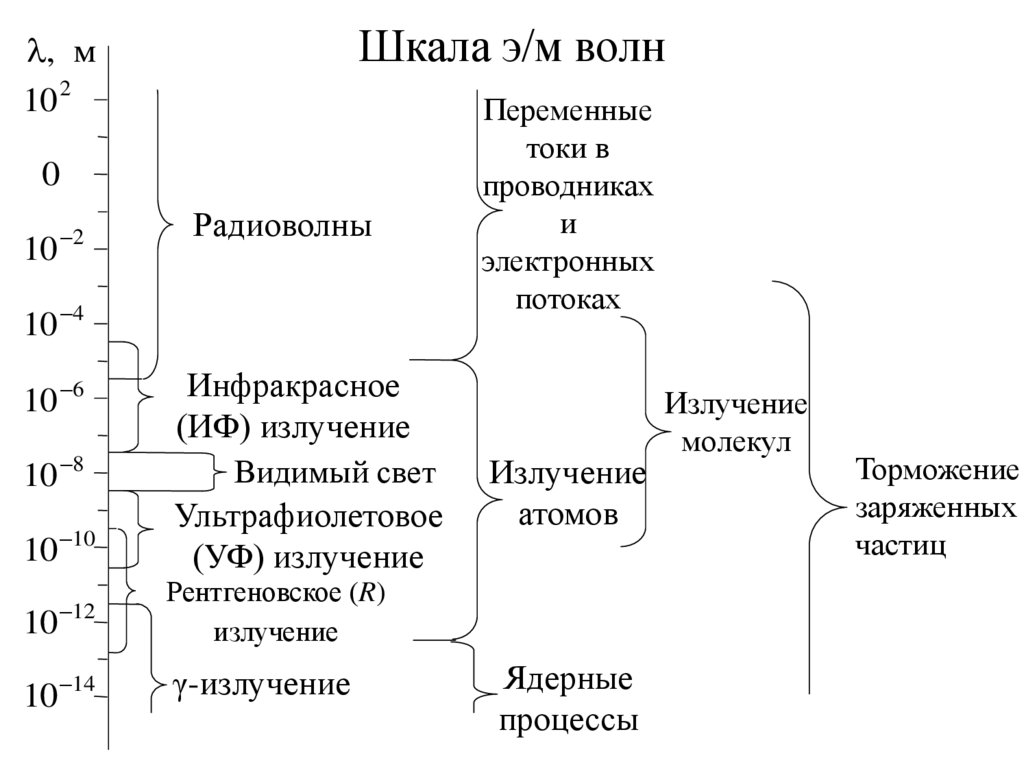
Шкала э/м волн, м
10 2
0
10
2
Радиоволны
10 4
10 6
10 8
10 10
10
10
Инфракрасное
(ИФ) излучение
Видимый свет
Ультрафиолетовое
(УФ) излучение
12
Рентгеновское (R)
излучение
14
γ-излучение
Переменные
токи в
проводниках
и
электронных
потоках
Излучение
атомов
Ядерные
процессы
Излучение
молекул
Торможение
заряженных
частиц
7.
Границы диапазона видимого светаопределяются
способностью
среднестатистического человеческого глаза
регистрировать э/м излучение в интервале λ =
380 ÷ 780 нм.
Нет принципиального различия между
соответствующими излучениями в области
перекрытия их диапазонов.
Из-за
сходства
процессов,
происходящих в источниках видимого света,
УФ-, ИК- и рентгеновского излучений, эти
диапазоны объединяют общим названием –
оптическое излучение.
8. Оптическое излучение, его интенсивность
Интенсивность света– модуль
среднего по времени значения плотности
потока электромагнитной энергии
1T
2
2
I S d t S ~ Em H m ~ nEm nA ,
T0
где T – период световой волны, S – среднее
по времени значение вектора Пойнтинга
Em = A – амплитуда светового
S E H,
вектора.
9. Интерференция электромагнитных волн
Монохроматическаяопределенную частоту.
волна
имеет
Интерференция
волн.
При
взаимодействии двух и более когерентных
волн происходит перераспределение энергии
и интенсивности в пространстве: в одних
местах возникают максимумы, в других –
минимумы интенсивности.
10.
Когерентныминазывают
такие
колебания (и волны) разность фаз Δα
которых постоянна во времени, а частота –
одинаковая (ω1 = ω2).
Если
при
сложении
волн
перераспределения энергии нет, говорим о
принципе суперпозиции: результирующее
колебание в данной точке пространства надо
искать как геометрическую сумму.
Рассмотрим сложение гармонических
колебаний одного направления равных
частот
x1 A1 cos 1t 1 ,
x2 A2 cos 2t 2
11.
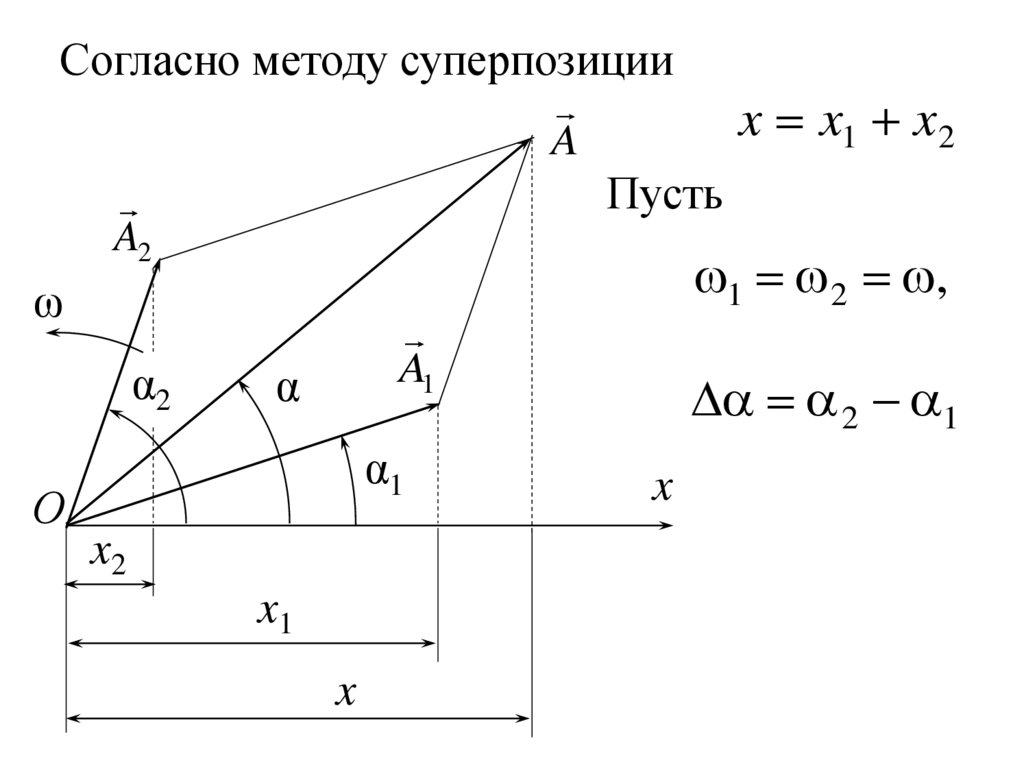
Согласно методу суперпозицииA
Пусть
A2
ω
α2
О
x x1 x 2
1 2 ,
A1
α
α1
x2
x1
x
2 1
x
12.
A2
2
A1
A
2
2
A1
2
A2
2 A1 A2 cos
2
A2
2 A1 A2 cos
При 2 m, m 0, 1, 2, амплитуда
A A1 A2 max
При 2m 1 , m 0, 1, 2,
амплитуда
то
A A1 A2 . Если
A 0 min
A1 A2 ,
13.
Интенсивностьрезультирующего
2
колебания
I~A
I I1 I 2 2 I1I 2 cos 2 1
I I1 I 2 2 I1I 2 cos
1. При 2 1 2 m, m 0, 1, 2,
– усиление интенсивности световой волны
I I1 I 2 2 I1I 2
I1 I 2
max
14.
2. При 2 1 2m 1 ,m 0, 1, 2, – ослабление интенсивности
световой волны
I I1 I 2 2 I1I 2
I1 I 2
min
3. Если Δα будет меняться от времени
2 1 t , то среднее значение
интенсивность
cos 2 1 0, тогда
световой волны
I I1 I 2 ,
т.е. интерференции нет.
15.
Интерференция характерна для волнлюбой природы и сравнительно просто
наблюдается на опыте для волн на
поверхности воды или для звуковых волн.
Наблюдать интерференцию световых
волн можно лишь при определенных
условиях.
В
случае
суперпозиции
когерентных
волн
интенсивность
результирующего колебания
I I1 I 2 2 I1I 2 cos
16.
Свет, испущенный обычными (нелазерными)
источниками,
не
бывает
монохроматическим.
Источники
некогерентны. Когерентные световые волны
можно получить и от обычных источников.
Общий принцип их получения: волну,
излучаемую одним источником света,
разделяют тем или иным способом на две
части и затем накладывают их друг на друга
подходящим способом.
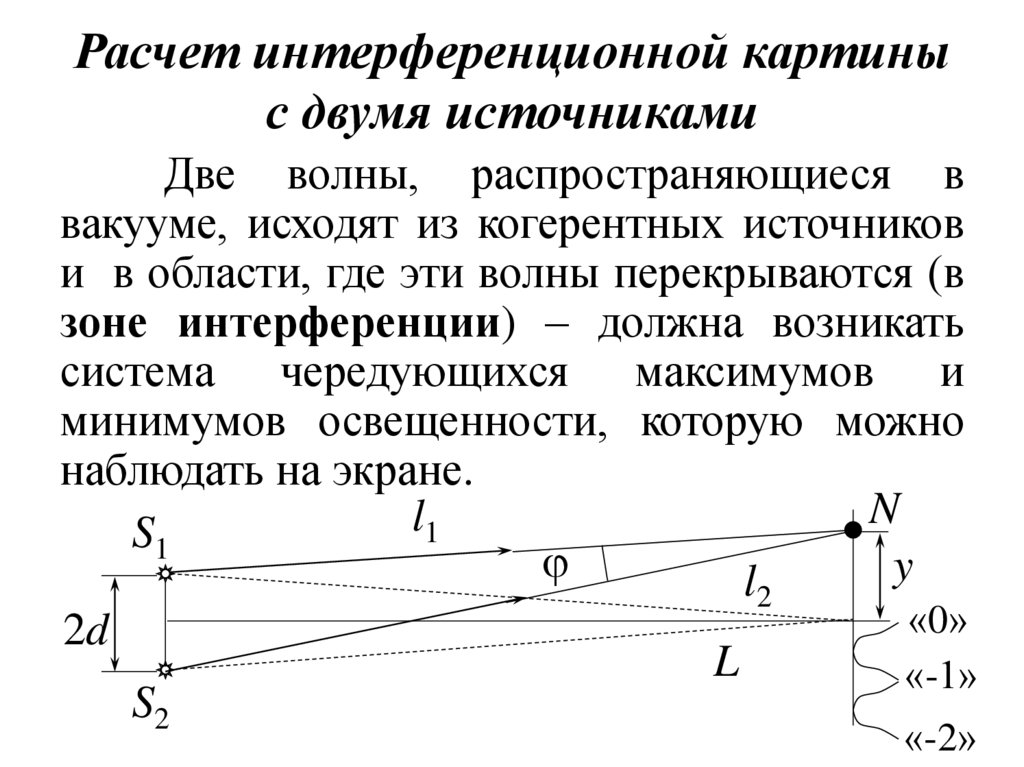
17. Расчет интерференционной картины с двумя источниками
Две волны, распространяющиеся ввакууме, исходят из когерентных источников
и в области, где эти волны перекрываются (в
зоне интерференции) – должна возникать
система чередующихся максимумов и
минимумов освещенности, которую можно
наблюдать на экране.
N
l
1
S1
y
l2
«0»
2d
L
«-1»
S2
«-2»
18.
Геометрическая разность хода –разность расстояний l2 и l1 от источников до
интересующей нас точки N. В случае, когда
волны от источников распространяются не в
вакууме, а в среде с показателем преломления
n,
под
Δ
следует
понимать
не
геометрическую, а оптическую разность
хода
(12.1)
n l 2 l1
Определим положение m-х максимумов
(расстояние ym). Сначала получим условия
интерференционных
максимумов
и
минимумов.
19.
f1 A1 cos 1t k1l1f 2 A2 cos 2 t k 2 l 2
1 2 ,
Разность фаз
k1 k2 k
2
k l2 l1 k l l ,
где волновое число
2
k
20.
АмплитудаA
2
2
A1
2
A2
2 A1 A2 cos
Интенсивность
I~A
2
I I1 I 2 2 I1 I 2 cos
Положим
l 2m m ,
2
тогда
m 0, 1, 2,
2 m
2 m
21.
A A1 A2 max,если A1 A2 , то A 2 A1 , I 4I 1
Положим
тогда
l 2m 1 ,
2
m 0, 1, 2,
2m 1
A A1 A2 min
если A1 A2 , то A 0,
I 0
22.
Условие максимума интерференцииm ,
m 0, 1, 2, (12.2)
где λ – длина волны в вакууме.
Из геометрии
2
l1
2
l2
L y d
2
2
L y d
2
(12.3)
2
Вычитая из второго уравнения (12.3) первое,
получаем
2
l2
2
l1
l2 l1 l2 l1 4 yd
(12.4)
23.
Учитывая, что L >> d , считаем, чтоl1 l2 2 L
Тогда
2 yd
l 2 l1
L
(12.5)
Подставив условие максимума (12.2) для
вакуума (n = 1), получаем положение m-х
максимумов
m L
ym
2d
(12.6)
24.
Ширина интерференционной полосы –расстояние
между
m-м
и
(m+1)-м
максимумами:
L
y ym 1 ym
2d
или
где
y ym 1 ym ,
2d L
δy не зависит от порядка максимума m
(12.7)
(12.8)
25. Пространственно-временная когерентность
Когерентность–
согласованное
протекание нескольких колебательных или
волновых процессов.
Временная когерентность: α1 – α2 = const (в
данной точке пространства не зависит от
времени).
Пространственная когерентность: (α1 – α2 )
для колебаний, происходящих в 2-х разных
точках так называемой псевдоволновой
поверхности остается неизменной.
26.
Псевдоволноваяповерхность
–
волновая поверхность монохроматического
источника.
ρког (lког) – радиус когерентности (длина
пространственной
когерентности)
–
расстояние
вдоль
псевдоволновой
поверхности, на длине которого фаза
случайным образом меняется на величину
порядка π (Δφ ~ π).
Лазер
–
источник
с
высокой
когерентностью
(пространственная
и
временная когерентность).
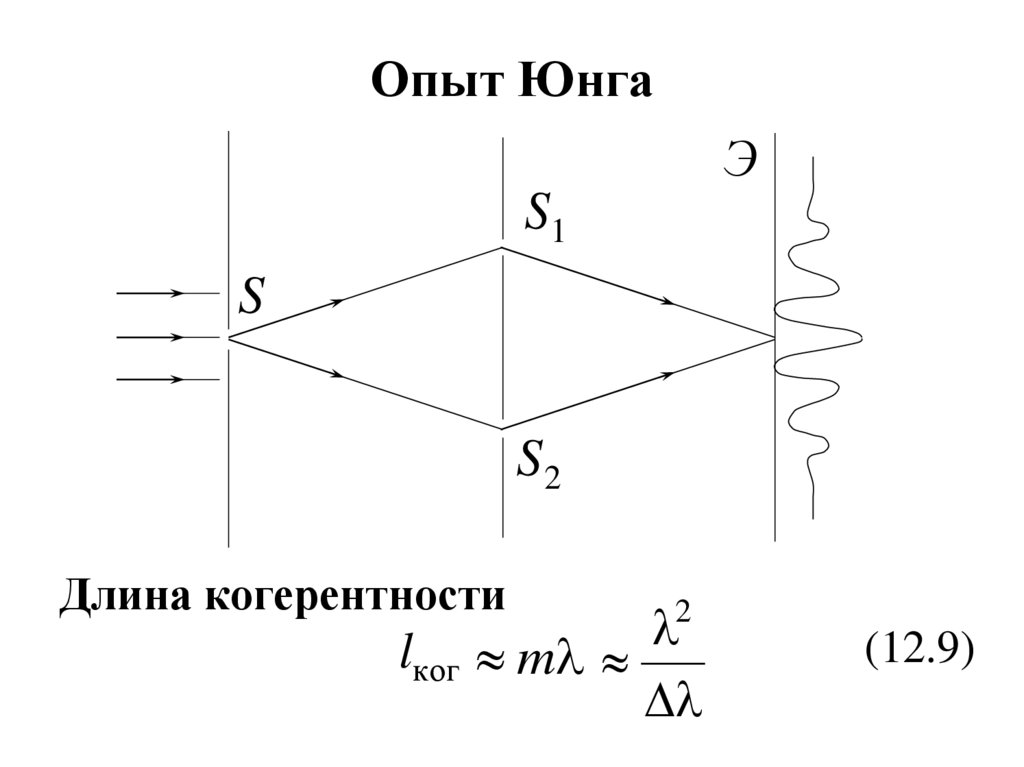
27. Опыт Юнга
ЭS1
S
S2
Длина когерентности
lког
m
2
(12.9)
28.
гдеm
–
максимальный
порядок
интерференции, соответствующий еще
видимой светлой полосе
m
,
(12.10)
cтепень монохроматичности света λ/Δλ
Ширина когерентности. Щели S1 и S2
становятся некогерентными источниками,
если
hког 2d
где 2d – расстояние между щелями
29.
Интерференционная картина исчезает, когдаширина щели S
s y
ширина полосы
L
y
2d
Тогда
L L
hког
y
s
(12.11)
где φ – угловая ширина щели S относительно
диафрагмы с двумя щелями.
30.
Получение устойчивой интерференционнойкартины возможно случае, если у исходной
световой волны:
• lког превышает оптическую разность хода
складываемых колебаний,
• hког превышает расстояние d между щелями.
l ког 2
hког 2d
(12.12)
Иродов И.Е. Волновые процессы.
Основные законы. — М. — С.-П.:
Физматлит, 1999, стр. 85-93.

















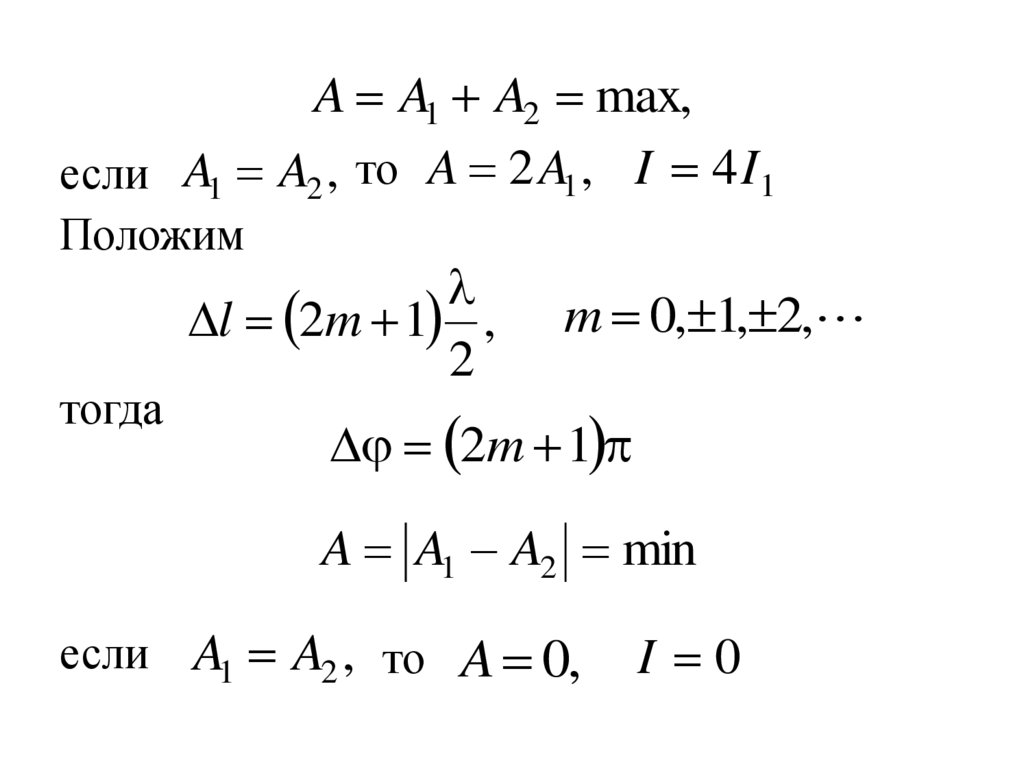








 Физика
Физика








