Интерференция света

1.

ИНТЕРФЕРЕНЦИЯ
СВЕТА

2.

Принцип суперпозиции волн
При наложении волн каждая из
них входит в результирующую
волну независимо друг от друга.
E E1 E2

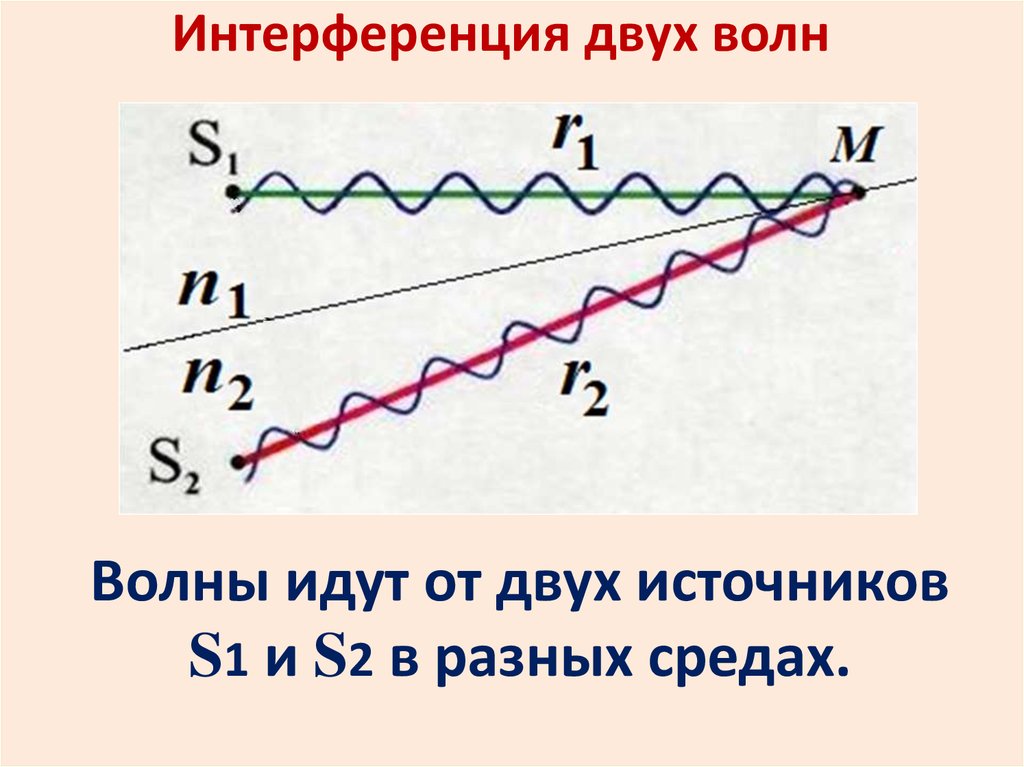
3. Интерференция двух волн

Волны идут от двух источников
S1 и S2 в разных средах.

4.

Пусть обе волны
монохроматические – одной
частоты ω.
И пусть световой вектор в точке М
направлен вдоль одной и той же
линии для обеих волн.

5.

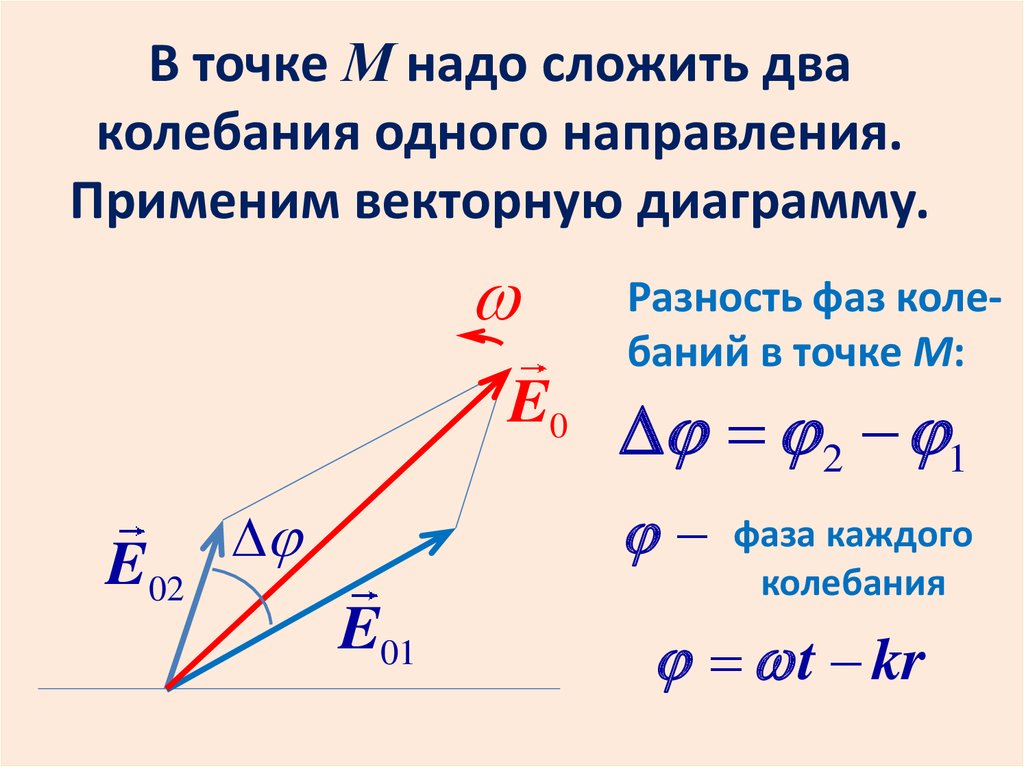
В точке М надо сложить два
колебания одного направления.
Применим векторную диаграмму.
E0
E02
Разность фаз колебаний в точке М:
2 1
E01
фаза каждого
колебания
t kr

6.

По теореме косинусов амплитуда
результирующего колебания
E E E 2 E01 E02 cos
2
0
2
01
2
02
Интенсивность результирующего
колебания
I I1 I 2 2 I1 I 2 cos
Интерференционное
слагаемое

7.

Это слагаемое может быть и >0 и
<0 в зависимости от разности фаз.
Если она все время изменяется
(например, ω1 ≠ω2), то среднее по
времени значение косинуса дает
нуль. Тогда просто
I I1 I 2
Нет никакой интерференции.

8.

Интерференция заключается в
перераспределении интенсивности
волны между точками пространства.
Она возникает только при наложении
когерентных волн.
Когерентные волны имеют в данной
точке постоянную разность фаз.
Это возможно, только если частоты
колебаний одинаковы (ω1=ω2).

9.

В результате интерференции в одних
точках пространства будут
наблюдаться максимумы
интенсивности. В этих точках волны
усиливают друг друга. В других
точках будут наблюдаться
минимумы интенсивности. Там
волны гасят друг друга. Для световых
волн это выглядит как светлые и
темные пятна.

10.

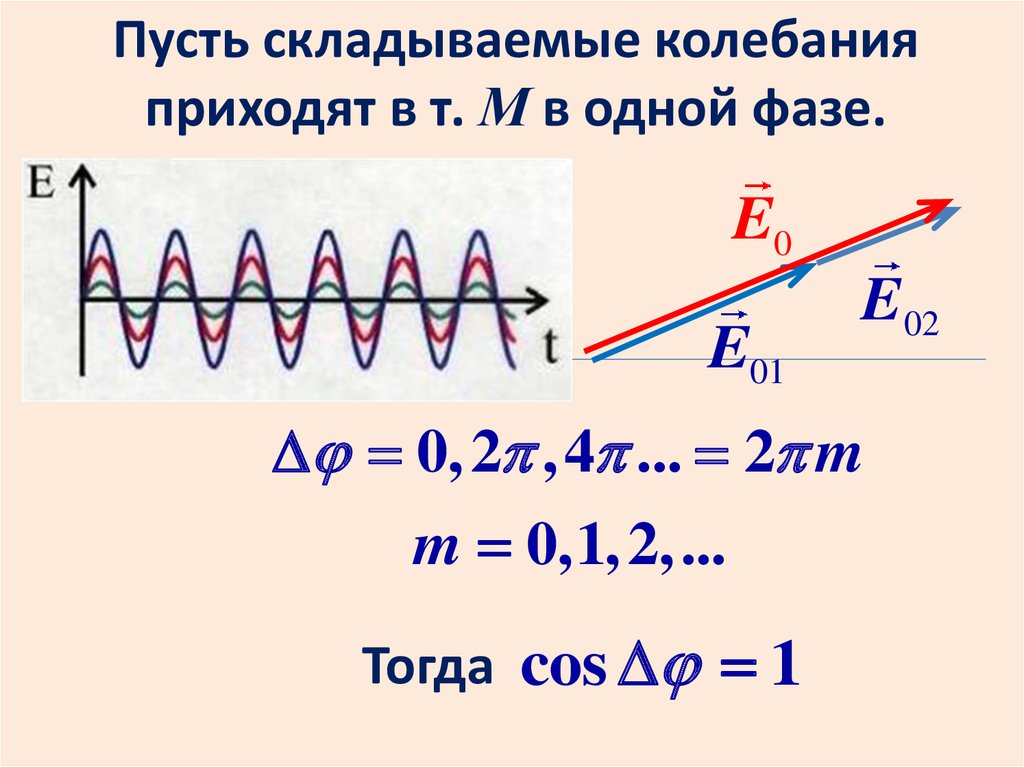
Пусть складываемые колебания
приходят в т. М в одной фазе.
E0
E01
E02
0, 2 , 4 ... 2 m
m 0,1, 2, ...
Тогда cos 1

11.

Интенсивность в точке М
Imax I1 I 2 2 I1 I 2
Это интерференционный максимум.
При
I1 I 2
Imax I1 I1 2 I1 I1 4 I1
Интенсивность в точке максимума в
4 раза больше, чем у каждой волны.

12.

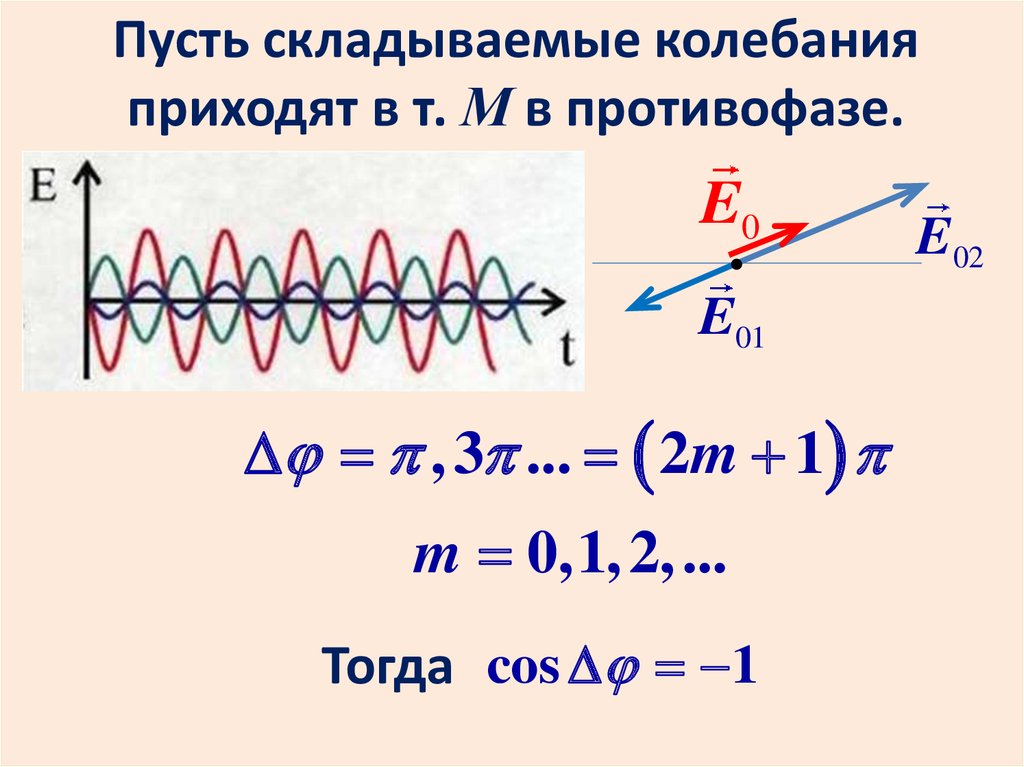
Пусть складываемые колебания
приходят в т. М в противофазе.
E0
E01
, 3 ... 2m 1
m 0,1, 2, ...
Тогда cos 1
E02

13.

Интенсивность в точке М
Imin I1 I 2 2 I1 I 2
Это интерференционный минимум.
При
I1 I 2
I 0

14.

Минимум
Максимум

15.

Условия максимума и минимума
при интерференции.
Пусть начальная фаза колебаний одинакова.
Распишем разность фаз в т. М:
1 2 t k1r1 t k2 r2 k2 r2 k1r
k
2
2
0
2 n
0
n2r2 n1r

16.

В скобках стоит разность
оптических путей волн.
2
0
L2 L1
Она называется оптической
разностью хода волн .
L2 L1

17.

Условие максимума:
Для максимума колебания должны быть
в одной фазе: = 2 m, m = 0,1,2…
2
0
2 m
max m 0
Если оптическая разность хода равна
целому числу длин волн, то в данной
точке будет интерференционный
максимум.

18.

Условие минимума:
Для минимума колебания должны быть в
противофазе: = (2m+1), m = 0,1,2…
2
0
2m 1
1
min m 0
2
Если оптическая разность хода равна
полуцелому числу длин волн, то в
данной точке будет
интерференционный минимум.

19.

Целое число m называют
порядком
интерференционного
максимума или минимума.

20. Виды интерференционных картин

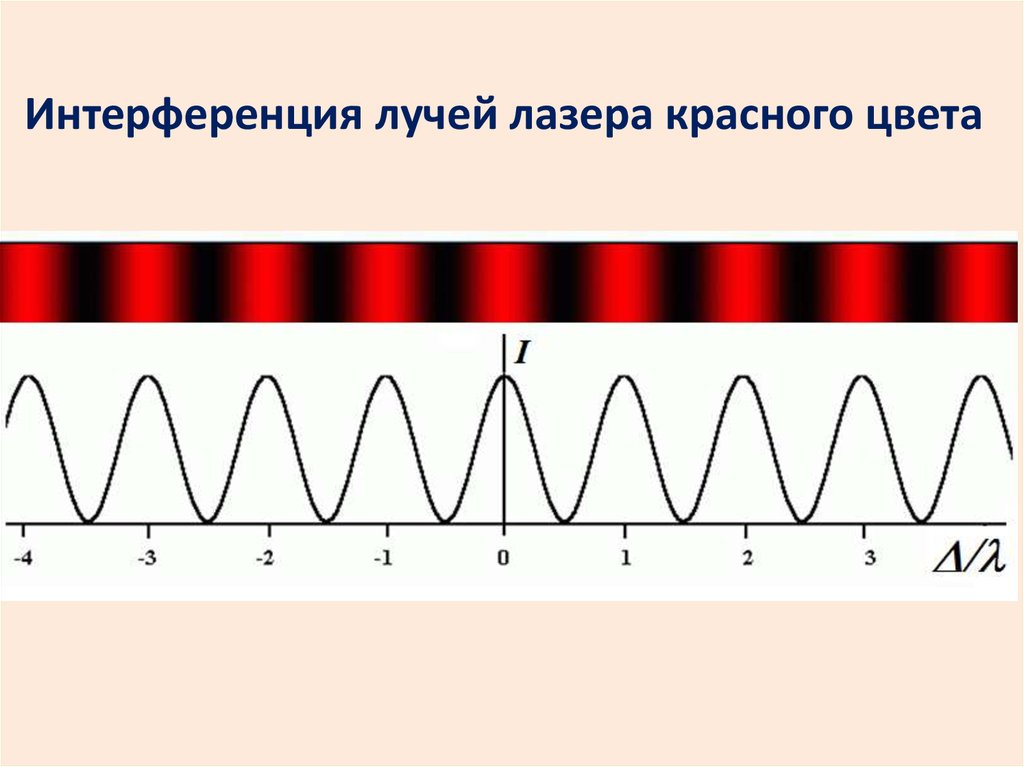
20

21.

Интерференция лучей лазера красного цвета

22.

Когерентность
Два разных источника никогда не
могут испускать когерентные волны.
Даже волна, испускаемая одним
источником, может быть
некогерентна самой себе.
Есть два типа нарушения
когерентности – пространственный и
временной.

23.

Причина пространственных нарушений когерентности – неточечность
реального источника волн. Разные
атомы, составляющие источник,
излучают несогласованно.

24.

Причина временных нарушений –
дискретность излучений атомов.
Атомы излучают не непрерывно, а
цугами.
Из-за этого фаза волны изменяется
скачками.

25.

Такой опыт впервые осуществил
Томас Юнг.

26.

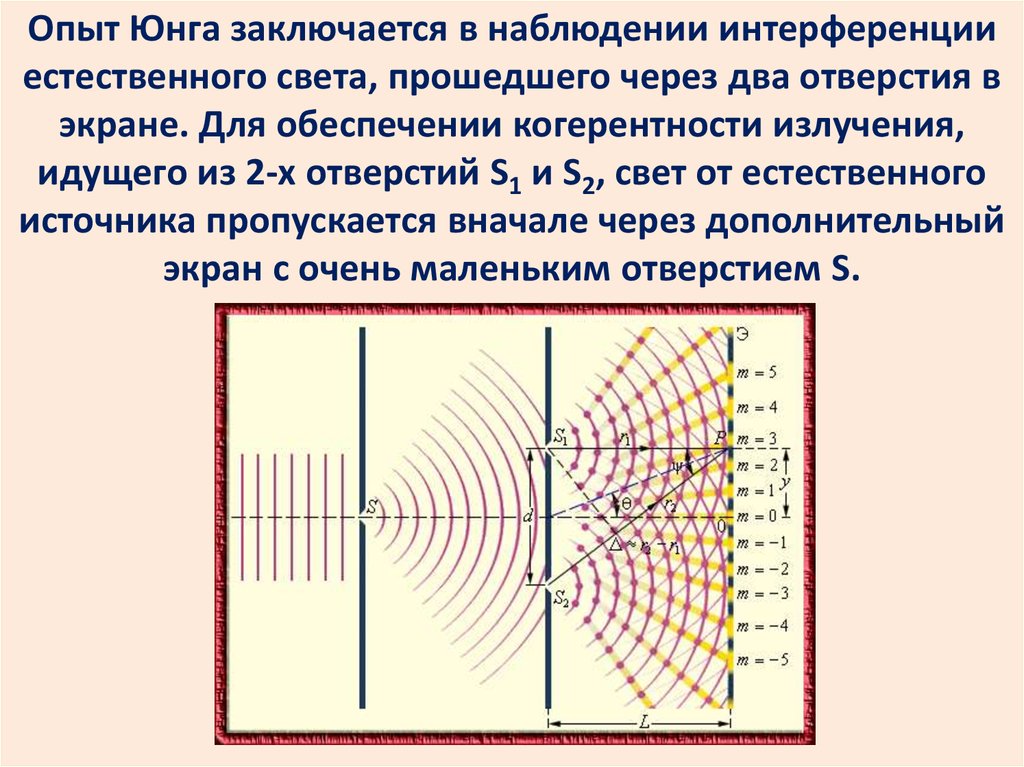
Опыт Юнга заключается в наблюдении интерференции
естественного света, прошедшего через два отверстия в
экране. Для обеспечении когерентности излучения,
идущего из 2-х отверстий S1 и S2, свет от естественного
источника пропускается вначале через дополнительный
экран с очень маленьким отверстием S.
27

27.

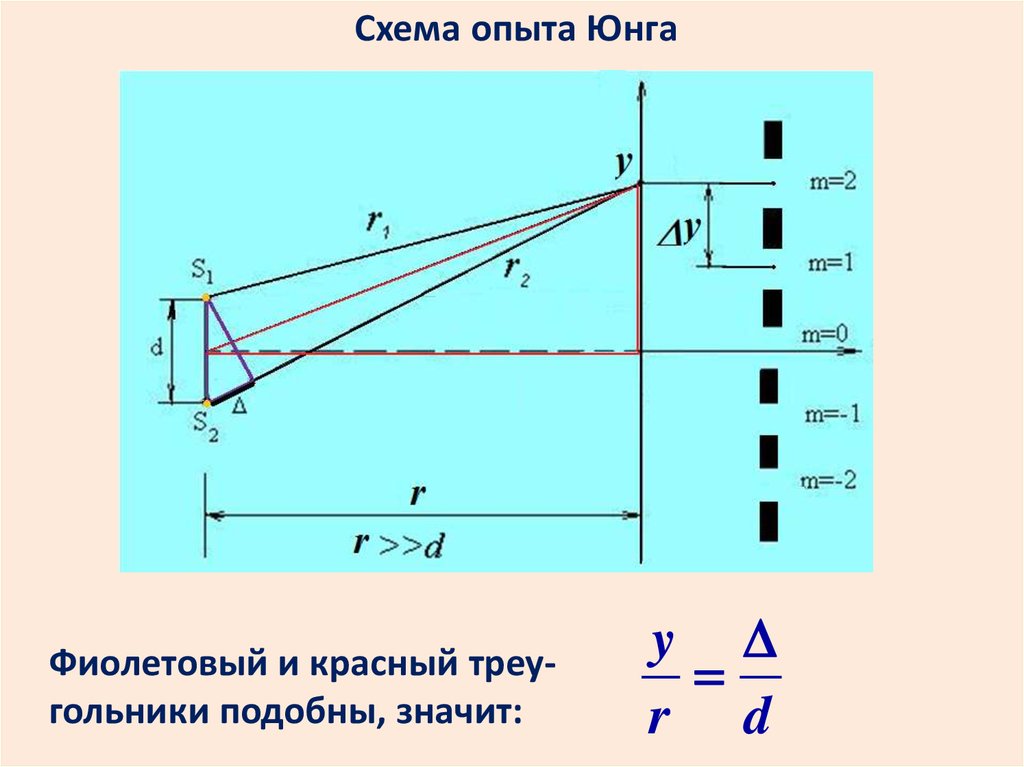
Схема опыта Юнга
Фиолетовый и красный треугольники подобны, значит:
y
r d

28.

Запишем это для двух соседних
максимумов с номерами m и m+1.
r
r
ym m m
d
d
r
r
ym 1 m 1 (m 1)
d
d
r
r
y ym 1 ym m 1 m
d
d

29.

Получили формулу для ширины
интерференционной полосы:
r
y .
d
По ней можно найти d.

30.

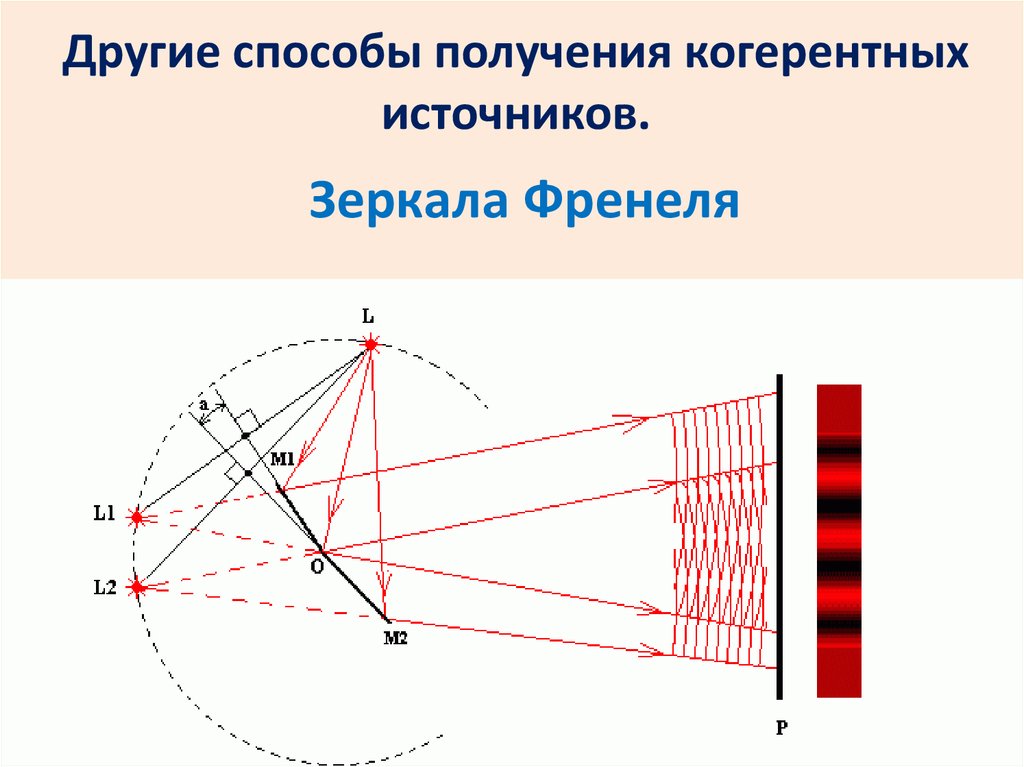
Другие способы получения когерентных
источников.
Зеркала Френеля

31.

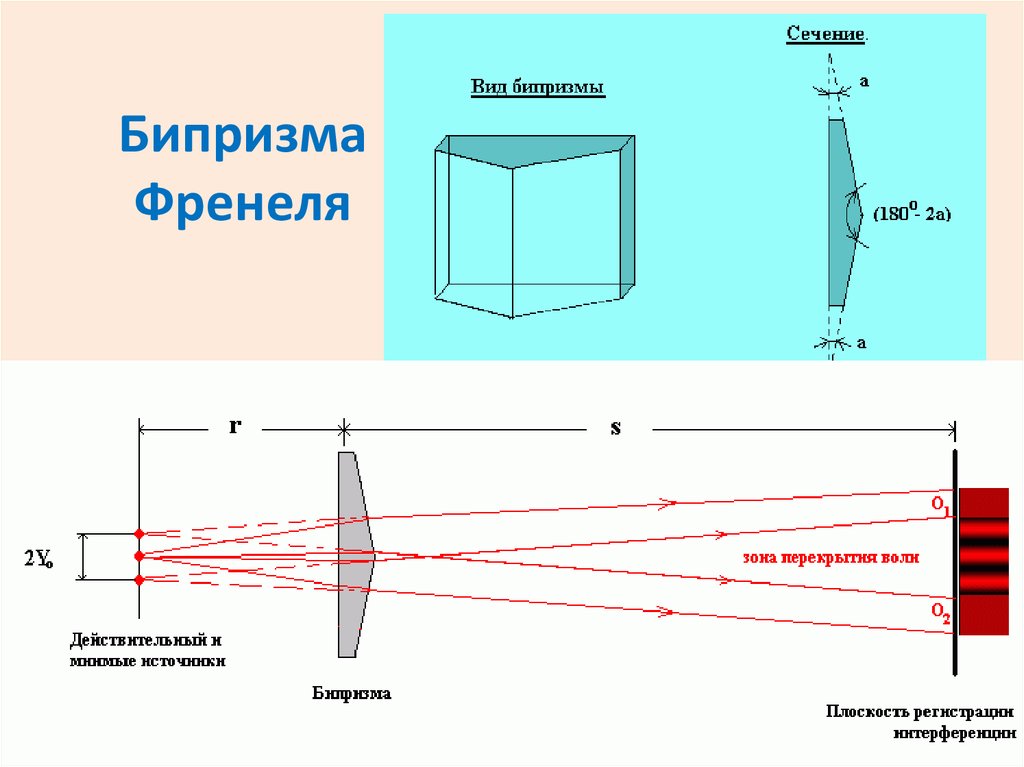
Бипризма
Френеля

32. Бипризма Френеля

Интерферометры
Интерферометры – это оптические
приборы, использующие законы
интерференции света, проходящего
через исследуемые вещества.
33

33. Интерферометры

Интерферометр Жамена
WMV-Видео «Интерферометр Жамена»
SWF-Модель «Интерферометр Жамена»
Интерференция света
34

34. Интерферометр Жамена

Интерферометр Рэлея
WMV-Видео «Интерферометр Рэлея»
SWF-Модель «Интерферометр Рэлея»
Интерференция света
35

35. Интерферометр Рэлея

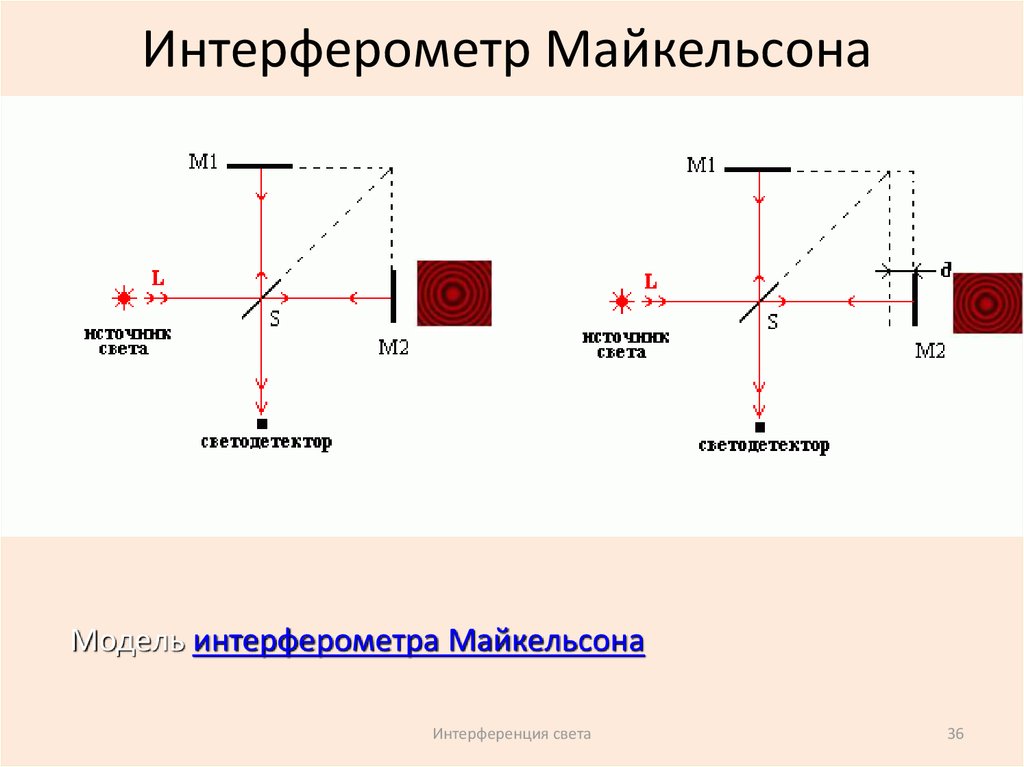
Интерферометр Майкельсона
Модель интерферометра Майкельсона
Интерференция света
36

36. Интерферометр Майкельсона

(видеоклип)
Интерференция света
38

37. Интерференционная картина в опыте Майкельсона с источником света лампой накаливания

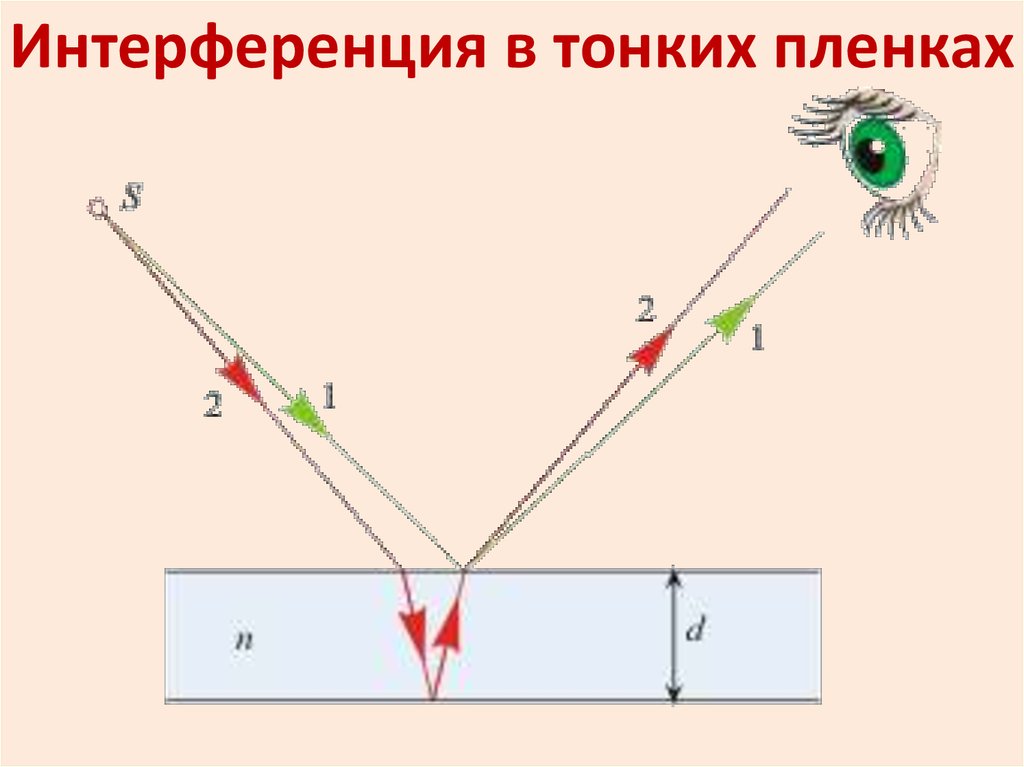
Интерференция в тонких пленках

38. Интерферометр Майкельсона (видеоклип)

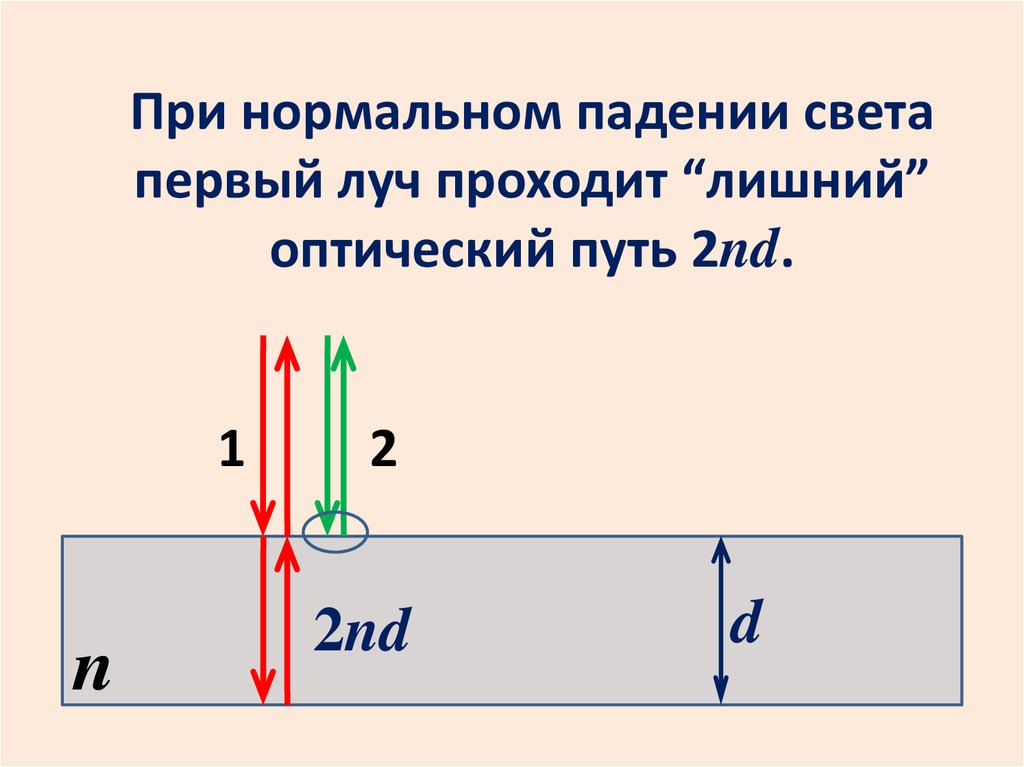
При нормальном падении света
первый луч проходит “лишний”
оптический путь 2nd.
1
n
2
2nd
d

39.

При отражении света от
оптически более плотной среды
фаза волны скачком изменяется
на радиан. Это соответствует
изменению оптической разности
хода на полволны. Говорят, что
луч “теряет” полволны. На
рисунке это делает луч 2.

40.

Оптическая разность хода
лучей на рисунке :
2nd
0
2

41.

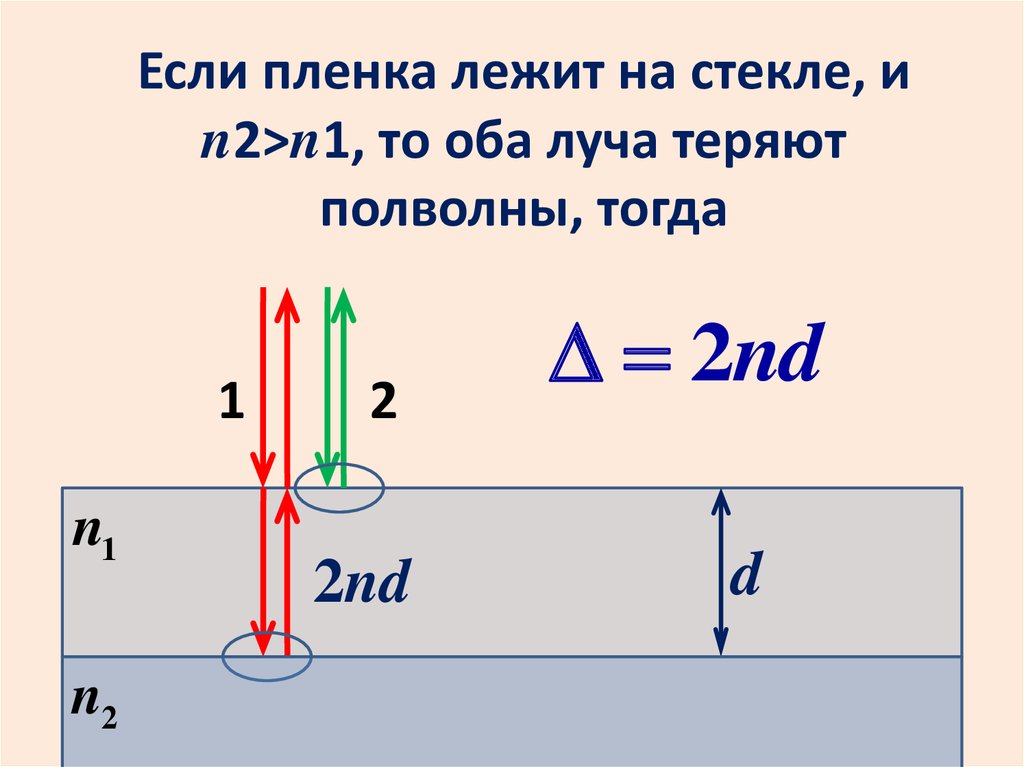
Если пленка лежит на стекле, и
n2>n1, то оба луча теряют
полволны, тогда
1
n1
n2
2
2nd
2nd
d

42.

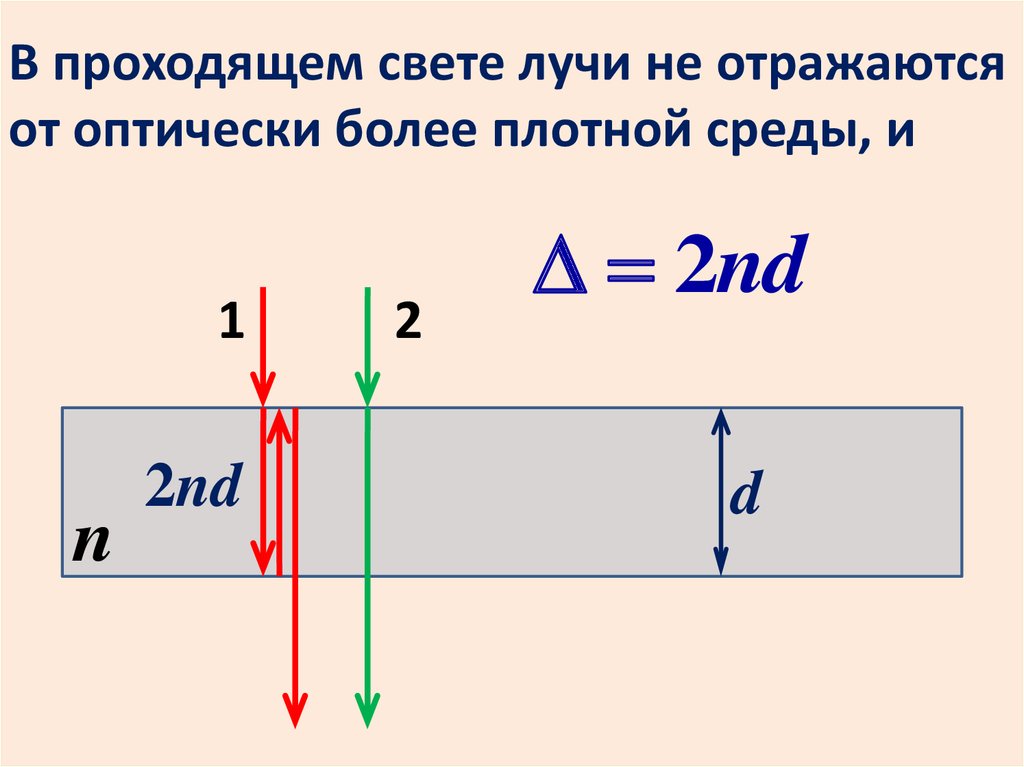
В проходящем свете лучи не отражаются
от оптически более плотной среды, и
1
n
2nd
2
2nd
d

43.

Лучи усиливают друг друга, когда
m 0 ,
и гасят, когда
2m 1
0
2
.

44.

Так как при отражении и
прохождении света
отличается на /2, то
максимуму на отражение
соответствует минимум на
прохождение и наоборот.

45.

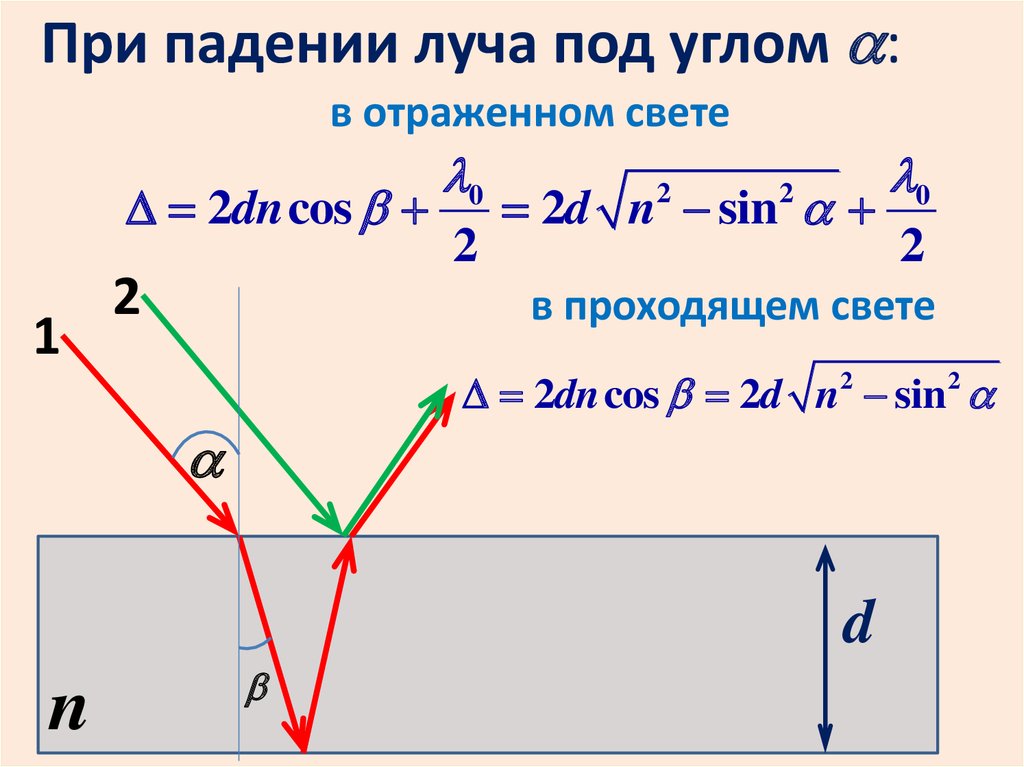
При падении луча под углом :
в отраженном свете
2dn cos
1
2
0
2
2d n sin
2
2
2
в проходящем свете
2dn cos 2d n2 sin2
d
n
0

46.

Рассеянный свет падает и отражается под
разными углами. Для каких-то углов могут
выполниться условия минимума, для
других – условия максимума. В результате
будут наблюдаться темные и светлые
кольца. Эти кольца называют полосами
равного наклона. Каждое кольцо
образуется лучами, падающими на пленку
под одинаковым углом с разных
направлений. Если свет белый, кольца
будут радужными.

47.

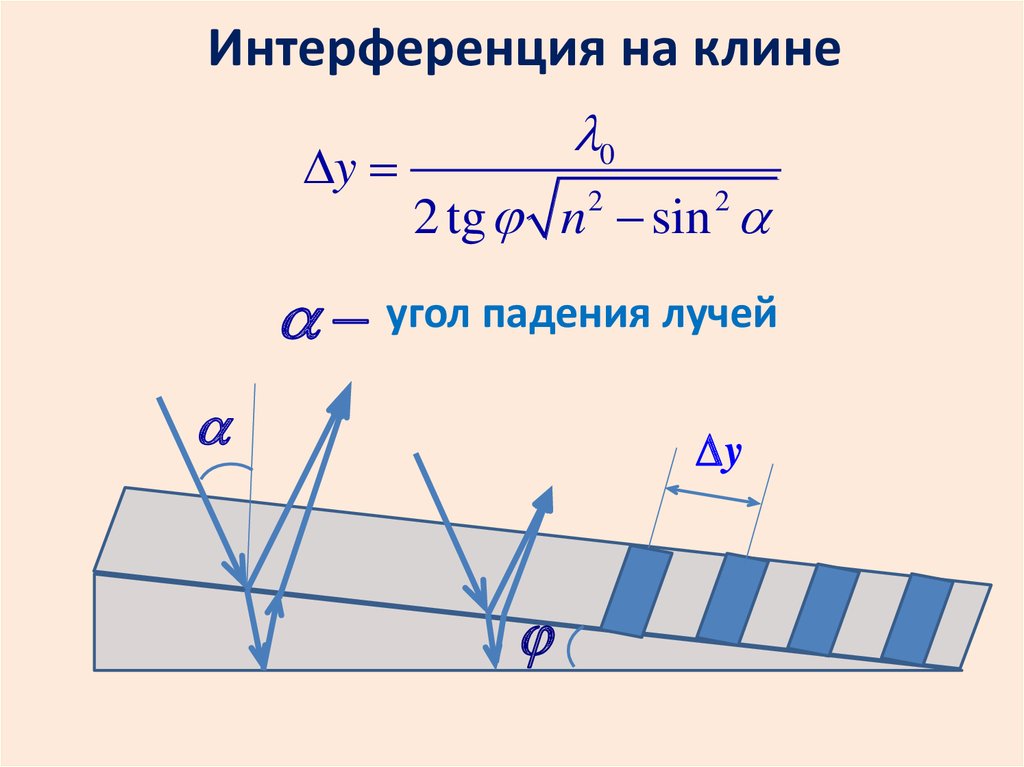
Интерференция на клине
y
0
2 tg n sin
2
2
угол падения лучей
y

48.

Полосы, образующиеся при интерференции на клине, называются полосами
равной толщины.

49. Интерференция на клине

Мыльный пузырь

50.

51. Мыльный пузырь

Интерференция света
53

52.

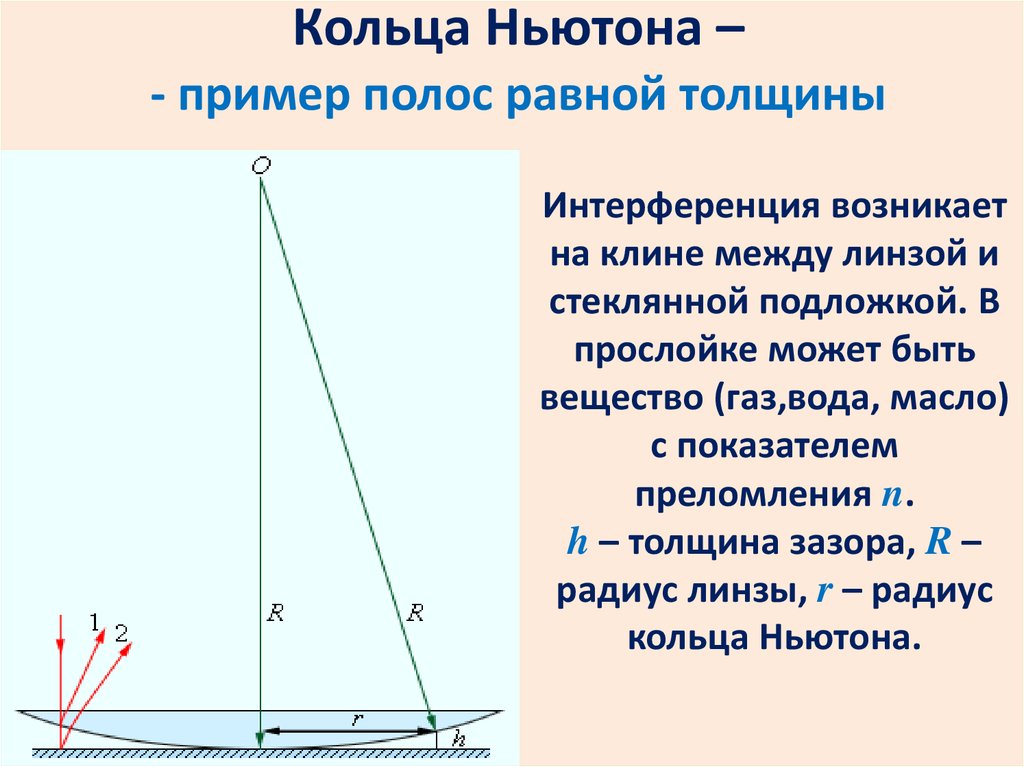
Кольца Ньютона –
- пример полос равной толщины
Интерференция возникает
на клине между линзой и
стеклянной подложкой. В
прослойке может быть
вещество (газ,вода, масло)
с показателем
преломления n.
h – толщина зазора, R –
радиус линзы, r – радиус
кольца Ньютона.

53.

Оптическая разность хода лучей: 2nh
2
длина волны в веществе клина
В отраженном
свете
В проходящем
свете
r
(2
m
1)
R
m
Светлые
2
Темные
rm mR
rm mR
rm (2m 1) R
m = 1, 2, 3,…. – номер кольца
2

54.

Для белого света кольца будут
радужными.
В отраженном свете в центре картины –
темное пятно (разность хода лучей /2),
в проходящем свете – светлое пятно.
Наблюдения в микроскоп

55.

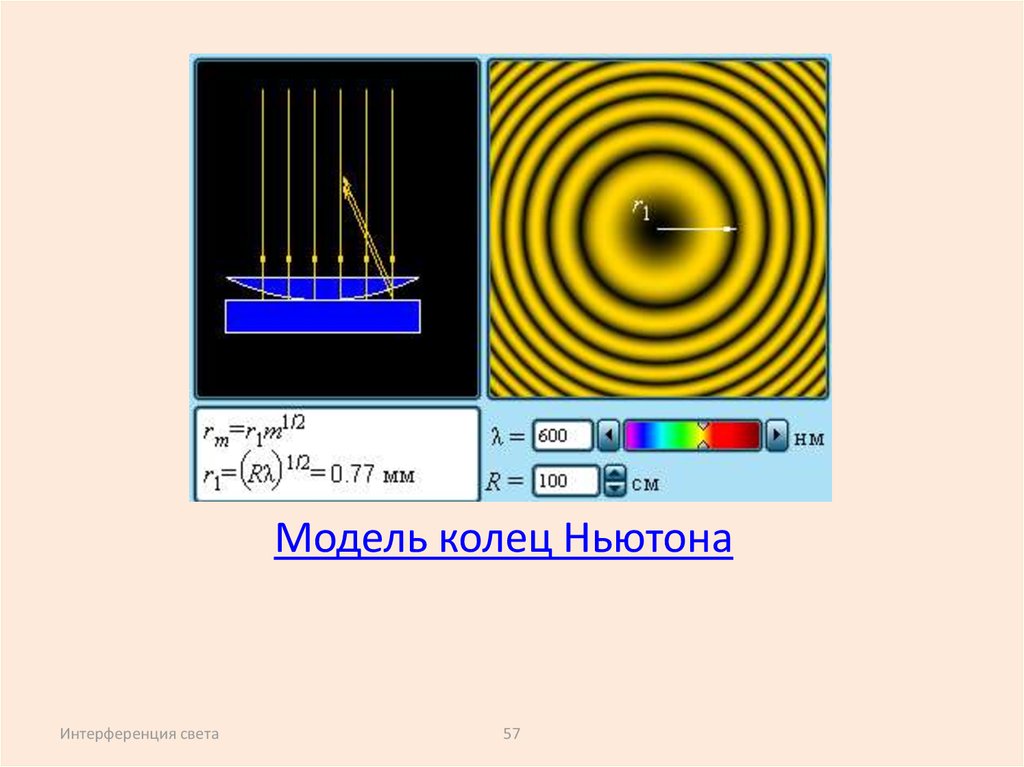
Модель колец Ньютона
Интерференция света
57

56. Наблюдения в микроскоп

Кольца Ньютона
(видеоклип)
58

57. Модель колец Ньютона

Применение интерференции
1.Измерение длин волн.
2.Измерение расстояний.
3.Измерение показателя преломления.
4.Контроль напыления микросхем
5.Просветление оптики.
Линзу оптического прибора покрывают
пленкой, такой чтобы выполнялось условие
минимума на отражение. Тогда весь свет
проходит внутрь.
nпленки nлинзы