Похожие презентации:
Плоская система сходящихся сил
1. Плоская система сходящихся сил
2. Определение равнодействующей геометрическим способом.
3. Пусть в точке О твердого тела к нему приложена система сходящихся сил: F1, F2, F3, F4.
Пусть в точке О твердого тела к нему приложена система сходящихся сил:F 1, F 2 , F 3 , F 4 .
Используя свойство векторной суммы сил, можно получить
равнодействующую любой сходящейся системы сил,
складывая последовательно силы, входящие в систему.
Вектор равнодействующей силы соединит начало первого вектора
с концом последнего.
0
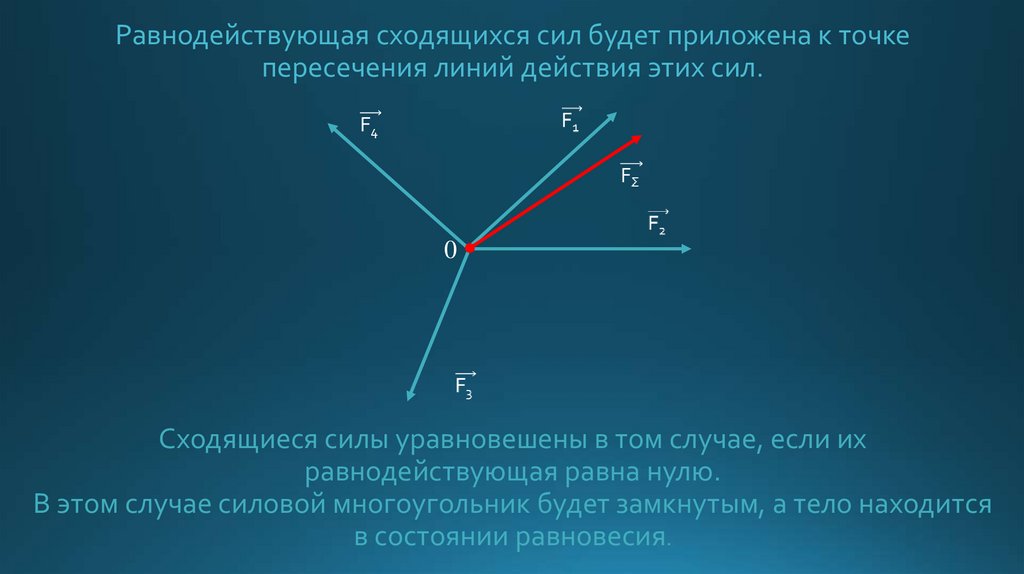
4. Равнодействующая сходящихся сил будет приложена к точке пересечения линий действия этих сил.
0Сходящиеся силы уравновешены в том случае, если их
равнодействующая равна нулю.
В этом случае силовой многоугольник будет замкнутым, а тело находится
в состоянии равновесия.
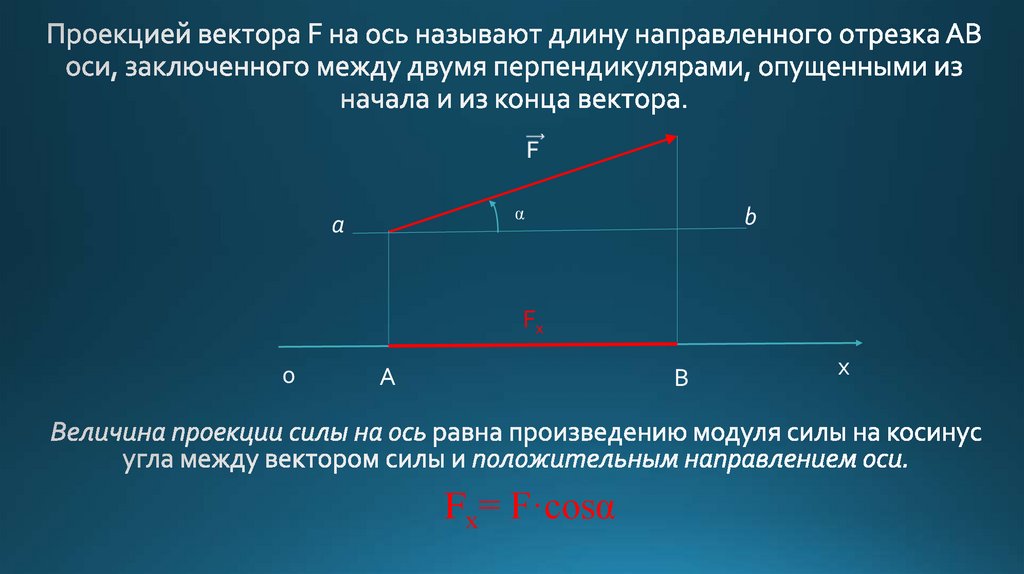
5. Проекция силы на ось.
6. Проекцией вектора F на ось называют длину направленного отрезка АВ оси, заключенного между двумя перпендикулярами, опущенными
αа
b
Fх
0
А
В
Fх= F·cosα
х
7. Проекция имеет знак: положительный, если отсчет длины проекции от ее начала к концу совпадает с положительным направлением оси,
Началовектора
Начало
вектора
Fх
F/х
(+)
(-)
Направление отсчета проекций
Положительное
направление оси
8. Если α=00 , т.е. сила параллельна оси и направлена в сторону положительного отсчета оси, то соs α =1 и поэтому Fx=F·cos00=F
0F1х= F1
F2х= -F2
F3х= 0
х
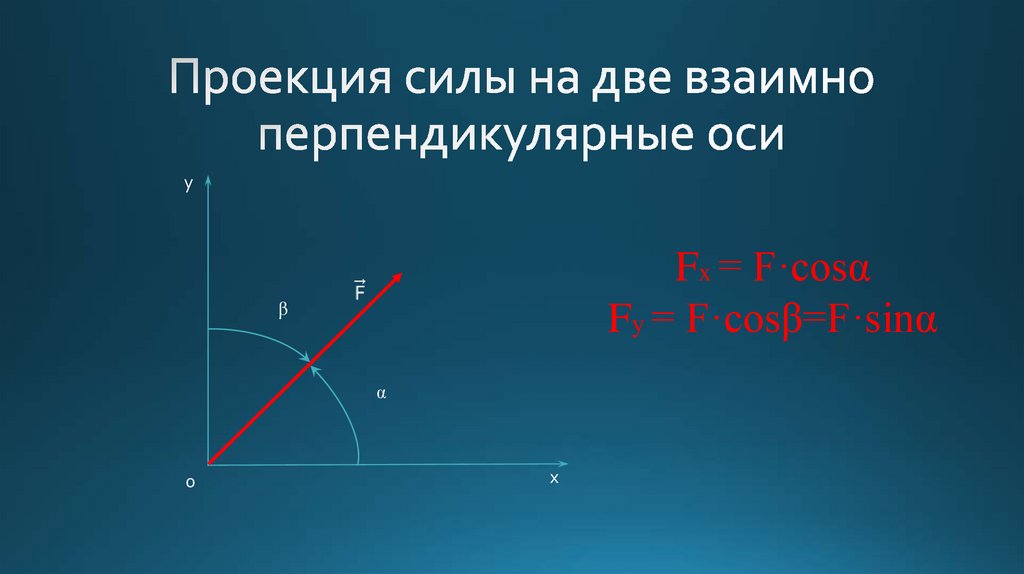
9. Проекция силы на две взаимно перпендикулярные оси
yFx = F·cosα
Fy = F·cosβ=F·sinα
β
α
0
x
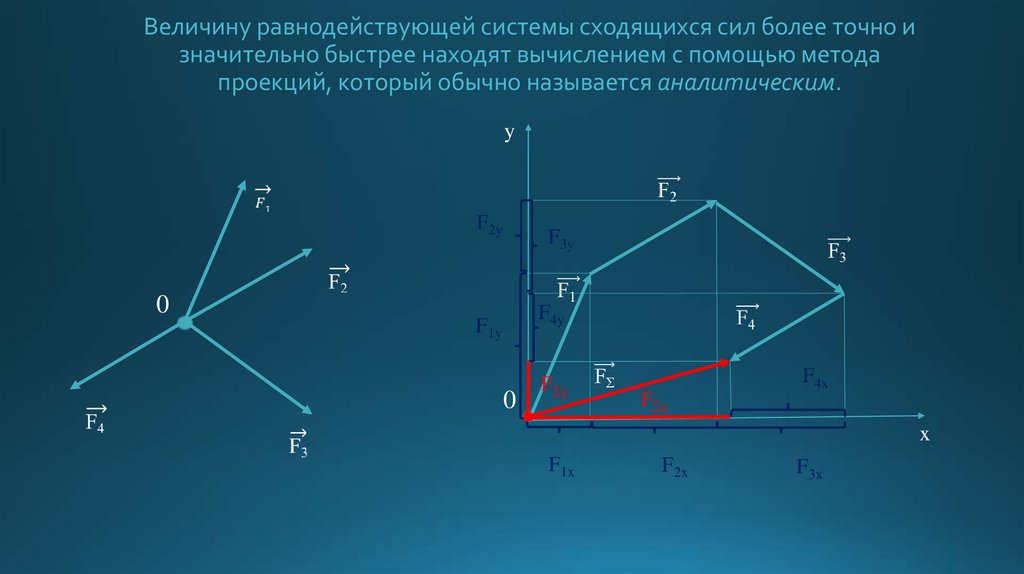
10. Определение равнодействующей системы сходящихся сил методом проекций. Аналитическое условие равновесия.
11. Величину равнодействующей системы сходящихся сил более точно и значительно быстрее находят вычислением с помощью метода
проекций, который обычно называется аналитическим.y
F2y
0
F3y
F4y
F1y
0
FΣy
F4x
FΣx
x
F1x
F2x
F3x
12.
yαy
αx
FΣy
x
0
FΣx









 Физика
Физика








