Код Фибоначчи - основа арифметики будущих компьютеров

1. 10 класс Код Фибоначчи - основа арифметики будущих компьютеров учебный материал ко Всероссийскому уроку информатики «Час кода

МОУ СОШ №12 с УИОП. Егорьевск
Владимир Утенков
10 класс
Код Фибоначчи - основа арифметики
будущих компьютеров
учебный материал ко Всероссийскому уроку информатики
«Час кода 1017»

2. Что такое числовая система

Позиционная система счисления – в ней количественный эквивалент цифры
зависит от ее положения в записи числа.
Базис позиционной системы счисления – последовательность чисел, на
которые умножают цифры в зависимости от их позиций.
Поясним эти понятия на примере всем хорошо знакомой десятичной
позиционной системы счисления:
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Размерность: 10.
Базис позиционной системы счисления: 1, 10, 100, 1000, 10….
то есть степени числа: 100, 101, 102, 103, … 10n…;
Пример:
2034510
↓
2∙104 + 0∙103 + 3∙102 + 4∙101 + 5∙100
Такая система счисления называется аддитивно-мультипликативной –
значение числа определяется как сумма ряда (аддитивно), а члены ряда
определяются умножением цифры на ее вес (мультипликативно).

3. Двоичная позиционная ЧС

Наиболее просто технически реализуется числовая система с двумя числами
в алфавите – двоичная.
Алфавит – 0, 1.
Размерность – 2.
Базис – 20=1, 21=2, 22=4, …, 2j, …
Пример:
1001012
↓
1∙25 + 0∙24 + 0∙23 + 1∙22 + 0∙21 + 1∙20 = 3710
Двоичная система является основой всей современной цифровой техники.

4. Недостатки двоичной ЧС

1. Трудность реализации в ней отрицательных чисел – приходится
использовать так называемый дополнительных код числа.
Процедура записи отрицательного двоичного числа:
- инвертировать запись числа, заменив 0 на 1, а 1 на 0;
- прибавить к числу единицу.
Пример:
1110 = 10112
Двоичный код числа -1110 вычисляется так:
1011 → 00001011 → 11110100 + 1 = 11110101
2. Двоичный код не имеет так называемой избыточности, то есть одна
ошибка в нем кардинально изменяет значение закодированного числа.
Ошибка
Пример:
4710 = 1011112 → 1010112 = 4310
В условиях, когда надежность технических систем все больше зависит от
надежности работы управляющих ими компьютерных систем и цифровых
систем связи, эффективные механизмы обнаружения и автоматического
исправления ошибок кодирования приобретают решающее значение.
Поэтому предлагаются числовые системы основанные на других принципах.

5. Нетрадиционные ЧС

Мы с вами пользуемся не только привычной нам десятичной позиционной
системой, но и системой, основанной на иных принципах. Пример измерение времени. Рассмотрим запись вида:
10 часов 12 минут 11 секунд вечера, 7 апреля 2016 года
Эта запись содержит:
- количество часов в 12-ричной системе с указанием времени суток
(вечер), правда количество часов можно было указать и в 24-ричной
системе как 22 часа);
- количество минут и секунд в 60-ричной системе:
- день месяца в системе, основание которого зависит от месяца (в апреле,
например, 30 дней, а в марте 31, в феврале 28 или 29 и т.д.);
- название месяца в 12-ричной системе;
- год в десятичной системе.
Кроме того, по календарю на 2016 год можно определить, что этот день
приходится на четверг. Это еще и так называемый лунный цикл из 28
дней, разбитый на 4 недели.
Еще один пример: в быту используется 12-ричная числовая система (число 12
называется дюжина) , так как она удобнее для деления, чем десятичная
(число 12 делится на 6, 4, 3, 2, а число 10 только на 5 и 2).

6. Числовой ряд Фибоначчи

Средневековый математик Фибоначчи придумал
числовой ряд построенный по следующим
правилам:
- два первых числа ряда: 1; 1;
- последующие числа ряда образуются как сумма
двух предыдущих, следующее число: 1+1 =2;
- следующее: 1+2=3;
- следующее: 2+3=5 и т. д.
Таким образом, ряд Фибоначчи имеет вид:
1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; …
Особенностью ряда Фибоначчи является то что
числа в нем быстро увеличиваются. Так член
ряда с номером 35 имеет значение 9 227 465.
Если последовательно делить очередное число
Фибоначчи на предыдущее, получается со все
большей точностью иррациональное число
примерно равное 1,612, которое называют
золотое сечение. Это отношение встречается в
пропорциях многих произведений искусства.
Леонардо Пизанский (род.
около 1170 года, ум.
около 1250 года) —
первый крупный
математик средневековой
Европы. Наиболее
известен под прозвищем
Фибоначчи.

7. Фибоначчиевая ЧС

Недостатки свойственные позиционной двоичной системе стимулировали
поиски других числовых систем, лишенных этих недостатков. В последние
десятилетия XX века советский ученый А. П. Стахов предложил числовую
систему с базисом из ряда Фибоначчи:
Алфавит: 0, 1.
Размерность: 2.
Базис позиционной системы счисления:
1, 2, 3, 5, 8, 13, 21, 34,…
Пример:
10110fib
↓
1∙8 + 0∙5 + 1∙3 + 1∙2 + 0∙1 = 1310
Оказывается в этой системе каждой последовательности из единиц и нулей
соответствует единственное число, но числу большему 2 соответствует
несколько последовательностей из единиц и нулей.
Пример:
310 = 1∙3 + 0∙2 + 0∙1 → 100fib
310 = 0∙3 + 1∙2 + 1∙1 → 011fib

8. Фибоначчиевая ЧС

У фибоначчиевой числовой системы есть интересное свойство: можно
преобразовывать одно и то же число во множество его представлений в
этой системе с помощью специальных фибоначчиевых операций свертки
и развертки, выполняемых над кодовым изображением числа:
свертка: 011 → 100;
развертка: 100 → 011.
Смысл этих операций легко понять, если вспомнить, что базисом
фибоначчиевой системы является ряд чисел, в котором следующее число
является суммой двух предыдущих, а так как ненулевое значение в
разряде означает, что это число из ряда и что два соседних с ним в сумме
должны быть ему равны: 5=3+2; 8=5+3; 13=8+5 и т.д.
Если над кодовым изображением числа произвести все возможные
развертки, то мы придем к специальному фибоначчиевому изображению,
называемому максимальной формой.
Пример:
для числа 9810 = 1000010001fib → 100 0010001 fib → 011 0010001 fib →
0110010001 fib → 0101110001 fib → 0101110001 fib → 0101101101 fib
→101101101 fib
В максимальной (или развернутой) форме рядом не встречаются два нуля.

9. Фибоначчиевая ЧС

Если над кодовым изображением числа произвести все возможные свертки,
то мы придем к специальному фибоначчиевому изображению,
называемому минимальной формой.
Пример:
для числа 2510 = 110101fib → 0110101fib → 1000101fib → 1000101fib
В минимальной форме рядом не встречаются две единицы.
Для исследования фибоначчиевой числовой системы автором разработана
компьютерная программа. Она написана на языке QBasic 4.5 и
откомпилирована:
Пуск
программы
Задание: перевести в фибоначчиевую форму числа: 7; 123; 445, 7 722 144.
Преобразовать в минимальную и максимальную формы число 100111010fib

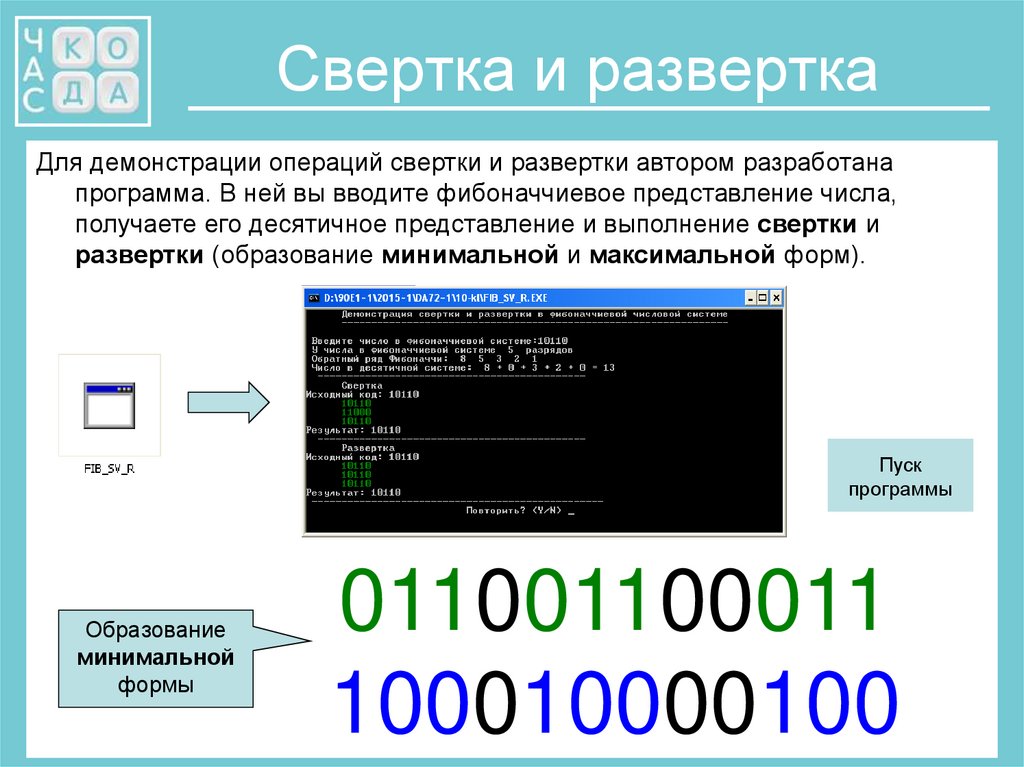
10. Свертка и развертка

Для демонстрации операций свертки и развертки автором разработана
программа. В ней вы вводите фибоначчиевое представление числа,
получаете его десятичное представление и выполнение свертки и
развертки (образование минимальной и максимальной форм).
Пуск
программы
Образование
минимальной
формы
011001100011
100010000100

11. Арифметика в фиб. ЧС

Для сложения чисел записанных в фибоначчиевой числовой системе
применяют следующий алгоритм:
1. Числа записывают одно над другим поразрядно, добавив нули слева:
1210 = A = 10101fib → 10101
710 = B = 1010fib → 01010
2. Единицы из числа A перемещают на место нулей числа B:
A = 10101
↓ ↓ ↓ →
B = 01010
00000
11111
3. Для числа B выполняют операции приведения к минимальной форме:
B = 11111 → 011111 → 100111 → 100111 → 101001
Проверим результат с помощью программы преобразования чисел в
фибоначчиевую форму:
A+B = 1210 +710 = 1910 = 101001fib
Ученые под руководством А. П. Стахова разработали алгоритмы вычитания,
умножения и деления в фибоначчиевой числовой системе. Смотри здесь.