Похожие презентации:
Квадратичная функция
1.
Квадратичнаяфункция
2.
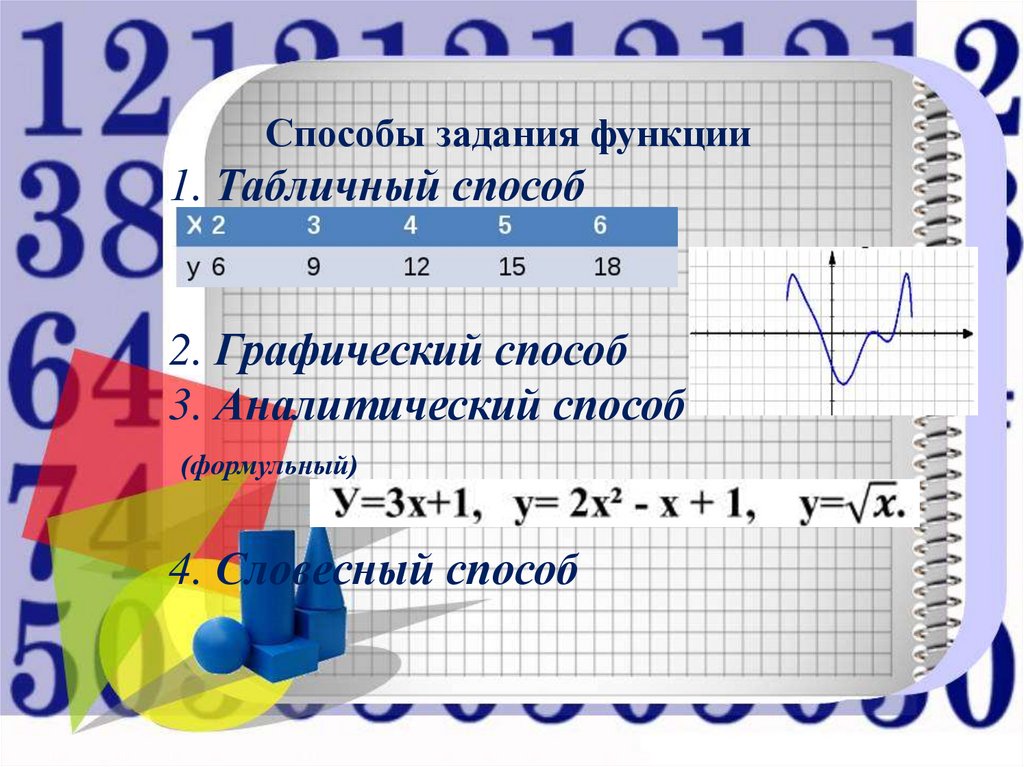
Способы задания функции1. Табличный способ
2. Графический способ
3. Аналитический способ
(формульный)
4. Словесный способ
3.
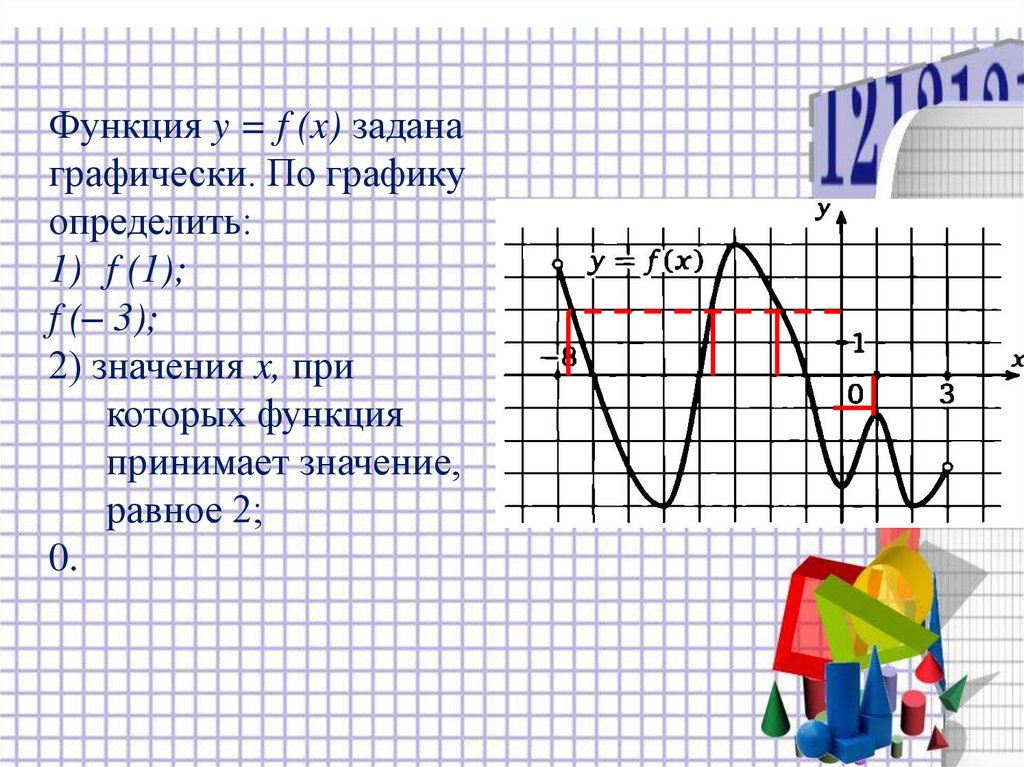
Функция y = f (x) заданаграфически. По графику
определить:
1) f (1);
f (– 3);
2) значения x, при
которых функция
принимает значение,
равное 2;
0.
4.
Найти значение функции f(x) =x3−3x2+x−2При х =2
f(2) =23−3⋅22+2−2= 8−12+2−2= −4.
Найти значение функции f(x) =3x2−5x+2
При х = − 1
f(−1) = 10
5.
Квадратичная функция6.
Квадратичная функцияу = ax2 + bx + c
Функция вида у = ax2 + bx + c, где а, b и с
– действительные числа, а ≠ 0, х –
действительная переменная, называется .
.
квадратичной функцией
Значения х при которых значение
функции у = ax2 + bx + c равно 0
называются нулями функции
7.
Квадратичная функция1) Найти значения функции
у = x2 − 7x + 6 при х = −2; х = 0
Решение:
у(−2) = (−2)2 − 7(− 2) + 6 = 24
у(0) = (0)2 − 7(0) + 6 = 6
2) При каких значениях х значение функции
у = x2 − 7x + 6 равно 0; −6
Решение:
а) у = 0 , то x2 − 7x + 6 = 0
х = 1, х = 6 − нули функции
б) у = −6 , то x2 − 7x + 6 = −6
x2 − 7x + 12 = 0 х = 3, х = 4





 Математика
Математика








