Похожие презентации:
Коллоидная химия
1. Коллоидная химия
проф. Назаров В.В.доц. Киенская К.И.
аcc. Яровая О.В.
2. Введение
3.
Коллоидная химия – наука о поверхностных явлениях и дисперсныхсистемах.
Литература
Основная:
1. Фролов Ю.Г. «Курс коллоидной химии. Поверхностные явления и дисперсные
системы», Москва, «Альянс», 2004, 463 с.
2. «Практикум и задачник по коллоидной химии» под ред. В.В. Назарова и
А.С. Гродского, Москва, ИКЦ «Академкнига», 2007, 373
Дополнительная:
1. Щукин Е.Д., Перцов А.В., Амелина Е.А. «Коллоидная химия», Москва, «Высшая школа»,
2004 г, 445 с.
2. Фридрихсберг Д.А. «Курс коллоидной химии. Учебник для ВУЗов», СПб, «Химия», 1995,
400 с.
3. Расчеты и задачи по коллоидной химии под ред. В.И.Барановой. М:, «Высшая школа»,
1989, 287 с.
4. Предмет коллоидной химии
Коллоидная химия – одна из немногих наук, название которой практически неотражает ее содержание. Термин «коллоидная» происходит от греческих слов:
κóλλα – клей; κολλάω – клею (клеить).
В 1861 г. Томас Грэм выделил растворы клеящих веществ в отдельную группу,
таким образом положив начало коллоидной химии и объектам ее исследования.
Позже оказалось, что не только клеящие вещества могут относиться к объектам
коллоидной химии. Более точное название этой науке дал П.А. Ребиндер - наука о
поверхностных явлениях и дисперсных системах.
Коллоидная химия
Поверхностные явления
Дисперсные системы
Дисперсная система
Дисперсионная средасплошная фаза
Дисперсная фазараздробленная фаза
5. Предмет коллоидной химии (2)
ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ:Адсорбция.
Адгезия, когезия, смачивание,
растекание.
Электрические явления и т.д.
ДИСПЕРСНЫЕ СИСТЕМЫ:
Суспензии, золи, аэрозоли.
Эмульсии, микроэмульсии.
Пены.
Мицеллярные растворы ПАВ.
Растворы полимеров.
ПРИЗНАКИ ОБЪЕКТОВ КОЛЛОИДНОЙ ХИМИИ
Гетерогенность (многофазность):
первичный признак,
качественная характеристика.
σ – межфазное натяжение
Песков Н.П.
Gs s
Дисперсность (раздробленность):
вторичный признак,
количественная характеристика.
s – площадь межфазной поверхности
Gs - поверхностная энергия
6. Количественные характеристики дисперсности
k-коэффициент формыФормы (предельные) элементов дисперсной
фазы
1. Определяющий размер элемента
дисперсной фазы: a
2. Дисперсность: D = 1/a
3. Удельная поверхность - отношение
площади межфазной поверхности к
объему (массе) дисперсной фазы:
ssp
ssp
s
s
s
; ssp'
V
m V
4. Кривизна поверхности: Н
Пленка:
Нить:
Куб:
Сфера:
ns 2 A2 2
2D
nV aA2 a
4 Aa 4
ssp
4D
Aa 2 a
ssp
2
6a
6
6D
a3
a
d2
6
ssp
6D
1 3 d
d
6
ssp
H
ssp kD
Сфера:
1 1
1
1 ds
; H
2 dV
2 r1
r2
H
Цилиндр: H
1
r
1
2rc
7.
Свободнодисперсные(жидкая и газообразная
дисперсионная среда)
По агрегатному состоянию
дисперсионной фазы и среды
Связнодисперсные
(твердая дисперсионная среда)
По кинетическим свойствам
Классификации дисперсных систем
По размерам частиц дисперсной фазы
По агрегативной устойчивости
Ультрамикрогетерогенные,
а = 10-9-10-7 м = 1 – 100 нм
Микрогетерогенные,
а = 10-7-10-5 м = 0,1 – 10 мкм
Грубодисперсные,
а > 10 мкм
Лиофильные
Лиофобные
cr a 2 kB T
cr a 2 kB T
8. Классификация дисперсных систем по агрегатному состоянию
H1
r
9.
КОСМЕТИКАИ ПАРФЮМЕРИЯ
КРЕМЫ,
ЗУБНЫЕ ПАСТЫ,
ШАМПУНИ И ДР.
МЕДИЦИНА
МИКРОКАПСУЛИРОВАНИЕ
ЭЛЕКТРОФОРЕЗ
НАНОМАТЕРИАЛЫ
ПОВЫШЕНИЕ
НЕФТЕОТДАЧИ
КОЛЛОИДНАЯ
ХИМИЯ
БУРОВЫЕ Р-РЫ,
ЗАВОДНЕНИЕ
КЕРАМИКА,
КАТАЛИЗАТОРЫ,
АДСОРБЕНТЫ
И ДР.
ЭЛЕКТРОНИКА
ПОЖАРОТУШЕНИЕ
ПЕНЫ
ФЛОТАЦИЯ,
МОЮЩИЕ
КОМПОЗИЦИИ
ПЛЕНКИ
ЛЕНГМЮРАБЛОЖДЕТТ
10. «Человек – ходячий коллоид»
11. Термодинамика поверхностных явлений
Общая характеристикаповерхностной энергии
12. Общая характеристика поверхностной энергии
Поверхностная энергия, как и любая другая энергия, рассчитывается как произведение фактора интенсивности σ на фактор емкости s: Gs = σsВеличина s определяется как s = sspV = (K/a)V = KDV, то есть размером и формой
элементов дисперсной фазы.
Поверхностное натяжение, в общем случае, определяется природой контактирующих фаз. При этом межфазная поверхность формируется наиболее конденсированной фазой – либо твердым телом ( в системах т-ж, т-г), либо жидкостью (ж-г, ж-ж).
Различие и общность поверхностей твердого тела и жидкости:
Различия:
1. Поверхность жидкости подвижна.
2. Поверхность жидкости энергетически
однородная (в покое).
1. Поверхность твердого тела неподвижна.
2. Поверхность твердого тела энергетически
неоднородная.
Общее заключается в том, что в обоих случаях на поверхности есть поверхностный слой
молекул, а, значит, есть и поверхностное натяжение и поверхностная энергия.
13. Поверхностное натяжение
Уравнение, вытекающее из первого и второго начал термодинамики,для дисперсной системы:
dG SdT Vdp ds i i dni dq
Энергия
Гиббса
Теплота
Механ.
Поверх.
«Химич.»
Электрич.
работа
энергия
энергия
энергия
где: S – энтропия; Т – температура; V – объем; р – давление; σ – поверхностное натяжение; s – площадь
межфазной поверхности; μi – химический потенциал компонента i; ni – число молей компонента i; φ –
электрический потенциал поверхности; q – заряд поверхности.
G
F
H
U
s p ,T ,n,q s V ,T ,n,q s S , p ,n,q s S ,V ,n,q
С точки зрения термодинамики поверхностное натяжение представляет собой
частную производную от любого термодинамического потенциала по площади
межфазной поверхности при постоянстве остальных параметров.
В частном случае, для чистых жидкостей:
G
G
const
Gs , то есть σ – свободная энергия единицы поверхности.
s
s p ,T ,n ,q
14. Поверхностное натяжение (2)
Поверхностное натяжение обусловлено нескомпенсированным полем молекулярных сил поверхностного слоя молекул.Термин поверхностное натяжение используется тогда, когда одна из фаз
является газообразной. В этом случае поверхностное натяжение определяется
межмолекулярными взаимодействиями внутри конденсированной фазы.
При контакте конденсированных фаз (т-ж, ж-ж) используют термин межфазное натяжение. Величина межфазного натяжения зависит от природы обеих
контактирующих фаз и определяется их взаимодействием – чем оно выше, тем
ниже межфазное натяжение.
Размерность поверхностного натяжения: Дж/м2 или Н/м.
В последней размерности поверхностное натяжение
можно рассматривать как силу, направленную тангенциально к поверхности и приходящуюся на единицу
длины периметра, ограничивающего эту поверхность.
Схема опыта Дюпре
15. Поверхностное натяжение (3)
Поверхностное натяжение (удельная поверхностная энергия)некоторых веществ на границе с воздухом
Т, К
, мДж/м2
Гелий (ж)
3
0,22
Азот (ж)
80
8,27
Аммиак (ж)
283
24,25
Гексан
298
17,9
Этанол
298
22,1
Бензол
298
28,2
Муравьиная кислота
298
36,6
Анилин
298
43,2
Вода
298
71,95
Лед
270
120,0
Ртуть
298
473,5
Вещество
16. Полная поверхностная энергия. Уравнение Гиббса-Гельмгольца
Есть чистая жидкость, ее объем V. Увеличим площадь поверхности этойжидкости при постоянстве других параметров (например, диспергируем ее
на несколько капель).
Рассчитаем, как изменится внутренняя энергия этой системы:
V1
V
T, V, n - const
V2
V=V1+V2+V3
V3
Уравнение из первого и второго начал термодинамики для данной системы:
dU TdS pdV ds dn
Учитывая, что dV=0 и dn=0: dU TdS ds
Полученное уравнение является однородным (под знаком дифференциала
стоят экстенсивные величины). Его можно сразу записать в интегральной
форме:
U T S s
17. Полная поверхностная энергия. Уравнение Гиббса-Гельмгольца (2)
Делим все части уравнения на величину изменения межфазной поверхности Δs:U s TSs ; U s U / s; Ss S / s; TSs qs ; U s qs
где: Us – полная поверхностная энергия; Ss – энтропия единицы поверхности; qs –
теплота образования единицы поверхности.
Gs
G
S
;
S
;
G
;
S
; U s TSs
s
s
s
T p ,n,q
T p ,n ,q
T p ,n ,q
После подстановки получаем уравнение Гиббса-Гельмгольца для полной поверхностной энергии:
Us T
T p ,n,q
Для расчетов по этому уравнению необходимо знать зависимость поверхностного
натяжения от температуры f T.
18. Зависимость термодинамических параметров поверхностного слоя от температуры
f Tqs TS s T
T
TSs qs ; qs 0
T 0
Ss 0
0;
T
qs f (T )
T
T
qs
U s f (T )
a
const
T
0 a(T T0 )
U s
2
2
T
T
2
T
T T
T
T 2
U s
0; U s f
T
T
2
0
2
T
19. Термодинамика поверхностных явлений
Поверхностное натяжение иадсорбция
20. Поверхностное натяжение и адсорбция
Адсорбция – самопроизвольное перераспределение вещества между объемной фазой иповерхностным слоем. Вещество (вещества), которое перераспределяется, называется
адсорбатом. Фаза, которая формирует поверхность, называется адсорбентом. В системах т-г и
т-ж адсорбентом является твердое тело, в системах ж-г и ж-ж – жидкость.
При физической адсорбции процесс адсорбции обратим и сопровождается снижением
межфазного натяжения.
Величину адсорбции А характеризуют количеством вещества (адсорбата) в поверхностном
слое, отнесенном к единице поверхности или единице массы адсорбента: моль/м2 или моль/кг
Правило фаз Гиббса при физической адсорбции и общее уравнение адсорбции
Адсорбция газов и паров на твердом
адсорбенте
F K Ф 2
F 2 2 2 2
A f (T , p)
Адсорбция из бинарного раствора
на твердом адсорбенте
F k ф 2
F 3 2 1 2
A f (T , c)
21. Поверхностное натяжение и адсорбция (2)
Изотерма адсорбции(основная зависимость)
T const
A f T (c)
A f T ( p)
Изобара и изопикна адсорбции
c const
p const
A f p (T )
Изобары, изопикны и изостеры получают
из семейства изотерм.
A f c (T )
Изостера адсорбции
A const
p f A (T )
c f A (T )
22. Адсорбция из раствора на твердом адсорбенте
Раствор красителя(метиленового голубого)
Исходный адсорбент
(силикагель)
Раствор и адсорбент
в контакте
Силикагель
после адсорбции
23. Метод избыточных величин Гиббса
с1, с2-концентрация растворителяи растворенного вещества (красителя),
соответственно.
xs – абсцисса, соответствующая
границе раздела фаз.
xs - xsα= h – толщина поверхностного
слоя.
Фаза α – жидкая фаза ( водный раствор
красителя).
Фаза β – фаза твердого адсорбента
(силикагеля).
А – абсолютная адсорбция;
Г – гиббсовская или избыточная
адсорбция.
Схема, иллюстрирующая
методы Гуггенгейма и Гиббса
24. Метод избыточных величин Гиббса (2)
Метод слоя конечной толщины(метод Гуггенгейма)
n2 n2 s n2ss V s c2 Vs c2s
V s sxs ; Vs sh
V s Vs V
Vs c2s
n2ss
A2
s
s
Абсолютная адсорбция – число молей
адсорбата в поверхностном слое,
отнесенное к единице поверхности (или
массы адсорбента) [моль/м2]
Метод избыточных величин
(метод избытков Гиббса)
n2 n2s n2 V c2 Vs (c2s c2 )
V sxs ; Vs sh
n2s Vs (c2s c2 ) Vs c2s Vs c2
2
s
s
s
2 A2 c2 h
A2
Гиббсовская адсорбция – избыток числа молей
компонента в объеме поверхностного слоя по
сравнению с числом молей этого компонента
в равном объеме объемной фазы, отнесенный
к единице поверхности (или массы адсорбента)
[моль/м2]
25. Метод избыточных величин Гиббса (3)
Отрицательная гиббсовскаяадсорбция
Для растворителя (первого компонента), в
соответствии с методом избытков Гиббса:
n1 n1s n1 V c1 Vs (c1s c1 )
n1s Vs (c1s c1 ) Vs c1s Vs c1
1
A1 hc1
s
s
s
1 0, так как с1s c1
Vs c1s
n1ss
A1
0
s
s
Таким образом, в общем случае:
i Ai
В каких случаях i
Ai ?
Vs (c2s c2 ) Vs c2s
2
A2 при с2s
s
s
c2
Различием между величинами гиббсовской и
абсолютной адсорбции можно пренебречь при:
1. при адсорбции газов и паров;
2. при адсорбции поверхностно-активных
веществ (ПАВ).
26. Фундаментальное адсорбционное уравнение Гиббса
Для адсорбционной системы запишемуравнение, вытекающее из первого и второго
начал термодинамики. Запишем его для
избытка внутренней энергии:
dU s TdS s ds i dnis
i
Так как под знаком дифференциала
находятся только экстенсивные величины (избытки), то:
s
s
s
U TS s i ni
i
Полный дифференциал от
тех же переменных:
dU s TdS s S s dT ds sd i dnis nis d i
i
i
Вычтем третье уравнение из первого:
0 S dT sd n d i
s
При Т=const: sd
s
i
i
n d
s
i
i
Делим на s и преобразуем:
i
0
d is d i - уравнение Гиббса,
i
nis
- избыточная адсорбция i-того
где: i
s
компонента.
27. Частное выражение уравнения Гиббса
Запишем уравнение Гиббса для случаяадсорбции из бинарного раствора:
d 1d 1 2 d 2
Для предельно разбавленного раствора
второго компонента:
d 1 0; d 2 d 2
d
2
Откуда:
d 2
Для разбавленного раствора:
2 20 RT ln c2 ; d 2 RTd ln c2 RT
dc2
c2
Окончательно:
2
c d
p d
или 2
RT dc
RT dp
Последнее уравнение справедливо при
физической адсорбции газов и паров.
1. Оба уравнения применимы либо в области разбавленных растворов, либо в области низких давлений
паров адсорбата.
2. Если вещество переходит из объемной фазы в
поверхностный слой, то есть Γ>0, то d 0.
dc
Это означает, что физическая адсорбция
сопровождается падением поверхностного натяжения.
3. Из полученного уравнения следует, что
размерность гиббсовской адсорбции будет моль/м2.
4. Если известна изотерма поверхностного натяжения σ=fT(c), то по полученному уравнению можно рассчитать изотерму гиббсовской адсорбции.
d
g
tg 0
dc c 0
d
tg
dc
c
tg
RT
28. Поверхностная активность
Поверхностная активность характеризуетспособность данного вещества снижать поверхностное натяжение данного растворителя:
d
g
; g tg 0
dc
c 0
По величине g все вещества делят на поверхностно-активные (ПАВ) и поверхностно
неактивные (ПИАВ):
d
0
dc
d
g 0; 0;
0
dc
1. Для ПАВ (С3H7COH): g 0; 0;
2. Для ПИАВ (KCl):
Молекулы специфических ПАВ имеют дифильное строение:
Кружок – полярная группа (-COONa, -OH,
-OSO3Na и др). Черта обозначает углеводородный радикал того или иного строения.
Зависимость поверхностного натяжения (а)
и гиббсовской адсорбции (б) от концентрации
водного раствора поверхностно-активного и
инактивного веществ: 1 – додециламин; 2 –
сульфат натрия.
29. Адгезия, смачивание и растекание жидкостей
30. Адгезия, смачивание и растекание
Адгезия - межфазное (межмолекулярное) взаимодействие 2-х разныхфаз, приведенных в контакт, сопровождающееся снижением
поверхностной энергии.
Количественной характеристикой адгезии является работа адгезии
(Wa, Дж/м2) - работа, затрачиваемая на разрыв адгезионного соединения.
Уравнение Дюпре для работы адгезии
Wa Ga Gin G fin 31 21 32
Wa 31 21 32
Здесь и далее индексы относятся:
«3» - к твердой фазе;
«2» - к жидкой фазе;
«1» - к газовой фазе.
σ31 - поверхностное натяжение твердой фазы;
σ21 – поверхностное натяжение жидкости;
σ32 – межфазное натяжение между твердым
телом и жидкостью.
Когезия – внутрифазное взаимодействие (межмолекулярное
взаимодействие между двумя частями одной фазы).
Количественной характеристикой когезии является работа когезии
(Wc, Дж/м2):
Wc 2 21
31.
Смачивание – межфазное взаимодействие между приведенными вконтакт тремя фазами (например, твердой, жидкой и газообразной).
Количественной характеристикой смачивания является угол
смачивания (краевой угол), обозначаемый буквой θ.
Уравнение Юнга для краевого угла
Из условия равновесия в точке контакта трех фаз
(пренебрегая действием силы тяжести):
31 32 21 cos ;
cos
31 32
21
Классификация смачивания:
1. cosθ > 0, θ < 900, смачивание; поверхность
лиофильная (гидрофильная).
2. cosθ < 0, θ > 900, несмачивание; поверхность
лиофобная (гидрофобная).
3. cosθ = 0, θ = 900, точка инверсии.
32.
Уравнение Дюпре-ЮнгаВыразим 31 32 из уравнения
Юнга
31 32 21 cos
и подставим в уравнение Дюпре:
Wa 21 31 32 21 21 cos
Получаем уравнение ДюпреЮнга:
Wa 21 (1 cos )
Разделим обе части уравнения на
величину 2 21 :
Wa
(1 cos )
21
2 21
2 21
Wa
(1 cos )
Wc
2
Предельные случаи:
1). 0 , cos 1 , Wa Wc
условие растекания
2). 90 , cos 0 ,
инверсия смачивания
Wa
1
Wc
2
Wa
0
Wc
3). 180 , cos 1 ,
реализовать невозможно, так как всегда
есть межмолекулярное взаимодействие и
Wa 0, Wc 0, 1800
33.
Растекание – предельный случай смачивания (θ = 00).Количественной характеристикой растекания является коэффициент
растекания (коэффициент растекания по Гаркинсу):
f Wa Wc
Выразим Wa и Wc через поверхностные натяжения и подставим:
f Wa Wc 31 32 21 2 21
f 31 32 21
Условия растекания:
00 , Wa Wc , f 0, 31 32 21 0
В некоторых случаях коэффициент растекания может быть больше
нуля ( f 0) за счет дополнительного взаимодействия между фазами (например, образование водородных связей).
34.
Основные факторы, влияющие наадгезию, смачивание и растекание:
cos
1). Температура:
1
0
31 32
21
T 21 cos
СПАВ
Изотерма смачивания водным раствором
ПАВ гидрофобной поверхности
2). Введение ПАВ в жидкую фазу:
c
21
32
cos
3). Шероховатость поверхности:
а). если θ<900, то шероховатость улучшает
смачивание;
б). если θ>900, то шероховатость ухудшает
смачивание.
1
0
СПАВ
Изотерма смачивания водным раствором
ПАВ гидрофильной поверхности
35.
Капля воды на гидрофобнойповерхности
Капля воды на гидрофильной
поверхности
Роль смачивания:
флотация,
гидрофобизация и
гидрофилизация
поверхностей,
моющие
композиции,
смачивание в
природе и др.
36. Гидрофобизация поверхности бумаги
Капли воды на поверхности бумаги:a. Исходная бумага (небеленая бумага
из древесины хвойных пород).
b. После обработки фторированным
соединением
CF3(CF2)5CH2CH2Si(OC2H5)3.
c. Нанесение частиц SiO2 (создание
шероховатости) + обработка
фторированным соединением.
Journal of Colloid and Interface Science,
325 (2008) 588–593.
1500
Частицы SiO2 на поверхности
волокон бумаги.
37.
Капля воды на супергидрофобной поверхности сплава алюминия(травление + химическая гидрофобизация). 159, 70
Водомерка на поверхности воды
38.
Эффект Марангони – растекание жидкости с меньшим поверхностнымнатяжением по поверхности жидкости с большим поверхностным натяжением (в
общем случае, это течение, обусловленное градиентом поверхностного
натяжения).
Правило Антонова – межфазное натяжение между двумя контактирующими
взаимно насыщенными жидкостями равно разности поверхностных натяжений их
взаимно насыщенных растворов на границе с воздухом.
f 3,1sat 2,1sat 3,2sat ;
при
f 0,
sat
sat
3,2
3,1sat 2,1
Примеры соблюдения правила Антонова при контакте жидкостей с водой
39.
Методы определения поверхностных и межфазных натяженийОпределение межфазного
натяжения - 32
ln
cr 2 VM
c
R T r
уравнение Кельвина
Определение поверхностного
натяжения - 31
Метод Цисмана
Методы определения
поверхностного натяжения - метод капиллярного поднятия
- уравнение Жюрена:
h
21
2 cos
grc
- метод максимального давления в
пузырьке
- уравнение Лапласа
p
- метод отрыва кольца
ds
dV
- сталагмометрический метод
40. Дисперсность и термодинамические свойства тел
41.
Правило фаз Гиббса и дисперсностьДисперсность (кривизна поверхности) – самостоятельный термодинамический параметр состояния системы, изменение которого вызывает из-менение
других равновесных свойств системы. Является интенсивным признаком.
Правило фаз Гиббса
с учетом дисперсности
F K 3
D0
C0
D
1
a
Cs
Cs
диспергирование
D0<D
С<C0
Диспергирование капель эмульсии
C
42.
Влияние дисперсности на внутреннее давление телКривизна вызывает изменение площади и положения
межфазной поверхности между двумя несмешивающимися жидкостями, что можно выразить приращением
поверхностной энергии σds.
При этом меняются объемы фаз 1 и 2 на dV1 и dV2, но
с учетом постоянства объема всей системы: dV1 dV2
Обобщенное уравнение первого и второго начал
термодинамики для энергии Гельмгольца системы:
dF p1dV1 p2 dV2 ds p1dV2 p2 dV2 ds
При равновесии между фазами dF=0 и тогда:
p1 p2 dV2 ds 0
T const;
V1 V2 V const
p2 p1 p;
или
p2 p1 dV ds
1 1
p
r1 r2
Уравнение Лапласа
p
ds
;
dV
43.
Влияние дисперсности навнутреннее давление тел (2)
Лиофильная поверхность Лиофобная поверхность
∆p
ds
0; p 0; p2 p1
dV
ds
2. H 0;
0; p 0; p2 p1
dV
ds
3. H 0;
0; p 0; p2 p1
dV
1. H 0;
h1>0
h2<0
4. Для сферической поверхности
радиуса r:
ds
2
2
; p
dV
r
r
5. Для цилиндрической поверхности
радиуса r:
ds
1
; p
dV
r
r
∆p
r
44.
Поверхностная энергия и равновесные формы телПринцип Гиббса-Кюри – термодинамически
устойчивой является та форма тела, при
которой система обладает наименьшей
поверхностной энергией Гиббса.
Для жидкостей (изотропные системы):
s
i
V const;
s
i i
min
i
min
при V
const
i
В изотропной системе все свойства,
в том числе и поверхностное натяжение,
в любой точке поверхности жидкости
имеют одно и тоже значение.
Термодинамически устойчивой формой
жидкого тела является сферическая форма,
поскольку она имеет наименьшую
поверхность при данном объеме.
45.
Поверхностная энергия и равновесные формы тел (2)Для кристаллов (анизотропные системы):
индекс i обозначает разные грани кристалла
si kli2 ; dsi 2kli dli ; ds
2
;
3
Vi 13 kli ; dVi kli2 dli ; dV li
2 i
p
li
Закон Вульфа – условием минимума поверхностной
энергии равновесного кристалла является пропорциональность удельных поверхностей его граней их
расстояниям от центра кристалла.
1
l1
2
l2
W const
1 : 2 :... l 1: l2 :...
W – константа Вульфа. Постоянна для
кристалла определенного размера, с его
увеличением уменьшается.
46.
Капиллярные явленияКапиллярные явления наблюдаются в
зазорах (капиллярах), содержащих жидкость, и у которых расстояние между
стенками соизмеримо с радиусом кривизны поверхности жидкости.
Для вогнутого цилиндрического мениска:
2
2
p p2 p1
èëè p1 p2 p '
r
r
2
p '
( 0 ) gh
r
h
2
r
; 0 cos
r ( 0 ) g r
h
2 cos
r0 ( 0 ) g
Уравнение Жюрена
p2
p1
p2
p1 p2
p1 p2
Лиофильная поверхность: cosθ > 0
Лиофобная поверхность: cosθ < 0
r – радиус мениска;
r0 – радиус капилляра.
47.
Капиллярные явления (2)Вогнутый мениск имеет цилиндрическую
форму:
p p2 p1 ; p1 p2 p '
r
r
d /2
p ' ( 0 ) gh;
cos
r
r
d – расстояние между пластинами
h
2 cos
d ( 0 ) g
Если в зазоре между двумя смачиваемыми плоскопараллельными пластинами
находится слой жидкости толщиной d, то за счет вогнутого цилиндрического
мениска они окажутся прижатыми друг к другу с силой F:
2 s cos
F ps
d
где: s – смоченная поверхность пластин.
48.
Зависимость термодинамической реакционной способности от дисперсностиТермодинамическая реакционная способность характеризует способность
вещества переходить в какое-либо иное состояние, например, переходить в другую
фазу, вступать в химическую реакцию.
Мерой термодинамической реакционной способности является свободная энергия.
Изменение свободной энергии, обусловленное изменением дисперсности:
dG SdT Vdp
При Т = const:
на 1 моль:
dG Vdp, G V p. Для индивидуального вещества в расчете
G V
p; GM VM p
n
n
После подстановки Δp из уравнения Лапласа получаем:
ds
ds
p
;
GM VM
Дисперсность (кривизна поверхности)
dV
dV
Для сферической кривизны радиуса r:
2 VM
GM
r
может вызывать как рост свободной
энергии, так ее снижение (в зависимости от знака кривизны).
49. Влияние дисперсности на давление паров (уравнение Кельвина)
Для 1 моля жидкости:ds
Gl VM p VM
dV
Для 1 моля пара:
p
p
Gv Vdp
ps
ps
RT
p
dp RT ln
p
ps
ds
p
RT ln
dV
ps
p VM ds
ln
ps
RT dV
Gl Gv ; VM
Для сферической капли:
ds
2
p 2 VM Уравнение
; ln
Кельвина
dV
r
ps
RTr
ln p / ps 0; p / ps 1; p ps
Для вогнутого мениска в капилляре (поре):
ds
2
p
2 VM Уравнение капилляр ; ln s
dV
r
p
RTr ной конденсации
ln ps / p 0; ps / p 1; ps p
50.
Влияние дисперсности частиц на их растворимостьДля неэлектролитов:
c
2 Vм
ln
RTr
cs
Для электролитов:
a
c
c
2 Vм
ln
ln v v ln
as
cs
cs
RTr
v
• С увеличением дисперсности растворимость растет (при положительной
кривизне).
• Растворимость зависит от знака кривизны поверхности. Для частиц
неправильной формы (в насыщенном растворе) участки с отрицательной
кривизной будут «зарастать», а с положительной кривизной – растворяться.
51.
Влияние дисперсности на равновесие химической реакцииС увеличением дисперсности повышается
активность компонента (его свободная
энергия). Константа химического равновесия изменяется в ту или другую сторону,
в зависимости от степени дисперсности
исходных веществ и продуктов реакции.
Kr
G RT ln
K
0
r
При повышении дисперсности
карбоната кальция
СаСО3 ↔ СаО + СО2
При повышении дисперсности
оксида кальция
СаСО3 ↔ СаО + СО2
52.
Влияние дисперсности на температуруфазового перехода
Изменение энергии Гиббса, связанное
с изменением дисперсности, при p = const:
dGr SdT ; Gr S T ; T Tr T
ds
ds
Gr VM
; S T VM
dV
dV
Энтропия фазового перехода:
H ph
S
T
После подстановки:
T V ds
T T Tr M
H ph dV
Для сферических частиц:
2 T VM
T Tr
H ph r
Влияние дисперсности
на поверхностное натяжение
Приближенное соотношение (при сравнительно малой кривизне), известное
как уравнение Толмена:
r /
1
2
1
r
где: σr и σ∞ - поверхностные натяжения при
радиусе кривизны r и для плоской поверхности; δ - толщина поверхностного слоя, имеющая порядок размера молекул.
При малых радиусах кривизны:
r Kr
где: К - коэффициент пропорциональности,
зависящий от температуры и природы фазы.
53. Получение дисперсных систем (энергетика диспергирования и конденсации)
54.
Получение дисперсных системДиспергирование:
Конденсация:
дробление, измельчение вещества с
использованием различных
механических устройств
(дробилки, диспергаторы, шаровые
и коллоидные мельницы и др.)
переход от гомогенной системы к
гетерогенной дисперсной системе в
результате ассоциации молекул,
атомов или ионов в агрегаты
(конденсация пара, кристаллизация
из раствора или расплава).
Достигаемый (минимальный)
размер частиц: до ~0,1 мкм.
Дисперсные системы с размерами
частиц от 10-9 до ~10-7 м
55.
Работа диспергированияКонденсированное
вещество
Объемное деформирование
(упругое и пластическое)
Образование
новых
поверхностей
При диспергировании работа W
затрачивается на деформирование
и создание новых поверхностей.
Работа упругого и пластического
деформирования:
Wdef kV
k – коэффициент, равный работе
объемного деформирования единицы
объема конденсированного тела.
Работа образования новой поверхности:
Ws s
56.
Работа диспергирования (2)Полная работа, затрачиваемая на диспергирование:
W Wdef Ws kV s
Уравнение Ребиндера
W k1d 3 k 2 d 2 d 2 (k1d k 2 )
При больших значениях d:
При малых значениях d:
W k1 d
W k 2 d 2
Эффект Ребиндера – адсорбционное понижение прочности твердых тел.
Уменьшение поверхностной энергии с помощью ПАВ, в результате чего
облегчается деформирование и разрушение твердого тела.
57.
Метод конденсацииГомогенная конденсация
Гетерогенная конденсация
образование новой фазы на
поверхностях зародышей,
возникающих
самопроизвольно в
результате флуктуаций
плотности и концентрации
вещества в системе
образование новой фазы на уже
имеющихся поверхностях
(стенках сосуда, частицах
посторонних веществ – ядрах
конденсации)
58.
Метод конденсации (2)Степень пересыщения для пара:
p
;
ps
для раствора:
c
cs
Для жидких и газообразных фаз энергию Гиббса образования
зародышей новой фазы можно выразить как сумму химической
(объемной) и поверхностной составляющих.
Химическая составляющая:
G v n( l v )
V
( l v )
VM
Поверхностная составляющая: G s s
Полное изменение энергии Гиббса при образовании зародыша:
G G v G s
V
( l v ) s
VM
59.
Метод конденсации (3)Для сферического зародыша:
4 r3
G
( l v ) 4 r 2
3 VM
При p < ps μl > μv
ΔG > 0,
новая фаза не может
образоваться самопроизвольно.
Для поиска экстремума на зависимости
ΔG=f(r) приравняем нулю первую
производную :
2
G 4 rкр
( ж п ) 8 rкр 0
r
Vм
Откуда:
v l
2 VM
rcr
rcr – критический радиус зародыша
в экстремальной точке.
RT ln p RT ln ps
2 VM
rcr
p 2 VM
ln cr ln
ps rcr RT
уравнение Кельвина
60.
Метод конденсации (4)Вторая производная от энергии Гиббса:
2 G 8 rcr 2 VM
8 8
2
r
VM
rcr
2 G
0 указывает на наличие максимума.
2
r
Свободная энергия образования
зародыша критического радиуса:
4 rcr3 2 VM
Gcr
3 VM
rcr
2
4 rcr
1
4 rcr2 ( 2 3 ) scr
3
16 3VM2
1
Gcr scr ; Gcr
3
3R 2T 2 ln 2 cr
2 G 8 rcr
( l v ) 8
2
r
VM
61.
Метод конденсации (5)Две стадии образования зародышей:
Зарождение центров
конденсации
Скорость зарождения
центров конденсации:
G1
I A1 exp
RT
ΔG1 – свободная энергия образования
центра конденсации.
Доставка вещества к
центру конденсации
Скорость доставки вещества
к центру конденсации:
E
U A2 exp
RT
Eη – энергия активации вязкого течения.
Общая скорость образования зародышей равна произведению
скоростей стадий, ее составляющих: 1 IU
62.
Метод конденсации (6)Скорость образования зародышей:
G1
RT
1 IU A3 exp
G1 E
A3 exp
RT
E
exp
RT
Скорость роста зародышей:
E
exp
RT
G2 E
B exp
RT
G2
RT
2 B exp
63. Адсорбционные равновесия
64. Адсорбционные равновесия Межмолекулярные взаимодействия при адсорбции
Классификация механизмов адсорбцииАдсорбция
Физическая
Физические
взаимодействия
(силы Ван-дер-Ваальса)
Химическая
Химическая реакция между
адсорбатом и адсорбентом
Ионнообменная
Обмен ионами между
адсорбатом и адсорбентом
65. Физические взаимодействия
Силы Ван-дер-ВаальсаДиполь-дипольное
взаимодействие
(силы Кеезома)
12 22
2
U att kBT
3
r6
70%
Дисперсионное
взаимодействие
(силы Лондона)
U att
C
r6
100%
Индукционное
взаимодействие
(силы Дебая)
12 22
2
U att kÁT
3
r6
2-9%
r
Энергия
притяжения
U att
Ñ
r6
U (r )
C
b
r6
r 12
Уравнение
Леннард-Джонса
Энергия
отталкивания
U rep
b
rm
66. Энергия взаимодействия атома адсорбата с поверхностью адсорбента
dU ad U att dNdN ndV
C
dN
6
r
1
x
1
2 Cn( 3 4 ) 2 Cn
3x
4x
12 x 3
dV sdr
U ad
s 2 rh 2 r (r x)
dV 2 r (r x)dr
dU ad
C
2 Cn
n
2
r
(
r
x
)
dr
(r x)dr
r6
r5
r x
dU ad 2 Cn 5 dr
r
x
dr xdr
2 Cn( 4 5 )
x r
x r
U ( x)
Cn
U (r )
6 x3
b
xm
C
b
r6 rm
Cn
6 x3
67. Адсорбция газов и паров на однородной поверхности
Закон ГенриЕсли адсорбат на поверхности адсорбента рассматривать как самостоятельную
фазу, то условиям равновесия соответствует равенство химических потенциалов
адсорбата в адсорбционном слое и в объемной фазе:
0
0 RT ln a ; RT ln a
0 RT ln a 0 RT ln a
0 0
a
exp
K ; T const
a
RT
a K a; c K c ; 1, c K c
c A;
p
pV nRT ; p cRT ; c
;
RT
A K с
A K p
Начальный участок изотермы адсорбции
68. Адсорбция газов и паров на однородной поверхности (2)
Теория ЛенгмюраОСНОВНЫЕ ПОЛОЖЕНИЯ:
1. Адсорбция протекает на адсорбционных центрах.
Адсорбционные центры энергетически эквиваленты,
(поверхность адсорбента энергетически однородная).
2. На адсорбционном центре адсорбируется только одна
молекула (мономолекулярная адсорбция).
3. Адсорбированные молекулы не перемещаются
по поверхности адсорбента (локализованная адсорбция).
4. Адсорбированные молекулы не взаимодействуют
друг с другом.
Если адсорбцию рассматривать как некую обратимую
квазихимическую реакцию, то для элементарного акта:
A B
К
AB
где К – константа адсорбционного равновесия.
Отклонения от закона Генри
69. Адсорбция на однородной поверхности (3)
A BK
К
AB
[ AB]
[ AB]
; K
[ A] [ B]
[ A] p
[ AB] A;
[ A] A A
A
K
( A A) p
Изотерма адсорбции Ленгмюра
Начальный участок
K p
K p
A K p K p
1 K p
K A K
1; A A
A Kp( A A) KpA KpA
A(1 Kp) A Kp
A A
K p
K c
; A A
1 K p
1 K c
Конечный участок
K p
1;
A A
A
1
A
K p
A
1 K p
70. Адсорбция на однородной поверхности (4)
Уравнение Ленгмюра в линейной формеA A
K p
1 K p
1
1 Kp
A
A Kp
1
1
1 1
A A A K p
ssp N A A s0
d ln K H 0
H 0 G 0
0
G RT ln K ;
; S
dT
RT 2
T
0
Изотерма в координатах уравнения Ленгмюра
71. Адсорбция на однородной поверхности (5)
Теория БЭТВывод уравнения БЭТ:
K
(Брунауэр, Эммет, Теллер)
Теория БЭТ была создана для
полимолекулярной адсорбции паров и
базируется на тех же исходных положениях,
что и теория Ленгмюра, за исключением
одного положения.
Вместо предположения о мономолекулярной адсорбции принимается, что каждая
адсорбированная молекула является новым
центром адсорбции.
A B
AB B
AB 2 B
AB;
K1
AB 2 ;
K2
AB3 ;
K
[ AB]
[ A] p
K1
[ AB 2 ]
[ AB] p
K2
[ AB 3 ]
[ AB 2 ] p
……………
Введем новые обозначения:
[ AB] AAB ; [ AB 2 ] AAB2 ; [ AB3 ] AAB3 ;
A
[ A] A0 - число незанятых центров
AB4
AB3
адсорбции.
Далее выразим адсорбцию из уравнений
для констант равновесия.
AB2
AB
Ā
Ā
Ā
Ā
Ā
Ā
P/Ps
72. Адсорбция на однородной поверхности (6)
AAB KA0 pРассчитываем общее число центров адсорбции
(фактически, емкость монослоя) A∞:
AAB2 K1 AAB p KK1 A0 p 2
AAB3 K2 AAB2 p KK1K2 A0 p
A A0 AAB AAB2 AAB
3
3
Вводим еще одно допущение :
все константы, начиная с K1, одинаковы
и равны константе конденсации.
a
K1 K2 K3 ... K L ; K L l
àv
liquid; al 1; av ps
vapor
KL
KL
1
1
; K1 K 2 K3 K L
ps
ps
Введем новую константу:
C
K
Kps ;
KL
K C KL C
A0 A0 Kp A0 KK1 p 2 A0 KK1 K 2 p3
1
1
p
K
K
K
;
K
C
;
x
1
2
3
p
p
p
s
s
s
A0 CA0 x CA0 x 2 CA0 x3
A0 [1 Cx (1 x x 2 x3 )]
Принимая, что число адсорбционных слоев
бесконечно большое и учитывая, что p/ps<1:
1 x x 2 x3
1
ps
1
1 x
Cx
1 x Cx
A A0 1
A
0
1 x
(1 x)
73. Адсорбция на однородной поверхности (7)
Рассчитываем суммарную величину адсорбции:A AAB 2 AAB2 3AAB3 ... A0 Kp A0 KK1 p2 A0 KK1K2 p3 ...
1
1
p
K
K
K
;
K
C
;
x
1
2
3
p
p
p
s
s
s
CA0 x 2CA0 x 2 3CA0 x3 ... CA0 x(1 2 x 3x 2 ...);
A
A
CxA0
;
2
(1 x)
A0 A
1 x
;
1 (C 1) x
A C p / ps
1 p / ps 1 C 1
Уравнение БЭТ
p
ps
A
1 2 x 3x 2 ...
A Cx(1 x)
;
(1 x) 2 [1 (C 1) x]
0, 05 p / ps 0,3
ssp A N A s0
x
1
(1 x)2
p
ps
Для определения удельной поверхности используется адсорбция паров азота и инертных газов при температуре кипения жидкого азота.
74. Адсорбция на однородной поверхности (8)
Анализ уравнения:Изотерма и уравнение БЭТ:
1. p / ps
A
A C p / ps
p
1 p / ps 1 C 1
ps
A C p / ps
p
p
p
1
1
C
p
p
p
s
s
s
A C ( p / ps ) A Kp
; C Kps
p
1 Kp
1 C
ps
2. Kp
A
1; A
1; A
A Kp
A Kp K p
1 Kp
Уравнение Генри и уравнение
Ленгмюра являются частными
случаями уравнения БЭТ.
75. Адсорбция на однородной поверхности (9)
Линейная форма уравнения БЭТA
Определение констант
A C p / ps
1 p / ps 1 C 1
p
ps
1 C 1 p / ps
p / ps
A 1 p / ps
A C
p / ps
1 C 1 p
A 1 p / ps A C A C ps
1
C 1 1
;
A C A C A
ssp A N A s0
76. Адсорбция на пористых материалах
Основные характеристикипористых материалов
а). Из золя SiO2
Сушка
Золь → Гель →
1. Удельная поверхность
ssp
s
s
s
'
ssp ; ssp
V
m V
Vp
V
100%; П '
Vp
m
Vp
V
Прокалка
→ Адсорбент
Адсорбент с корпускулярной структурой (силикагель)
б). Из порошка (например, оксида металла)
Порошок Al2O3 → Паста
2. Пористость
П
Ксерогель
П
3. Радиус (размер) пор rp
(распределение пор по размерам)
Получение пористых материалов
I. В качестве исходного материала используется вещество в высокодисперсном
состоянии (золь, порошок и др.).
Формовка
→
Гранулы
Сушка
→
Прокалка
→ Пористый материал
в). Из золя алюмосиликата
Кристаллизация
Золь → Гель → → → Адсорбент с кристаллической структурой
Пример: цеолиты, поры 0,4-1,2 нм;
Na2O∙xSiO2∙yAl2O3∙nH2O
II. В качестве исходного используется непористый материал.
а). Никель Рэнея (губчатая структура);
б). Активированный уголь (губчатая струк-ра)
77. Классификация пор по Дубинину
Макропорыrp 200 nm
1. Уравнение Генри
A K c
2. Уравнение Ленгмюра
ПОРЫ
Мезопоры
2 rp 200 nm
Теория капиллярной
конденсации
ln
Kc
A A
1 Kc
3. Уравнение БЭТ
A
A C ( p / ps )
(1 p / p s )[1 (C 1) p / ps ]
ps 2 VM cos
p
RTrp
Уравнение Кельвина
Микропоры
rp 2 nm
Теория объемного
заполнения микропор
Дубинина
R nT n
n
ln A ln A0 n ln( ps / p)
E
Обобщенное уравнение
изотермы адсорбции
78. Теория капиллярной конденсации
lnp VM ds
ps
RT dV
ds
2cos
dV
rp
Уравнение капиллярной конденсации Кельвина
(для сферического вогнутого мениска)
ln
ps 2 VM cos
p
RTrp
Капиллярная конденсация возможна при:
1) наличии мезопор;
2) полимолекулярной адсорбции на стенках пор, что ведет к
возникновению пленки жидкости;
3) смачивании жидким адсорбатом стенок пор; θ < 90 ; ln (ps /p) > 0; ps > p.
79. Теория капиллярной конденсации (2)
Форма мезопор и уравнение капиллярной конденсацииЦилиндрические
закрытые
Цилиндрические
открытые
Конические
закрытые
ds
const
dV
ds
const
dV
ds
const
dV
ln
ln
ps 2 VM cos
p
RTrp
Адсорбция и десорбция
ln
ps 2 VM cos
p
RTrp
Адсорбция и десорбция
ps 2 VM cos
p
RTrp
Адсорбция
ln
ps 1 VM cos
p
RTrp
Десорбция
80. Теория капиллярной конденсации (3)
Капиллярно-конденсационный гистерезисРеальные мезопористые тела, как правило, содержат все типы пор разных размеров,
поэтому типичные изотермы адсорбции (1) и десорбции (2) имеют следующий вид:
81. Теория капиллярной конденсации (4)
Кривые распределения пор по размерамИнтегральная и дифференциальная кривые распределения пор по размерам
рассчитываются по изотерме десорбции, поскольку в этом случае форма кривизны
менисков одинакова (сферическая) во всех порах и можно использовать одно и тоже
уравнение:
ln
ps 2 VM cos
pi
RTrpi
rpi
2 VM cos
p
RT ln s
pi
V pi AV
i M
rpi
Интегральная кривая
V p f (rp )
Дифференциальная кривая
dV p
drp
f (rp )
82. Теория капиллярной конденсации (5)
Кривые распределения пор по размерамИнтегральная кривая
Дифференциальная кривая
83. Особенности адсорбции в микропорах
1). размер пор и молекул адсорбатасоизмеримы;
2). наличие «ситового» эффекта;
3). повышенная теплота адсорбции;
4). повышенная селективность адсорбции.
Изотерма адсорбции бензола
на микропористом активном угле.
84. Потенциальная теория Поляни
Данная теория была предложена для термодинамического описания полимолекулярной адсорбции. В соответствии с этой теорией, адсорбат на поверхности адсорбента рассматривается как жидкость, находящаяся в поле действия молекулярных сил адсорбента. За меру интенсивности адсорбционного взаимодействия принятадсорбционный потенциал (ε).
1 моль пара
p
ps
ε
ps
p
V AVM
[Дж/моль]
Жидкий адсорбат
RT ln
Твердый адсорбент
Адсорбционный потенциал представляет собой работу переноса 1 моль пара
адсорбата, находящегося в равновесии с чистым жидким адсорбатом в отсутствие
адсорбента (давление ps), в равновесную с адсорбентом паровую фазу (давление р).
Адсорбционный потенциал является функцией адсорбционного объема V как
меры расстояния от поверхности адсорбента до адсорбированных молекул.
85. Потенциальная теория Поляни (2) и ТОЗМ
На основе изотермы адсорбции A = fT(p) рассчитываетсяхарактеристическая (потенциальная) кривая:
f (V )
Температурная инвариантность
0
T V
- адсорбционный потенциал
не зависит от температуры
A f T ( p)
- получена экспериментально
A f T ( p)
- можно рассчитать
1
2
V A1 VM 1 А2 VM 2
Т1
RT1 ln
Т2
ps1
p
RT2 ln s 2
p1
p2
Аффинность
const - коэффициент аффинности
0 V
0 f (V ) - для стандартного адсорбата
β - коэффициент аффинности
известно
f (V )
и
A f ( p)
для другого адсорбата на этом же адсорбенте
можно рассчитать
RT ln ps p ;
V A VM
86. Теория объемного заполнения микропор Дубинина (2)
Базируется на 2-х функциях и 2-х положениях:p
1. RT ln s
1.
0
p
T
V
2.
0 V
2. V AVM
Используя уравнение распределения Вейбула:
n
n
V V0 exp ; A A0 exp
E
E
Е – характеристическая энергия; n = 1 - 6.
A0
A
E
exp ; 0 e; exp e; E;
A
A
E
E
0 V E0
n
RT p
ln A ln A0 n ln s
E p
n
n
n
n
- обобщенное уравнение теории объемного
заполнения микропор Дубинина.
87. Теория объемоного заполнения микропор Дубинина (3)
Для многих активных углей n = 2 и тогда:2
R 2T 2 ps
R2
ln A ln A0 2 ln ; E E0 ; B 2
E p
E0
2
BT 2 ps
ln A ln A0 2 ln - уравнение Дубинина-Радушкевича
p
BT 2
tg 2 ; A0VM V ' [м3/кг]
88. Адсорбция поверхностно-активных веществ (ПАВ)
Адсорбция поверхностноактивных веществ (ПАВ)89. Адсорбция ПАВ
При адсорбции ПАВ на границераствор – газовая фаза:
g 0,
d
0, 0, c s c
dc
Vs (c s c)
s
Vs c s
A
s
где Vs – объем поверхностного слоя;
cs и c – равновесные концентрации в
поверхностном слое и в объеме раствора;
g - поверхностная активность
d
g
dc c 0
Обозначение молекулы ПАВ:
○------
Правило Дюкло-Траубе:
В гомологическом ряду ПАВ увеличение
длины углеводородного радикала на одну
метиленовую группу (-СН2-) приводит к
возрастанию поверхностной активности
приблизительно в 3,2 раза (для водных
растворов).
gn 1 / gn 3, 2
В общем случае:
gn 1 / gn exp[ Na / ( RT )] const
Для полярных растворителей:
gn 1 / gn 1
Для полярных растворителей:
gn 1 / gn 1
90. Зависимость поверхностного натяжения от концентрации раствора
1. Область низких концентраций:c d
A K c,
, A
RT dc
c d
K c,
RT dc
c
0
0
d RTK dc,
И
d RTK dc
( 0 ) RTK c
0 RTK c
Поверхностная активность определяется
адсорбционной способностью (KГ).
Изотермы адсорбции и поверхностного
натяжения.
d
g
tg RTK
dc c 0
g n 1 K n 1
gn
K n
91. Зависимость поверхностного натяжения от концентрации раствора (2)
2. Область более высоких концентраций:A A
Kc
c d
,
, A
1 Kc
RT dc
c d
Kc
A
RT dc
1 Kc
Kdc
1 Kc
c
Kdc
d A RT
1 Kc
0
0
d A RT
0 A RT ln 1 Kc
0 A RT ln 1 Kc
(уравнение Шишковского)
Изотермы поверхностного натяжения и
адсорбции
0 a ln 1 bc
92. Уравнения состояния поверхностных адсорбционных пленок
1. Область низких концентраций:2. Область более высоких концентраций:
0 A RT ln 1 Kc
0 RTK c, 0 RTK c
0 , K c A, RTA
mol
A 2 ,
m
1
sM
A
m
mol
Kc
1, ln 1 Kc Kc,
2
sM RT , pV RT
где: π – поверхностное давление;
sM – площадь поверхности, занимаемая
одним молем.
Адсорбционная пленка ведет себя как
идеальный двумерный газ.
α и β учитывают межмолекулярные
взаимодействия и собственный размер
молекул (как a и b).
RT
1
A Kc
1 1
1
1
1 1
;
A A A Kc A Kc A A
RT
1 1
sM
A A
(sM ) RT ,
p(V b) RT
3. Область высоких концентраций:
( / sM2 )( sM ) RT
( p a / V 2 )(V b) RT
93. Типы поверхностных пленок и определение их характеристик
Принципиальная схема весов Ленгмюра:1 – кювета; 2, 3 – неподвижная и подвижная
планки; 4 – чашечка для разновесов.
Весы Ленгмюра позволяют измерять
поверхностное давление π как функцию
sM.
1. С11H23COOH; 2. C13H27COOH;
3. C15H31COOH
Изотермы поверхностного давления карбоновых
кислот: 1 - лауриновая; 2 – миристиновая; 3 –
пальмитиновая.
/ N A sM0 / N A 1/ ( A N A ); 0, 205 nm 2
V
M0 A VM A M /
sM
CH 2 0,143(0,154) nm
94. Адсорбционные взаимодействия
Ионообменная адсорбция95. Ионообменная адсорбция
Ионный обмен открыт в 1850 г.(Томсон, Уэй).
Ионный обмен – обмен ионами между
раствором и адсорбентом.
Адсорбенты – иониты (катиониты,
аниониты).
Ионит имеет «каркас» (полимерный),
сшитый ковалентными связями. К каркасу
присоединены функциональные группы –
кислотные или основные.
Ионный обмен (катионов или
анионов) обеспечивает диссоциация
функциональных групп.
Ионит несет отрицательный
(катионит) или положительный (анионит)
заряды, компенсируемые противоионами,
которые и участвуют в ионном обмене.
Классификация ионитов
I. По происхождению
1. Природные (кристаллические алюмосиликаты – шабазит, глауконит и др.; почвенный
гумус).
2. Синтетические (на основе полимеров).
II. По составу
1. Неорганические. 2. Органические.
III. По знаку заряда обмениваемых ионов
1. Катиониты. 2. Аниониты. 3. Амфолиты.
96.
Синтез ионитов(ионообменных смол)
3. Реакция полимеризации (анионит)
1. Реакция поликонденсации (катионит КУ-1)
Смесь фенола и формальдегида – поликонденсация – фенолформальдегидная смола.
Функциональные группы –OH и –SO3H.
2. Реакция полимеризации (катионит КУ-2)
Сополимеризация стирола и дивинилбензола.
Функциональные группы (–SO3H) вводят после
полимеризации.
В анионите – функциональные группы на
основе азота, например, на основе четвертичного аммониевого основания.
Химически более стойкими являются иониты,
полученные по реакции полимери-зации.
97.
Основные физико-химические свойства1. Емкость – способность адсорбировать
определенное количество ионов.
2. Кислотно-основные свойства –
определяются константами диссоциации
функциональных групп.
3. Селективность – способность избирательно
адсорбировать определенные ионы или
группу ионов.
4. Набухаемость – влияет на селективность
адсорбции.
Емкость
Различают:
1. Статическая или полная обменная емкость
(ПОЕ).
2. Динамическая обменная емкость (ДОЕ).
ПОЕ – общее количество ионогенных групп
ионита, выраженное в эквивалентах и
отнесенное к единице массы (или объема)
ионита (у природных – 0,2-0,3 мг-экв/г; у
синтетических – 3-10 мг-экв/г).
ДОЕ – емкость до проскока извлекаемого
(адсорбируемого)
иона;
зависит
от
технологических условий.
98.
Ионообменная колонкаОпределение ПОЕ и ДОЕ
-SO3H + NaCl → -SO3Na + HCl
1. отводная трубка;
2. емкость;
3. стеклянный
стержень;
4. трубка;
5. колонка с ионитом;
6. кран.
с – концентрация адсорбирующегося иона в
растворе, выходящем из колонки; V – объем
раствора, выходящего из колонки.
Площадь ABCDE ~ ПОЕ.
Площадь ABCE ~ ДОЕ.
99.
Кислотно-основные свойстваКатиониты:
1. Сильнокислотные (-SO3H).
2. Слабокислотные (-OH, -COOH).
Аниониты:
1. Сильноосновные (-N(CH3)3Cl).
2. Слабоосновные (-NH2, =NH, ≡N).
Кислотно-основные свойства определяют
рабочий интервал значений рН.
Константа равновесия ионного обмена
z2 M1 z1M 2
K
z1M 2 z2 M1
2-SO3H + Ca2+ ↔ (-SO3)2 + 2H+
z2 = 2; z1 = 1; M 1 = H+; M2 = Ca2+
Термодинамическая и концентрационная
константы равновесия:
a2z1 a1z2
c2z1 c1z2
K a z2 z1 ; K c z2 z1
a1 a2
c1 c2
Константа Никольского:
K
1
z1 z2
c
K'
1
z1
1
z2
2
1
z1
1
c1 c
1
z2
2
c c
100. Электрические явления на поверхностях
Двойной электрический слой101. Двойной электрический слой (ДЭС)
При контакте двух фаз, из которых хотя бы одна является жидкой, намежфазной границе, как правило, возникает двойной электрический слой
(ДЭС), который состоит из двух слоев зарядов противоположного знака.
Механизмы формирования ДЭС:
1. Переход зарядов из одной фазы в другую.
2. Преимущественная адсорбция ионов одного знака заряда из объема одной
из фаз.
3. Ориентирование полярных молекул на межфазной границе.
Правило Фаянса-Панета:
Структуру кристаллической решетки
могут достраивать те ионы, которые
есть в ее составе или изоморфные.
Правило Кёна:
Из двух соприкасающихся фаз положительно заряжается та, которая имеет большую диэлектрическую проницаемость.
102.
Термодинамические уравнения ЛиппманаДля дисперсной системы с ДЭС запишем уравнение, вытекающее из первого и второго начал термодинамики (без учета химической энергии):
dG SdT ds dq
(1)
dG ds dq
При T = const:
(2)
Полный дифференциал энергии Гиббса:
dG ds sd dq qd
(3)
Вычитаем уравнение (2) из уравнения (3): sd qd 0
(4)
Разделим все члены уравнения на площадь поверхностного слоя s:
d
q
q s - первое уравнение Липпмана, где q s - заряд единицы поверхности.
d
s
При самопроизвольном формировании ДЭС знаки заряда и потенциала совпадают
и тогда d / d 0 , то есть формирование ДЭС ведет к снижению поверхностного натяжения. При qs = 0, φ = φ(0), где φ(0) – потенциал нулевого заряда.
103.
Термодинамические уравнения Липпмана (2)Запишем выражение для дифференциальной емкости ДЭС как конденсатора и
подставим в него заряд из первого уравнения Липпмана:
dq
d
C
; qs
d
d
Получаем второе уравнение Липпмана:
d 2
C
d 2
Уравнения Липпмана позволяют рассчитать заряд поверхности и электрическую
емкость ДЭС, если известна зависимость σ = f(φ), называемая электрокапиллярной
кривой.
При адсорбции катионов (потенциалопределяющие ионы):
d d ; qs Fz ; d q s d Fz d
a
RT
ln 0
Fz
Fz asol
- уравнение электродного потенциала Нернста
104.
Уравнение электрокапиллярной кривойЕсли ДЭС представляет собой плоский конденсатор, то:
q
C s ; qs C
Подставим qs в первое уравнение Липпмана и поделим переменные:
d
C ; d C d
d
Интегрируем в пределах от σ до максимального значения σмакс и от φ до точки
нулевого заряда φ(0)
( 0 )
max
2
2 (0)
d C d ; max - C 2 2
max
C 2
2
(0)
- уравнение электрокапиллярной
2
кривой
Проверка уравнения проводилась с использованием
капиллярного электрометра.
105.
Схема капиллярного электрометра1 – капиллярная трубка
с ртутью;
2 – сосуд с ртутью;
3 – шланг;
4 – стакан с раствором
электролита;
5 – сосуд с каломельным
электродом;
6 – реостат;
7 – источник тока
(аккумулятор).
106. Теории строения ДЭС
1. Теория ГельмгольцаСтроение ДЭС подобно строению плоского конденсатора. Один слой зарядов находится на
межфазной поверхности, имеющей потенциал 0.
Ионы, образующие этот слой
называются потенциалопределяющими. Заряд этого слоя компенсируется зарядом второго
слоя ионов, называемых противоионами.
2. Теория Гуи-Чепмена
Все противоионы участвую в тепловом движении, удерживаются возле межфазной
поверхности за счет электростатических сил и образуют диффузный (размытый) слой.
3. Теория Штерна
Одна часть противоионов удерживается у поверхности за счет электростатического и
адсорбционного взаимодействий, образуя адсорбционный слой (слой Гельмгольца). Другая
часть противоионов находится в растворе, примыкающем к поверхности, и образует
диффузный слой (слой Гуи) из-за их участия в тепловом движении.
107.
Теория Гуи-Чепмена1. Концентрация ионов в диффузной части ДЭС на расстоянии х от границы раздела фаз
пропорциональна фактору Больцмана:
cxi c0i e Wx / RT ; Wxi zi F x
где Wxi - работа, необходимая для перемещения 1 моля ионов из объема раствора на
расстояние х от границы раздела фаз; φх - потенциал на расстоянии х, который в
граничных условиях изменяется от φх = φδ (потенциал диффузного слоя) при х = δ до
φх = 0 при х = ∞.
2. При условии, что z+ > 0 и z- < 0, объемная плотность
заряда в диффузном слое равна:
zi F x
x Fzi cxi Fzi c0i exp
RT
i
i
3. Уравнение Пуассона:
2 2 2
2 2 2
x
y
z
0
2
108.
Теория Гуи-Чепмена (2)4. Уравнение Пуассона-Больцмана:
zi F x
2 2 2
1
Fz
c
exp
i 0i
2
2
2
x
y
z
0 i
RT
Решаем уравнение Пуассона-Больцмана при следующих допущениях:
• двойной электрический слой является плоским, то есть пренебрегаем кривизной
поверхности
d 2
2
2
dx
• диэлектрическая проницаемость является одинаковой в растворе и ДЭС;
• ионы представляют собой точечные заряды (не имеют объема);
• при переводе противоионов из объема раствора в ДЭС совершается работа только
против электростатических сил;
• рассматривается случай слабозаряженной поверхности:
zi F
RT
1;
φδ < 25 мВ
109.
Теория Гуи-Чепмена (3)Экспонента может быть разложена в ряд Маклорена:
e y 1 y y 2 / 2! y 3 / 3! ...; e y 1 y; y
1
С учетом этого избавимся от экспоненты в выражении для объемной плотности заряда:
zi F x
F 2c0i zi2
zi F x
zi F x
y
; x Fzi c0i exp
x
Fzi c0i 1
Fzi c0i
RT
i
RT
i
RT
i
i
RT
Так как сумма зарядов в объеме раствора по условиям электронейтральности
равна нулю, то
F2
2F 2 I
1
2
Fz
c
0;
c
z
;
I
c0i zi2 - ионная сила
i i 0i
x
0i i x
x
RT i
RT
2 i
110.
Теория Гуи-Чепмена (4)Уравнение Пуассона-Больцмана принимает вид:
x
d 2
2F 2 I
d 2
2F 2 I
2
2
;
x ;
dx 2
0 0 RT x dx 2
0 RT
Для того, чтобы провести интегрирование, преобразуем полученное уравнение:
d (d dx)
d
dx
d d
d
2
2
2
2 x ; d
dx
d
;
d
x d
x
x
dx
d
d
dx dx
dx
Первое интегрирование:
d
dx
0
d d
1 d 2 x2
2
d
x d ;
dx dx
2
dx
2
0
Извлекаем корень с учетом того, что dφ/dx < 0 :
d
x
dx
2
111.
Теория Гуи-Чепмена (5)Делим переменные и интегрируем второй раз:
d
dx;
x
d
x
dx; ln x ln x
x e ( x ) - уравнение Гуи-Чепмена
x e x
Если расстояние х отсчитывать от начала диффузной
части ДЭС (от слоя Гельмгольца), то
x e x
Для высоких потенциалов и больших расстояний
от поверхности:
zF
1;
RT
zF x
RT
1;
x
4 RT x
e
zF
[exp( zF /( 2RT )] 1
[exp( zF /( 2RT )] 1
При очень высоких потенциалах (φδ > 100 мВ) γ ≈ 1. В этом случае φх не
зависит от потенциала диффузного слоя φδ.
112. Теория Гуи-Чепмена (6)
Толщина диффузного слояx e
x
2F 2 I
2F 2 I
;
; =
0 RT
0 RT
2
1
x e
0 RT
2F 2 I
= e
/ e
Факторы, влияющие на толщину диффузного слоя:
0 RT
2F 2 I
; I
1
coi zi2
2 i
1. ε (влияет на диссоциацию).
2. εT – это произведение может и уменьшаться с ростом температуры.
3. I – зависит не только от концентрации,
но от заряда ионов.
113.
Теория Штерна1. Противоионы образуют два слоя (слой Гельмгольца
и слой Гуи).
2. Учтены собственные размеры ионов – толщина δ
определяется радиусами гидратированных ионов.
3. Учтена специфическая адсорбция ионов в слое
Гельмгольца; ионы удерживаются за счет
электростатических и адсорбционных
взаимодействий.
Ai A i
δ - толщина слоя Гельмгольца;
- потенциал диффузного слоя;
λ - толщина диффузного слоя.
Ki ci
z F
; Ki exp i
1 Ki ci
RT
q Fzi Ai ; qs q q 0
Учет специфической адсорбции в слое Гельмгольца позволил объяснить явление
перезарядки поверхности.
114.
Перезарядка поверхностипри специфической адсорбции
ионов
а – исходное состояние;
б – после введения части электролита;
в – изоэлектрическое состояние;
г – состояние перезарядки поверхности.
115. Перезарядка при химическом взаимодействии ионов
а – исходное состояние;б – после введения части электролита;
в – состояние перезарядки поверхности.
116.
Формулы ДЭС (формулы мицелл)117.
Формулы ДЭС (2)AgI m nAg+ | n - x NO3- |xNO3 AgI m nI | n - x K |xK
SiO2 m n( SiO )| n - x Na |xNa
SiO
n
(
SiOH
)|
n
x
Cl
|
x
Cl
2 m
2
118. Электрокинетические явления
119.
Электрофорез – движение частиц дисперсной фазы под действием приложенногоэлектрического поля. (Рейсс, 1808 г., см. рис. а)
Электроосмос – движение жидкой дисперсионной среды в пористом теле под
действием приложенного электрического поля. (Рейсс, 1808 г., см. рис. б)
а
б
h
+
-
Потенциал седиментации или потенциал Дорна – возникновение разности
потенциалов по высоте столба суспензии, содержащей оседающие частицы. (Дорн,
1878 г)
Потенциал течения (протекания) или потенциал Квинке – возникновение
разности потенциалов, например, по длине капилляра при протекании в нем
дисперсионной среды за счет перепада давления. (Квинке, 1859 г.)
120.
Электрокинетический потенциал или ζ–потенциал (дзетапотенциал) – потенциал, возникающий на плоскости скольженияпри отрыве части диффузного слоя ДЭС.
ζ –потенциал зависит от:
• природы контактирующих фаз
• рН дисперсионной среды
• температуры
• диэлектрической проницаемости среды
• типа электролита
(индифферентный/неиндифферентный)
• ионной силы (концентрации электролита)
x
x l e x e ;
ln ln Bx I
1
0 RT
2F 2 I
121. Вывод уравнения Гельмгольца-Смолуховского (на примере электроосмоса)
1.2.
3.
4.
Ограничения, вводимые при выводе уравнения Гельмгольца-Смолуховского:
Толщина ДЭС значительно меньше радиуса кривизны поверхности твердой фазы r
(радиуса частиц, пор, капилляров).
Слой жидкости, прилегающий к твердой фазе, неподвижен; движение жидкой фазы
ламинарное (при электроосмосе).
Твердая фаза является диэлектриком, а жидкая фаза проводит электрический ток.
Распределение зарядов в ДЭС не зависит от приложенной разницы потенциалов.
Электрическая сила dFel, действующая на слой жидкости
толщиной dx (в расчете на единицу площади поверхности):
d 2
dFel Edq E dx E 0 2 dx
dx
где: dq – заряд слоя жидкости dq; E – напряженность электрического поля; ρ –
объемная плотность заряда, выраженная с использованием уравнения
Пуассона.
Сила трения Ffr и ее дифференциал в соответствии с законом
Ньютона (в расчете на единицу поверхности):
du
d 2u
Ffr ; dFfr 2 dx
dx
dx
где: u – линейная скорость движения жидкости; η – вязкость жидкости.
122. Вывод уравнения Гельмгольца-Смолуховского (2)
При установившемся движении (в стационарном состоянии):dFel dFfr
0 E d 2
d 2u
2
dx
dx 2
èëè
Пределы интегрирования:
1. При x = l, φ = ζ и u = 0; 2. При x = ∞, φ∞ = 0, u∞ = u0, (dφ/dx)∞ = 0, (dφ/dx)∞ = 0
После двойного интегрирования:
u0
0 E
Полученное уравнение справедливо как для электроосмоса, так и для электрофореза.
Расчет ζ-потенциала по скорости электрофореза:
u0
0 E
или
ueph
u0
u
; eph
E
0
ueph - электрофоретическая подвижность
123.
Определение ζ-потенциала методом макроэлектрофореза+
5
3
Схема установки для проведения
макроэлектрофореза.
1 – U-образная трубка; 2 – краны;
3 – электроды; 4 – гайка крепления;
5 – воронка; 6 – зажим; 7 – шланг.
6
ueph
2
4
7
ueph
0
a - смещение границы раздела золь – контактная
V
L
1
a
aL
;
E V
жидкость за время ;
- приложенная разность потенциалов;
- расстояние между электродами.
Дисперсная система должна быть
седиментационно и агрегативно устойчивой.
124.
Эффекты, не учитываемые уравнением Гельмгольца-Смолуховскогодля электрофореза
Электрофоретическое торможение
Обусловлено сопротивлением
движению частицы обратным потоком
противоионов, которые увлекают за
собой жидкость.
При r ~ вводят поправку Гюккеля
– множитель k = 1 ÷ 3/2
u0
k
0 E
Релаксационный эффект
Проявляется в нарушении
симметрии диффузного слоя
вокруг частицы при относительном
движении фаз в противоположные
стороны.
- +--+- --+--+ ++ ++ + +
- + +++ - -+ -++ +- -+ E
Вследствие данных эффектов, экспериментально измеренные значения
электрофоретической подвижности получаются заниженными.
125.
Определение ζ-потенциала методом электроосмосаПереход к объемной скорости электроосмоса v :
v u0 s
E
откуда
0 E s
V
L
; V IR; R
L
s v
IL
I
E
Ls v s v
После подстановки E в выражение для v :
1 - корпус; 2 - штуцеры; 3 - капилляры;
4 - накидная гайка; 5 - мембрана;
6 - втулка; 7 - прокладки из
фильтровальной бумаги;
8 - электроды, подсоединяемые
к источнику постоянного тока;
9 – агар-агаровые электродные мостики;
10 - стаканы с раствором сульфата меди.
v
0 s I
I
v
0 ; v ; при r
s v
v
0 I
s - поперечное сечение всех пор (капилляров);
v - удельная электропроводность жидкой фазы;
I - сила тока;
R - сопротивление;
r - радиус пор мембраны;
- толщина диффузного слоя.
126.
Эффекты, не учитываемые уравнениемГельмгольца-Смолуховского для электроосмоса
Если радиусы пор (капилляров) сопоставимы с толщиной диффузного
слоя, то в уравнение вводят поправку на поверхностную проводимость κs,
которая всегда положительна.
v ( v s )
0 I
Поверхностная проводимость κs – удельная электропроводность в
неподвижной части двойного электрического слоя.
127.
Потенциалы течения и седиментацииПотенциал течения
U
0 p
U - разность потенциалов (потенциал течения);
- удельная электропроводность жидкой фазы;
p - перепад давления.
Потенциал седиментации
E
0cv ( 0 ) g
E - напряженность электрического поля;
cv - объемная доля дисперсной фазы;
- плотность частиц;
0- плотность дисперсионной среды.
128. Кинетические свойства дисперсных систем
Седиментация129.
Кинетические свойстваСедиментация в поле тяжести
Седиментация – оседание частиц дисперсной фазы.
Обратная седиментация – всплывание частиц дисперсной фазы.
На каждую частицу в дисперсной системе действует сила тяжести
(гравитационная сила) и подъемная сила Архимеда:
FA V 0 g
Fg mg V g ;
Равнодействующая сила, вызывающая седиментацию:
Если ρ > ρ0, то Fs > 0
Fs Fg FA V ( 0 ) g
частица оседает
При ламинарном режиме движения сила трения равна:
Если ρ < ρ0, то Fs < 0
F fr Bu
частица всплывает
Сила, действующая на частицу во время движения:
F Fs Ffr Vg ( 0 ) Bu
При постоянной скорости движения частицы:
V ( 0 ) g
F 0; u
B
9 u
2 g ( 0 ) r 2
r
u
2 0 g
Для сферической частицы в соответствии
9
с законом Стокса:
B 6 r
130.
Условия соблюдения закона Стокса1. Частицы осаждаются независимо друг от друга (разбавленные дисперсные
системы).
2. Частицы имеют сферическую форму. Если частицы неправильной формы,
то необходимо вводить фактор формы или использовать эквивалентный
радиус частицы.
3. Движение частиц происходит в ламинарном режиме.
4. В системе присутствует только внутреннее (вязкое) трение.
5. Размеры частиц лежат в интервале от 1 до 100 мкм.
Способность к седиментации характеризуют
константой седиментации:
Для сферических частиц:
Ss
Ss
4
3
mrel V ( 0 ) U
B
B
g
( 0 )r 3 2( 0 )r 2
6 r
9
131.
Седиментационный анализПринцип седиментационного
анализа состоит в измерении
скорости осаждения частиц,
обычно, в жидкой среде.
На практике седиментационный анализ сводится к
получению зависимости массы осевших частиц от
времени (кривая седиментации) m = f(τ) и ее
математической обработке.
Монодисперсная система
Бидисперсная система
ri
9 h
2 0 g i
m1 r1
m
mmax
m
9 u
u ; tg = max u; r
2 0 g
h
h
132.
Седиментационный анализ (2)Полидисперсная система
m1 r1; m1 m2 r1 , r2 ; m1 m2 m3 r1 r3
Общая масса частиц, осевших к моменту
времени i:
dm
m i mi
i - уравнение Одена
d
mi ri rmax
m1
100% Q1 ;
mmax
m2
2 u2 r2 ;
100% Q2 ;
mmax
………………………………
1 u1 r1 ;
Q f r - интегральная кривая
распределения частиц
по размерам (по радиусам)
133.
Интегральная и дифференциальная кривые распределенияИнтегральная кривая
m
Qi i 100%
mmax
di
Дифференциальная кривая
dQ
Fi
dd d d i
18 h
0 g i
Q1 d1 dmax
Q2 d 2 d max
Q Q2 Q1 d2 d1
dn – наивероятнейший диаметр
134.
Аналитическая обработка кривой седиментацииАналитический метод Н.Н. Цюрупы
m
Q
0
Qm
Qm
Qm - уравнение кривой
седиментации
При , Q Qm (количество частиц,
которое осядет за бесконечно большое время.
При = 0 («половинное время осаждения»),
Q = Qm/2.
dQ i
dQ i
Q
Q
Q i Qi
i
i
i
i;
d i
d
Q Qm
0
i
di
2
18 h
0 g i
i
d 02
Qi Qm
Qm i2 - уравнение интегральной
Qm 2
2
i 0
d 0 di
кривой распределения
dQi
di d04
8Qm
8Qm
2
Fi
8Qm 2
(1
)
i - уравнение дифференциальной
i
i
i
2 3
dd
(d 0 di )
d0
d0
кривой распределения
135.
Аналитическая обработка кривой седиментацииd0
18 h
; d min d0 (0,1 Qm 1)1/2 ; dн d0 2, 24; d max 3d0
0 g 0
PI
d max
3
d min (0,1 Qm 1)1/2
- степень полидисперсности
Параметры и i при разных соотношениях di/d0
di/d0
i2
i
di/d0
i2
i
di/d0
i2
i
0,1
0,980
0,097
0,6
0,541
0,239
1,4
0,114
0,054
0,2
0,925
0,177
0,7
0,451
0,209
1,6
0,079
0,036
0,3
0,842
0,232
0,8
0,372
0,182
1,8
0,056
0,023
0,4
0,743
0,255
0,9
0,305
0,155
2,0
0,040
0,016
0,45
0,692
0,260
1,0
0,250
0,125
2,5
0,019
0,007
0,5
0,640
0,256
1,2
0,168
0,083
3,0
0,010
0,003
136.
Сравнение методов обработки кривых седиментацииМетод касательных
Графический метод.
Требуется большое количество
экспериментальных точек на
кривой седиментации.
Необходимы точные графические
построения.
Позволяет построить кривые
распределения для систем с
нелогарифмическим
мономодальным, а также с
бимодальным распределением
частиц по размерам.
Метод Н.Н. Цюрупы
Аналитический метод.
Для построения кривых
распределения требуется меньшее
количество экспериментальных
точек.
Метод прост и нетрудоемок.
Расчет является корректным
только для систем, в которых
распределение частиц по размерам
близко к логарифмически
нормальному.
137.
Средние размеры частиц и функции распределенияСреднечисленный диаметр
n
d n i di f ni di
i ni
i
i
Среднеповерхностный диаметр
ni di2
ds
d f si di
2 i
n
d
i i i
i
i
Среднемассовый (среднеобъемный) диаметр
ni di3
dw
d f wi di
3 i
i ni di
i
i
Дифференциальные кривые численного (1),
Степень полидисперсности и индекс вариации
поверхностного (2) и массового (3)
dn
распределения частиц по размерам.
Нормальное распределение (Гаусса)
2
100
1 d d
FG d
exp
2
2
; K n 100%
dw
dn
Логарифмически нормальное распределение
1 ln d ln d 2
1
g
FG ln d
exp
ln
2
ln g 2
g
138.
Экспериментальные методы в седиментационном анализеПипеточный
прибор
Седиментометр
Вигнера
Схема установки с торсионными весами
4
5
6
3
2
1
7
8
1 – арретир; 2 – стрелка весов; 3 – риска; 4 – рычаг
уравновешивания; 5 – стрелка циферблата;
6 – крючок для чашки; 7 – цилиндр; 8 – чашка.
139.
Седиментация в центробежном полеДля осуществления седиментации
ультрамикрогетерогенных систем
и систем с малой разностью – 0
Центробежная сила:
mrel u 2
Fc mrel a
mrel 2 R
R
dx
При равновесии между
B
mrel 2 x
d
центробежной силой и силой трения:
Разделим переменные и проинтегрируем
от начального расстояния х0 до х и,
соответственно, от τ = 0 до τ:
r
9 ln(
dx mrel 2
2
d
S
d
s
0 x
B 0
0
x
x mrel 2
ln
S s 2
x0
B
Для частиц сферической формы,
подчиняющихся закону Стокса:
x 2r 2 ( 0 ) 2
ln
;
x0
9
Пренебрегаем силой
тяжести, поскольку
Fc >> Fs
x
x0
)
2( 0 ) 2
x x0 exp( S s 2 )
140. Кинетические свойства дисперсных систем
Молекулярно-кинетическиесвойства
141.
Природа броуновского движенияБроуновское движение – участие частиц дисперсной фазы
ультрамикрогетерогенных систем в тепловом движении.
Является следствием теплового движения молекул дисперсионной среды и прямым
отражением законов статистики.
Броуновское движение – следствие случайных микроотклонений (флуктуаций),
эффект которых возрастает с уменьшением размеров системы, и наглядное
проявление отклонений от второго закона термодинамики в микросистемах.
Число ударов велико
и результирующий
импульс равен нулю.
Частицы с большой
массой обладают
инерционностью и
мало чувствительны
к ударам молекул.
Большая частица
Число ударов мало,
велика вероятность
неравномерного
распределения
импульсов.
Частица приобретает
колебательное,
поступательное
Маленькая частица и вращательное
движение.
142.
Среднеквадратичный сдвиг при броуновском движенииКвадрат среднего расстояния, проходимого частицей за любой промежуток
2
2
2
2
времени (трехмерное пространство):
l x y z
Под микроскопом наблюдают проекцию
смещения частицы на плоскость:
2
2
l x y
2
2
2
2
2
При равновероятных отклонениях частицы: x y 2 ; l 2 ;
2
1
2l
2
- средний сдвиг по выбранному направлению (по x или y)
Для экспериментального определения
используют среднеквадратичные
расстояния, проходимые частицей:
l12 l22 l32 ... ln2
l
n
2
n – число отрезков ломаной
кривой движения или число
измерений расстояния,
проходимого частицей
через равные промежутки
времени.
143.
Закон Эйнштейна-Смолуховского«Если частицы участвуют в тепловом движении, то
для них должны быть справедливы законы диффузии»
Возьмем трубку с поперечным сечением s, наполненную золем, концентрация
частиц которого уменьшается слева направо. Стрелкой отмечено направление
диффузии частиц:
Количество дисперсной фазы, которое за время τ
переместится из объема 1 вправо: Q1 1 2 1 s
Q2 1 2 2 s
Из объема 2 влево:
Поскольку │Q1│>│Q2│ (ν1 > ν2), то суммарное
количество перенесенного вещества через
плоскость MN вправо равно:
Q 1 2 1 s 1 2 2 s
В пределе: lim
2 ( 1 2 ) s
1
2
2
1 2
d
d
0.
при
этом
в
направлении
диффузии:
;
dx
dx
1 2
0
1
s
144.
Закон Эйнштейна-Смолуховского (2)d
d
s. В соответствии с первым законом Фика: Q D
s .
dx
dx
2 d
d
Приравняв правые части этих уравнений: 1 2
s D
s ,
dx
dx
Тогда: Q 1 2
2
получаем закон Эйнштейна-Смолуховского:
Согласно уравнению Эйнштейна:
где В – коэффициент трения
D
2
2 D
kBT
RT
;
B
N AB
2
Если движение частиц подчиняется закону Стокса:
B 6 r;
2
kBT
3 r
2kBT
2 RT
B
N AB
145.
Экспериментальная проверка законаЭйнштейна-Смолуховского
Расчет известных констант, таких как число Авогадро и заряд электрона,
исходя из экспериментальных данных, которые обрабатывали, используя
закон Эйнштейна-Смолуховского
• Зеддиг (1908) – связь среднего сдвига с температурой.
• Сведберг (1909) – измерение среднего сдвига частиц золота в
зависимости от времени и вязкости среды.
• де Бройль (1909) – измерение скорости движения частиц табачного
дыма в горизонтальном электрическом поле и среднего сдвига при
броуновском движении.
• Милликен (1910) – исследование поведения аэрозолей в вертикальном
электрическом поле.
• Перрен (1910) – определение числа Авогадро при исследовании
броуновского движения коллоидных частиц гуммигута в воде.
146.
Следствия из теории броуновского движенияУльтрамикрогетерогенные системы должны подчиняться тем же законам
молекулярно-кинетической теории, каким следуют молекулярные системы
(газы и растворы).
Величины, которые можно
рассчитать на основе МКТ:
1. Средняя скорость движения частицы.
2. Энергия коллоидной частицы.
3. Размер частиц дисперсной фазы.
4. Молекулярная масса макромолекул
полимеров.
Для аэрозолей справедливо
где N – число частиц аэрозоле.
pV
D
N
RT
NA
kBT
6 r
mD
k BT
ln( x x 0 ) mD
2
kBT
Ss
Необходимо учитывать, что
для ультрамикрогетерогенных
систем правило фаз Гиббса
имеет вид F=K-Ф+3
147.
Седиментационно-диффузионное равновесиеОседание частиц в дисперсной системе, представляющей собой статистическое
множество частиц, приводит к возникновению градиента концентрации.
Этот градиент концентрации вызывает диффузионный поток, направленный
снизу вверх, который равен:
kBT d
Q
d
idif
s
D
dx
B
dx
Седиментационный поток, (при
постоянной скорости движения частицы)
m g
Vg ( 0 )
is u rel
направленный сверху вниз, равен:
B
B
idif
is
kBT d
k BT
d
mrel g dx
Vg ( 0 ) dx
Характер поведения частиц определяется их размером и плотностями частиц и среды
При d > 10 мкм, idif<<is – можно
не учитывать диффузию частиц
При d < 1 мкм, idif >> is – можно
пренебречь седиментацией частиц
.
148.
Седиментационно-диффузионное равновесие (2)Седиментационно-диффузионное равновесие – состояние системы, когда
седиментационный поток равен диффузионному потоку.
idif
k T d
Q
d
D
B
;
s
dx
B dx
Приравняем потоки, заменив
x на h (расстояние по высоте):
Разделим переменные:
is u
k BT
d
mrel g
Vg ( 0 )
B
B
d
mrel g V ( 0 ) g
dh
mrel g
V ( 0 ) g
dh
dh
k BT
k BT
Проинтегрируем в пределах от ν0 до νh и, соответственно, от h = 0 до h:
h
vh
mrel gh
V ( 0 ) g
V ( 0 ) g
d
kBT 0 dh; ln 0 kBT kBT h
h
0
mот gh
V ( 0 ) gh
exp
0
k
T
k
T
B
B
h 0 exp
уравнение Лапласа или
гипсометрический закон
149.
Седиментационная устойчивость дисперсных системКинетическая
седиментационная устойчивость
(KSS)
Величина, обратная константе
седиментации.
Измеряется в обратных сведбергах
(обр. сведберг = 1013 с).
Обеспечивается
гидродинамическими факторами
(вязкостью и плотностью среды;
плотностью и размером частиц).
KSS
1
B
9
2
S s mrel 2r ( 0 )
Термодинамическая
седиментационная устойчивость
(TSS)
Мерой TSS является
гипсометрическая высота he
(высота, на которой концентрация
частиц уменьшается в е раз).
Обусловлена статистическими
законами диффузии и связана с
седиментационно-диффузионным
равновесием. Зависит от
температуры, но не зависит от
вязкости среды.
he
k BT
k BT
mrel g V ( 0 ) g
150. Оптические свойства дисперсных систем
151.
Оптические свойства дисперсных системЭлектромагнитное излучение
(световой пучок)
Система с жидкой
дисперсионной средой
Дифракция
Преломление
(рефракция)
Рассеяние
(эффект Тиндаля)
Поглощение
152.
Рассеяние света в дисперсных системахЭффект Тиндаля – рассеяние света, обусловленное наличием
неоднородностей (частиц дисперсной фазы).
Возможно при условиях:
1. Расстояние между частицами дисперсной фазы больше, чем длина
волны.
2. Размеры частиц дисперсной фазы меньше, чем длина волны.
153.
Рассеяние света в дисперсных системах (2)Статическое (упругое)
светорассеяние
Динамическое (квазиупругое)
светорассеяние
Используются:
1. Теория Рэлея (1871 г) (при d < λ/20).
2. Теория Рэлея–Ганса-Дебая при
λ/20 < d < λ.
3. Теория Ми при d ~ λ.
Измеряется усредненная во времени
общая интенсивность рассеянного света, как функция угла рассеяния.
Определяют массу и характерный
линейный размер частиц, а также по
угловой зависимости интенсивности
можно получить информацию о форме
и внутренней структуре частиц.
Два варианта метода:
1. Метод квазиупругого рассеяния основан на анализе спектра рассеянного света по сравнению со спектром
источника (эффект Доплера).
2. Метод фотон-корреляционной
спектроскопии – основан на измерении автокорреляционной функции
интенсивности рассеянного света.
Определяют коэффициенты диффузии частиц, размер частиц и распределение по размерам.
154.
Теория Рэлея1.
2.
3.
4.
Теория Рэлея используется при следующих условиях:
Дисперсная фаза является диэлектриком. Частицы сферические.
Вторичным рассеянием можно пренебречь (частицы находятся далеко
друг от друга). Используется неполяризованный свет.
Размер частиц не превышает 0,05λ длины волны падающего света.
Коэффициент преломления дисперсной фазы близок к единице.
Уравнение Рэлея:
n12 n02
9 2 V 2
2
I
F 4 2 (1 cos ) I 0 ; F 2
2
2
R
n1 2n0
cV
V 2
I sc 24 F 4 I 0 24 3 F V 4 I 0 ;
3
2
I sc
cV
24 3 F V 4
I0
155.
Теория Рэлея (2)Турбидиметрия
Измерение оптической плотности
исследуемой системы.
D lg
I0
1
l
I t 2,3
Закон Бугера-Ламберта-Бера
Схема
фотоэлектрокалориметра:
1 – источник света;
2 – зеркала;
3 – кювета с исследуемой
системой и кювета
сравнения;
4 – призмы.
Нефелометрия
Измерение интенсивности
рассеянного света как функции
угла рассеяния.
cV
V 2
I sc 24 F 4 I 0 24 3 F V 4 I 0
3
Уравнение Рэлея
Схема
нефелометра:
1 – источник света;
2 – зеркала;
3 – кювета
с исследуемой системой
и кювета сравнения;
4- призмы;
5 – подвижные экраны.
156.
Турбидиметрический методОслабление интенсивности света за счет
рассеяния при прохождении пути dx:
dI Idx
- коэффициент пропорциональности,
характеризующий способность системы
рассеивать свет (мутность).
Проинтегрируем в пределах от I0 до Iп и соответственно от х = 0 до толщины слоя l:
It
l
dI
I I 0 dx; ln It ln I0 l; It I 0 exp l
0
I
I
l
2,3D
ln 0 l; 2,3lg 0 2,3D l; D
; =
2,3
l
It
It
I
Из баланса: It I 0 I sc ; делим на I0 и логарифмируем: 2,3D ln 1 sc
I0
I sc I sc' l
2,3D
При I sc I 0 , 2,3D
l;
I0
I0
l
157.
Определение размеров частиц турбидиметрическим методом (метод Рэлея)1.
2.
3.
4.
Условия применения метода:
Ослабление интенсивности света происходит только за счет рассеяния.
Отсутствие поглощения и вторичного светорассеяния.
Частицы являются диэлектриком.
Диаметр частиц не превышает 0,05λ.
2
cV
2,3D
3 V
24 F 4 I 0 24 3 F V 4 I 0 ;
l
При V = const,
(размер частиц)
При cV = const,
(объемная
концентрация золя)
D1 1 cV 1
D2 2 cV 2
D1 V1 d13
D2 V2 d 23
Определение радиуса частиц:
1/3
4
I sc
cV V
4 3
3
24 F 4 ; V r ; r
r
;
lim
;
c 0
4
4
I0
3
32
F
c
32
c
F
V 0
cV 0 V cV
V
4
1/3
158.
Определение размеров частиц турбидиметрическим методом (метод Геллера)Условия применения:
1. Падение интенсивности света происходит только за счет рассеяния.
2. Показатели преломления частиц и среды различаются незначительно.
3. Диаметр частиц лежит в интервале от 0,05λ до 0,33λ.
D k m
Z
8 r
av
av
;
vac.max vac.min
2n0
m
Z
m
Z
3,812
3,686
3,573
3,436
3,284
3,121
2,960
2,0
2,5
3,0
3,5
4,0
4,5
5,0
2,807
2,657
2,533
2,457
2,379
2,329
-
5.5
6,0
6,5
7,0
7,5
8,0
-
159.
Определение молекулярной массы полимеров нефелометрическим методом(метод Дебая)
Метод применим для разбавленных растворов гибкоцепных полимеров, в
предположении, что рассеивающими центрами являются сами макромолекулы, которые не взаимодействуют между собой.
Hc
1
2 A2 c
M
Уравнение Дебая
32 3n02 (n n0 ) / c
2
H
3 4 vac N A
Мицеллярная масса ПАВ
Число агрегации
H (c KKM )
1
2 A2 (c KKM );
- KKM
M mic
m M mic M
Метод является абсолютным, не требует калибровки. Позволяет определить
среднеобъемное (массовое) значение массы (или размера) частицы, оценить
форму и конформацию макромолекул полимера.
160.
Методы динамического (квазиупругого) светорассеянияАнализ спектра рассеянного света по
сравнению со спектром источника
Спектр рассеянного света представляет
собой пик, описываемый уравнением
распределения Лоренца.
1/2
Dq ; q
2
4 n0
0
Фотон-корреляционная
спектроскопия
Автокорреляционная функция интенсивности рассеянного света:
sin
2
G( ) I (t ) I (t )
Уширение спектра рассеянного света
(эффект Доплера)
ω0 – частота
источника
излучения
2
G( )
A
B
exp
2
I
c
c
kБT
k БT
1
;
D
;
D
Dq 2
B
6 r
161.
Метод фотон-корреляционной спектроскопииСхема спектрометра динамического рассеяния света
(1) He-Ne лазер; (3) фокусирующий узел; (5) оптическая скамья;
(6) жесткое основание; (7) термостат; (8) адаптер кювет;
(10) прецизионный гониометр; (11) поворотная консоль
гониометра; (12) сменная диафрагма выбора апертуры;
(13) приемная оптическая система; (14) фотоприемный блок;
(15) фотоумножитель, работающий в режиме счета фотонов,
быстрый усилитель-дискриминатор
www. photocor.ru
162.
Метод фотон-корреляционной спектроскопии (2)c
1
;
2
Dq
D
kBT
6 r
163.
Световая и электронная микроскопияВизуальный анализ – размеры частиц не менее 1-5 мм
Оптическая микроскопия
Размеры частиц ≥ 0,5 мкм.
При использовании иммерсионных
препаратов и источников света с
более короткими длинами волн
(УФ-диапазон) можно исследовать
образцы с размерами частиц порядка
0,1 мкм.
d
k
n sin
Электронная микроскопия
Размеры частиц 1нм – 5 мкм
(увеличение от 5 000 до 500 000
диаметров образца).
Разность потенциалов от 30 до 100 кВ.
Длина волны электронов 0,54.10-2 нм
(при разности потенциалов 50 кВ)
1,23
h
; 1/ 2
U
mv
164.
Световая и электронная микроскопия (2)Схема хода лучей в оптическом (а)
и электронном (б) микроскопах:
1 – источник света;
2 – конденсорные линзы;
3 – исследуемый объект;
4 – линзы объектива;
5 – промежуточное изображение;
6 – проекционные линзы (окуляр);
7 – конечное изображение;
8 – фотопластинки;
9 – катод электронной пушки;
10 – анод электронной пушки.
165.
Световая и электронная микроскопия (3)Анализ дисперсности частиц
• полуколичественный метод сравнения
• метод счета
Для сферы
радиуса r:
r 3
3m
4 n
Для куба с
размером ребра l:
l
3
m
n
Требования к препарату порошка или суспензии:
• определенное количество частиц (контуры изображения частиц
не накладываются друг на друга, но проба является представительной);
• частицы находятся в одной оптической плоскости;
• препарат готовят из седиментационно устойчивой системы.
166.
Световая и электронная микроскопия (3)Просвечивающая электронная
микроскопия (ПЭМ, ТЕМ)
Двумерное представление реальной
структуры.
Определение размеров и формы
единичных частиц и расчет
распределения частиц по размерам.
Сканирующая электронная
микроскопия (СЭМ, SEM)
Трехмерное представление структуры.
Разрешающая способность до 1 нм.
Определение размеров, формы и
структуры частиц, а также рельефа
поверхности.
167.
УльтрамикроскопияОсвещение объекта
Сбоку.
Ультрамикроскопия.
Частицы от 2-3 нм.
Сверху или снизу.
Обычная микроскопия.
Частицы от 0,5 мкм.
Расчет размеров частиц
Для сферы
радиуса r:
r
3
3c
4 v
с – массовая концентрация системы;
v – частичная концентрация системы;
х – расстояние между частицами.
Для куба с
размером ребра l:
cx
l
c
l 3
c
v
168.
Схема щелевого ультрамикроскопаСхема щелевого ультрамикроскопа
1 – световой поток;
2 – щелевая диафрагма;
3 – фокусирующая линза;
4 – кювета с исследуемым золем;
5 – объектив; 6-окуляр.
Ход лучей в конденсоре темного поля
1 – световой поток;
2 – центральная диафрагма;
3 – плоско-выпуклые линзы;
4 – кювета с исследуемым золем.
169. Агрегативная устойчивость и коагуляция дисперсных систем
170.
Общие вопросы устойчивостиУстойчивость дисперсных систем – постоянство их свойств во времени.
Основными свойствами являются дисперсность, распределение частиц
дисперсной фазы по объему и межчастичные взаимодействия.
Устойчивость
Седиментационная
Устойчивость к осаждению
(отсутствие осаждения)
Кинетическая
Агрегативная
Агрегативная
устойчивость
Устойчивость к агрегации
(отсутствие агрегации)
Термодинамическая
171. Факторы седиментационной устойчивости
Кинетическая седиментационная устойчивость:1
m 2r 0
9
KSS ; C
; KSS 2
C
B
9
2r 0
2
, r , 0
Термодинамическая седиментационная устойчивость:
k BT ln
h
mg
c0
ch
;
с0
kT
k BT
e, he B
сh
mg 4 / 3 r 3 0 g
, r , 0 , T
172.
Классификация дисперсных систем по РебиндеруДисперсные системы
Лиофильные
Gs s
Лиофобные
Самопроизвольное образование
гетерогенной свободнодисперсной
системы (самопроизвольное
диспергирование одной из фаз)
Принудительное образование
гетерогенной свободнодисперсной
системы (образование в результате
диспергирования и конденсации с
пересыщением)
Крайне низкая Gs.
Термодинамически устойчивы.
Избыток поверхностной энергии.
Характерны процессы, приводящие
к снижению Gs.
173.
При образовании лиофильных дисперсных систем ΔG<0:G H T S ;
H T S 0;
H T S
Изменение энтальпии характеризует межфазное взаимодействие, в результате
которого снижается межфазное натяжение.
Остаточная поверхностная энергия компенсируется энтропийной составляющей, что возможно только для систем, частицы которых способны к тепловому
(броуновскому) движению.
Условие термодинамической агрегативной устойчивости дисперсной системы:
G
0;
ds
G
0
dr
174.
k BTcr 2
a
cr от 10-4 до 1 мДж/м2
Критерий Ребиндера-Щукина
cr - критическое межфазное натяжение,
при котором обеспечивается термодинамическая устойчивость дисперсных систем.
Лиофильные системы:
межфазное натяжение ≤ cr.
cr a k BT ; G
2
Лиофобные системы:
межфазное натяжение > cr.
s
cr a ; Ekin
2
k BT
Фактически, критерий Ребиндера-Щукина устанавливает определенное
соотношение между поверхностной и кинетической энергией частиц.
175. Агрегативная устойчивость и коагуляция дисперсных систем
Растворы ПАВ как лиофильныедисперсные системы
176. Лиофильные дисперсные системы
Особенности строения молекул ПАВМолекула ПАВ имеет дифильное строение и состоит из полярной
(функциональной) группы и углеводородного радикала:
Гидрофобный радикал
Гидрофильная группа
Классификация ПАВ
По химическому строению
Ионные
Неионные
По коллоидно-химическим свойствам
Истинно растворимые
Коллоидные
177. Классификация ПАВ (продолжение)
ИонныеАнионные
Неионные ПАВ:
Амфотерные Катионные
Анионные ПАВ:
а) карбоновые кислоты и их соли –
RCOOH, RCOOM (M-катион);
б) алкилсульфаты ROSO2OM;
в) алкиларилсульфонаты RArSO2OM;
г) др. классы ПАВ, содержащие
поверхностноактивный анионю
Катионные ПАВ:
а) соли алифатических и ароматических аминов;
б) соли алкилзамещенных четвертичных аммониевых оснований
ROH+nH2C
CH2
O
Коллоидные ПАВ – все типы ПАВ,
способные к мицеллообразованию при
достижении ККМ.
Истинно растворимые ПАВ – ни при
каких концентрациях не образуют мицелл
Амфотерные ПАВ:
ОН-
RO(OCH2CH2)nH
Н+
RNH(CH2)nCOO- RNH(CH2)nCOOH RN+H2(CH2)nCOOH
178. Мицеллообразование в растворах ПАВ. Солюбилизация
Строение мицелл (схемы)Изменение формы прямых мицелл
с ростом концентрации ПАВ
а
Прямые мицеллы:
полярные растворители; числа агрегации 50-500;
ΔH < TΔS; ΔS > 0,
ΔH ~ 0.
б
Обратные мицеллы:
неполярные растворители; числа агрегации 3-40;
водородные связи;
ΔH < TΔS; ΔH < 0.
ККМ – критическая концентрация
мицеллобразования.
в
Мицеллы сферические (а), дискообразные (б) и
цилиндрические (в).
Солюбилизация – явление растворения веществ
в мицеллах ПАВ
179. Элементы термодинамики мицеллообразования
Согласно закону действия масс,процесс мицеллообразования можно
представить так:
mK nR
M ( n m)
Константа равновесия равна:
a
c
K m M n m Mn m M n
aK aR cK cR_ K R
Энергия Гиббса, приходящаяся на 1
моль ПАВ, составит:
RT
GM
ln K
n
RT
RT
RT
GM0 [ ln aM
ln(cKm cRn )
ln m M n ]
n
n
n K R
Принимая, что cK cR KKM ; aM 1
можно записать:
GM0
RT
m
ln KKM m n (1 ) RT ln KKM
n
n
0
ln K
m d ln KKM H M
1
T
dT
RT 2
n
H M0
m
const
1 ln KKM
RT
n
H M0 GM0
G H T S ; S
T
0
M
S (1
0
M
0
M
0
M
m
ln KKM
) R[ln KKM T (
)m ]
n
T
1. Неионное ПАВ: m = 0.
2. Ионное ПАВ, полная диссоциация: m = 0.
3. Ионное ПАВ, полная ассоциация в мицелле,
но полная диссоциация в растворе: m = n.
4. Ионное ПАВ, реальный случай; 0,6<m/n<0,9.
180. Методы определения ККМ
Все методы определения ККМ базируются на анализе зависимости какоголибо свойства раствора ПАВ от егоконцентрации.
Зависимость удельной электропроводности
раствора ионного ПАВ от концентрации.
τ – мутность; n – коэффициент преломления; π – осмотическое давление; λ – эквивалентная электропроводность; σ – поверхностное натяжение.
ККМ2 соответствует концентрации, при
которой меняется форма мицелл.
181.
Факторы, влияющие навеличину ККМ
Определение мицеллярной
массы методом Дебая
длина углеводородного радикала;
R
KKM
RT ln KKM a b n
характер полярной группы
(ионная или неионная);
температура;
введение неэлектролитов;
введение индифферентных
электролитов:
RT ln KKM a b n k ln c
H (c KKM )
1
2 A2 (c KKM )
KKM
МM
182. Агрегативная устойчивость и коагуляция дисперсных систем
Лиофобные системы183.
Лиофобные системыПроцессы, которые могут протекать в дисперсных системах
184.
Снижение Gs за счет уменьшения площади межфазной поверхности sПроцессы укрупнения частиц
Изотермическая перегонка
(перенос вещества от мелких
частиц к крупным)
Коалесценция – слияние частиц
(характерно для капель эмульсий)
Коагуляция
(потеря агрегативной устойчивости
из-за слипания или слияния частиц)
Гетерокоагуляция – слипание
частиц различной природы
Флокуляция – образование агрегатов
из частиц, разделенных прослойками среды
(например, в присутствии полимеров)
Адагуляция – адгезионное взаимодействие
частиц дисперсной фазы с макроповерхностью
185.
Факторы агрегативной устойчивостиЛиофобная
дисперсная
система,
будучи термодинамически неустойчивой,
может быть кинетически устойчивой
благодаря наличию
энергетического
барьера
между частицами (барьера
отталкивания).
Из теории бинарных столкновений:
E
d
2
Pk exp
d
kBT
1. Быстрая (диффузионная) коагуляция:
P = 1, ΔЕ = 0.
2. Медленная (барьерная) коагуляция:
ΔЕ ≠ 0.
Все факторы, ведущие к снижению
межфазного натяжения и возникновению
энергетического (потенциального) барьера, являются факторами устойчивости.
Факторы устойчивости:
1. Электростатический (ионносольватный).
2. Адсорбционно-сольватный
3. Структурно-механический
4. Энтропийный
5. Гидродинамический
Агрегативная устойчивость реальных
систем обеспечивается, как правило,
несколькими факторами одновременно.
186.
Кинетика коагуляции по СмолуховскомуПредполагается, что при коагуляции происходит взаимодействие только двух
частиц, что позволяет применить для описания кинетики коагуляции теорию бимолекулярных химических реакций. Так как рассматривается быстрая коагуляция в монодисперсной системе, то для расчета скорости коагуляции надо найти общее число
столкновений частиц в единице объема.
Выделяем одну центральную m-мерную частицу и записываем выражение для
диффузионного стационарного потока n-мерных частиц, средняя концентрация
которых в системе равна n , через сферическую поверхность с расстояний x от центра
m-мерной частицы (в соответствии с первым законом Фика):
d n
d
s Dnm n 4 x 2
dx
dx
где Dnm – коэффициент диффузии движущейся центральной частицы, который равен
сумме коэффициентов диффузии сталкивающихся n- и m-мерной частиц:
I Dnm
( n m )2 n2 2 n m m2
Dnm
Dn Dm
2
2
2
2
187.
Кинетика коагуляции по Смолуховскому (2)Пусть в начальный момент времени в единице объема находится суммарное число
n-мерных частиц, равное n . При этом расстояние между ними х = ∞.
При столкновении x = Rnm (сумма радиусов частиц), а в начале координат концентрация частиц снижается до n = 0, так как каждое столкновение приводит к агрегации.
Проинтегрируем от Rnm до x и от 0 до v n :
v
n
dx
I 2 4 Dnm dvn ; I 4 Dnm Rnm vn
x
Rnm
0
Приняв, что Dn Dm D; Dnm 2D; Rnm R, общее число столкновений в единицу времени в единице объема (скорость быстрой коагуляции:
d
8 DR 2
d
где νΣ – суммарная концентрация частиц разных размеров в данный момент.
Для данной дисперсной системы 8πDR = const = k, где k – константа скорости коагуляции.
С учетом этого мы получаем уравнение, аналогичное уравнению для скорости бимолекулярной реакции:
d
k 2
d
188.
Кинетика коагуляции по Смолуховскому (3)Делим переменные и интегрируем в пределах от v v0 при τ = 0 до v∑ при τ:
dv
0
1 1
2 kd ;
k ;
v
0
1 k 0
v0
0
v
Смолуховский ввел время (период) половинной коагуляции θ – время коагуляции, в
течение которого общая концентрация частиц уменьшается до половины от начальной
концентрации первичных (единичных) частиц.
,
0
2
0
1
, 1 k 0 2, k 0 .
1 k 0
С учетом последнего соотношения получаем
уравнение Смолуховского:
v
v0
1
Линейная форма этого уравнения:
ctg
v0
1
v
189.
Кинетика коагуляции по Смолуховскому (4)Общее число частиц v∑ в единице объема системы можно представить как сумму геометрической прогрессии:
v0
/
v
i 1 2 3 ... 1 1q 1q 2 ...; q
1
1 /
i
1
Сумма прогрессии равна
, откуда находим концентрацию одинарных частиц:
1 q
/ 0
1 1 q 1
1 / 1 /
По аналогии:
2 1q
0
2
1 /
0 /
0
/
2
3
1 / 1 / 1 /
Число частиц каждого порядка (m-мерных частиц):
0 ( ) m 1
m
(1 ) m 1
190.
Факторы, влияющие на скорость коагуляцииБыстрая коагуляция
k f 8 DR; R 2r; k f 16 Dr;
D
kf
kBT
kT
B ;
B
6 r
8k B T
3
; á
3
8k BT 0
T , , 0
E
1
W
exp
ksl P
k
T
B
kf
Медленная коагуляция
E
ksl k f P exp
k
T
B
ksl
E
8kBT
P exp
3
k
T
B
sl
E
3
exp
8kBT 0 P
k
T
B
T , , 0 , P, E
Фактор устойчивости
(коэффициент стабильности)
191. Агрегативная устойчивость и коагуляция дисперсных систем
Лиофобные системы. Теория ДЛФО192.
Расклинивающее давлениеРасклинивающее давление возникает при
сильном уменьшении толщины пленки
(прослойки) в результате перекрывания
(взаимодействия) поверхностных слоев.
Пленка – часть системы,
находящаяся между двумя
межфазными поверхностями.
h – толщина пленки; δ – толщина поверхностного слоя.
193.
Расклинивающее давление (2)Избыточные термодинамические функции тонкой пленки зависят от ее
толщины h.
Избыточная энергия Гиббса:
G
dG SdT ( 1, 2 2,3 )ds i dni
dh
h
Расклинивающее давление
в пленке толщиной h:
1 G
(h) p - p0
s h T ,n j ,s
Расклинивающее давление можно рассматривать как разность гидростатических давлений в пленке и в окружающей пленку фазе, или как приращение
энергии Гиббса на данном расстоянии между поверхностными межфазными
слоями, пересчитанное на единицу толщины пленки и отнесенное к единице
площади перекрывания поверхностных слоев.
194.
Расклинивающее давление (3)Расклинивающее
давление П(h)
П(h) < 0,
h < 2δ
отрицательное
расклинивающее
давление
(силы притяжения)
Толщина прослойки
между поверхностями
самопроизвольно
уменьшается
П(h) = 0,
h > 2δ
взаимодействия
между частицами нет
П(h) > 0,
h < 2δ
положительное
расклинивающее
давление
(силы отталкивания)
Толщина прослойки
между поверхностями
самопроизвольно
увеличивается
195.
Расклинивающее давление (4)Поскольку поверхностные силы имеют различную природу,
то расклинивающее давление является суммарным параметром.
(h) m (h) el (h) s (h) a (h) st (h)
Составляющие расклинивающего давления:
Пm – молекулярная;
Пel – электростатическая;
Пs – структурная;
Пa – адсорбционная;
Пst – стерическая;
классическая
теория ДЛФО
обобщенная
теория ДЛФО
В рамках данного курса рассматривается только классическая теория ДЛФО.
196.
Основные положения теории ДЛФОТеория ДЛФО – теория устойчивости лиофобных дисперсных систем,
разработанная в 1937-1941 гг. Дерягиным и Ландау, и несколько позже Фервеем
и Овербеком.
Теория ДЛФО позволяет количественно описать действие различных
факторов стабилизации лиофобных дисперсных систем. Для этого рассматривают поверхностные силы, возникающие между двумя сближающимися частицами.
Теория ДЛФО является физической теорией (химическое взаимодействие
не рассматривается). Также ее можно считать кинетической теорией, так как
она рассматривает процесс взаимодействия частиц по отдельным стадиям –
перекрывание их поверхностных слоев и возникновение расклинивающего
давления. При этом используется понятие потенциального барьера, аналогичное энергии активации в химической кинетике.
197.
Основные положения теории ДЛФО (2)U U el U m
Энергия отталкивания Uel
dU el el dh
Отталкивание
обусловлено только
электростатическими силами
Энергия притяжения Um
dU m m dh
Притяжение
обусловлено
силами Ван-дер-Ваальса
(дисперсионное взаимодействие)
198.
Энергия электростатического отталкиванияd el d ;
0
Ï
el
d
2
x
Из теории Гуи-Чепмена для слабозаряженных
частиц и пренебрегая кривизной поверхности:
2F 2 I
x
0 2 ; x e
RT
el
ДЭС не перекрываются
ДЭС перекрываются
Для низких потенциалов
при h=2x
el 2 0 2 2 e h
2 x
0 2 d 2 0 2 x2
0
Для высоких потенциалов
при h=2x
el 64с0 RT 2e h ;
zF
exp
2 RT
zF
exp
2 RT
1
1
199.
Энергия электростатического отталкивания (2)Получим выражение для энергии электростатического отталкивания пластин:
U el Ï el dh 2 0 e
2
h
h
Для низких потенциалов:
U el (h) 2 0 2e h
2 h
2 0 2 2 h
dh
e d ( h)
h
Для высоких в потенциалов:
U el (h)
64c0 RT
Для частиц с искривленной поверхностью
необходимо учитывать их взаимную
F (h) CU pl (h);
ориентацию и радиус кривизны.
Для сферических частиц
при r1 = r2
при r1 ≠ r2
2 r1r2
C
r1 r2
C r
2 e h
U (h) F (h)dh
h
U э 2 0 r 2 ln 1 exp( h)
200.
Энергия молекулярного притяженияДисперсионное взаимодействие между двумя частицами определяется
суммированием взаимодействий между молекулами или атомами в обеих
частицах (теория де Бура и Гамакера).
Уравнение энергии притяжения одной молекулы (атома)
U ads
Cn
6 x3
к поверхности адсорбента (в данном случае, частицы)
Просуммируем энергию притяжения всех молекул
(атомов) левой пластины к правой пластине:
Cn
1
dU m (h)
ndr
3
6 ( r h)
r
Cn
1
Cn 2
U m ( h)
ndr
3
6 ( r h)
12h 2
r 0
x r h
A
U m (h) 12 2
12 h
A12 Cn ;
2
2
A A1 A0 2A01
*
A*
U m ( h)
12 h2
201.
Общее уравнение энергии взаимодействияЭнергия взаимодействия между двумя параллельными пластинами,
приходящаяся на единицу площади поверхности
Для больших потенциалов
Для малых потенциалов
*
A
U (h) 2 0 2e h
12 h
U ( h)
64c0 RT
*
A
2e h
12 h 2
Энергия взаимодействия между
двумя сферическими частицами
*
A
r
U (h) 2 0 r 2 ln 1 exp( h)
12h
Справедливо для частиц с низким значением
электрического потенциала и при условии, что
радиус частицы значительно больше толщины
диффузного слоя ДЭС r 1/
202.
Потенциальные кривые взаимодействия частицАгрегативно
устойчивая система
Агрегативно неустойчивые системы
Возникновение
контактов во
втором
минимуме
Наличие высокого
потенциального барьера
Возникновение
контактов в
первом
минимуме
203.
Электролитная коагуляцияПри уменьшении поверхностного потенциала и/или уменьшении
толщины ДЭС снижается вклад электростатической составляющей.
При этом происходит снижение величины потенциального барьера,
что приводит к потере агрегативной устойчивости и коагуляции частиц.
Концентрационный механизм
Нейтрализационный механизм
Энергия отталкивания снижается
за счет сжатия диффузной части ДЭС
при введении индифферентного (не
взаимодействующего с поверхностью
частиц) электролита (повышается
ионная сила дисперсионной среды).
Энергия отталкивания снижается
за
счет
снижения
потенциала
диффузного слоя при введении неиндифферентного (специфически адсорбирующегося на поверхности частиц)
электролита.
x
U el (h) 2 0 exp
2
x
U el (h) 2 0 exp
2
204.
Концентрационный механизм коагуляцииВведение индифферентных электролитов (как правило, содержат
однозарядные ионы), ионы которых не адсорбируются в слое Гельмгольца,
приводит к увеличению ионной силы I. При этом сжимается диффузная
часть ДЭС.
x
e x e
при с2 > c1, λ2 < λ1
x
U el (h) 2 0 2 exp
1/
I
0 RT
2F 2 I
1
c0i zi2
2
x e
e
/ e
205.
Нейтрализационный механизм коагуляцииПри добавлении неиндифферентного электролита происходит нейтрализация
заряда поверхности и падение абсолютной величины поверхностного потенциала
и потенциала диффузной части ДЭС. При высоких концентрациях электролита
может наступить перезарядка поверхности – формирование нового ДЭС,
в котором адсорбировавшиеся ионы играют роль потенциалопределяющих.
Неиндифферентные
электролиты содержат:
ионы Н+ и ОН- (для оксидов и гидроксидов), многозярядные ионы; ионогенные ПАВ и полиэлектролиты.
Изоэлектрическая точка:
концентрация электролита,
при которой электрокинетический потенциал равен
нулю.
206.
Нейтрализационный механизм коагуляцииВ ситуации, когда не происходит образования недиссоциирующего соединения
с потенциалобразующими ионами, накопление специфически адсорбирующихся
ионов в слое Гельмгольца приводит к падению абсолютной величины потенциала
диффузного слоя. Сверхэквивалентная адсорбция таких ионов может привести как к
изоэлектрическому состоянию, так и к перезарядке. В этом случае вплоть до
изоэлектрического состояния адсорбция является ионообменной.
207.
Порог коагуляцииПорог быстрой (медленной) коагуляции – наименьшая концентрация электролита, при которой
начинается быстрая (медленная) коагуляция.
Для осуществления быстрой коагуляции требуется такая концентрация электролита, после увеличения которой скорость коагуляции остается постоянной.
Турбидиметрический метод
определения порогов
быстрой коагуляции
208.
Правило Эйлерса-КорфаПри концентрации электролита ccr, равной порогу быстрой
коагуляции, и h = hcr (для слабозаряженных поверхностей):
A*
2
2 0 cr exp( cr hcr )
U h hcr 0;
12 hcr
hcr
dU
0;
dh h hcr
2 A*
2 0 cr exp( cr hcr ) ( cr )
12 hcr3
2
2 2 cr / cr
hcr 2 / cr ; 2 0 cr e
ccr
2
B const;
cr
2
B - условие агрегативной устойчивости;
2
B - условие коагуляции.
F 2 z 2ccr
;
0 RT
2
cr
A* cr2
12 22
ccr
0 RT 4
B2 F 2 z 2
K
4
z2
209.
Правило Щульце-ГардиПри больших потенциалах поверхности (сильнозаряженные частицы)
теория ДЛФО дает следующие соотношения:
ccr
cr3
const;
ccr z 6 const;
ccr
const
z6
- закон Дерягина
Правило Шульце-Гарди: значения порогов коагуляции, вызываемой
электролитами с зарядами противоионов 1, 2 и 3 находятся в соотношении:
1 : 1/20 : 1/500
Закон Дерягина:
1 : (1/2)6 : (1/3)6 = 1 : 1/64 : 1/729
210. Эмульсии
211. Эмульсии
Эмульсии – дисперсные системы, в которых одна жидкая фазадиспергирована в другой жидкой фазе, несмешивающейся с первой.
Эмульсии существуют только в присутствии стабилизаторов, в роли
которых могут выступать ПАВ, полимеры и высокодисперсные порошки.
Классификации эмульсий
по агрегативной устойчивости
по типу
по концентрации
Макроэмульсии
(лиофобные системы)
Прямые
Разбавленные
Обратные
Концентрированные
Бинепрерывные
Высококонцентрированные
Микроэмульсии
(лиофильные системы)
Множественные
212.
Классификация эмульсий по агрегативной устойчивостиМакроэмульсии
Микроэмульсии
Размер капель в макроэмульсиях
лежит в интервале 1-100 мкм
Размер капель в макроэмульсиях
лежит в интервале 1-100 нм
Макроэмульсии являются типично
лиофобными системами.
Величина межфазного натяжения
на границе жидкость-жидкость
обычно составляет 10-20 мДж/м2
Микроэмульсии являются лиофильными
системами. Величина межфазного
натяжения на границе жидкость-жидкость
составляет менее 1 мДж/м2
k BT
cr 2
a
k BT
cr 2
a
213.
Классификация эмульсий по типуПрямые (масло (м) в воде (в)) – м/в
Обратные (вода (в) в масле(м)) – в/м
Множественные (прямые и обратные)
Бинепрерывные
214.
Определение типа эмульсииСуществует несколько способов определения типа эмульсий. Рассмотрим 3
наиболее известных способа как отличить прямую эмульсию от обратной.
1). Метод разбавления. Прямые эмульсии легко разбавляются водой, при этом
изменяется только концентрация дисперсной фазы, разделения фаз не происходит.
Обратные эмульсии не смешиваются с водой и хорошо разбавляются органическими
растворителями.
2). Использование красителей. Водорастворимые красители легко растворяются в
прямых эмульсиях (водной дисперсионной среде), окрашивая их в соответствующий
цвет; маслорастворимые красители легко растворяются в обратных эмульсиях.
3). Измерение электропроводности. Прямые эмульсии хорошо проводят электрический ток; их электропроводность на несколько порядков выше, чем электропроводность обратных эмульсий.
215.
Обращение эмульсийПри достаточно высоких концентрациях дисперсной фазы (более 20 % объемных)
под действием внешних условий возможна смена типа эмульсии – обращение фаз.
Создание благоприятных условий для эмульсии обратного типа, как правило, и
приводит к обращению фаз. Процесс обращения эмульсии проходит через образование бинепрерывной структуры, как показано на рисунке 1.
бинепрерывная
эмульсия
обратная
эмульсия
прямая эмульсия
Рис. 1. Обращение эмульсий.
Рис. 2. Температура инверсии фаз.
216.
Стабилизация эмульсий поверхностно-активными веществамиКак правило, чем ближе фазы по полярности, тем устойчивее система. Однако
при получении стабильных эмульсий только низкого значения межфазного натяжения
недостаточно. Это можно проиллюстрировать следующими примерами.
Неустойчивая
эмульсия
бутилацетат
σ0=10 мДж/м2
вода
Образование эмульсии
декан
декан
ПА
ПАВ
В
σ0=51 мДж/м2
σПАВ=12 мДж/м2
вода
вода
217.
Стабилизация ПАВПосадочная площадка молекулы ПАВ на границе жидкость-жидкость в случае
эмульсионных систем существенно зависит от природы масла. Так, для додецилсульфата натрия при стабилизации прямых эмульсий, получены следующие данные:
Масло
Посадочная площадка, Å2
Гексан
45,2
Октан
48,3
Декан
49,0
Циклогексан
48,3
Бензол
64,9
Четыреххлористый углерод
53,1
Все эти значения посадочной
площадки существенно выше
значений s0 на границе жидкостьгаз (28 Å2), что говорит о том,
что адсорбционные слои на
границе жидкость-жидкость
более рыхлые и разреженные.
218.
Стабилизация ПАВМодель дуплексной пленки
Модель ориентированных
клиньев Банкфорта
ПАВ должно быть растворено
в дисперсионной среде
σ1 σ2
Роль стерического фактора
олеиновый спирт
цетилсульфат натрия
Молекула ПАВ
с 1 большой «головкой»
Стабилизация прямых эмульсий
цетиловый спирт
Молекула ПАВ
с 2 «хвостами»
«хорошо»
«плохо»
Стабилизация обратных эмульсий
219.
Стабилизация полимерами и высокодисперсными порошкамиСтабилизация порошками
В качестве стабилизаторов в данном случае используются высокодисперсные частицы, нерастворимые в
дисперсионной среде. Большую роль
в такой стабилизации играет величина
углов смачивания. Таким образом
получают «бронированные» эмульсии,
обладающие повышенной прочностью.
BaSO4
масло
Капля эмульсии
Стабилизация полимерами
220.
В дисперсных системах вода может находиться в различных состояниях.Рассмотрим некоторых из этих состояний в системах, содержащих ПАВ.
гидратная вода
Молекулы гидратной воды
располагаются вблизи головок
молекул ПАВ. Такая вода легко
может быть удалена при сушке.
По своим физическим свойствам такая вода ничем не отличается от обычной.
221.
Микроэмульсионная водаСолюбилизированная вода
солюбилизированная
вода
микроэмульсионная
вода
Солюбилизированная вода, как правило,
обладает повышенными вязкостью
и плотностью.
Системы с солюбилизатом прозрачны
и однородны.
Микроэмульсионные системы
однородны, опалесцируют
и окрашены в голубоватый цвет.
Микроэмульсии обратимо
реагируют на изменение
температуры.
222.
МикроэмульсииФазовая диаграмма
для типичной микроэмульсионной системы
Микроэмульсию обычно получают
в присутствии нескольких ПАВ
(основного и со-ПАВ). Часто
микроэмульсионная область находится
в равновесии с водной и масляной
фазами.
Микроэмульсионные системы
очень чувствительны к изменению
температуры и введению электролитов.
В настоящее время микроэмульсии
находят самое разнообразное применение:
для повышения нефтеотдачи, в медицине
и косметологии, при синтезе наночастиц
металлов и др.
223. Структурообразование и структурно-механические свойства дисперсных систем
Механизм структурообразования224.
СтруктурообразованиеОсновные типы структур
Структура – такое пространственное взаимное расположение составных
частей (атомов, молекул, частиц), когда невозможно изменить расположение
любой частицы, не изменив расположение всех остальных. Тип структуры,
которая может сформироваться в дисперсной системе с жидкой дисперсионной
средой в основном определяется агрегативной устойчивостью.
Структуры первого типа
Характерны для агрегативнонеустойчивых систем.
Возникновение трехмерного
каркаса из частиц дисперсной
фазы, которые находятся в
контакте друг с другом.
Структуры второго типа
Характерны для агрегативноустойчивых систем.
Возникновение стесненных
условий, в которых все частицы
занимают в пространстве
положения, характеризующиеся
минимумом энергии.
225.
Структуры первого типаОбразование структур обусловлено избыточной поверхностной
энергией и происходит самопроизвольно. В объеме возникает
рыхлая неупорядоченная структура из агрегированных частиц.
Согласно теории ДЛФО возможны два варианта образования
агрегатов.
В случае, когда высота потенциального барьера больше, чем
(10-15)kBТ, а глубина второго энергетического минимума
не менее (1-1,5)kBТ, то происходит взаимная фиксация частиц
на расстоянии, соответствующем положению второго
энергетического минимума. При этом между частицами остается
прослойка дисперсионной среды (поверхностных слоев).
В случае, когда вся потенциальная кривая лежит в области
отрицательных значений (на всех расстояниях преобладают
силы притяжения), происходит сближение частиц вплоть до
их непосредственного соприкосновения (фиксация в первом
энергетическом минимуме).
226.
Типы межчастичных контактовПрочность связей между частицами характеризуют средней силой их
сцепления (прочностью единичного контакта) F1 , соответствующей
усилию, необходимому для разъединения двух частиц.
Коагуляционные
Атомные
Образуются между
частицами при их
фиксации во втором
энергетическом
минимуме. После
механического
разрушения способны к
самопроизвольному
восстановлению.
Возникают при
взаимодействии частиц в
первом энергетическом
минимуме, при
непосредственном
контакте частиц друг с
другом. Разрушаются
обратимо.
F1 10-11 10-9 Н
F1 10-9 10-6 Н
Фазовые
Образуются при
«срастании» частиц,
находящихся в первом
энергетическом
минимуме. Становится
возможным непрерывный
переход из объема одной
частицы в другую.
Разрушаются
необратимо.
F1 10-6 Н
227.
Классификация структур первого типаКоагуляционнотиксотропные структуры
Возникают в результате сцепления
частиц через прослойки среды (во
втором энергетическом минимуме) за
счет коагуляционных контактов, или
при частичном вытеснении прослоек
среды (в первом энергетическом
минимуме) за счет атомных контактов.
Характеризуются высокой
дефектностью, пространственный
каркас относительно непрочен.
Основной особенностью является
обратимость – способность
самопроизвольно восстанавливаться
после механического разрушения
(тиксотропия).
Конденсационнокристаллизационные структуры
Кристаллические частицы связаны друг с
другом фазовыми контактами.
Характеризуются высокой прочностью и
необратимым характером разрушений.
Образованию конденсационных структур
всегда предшествует стадия формирования
структур коагуляционного типа.
228.
Структуры второго типаВозникновение структуры происходит за счет образования стесненных условий
при действии сил отталкивания между частицами. Критерием стесненных условий
является перекрытие поверхностных слоев (диффузные части ДЭС, сольватные слои,
адсорбционные слои ПАВ и полимеров).
Частица занимает
некий эффективный
объем Vef Vr Vs .
Vef может быть >> Vr.
Поэтому следует
использовать не φ, а
ef s
H 2
, ef max
H 2
ef max
φmax – объемная концентрация,
соответствующая плотной
упаковке частиц.
229.
Лиотропные жидкие кристаллыЖидкокристаллическое состояние – формирование структуры второго типа
в агрегативно-устойчивых и лиофильных системах при достижении стесненных условий. Характеризуется наличием дальнего порядка в расположении
частиц.
Жидкокристаллическое состояние –
наиболее совершенная структура
второго типа (в плане закономерного
расположения частиц в объеме),
поскольку частицы дисперсной фазы
близки к монодисперсным и
участвуют в броуновском движении.
Элементами дисперсной фазы лиотропных жидких кристаллов могут быть
твердые частицы (особенно с ярко выраженной анизометрией), мицеллы
ПАВ, супрамолекулы, молекулы жесткоцепных полимеров.
230. Структурообразование в дисперсных системах и их структурно-механические (реологические) свойства
231.
Реологические свойстваОсновные понятия и идеальные законы реологии
Реология – наука о деформациях и течении материальных систем под
действием механических напряжений. Исследует структурно-механические
(реологические) свойства систем по проявлению деформации под действием
внешних механических напряжений. (Rheos – течь, logos – наука; Бингам).
Деформация (γ) – относительное смещение точек системы, при котором
не нарушается ее сплошность (безразмерная величина).
Вязкость (η) – величина, характеризующая сопротивление жидкости
течению (Па.с).
Кривая течения – зависимость скорости деформации от приложенного
механического напряжения f P .
Реологические кривые – зависимости скорости деформации и вязкости от
приложенного механического напряжения.
232.
Основные понятия и идеальные законы реологии (2)Напряжения (Р)
(Па=Н/м2)
Нормальные
(направленные
перпендикулярно
к поверхности)
Тангенциальные
(направленные
по касательной
к поверхности)
Приводят к объемной
деформации
(растяжение или сжатие)
Приводят к сдвиговой
деформации
Первая аксиома реологии – при всестороннем равномерном (изотропном)
сжатии все материальные тела ведут себя одинаково – как идеальные
упругие тела.
Вторая аксиома реологии – любая материальная система обладает всеми
реологическими свойствами (прочность, упругость, пластичность и вязкость).
233.
Основные понятия и идеальные законы реологии (3)Деформации
Упругая деформация
(исчезает после снятия напряжения);
упругие (гуковские) и эластические
(запаздывающие упругие)
Остаточная деформация
(необратима, изменения
в системе остаются после
снятия напряжения);
вязкое и пластическое течение
Объемные деформации l l l0
l0
l0
(растяжение, сжатие).
Пластическая деформация
(остаточная деформация, при
которой не происходит
разрушения тела)
Сдвиговые:
y
tg
x
Деформации изгиба и кручения.
Течение – вид деформации, при
котором величина деформации
непрерывно увеличивается при
постоянном напряжении.
234.
Основные понятия и идеальные законы реологии (4)Элементарные реологические модели
Идеально упругое тело Гука –
пружина, деформационное поведение которой
описывается законом Гука. Модуль Юнга – Е,
характеризует жесткость материала.
Характерна полная обратимость деформаций.
P E
Идеально вязкое тело Ньютона перфорированный поршень в цилиндре, заполненном
идеально вязкой жидкостью. Скорость деформации
(перемещения цилиндра) описывается законом Ньютона.
P
Идеально пластическое тело Сен-Венана – Кулона твердое тело, скользящее по плоскости. Движение
тела начнется только при приложении к нему
напряжения РТ - предела текучести, компенсирующего
действие «сухого трения».
Р РТ, = 0; Р РТ, 0
P
235.
Моделирование реологических свойствУпруговязкое тело
Вязкоупругое тело
Модель Максвелла
Модель Кельвина-Фойгта
Упругопластическое тело
236.
Моделирование реологических свойств (2)Модель Максвелла – модель упруговязкого тела (последовательное сочетание
моделей Гука и Ньютона – упругого и вязкого элементов). Позволяет показать
наличие упругих свойств у жидкости.
;
P P d
d P
1 dP P
d d d
;
. При Р = const,
;
E
d
1
d
E
d
d
d
d
1
1
1
1
const;
E1 P 0 ; 1 P 1
E
1 dP P
dP
0;
1 d
E1 d 1
P
1
P P0 exp / ; 1 / E1
λ – время релаксации, за которое начальное напряжение Р0 при постоянной
деформации уменьшается в е раз.
237.
Моделирование реологических свойств (3)Модель Кельвина-Фойгта – модель вязкоупругого тела (параллельное
соединение моделей Гука и Ньютона – упругого и вязкого элементов).
Отражает поведение вязкоупругих тел, обладающих эластичностью.
При Р=Р0 деформация развивается во времени
постепенно: d P P0 P P0 E2
d 2
2
2 2
P0
(1 e )
E2
Эластичность тела характеризуют:
θ – время запаздывания или
релаксация деформации;
Е2 – модуль эластической
деформации
2 E2 ; E2 P 1
Упругое последействие описывается
уравнением, в котором Р0 = 0:
1 exp( )
P P P
Деформация полностью исчезает
только через бесконечно долгое
время. Поэтому всегда существует
некоторая остаточная деформация.
238.
Моделирование реологических свойств (4)Модель упруго-пластического тела – последовательное соединение моделей
Максвелла и Кельвина-Фойгта. Позволяет смоделировать систему, обладающую упругой деформацией, эластичностью, способностью к релаксации
напряжений.
При Р = const деформация развивается во
времени в соответствии с уравнением:
P P
P
1 e /
E1 1
E2
На основании кривой деформации
можно рассчитать: E1 P / 0
1. Модуль упругости
2. Модуль медленной эластической
деформации: E2 P / 3
3. Равновесный модуль
эластичности: E3 P / 0 3
4. Степень эластичности
3
0 3
100%
E1
100%
E1 E2
5. Другие характеристики (η1, η2, θ).
239.
Моделирование реологических свойств (5)Модель Бингама – модель вязкопластического тела (к параллельному
сочетанию моделей Ньютона и Сен-Венана-Кулона последовательно
присоединен элемент Гука).
ctg *
*
P P PT
d P PT
;
E
*
d
*
P PT * - уравнение Бингама
Соотношение между ньютоновской
и пластической вязкостью:
( PT * ) * PT
При малых напряжениях развиваются
только упругие деформации, а при
достижении Р > РТ имеет место
пластическая деформация, растущая
до бесконечности.
Скорость деформации равна нулю при
Р < РТ, и только при Р > РТ она
возрастает с увеличением напряжения.
Напряжение Р разбивается на две
составляющие: напряжение РТ необходимое для разрушения структуры
и напряжение Р-РТ, осуществляющее
собственно течение.
При РТ = 0 уравнение Бингама переходит
в закон Ньютона.
240.
Классификация дисперсных систем по структурно-механическимсвойствам
Дисперсные системы
Твердообразные системы
РТ > 0
Жидкообразные системы
РТ = 0
Ньютоновские
жидкости
Неньютоновские
жидкости
Нестационарные
Стационарные
Псевдопластические
Бингамовские
системы
Небингамовские
системы
Псевдопластические
Дилатантные
Дилатантные
241.
Классификация (2)Жидкообразные системы
1 – ньютоновская жидкость;
2 – псевдопластическая жидкость;
3 – дилатантная жидкость.
Твердообразные системы
1 – бингамовское тело;
2 – псевдопластическое
твердообразное тело
3 – пластическое дилатантное тело
Уравнение Оствальда-Вейля
P k n ; P k n 1
P PT k n
242.
Классификация (3)Ньютоновские
жидкости
Дилатантные
жидкости
Псевдопластические
жидкости
γ·
P
η
P
P k n 1 const
P k n 1; n 1
P k n 1; n 1
243.
Классификация (4)Нестационарные неньютоновские жидкости
Тиксотропные
жидкости
Реопектические
жидкости
f P,
f P,
Реопексия – возрастание прочности
структуры (вязкости) со временем
при действии напряжения сдвига.
1 – равновесная кривая;
2 – неравновесная кривая.
244.
Ньютоновские системыУравнение Эйнштейна
Допущения:
1. Система несжимаема.
2. Отсутствует скольжение
между частицами и жидкостью.
3. Ламинарный режим.
4. Частицы не взаимодействуют
между собой.
Общий вид уравнения Эйнштейна
0 (1 )
α – коэффициент формы частиц.
Для твердых сферических частиц
0
0 (1 2,5 );
2,5
Коэффициент формы для несферических частиц обычно больше 2,5, поскольку объем
вращения несферической частицы превышает объем самой частицы. Уравнение
Эйнштейна не учитывает наличия у частиц поверхностных слоев, таких как ДЭС,
адсорбционные и сольватные слои. Увеличение вязкости, обусловленное наличием таких
слоев, называют электровязкостным, адсорбционным и сольватным эффектами.
0 1 ef ;
ef n (4 / 3) (r )3
1
3
n (4 / 3) r
r
n – число частиц в единице объема; δ – толщина поверхностного слоя.
3
245.
Ньютоновские системыУравнения Штаудингера и Марка-Куна-Хаувинка
Уравнение Штаудингера справедливо для растворов
полимеров с короткими и жесткими цепями, которые
могут сохранять палочкообразную форму:
sp
0
KMc
0
η/η0 – относительная вязкость; ηsp = (η-η0)/ η0 - удельная вязкость;
sp ñ) - характеристическая вязкость.
ηsp/с – приведенная вязкость; [ ] lim(
c 0
Гибкие длинные молекулярные цепи
полимеров часто сворачиваются в клубки,
что уменьшает сопротивление их движению.
При этом зависимость вязкости от
молекулярной массы полимера оказывается
нелинейной. Поэтому более правильно
связывать с молекулярной массой
полимера характеристическую вязкость.
[ ] KM a ;
[ ] lim ( уд с)
c 0
Уравнение Марка-Куна-Хаувинка
Постоянная а отражает форму и плотность
клубка макромолекулы, зависит от природы
растворителя и гидродинамического
взаимодействия в объеме клубка. а=(0,5-1,0)
246.
Кривые течения реальных структурированных системРеологические кривые жидкообразной псевдопластической системы
При малых напряжениях сдвига (Р РК)
система ведет себя как ньютоновская жидкость,
ее вязкость max постоянна. Такое реологическое
поведение – течение структурированных систем с
постоянной вязкостью, называется ползучестью.
При Р РК происходит разрушение
структурной сетки. При достижении РМ,
происходит полное разрушение всех
элементов структуры, и в системе остаются
преимущественно индивидуальные частицы.
247.
Кривые течения реальных структурированных систем (2)Реологические кривые системы с твердообразной коагуляционной структурой
При малых напряжениях сдвига (Р РСТ)
система ведет себя как идеально упругое тело
(бесконечно большая вязкость).
При Р РCT может наблюдаться ползучесть, а
дальнейшее увеличение напряжения ведет к
разрушению структуры и падению вязкости.
При Р РKP разрушается само тело.
РCT – статическое предельное напряжение
сдвига;
РT – предел текучести по Бингаму
(динамический);
РKP – предел прочности.
248.
Методы измерения вязкости (кривых течения)Капиллярный
вискозиметр Уббелоде
Реовискозиметр
Хепплера
1 – индикатор; 2 – арретир; 3 – чашечка для
груза; 4 – коромысло; 5 – шарнир; 6 – маятник;
7 – зажим; 8 – термостат; 9 – шарик,
укрепленный на стержне; 10 – пробирка.
Уравнение Пуазейля:
r 4 P 1
P
; k
8 l
V
2r 2 g 0
9h
k ' 0 ; kP ; k
st
P st
249.
Методы измерения вязкости (кривых течения) (2)Схема ротационного вискозиметра
N / k1 ;
P
k1
P
; P k2 F
N
N – число оборотов лимба за время τ;
k1 – константа прибора (определяется по
эталонной жидкости);
k2 – константа, зависящая от размеров
внутреннего и внешнего цилиндров;
F – масса груза.
1 – лимб; 2 – блок; 3 – стопор; 4 – внутренний
цилиндр; 5 – внешний цилиндр; 6 – подъемная
площадка; 7 – винт; 8 – маховик; 9 –
подъемный механизм; 10 – стопорный винт.



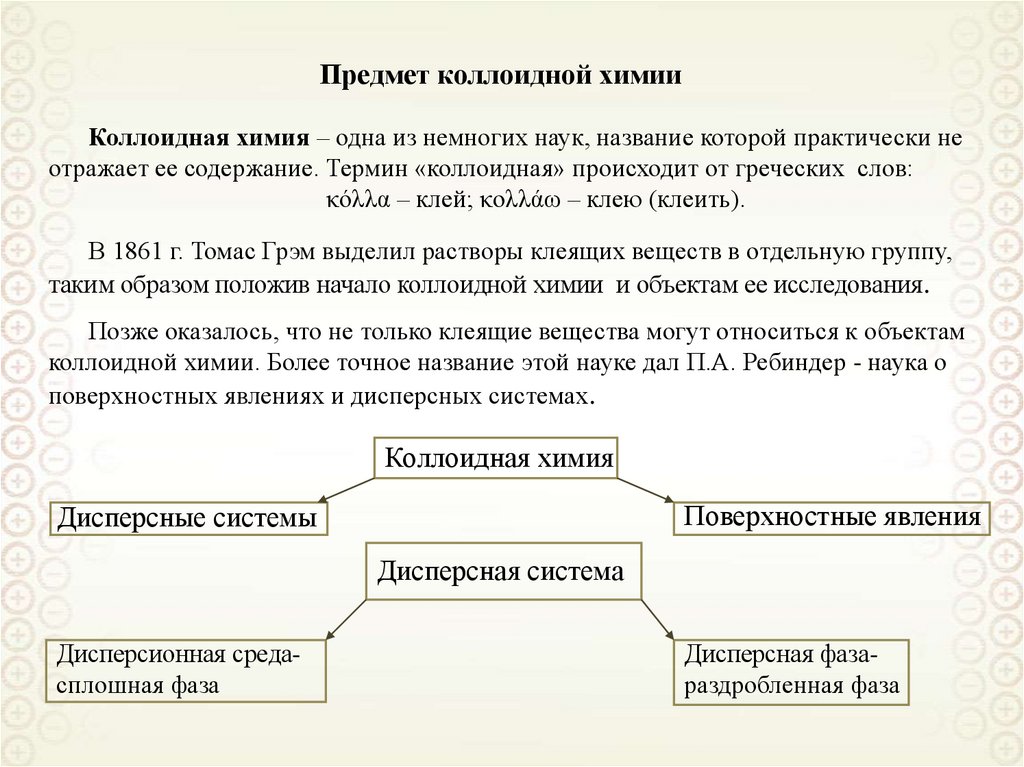


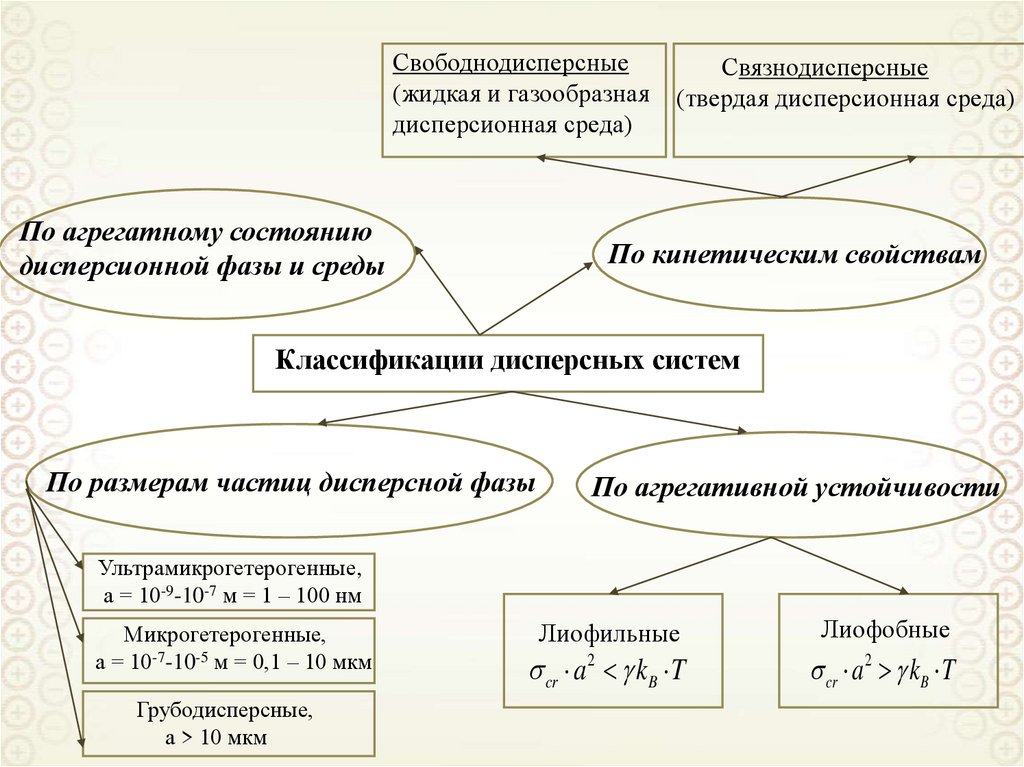

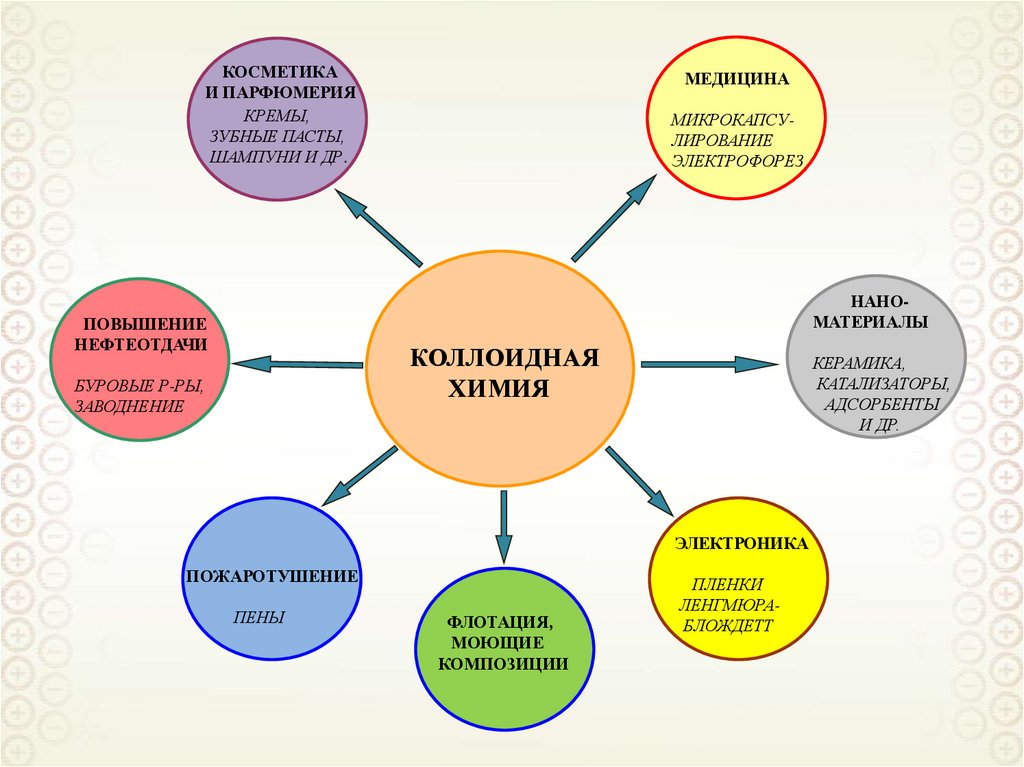











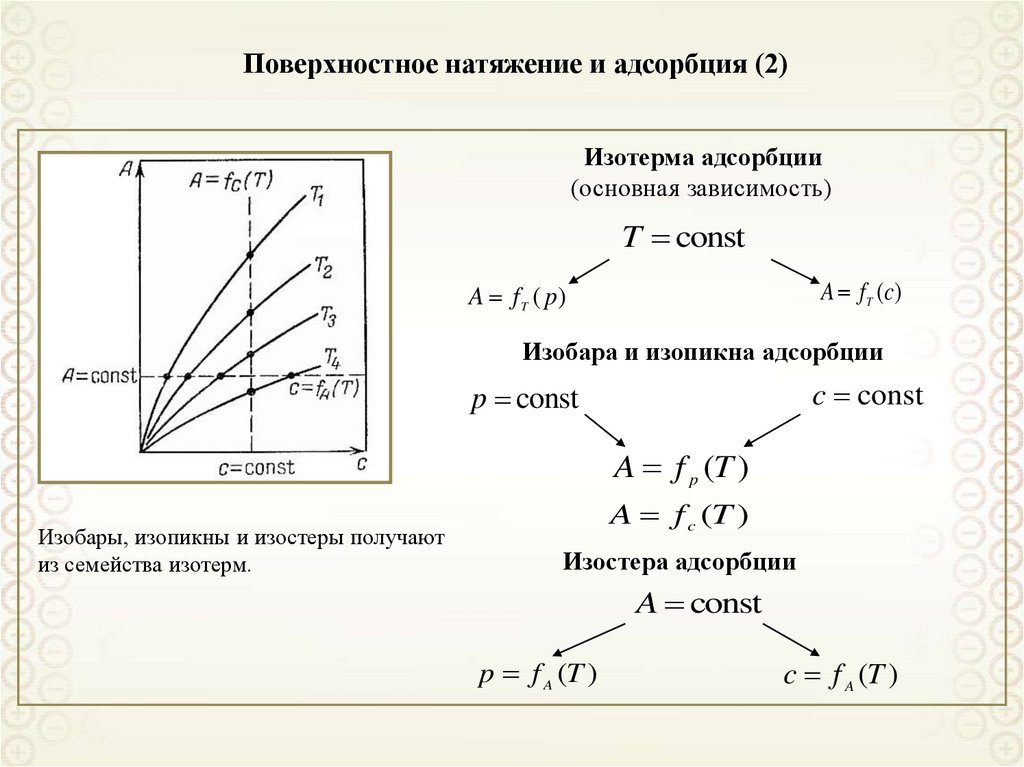

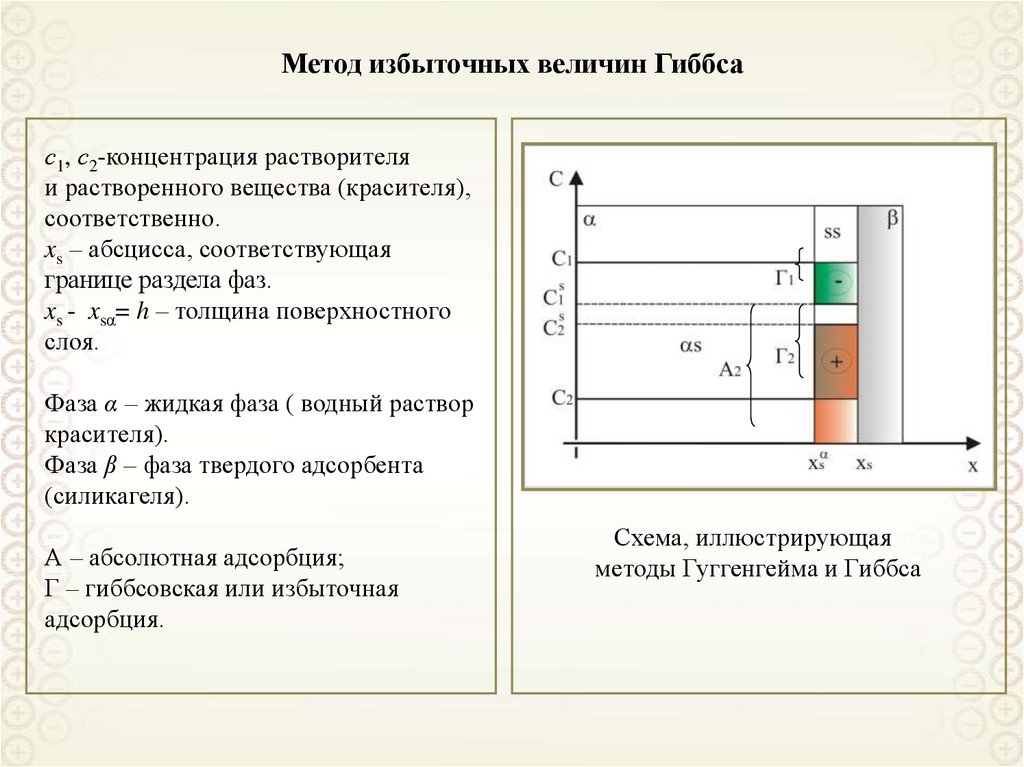










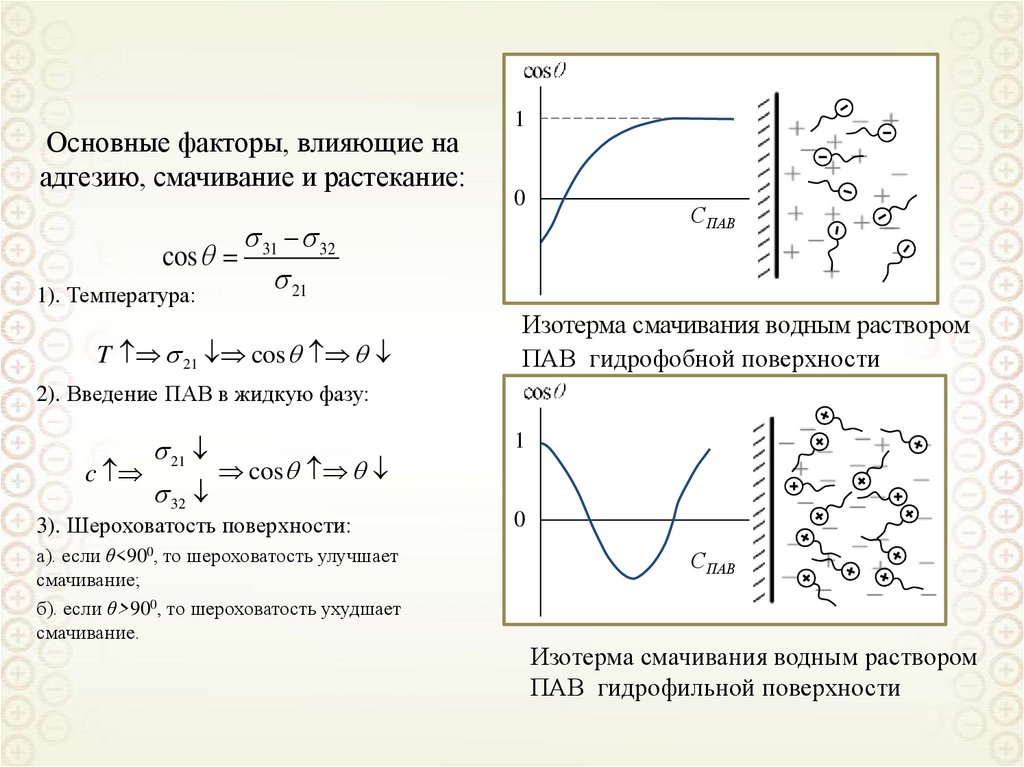



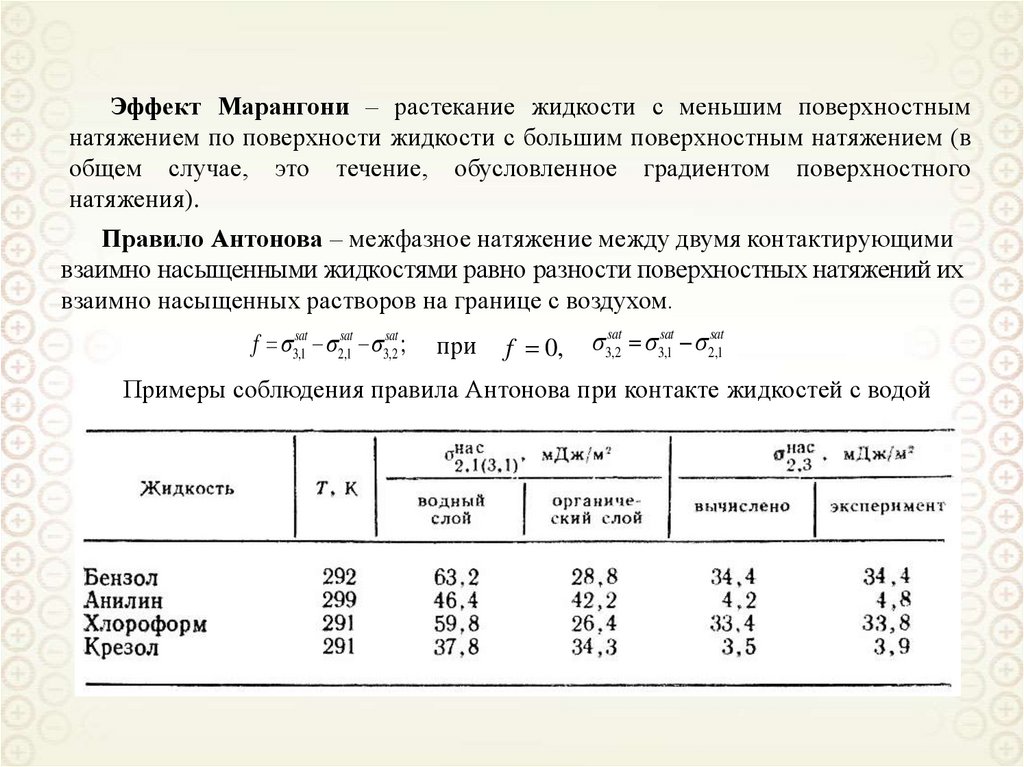


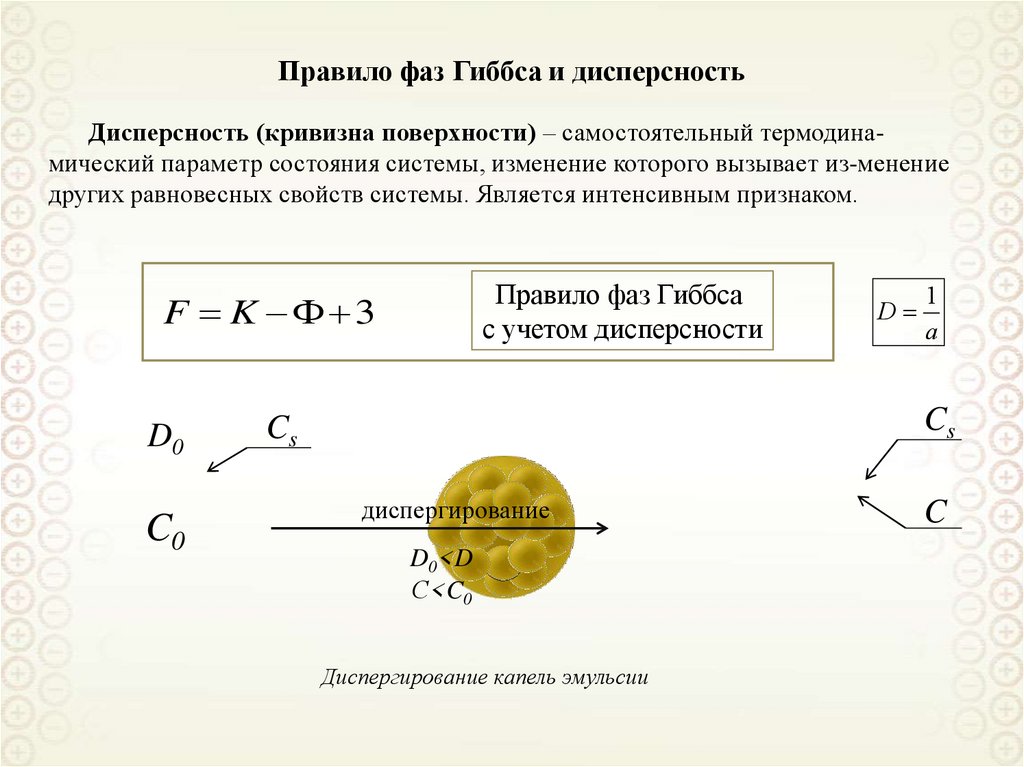









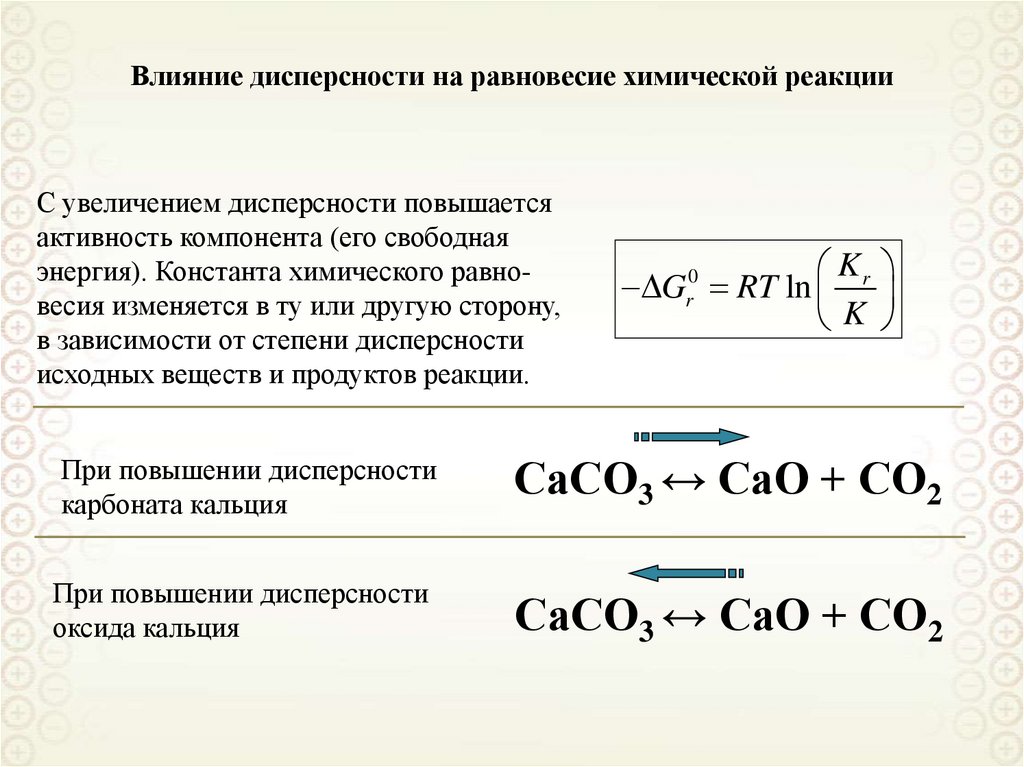








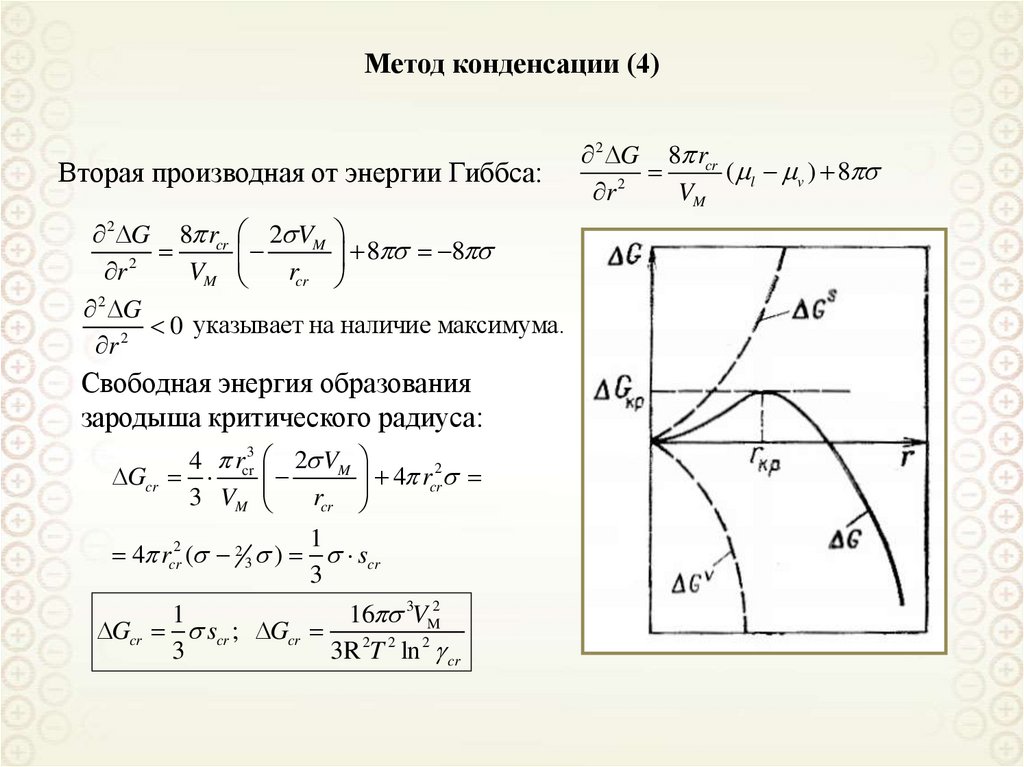

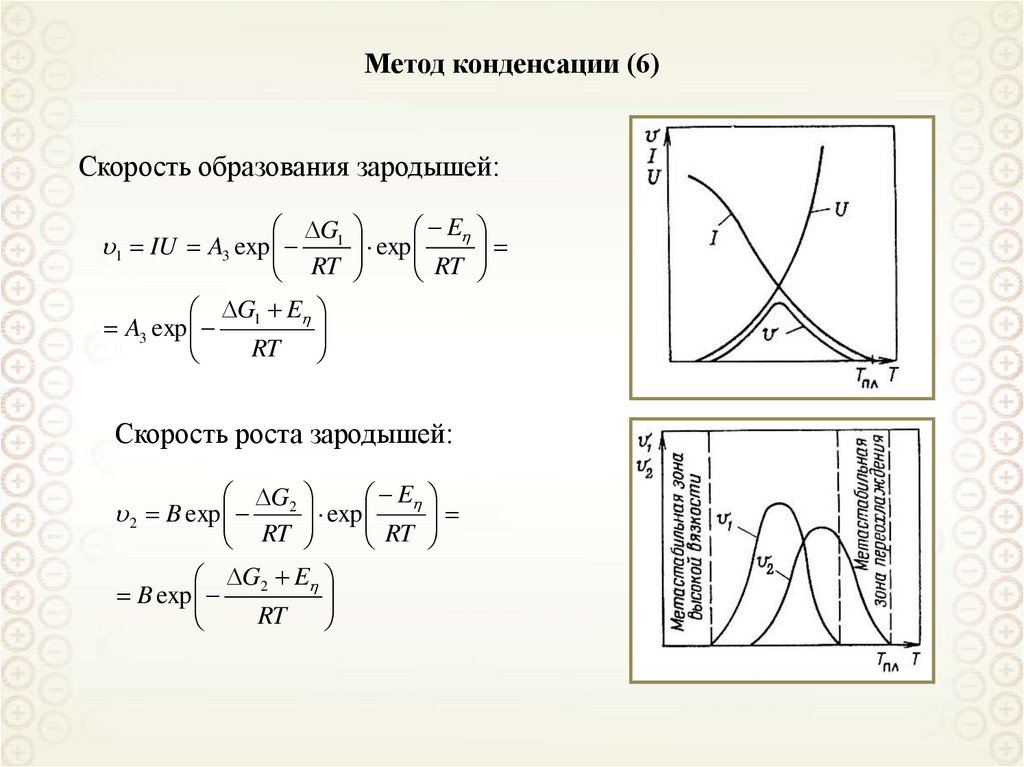

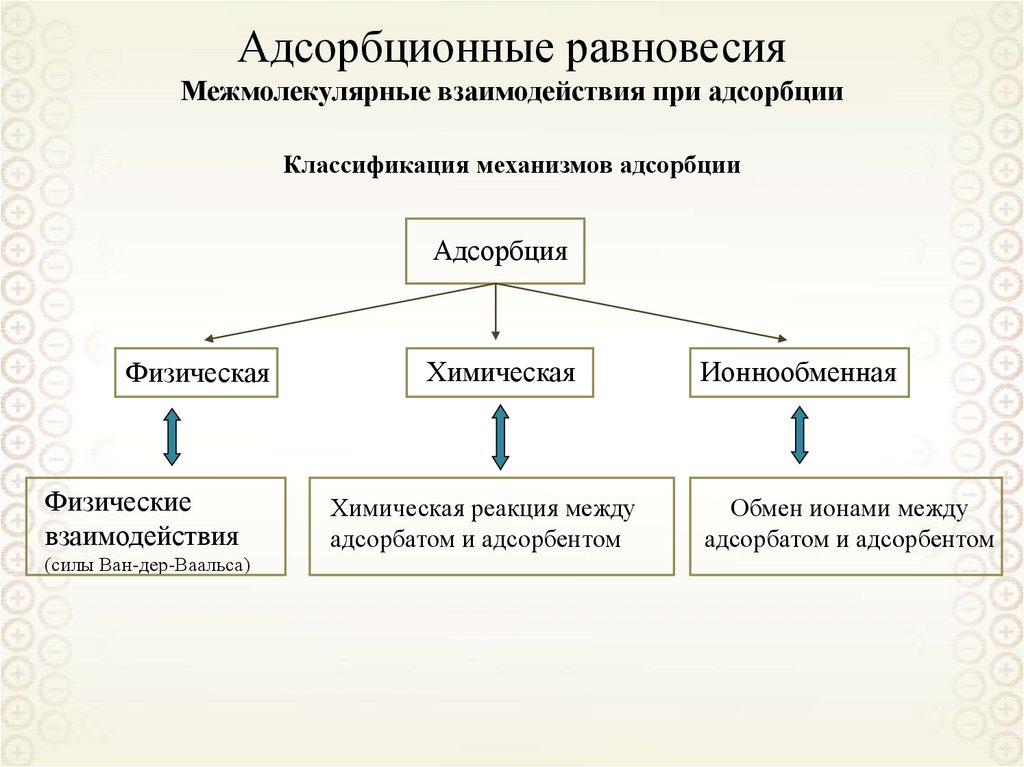
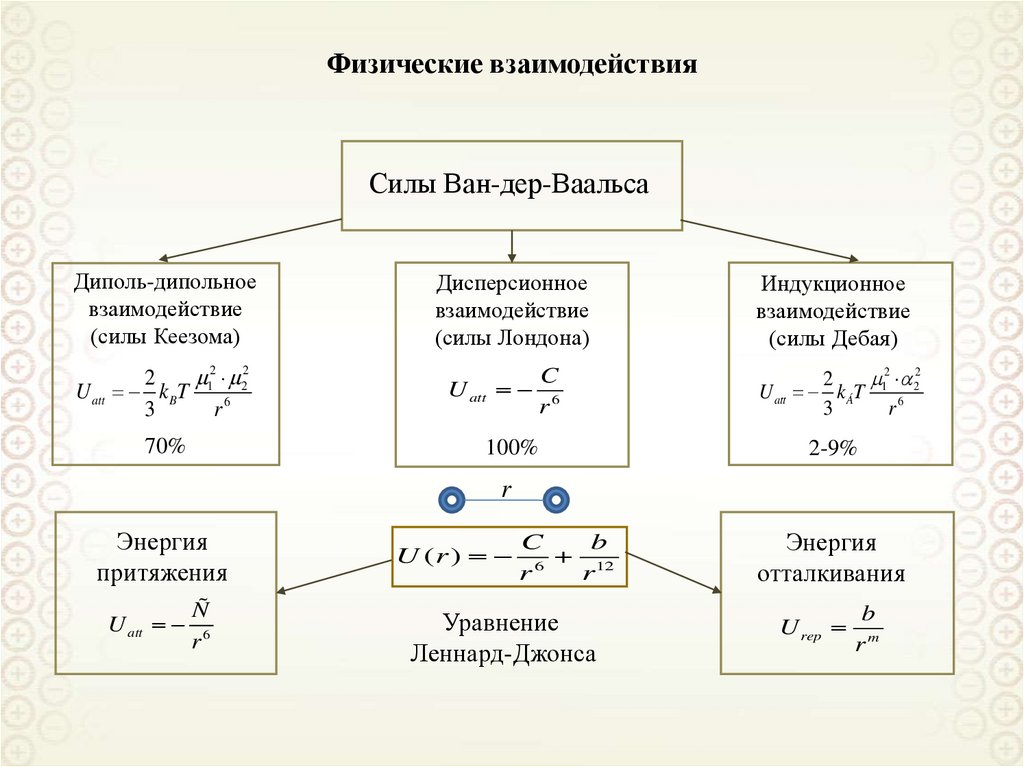




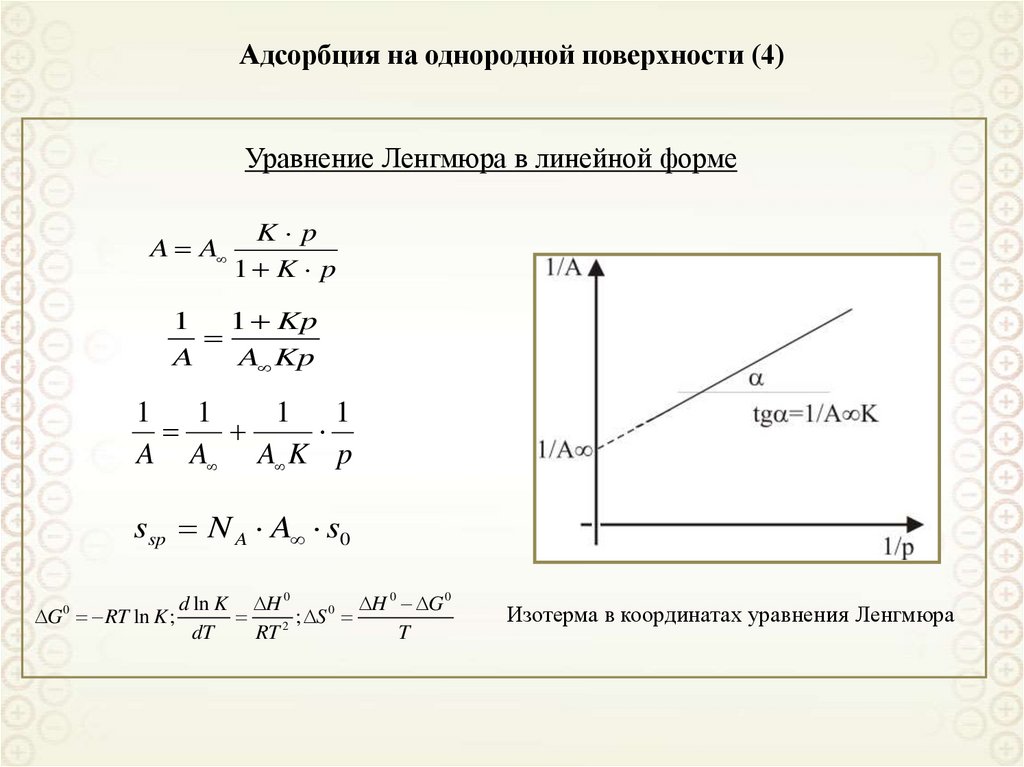




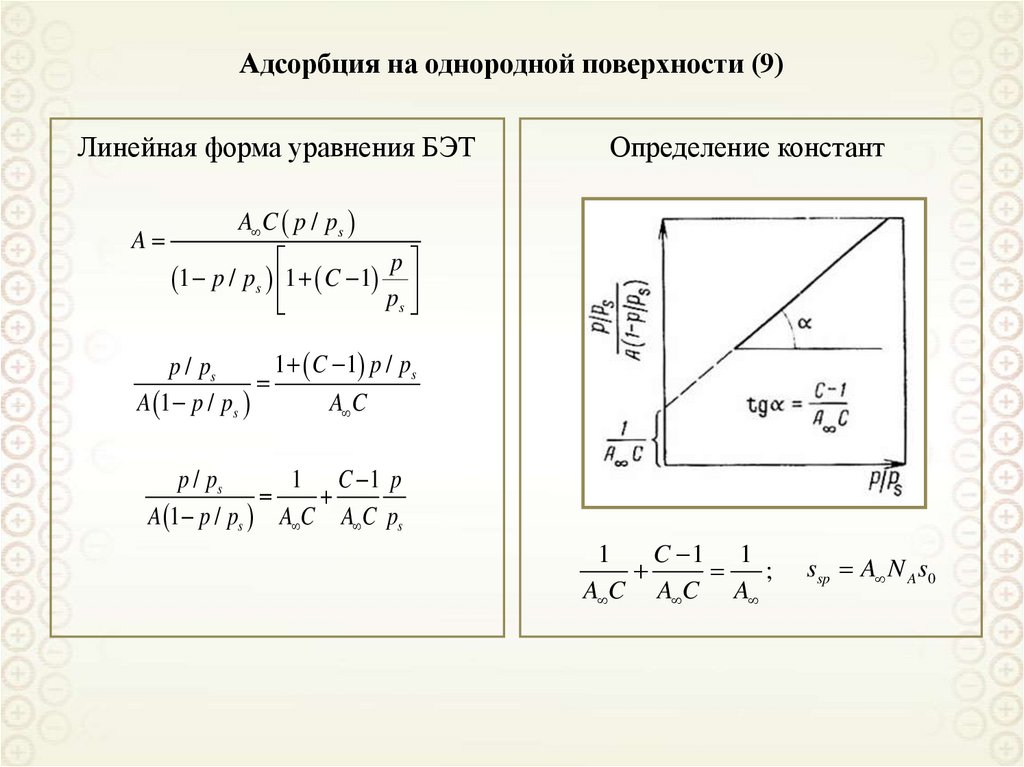



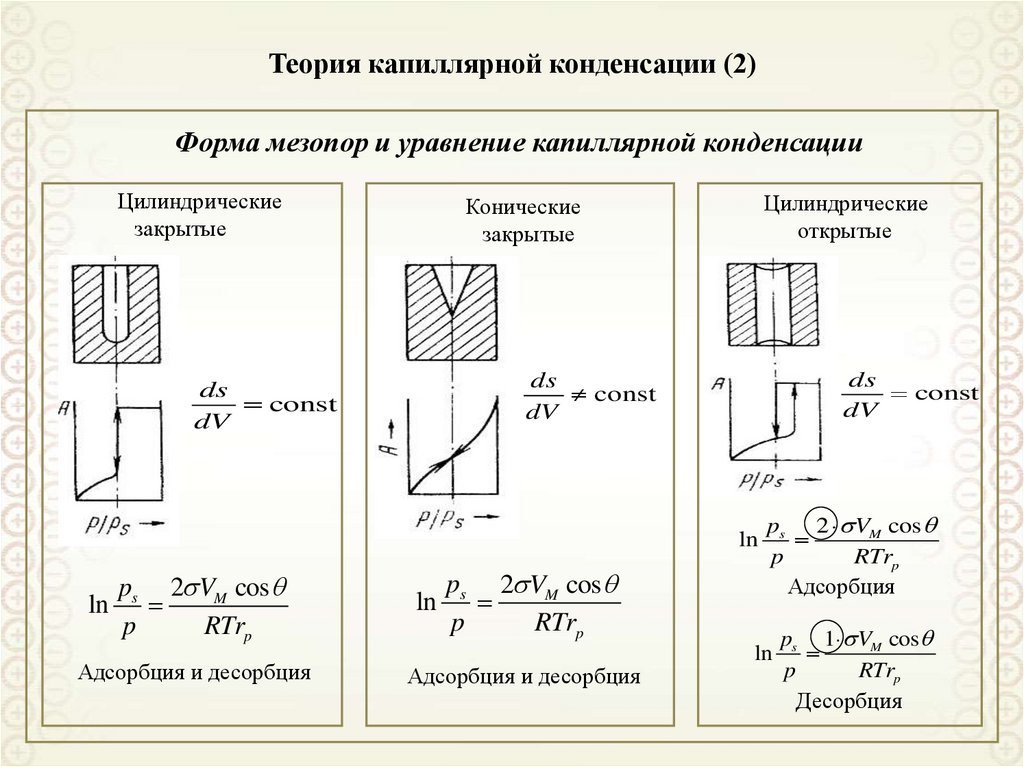
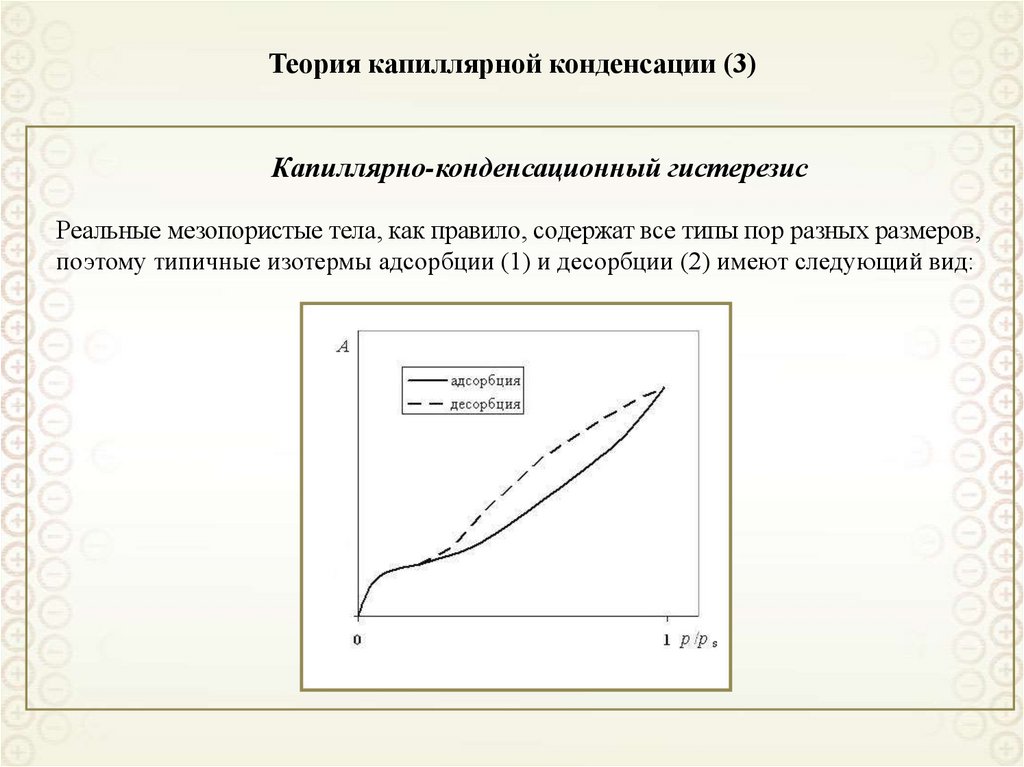


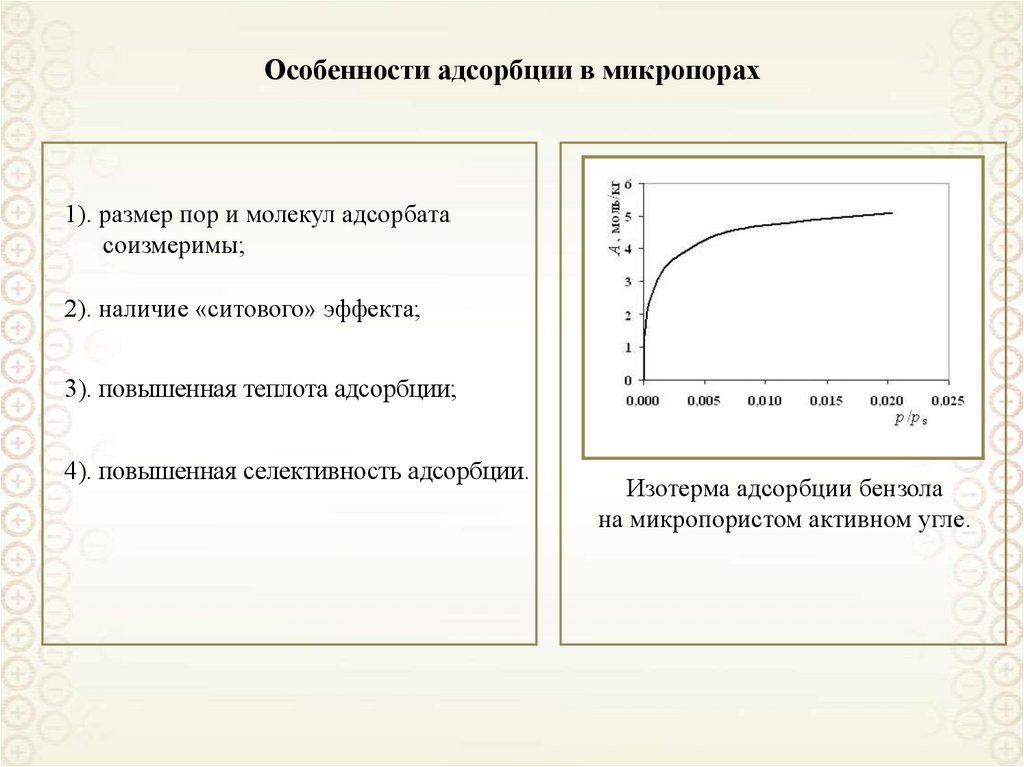
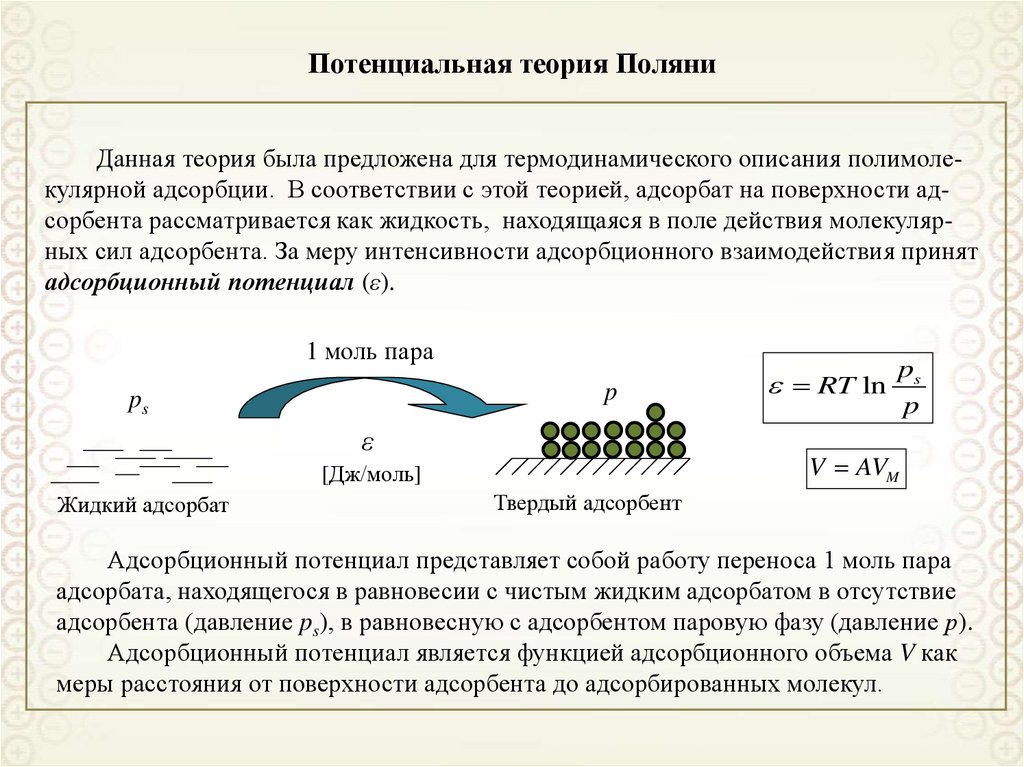






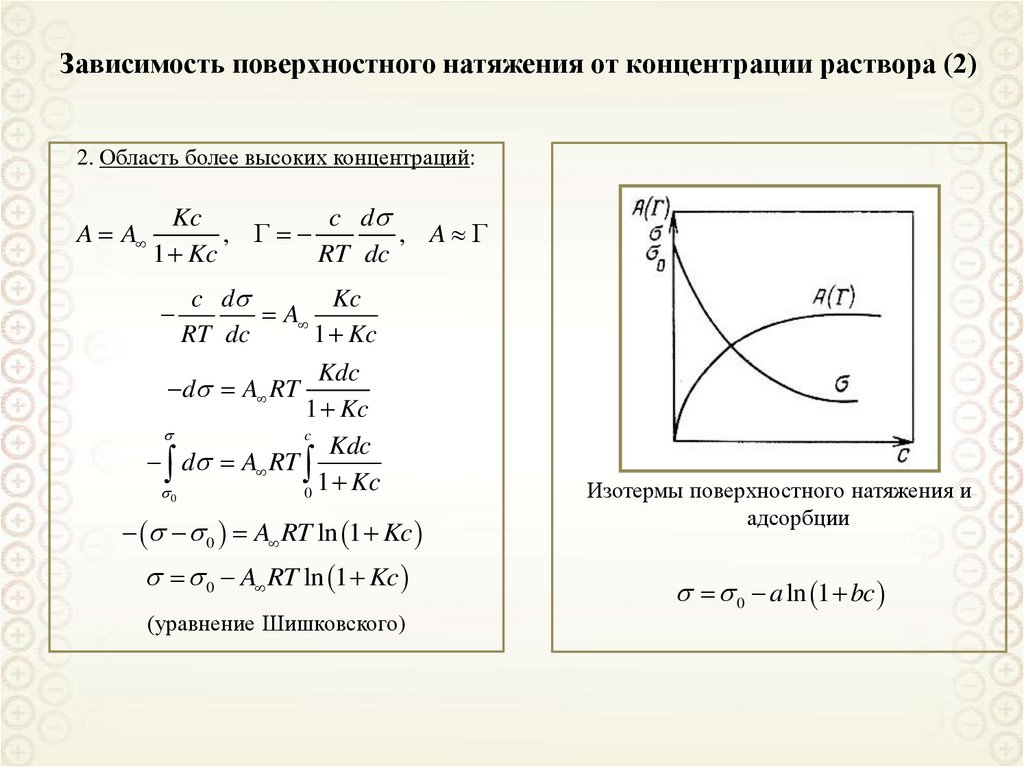




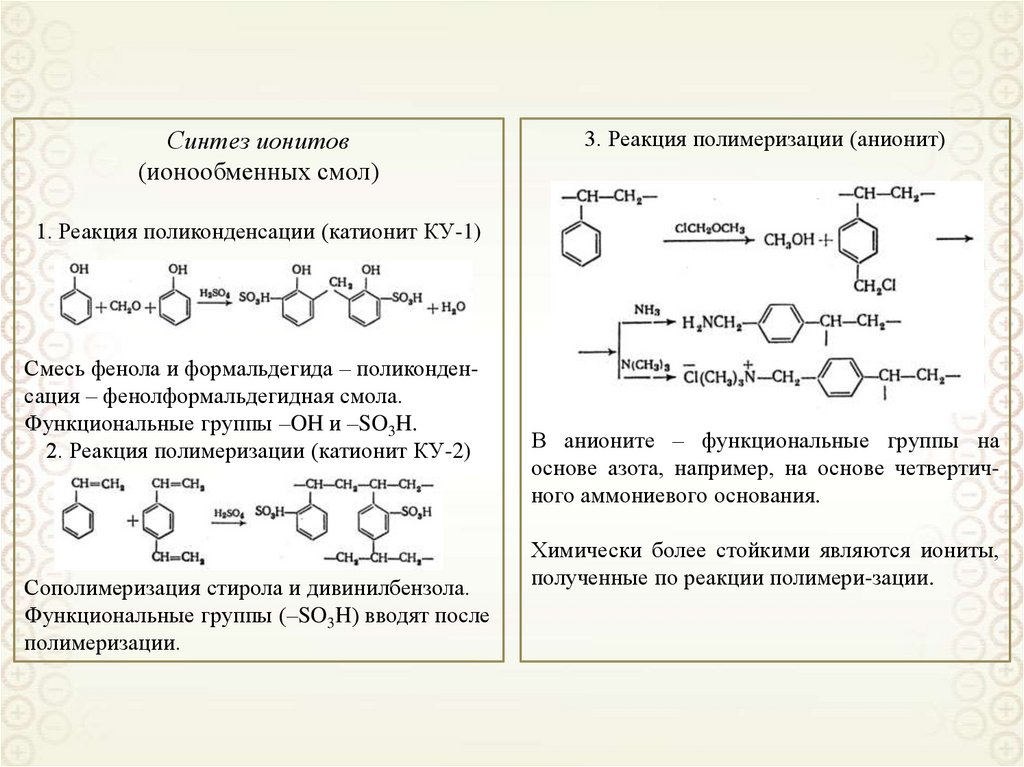

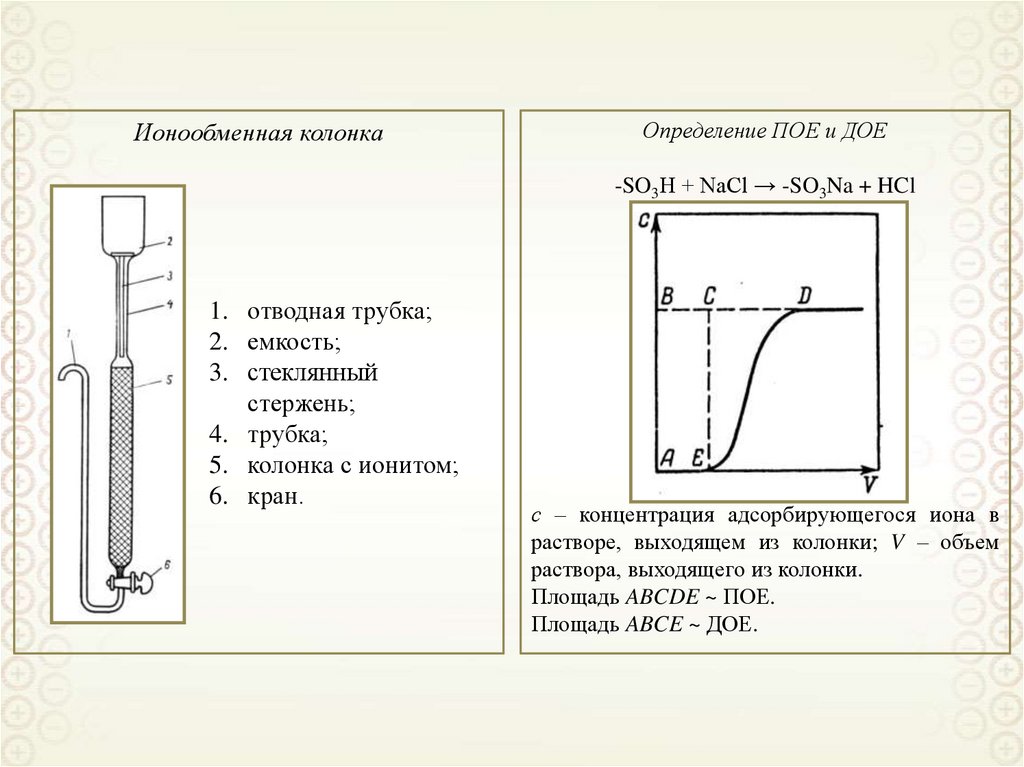





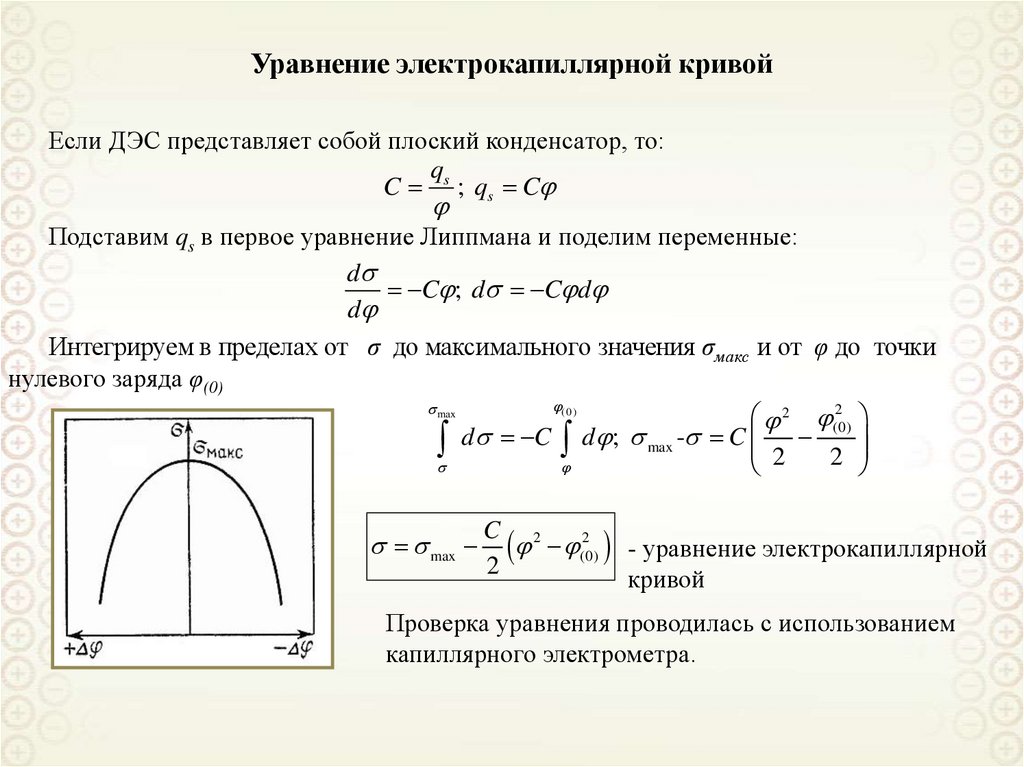
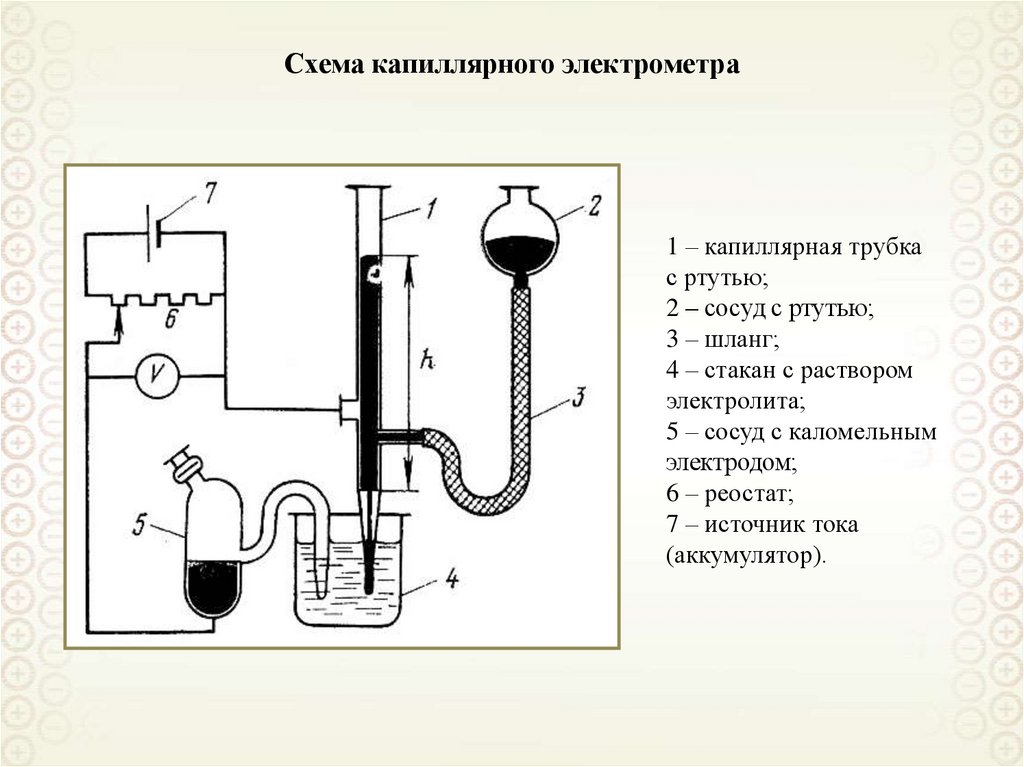








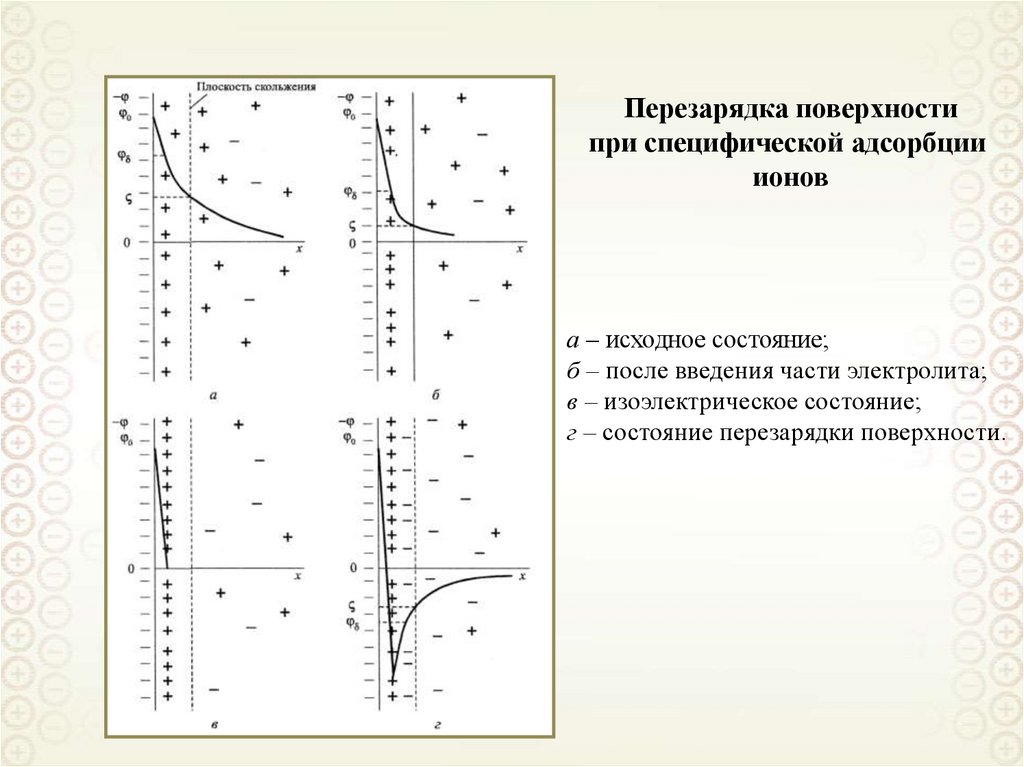




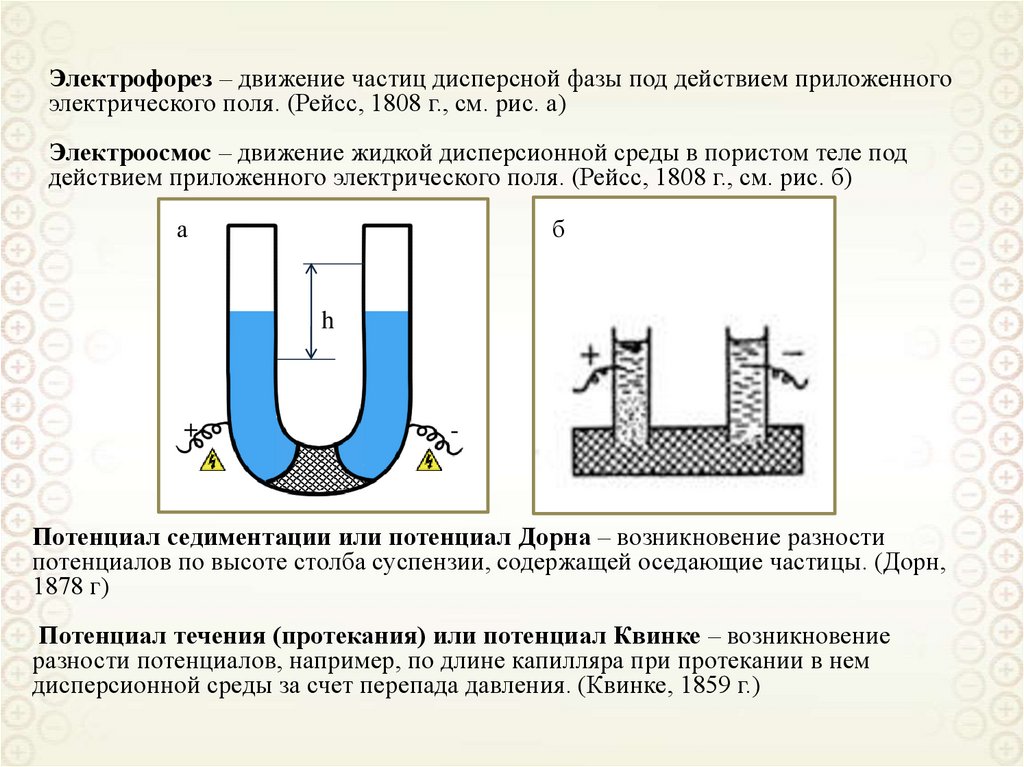



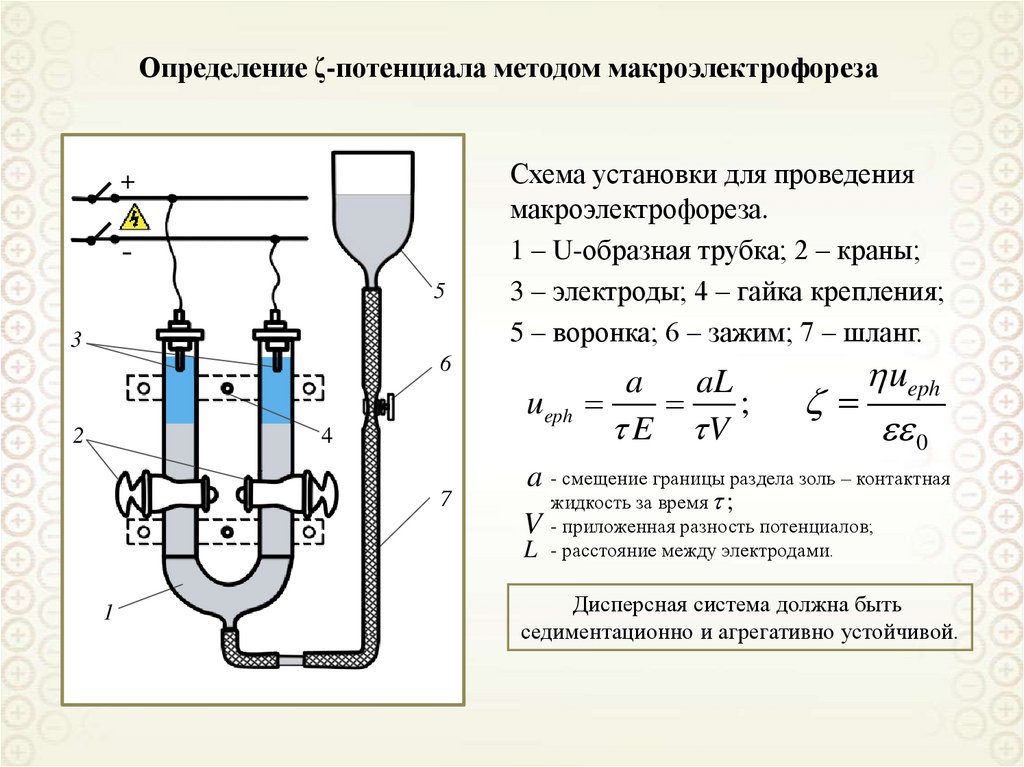









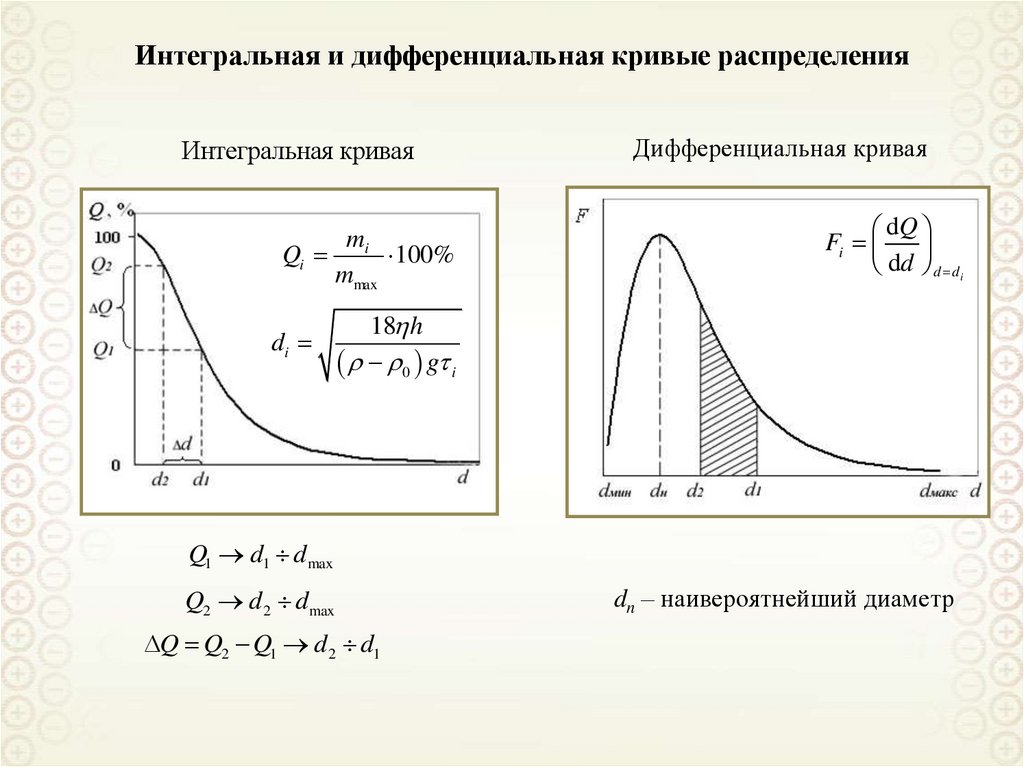



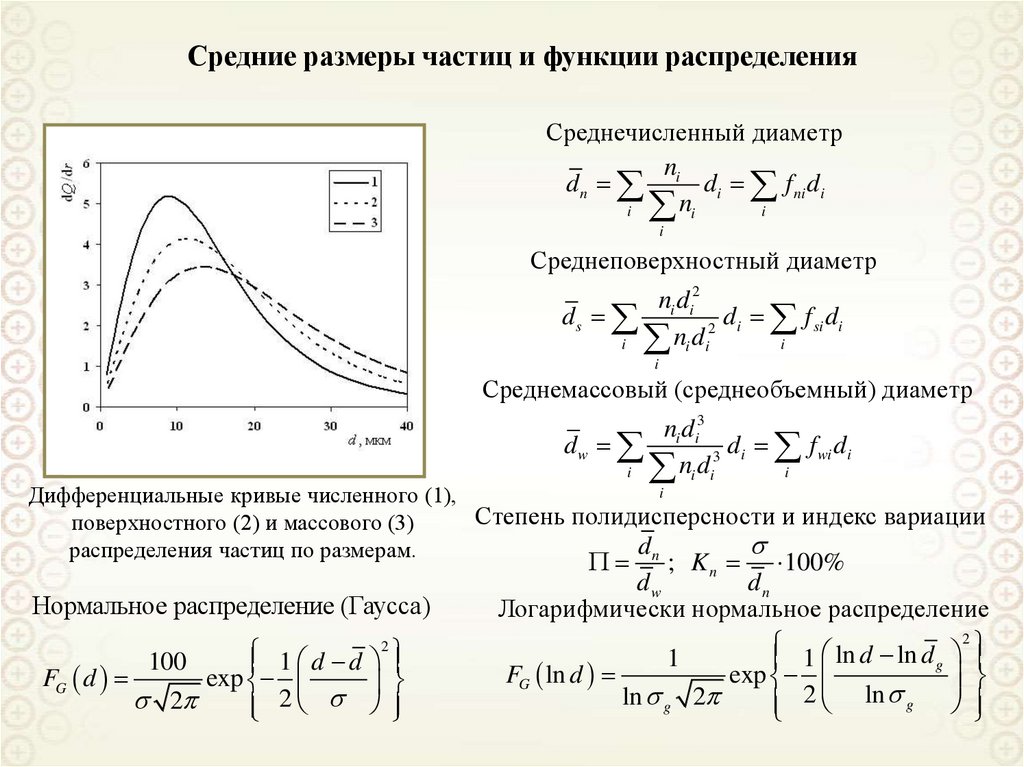
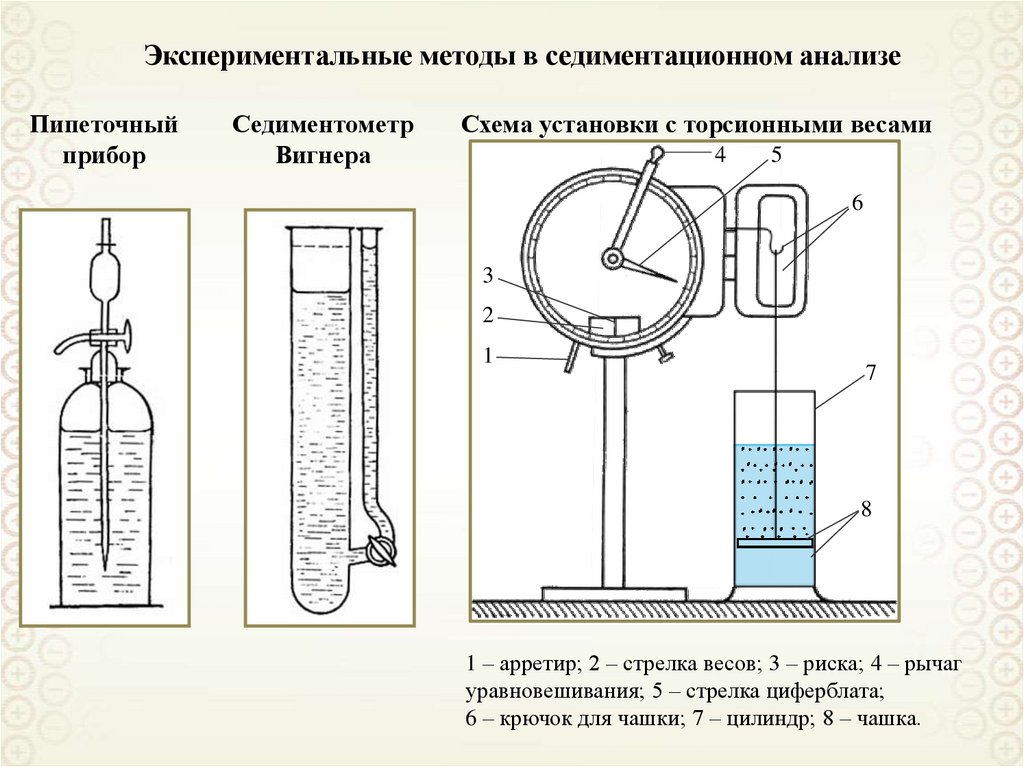


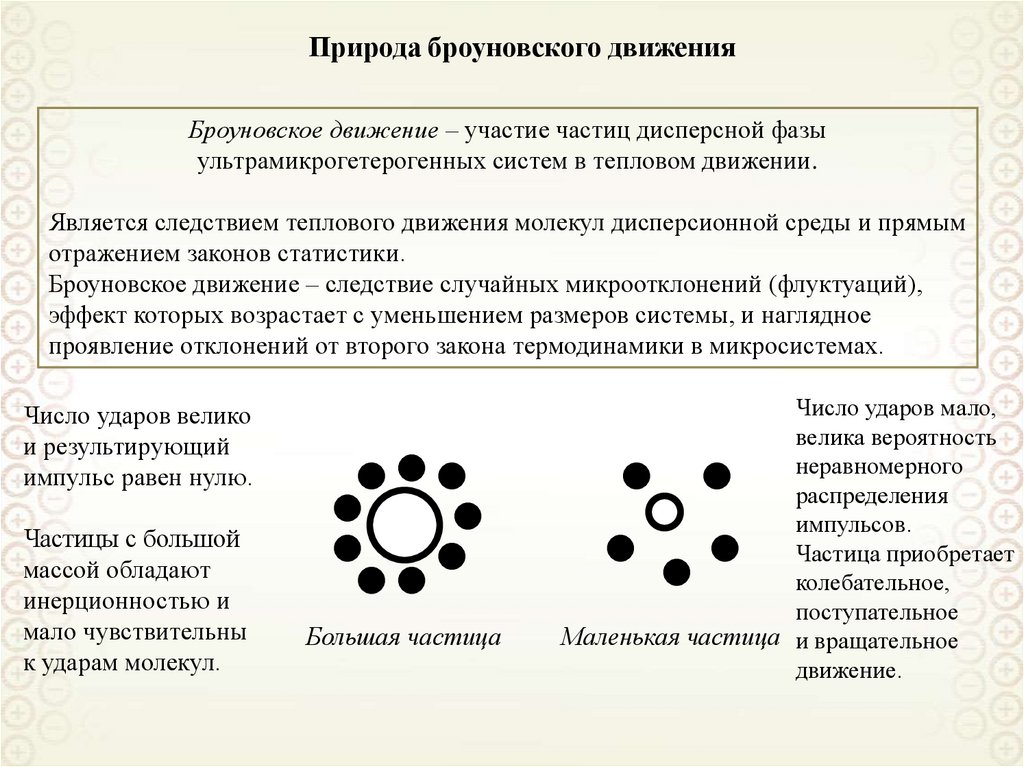




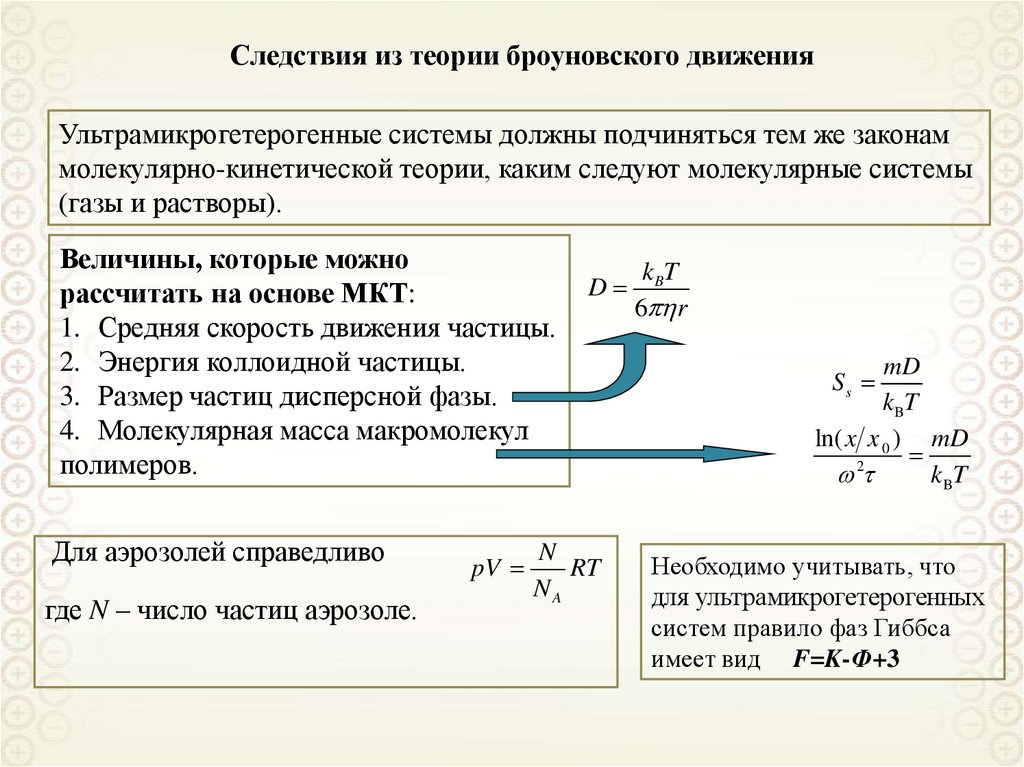




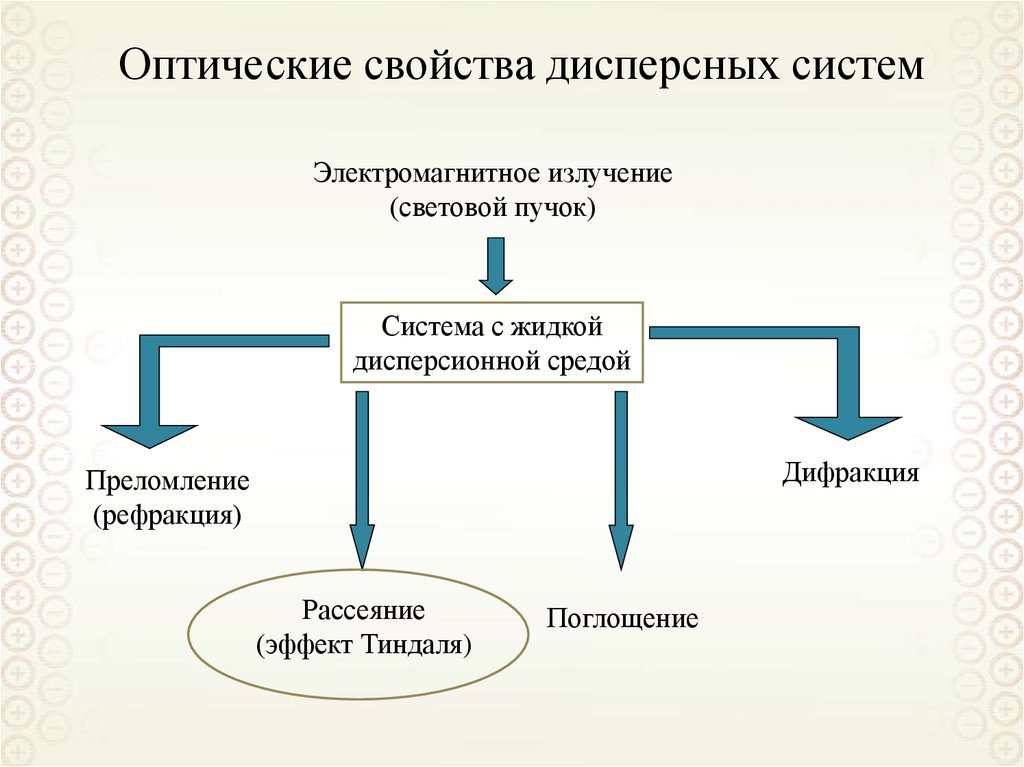
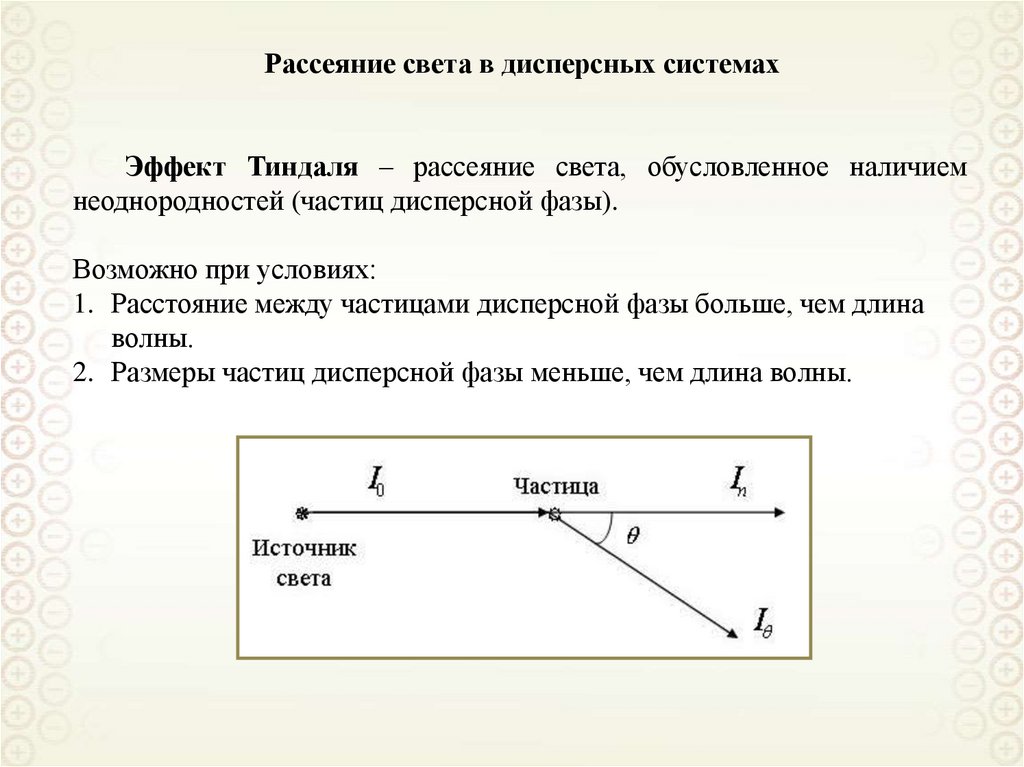








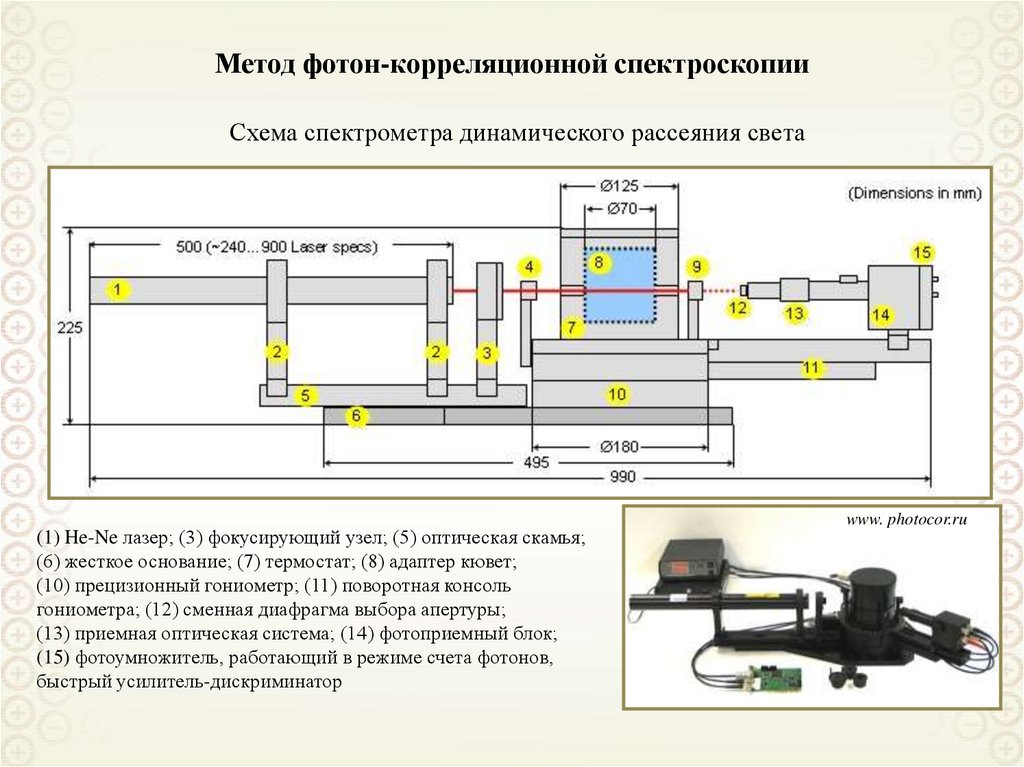
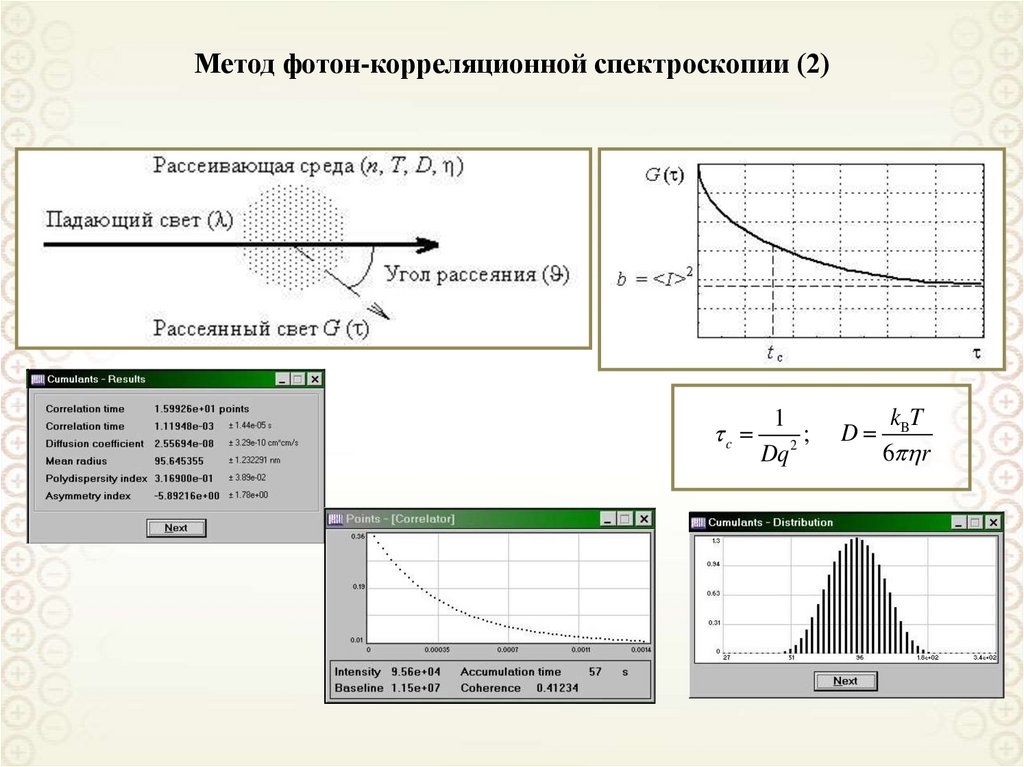

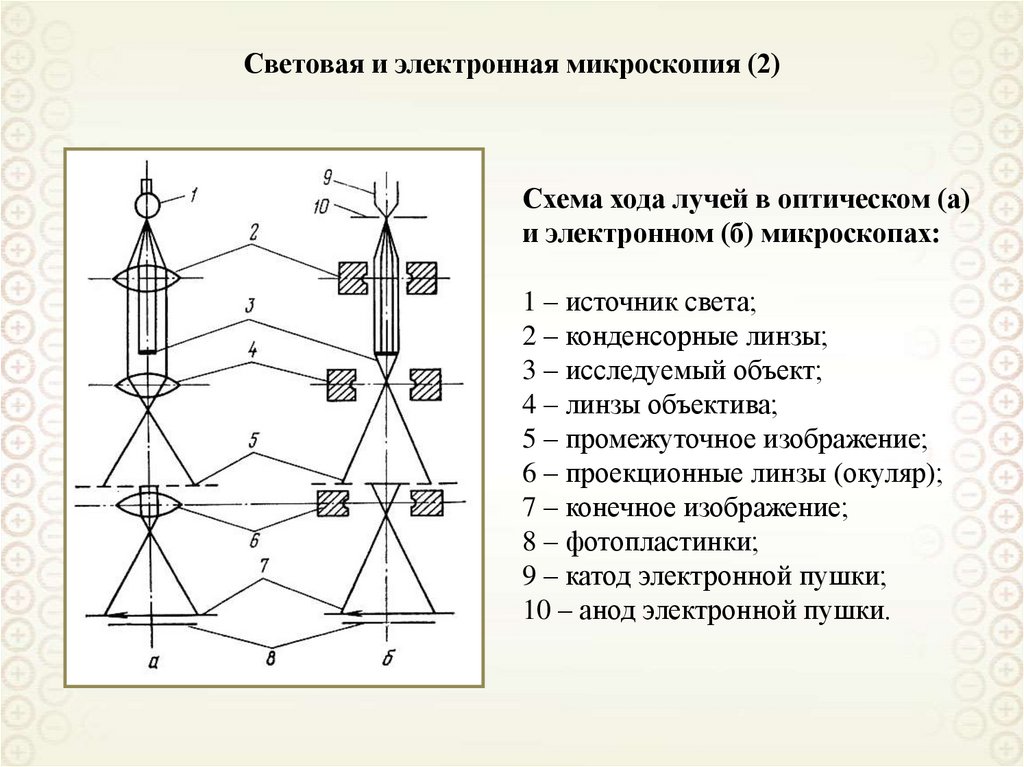
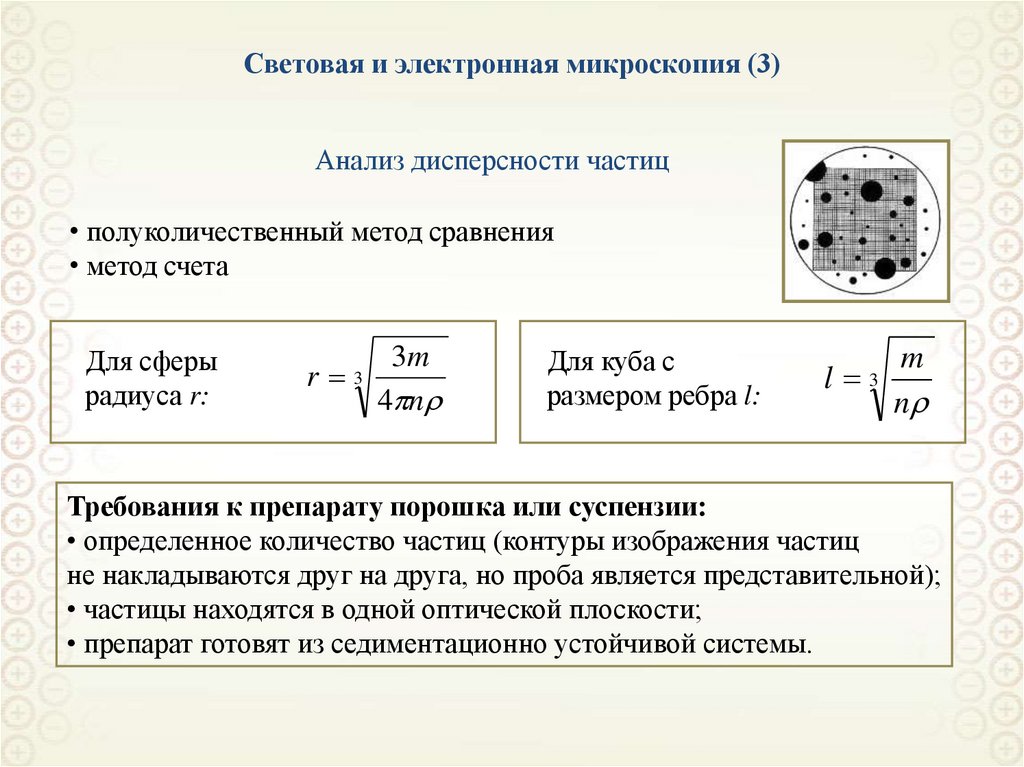

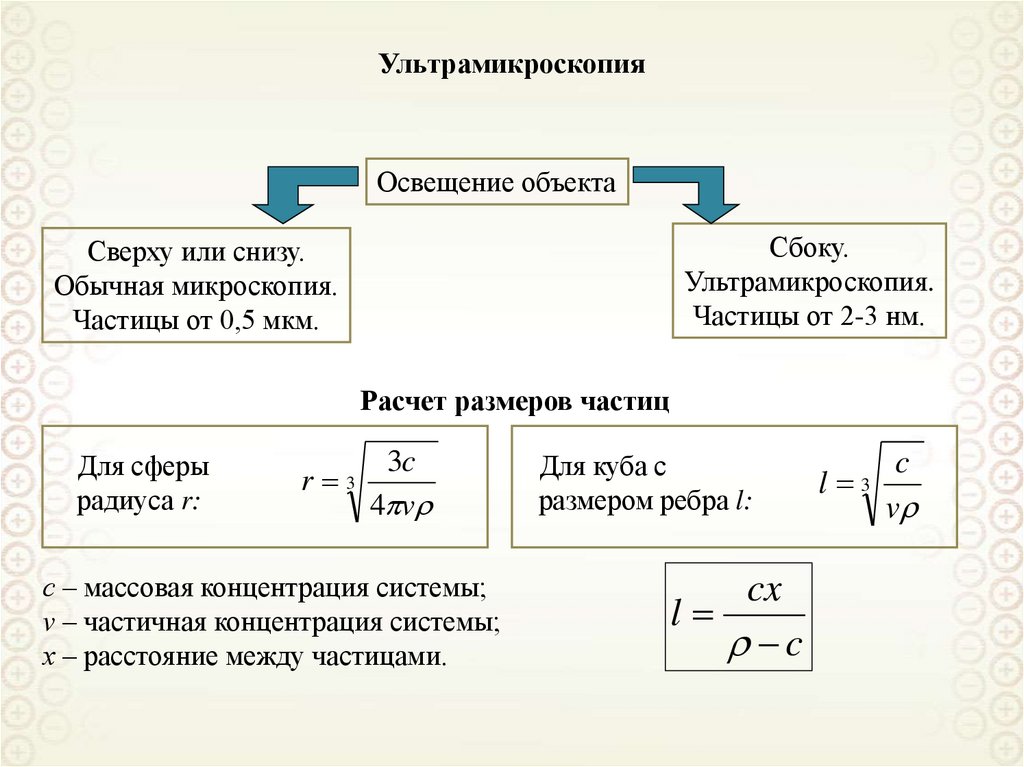
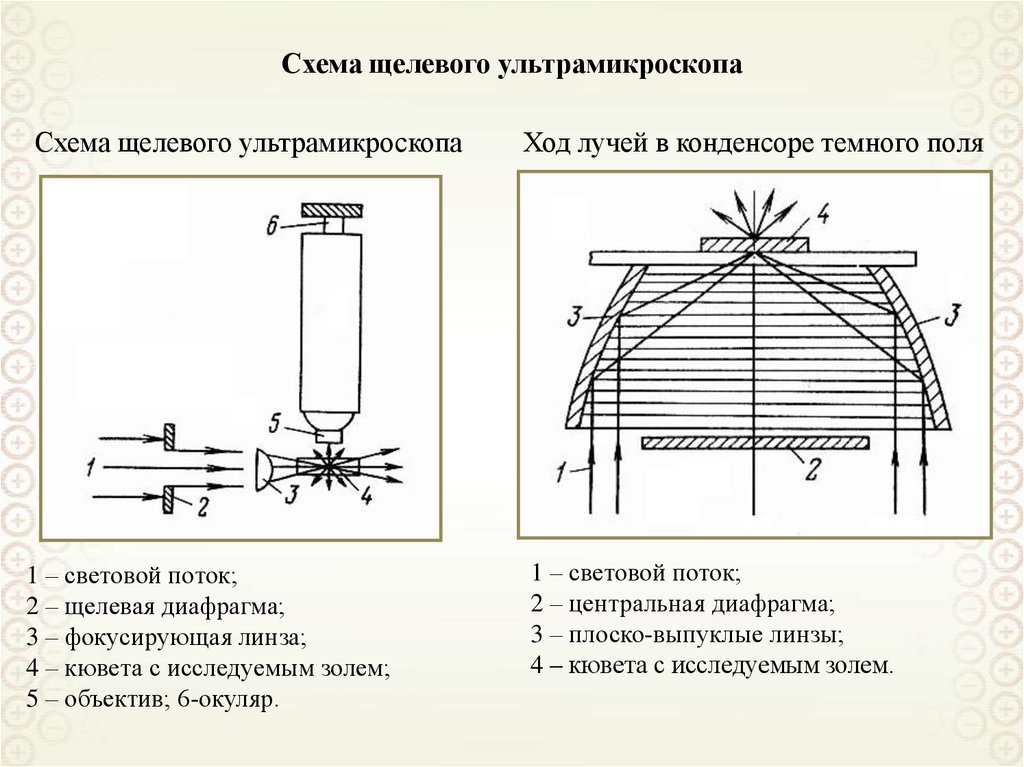

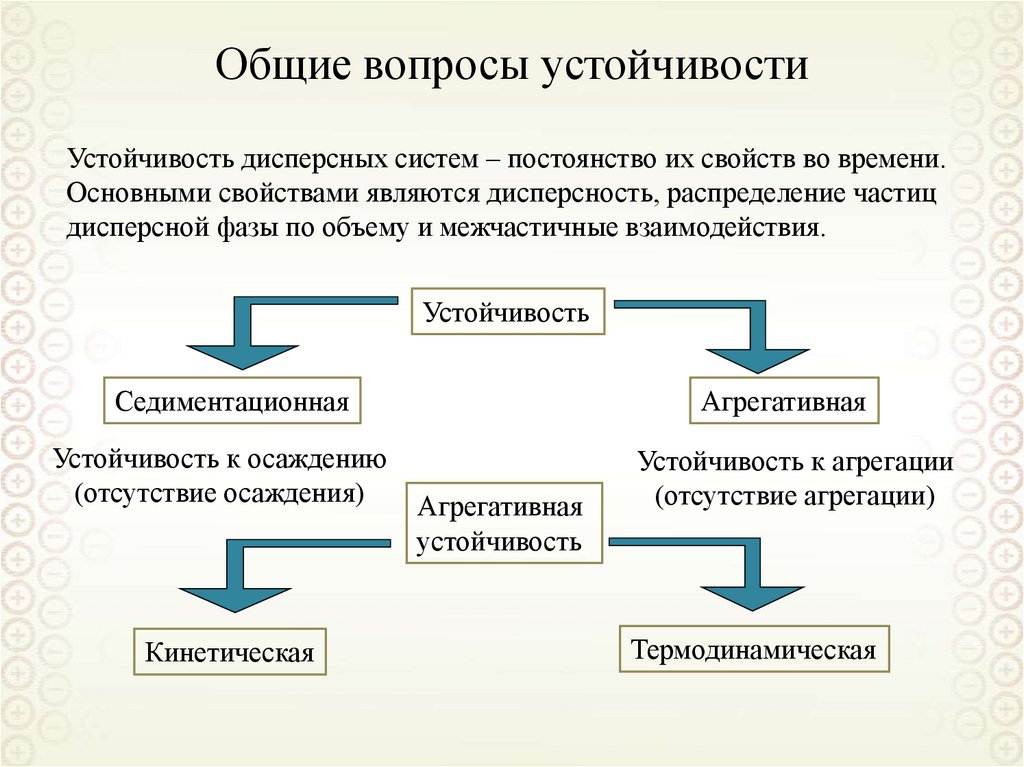

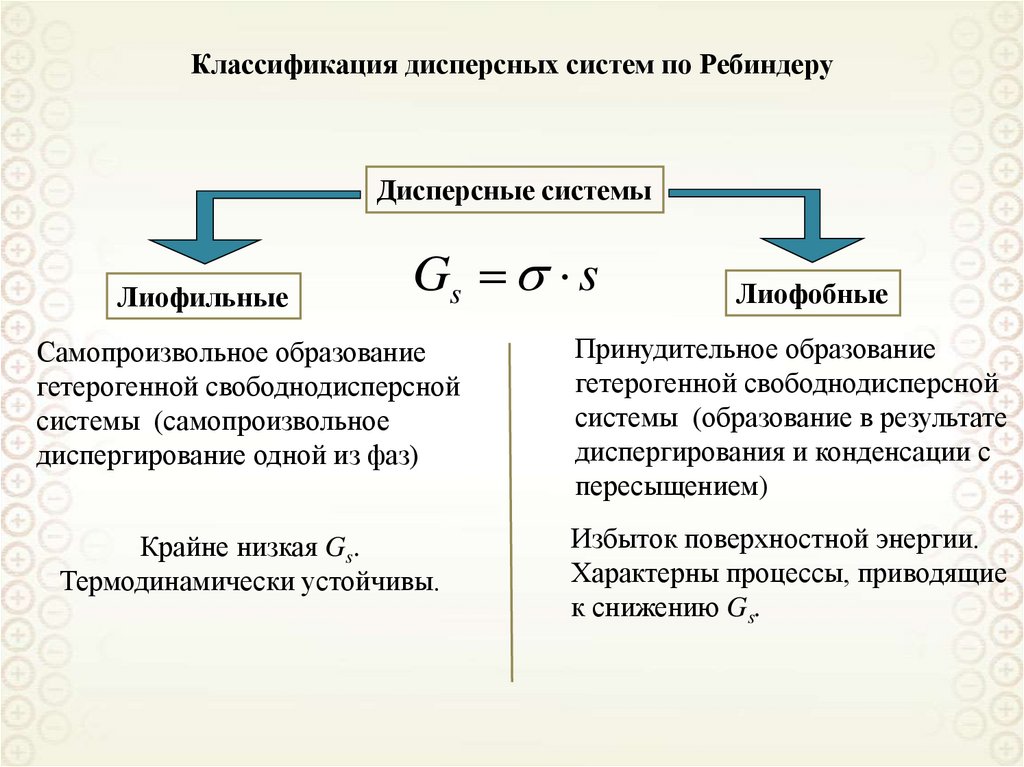



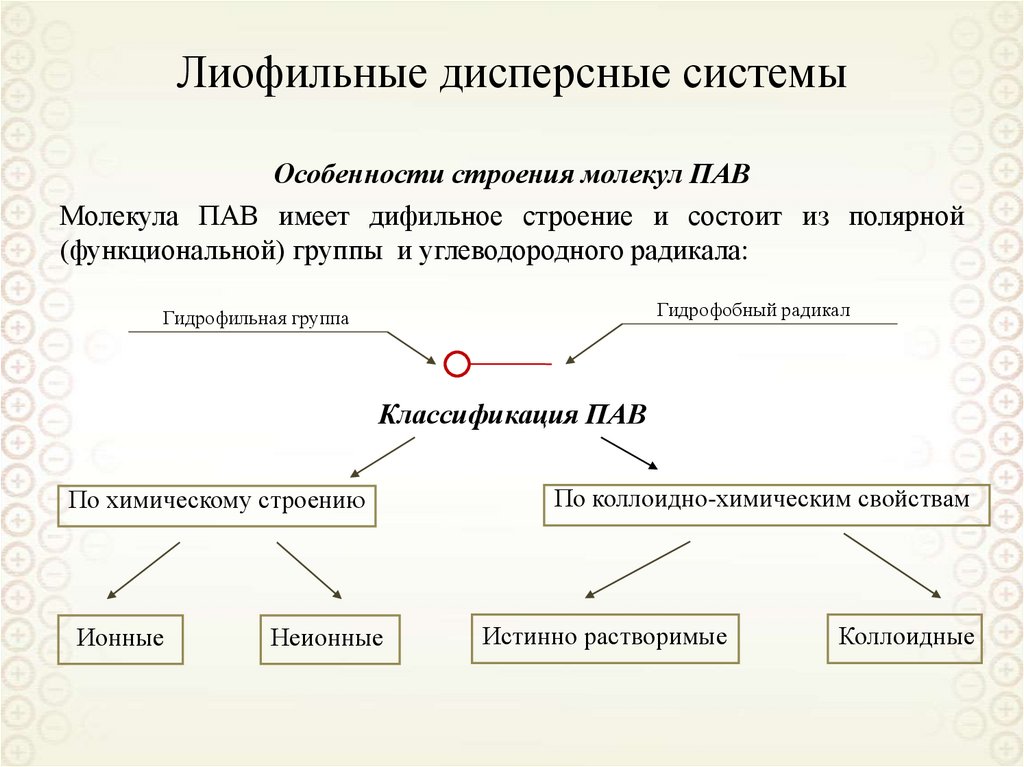







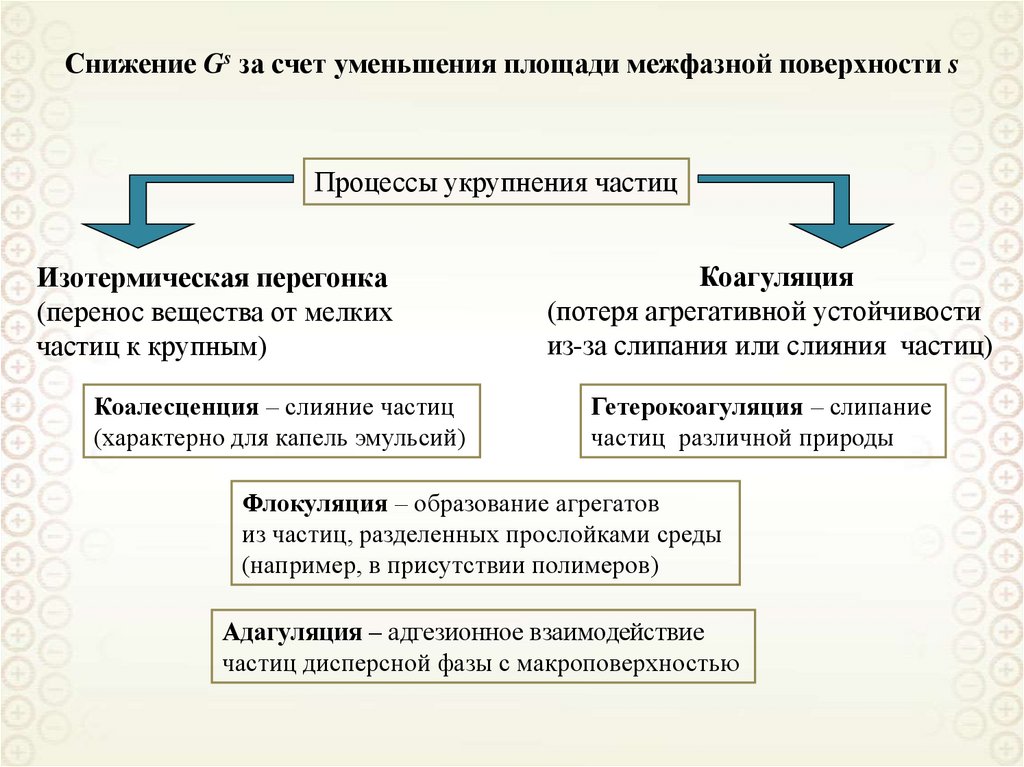




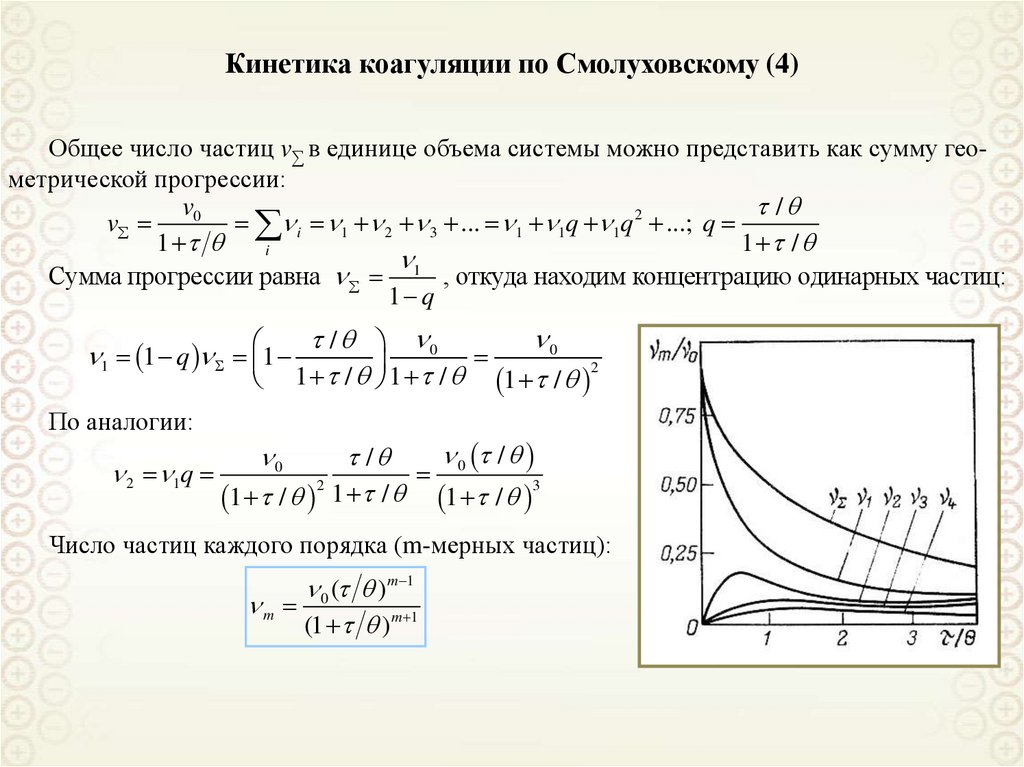


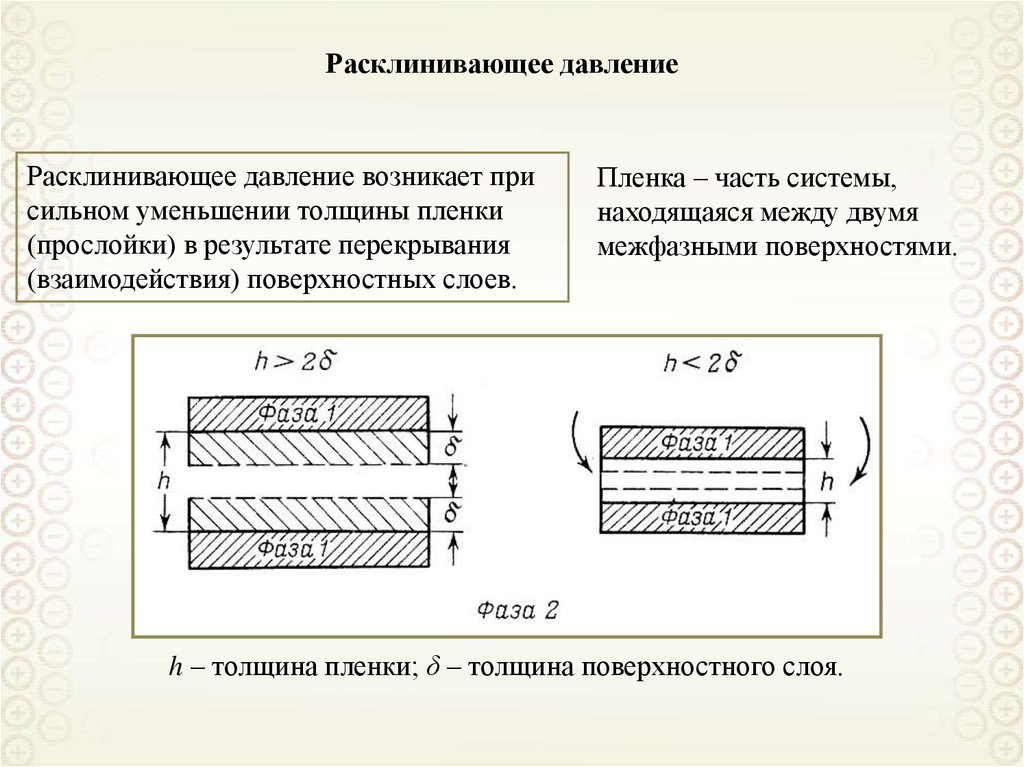




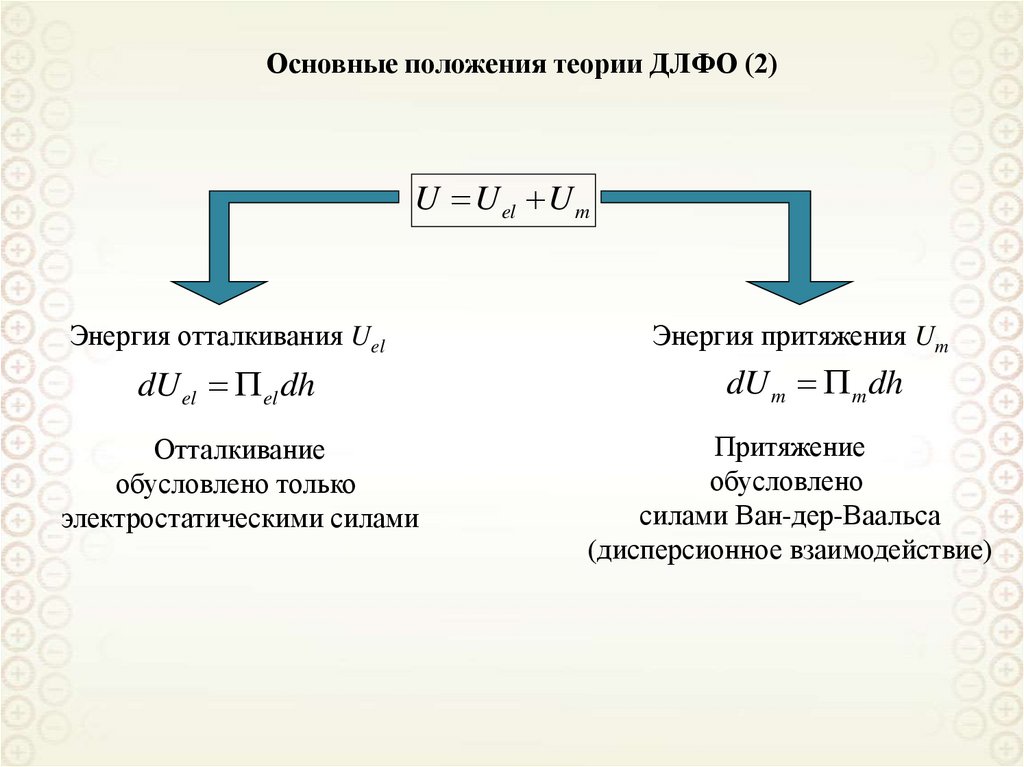
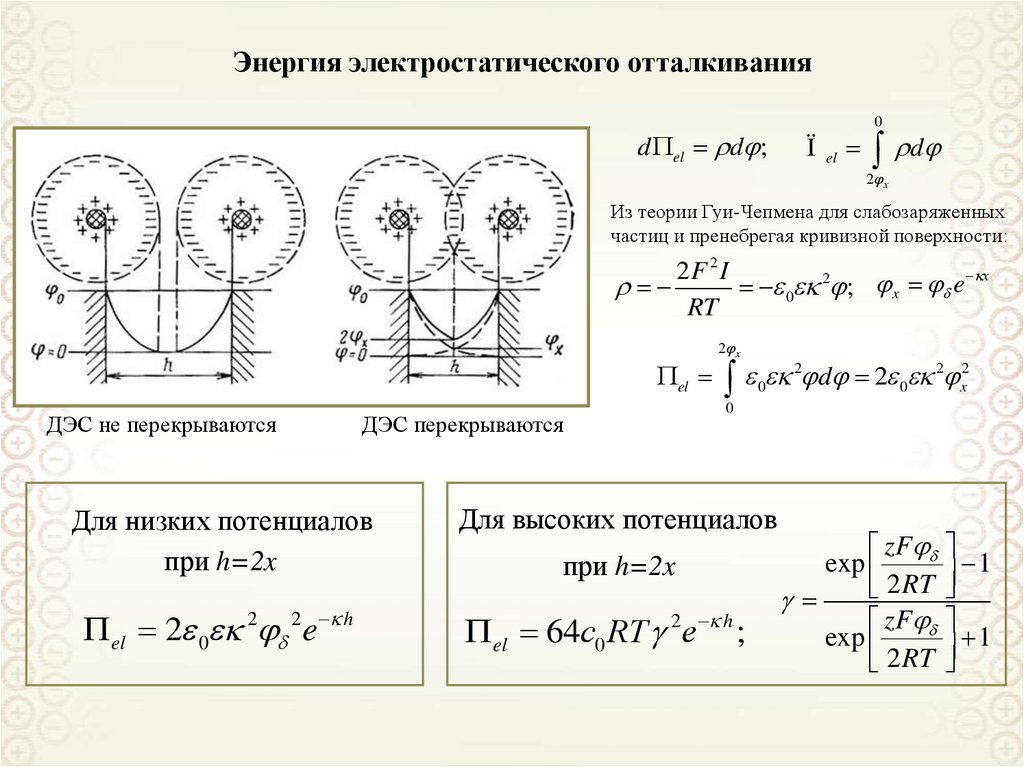



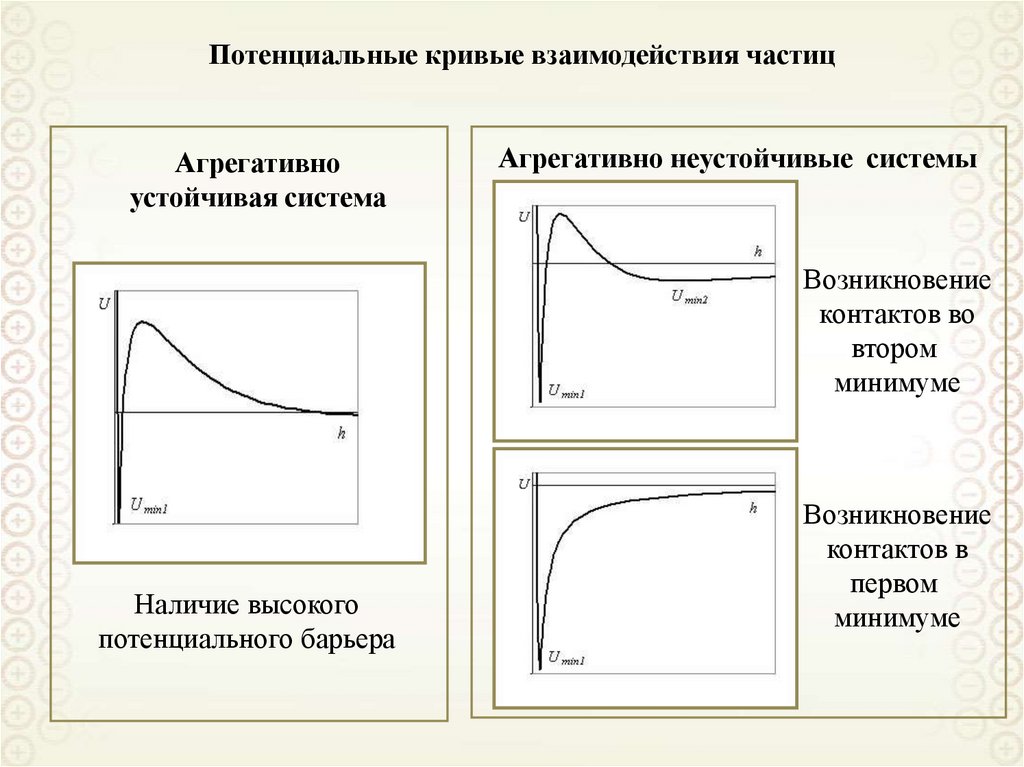

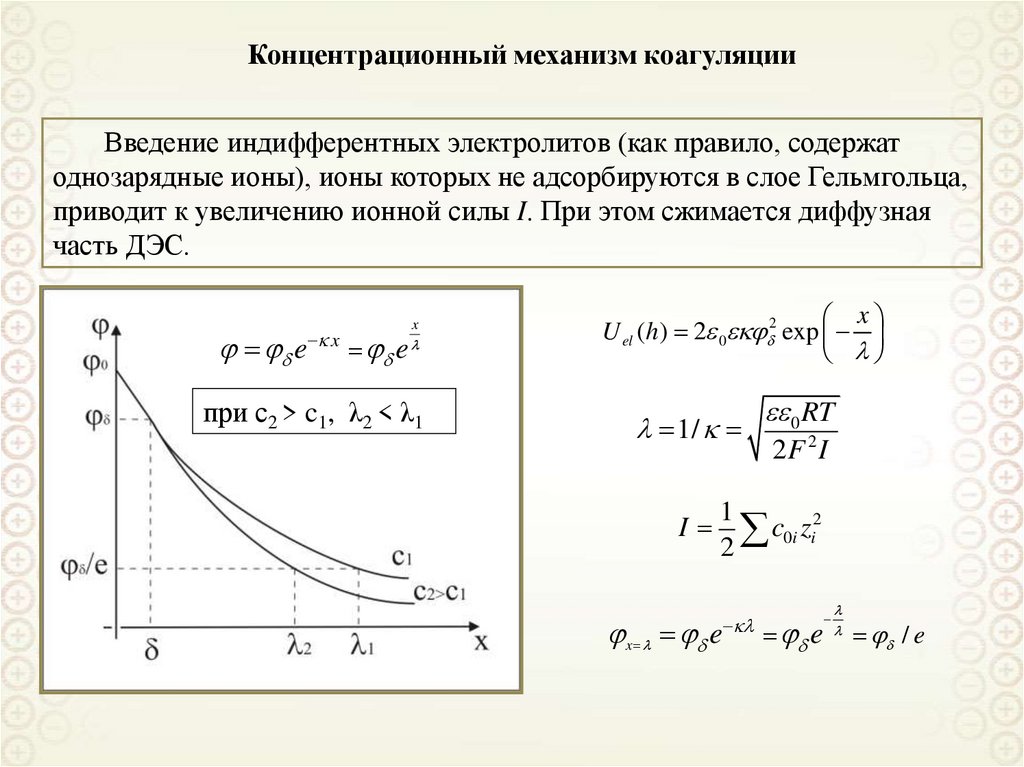


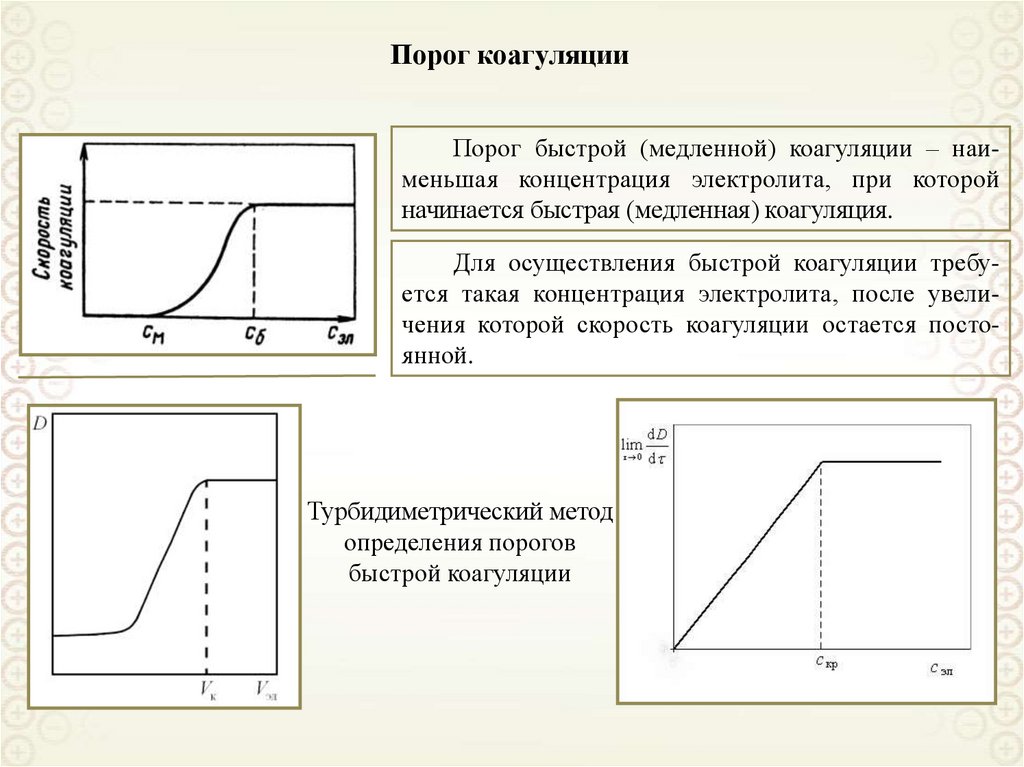
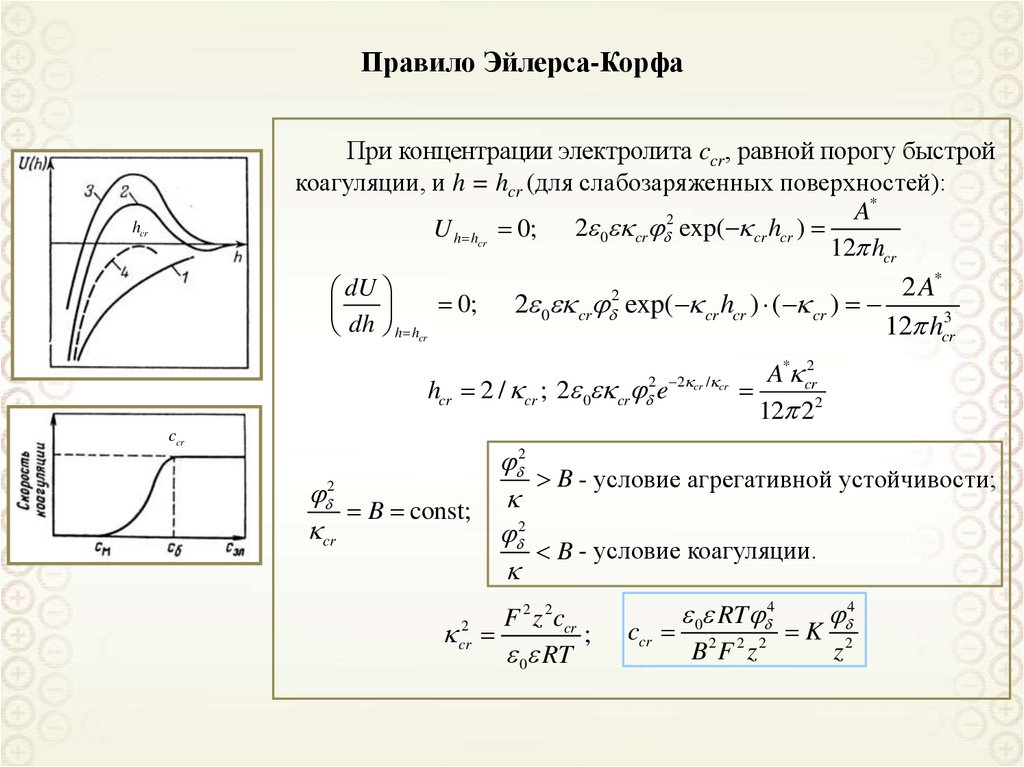






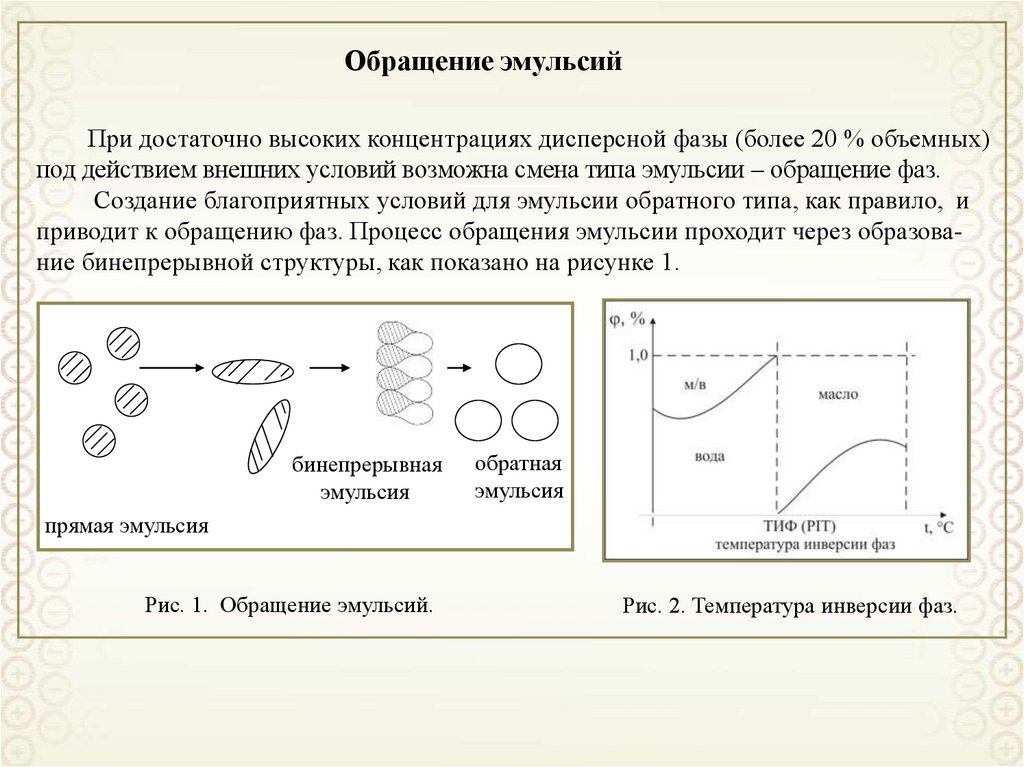
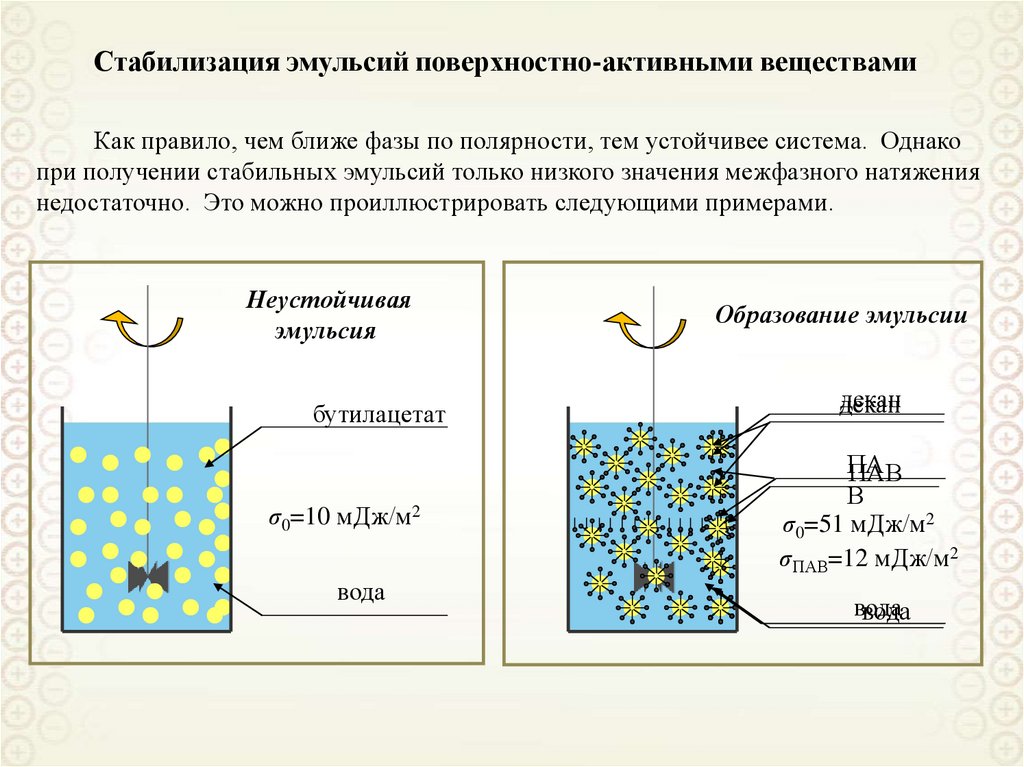




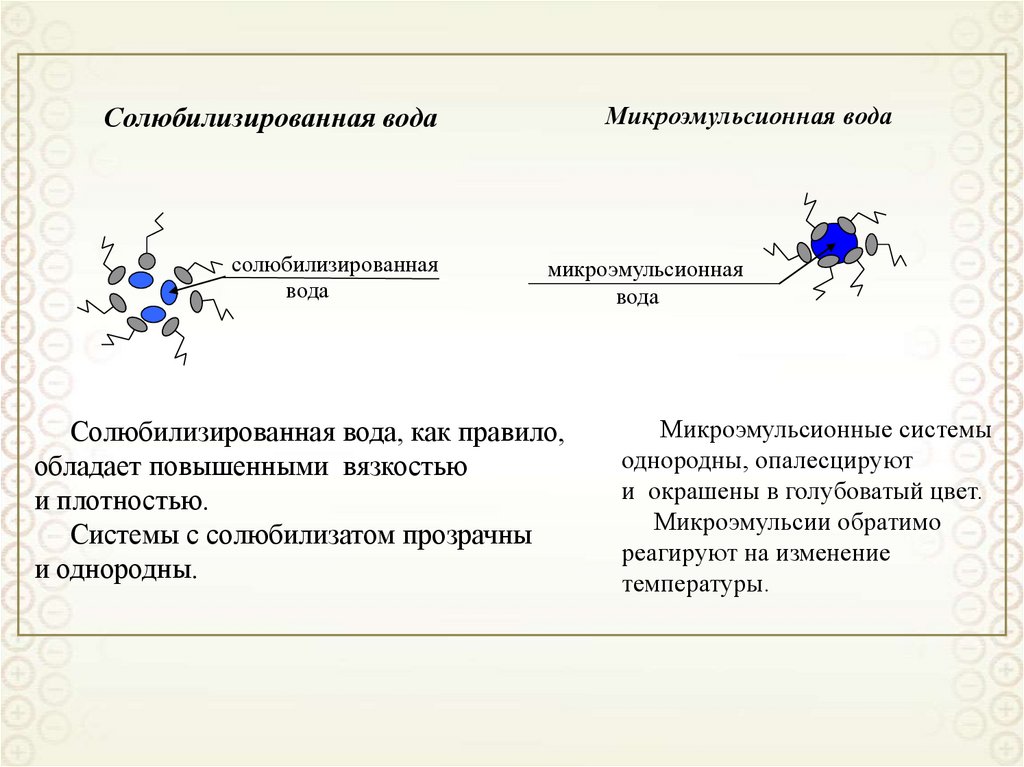



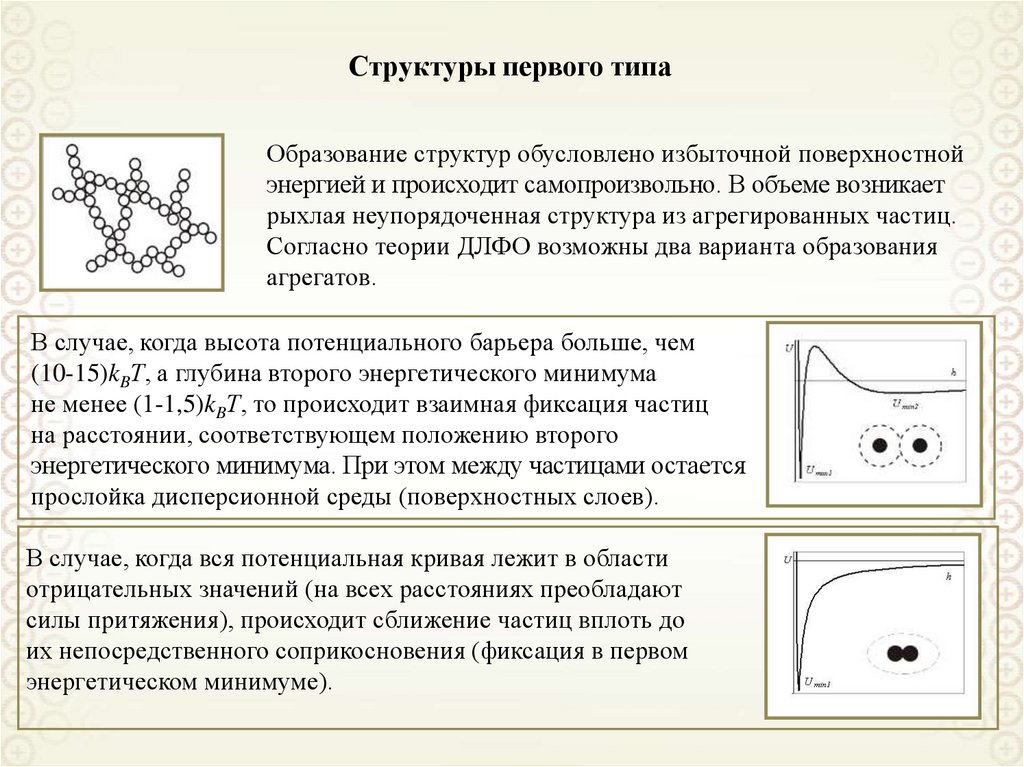


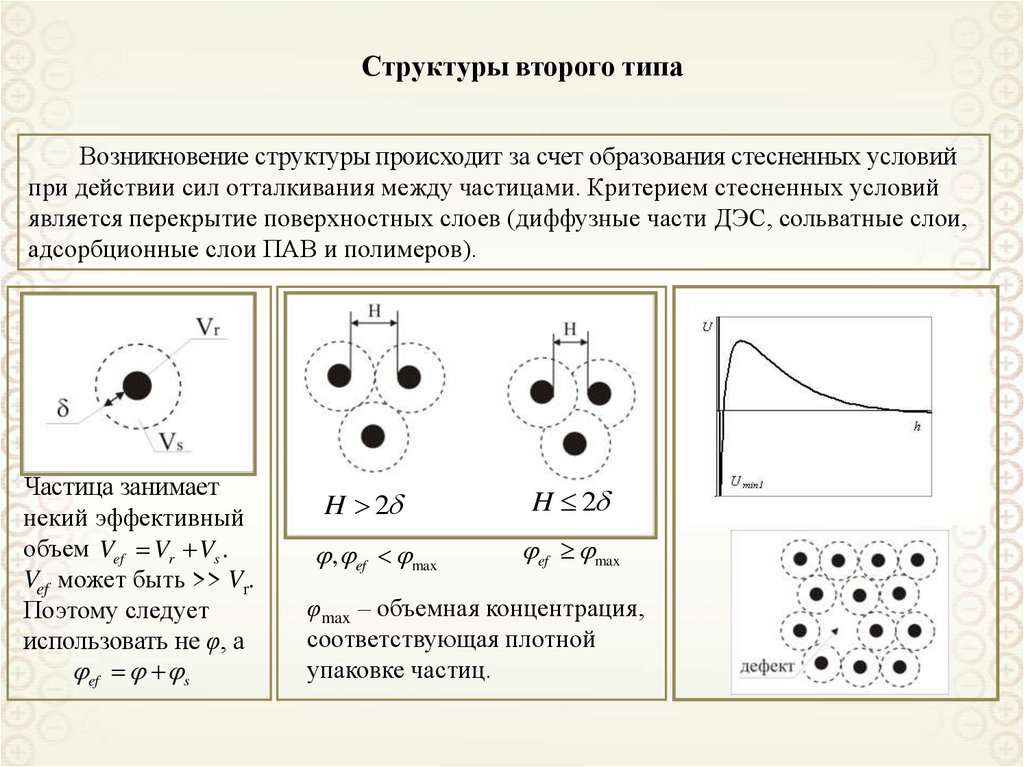



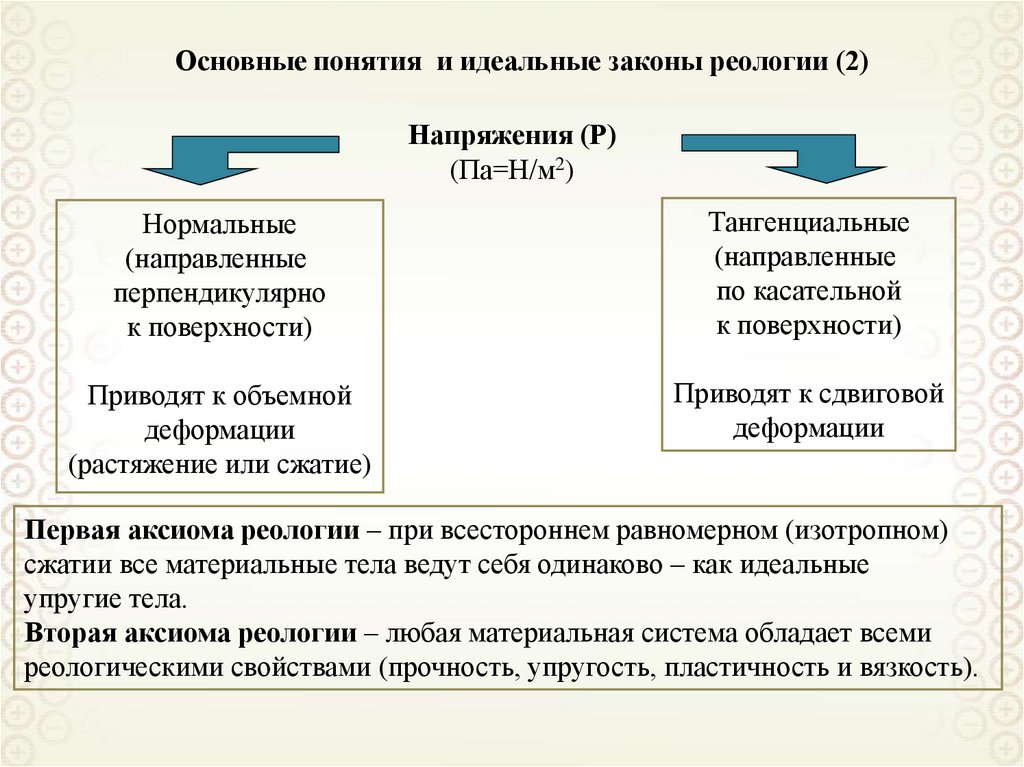
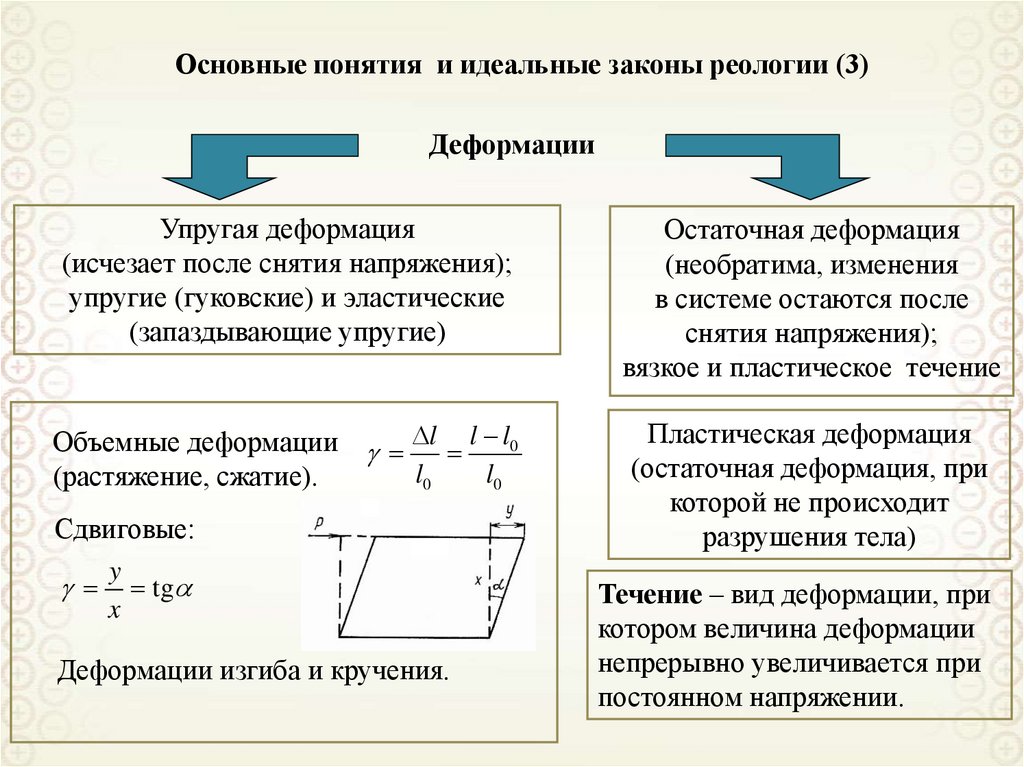






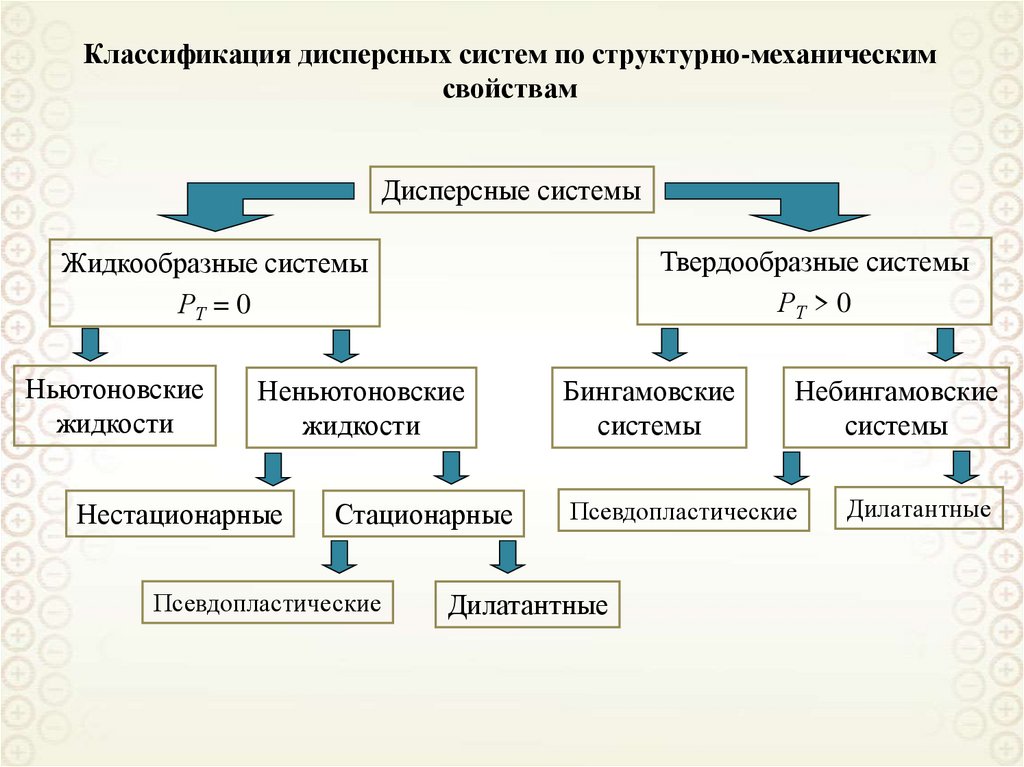

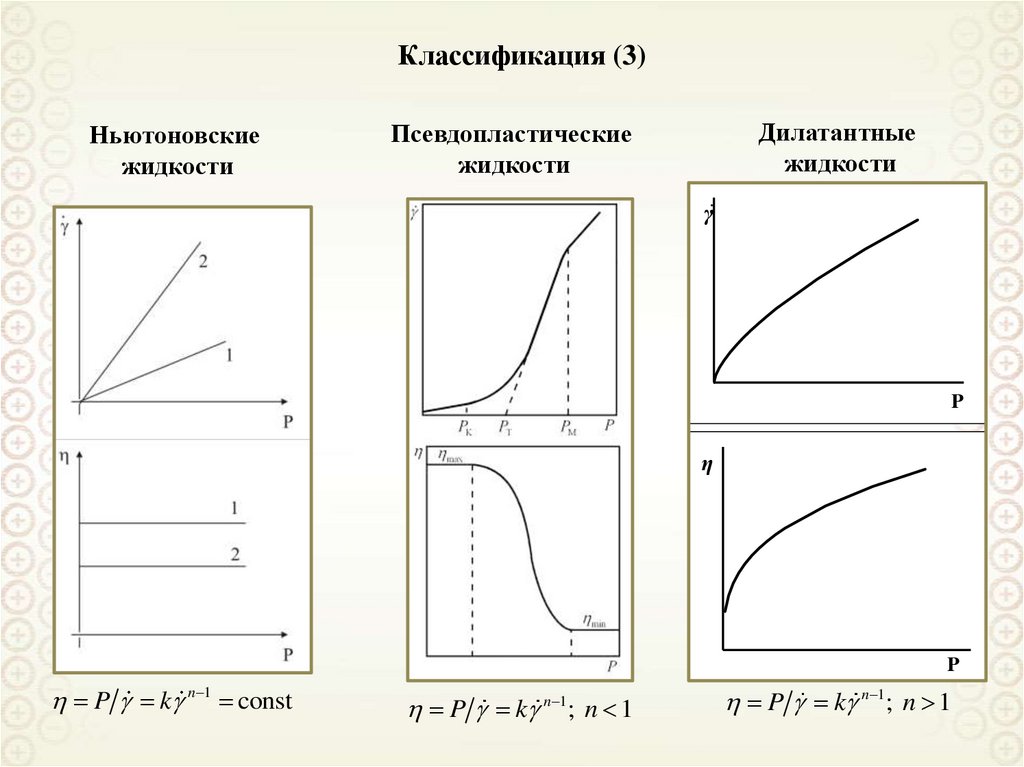





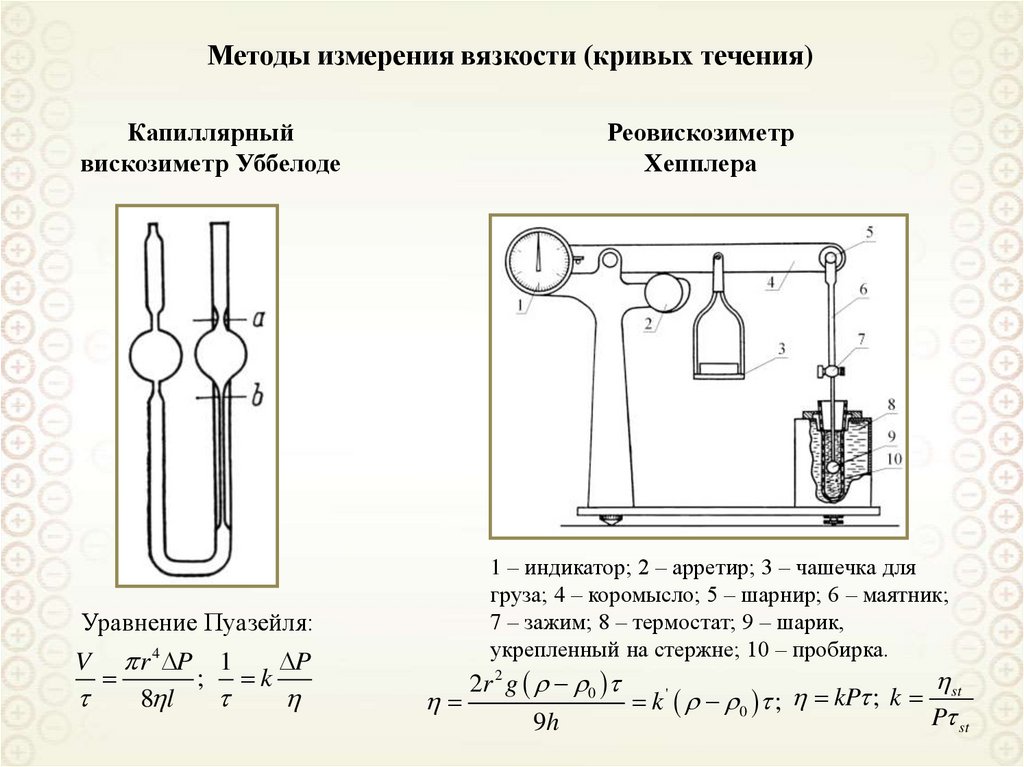
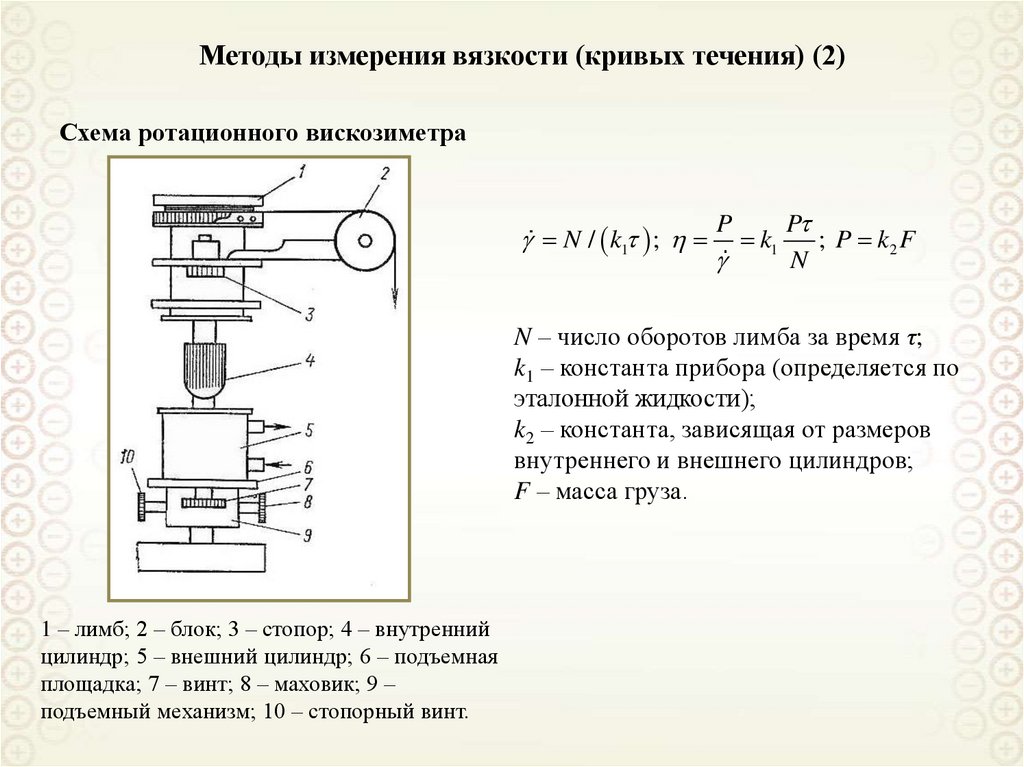
 Химия
Химия








