Адсорбция из раствора на твердом адсорбенте

1. Адсорбция из раствора на твердом адсорбенте

Раствор красителя
(метиленового голубого)
Исходный адсорбент
(силикагель)
Раствор и адсорбент
в контакте
Силикагель
после адсорбции

2. Метод избыточных величин Гиббса (2)

Метод слоя конечной толщины
(метод Гуггенгейма)
Метод избыточных величин
(метод избытков Гиббса)
A2
Абсолютная адсорбция – число молей
адсорбата в поверхностном слое,
отнесенное к единице поверхности (или
массы адсорбента) [моль/м2]
Гиббсовская адсорбция – избыток числа молей
компонента в объеме поверхностного слоя по
сравнению с числом молей этого компонента
в равном объеме объемной фазы, отнесенный
к единице поверхности (или массы адсорбента)
[моль/м2]

3. Метод избыточных величин Гиббса (3)

Отрицательная гиббсовская
адсорбция
В каких случаях
?
Для растворителя (первого компонента), в
соответствии с методом избытков Гиббса:
Различием между величинами гиббсовской и
абсолютной адсорбции можно пренебречь при:
1. при адсорбции газов и паров;
2. при адсорбции поверхностно-активных
веществ (ПАВ).
Таким образом, в общем случае:

4. Частное выражение уравнения Гиббса

Запишем уравнение Гиббса для случая
адсорбции из бинарного раствора:
Для предельно разбавленного раствора
второго компонента:
Откуда:
Для разбавленного раствора:
Окончательно:
Последнее уравнение справедливо при
физической адсорбции газов и паров.
1. Оба уравнения применимы либо в области разбавленных растворов, либо в области низких давлений
паров адсорбата.
2. Если вещество переходит из объемной фазы в
поверхностный слой, то есть Γ>0, то
.
Это означает, что физическая адсорбция
сопровождается падением поверхностного натяжения.
3. Из полученного уравнения следует, что
размерность гиббсовской адсорбции будет моль/м2.
4. Если известна изотерма поверхностного натяжения σ=fT(c), то по полученному уравнению можно рассчитать изотерму гиббсовской адсорбции.

5. Поверхностная активность

Поверхностная активность характеризует
способность данного вещества снижать поверхностное натяжение данного растворителя:
По величине g все вещества делят на поверхностно-активные (ПАВ) и поверхностно
неактивные (ПИАВ):
1. Для ПАВ (С3H7COH):
2. Для ПИАВ (KCl):
Молекулы специфических ПАВ имеют дифильное строение:
Кружок – полярная группа (-COONa, -OH,
-OSO3Na и др). Черта обозначает углеводородный радикал того или иного строения.
Зависимость поверхностного натяжения (а)
и гиббсовской адсорбции (б) от концентрации
водного раствора поверхностно-активного и
инактивного веществ: 1 – додециламин; 2 –
сульфат натрия.

6. Адсорбция поверхностно-активных веществ (ПАВ)

Адсорбция поверхностноактивных веществ (ПАВ)

7. Адсорбция ПАВ

При адсорбции ПАВ на границе
раствор – газовая фаза:
где Vs – объем поверхностного слоя;
cs и c – равновесные концентрации в
поверхностном слое и в объеме раствора;
g - поверхностная активность
Правило Дюкло-Траубе:
В гомологическом ряду ПАВ увеличение
длины углеводородного радикала на одну
метиленовую группу (-СН2-) приводит к
возрастанию поверхностной активности
приблизительно в 3,2 раза (для водных
растворов).
В общем случае:
Для полярных растворителей:
Для полярных растворителей:
Обозначение молекулы ПАВ:
○------

8. Зависимость поверхностного натяжения от концентрации раствора

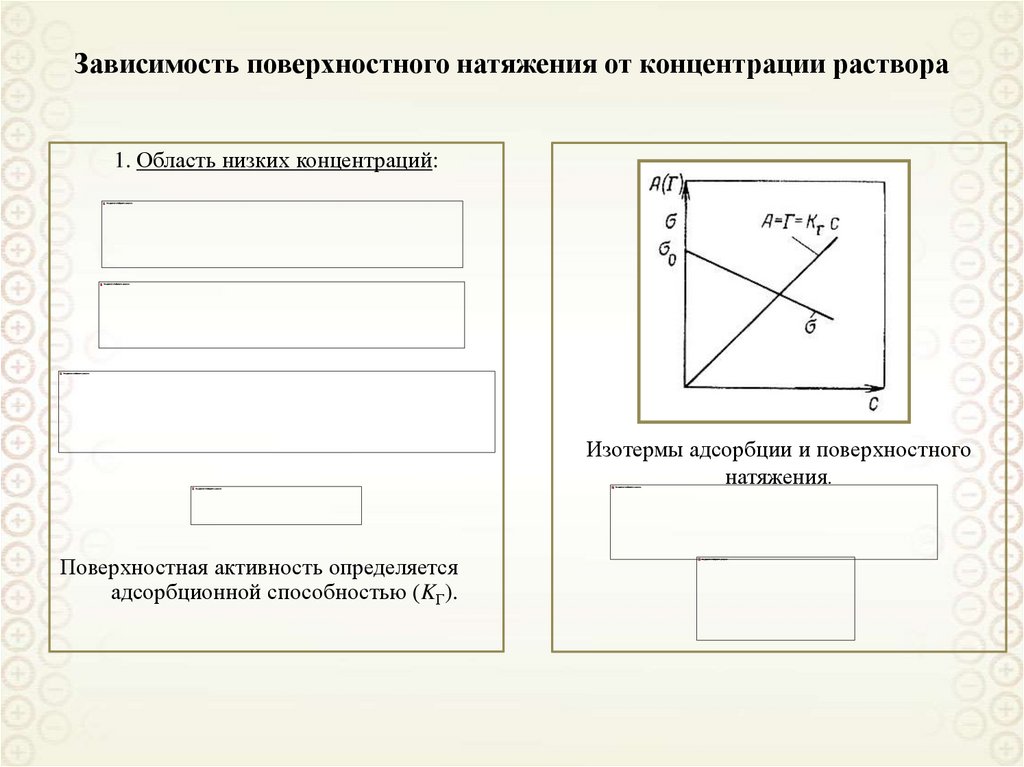
1. Область низких концентраций:
И
Изотермы адсорбции и поверхностного
натяжения.
Поверхностная активность определяется
адсорбционной способностью (KГ).

9. Зависимость поверхностного натяжения от концентрации раствора (2)

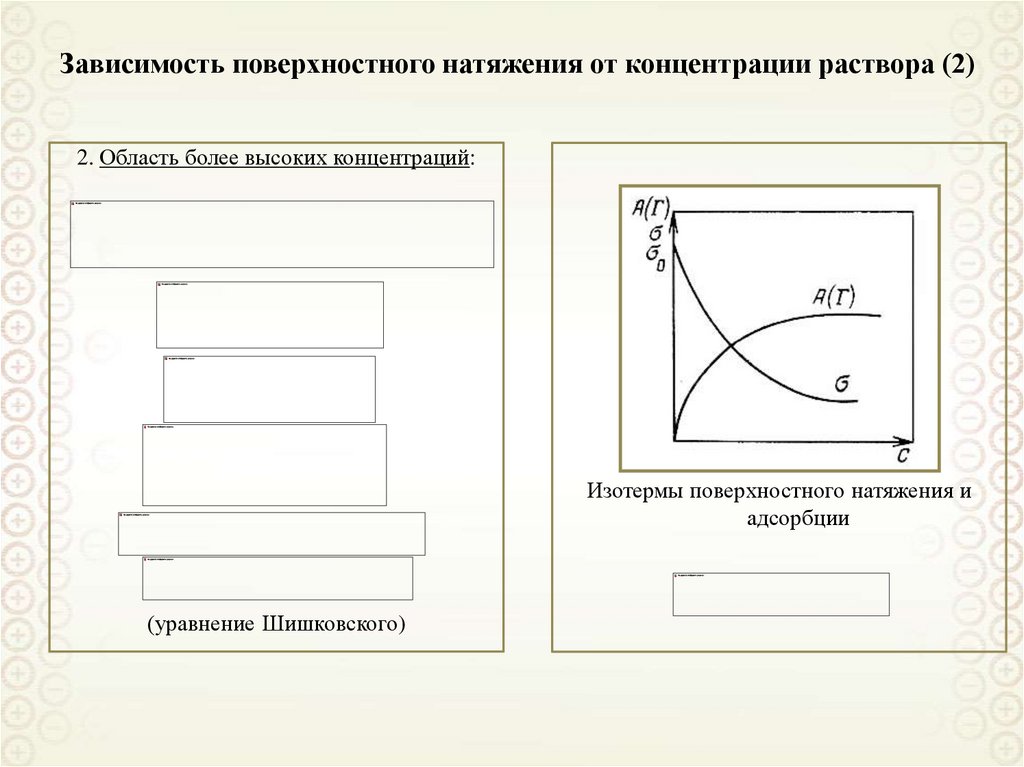
2. Область более высоких концентраций:
Изотермы поверхностного натяжения и
адсорбции
(уравнение Шишковского)

10. Уравнения состояния поверхностных адсорбционных пленок

1. Область низких концентраций:
где: π – поверхностное давление;
sM – площадь поверхности, занимаемая
одним молем.
Адсорбционная пленка ведет себя как
идеальный двумерный газ.
α и β учитывают межмолекулярные
взаимодействия и собственный размер
молекул (как a и b).
2. Область более высоких концентраций:
3. Область высоких концентраций:

11. Типы поверхностных пленок и определение их характеристик

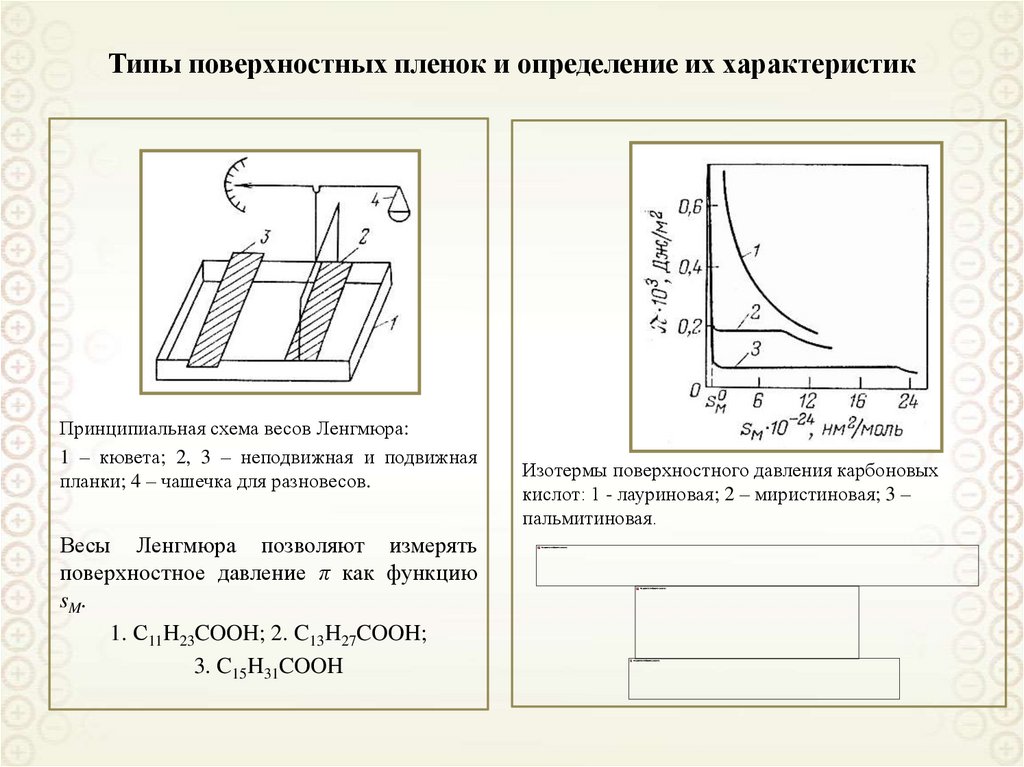
Принципиальная схема весов Ленгмюра:
1 – кювета; 2, 3 – неподвижная и подвижная
планки; 4 – чашечка для разновесов.
Весы Ленгмюра позволяют измерять
поверхностное давление π как функцию
sM.
1. С11H23COOH; 2. C13H27COOH;
3. C15H31COOH
Изотермы поверхностного давления карбоновых
кислот: 1 - лауриновая; 2 – миристиновая; 3 –
пальмитиновая.

12. Адсорбционные взаимодействия

Ионообменная адсорбция

13. Ионообменная адсорбция

Ионный обмен открыт в 1850 г.
(Томсон, Уэй).
Ионный обмен – обмен ионами между
раствором и адсорбентом.
Адсорбенты – иониты (катиониты,
аниониты).
Ионит имеет «каркас» (полимерный),
сшитый ковалентными связями. К каркасу
присоединены функциональные группы –
кислотные или основные.
Ионный обмен (катионов или
анионов) обеспечивает диссоциация
функциональных групп.
Ионит несет отрицательный
(катионит) или положительный (анионит)
заряды, компенсируемые противоионами,
которые и участвуют в ионном обмене.
Классификация ионитов
I. По происхождению
1. Природные (кристаллические алюмосиликаты – шабазит, глауконит и др.; почвенный
гумус).
2. Синтетические (на основе полимеров).
II. По составу
1. Неорганические. 2. Органические.
III. По знаку заряда обмениваемых ионов
1. Катиониты. 2. Аниониты. 3. Амфолиты.

14.

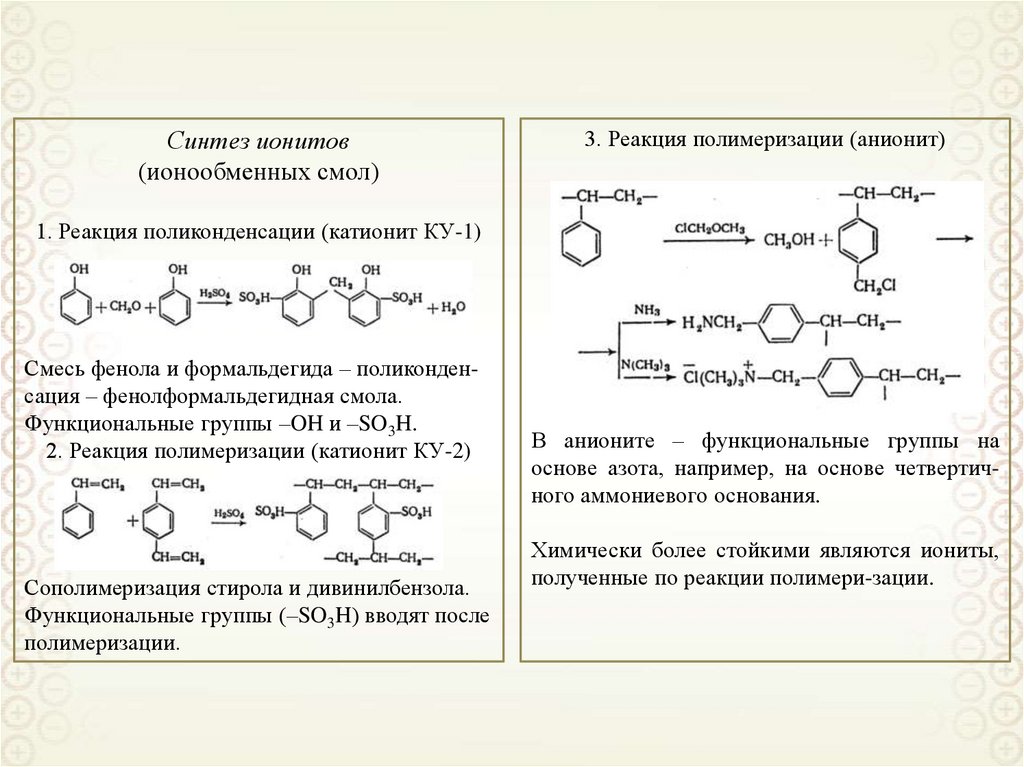
Синтез ионитов
(ионообменных смол)
3. Реакция полимеризации (анионит)
1. Реакция поликонденсации (катионит КУ-1)
Смесь фенола и формальдегида – поликонденсация – фенолформальдегидная смола.
Функциональные группы –OH и –SO3H.
2. Реакция полимеризации (катионит КУ-2)
Сополимеризация стирола и дивинилбензола.
Функциональные группы (–SO3H) вводят после
полимеризации.
В анионите – функциональные группы на
основе азота, например, на основе четвертичного аммониевого основания.
Химически более стойкими являются иониты,
полученные по реакции полимери-зации.

15.

Основные физико-химические свойства
1. Емкость – способность адсорбировать
определенное количество ионов.
2. Кислотно-основные свойства –
определяются константами диссоциации
функциональных групп.
3. Селективность – способность избирательно
адсорбировать определенные ионы или
группу ионов.
4. Набухаемость – влияет на селективность
адсорбции.
Емкость
Различают:
1. Статическая или полная обменная емкость
(ПОЕ).
2. Динамическая обменная емкость (ДОЕ).
ПОЕ – общее количество ионогенных групп
ионита, выраженное в эквивалентах и
отнесенное к единице массы (или объема)
ионита (у природных – 0,2-0,3 мг-экв/г; у
синтетических – 3-10 мг-экв/г).
ДОЕ – емкость до проскока извлекаемого
(адсорбируемого)
иона;
зависит
от
технологических условий.

16.

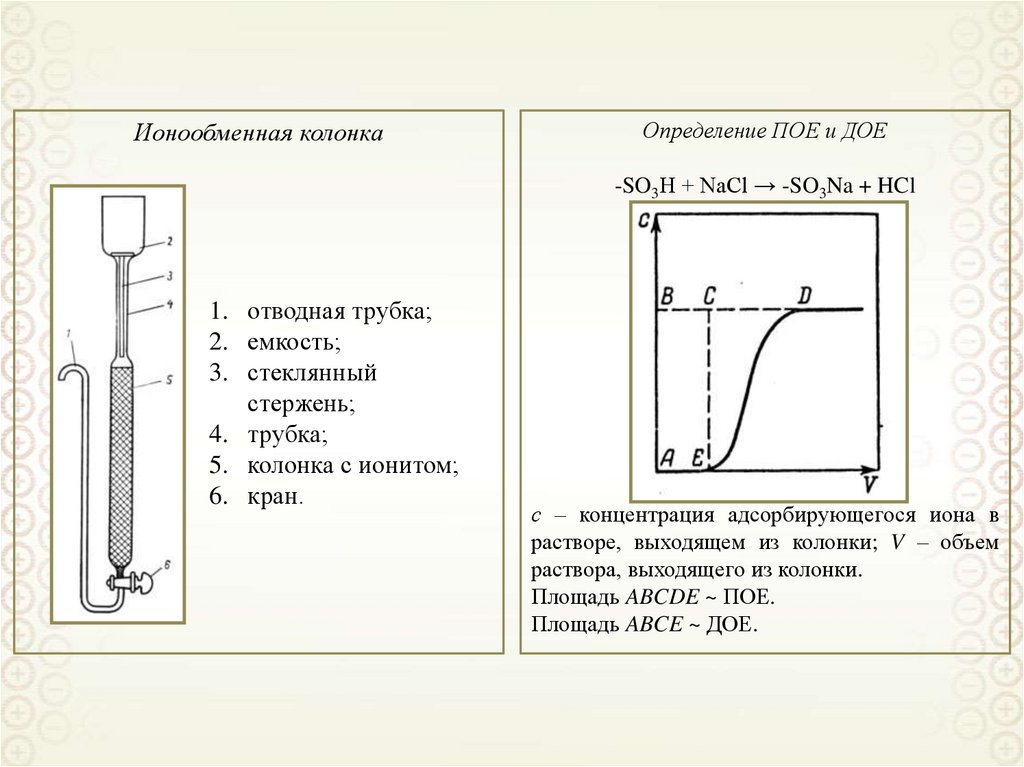
Ионообменная колонка
Определение ПОЕ и ДОЕ
-SO3H + NaCl → -SO3Na + HCl
1. отводная трубка;
2. емкость;
3. стеклянный
стержень;
4. трубка;
5. колонка с ионитом;
6. кран.
с – концентрация адсорбирующегося иона в
растворе, выходящем из колонки; V – объем
раствора, выходящего из колонки.
Площадь ABCDE ~ ПОЕ.
Площадь ABCE ~ ДОЕ.

17.

Кислотно-основные свойства
Константа равновесия ионного обмена
K
Катиониты:
1. Сильнокислотные (-SO3H).
2. Слабокислотные (-OH, -COOH).
Аниониты:
1. Сильноосновные (-N(CH3)3Cl).
2. Слабоосновные (-NH2, =NH, ≡N).
Кислотно-основные свойства определяют
рабочий интервал значений рН.
2-SO3H + Ca2+ ↔ (-SO3)2 + 2H+
z2 = 2; z1 = 1;
= H+; M2 = Ca2+
Термодинамическая и концентрационная
константы равновесия:
Константа Никольского:

18. Электрические явления на поверхностях

Двойной электрический слой

19. Двойной электрический слой (ДЭС)

При контакте двух фаз, из которых хотя бы одна является жидкой, на
межфазной границе, как правило, возникает двойной электрический слой
(ДЭС), который состоит из двух слоев зарядов противоположного знака.
Механизмы формирования ДЭС:
1. Переход зарядов из одной фазы в другую.
2. Преимущественная адсорбция ионов одного знака заряда из объема одной
из фаз.
3. Ориентирование полярных молекул на межфазной границе.
Правило Фаянса-Панета:
Структуру кристаллической решетки
могут достраивать те ионы, которые
есть в ее составе или изоморфные.
Правило Кёна:
Из двух соприкасающихся фаз положительно заряжается та, которая имеет большую диэлектрическую проницаемость.

20.

Термодинамические уравнения Липпмана
Для дисперсной системы с ДЭС запишем уравнение, вытекающее из первого и второго начал термодинамики (без учета химической энергии):
(1)
При T = const:
(2)
Полный дифференциал энергии Гиббса:
(3)
Вычитаем уравнение (2) из уравнения (3):
(4)
Разделим все члены уравнения на площадь поверхностного слоя s:
- первое уравнение Липпмана, где
- заряд единицы поверхности.
При самопроизвольном формировании ДЭС знаки заряда и потенциала совпадают
и тогда
, то есть формирование ДЭС ведет к снижению поверхностного натяжения. При qs = 0, φ = φ(0), где φ(0) – потенциал нулевого заряда.

21.

Термодинамические уравнения Липпмана (2)
Запишем выражение для дифференциальной емкости ДЭС как конденсатора и
подставим в него заряд из первого уравнения Липпмана:
Получаем второе уравнение Липпмана:
Уравнения Липпмана позволяют рассчитать заряд поверхности и электрическую
емкость ДЭС, если известна зависимость σ = f(φ), называемая электрокапиллярной
кривой.
При адсорбции катионов (потенциалопределяющие ионы):
- уравнение электродного потенциала Нернста

22.

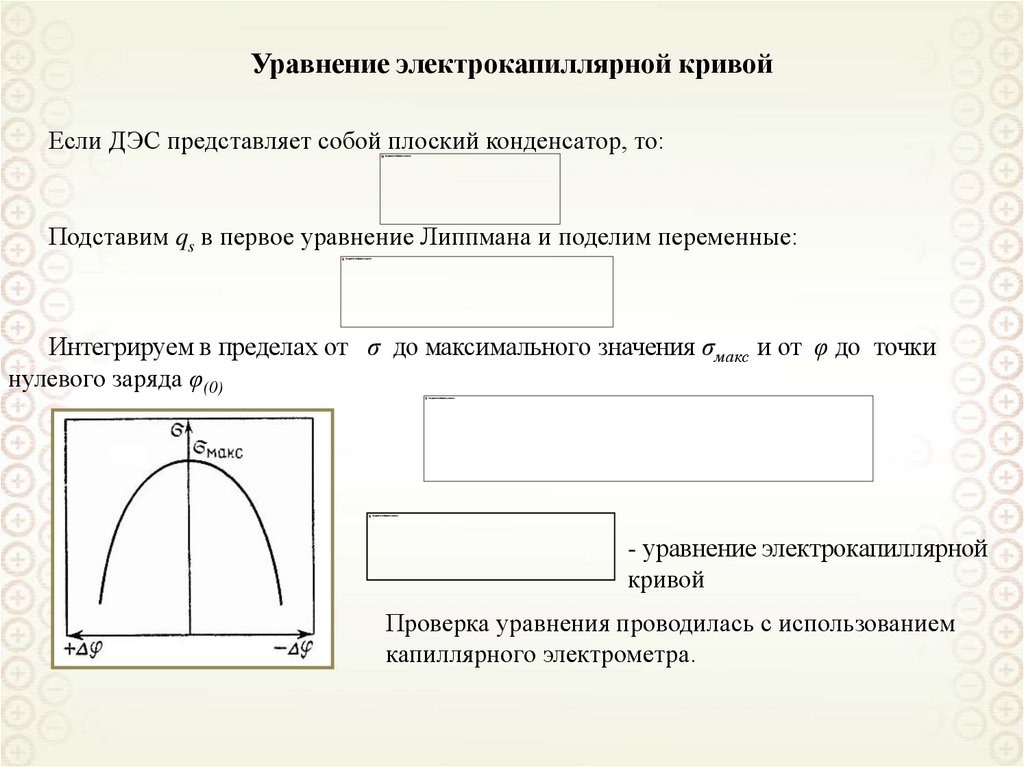
Уравнение электрокапиллярной кривой
Если ДЭС представляет собой плоский конденсатор, то:
Подставим qs в первое уравнение Липпмана и поделим переменные:
Интегрируем в пределах от σ до максимального значения σмакс и от φ до точки
нулевого заряда φ(0)
- уравнение электрокапиллярной
кривой
Проверка уравнения проводилась с использованием
капиллярного электрометра.

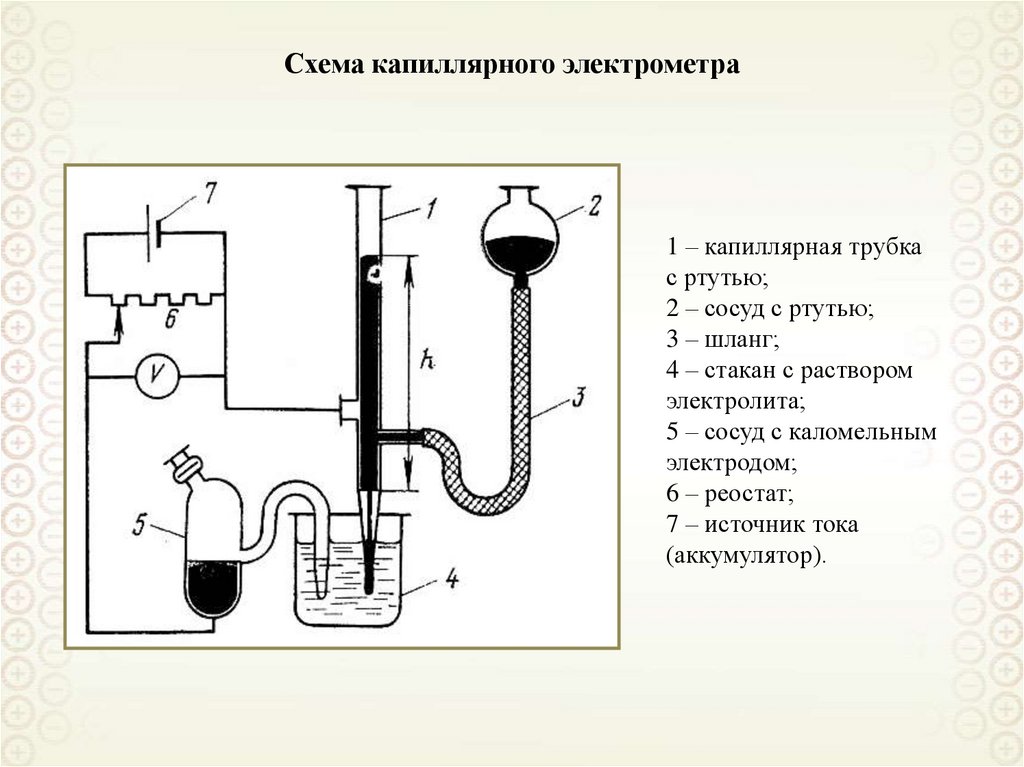
23.

Схема капиллярного электрометра
1 – капиллярная трубка
с ртутью;
2 – сосуд с ртутью;
3 – шланг;
4 – стакан с раствором
электролита;
5 – сосуд с каломельным
электродом;
6 – реостат;
7 – источник тока
(аккумулятор).

24. Теории строения ДЭС

1. Теория Гельмгольца
Строение ДЭС подобно строению плоского конденсатора. Один слой зарядов находится на
межфазной поверхности, имеющей потенциал 0.
Ионы, образующие этот слой
называются потенциалопределяющими. Заряд этого слоя компенсируется зарядом второго
слоя ионов, называемых противоионами.
2. Теория Гуи-Чепмена
Все противоионы участвую в тепловом движении, удерживаются возле межфазной
поверхности за счет электростатических сил и образуют диффузный (размытый) слой.
3. Теория Штерна
Одна часть противоионов удерживается у поверхности за счет электростатического и
адсорбционного взаимодействий, образуя адсорбционный слой (слой Гельмгольца). Другая
часть противоионов находится в растворе, примыкающем к поверхности, и образует
диффузный слой (слой Гуи) из-за их участия в тепловом движении.

25.

Теория Гуи-Чепмена
1. Концентрация ионов в диффузной части ДЭС на расстоянии х от границы раздела фаз
пропорциональна фактору Больцмана:
где Wxi - работа, необходимая для перемещения 1 моля ионов из объема раствора на
расстояние х от границы раздела фаз; φх - потенциал на расстоянии х, который в
граничных условиях изменяется от φх = φδ (потенциал диффузного слоя) при х = δ до
φх = 0 при х = ∞.
2. При условии, что z+ > 0 и z- < 0, объемная плотность
заряда в диффузном слое равна:
3. Уравнение Пуассона:

26.

Теория Гуи-Чепмена (2)
4. Уравнение Пуассона-Больцмана:
Решаем уравнение Пуассона-Больцмана при следующих допущениях:
• двойной электрический слой является плоским, то есть пренебрегаем кривизной
поверхности
• диэлектрическая проницаемость является одинаковой в растворе и ДЭС;
• ионы представляют собой точечные заряды (не имеют объема);
• при переводе противоионов из объема раствора в ДЭС совершается работа только
против электростатических сил;
• рассматривается случай слабозаряженной поверхности:
φδ < 25 мВ

27.

Теория Гуи-Чепмена (3)
Экспонента может быть разложена в ряд Маклорена:
С учетом этого избавимся от экспоненты в выражении для объемной плотности заряда:
Так как сумма зарядов в объеме раствора по условиям электронейтральности
равна нулю, то
- ионная сила

28.

Теория Гуи-Чепмена (4)
Уравнение Пуассона-Больцмана принимает вид:
Для того, чтобы провести интегрирование, преобразуем полученное уравнение:
Первое интегрирование:
Извлекаем корень с учетом того, что dφ/dx < 0 :

29.

Теория Гуи-Чепмена (5)
Делим переменные и интегрируем второй раз:
- уравнение Гуи-Чепмена
Если расстояние х отсчитывать от начала диффузной
части ДЭС (от слоя Гельмгольца), то
Для высоких потенциалов и больших расстояний
от поверхности:
При очень высоких потенциалах (φδ > 100 мВ) γ ≈ 1. В этом случае φх не
зависит от потенциала диффузного слоя φδ.

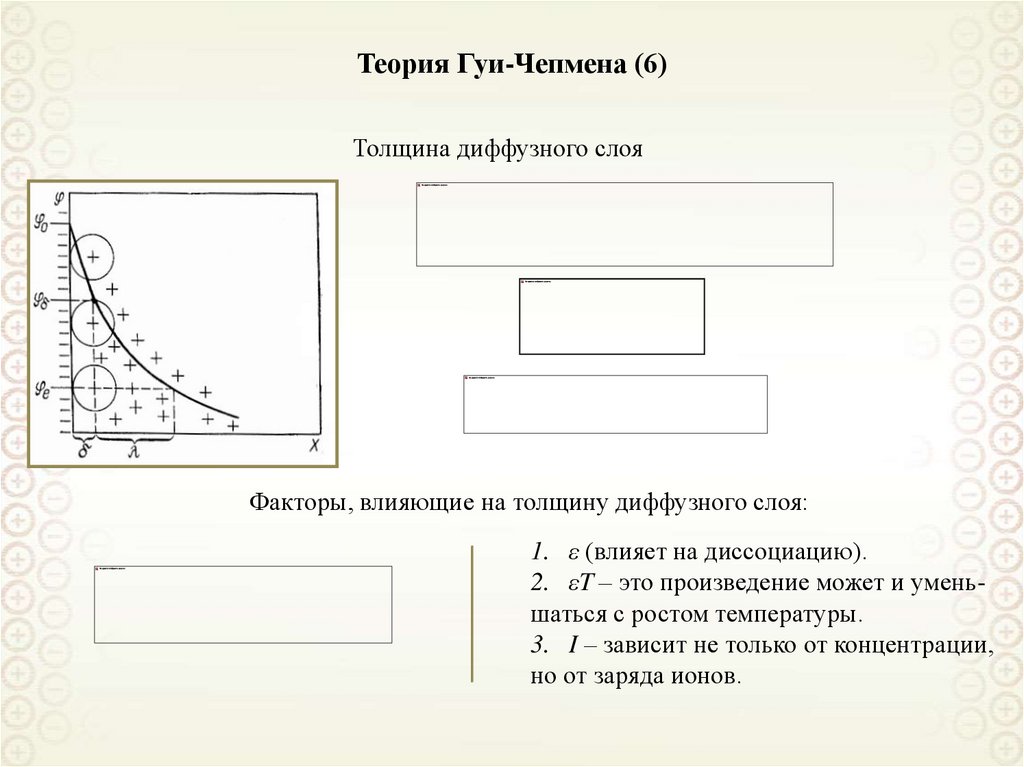
30. Теория Гуи-Чепмена (6)

Толщина диффузного слоя
Факторы, влияющие на толщину диффузного слоя:
1. ε (влияет на диссоциацию).
2. εT – это произведение может и уменьшаться с ростом температуры.
3. I – зависит не только от концентрации,
но от заряда ионов.

31.

Теория Штерна
1. Противоионы образуют два слоя (слой Гельмгольца
и слой Гуи).
2. Учтены собственные размеры ионов – толщина δ
определяется радиусами гидратированных ионов.
3. Учтена специфическая адсорбция ионов в слое
Гельмгольца; ионы удерживаются за счет
электростатических и адсорбционных
взаимодействий.
δ - толщина слоя Гельмгольца;
- потенциал диффузного слоя;
λ - толщина диффузного слоя.
Учет специфической адсорбции в слое Гельмгольца позволил объяснить явление
перезарядки поверхности.

32.

Перезарядка поверхности
при специфической адсорбции
ионов
а – исходное состояние;
б – после введения части электролита;
в – изоэлектрическое состояние;
г – состояние перезарядки поверхности.

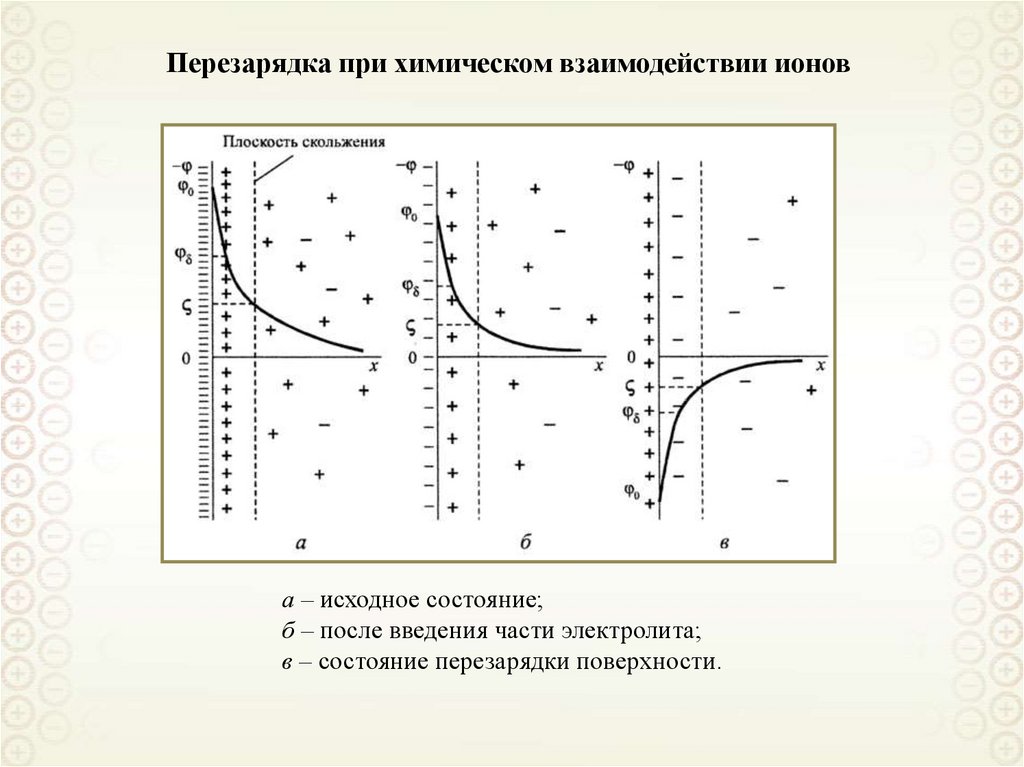
33. Перезарядка при химическом взаимодействии ионов

а – исходное состояние;
б – после введения части электролита;
в – состояние перезарядки поверхности.

34.

Формулы ДЭС (формулы мицелл)

35.

Формулы ДЭС (2)

36. Электрокинетические явления

37.

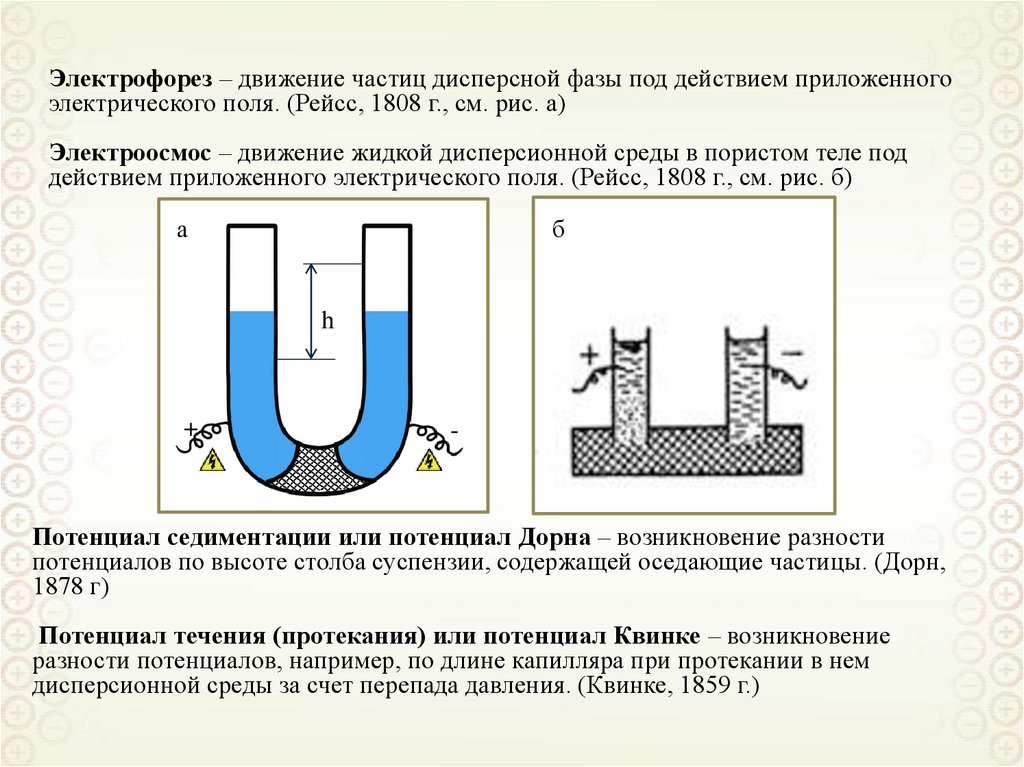
Электрофорез – движение частиц дисперсной фазы под действием приложенного
электрического поля. (Рейсс, 1808 г., см. рис. а)
Электроосмос – движение жидкой дисперсионной среды в пористом теле под
действием приложенного электрического поля. (Рейсс, 1808 г., см. рис. б)
а
б
h
+
-
Потенциал седиментации или потенциал Дорна – возникновение разности
потенциалов по высоте столба суспензии, содержащей оседающие частицы. (Дорн,
1878 г)
Потенциал течения (протекания) или потенциал Квинке – возникновение
разности потенциалов, например, по длине капилляра при протекании в нем
дисперсионной среды за счет перепада давления. (Квинке, 1859 г.)

38.

Электрокинетический потенциал или ζ–потенциал (дзетапотенциал) – потенциал, возникающий на плоскости скольжения
при отрыве части диффузного слоя ДЭС.
ζ –потенциал зависит от:
• природы контактирующих фаз
• рН дисперсионной среды
• температуры
• диэлектрической проницаемости среды
• типа электролита
(индифферентный/неиндифферентный)
• ионной силы (концентрации электролита)

39. Вывод уравнения Гельмгольца-Смолуховского (на примере электроосмоса)

1.
2.
3.
4.
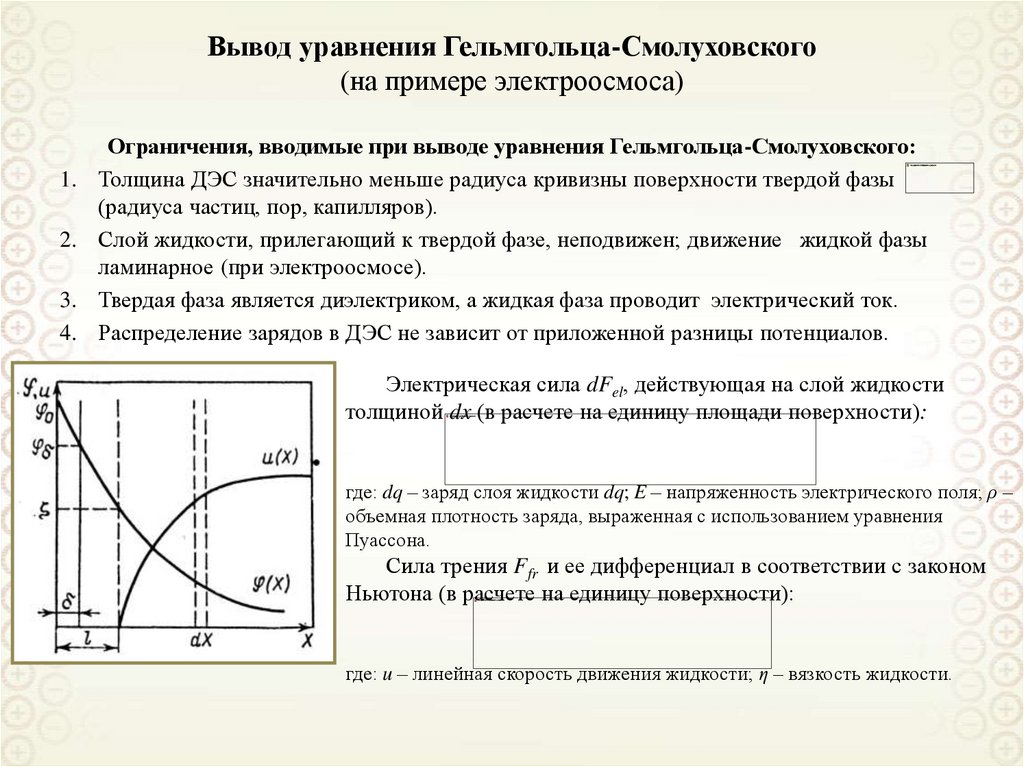
Ограничения, вводимые при выводе уравнения Гельмгольца-Смолуховского:
Толщина ДЭС значительно меньше радиуса кривизны поверхности твердой фазы
(радиуса частиц, пор, капилляров).
Слой жидкости, прилегающий к твердой фазе, неподвижен; движение жидкой фазы
ламинарное (при электроосмосе).
Твердая фаза является диэлектриком, а жидкая фаза проводит электрический ток.
Распределение зарядов в ДЭС не зависит от приложенной разницы потенциалов.
Электрическая сила dFel, действующая на слой жидкости
толщиной dx (в расчете на единицу площади поверхности):
где: dq – заряд слоя жидкости dq; E – напряженность электрического поля; ρ –
объемная плотность заряда, выраженная с использованием уравнения
Пуассона.
Сила трения Ffr и ее дифференциал в соответствии с законом
Ньютона (в расчете на единицу поверхности):
где: u – линейная скорость движения жидкости; η – вязкость жидкости.

40. Вывод уравнения Гельмгольца-Смолуховского (2)

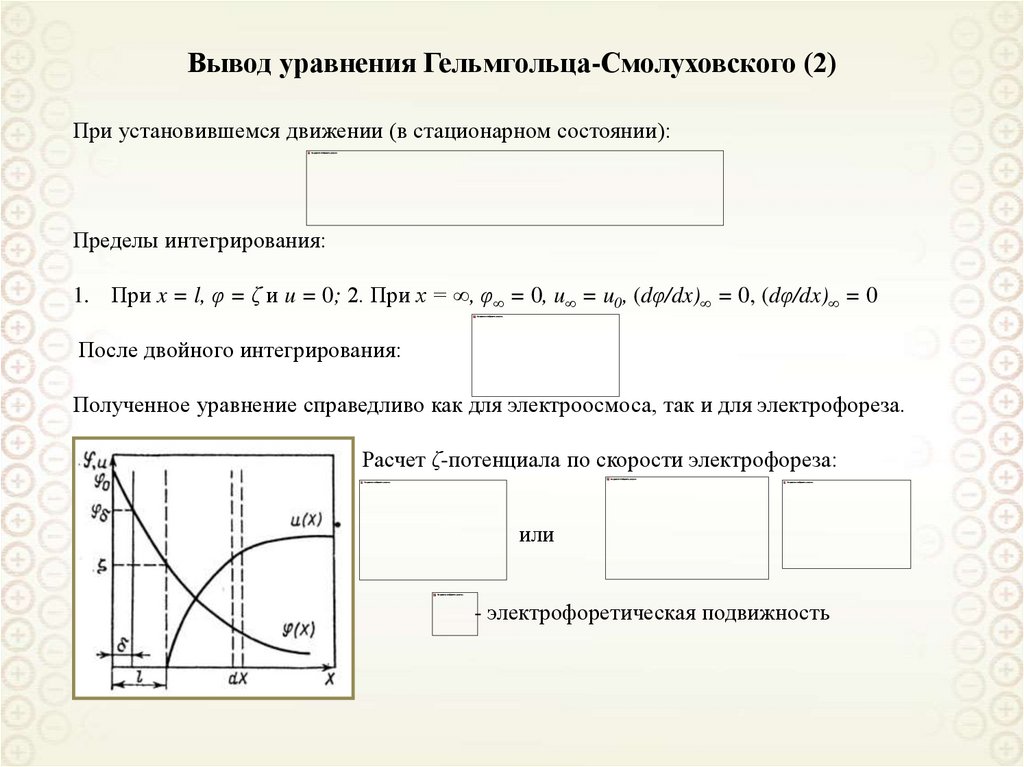
При установившемся движении (в стационарном состоянии):
Пределы интегрирования:
1. При x = l, φ = ζ и u = 0; 2. При x = ∞, φ∞ = 0, u∞ = u0, (dφ/dx)∞ = 0, (dφ/dx)∞ = 0
После двойного интегрирования:
Полученное уравнение справедливо как для электроосмоса, так и для электрофореза.
Расчет ζ-потенциала по скорости электрофореза:
или
- электрофоретическая подвижность

41.

Определение ζ-потенциала методом макроэлектрофореза
+
5
3
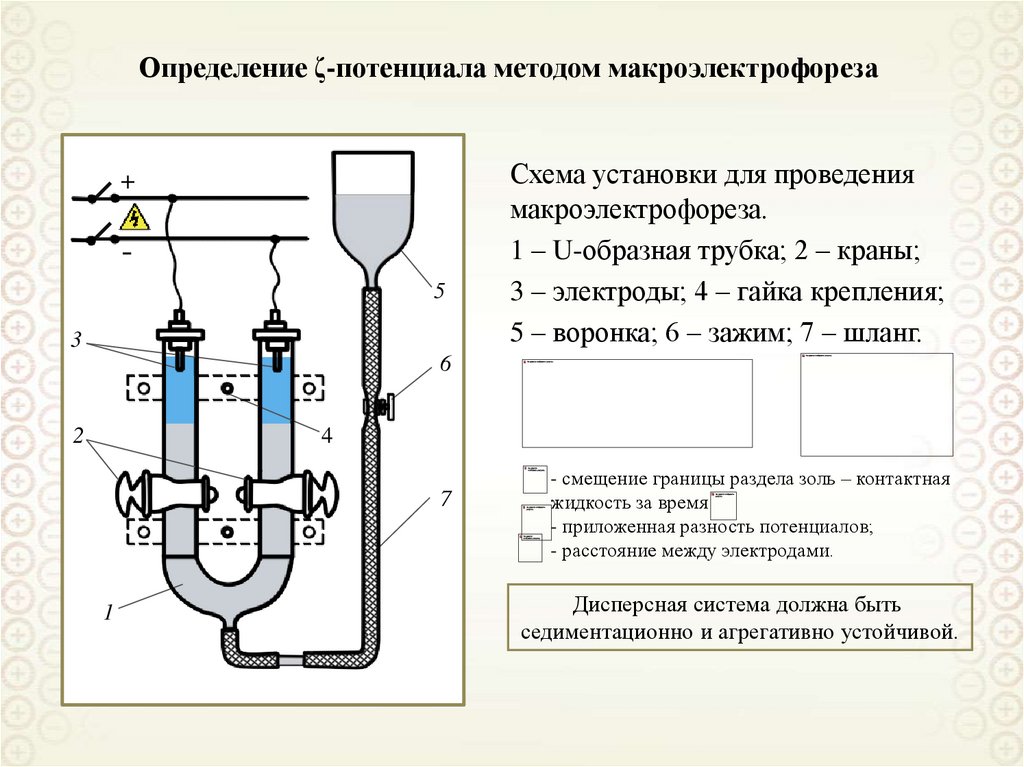
Схема установки для проведения
макроэлектрофореза.
1 – U-образная трубка; 2 – краны;
3 – электроды; 4 – гайка крепления;
5 – воронка; 6 – зажим; 7 – шланг.
6
2
4
7
1
- смещение границы раздела золь – контактная
жидкость за время
- приложенная разность потенциалов;
- расстояние между электродами.
Дисперсная система должна быть
седиментационно и агрегативно устойчивой.

42.

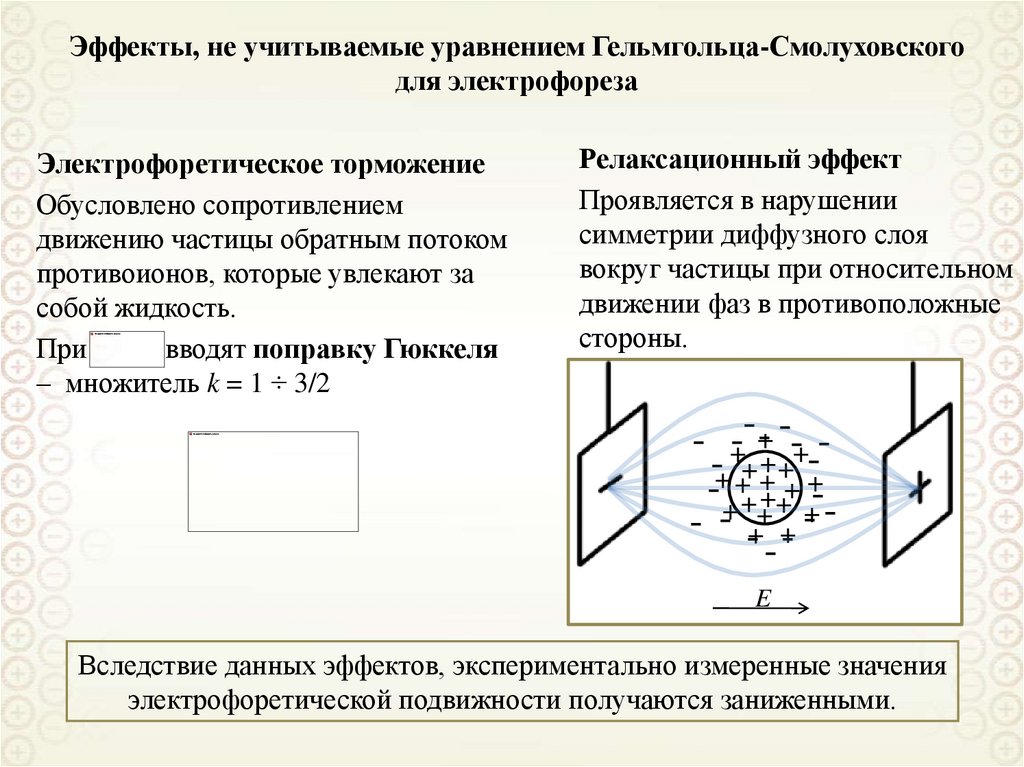
Эффекты, не учитываемые уравнением Гельмгольца-Смолуховского
для электрофореза
Электрофоретическое торможение
Обусловлено сопротивлением
движению частицы обратным потоком
противоионов, которые увлекают за
собой жидкость.
При
вводят поправку Гюккеля
– множитель k = 1 ÷ 3/2
Релаксационный эффект
Проявляется в нарушении
симметрии диффузного слоя
вокруг частицы при относительном
движении фаз в противоположные
стороны.
- +--+- --+--+ ++ ++ + +
- + +++ - -+ -++ +- -+ E
Вследствие данных эффектов, экспериментально измеренные значения
электрофоретической подвижности получаются заниженными.

43.

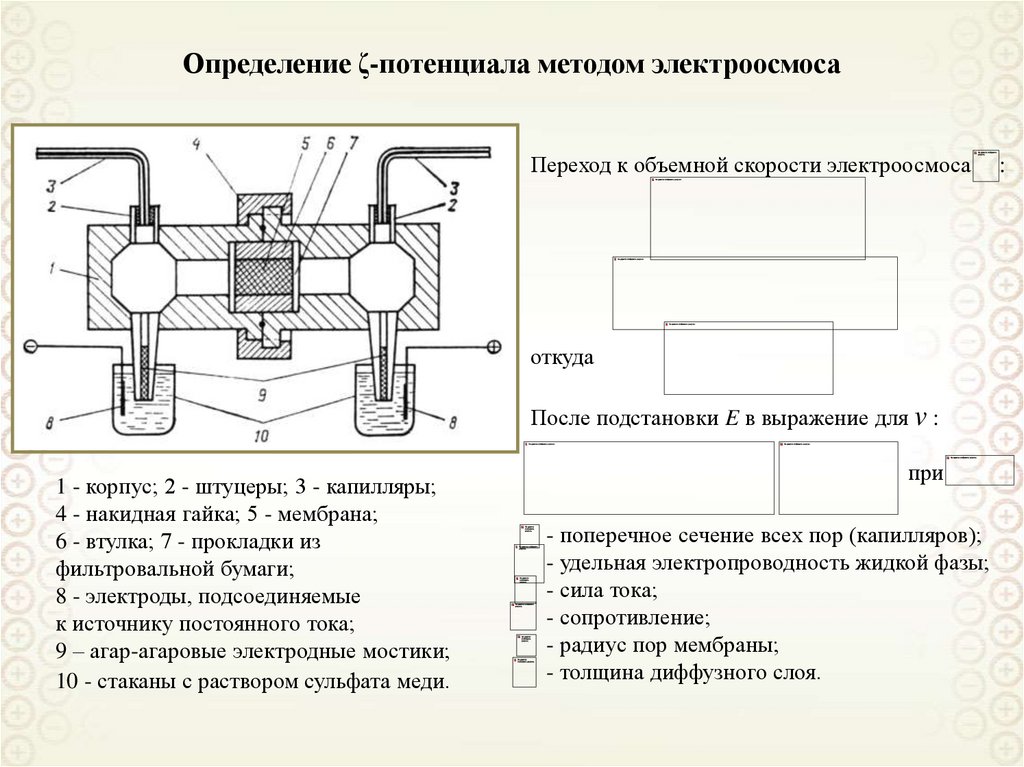
Определение ζ-потенциала методом электроосмоса
Переход к объемной скорости электроосмоса
откуда
После подстановки E в выражение для v :
1 - корпус; 2 - штуцеры; 3 - капилляры;
4 - накидная гайка; 5 - мембрана;
6 - втулка; 7 - прокладки из
фильтровальной бумаги;
8 - электроды, подсоединяемые
к источнику постоянного тока;
9 – агар-агаровые электродные мостики;
10 - стаканы с раствором сульфата меди.
при
- поперечное сечение всех пор (капилляров);
- удельная электропроводность жидкой фазы;
- сила тока;
- сопротивление;
- радиус пор мембраны;
- толщина диффузного слоя.
:

44.

Эффекты, не учитываемые уравнением
Гельмгольца-Смолуховского для электроосмоса
Если радиусы пор (капилляров) сопоставимы с толщиной диффузного
слоя, то в уравнение вводят поправку на поверхностную проводимость κs,
которая всегда положительна.
Поверхностная проводимость κs – удельная электропроводность в
неподвижной части двойного электрического слоя.

45.

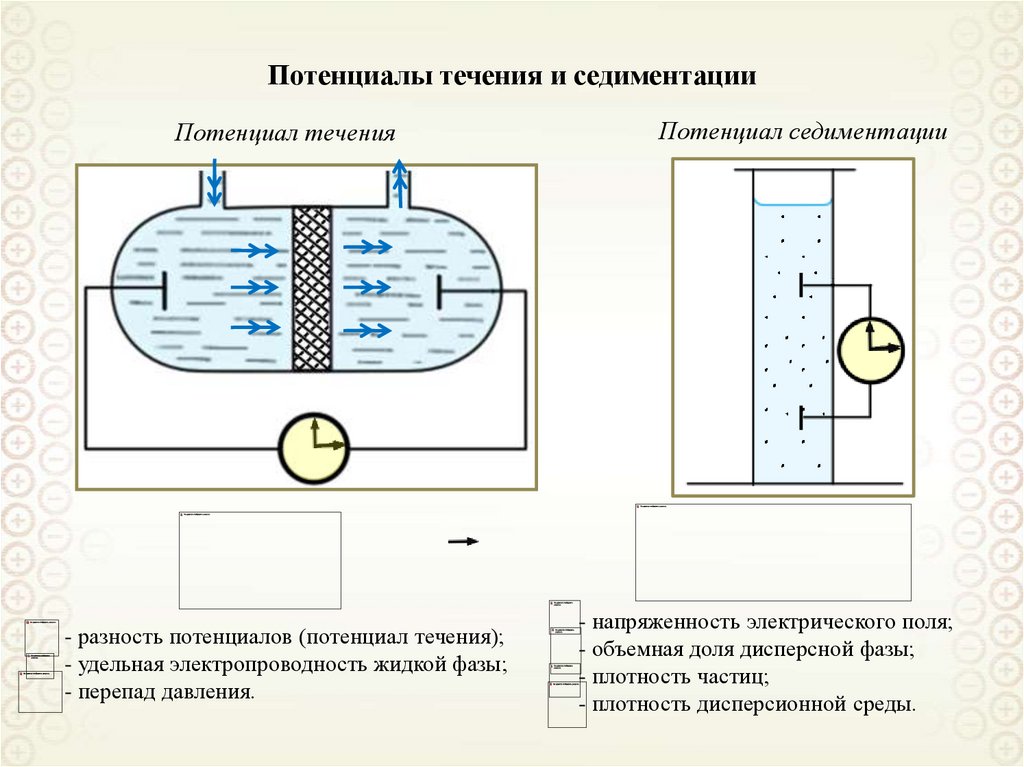
Потенциалы течения и седиментации
Потенциал течения
- разность потенциалов (потенциал течения);
- удельная электропроводность жидкой фазы;
- перепад давления.
Потенциал седиментации
- напряженность электрического поля;
- объемная доля дисперсной фазы;
- плотность частиц;
- плотность дисперсионной среды.

46. Кинетические свойства дисперсных систем

Седиментация