Устойчивость систем автоматического управления

1. Устойчивость САУ

2. САУ устойчива если после кратковременного возмущения она возвращается в прежнее или занимает новое устойчивое положение.

3. ПРИМЕРЫ Устойчива

∆х
р
∆х
t

4. Неустойчива

∆х
∆х
р
t

5. Устойчива “в малом”

∆x
t

6.

Линейные САУ описываются линейными
дифференциальными уравнениями
(ДУ). Для решения ДУ следует найти
корни его характеристического
уравнения:

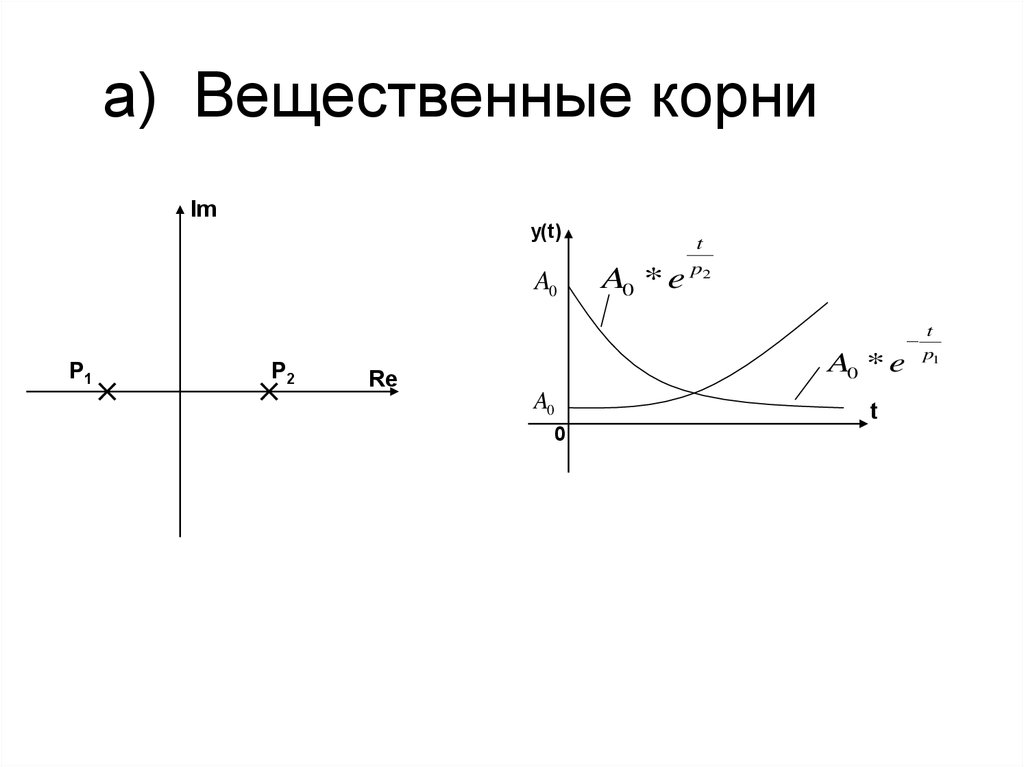
7. a) Вещественные корни

Im
y(t)
A0
A0 * e
t
p2
P1
P2
A0 * e
Re
A0
t
0
t
p1

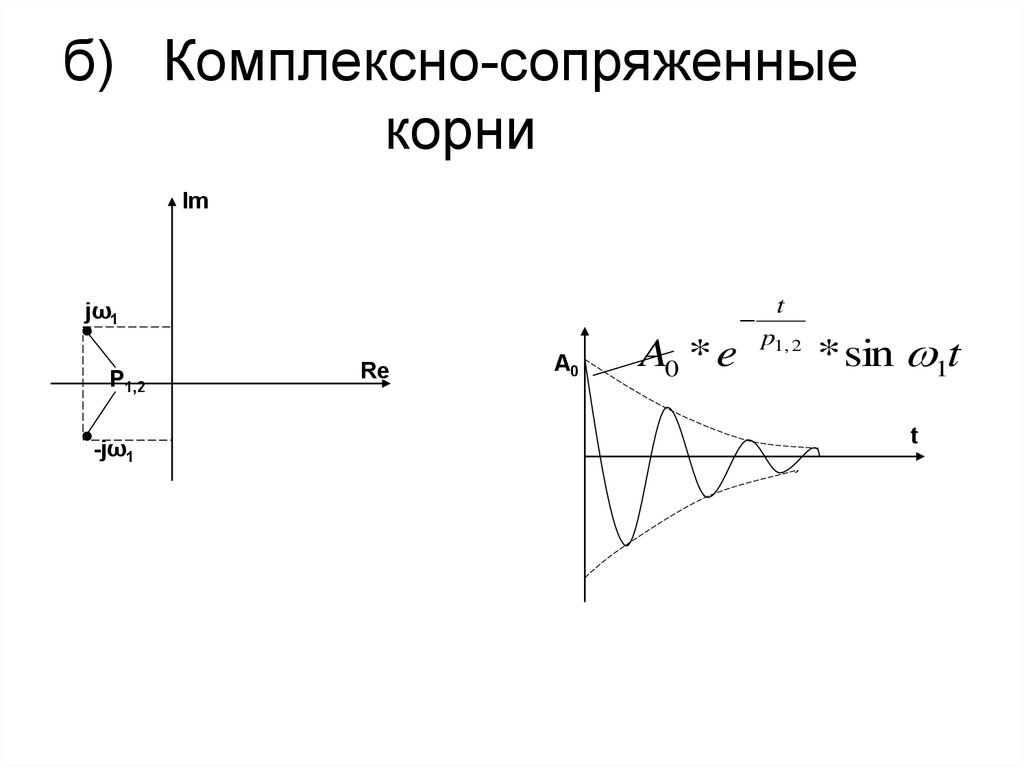
8. б) Комплексно-сопряженные корни

Im
jω1
P1,2
-jω1
Re
A0
A0 * e
t
p1, 2
* sin 1t
t

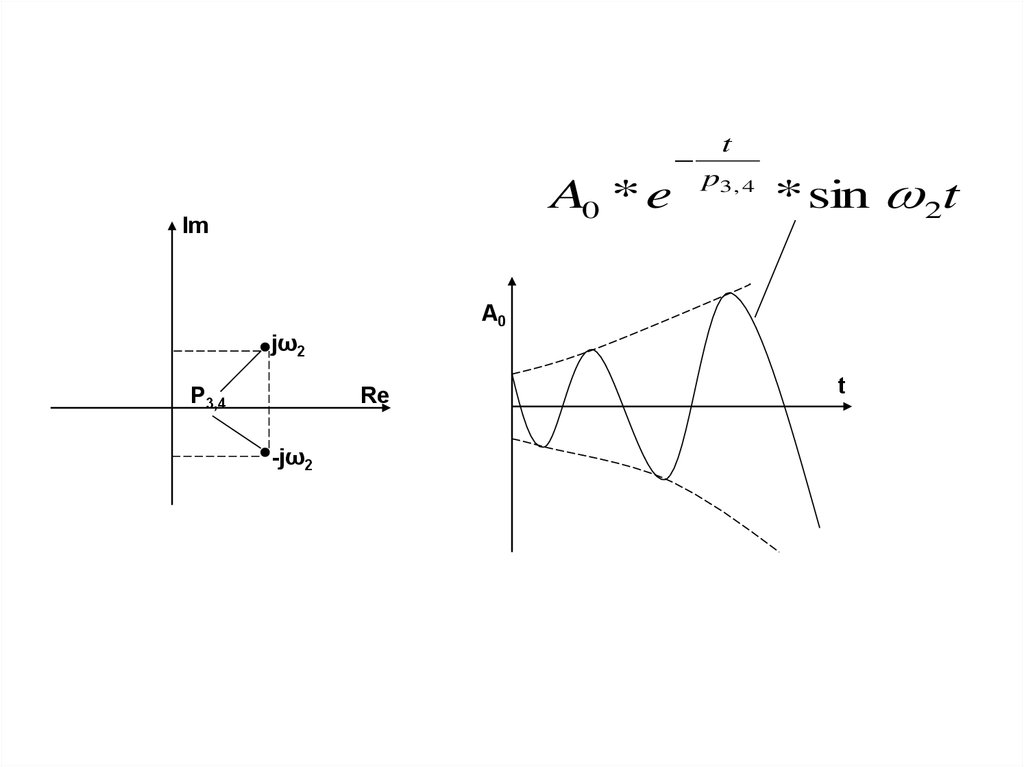
9.

A0 * e
Im
t
p3 , 4
* sin 2t
A0
jω2
Re
P3,4
-jω2
t

10.

Итак, чтобы САУ была устойчивой
необходимо и достаточно, чтобы все
корни ее характеристического
уравнения находились в левой
полуплоскости комплексной плоскости.

11.

Критерии устойчивости САУ – это
некоторые признаки позволяющие не
решая характеристического уравнения
оценить устойчивость САУ.

12. ВНИМАНИЕ

• Характеристическое уравнение
замкнутой САУ – это знаменатель ее
передаточной функции Ф(s)
приравненный “0”.
• Характеристическое уравнение
разомкнутой САУ - это знаменатель ее
передаточной функции Wp(s)
приравненный “0”.

13. А. Алгебраические критерии устойчивости САУ

I.
Критерий Гурвица (1895г.).
Пусть дано ХУ замкнутой САУ
anpn+an-1pn-1+…+a0=0
(1)

14. Составим определитель Гурвица из коэффициентов ХУ:

∆n=
an 1
a n 3
a n 5
...
0
an
0
...
...
an 2
an 1
...
...
a n 4
a n 3
...
...
...
...
...
...
0
0
...
...
...
...
...
...
...
...
a1
a2
0
a0
(2)

15. Как видно из (2):

• На главной диагонали определителя Гурвица
располагаются сверху вниз коэффициенты
ХУ начиная со второго.
• Выше элементов главной диагонали
выписываются коэффициенты при младших
степенях “р” по мере их убывания.
• Ниже элементов главной диагонали
выписываются коэффициенты при старших
степенях “р” по мере их возрастания.
• Остальные элементы определителя Гурвица
равны “0”.

16. Составим главные диагональные миноры

∆1= an-1
∆2 =
∆3=
an 1
an 3
an
an 2
an 1
a n 3
a n 5
an
0
an 2
an 1
an 4
a n 3

17. 1. Критерий Гурвица:

Для устойчивости линейной САУ
необходимо и достаточно, чтобы при
аn>0 все главные диагональные миноры
определителя Гурвица были бы
положительны.

18. Примеры

1. n=1 a1p+a0=0
Условия устойчивости
a1>0 ∆1=a0>0
2. n=2 a2p2+a1p+a0=0
Условия устойчивости
a2>0
∆1=a1>0
∆2= a1 0 = a1a0>0
a2
a0

19.

3. n=3 a3p3+a2p2+a1p=0
Условия устойчивости
a3>0
∆1=a2>0
∆2 = a2 a0 =a2a1-a3a0>0
a3
a1
a2
a0
0
∆3= a3
a1
a2
0
a0
0
=a0*∆2>0

20. Недостаток критерия Гурвица

• С увеличением “n” раскрывать
определители становится трудно.

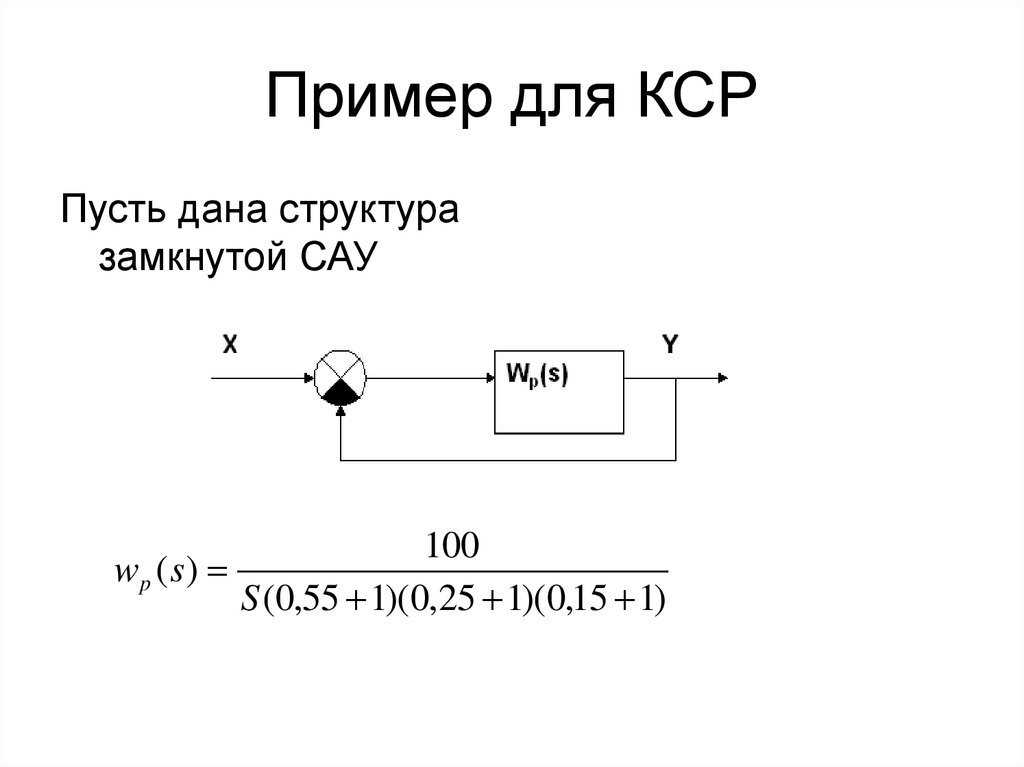
21. Пример для КСР

Пусть дана структура
замкнутой САУ
100
wp ( s)
S (0,55 1)(0,25 1)(0,15 1)

22. Необходимо с помощью критерия Гурвица определить устойчивость САУ. План исследований:

• 1. Найти передаточную функцию замкнутой
САУ.
• 2. Определить ХУ замкнутой САУ и его
коэффициенты.
• 3. Составить определитель Гурвица.
• 4. Определить все главные диагональные
миноры и оценить устойчивость САУ по
критерию Гурвица.

23. 2. Критерий Рауса

Пусть дано ХУ замкнутой САУ “n”–го
порядка:
anpn + an-1pn-1 +… +a1p + a0 = 0

24. Составим таблицу Рауса из коэффициентов ХУ:

-
c11 = an
c21 = an-2
c31 = an-4
c41 = an - 6
-
c12 = an-1
c22 = an-3
c32 = an-5
c42 = an - 7
c11
r3 =
c12
c13 = c21 –
- r3*c22
c23 = c31 –
r3*c32
c33 = c41 – r3
*c42
…
c12
c13
c14 = c22 –
r4*c23
c24 = c32 –
r4*c33
c34 = c42 – r4
* c43
…
…
…
…
…
r4 =
…

25. Критерий Рауса

Для устойчивости линейной САУ
необходимо и достаточно, чтобы
коэффициенты первого столбца
таблицы Рауса были положительны,
т.е.:
С11> 0
c12 > 0
…
c1,n+1 > 0

26. Пример I для КСР

Пусть ХУ замкнутой САУ:
P6 + 6p5 + 21p4 + 44p3 + 62p2 + 52 + 100 =0
Необходимо исследовать устойчивость этой
системы используя критерий Рауса.

27. План исследования

1. Составим таблицу Рауса и заполним
ее первые две строки.
2. Вычислим последовательно
коэффициенты последующих строк.
3. Оценим знаки первого столбца
таблицы и устойчивость САУ.

28. Итак, составим таблицу Рауса

-
a6 = 1
a4 = 21
a2 = 62
a0 = 100
-
a5 = 6
a3 = 44
a1 = 52
0
r3 =
1
6
r4 =
6
13,65
21 -
44
6
= 13,65
62 -
52
6
= 53,3
100

29. Задание по КСР:

Завершить заполнение таблицы Рауса и
оценить устойчивость САУ.

30. Б. Частотные критерии устойчивости САУ

I. Критерий Михайлова (1938)
Дано ХУ замкнутой линейной САУ:
А(s) = ansn + an-1sn-1 + … + a0 = 0 (1)
A(s)
корни ХУ
s
0

31. Представим полином (1) в виде:

A(s) = an (s – s1) (s –s2) … (s - sn)
Где si – корни ХУ
i = 1, 2 … n
Положим s = jω, тогда:
А(jω) = an (jω – s1)(jω – s2)… (jω - sn)
(2)
(3)

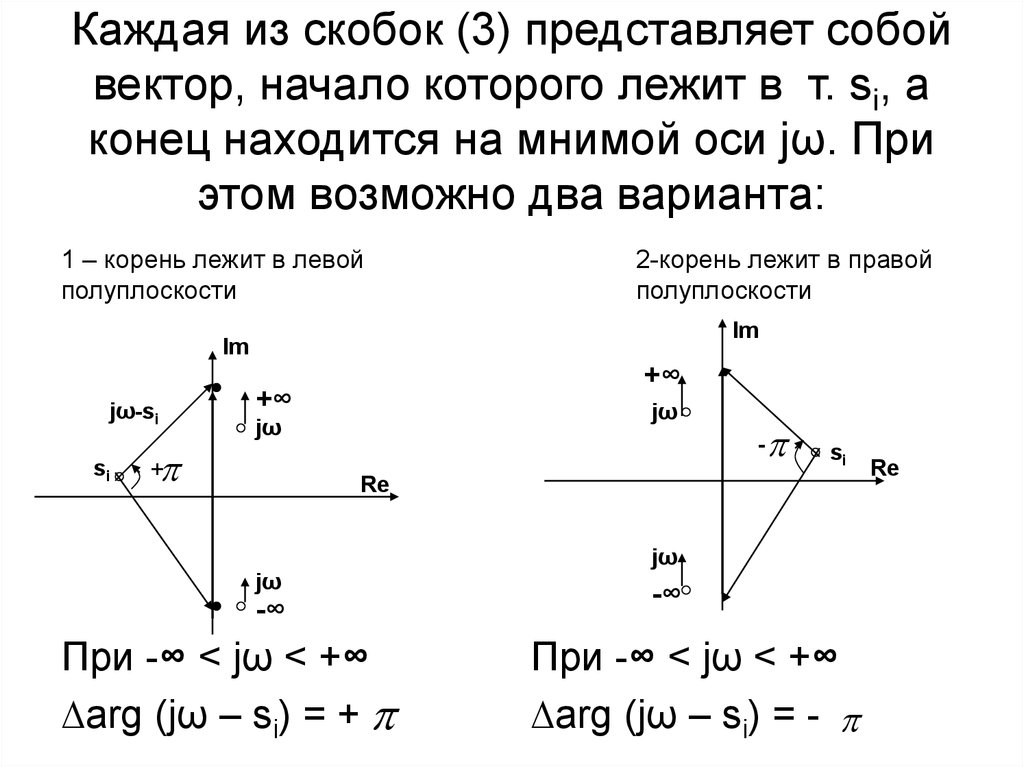
32. Каждая из скобок (3) представляет собой вектор, начало которого лежит в т. si, а конец находится на мнимой оси jω. При этом возможно два вариант

Каждая из скобок (3) представляет собой
вектор, начало которого лежит в т. si, а
конец находится на мнимой оси jω. При
этом возможно два варианта:
1 – корень лежит в левой
полуплоскости
Im
Im
jω-si
si
2-корень лежит в правой
полуплоскости
+∞
+∞
jω
jω
+
-
si
Re
jω
jω
-∞
При -∞ < jω < +∞
∆arg (jω – si) = +
-∞
При -∞ < jω < +∞
∆arg (jω – si) = -
Re

33.

Итак, если ХУ A(s) = 0 содержит L корней в
правой полуплоскости, то
∆arg A(jω) = (n-2L) = (n-L) - L

34.

Для устойчивости линейной САУ необходимо,
чтобы L = 0, т.е.:
∆arg A(jω) = n
(4)

35.

2
Критерий Михайлова является графической
интерпретацией выражения (4).
При этом рассматриваются лишь
положительные частоты, т.е.:
∆arg A(jω) = n *
0
2
(5)

36. Критерий Михайлова

Для устойчивости линейной САУ
необходимо и достаточно, чтобы
годограф Михайлова (5) А(jω),
начинаясь при ω = 0 на действительной
оси с ростом “ω” от “0” до “∞” обходил
последовательно “n” квадрантов против
часовой стрелки (где n – порядок
характеристического уравнения).

37.

Im
I
I
II
II
n=1
n=5
n=2
Re
ω=0
ω=0
n=2
Re
n=4
n=3
n=4
III
IV
Системы устойчивы
n=3
III
n=1
IV
Системы не устойчивы

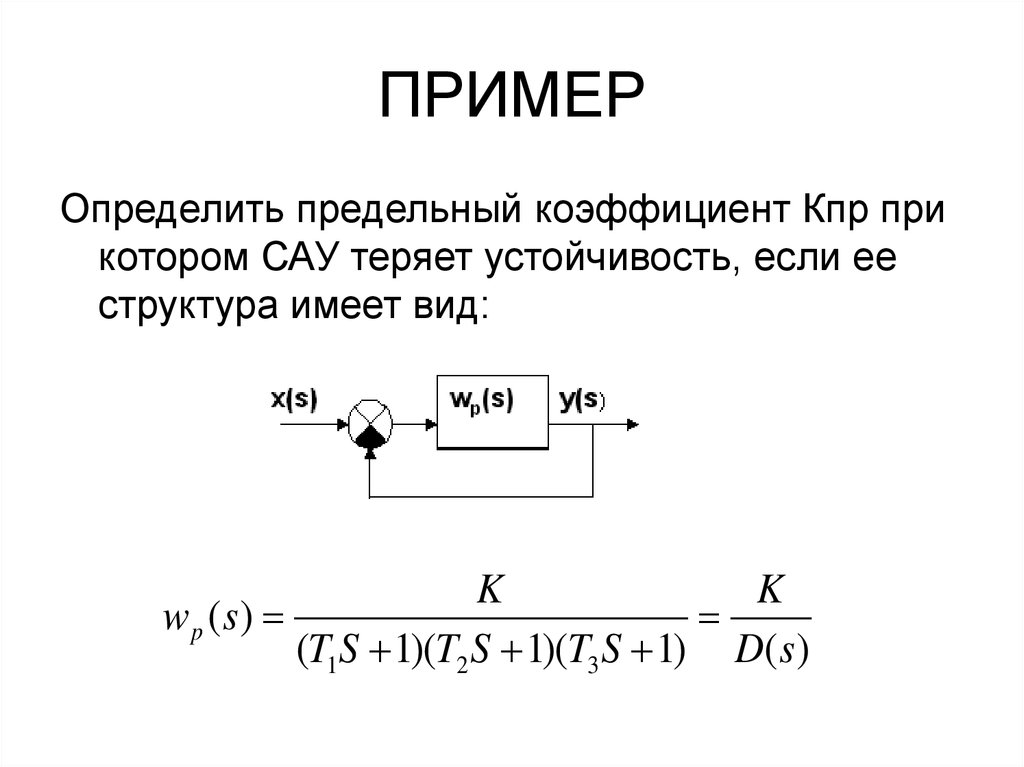
38. ПРИМЕР

Определить предельный коэффициент Кпр при
котором САУ теряет устойчивость, если ее
структура имеет вид:
K
K
wp ( s)
(T1S 1)(T2 S 1)(T3 S 1) D( s)

39.

1. Найдем передаточную функцию
замкнутой САУ:
Wp ( s)
K
Ф( s )
1 Wp ( s) D( s) K
2. ХY САУ – это знаменатель ее
передаточной функции приравненный
к 0 т.е.:
A( s) D( s) K 0

40.

3. Годограф Михайлова (при s = jω):
А(jω) =D(jω) + К
0<ω<∞
4. Построим, вначале, D(jω):
D(jω) = (Т1jω+1)(T2jω+1)(T3jω+1)=Re(ω) + jIm(ω)
Re(ω) = 1 – (T1T2 + T1T3 + T2T3)ω2
Im(ω) = (T1 + T2 + T3)ω –T1T2T3ω3

41.

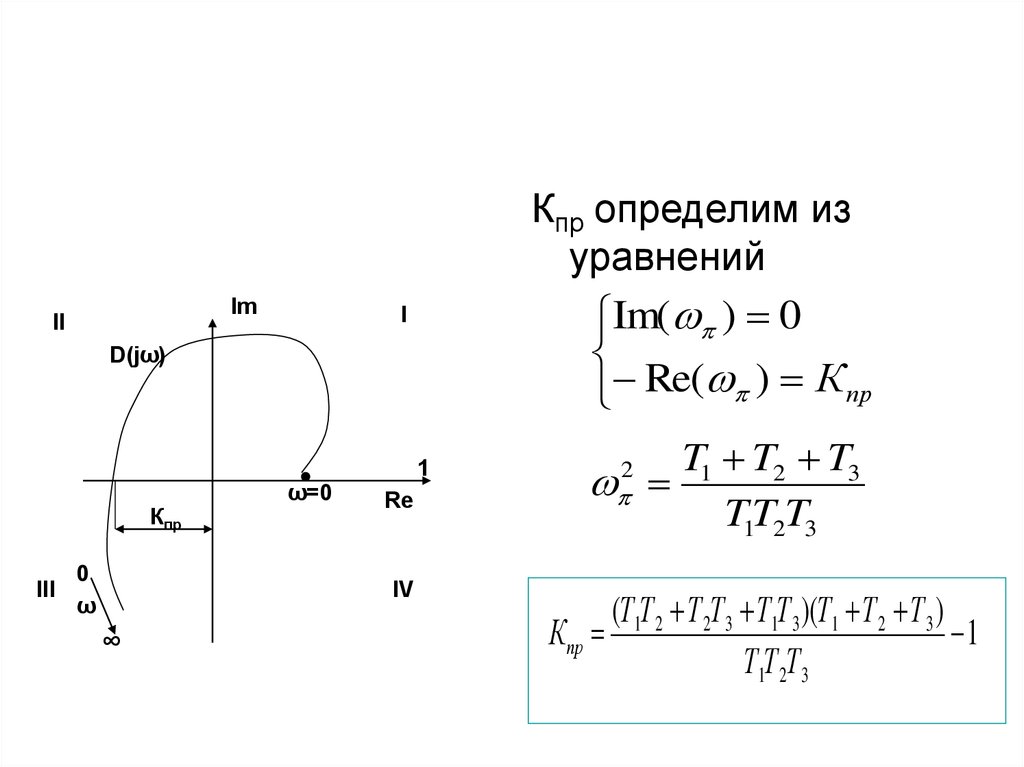
Im
II
Кпр определим из
уравнений
Im( ) 0
Re( ) К пр
I
D(jω)
Кпр
III
0
ω
ω=0
1
Re
IV
∞
T1 T2 T3
T1T2T3
2
(Т1Т 2 Т 2Т 3 Т1Т 3 )(Т1 Т 2 Т 3 )
К пр
1
Т1Т 2Т 3

42. НЕДОСТАТОК критерия Михайлова

Годограф Михайлова не имеет
физической сущности (его нельзя
получить экспериментально). Между
тем при исследовании сложных систем
хотелось бы опираться на
характеристики получаемые не только
аналитически, но и экспериментально.

43. 2. Критерий Найквиста (1932)

Основан на использовании wp(s), которую
можно получить экспериментально.
Пусть:
Тогда:
M ( s)
Wp (s)
N ( s)
Ф( s )
Wp ( s)
1 Wp (s)
- ПФ разомкнутой САУ
M ( s)
M ( s) N ( s)
- ПФ замкнутой САУ

44.

Образуем функцию:
M ( s) N ( s)
F ( s ) 1 wp ( s )
N ( s)
- XY замкнутой САУ
- XY разомкнутой САУ

45. РАССМОТРИМ

1-й случай – разомкнутая САУ устойчива.
Тогда, согласно критерию Михайлова:
∆arg N(jω) = n*
0<ω<∞
2

46.

Чтобы система и в замкнутом состоянии
была устойчива необходимо чтобы:
M
(
j
)
N
(
j
)
n
*
∆arg
2
0<ω<∞
Это значит что: ∆arg F(jω)= 0
0<ω<∞

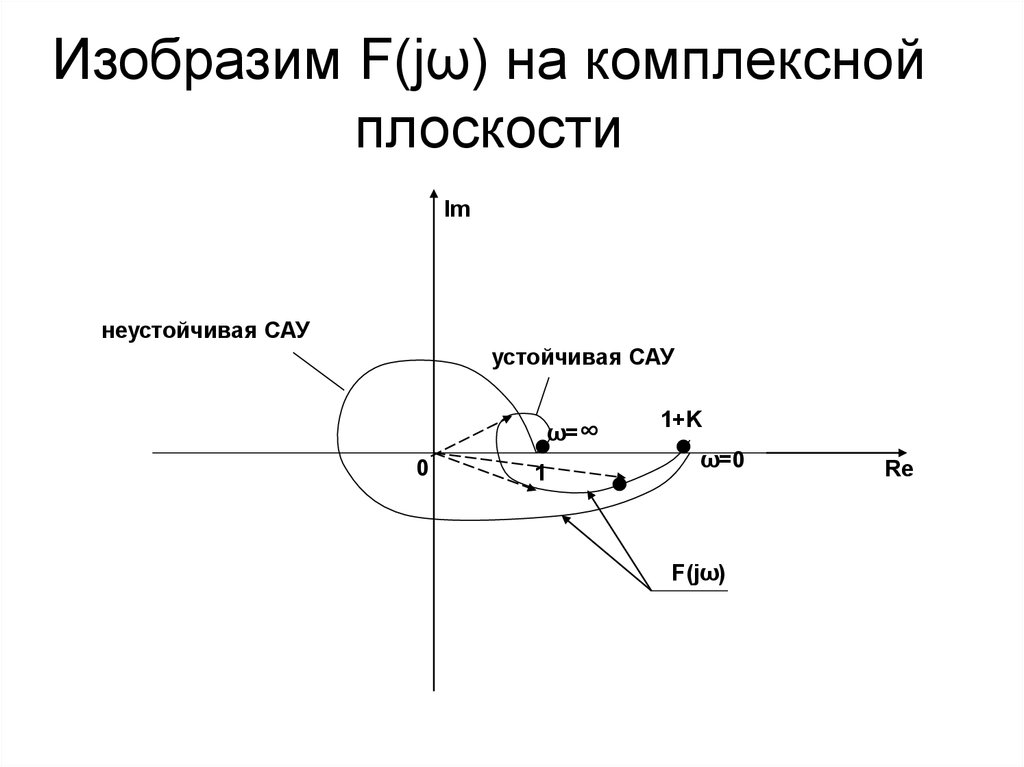
47. Изобразим F(jω) на комплексной плоскости

Im
неустойчивая САУ
устойчивая САУ
ω=∞
0
1
1+K
ω=0
F(jω)
Re

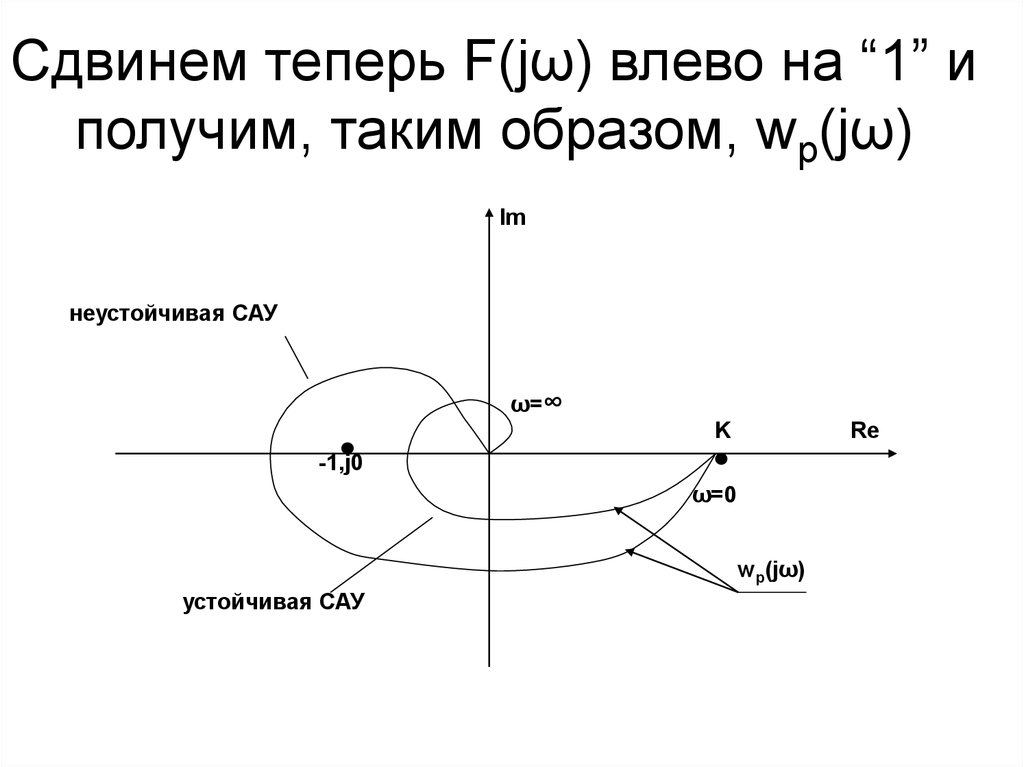
48. Сдвинем теперь F(jω) влево на “1” и получим, таким образом, wp(jω)

Im
неустойчивая САУ
ω=∞
K
Re
-1,j0
ω=0
wp(jω)
устойчивая САУ

49. Критерий устойчивости Найквиста:

Если разомкнутая САУ устойчива, то для
ее устойчивости в замкнутом состоянии
необходимо и достаточно, чтобы АФЧХ
wp(jω) при 0<ω<∞ не охватывала точку с
координатами (-1; j0).

50. ПРИМЕР

Найти, используя критерий Найквиста,
предельный коэффициент Кпр при
котором САУ потеряет устойчивость
если:
K
Wp ( s)
(T1S 1)(T2 S 1)(T3 S 1)

51. По критерию Найквиста САУ находится на границе устойчивости если:

Кпр
(T1 j 1)(T2 j 1)(T3 j 1)
1
Kпр
Re( ) j Im( )
Полагая Im(ω ) = 0 найдем:
T1 T2 T3
T1T2T3
2

52.

Подставив 2 в Re(ω ) найдем:
(Т1Т 2 Т1Т 3 Т 2Т 3 )(Т1 Т 2 Т 3 )
К пр
1
Т1Т 2Т 3
Т.е. результат такой же, как и при
использовании критерия Михайлова.

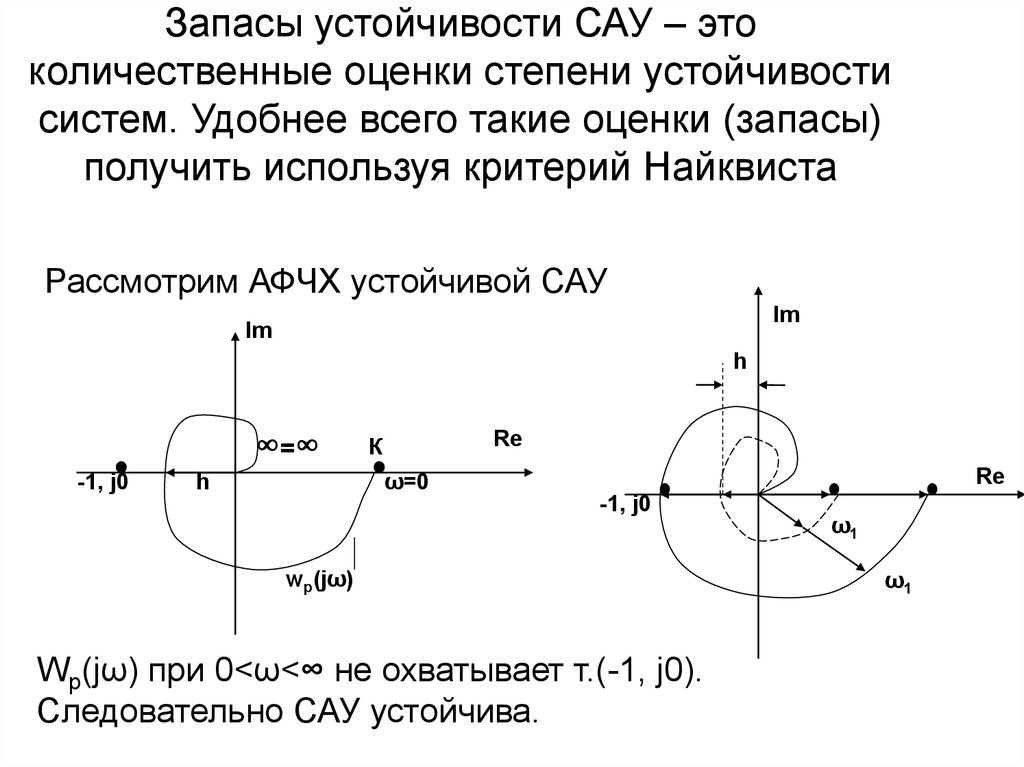
53. Запасы устойчивости САУ – это количественные оценки степени устойчивости систем. Удобнее всего такие оценки (запасы) получить используя к

Запасы устойчивости САУ – это
количественные оценки степени устойчивости
систем. Удобнее всего такие оценки (запасы)
получить используя критерий Найквиста
Рассмотрим АФЧХ устойчивой САУ
Im
Im
h
∞=∞
-1, j0
Re
К
Re
ω=0
h
-1, j0
wp(jω)
Wp(jω) при 0<ω<∞ не охватывает т.(-1, j0).
Следовательно САУ устойчива.
ω1
ω1

54. САУ может потерять устойчивость по двум причинам:

а) увеличения К без изменения фаз - все
вектора wp(jω) увеличиваются и когданибудь САУ станет неустойчивой.
Очевидно, что увеличивать К можно
1
в h раз т.ч.
1
h
∆А=
- запас устойчивости САУ по
амплитуде.

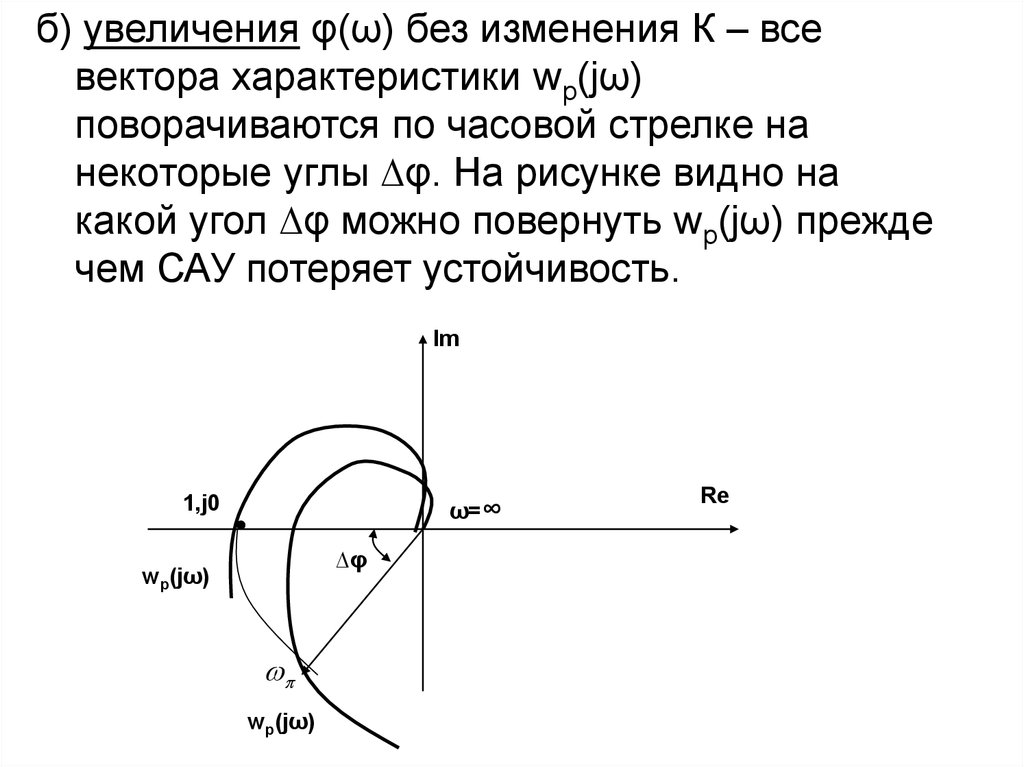
55.

б) увеличения φ(ω) без изменения К – все
вектора характеристики wp(jω)
поворачиваются по часовой стрелке на
некоторые углы ∆φ. На рисунке видно на
какой угол ∆φ можно повернуть wp(jω) прежде
чем САУ потеряет устойчивость.
Im
ω=∞
1,j0
∆φ
wp(jω)
wp(jω)
Re

56.

Проводя окружность радиусом “1” можно
найти ту точку ω , которая попадет в
точку (-1; j0) если на частоте ω φ(ω )
увеличится на угол ∆φ.
Следовательно ∆φ – запас устойчивости
САУ на фазе.

57. Итак, существуют две количественные оценки степени устойчивости САУ

1) Запас “по амплитуде” - ∆А=
1
h
2) Запас “по фазе” - ∆φ
Недостаток частотных критериев
устойчивости – сложно строить кривые
А(jω) и wp(jω)

58. Анализ устойчивости САУ по логарифмическим характеристикам

АФЧХ можно построить в
логарифмическом масштабе в виде
двух характеристик:
L(ω) – логарифмической
амплитудной частотной характеристики
φ(ω) – фазовой частотной
характеристики.

59.

Тогда анализ устойчивости заметно
упрощается. Особенно просто строятся
т.н. асимптотические L(ω) – в виде
кусочно-прямолинейных характеристик.

60. РАССМОТРИМ вначале два элемента таких кусочно-ломанных L(ω)

РАССМОТРИМ
вначале два элемента таких кусочноломанных
L(ω)
L(ω)
Пусть:
60
40
20
1
1
0,1
1
ωc= T
10
φ(ω)
1
TS 1
ω
100
1000
2
-20дб/дек
0
Тогда:
W ( j )
A( )
1
j T 1
1
2T 2 1
L( ) 20 lg A( ) 20 lg 1 20 lg 2T 2 1
-450
-900
W ( s)
φ(ω)= -arctgωT

61.

Пусть:
Тогда:
1
W ( s)
TS 1
1
W ( j )
j T 1
A( )
1
2T 2 1
L( ) 20 lg A( ) 20 lg 1 20 lg 2T 2 1

62.

Приближенно:
при ω <
1
при ω > T
Итак L(ω) состоит из двух прямых
(асимптот):
1
1 – совпадающей с осью ω при ω < T
20 lg 1 0
L( )
20 lg 1 20 lg T
1
T
2 – имеющей наклон –20 дб/дек при ω >
1
T

63.

Частота ω = = ωс называется
сопрягающей.
1
T
На сопрягающей частота ωс =
φ(ω) = - arctg1 = -450
1
T
При ω→∞ φ(ω) = -arctg∞→ -900
ω→0 φ(ω) = -arctg0 →00

64. Итак, чтобы построить L(ω) и φ(ω) для этого элемента – w(jω) = нужно:

Итак, чтобы построить L(ω) и φ(ω) для
1
этого элемента – w(jω) = j T 1
нужно:
1. Найти сопрягающую частоту:
2. Вдоль оси ω построить участок 1 для
ω < ωс
3. Построить участок 2 с наклоном 20дб/дек для
ω < ωс

65.

4. По формуле φ(ω)= -arctgωT
задаваясь разными частотами 0<ω<∞
построить фазовую частотную
характеристику L(ω)

66.

Пусть теперь:
W ( s) TS 1
Тогда:
W ( j ) j T 1
A( ) 2T 2 1
Приближенно:
20 lg 1 0 при ω <
L( )
20 lg T при ω >
1
T
1
T

67.

Т.О. и здесь L(ω) состоит из двух
участков:
1 – вдоль оси ω до ω ≤ ωс =
1
T
2 – с наклоном +20дб/дек при ω >
1
Т

68.

L(ω)
40
+20дб/дек
20
1
II
I
10
100
φ(ω)
ω
1000
φ(ω)= +arctgωT
+900
+450
ω
1
10
100

69. Построение асимптотических L(ω) и φ(ω) для сложных САУ.

Пусть например:
100 (0,1S 1)
wp ( s)
S(S 1)(0,01S 1)
Заменив S→jω получим амплитуднофазовые частотные характеристики:
100(0,1j 1)
W(j )
j (j 1)(0,01j 1)

70.

Представим последнюю характеристику в виде
произведения характеристик элементарных
звеньев:
100
1
1
w( j )
*
* (0,1 j 1) *
0,01 j 1
j
j
1
3дифференцирующее
1интегратор
2 инерционное
звено
звено
4 инерционное
звено

71. Определим сопрягающие частоты:

wc1 1 1
c
1 1
wc 2
0,1 c
1 1
wc 3
0,01 c

72.

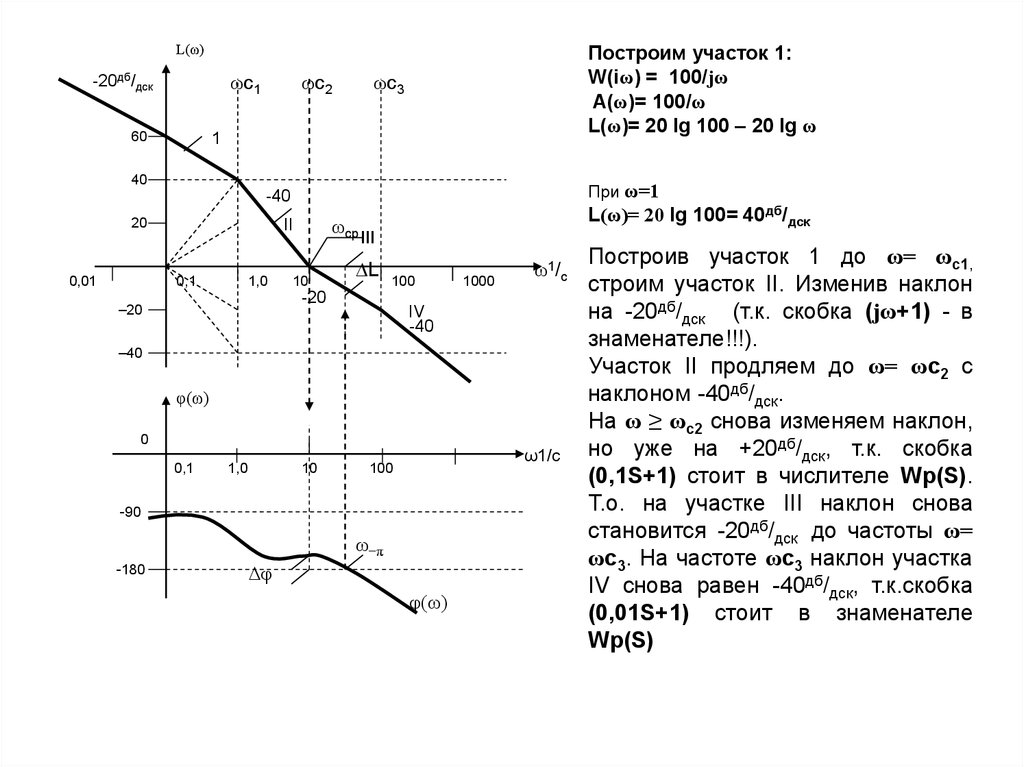
L(ω)
-20дб/дск
ωс1
60
ωс2
Построим участок 1:
W(iω) = 100/jω
A(ω)= 100/ω
L(ω)= 20 lg 100 – 20 lg ω
ωс3
1
40
При ω=1
-40
20
0,01
ωср
II
0,1
1,0
10
L(ω)= 20 lg 100= 40дб/дск
III
∆L
100
-20
–20
1000
ω1/с
IV
-40
–40
φ(ω)
0
0,1
1,0
10
ω1/c
100
-90
ω−π
-180
∆φ
φ(ω)
Построив участок 1 до ω= ωс1,
строим участок II. Изменив наклон
на -20дб/дск (т.к. скобка (jω+1) - в
знаменателе!!!).
Участок II продляем до ω= ωс2 с
наклоном -40дб/дск.
На ω ≥ ωс2 снова изменяем наклон,
но уже на +20дб/дск, т.к. скобка
(0,1S+1) стоит в числителе Wp(S).
Т.о. на участке III наклон снова
становится -20дб/дск до частоты ω=
ωс3. На частоте ωс3 наклон участка
IV снова равен -40дб/дск, т.к.скобка
(0,01S+1) стоит в знаменателе
Wp(S)

73. Фазовая характеристика φ(ω) САУ

складывается из фазовых характеристик
отдельных звеньев Wp(S):
• φ(ω) = –90°−(arctg1ω)+(arctg0,1ω) –
(arctg0,01ω)

74. Для ее построения удобно построить таблицу

ω1=1
ω2=10
ω3=100
ω4
ω5
φ1
-90
-90
-90
-90
-90
φ2
φ3
-45
+
-45
+
+
+
φ4
φ
-
-
-45
-
-
Фазовая характеристика строится по точкам под
амплитудной,
причем масштаб по оси “ω” тот же.

75.

• Об устойчивости САУ судят по
расположению точек пересечения L(ω)
оси частот ωср –частота среза и φ(ω)
оси -180°.

76. Критерий устойчивости по ЛАЧХ

• Для устойчивости линейных САУ необходимо и
достаточно, чтобы:
ωср < ω−π
• Логарифмические характеристики позволяют
определить запасы устойчивости:
∆L (дб) – запасы по амплитуде
∆φ (град) – запас по фазе
как это показано на рисунке.