Похожие презентации:
Расширение множества натуральных чмсел
1.
Л. А. Янкина,канд. пед. наук, доцент
2.
1. Задача расширенияпонятия числа
2. Положительные
рациональные числа
3. Действительные числа
3.
Задача расширения понятиячисла
Большинство применений
математики сводится к двум
основным задачам:
- подсчет числа элементов конечного
множества;
- измерение величин.
4.
4 арбуза9 грузовиков
5.
4 куска ткани6.
Для решения первой задачидостаточно множества целых
неотрицательных чисел:
N0 = {0, 1, 2, 3, …}
7.
18 см < d < 19 смДля измерения величин натуральных
чисел недостаточно
8.
Счетпредметов
Измерение
величин
Натуральные
числа
Дробные
числа
Иррациональные
числа
9.
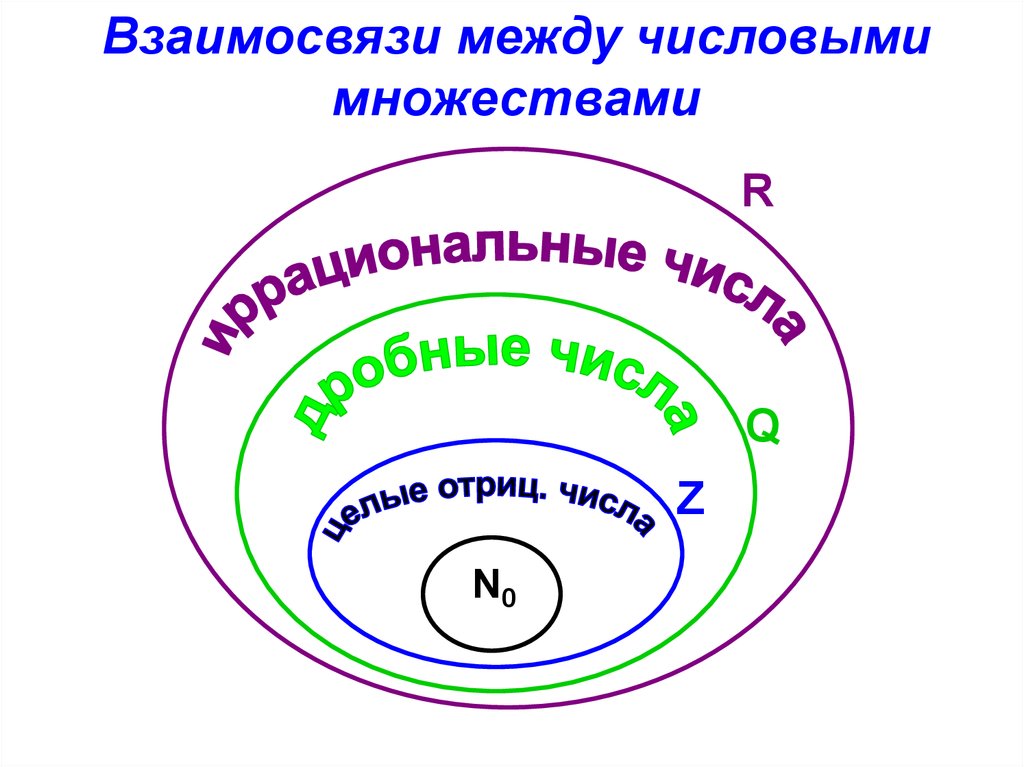
Взаимосвязи между числовымимножествами
R
Q
Z
N0
10.
Расширение множестванатуральных чисел
R
R+
Q+
N
11.
ПОЛОЖИТЕЛЬНЫЕРАЦИОНАЛЬНЫЕ ЧИСЛА
1. Понятие дроби
2. Понятие положительного
рационального числа
3. Арифметические действия над
положительными рациональными
числами
4. Свойства множества положительных
рациональных чисел
12.
Понятие дробиДан отрезок а, выберем единичный отрезок е.
При измерении длины отрезка а могут
возникнуть следующие ситуации:
1. Единичный отрезок е укладывается в
отрезке а целое число раз (n раз):
mе(а) = n или а = nе
Длина отрезка а при единице длины е
выражается натуральным числом n
Отрезки а и е в этом случае называются
соизмеримыми
13.
2. Единичный отрезок е не укладывается вотрезке а целое число раз. Разобьем отрезок
е на n равных частей и выберем в качестве
единицы длины n-ную часть отрезка е:
1
mе1(е) = n или е = nе1, е1 = е
n
Если n-ная часть отрезка е укладывается в
отрезке а целое число раз (m раз), то
mе(а) =
m
n
или а =
m
n
е
Длина отрезка а выражается парой
натуральных чисел (m; n)
14.
Пару чисел, записанную в видеm
,
n
называют обыкновенной дробью, здесь
m, n N, m – числитель, n – знаменатель.
Знаменатель определяет, какую часть единицы
измерения следует рассмотреть, числитель –
указывает, сколько таких частей нужно взять
Длина отрезка а при единице длины е
выражается обыкновенной дробью
Отрезки а и е в этом случае называются
соизмеримыми
15.
3. Единичный отрезок е и любая егочасть не укладываются в отрезке а
целое число раз. То есть его длину
нельзя выразить ни натуральным, ни
дробным числом.
В этом случае отрезок а не соизмерим
ни с каким единичным отрезком.
Длина такого отрезка выражается
иррациональным числом.
16.
Рассмотрим отрезок а, выберемединичный отрезок е
а
е
е1
1
18
е = 4е1 е1 = е, а =
е
4
4
1
9
е = 2е2 е2 = е, а =
е
2
2
1
36
е = 8е3 е3 = е, а =
е и т. д.
8
8
17.
Длина отрезка а может быть выраженабесконечным множеством дробей:
9 18 36
, , ,...
2 4 8
Вообще, если при единице длины е
m
длина отрезка а выражена дробью
, то
n
она может быть выражена и любой
mk
дробью вида
, где k N
nk
18.
Дроби, выражающие длину одного итого же отрезка при единице длины е,
называют равными дробями (или
эквивалентными, или равносильными)
19.
Теорема (признак определенияравенства дробей)
p
m
Для того чтобы дроби
и
n
q
выражали длину одного и того же
отрезка, необходимо и достаточно,
чтобы выполнялось равенство mq = np,
т.е.
p
m
=
mq = np.
n
q
9 18
Пример:
, т. к. 9 · 4 = 2 · 18
2 4
20.
Основное свойство дробиЕсли числитель и знаменатель дроби
умножить или разделить на одно и то
же натуральное число, то получится
дробь, равная данной:
m mk , k N
n nk
На этом свойстве основано
сокращение дробей и приведение
дробей к общему знаменателю
21.
Сокращение дроби – это замена даннойдроби другой, равной данной, но с
меньшим числителем и знаменателем
Чтобы сократить дробь, надо ее
числитель и знаменатель разделить на
одно и то же число отличное от 0
Дробь является сократимой, если ее
числитель и знаменатель имеют общий
делитель больше единицы. Если числитель
и знаменатель дроби одновременно делятся
только на единицу, то дробь называют
несократимой
22.
5Пример 1:
несократимая дробь, т. к.
17
D (5; 17) = 1, т.е. 5 и 17 взаимно простые.
48
Пример 2: сократить дробь
80
48 3
D (48; 80) = 16,
80 5
23.
Приведение дробей к общемузнаменателю – это замена данных
дробей равными им дробями,
имеющими одинаковые знаменатели
m
p
Общим знаменателем двух дробей и
n
q
является общее кратное чисел n и q, а
наименьшим общим знаменателем – их
наименьшее общее кратное К(n, q)
24.
Пример: Привести к наименьшемуобщему знаменателю дроби 8 и 4
15
35
15 = 3 · 5, 35 = 5 · 7, K(15, 35) = 3 · 5 · 7 = 105
8
8 7
56
15 15 7 105
4
4 3
12
35 35 3 105
25.
Дробь называется правильной, еслиеё числитель меньше знаменателя, и
неправильной, если ее числитель
больше знаменателя или равен ему
правильные
неправильные
1 3 8 9 12 1 40
8 5 8 7 36 1 5
26.
Упражнения3 1 9 3 5 12
, , , , ,
На множестве дробей 4 5 12 15 25 6 задано
отношение равенства. Постройте граф этого
отношения. Каковы особенности этого графа? С
чем они связаны?
Приведите дроби к наименьшему общему
1
7
5
15
23
1
знаменателю: а) и
б)
и
в)
и
3
102
16
844
Найдите несократимую дробь, равную
108
402
следующей: а)
б)
144
455
г) 45 56 45 14
70 72
780
в)
2730
д) 38 53 38 25
19 42
171
270
27.
28.
- Обыкновеннаядробь,
числитель,
знаменатель
m
n
m, n N
- Правильная
дробь
m<n
- Неправильная
дробь
m n
- Сократимая
дробь
D(m; n) 1
- Несократимая
дробь
D(m; n) = 1
29.
Одному и тому же отрезку можнопоставить в соответствие
бесконечное множество равных
дробей, выражающих его длину при
выбранной единице е. Но длина
отрезка должна представляться
единственным числом. Поэтому
равные дроби считают различными
записями одного и того же числа, а
само число называют
положительным рациональным
числом.
30.
Положительным рациональнымчислом называется класс равных
дробей, а каждая дробь,
принадлежащая этому классу, есть
запись (представление) этого числа
1 2 3 4 1 2 3 4
, , , ,... , , , ,...
Примеры: 2 4 6 8 , 3 6 9 12
Множество всех положительных
рациональных чисел принято обозначать
символом Q+.
31.
Отношение равенства намножестве Q+
Если положительное рациональное
m
n ,
число а представлено дробью
а
положительное рациональное число b –
p
m p
другой дробью q , то а = b n q тогда
и только тогда, когда mq = np.
32.
Среди всех записей любогоположительного рационального
m
числа выделяется дробь n ,
которая является несократимой
(т. е. Д(m; n) = 1)
33.
ТеоремаДля
любого
положительного
рационального числа а найдётся одна и только
одна
несократимая
дробь,
являющаяся
записью этого числа
34.
mЗадача. Пусть n - запись некоторого
рационального числа. Построить отрезок, длина
которого выражается этим числом.
Алгоритм
1) выбрать единицу длины е
2) разделить единичный отрезок е на n равных
частей
3) построить луч Ох и на нем от точки О
отложить m отрезков, равных n-ной части
отрезка е – получим точку А.
m
Отрезок ОА – искомый: ОА = n е
35.
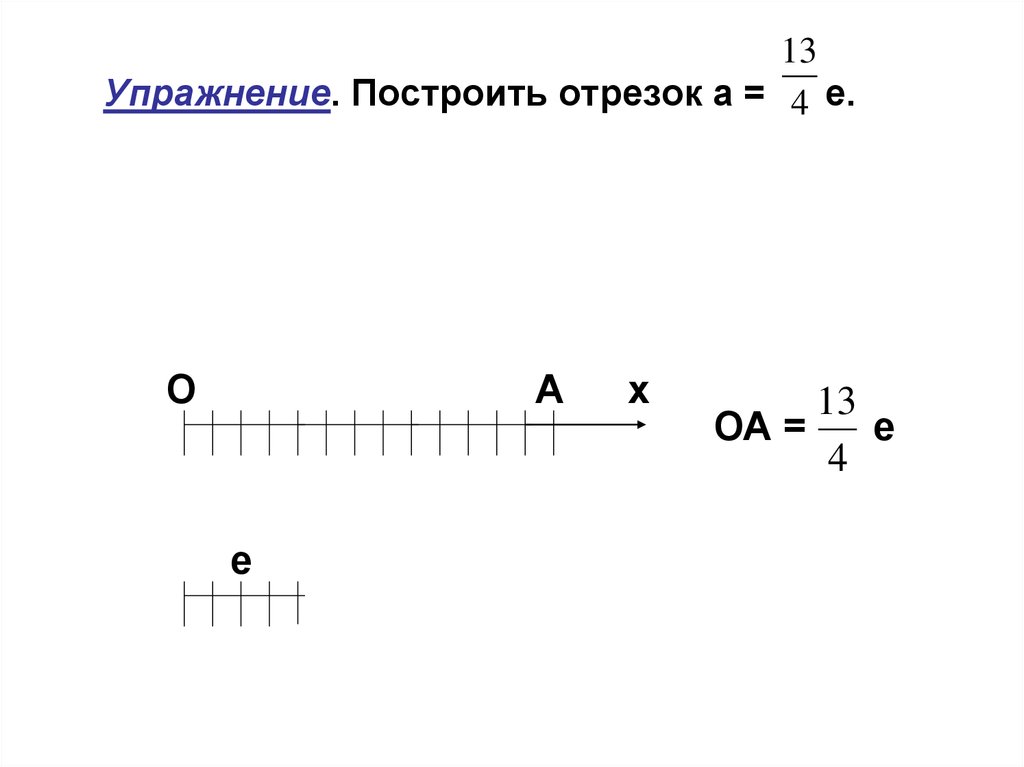
13Упражнение. Построить отрезок а = 4 е.
О
А
е
х
13
ОА =
е
4
36.
37.
Рассмотрим отрезки а, b и с,е – единичный отрезок
а
е
b
с
m
р
а = n е, b = n е,
где е = nе1 и
1
е1 = n е
р
m
с=а+b=
е+
е = mе1 + ре1 = (m + р)е1 =
n
n
m р
=
е
n
38.
Определение. Если положительныерациональные числа а и b представлены
m
p
дробями n и n , то их суммой называется
число а + b, которое представляется
m p
дробью n
р
m
+
n
n
m р
=
n
(1)
Если же числа а и b представлены дробями с
различными знаменателями, то сначала надо
привести их к одному знаменателю, а затем
применять правило (1)
39.
Чтобы сложить дроби, нужно привестиих к общему знаменателю, затем
сложить их числители и полученную
сумму взять числителем, а найденный
общий знаменатель – знаменателем
Пример:
2 3
4
20 15 8
20 15 8 43
7 14 35
70 70 70
70
70
40.
В общем виде правило сложения можнозаписать так:
m p mq np
n q
nq
Если D(n, q) = 1, К(n, q) = n · q
41.
Теорема (о существовании иединственности суммы)
Сумма любых двух положительных
рациональных чисел существует и
единственна
42.
Отношение «больше»Пусть а, b Q+.
Определение. Число а больше числа b,
если существует такое число с Q+,
что а = b + с:
а > b ( с Q+) а = b + с
Отношение «меньше» определяется
аналогично
43.
Практические приемы установленияотношения «больше»
m
р
1)Если а = n , b = n , то а > b тогда и
только тогда, когда m > р.
13
9
Пример: 14 > 14 , так как 13 > 9.
m
n
m
q
2) Если а = , b = , а > b тогда и
только тогда, когда n < q.
13 13
Пример: 14 > 15 , так как 14 < 15.
44.
pm
3) Если а = n , b = q , то а > b тогда
и только тогда, когда mq > nр.
11
7
Пример: 8 > 13 , т.к. 7 · 13 > 8 · 11
Теорема. ( а, b Q+) а b а b b > а
45.
Отношение «больше» обладаетсвойствами:
1) антисимметричности:
( а, b Q+) а b и а b b > а
2) транзитивности:
( а, b, с Q+) а b и b > с а с
Отношение «больше» является
отношением порядка на множестве Q+
46.
Свойства сложения1) Коммутативный закон сложения
( а, b Q+) а + b = b + а
2) Ассоциативный закон сложения
( а, b, с Q+) (а + b) + с = а + (b + с)
3) Сократимость сложения
( а, b, с Q+) а + с = b + с а = b
4) Монотонность сложения
( а, b, с Q+) а > b а + с > b + с
47.
5)6)
( а, b Q+) а + b а
( а Q+) а + 0 = 0 + а = а
В связи с определением сложения
рациональных чисел возникает
возможность уточнить смысл
1
5
записей вида 3 4 , 12 7 – смешанных
чисел
48.
mРассмотрим неправильную дробь n
m n
m
а) m n n - запись натурального числа.
15
Например, 3 = 5.
б) m n
Разделим m на n с остатком:
m = nq + r, где r < n.
m
nq r nq r
r
q
Тогда n =
n
n n
n
49.
rТак как r < n, то дробь n правильная.
Таким
образом,
m
n
неправильную дробь
можно
представить
в
виде
суммы
натурального числа q и правильной
r
дроби n . Это действие называют
выделением
целой
неправильной дроби.
части
из
50.
Пример:13 4 3 1 4 3 1
1
1
3 3
4
4
4
4
4
4
смешанная дробь
51.
Справедливои
обратное
утверждение: всякую смешанную
дробь можно записать в виде
неправильной дроби:
1
1 3 4 1 4 3 1 13
3 3
Пример: 4
4 1 4 4
4
4
1 3 4 1
3
или 4
4
52.
Разностью положительныхрациональных чисел а и b называется
такое положительное рациональное
число с, что а = b + с
а–b=с а=b+с
Операцию, в результате которой находят
разность положительных рациональных
чисел а и b, называют вычитанием.
Вычитание положительных рациональных
чисел - операция, обратная сложению
53.
Теорема (о существовании иединственности разности)
Разность а – b положительных
рациональных чисел существует тогда
и только тогда, когда а > b. Если
разность а – b существует, то она
единственна
54.
Используя определение и условиесуществования разности, можно получить
правило
вычитания
положительных
рациональных чисел, представленных
m
p
дробями n и n , где m > p:
p m p
m
n – n = n
(2)
Если же числа а и b представлены
дробями с разными знаменателями, то
нужно сначала привести эти дроби к
общему знаменателю, а затем применить
формулу (2)
55.
Правила вычитания1) правило вычитания числа из суммы
а > с (а + b) – с = (а – с) + b
или
b > с (а + b) – с = а + (b – с)
56.
2) правило вычитания суммы из числаа – (b + с) = (а – b) – с
3) правило вычитания разности из числа
а – (b – с) = (а – b) + с
4) а – 0 = а, а – а = 0
57.
Если положительные рациональные числаm
n
представлены дробями
произведение есть число,
mp
дробью nq :
p
q , то их
и
представленное
m p mp
·
n q = nq
т.е. произведением двух дробей называется
дробь, числитель которой равен произведению
числителей этих дробей, а знаменатель –
произведению знаменателей.
58.
3 5 3 5 5Примеры: 1)
4 6 4 6 8
1 4 22 4 88
4
2) 7
4
3 7 3 7 21
21
59.
Теорема (о существовании иединственности произведения)
Произведение любых двух
положительных рациональных чисел
существует и единственно
60.
Законы умножения1) Коммутативный закон умножения
( а, b Q+) а · b = b · а
2) Ассоциативный закон умножения
( а, b, с Q+) (а · b) · с = а · (b · с)
3) дистрибутивный закон умножения
относительно сложения
( а, b, с Q+) а · (b + с) = а · b + а · с
4) дистрибутивный закон умножения
относительно вычитания
( а, b, с Q+) а · (b - с) = а · b - а · с
61.
5) Сократимость умножения( а, b, с Q+) а · с = b · с а = b
6) Монотонность умножения
( а, b, с Q+) а > b а · с > b · с
7) а · 1 = 1 · а = а,
а·0=0·а=0
62.
Деление положительных рациональныхчисел - операция, обратная умножению
Операцию, в результате которой находят
частное положительных рациональных
чисел а и b, называют делением.
Частным положительных рациональных
чисел а и b называется такое
положительное рациональное число с,
что а = b · с
а:b=с а=b·с
63.
Правило деленияm p m q
:
n q n p
Теорема (о существовании и
единственности частного)
Частное любых двух положительных
рациональных чисел существует и
единственно
64.
Свойства деления1) правило деления произведения на
число:
(а · b) : с = (а : с) · b или (а · b) : с = а · (b : с)
2) правило деления числа на произведение
а : (b · с) = а : b : с
3) дистрибутивный закон деления
относительно сложения
(а + b) : с = а : с + b : с
4) дистрибутивный закон деления
относительно вычитания
(а - b) : с = а : с - b : с
65.
5) а : 1 = а, а : а = 1 а · 0 = 0 · а = 0На 0 делить нельзя
Замечание. Знак черты в дроби можно
рассматривать как знак действия
деления:
m
= m : n.
n
66.
Термин «рациональное число»произошел от латинского слова r а t i о,
что в переводе на русский означает
«отношение» (частное).
67.
СВОЙСТВА МНОЖЕСТВАПОЛОЖИТЕЛЬНЫХ РАЦИОНАЛЬНЫХ
ЧИСЕЛ
N
Q+
1. N Q+
дробные
числа
Пример: натуральное число 6 можно
представить в виде следующих дробей:
6 12 18 24
1 , 2 , 3 , 4 и т.д.
68.
2. Множество Q+ не ограничено снизу,т.е. в нем нет наименьшего числа
3. Множество Q+ не ограничено сверху,
т.е. в нем нет наибольшего числа
4. Множество Q+ упорядочено
Множество Q+ упорядочивает заданное
на нем отношение «больше» (или
«меньше»), которое является
отношением порядка, так как оно
антисимметрично и транзитивно.
69.
5. Множество Q+ плотно, т.е. между любымидвумя различными числами а и b из Q+
заключено бесконечно много чисел этого же
множества
6. Множество Q+ замкнуто относительно
четырех арифметических операций
т.е. сумма, разность, произведение, частное
(кроме частного при делении на 0, которое не
имеет смысла) любых двух положительных
рациональных чисел является
положительным рациональным числом.
70.
Основные задачи на дроби1.Нахождение дроби от числа
25
В классе 25 учеников.
2 учащихся класса
5
ходило в кино.
Сколько учеников
ходили в кино?
2
25 ·
5
?
2
5
= 10 (уч.)
71.
2.Нахождение числа по данному значениюдроби
10 учеников класса
ходили в кино, что
2
составляет
всех
5
учащихся класса.
Сколько всего
?
10
2
5
учеников в классе?
2
5
10 :
= 10 ·
= 25 (уч.)
5
2
72.
3.Нахождение отношения двух чиселВ классе 25 учеников.
10 учеников ходили в
кино. Какую часть
всех учеников класса
составляют ученики,
ходившие в кино?
10
2
=
25
5
25
10
?
73.
Проценты1
1%=
= 0,01
100
12
12 % =
= 0,12
100
100
100 % =
= 1
100
2
2%=
= 0,02
100
40
40 % =
= 0,4
100
115
115 % =
= 1,15
100
Чтобы проценты выразить дробью, нужно
число процентов разделить на 100 и отбросить
знак %.
Чтобы число выразить в процентах, нужно
число умножить на 100 и приписать знак %.
74.
Основные задачи на проценты1.Нахождение процентов от числа
25
В классе 25 учеников.
40 % учащихся класса
?
ходили в кино.
Сколько учеников
40 %
ходили в кино?
25 · 40 % = 25 · 0,4 = 10 (уч.)
75.
2.Нахождение числа по данному значениюпроцентов
10 учеников класса
ходили в кино, что
?
10
составляет 40 % всех
учащихся класса.
40 %
Сколько всего
учеников в классе?
10 : 40% = 10 : 0,4= 100 : 4 = 25 (уч.)
76.
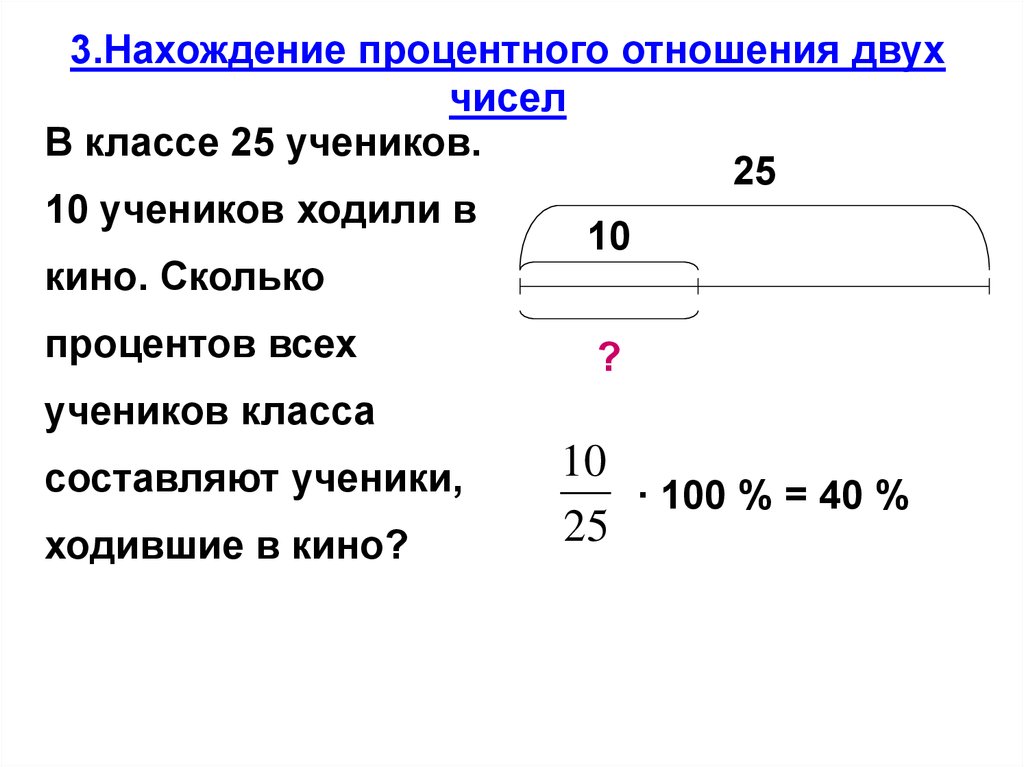
3.Нахождение процентного отношения двухчисел
В классе 25 учеников.
25
10 учеников ходили в
10
кино. Сколько
процентов всех
?
учеников класса
составляют ученики,
ходившие в кино?
10
· 100 % = 40 %
25
77.
Множество положительныхрациональных чисел
как расширение множества натуральных
чисел
Условия расширения:
1. N Q+
2. Согласованность операций,
т.е. результаты арифметических действий,
произведенных по правилам, существующим для
натуральных чисел, должны совпадать с
результатами действий над ними, но
выполненных по правилам, сформулированным
для положительных рациональных чисел.
78.
3. Выполнимость в Q+ операции, невсегда осуществимой в N
Деление, которое не всегда
выполняется во множестве N, во
множестве Q+ выполняется всегда
79.
УпражнениеРешить уравнение, используя
зависимость между компонентами и
результатами действий:
3
1 3 4
3 1
66 : 5 3 : 1 х 7
5
5 5 15
20 4
80.
81.
mДесятичной называется дробь вида
n ,
10
где m, n N.
m
При записи дроби 10 n последние n
цифр десятичной записи числа m
отделяют запятой.
4362
Примеры:
43,62
2
10
47 00047
0,0047
4
4
10
10
82.
Утверждение: Если к десятичной дробиА,an-1 ... a0 приписать справа любое
число нулей, то получится десятичная
дробь, равная данной, т.е.
А,an-1 ... a0 = А,an-1 ... a000…0
83.
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАДДЕСЯТИЧНЫМИ ДРОБЯМИ
Сложение и вычитание
2,5400
+
3,7126
3,7126
2,5400
6,2526
1,17 2 6
84.
Умножение3
,
21
5,4
+
12 8 4
16 0 5
17,334
Примеры: 1) 5,426·102 = 542,6
2) 5,42·103 = 5420
85.
ДелениеПримеры: 1) 24,48 : 1,2 = 244,8 : 12 = 20,4
244,8 12
24
2 0, 4
48
48
0
2) 542,6 : 102 = 5,426
3) 5,4 : 103 = 0,0054
86.
ПЕРЕВОД ОБЫКНОВЕННЫХ ДРОБЕЙ ВДЕСЯТИЧНЫЕ
И ДЕСЯТИЧНЫХ – В ОБЫКНОВЕННЫЕ
412 412 103
4,12 2
10
100 25
87.
Чтобы перевести обыкновенную дробь вдесятичную, нужно разделить числитель на
знаменатель
m
Любую ли дробь вида n (m, n N)
можно записать в виде конечной
десятичной дроби, т.е. дроби, у которой
после запятой стоит конечное число
цифр?
88.
Теорема. Для того чтобы несократимаядробь
m
n
была равна десятичной,
необходимо и достаточно, чтобы в
разложение ее знаменателя n на
простые множители входили лишь
простые числа 2 и 5 (или лишь одно из
них).
89.
Примеры: 1)160
2
80
2
40
2
20
2
10
2
5
5
1
7
7
5 0,04375
2 5
160
90.
99
2)
14 2 7
3)
- дробь нельзя
превратить в конечную
десятичную
195
3
3
260
4 2 2
260 = 22 · 5 · 13
0,75
91.
Упражнения1234 6969
1. Запишите дроби 10 , 10
37
, 10
в виде
десятичных.
2. Запишите числа 7,11; 0,45; 13,745 в виде
несократимых обыкновенных дробей.
3. Какими будут численные значения
следующих величин, если в качестве единицы
длины взять 1 м: а) 23 см 2 мм; в) 90 дм 16 см 8
мм; б) 5м 17 дм; г)1 км 120м?
92.
4. Невыполняя
вычислений,
сравните
следующие произведения:
а) 19,91 •199,2 и 1,991·1992;
б) 1,992 •199,3 и 1,992 •1993.
5. Что больше: 35% от 40 или 40% от 35?
6. Увеличьте число: а) 60 на 10%; 6) 80 на 2,5%.
7. Число х увеличили на 45%. Во сколько раз
увеличили число?
8. Число х увеличили в 2,4 раза. На сколько
процентов увеличили число?
93.
9. Туристы прошли 75% маршрута и имосталось пройти еще 5,5 км. Какова длина
маршрута?
10. Какие из следующих чисел можно записать
в виде конечных десятичных дробей:
7
12
21 12
;
;
;
.
352 56 75 96
94.
БЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ ПЕРИОДИЧЕСКИЕ ДРОБИПример 1
10
1,42857141… =
7
= 1,(42857141)
10 7
7 1,42857141
30
28
20
14
60
56
40
35
50
49
10
95.
Пример 231
2,8181… =
11
= 2,(81)
31 11
22 2,8181
90
88
20
11
90
88
20
11
90
96.
Пример 353
4,4166… =
12
= 4,41(66)
53 12
48 4,4166
50
48
20
12
80
72
80
72
80
97.
Пример 40,25 = 0,250000…. = 0,25(0)
Дробь называется периодической,
если начиная с некоторой цифры, она
образуется бесконечным повторением
одной и той же цифры или группы
цифр. Повторяющуюся группу цифр
заключают в скобки и называют
периодом этой дроби.
Каждое положительное рациональное
число можно представить в виде
бесконечной десятичной
периодической дроби.
98.
Если период следует сразу послезапятой, то такую дробь называют
чисто периодической.
Если перед периодом стоят один
или несколько знаков, то дробь смешанная периодическая
99.
Преобразование бесконечнойпериодической дроби в обыкновенную
Чисто периодическая бесконечная
десятичная дробь, меньше единицы,
равна такой обыкновенной дроби,
числитель которой равен периоду, а
знаменатель состоит из стольких
девяток, сколько цифр в периоде
дроби
3
1
Пример: 5,33… = 5,(3) = 5 5
9
3
100.
Смешанная периодическая дробь, меньшеединицы, равна такой обыкновенной дроби,
числитель которой равен разности между
числом, записанным цифрами, стоящими до
начала второго периода, и числом,
записанным цифрами, стоящими до начала
первого периода; знаменатель состоит из
такого числа девяток, сколько цифр в
периоде, и такого числа нулей, сколько цифр
стоит до начала первого периода
К периодическим десятичным дробям можно
отнести все конечные десятичные дроби, как
дроби, имеющие в периоде число 0.
101.
46 442
7
Пример: 3,4(6) = 3
3
3
90
90
15



























































































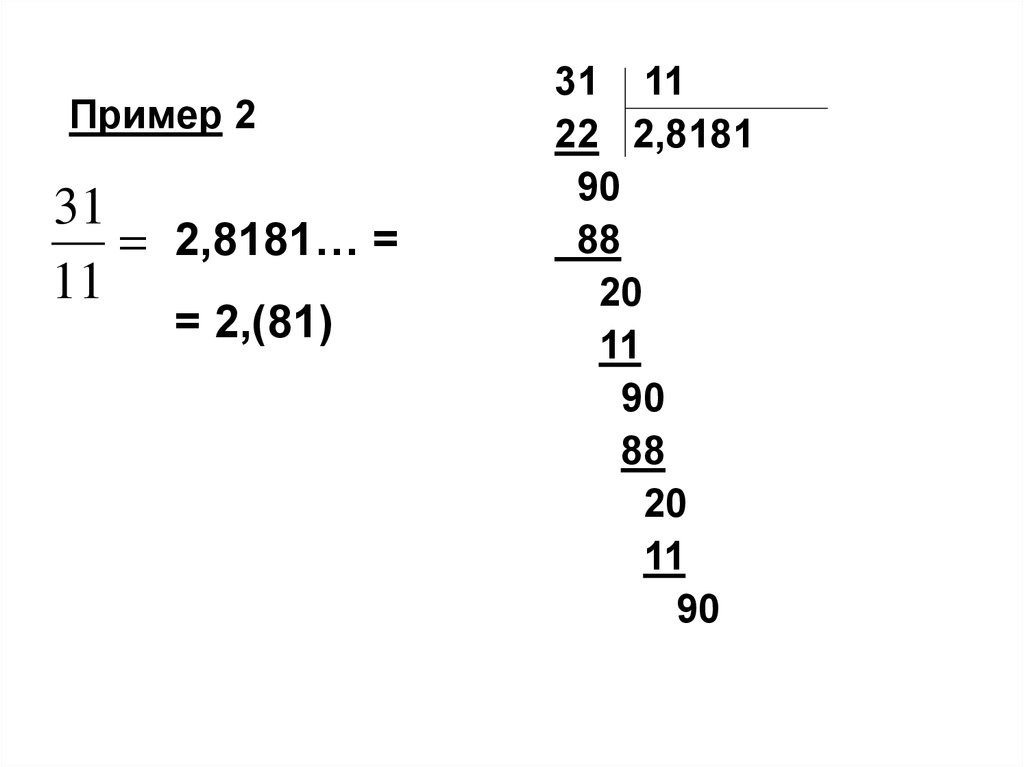







 Математика
Математика








