Похожие презентации:
Действительные числа. Множество действительных чисел
1. Действительные числа
Число, выраженное десятичнымзнаком, прочтёт и немец, и русский, и
араб, и янки одинаковою
Д. Менделеев
2. Оглавление
Множество действительных чиселНатуральные числа
Целые числа
Рациональные числа
Иррациональные числа
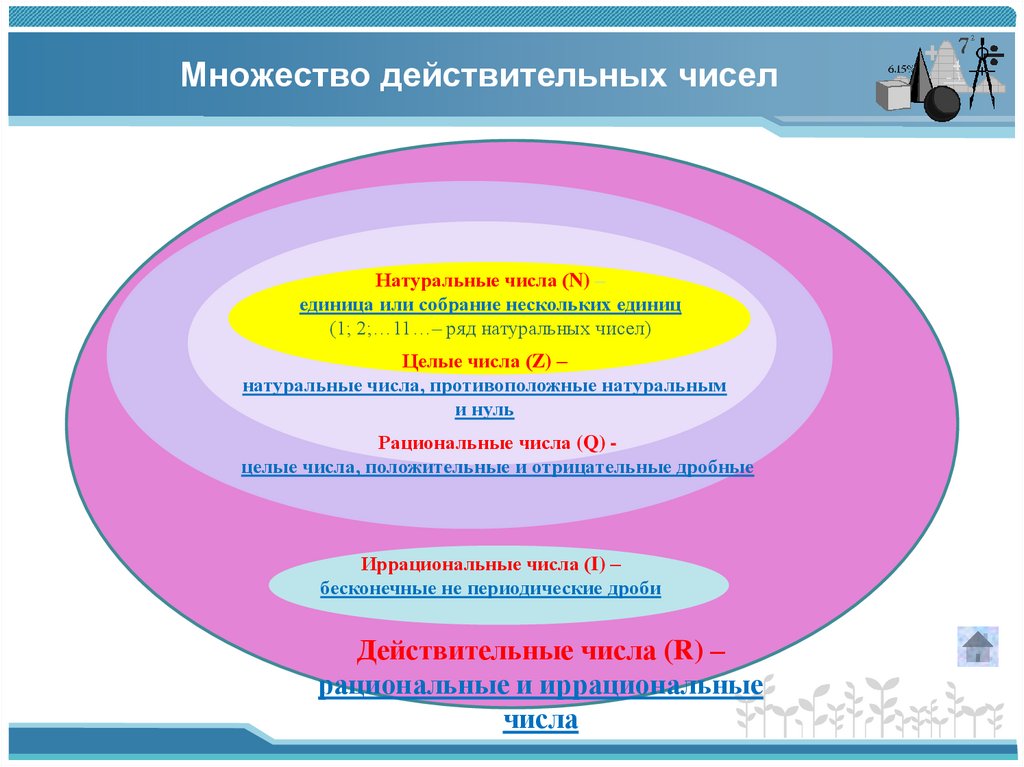
3. Множество действительных чисел
Натуральные числа (N) –единица или собрание нескольких единиц
(1; 2;…11…– ряд натуральных чисел)
Целые числа (Z) –
натуральные числа, противоположные натуральным
и нуль
Рациональные числа (Q) целые числа, положительные и отрицательные дробные
Иррациональные числа (I) –
бесконечные не периодические дроби
Действительные числа (R) –
рациональные и иррациональные
числа
4. Натуральные числа (N)
Простые -делятся насебя и на единицу
Составные - остальные
Четные - делящиеся на
2 и число 0. (2п)
Нечетные – остальные
(2п+1; 2п-1).
2-единственное простое
четное число!!! Любое
составное число можно
разложить на простые
множители
Найдите неточность
или ошибку на
слайде.
5. Задание 1
• Найти НОД иНОК чисел
(34; 68)
(54; 72);
(96; 124)
• НОД (34; 68)=17
• НОД (54; 72)=18
• НОД (96; 124)=4
• НОК (34; 68)=68
• НОК (54; 72)=216
• НОК (96; 124)=2976
Найдите неточность или ошибку на
слайде.
6. Целые числа (Z)
• Целые числа=натуральные числа + импротивоположные числа+0
Целые числа бывают положительными,
отрицательными.
Число 0 не имеет
знака!
7. Рациональные числа (Q)
Доля(часть) единицы или собраниенескольких одинаковых долей
единицы называется обыкновенной
дробью
Дробь, у которой знаменатель есть
единица с одним или несколькими нулями,
называется десятичной дробью
Найдите неточность или ошибку на
слайде.
¼=0,75 – конечная десятичная
дробь
2/3 = 0,666…= 0,(6) –
бесконечная периодическая
дробь
0,(68) – чистая периодическая
дробь
1, 4(35) – смешанная
периодическая дробь
8. Задание 2
Перевести в
десятичную дробь
5/7; 31/6
• Перевести в
обыкновенную
дробь 0,(3); 0,2(3)
0, (714285)
5, 1(6)
1/3
4/33
Найдите неточность или ошибку
на слайде.
9. Иррациональные числа (I)
10. Задание 3
• Извлечь квадратныйкорень из чисел
425104;
1,7424;
21697,29
• 652; 1,32; 147,3
11. Правило перевода периодической дроби в обыкновенную
Чтобы обратить чистую периодическую дробь в обыкновенную,
нужно ее период сделать числителем, а в знаменателе записать
цифру 9 столько раз, сколько цифр в периоде.
23
1, 23 1
99
Чтобы обратить смешанную периодическую дробь в
обыкновенную, нужно из числа, стоящего после запятой до
второго периода, вычесть число, стоящее после запятой до
первого периода, и эту разность сделать числителем, а в
знаменатель записать цифру 9 столько раз, сколько цифр в
периоде, со столькими нулями справа, сколько цифр между
запятой и первым периодом.
437 4
433
1,4 37 1
990
1
990










 Математика
Математика








