Похожие презентации:
Модель Бельтрами-Клейна
1. Модель Бельтрами-Клейна
После создания неевклидовой геометрииона долгое время не признавалась
учеными. И первой, сразу возникшей
проблемой, стало доказательство
непротиворечивости геометрии
Лобачевского. Первые исследования по
вопросу непротиворечивости геометрии
Лобачевского были проведены
итальянским математиком Бельтрами
(1835-1900). В 1868 году Бельтрами
показал, что геометрия Лобачевского
выполняется в малом на псевдосфере
Э. Бельтрами
2.
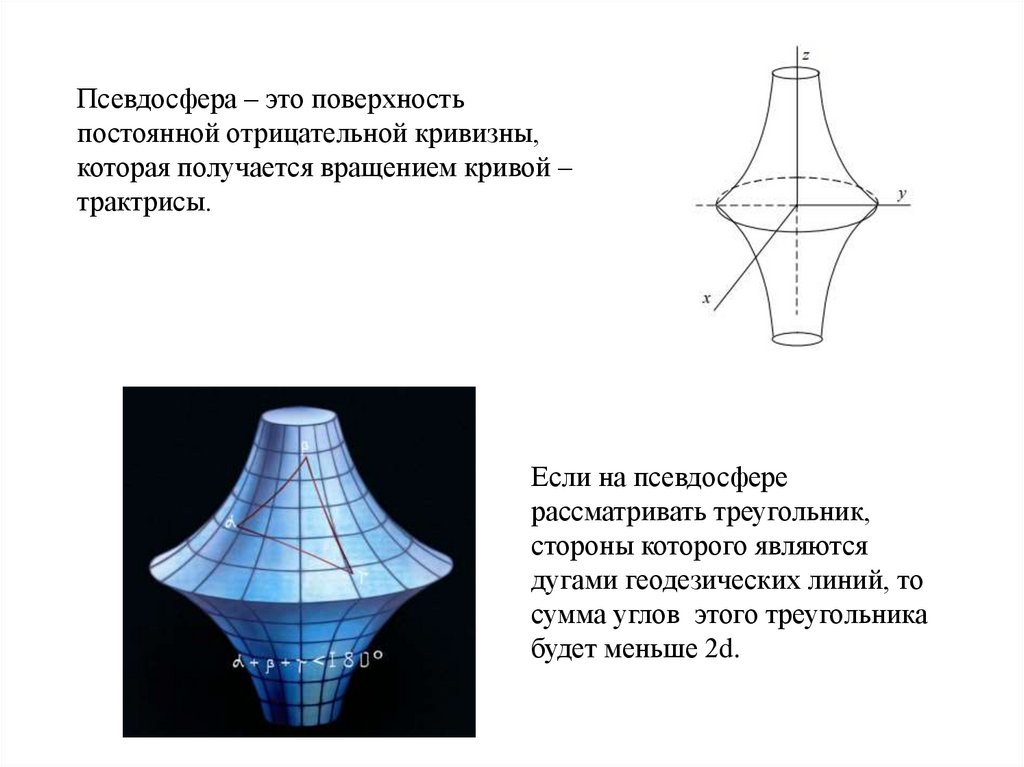
Псевдосфера – это поверхностьпостоянной отрицательной кривизны,
которая получается вращением кривой –
трактрисы.
Если на псевдосфере
рассматривать треугольник,
стороны которого являются
дугами геодезических линий, то
сумма углов этого треугольника
будет меньше 2d.
3.
Простую модель всей плоскости Лобачевского построил в1871г.
Ф.Клейн, взяв в качестве плоскости Лобачевского
открытый круг
евклидовой плоскости.
4. Основные объекты
• Плоскостью лобачевского в моделиБельтрами-Клейна является внутренность
круга евклидовой плоскости.
• Под точками плоскости Лобачевского будем
понимать евклидовы точки,
принадлежащие этому открытому кругу,
под прямыми – хорды окружности без
концов.
5.
Окружность называетсяабсолютом,
точки окружности не принадлежат
плоскости
Лобачевского, их называют
несобственными,
а внешние точки – идеальными.
Между моделями Бельтрами и
Клейна
можно установить изоморфизм,
поэтому
модель Клейна называют моделью
Бельтрами–Клейна.
6. Основные отношения
• Отношение P1- принадлежность точки прямой:точка Р принадлежит прямой А0В0, если евклидова
точка Р принадлежит евклидовой хорде А0В0.
• Отношение P3 – лежать между для трех точек прямой
вводится аналогично: точка Р плоскости Лобачевского
лежит между точками А и В, если точка Р лежит
между евклидовыми точками А и В.
Аксиомы I – II групп системы аксиом выполняются, так
как они являются истинными предложениями на
евклидовой плоскости, аксиомы непрерывности
выполняются внутри круга, так как во множестве точек
и хорд открытого круга евклидовой плоскости
выполняется теорема Дедекинда.
7.
Перейдем к аксиомам конгруэнтности III группы.• Отношение конгруэнтности будем определять через движение.
Будем говорить, что отрезок DC равен (конгруэнтен) отрезку MN, если
существует движение плоскости Лобачевского (L-плоскости) которое
отрезок DC переводит в отрезок MN. Аналогично, угол hk равен углу h'k',
если существует движение L-плоскости, которое угол hk переводит в угол
h'k', т.е. h →h' ,k → k' или h → k' ,k → h' .
8.
Движения L-плоскости в модели Бельтрами – Клейна определяются черезпроективные преобразования расширенной евклидовой плоскости
являющейся моделью проективной плоскости. Среди всех проективных
преобразований расширенной евклидовой плоскости выделим те, которые
абсолют оставляют инвариантным, а внутренние точки переводят во
внутренние, т.е. точки открытого круга переводят в точки открытого круга.
Множество всех таких преобразований образует подгруппу группы всех
проективных преобразований, ее и назовем группой движений плоскости
Лобачевского (L-плоскости) в модели Бельтрами – Клейна: D={f, g, …}.
Очевидно, тождественное преобразование id принадлежит D. Нетрудно
доказать, что такие проективные преобразования существуют. Как и на
евклидовой плоскости, справедливо предложение о том, что всякое движение
L-плоскости можно представить в виде композиции осевых симметрий.
9.
Роль симметрий относительно прямой а вмодели Бельтрами – Клейна выполняют
гомологии с осью а, а центром гомологии
является полюс S прямой а относительно
абсолюта, т.е. S – идеальная точка.
Гомоло́гия — проективное преобразование
проективной плоскости, которое оставляет
неподвижными все точки некоторой
прямой, называемой осью гомологии.
Свойства гомологии
1. Точки M, O, М ′ лежат на одной прямой.
2. Соответствующие прямые пересекаются
на оси гомологии.
10.
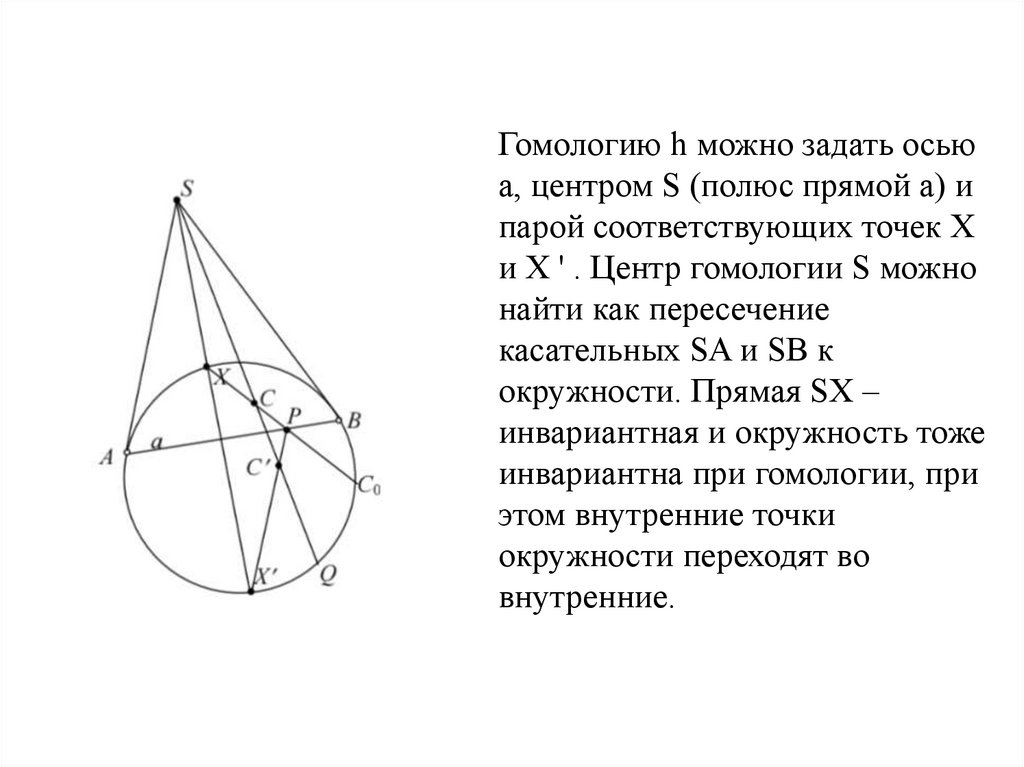
Гомологию h можно задать осьюа, центром S (полюс прямой а) и
парой соответствующих точек Х
и Х ' . Центр гомологии S можно
найти как пересечение
касательных SA и SB к
окружности. Прямая SX –
инвариантная и окружность тоже
инвариантна при гомологии, при
этом внутренние точки
окружности переходят во
внутренние.
11.
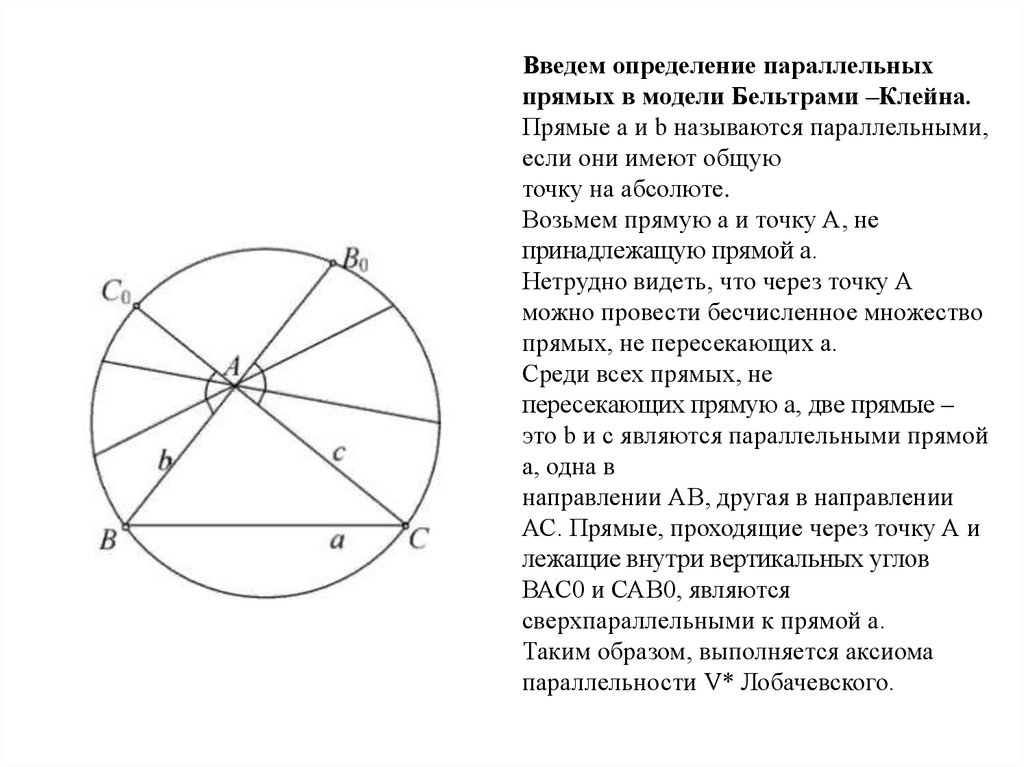
Введем определение параллельныхпрямых в модели Бельтрами –Клейна.
Прямые а и b называются параллельными,
если они имеют общую
точку на абсолюте.
Возьмем прямую а и точку А, не
принадлежащую прямой а.
Нетрудно видеть, что через точку А
можно провести бесчисленное множество
прямых, не пересекающих а.
Среди всех прямых, не
пересекающих прямую а, две прямые –
это b и c являются параллельными прямой
а, одна в
направлении АВ, другая в направлении
АС. Прямые, проходящие через точку А и
лежащие внутри вертикальных углов
ВАС0 и САВ0, являются
сверхпараллельными к прямой а.
Таким образом, выполняется аксиома
параллельности V* Лобачевского.
12.
Некоторые факты планиметрии Лобачевского в модели Бельтрами –Клейна.
1. Расстояние между двумя точками d (A, B) , определяется в этой модели
по формуле:
(АВ,MN) – сложное отношение четырех точек, k – постоянная величина. Так
как сложное отношение четырех точек прямой является инвариантом группы
проективных преобразований, то и d (A, B ) , по формуле является
инвариантом группы движений плоскости Лобачевского.
13.
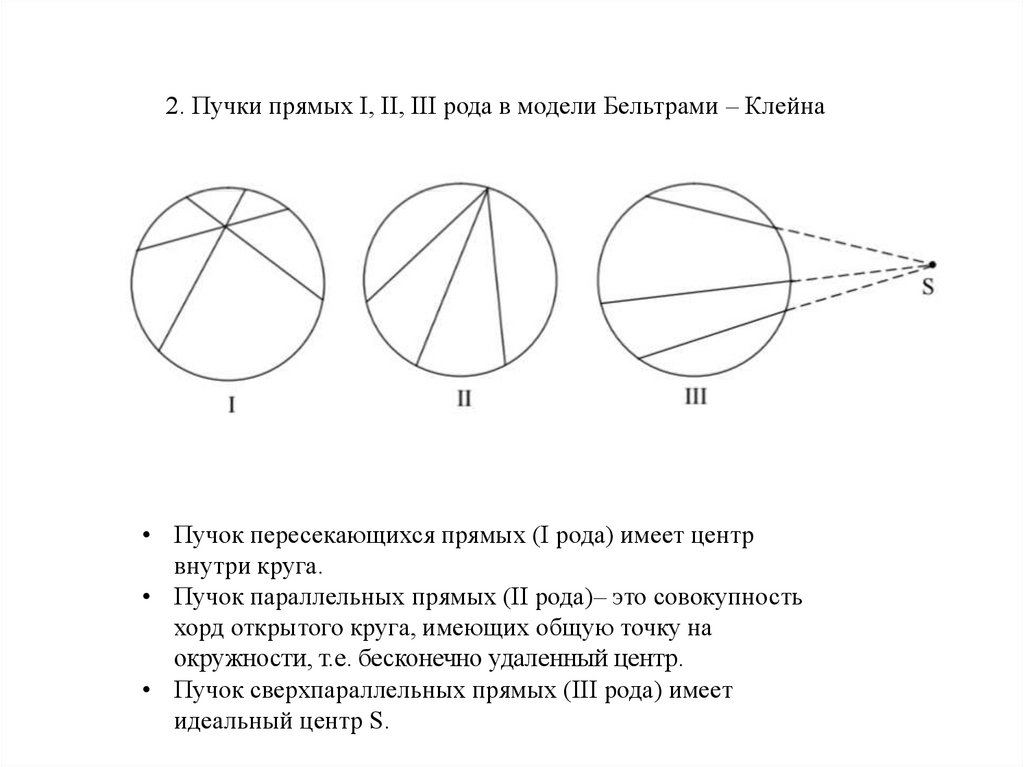
2. Пучки прямых I, II, III рода в модели Бельтрами – Клейна• Пучок пересекающихся прямых (I рода) имеет центр
внутри круга.
• Пучок параллельных прямых (II рода)– это совокупность
хорд открытого круга, имеющих общую точку на
окружности, т.е. бесконечно удаленный центр.
• Пучок сверхпараллельных прямых (III рода) имеет
идеальный центр S.









 Математика
Математика








