Похожие презентации:
Функции в жизни человека
1.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЁЖНОЙ ПОЛИТИКИ КРАСНОДАРСКОГО КРАЯГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
КРАСНОДАРСКОГО КРАЯ
«АПШЕРОНСКИЙ ЛЕСХОЗ - ТЕХНИКУМ»
Индивидуальный образовательный проект
на тему: "Функции в жизни человека"
Выполнил студент
Остапенко Денис Андреевич
Форма обучения: очная,
группа 19
Руководитель: Фоменко Н.В.
преподаватель математики
Апшеронск 2019
2.
Цель: исследование сфер применения функции.Задачи:
1. Доказать, что функциональные зависимости
существуют во всех сферах жизни;
2. Расширить знания о функции и методах решения
уравнений;
3. Узнать, какие явления из жизни и некоторых наук
описывает функция;
4. Научиться применять полученные знания в
нестандартных ситуациях на основе рассмотрения
примеров из реальной жизни, при решении
практико-ориентированных задач.
Продукт: Буклет «Функции в жизни человека»
3. Возникновение функции
Понятие функция сложилосьне сразу, а прошло долгий
путь развития. В работе
французского математика П.
Ферма «Введение в изучении
плоских и телесных мест»
(1636) говорится: «Всякий
раз, когда в заключительном
уравнении
имеются
две
неизвестных
величины,
налицо имеется место». По
существу здесь идёт речь о
функциональной зависимости
и
её
графическое
изображении
(«место
у
Ферма означает линию).
Изучение линий по их
уравнениям в «Геометрии»
французского математика Р.
Декарта
(1637)
также
указывает
на
ясное
представление о взаимной
зависимости
двух
переменных величин.
У английского
математика И.
Барроу («Лекции по
геометрии», 1669) в
геометрической форме
устанавливается взаимная
обратность действий
дифференцирования и
интегрирования
(разумеется, без
употребления самих этих
терминов).
4. Возникновение функции
Однако термин«Функция»
впервые появляется
лишь в 1692 у
немецкого
учёного
Г.
Лейбница и притом
не
совсем
в
современном
понимании
его.
Лейбниц называет
функции
различные отрезки,
связанные с кривой
линией ( например,
абсциссы её точек).
Первое определение
функций
в
смысле,
близком к современному,
находим у швейцарского
математика
И.
Бернулли
(1718):
«функция-это величина,
составленная
из
переменной
и
постоянной». В основе
этого
не
вполне
отчётливого определения
лежит
идея
задания
функций аналитической
формулой.
Близко к современному и
определение
русского
математика
М.И.
Лобачевского. "Общее понятие
требует,
чтобы
функции
от х назвать число, которое даётся
для
каждого
х
и
вместе х постепенно изменяется.
Значение функций может быть
дано
или
аналитическим
выражением
или
условием,
которое
подаёт
средство
и
испытывать все числа и выбирать
одно из них, или, наконец,
зависимость может существовать
и оставаться неизвестной". Таким
образом современное определение
функций
обычно
приписываемое
Дирихле
и
высказанное
им
в
1837,
нелднократно предлагалось и до
него.
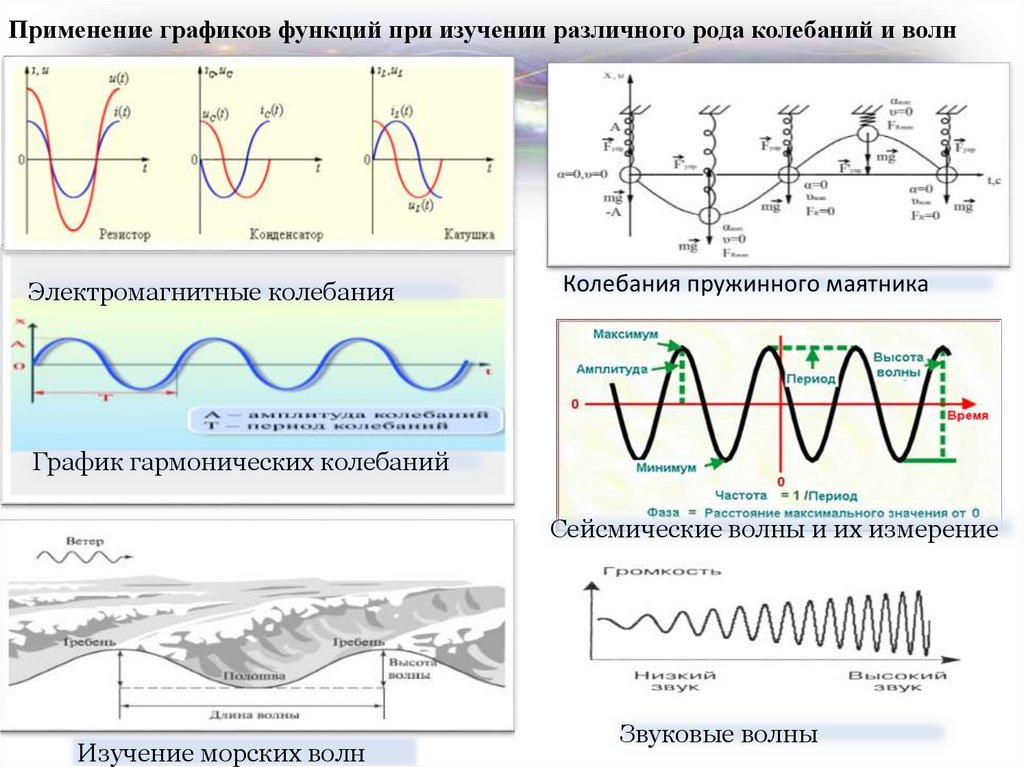
5. Применение графиков функций при изучении различного рода колебаний и волн
Электромагнитные колебанияКолебания пружинного маятника
График гармонических колебаний
Сейсмические волны и их измерение
Изучение морских волн
Звуковые волны
6. Функции в точных науках
Такиефункции
как: линейные (y=kx+b),
квадратные
(у=кх^2),
переодические функции,
логорифмические
функции, применяются в
таких науках как: Физика,
Оптика,
Астрономия.
Также
эти
функции
используются
для
изучения
Звука,
Потенциальной энергии
и Електричества.
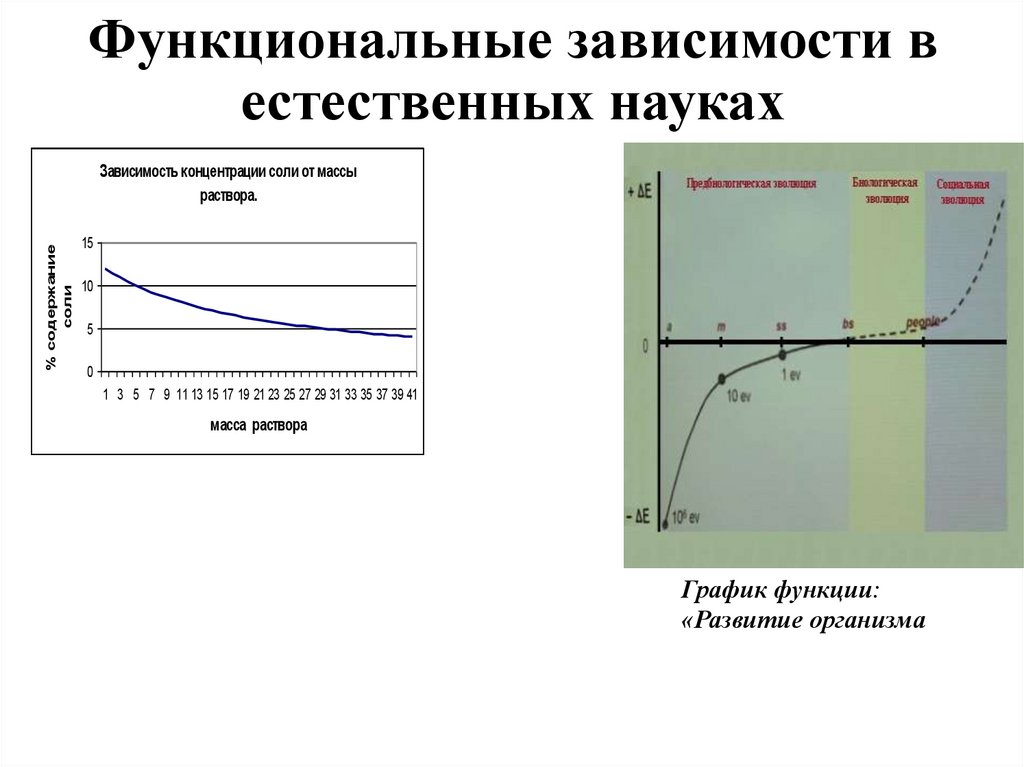
7. Функциональные зависимости в естественных науках
% содержаниесоли
Зависимость концентрации соли от массы
раствора.
15
10
5
0
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41
масса раствора
График функции:
«Развитие организма
8. ПРИМЕНЕНИЕ ФУНКЦИИ В ИСТОРИИ И ФИЛОЛОГИИ
История: «Графикинформационного бума»
Филология: «Чем дальше
в лес,
тем больше дров»
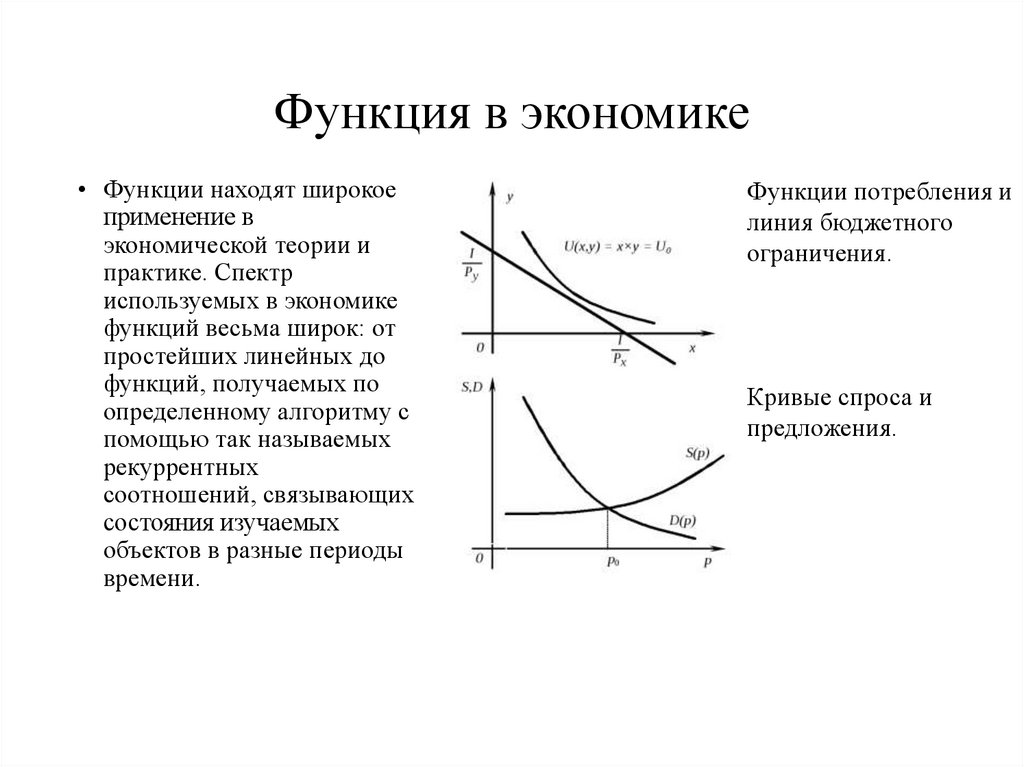
9. Функция в экономике
• Функции находят широкоеприменение в
экономической теории и
практике. Спектр
используемых в экономике
функций весьма широк: от
простейших линейных до
функций, получаемых по
определенному алгоритму с
помощью так называемых
рекуррентных
соотношений, связывающих
состояния изучаемых
объектов в разные периоды
времени.
Функции потребления и
линия бюджетного
ограничения.
Кривые спроса и
предложения.
10. Функция в жизни
Статистика11.
ЗаключениеФункция является неотъемлемой частью нашей
жизни и наук в целом, так как функциональные
зависимости, действительно, существуют во всех
сферах жизни человека.
12. благодарим за внимание!
БЛАГОДАРИМ ЗАВНИМАНИЕ!








 Математика
Математика








