Похожие презентации:
Построение сечений многогранников (2)
1.
1. Найти точку пересечения прямой АВ и плоскости β.β
а)
α
В
А
α
АВ
б)
β
А
В
2.
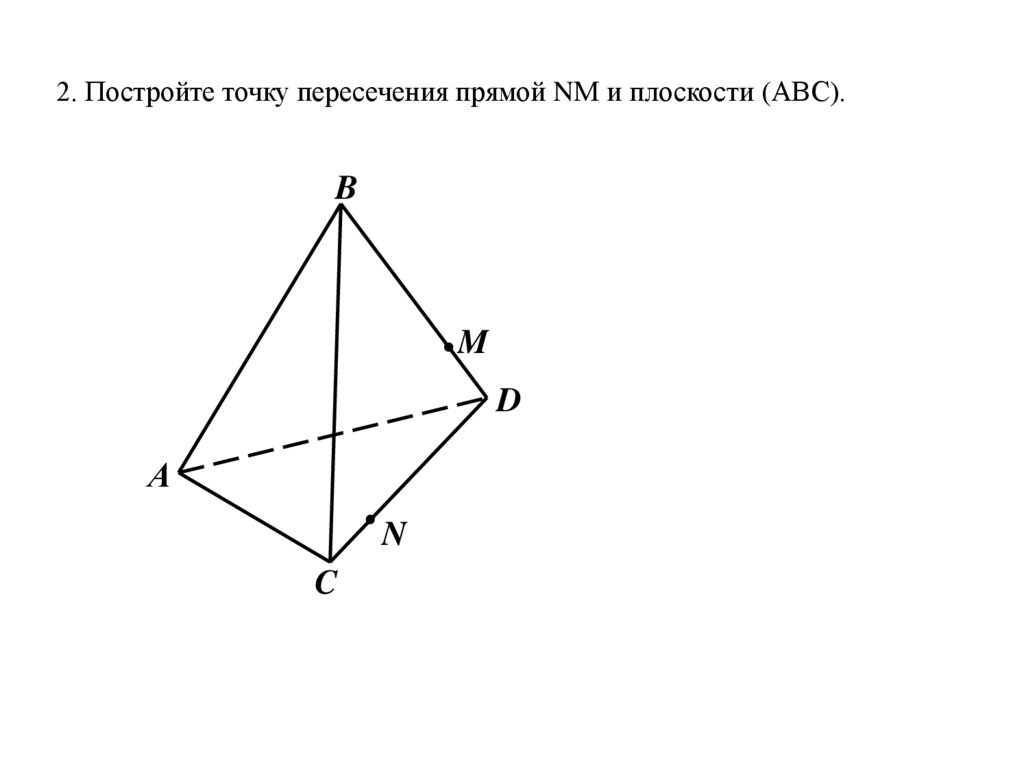
2. Постройте точку пересечения прямой NМ и плоскости (АВС).B
M
D
А
N
C
3.
3. а) Постройте точкупересечения прямой КМ и
плоскости (АВС).
б) Постройте точку
пересечения прямой КМ и
плоскости (АD₁D).
в) Постройте точку
пересечения прямой NМ и
плоскости (АВВ₁).
К
M
N
4.
Секущейплоскостью
многогранника называется
любая плоскость, по обе
стороны от которой имеются
точки
данного
многогранника.
Секущая
плоскость
пересекает
грани
многогранника по отрезкам.
Многоугольник, сторонами
которого
являются
эти
отрезки,
называется
сечением многогранника.
5.
4. На ребрах BB BC AB куба ABCDA₁B₁C₁D₁ отмечены точки M, N и K.Построить сечение куба плоскостью (MNK).
D₁
C₁
A₁
B₁
/
/
M
D
A
/
/
K
/
/
B
C
N
6.
Если две параллельные плоскости пересечены третьей, толинии их пересечения параллельны
5. N – середина ребра СС₁ куба ABCDA₁B₁C₁D₁. Построить сечение куба
плоскостью (AD₁N).
7.
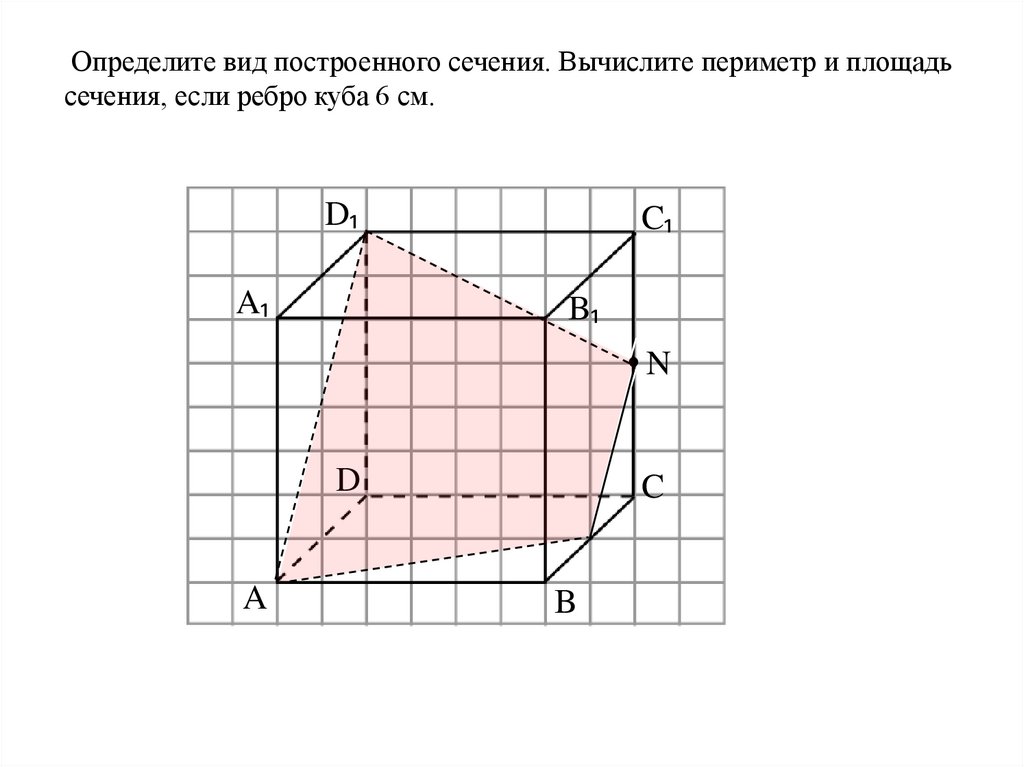
Определите вид построенного сечения. Вычислите периметр и площадьсечения, если ребро куба 6 см.
D₁
A₁
C₁
B₁
/
/
D
A
N
C
B
8.
6. Построить сечение куба ABCDA₁B₁C₁D₁, проходящее через точки M, Nи L ребер соответственно AA₁, D₁C₁ и AB.
N
/
D₁
/
A₁
/
M/
B₁
D
A
C₁
C
/
L/
B
Метод следов
Метод построения
сечения, при
котором находят
след секущей
плоскости на
каждой грани,
называется
методом следов.
9.
7. Построить сечение куба ABCDA₁B₁C₁D₁, проходящее через точки M, Nребер соответственно В₁С₁, D₁C₁ и параллельное прямой АА₁.
D₁
A₁
N
/
/
/
/
B₁
D
A
C₁
M
C
B
10.
8. Построить сечение прямоугольного параллелепипеда ABCDA₁B₁C₁D₁,плоскостью BKL, где точка K- середина ребра AA₁, а точка L –
середина CC₁. Докажите, что построенное сечение – параллелограмм.
D₁
A₁
B₁
/
К/
A
C₁
D
/
/
L
C
B
11.
12.
13.
14.
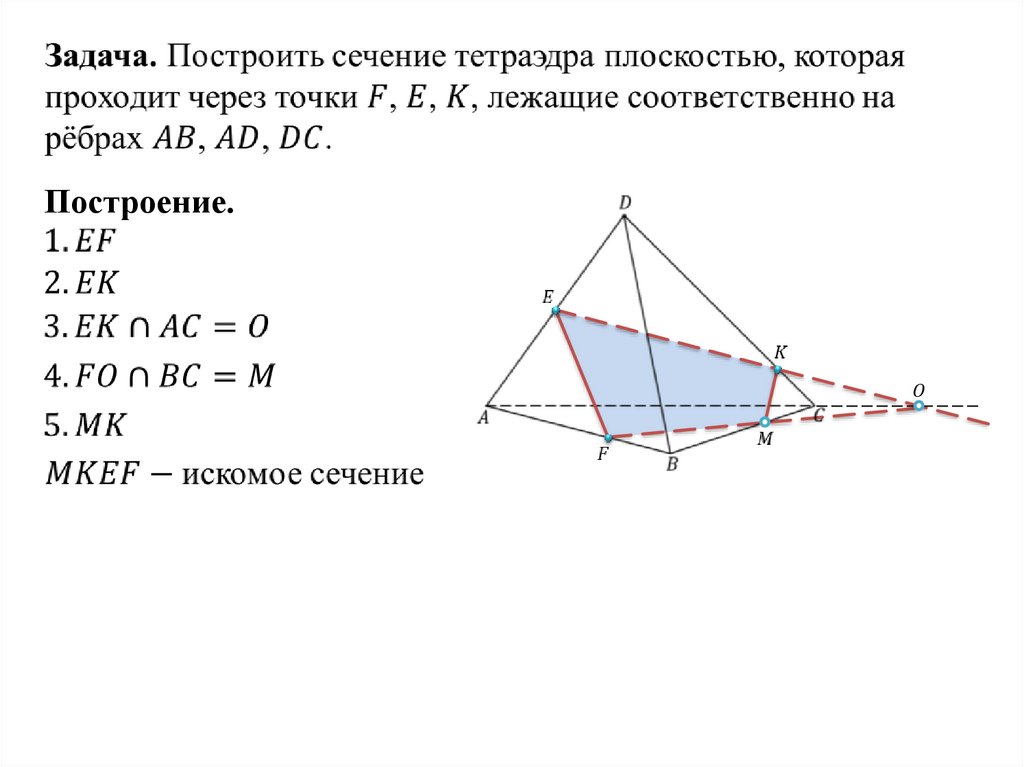
Построение.15.
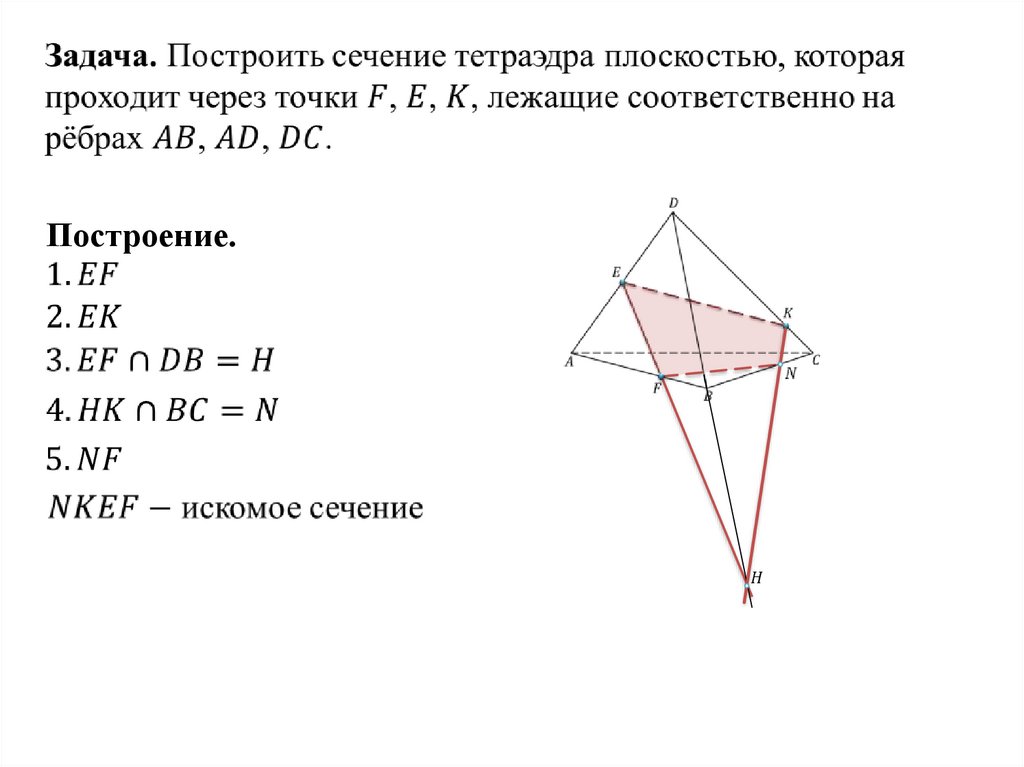
Построение.16.
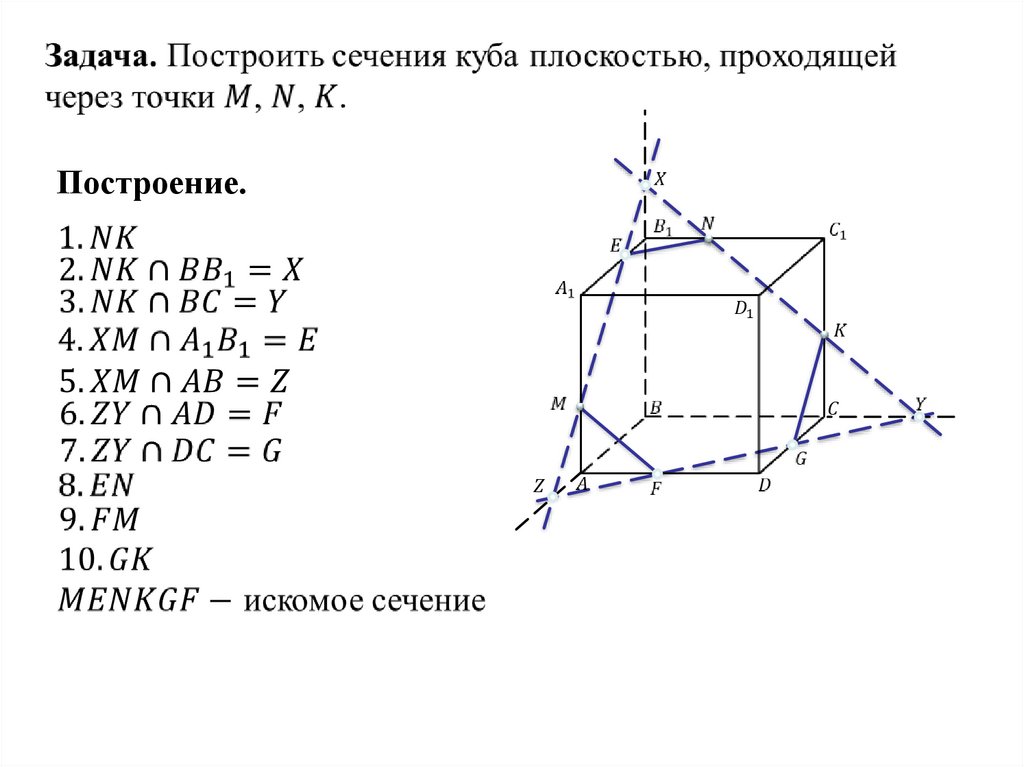
Построение.17.
MP
M
N
P
M
N
N
P
N
M
N
M
P
N
P
P
M
18.
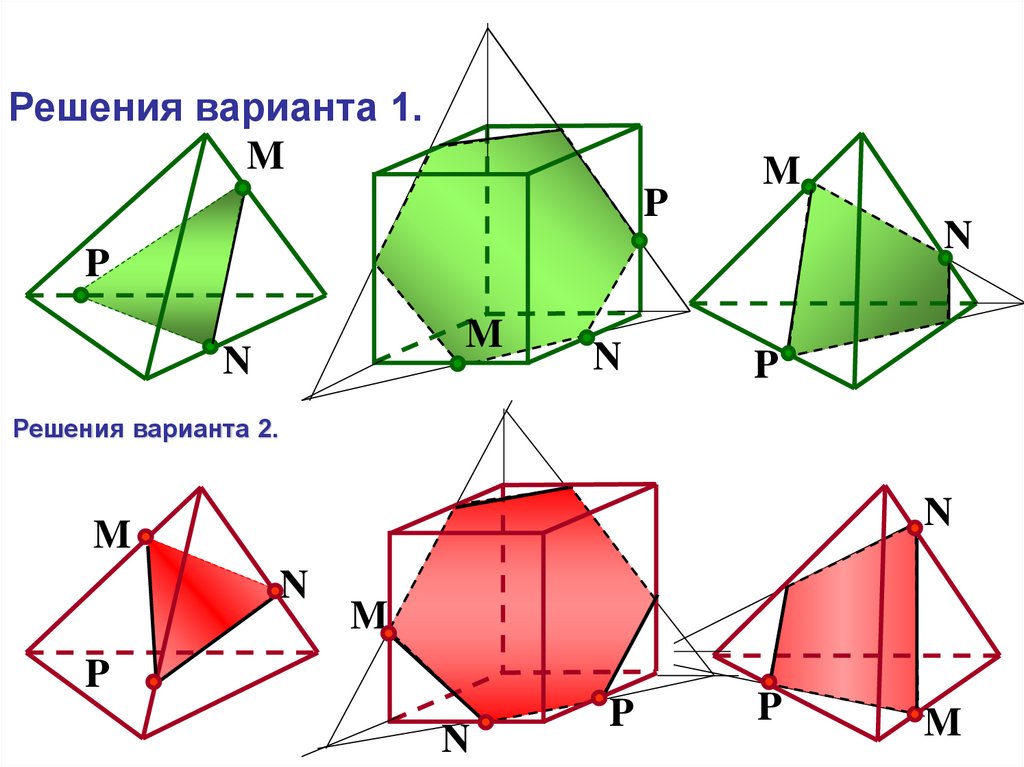
Решения варианта 1.M
P
M
N
P
M
N
N
P
Решения варианта 2.
N
M
N
M
P
N
P
P
M










 Математика
Математика








